第一作者简介:雷少飞(1989-),男,陕西合阳人,中国石油大学(华东)在读博士,主要从事钻井液防漏堵漏、储集层保护等方面的研究工作。地址:山东省青岛市黄岛区长江西路66号,中国石油大学(华东)石油工程学院,邮政编码:266580。E-mail: b19020017@s.upc.edu.cn
针对裂缝性地层封堵层形成机理和封堵规则尚不明晰的问题,基于封堵实验和颗粒物质力学方法研究了裂缝性地层封堵层的形成过程,分析了封堵层组成及颗粒配比,揭示了封堵层形成的本质及破坏的驱动能量,提出了钻井液防漏堵漏颗粒优选规则。研究表明封堵层的形成过程经历了从惯性流、弹性流到准静态流的流态变化过程。封堵层由封端颗粒、架桥颗粒和填充颗粒组成,3种堵漏颗粒的配比是设计堵漏体系的重要依据。封堵层形成的本质是体系发生非平衡性Jamming相态转变,封堵层颗粒体系对压力的响应由熵力驱动,熵越大封堵层越稳定。根据提出的规则优选了堵漏材料、优化了堵漏体系,封堵效果优于其他常用规则,可有效提高封堵层承压能力,为解决裂缝性地层漏失提供了理论和技术依据。
As formation mechanisms of plugging zone and criteria for fracture plugging remain unclear, plugging experiments and methods testing granular material mechanical properties are used to study the formation process of the plugging zone in fractured formations, analyze composition and ratios of different sizes of particles in the plugging zone, and reveal the essence and driving energy of the formation and damage of the plugging zone. New criteria for selecting lost circulation materials are proposed. The research results show that the formation of the plugging zone has undergone a process from inertial flow, elastic flow, to quasi-static flow. The plugging zone is composed of fracture mouth plugging particles, bridging particles and filling particles, and the proportion of the three types of particles is an important basis for designing drilling fluid loss control formula. The essence of the construction of the plugging zone is non-equilibrium Jamming phase transition. The response of the plugging zone particle system to pressure is driven by entropy force; the greater the entropy, the more stable the plugging zone. Lost circulation control formula optimized according to the new criteria has better plugging effect than the formula made according to conventional plugging rules and effectively improves the pressure-bearing capacity of the plugging zone. The research results provide a theoretical and technical basis for the lost circulation control of fractured formations.
井漏是钻井过程中钻井液大量流入地层的现象。井漏不仅损耗大量钻井液, 延长钻井周期, 处理不当还可能导致井塌、井喷、卡钻等复杂情况, 甚至导致井眼报废[1]。据统计, 全球有26%的油气井存在井漏问题, 每年用于堵漏的费用高达20亿美元[2, 3]。2017— 2019年, 中国石油天然气集团有限公司年均井漏损失时间约占钻井事故总损失时间的70%, 每年直接经济损失超40亿元[4]。墨西哥湾钻井作业中有12%的非生产时间由井漏导致; 伊拉克Rumaila油田在钻井过程中至少有45%的井发生严重或失返性漏失[5, 6, 7]。随着油气勘探开发向深层、超深层、海洋深水等领域拓展, 地质条件更加苛刻, 井漏问题更加突出。
为了有效控制和消除井漏问题, 国内外学者相继提出了针对孔隙性和裂缝性地层的堵漏颗粒粒度优选规则[8]。适用于孔隙性地层的封堵规则主要有1/3架桥规则[9]、理想充填理论[10, 11, 12]和Vickers准则[13]等。适用于裂缝性地层的封堵规则主要有D50准则[14]、Mortadha准则[15]、Omid双模准则[16]等。这些规则皆从实验角度提出了堵漏颗粒粒径与地层孔隙或裂缝之间的匹配关系, 形成了堵漏颗粒粒径分布优选方法, 但是仍存在封堵层形成机理不清、承压能力不足和一次堵漏成功率较低等问题。
本文采用堵漏实验装置和颗粒物质力学方法研究裂缝性地层封堵层的形成过程, 分析封堵层组成及颗粒配比, 揭示封堵层形成的本质及驱动能量, 形成堵漏颗粒优选规则。依据新规则设计优选新型堵漏材料, 优化堵漏体系。研究结果可为处理裂缝性地层漏失提供理论和技术支撑。
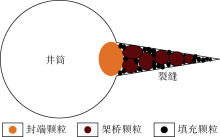
采用可视化堵漏实验装置和颗粒流(PFC)软件, 模拟了裂缝性地层封堵层的形成过程。可视化堵漏实验系统如图1所示。
封堵层形成时, 堵漏体系颗粒间接触力沿着链状路径(即力链)传递, 经历颗粒— 力链— 封堵层的多尺度结构变化过程[17], 宏观上表现为从类流态到类固态的转变。根据封堵过程中堵漏颗粒之间的力链形成状态, 堵漏体系流态可以划分为惯性流、弹性流和准静态流[18, 19]。
惯性流处于封堵层形成的早期。当堵漏颗粒进入漏失地层裂缝时, 堵漏体系在压差的作用下以流体状态运动。如图2所示, 随着颗粒在裂缝内不断堆积, 颗粒发生频繁碰撞, 颗粒间通过相互碰撞传递动量。此时, 堵漏颗粒间不能形成稳定的力链, 此状态为惯性流。
弹性流处于封堵层形成的中期。如图3所示, 随着颗粒继续在裂缝内不断堆积, 封堵层局部生成相对稳定的力链, 堵漏颗粒流态从惯性流转变为弹性流。此时, 封堵层局部虽然形成相对稳定的力链, 但是弱力链较多, 仍然有许多颗粒未与其他颗粒接触, 且颗粒受到的剪切速率较高, 碰撞较为剧烈。在弱力链中, 颗粒轻微接触, 变形极小, 微量切应力就可以把弱力链打破(见图4)。
准静态流处于封堵层形成的晚期。如图5所示, 随着颗粒在裂缝内持续架桥堆积, 颗粒被挤压到一起形成整体稳定的力链, 继而形成稳定的封堵层。此时, 整个封堵层可看作是连续的固体, 颗粒间力链中的接触应力与剪切速率无关, 称为准静态流。准静态流中强力链占比较大, 颗粒处于自锁状态, 可承受一定的切向力。
封堵层形成过程中的惯性流、弹性流和准静态流3种流态的转变, 涉及颗粒的碰撞、黏结、流动等物理过程, 与堵漏颗粒的粒径、物性(刚度、黏弹性)及地层应力等有关。因此, 在制备堵漏体系时, 应根据地层裂缝特征, 优选具有合适的粒径分布、物性的堵漏材料, 以达到最佳的堵漏效果。
国内外学者针对不同粒径堵漏颗粒在封堵层中的作用, 相继提出了不同的堵漏机理, 包括:应力笼理论、提高裂缝闭合应力机理和提高裂缝延伸压力机理[20, 21, 22, 23]。这些机理分析了不同粒径的堵漏颗粒在裂缝入口、裂缝中部和裂缝尾部形成封堵层、提高地层承压能力的力学机理。按照粒径及作用可将堵漏颗粒分为封端颗粒、架桥颗粒和填充颗粒(见图6)。封端颗粒用量较少, 主要在裂缝入口附近形成堵塞隔层, 调控井周应力, 保护缝内封堵层免受压力波动的影响。架桥颗粒对封堵成功起决定性作用, 主要在裂缝中部形成架桥堵塞隔层, 提高裂缝闭合应力。填充颗粒主要有两方面作用:①架桥颗粒形成架桥封堵后, 用以填充封堵层孔隙, 提高封堵层致密性; ②填充颗粒粒径较小, 可在裂缝尾部形成封堵, 隔离裂缝尖端, 防止产生诱导裂缝。
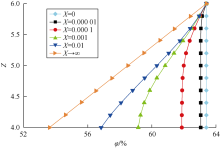
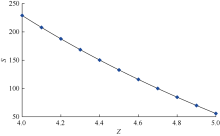
假设封堵层中封端颗粒、架桥颗粒和填充颗粒分别为大小相同的球形颗粒。参照文献[24, 25, 26]的计算方法, 可得到堵漏颗粒的Z-φ 相图(见图7)。图中, Z为力学配位数, φ 为颗粒体积分数, X为颗粒熵压缩率。由图7可知, 不同熵压缩率的Z-φ 曲线组成了一个三角形区域。若封堵层中堵漏颗粒的配位数和熵压缩率在三角形区域内, 则堵漏颗粒可形成具有一定承压能力的封堵层, 堵漏成功, 否则堵漏失败。
当封堵层中封端颗粒和架桥颗粒(统称粗颗粒)处于最紧密堆积状态时, 即X=0时, 封堵层中粗颗粒的体积分数为:
${{\varphi }_{\text{c}}}=\varphi \left( X=0, Z \right)=\frac{6}{6+2\sqrt{3}}\text{=}63.4\text{ }\!\!%\!\!\text{ }$ (1)
填充颗粒充满粗颗粒间的孔隙, 处于疏松堆积状态, 即X→ ∞ , 此时可得粗颗粒间孔隙中填充颗粒的体积分数为:
${{\varphi }_{\text{f}}}\text{=}\varphi (X\to \infty , Z)\approx \frac{\text{4}}{4+2\sqrt{3}}\text{=}53.6\text{ }\!\!%\!\!\text{ }$ (2)
假设封堵层的体积为V, 则粗颗粒间孔隙体积和粗颗粒体积分别为:
${{V}_{\text{cv}}}=\left( 1-{{\varphi }_{\text{c}}} \right)V$ (3)
${{V}_{\text{cs}}}={{\varphi }_{\text{c}}}V$ (4)
则填充颗粒体积为:
${{V}_{\text{fs}}}={{\varphi }_{\text{f}}}{{V}_{\text{cv}}}$ (5)
填充颗粒的配比, 即填充颗粒体积与堵漏颗粒总体积之比为:
${{\varphi }_{\text{p}}}=\frac{{{V}_{\text{fs}}}}{{{V}_{\text{cs}}}+{{V}_{\text{fs}}}}$ (6)
将(1)— (5)式代入(6)式可得, 堵漏体系中填充颗粒的配比约为25%, 则封端颗粒和架桥颗粒的总配比约为75%。
封堵层的形成是堵漏材料由无相互作用的无刚性类液体体系转变为有相互作用的刚性非晶Jammed固态的过程, 同时保持液态的无序结构, 其本质是一种非平衡的Jamming相态转变。
如果只考虑相互作用中纯排斥部分, 在一定的地层压力下, 封堵层Jamming态颗粒体积分数存在一个特殊的状态点, 通常被称作J点, 此时所有的颗粒都刚好接触, 如图8所示。当堵漏颗粒体积分数小于J点体积分数时, 堵漏颗粒之间没有形成稳定的接触。当堵漏颗粒体积分数增大至J点体积分数时, 堵漏材料刚好完全接触, 封堵层形成; 随着漏失过程的进行, 堵漏颗粒体积分数进一步增大, 堵漏颗粒之间相互交叠形成贯穿系统的力链网, 从而形成具有一定力学刚度的致密固体封堵层。J点体积分数可由下式计算得到:
${{\varphi }_{\text{J}}}\text{=}\frac{{{V}_{\text{cs, J}}}+{{V}_{\text{fs, J}}}}{V}$ (7)
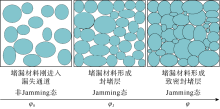
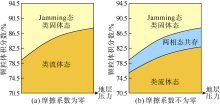
对于三维纯排斥无摩擦相互作用的球形颗粒封堵层, 堵漏颗粒体系Jamming相图如图9a所示。当颗粒体积分数小于J点体积分数时, 堵漏颗粒体系呈类流体状态。当颗粒体积分数大于J点体积分数时, 堵漏颗粒体系像非晶固体一样, 所有颗粒都自锁在力链中无法自由移动。
实际上, 堵漏颗粒有刚性颗粒、弹性颗粒、纤维颗粒等多种类型, 颗粒物性(摩擦系数、黏弹性等)也各不相同。因此, 在封堵层形成过程中, 堵漏颗粒间除了纯排斥力, 还有摩擦力、黏结力等相互作用力。堵漏颗粒间摩擦力、黏结力等相互作用力会降低J点体积分数[25], 促使堵漏颗粒在漏失通道内迅速形成封堵层, J点会变成一个由J线包围的区域, 如图9b所示。随着摩擦力和黏结力的增加, 堵漏颗粒由非Jamming态转化为Jamming态所需的颗粒体积分数随之下降, 封堵层形成的时间也会随之缩短。因此, 在进行防漏堵漏作业时, 应选择摩擦系数较大和具有黏结特性的凝胶或树脂颗粒, 加快封堵层的形成, 有效减少钻井液漏失。
相对于固体物质, 堵漏颗粒组成的封堵层在较小的扰动下会产生较大的非线性响应。在热平衡态下, 固体物质系统的内能对自由能的贡献远远超过熵, 物质的结构和性能主要由内能的极小值决定。但是, 堵漏颗粒的内能比温度与熵的乘积小很多, 平衡态的结构由熵的极大值决定[27]。堵漏颗粒体系熵偏离极大值时所产生的力为熵力, 堵漏颗粒对外界微扰的响应由这种熵力驱动[28]。堵漏颗粒间以接触力相互作用, 组成一个系统, 在封堵层形成过程中, 堵漏颗粒流态由惯性流、弹性流转变为准静态流, 进入由颗粒熵表征的无序状态[29]。
配位数是堵漏颗粒体系内中每个颗粒周围与其接触的平均颗粒数。配位数小于2的颗粒对封堵层承压能力基本无贡献。在一定的孔隙度条件下, 配位数主要受堵漏颗粒间摩擦系数、地层裂缝维度等影响。堵漏颗粒的摩擦系数一般为0.1~1.0, 在此区间内堵漏颗粒的配位数随摩擦系数增大出现显著下降趋势[26]。图10为堵漏颗粒熵随配位数的变化关系, 可以看出, 堵漏颗粒熵与配位数呈负相关。因此, 进行防漏堵漏作业时, 应选择摩擦系数较大的堵漏材料, 使堵漏颗粒体系熵达到极大值, 从而使封堵层呈现最稳定状态。
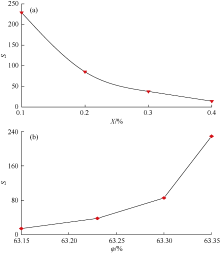
图11为堵漏颗粒熵随熵压缩率和颗粒体积分数的变化关系。由图11a可知, 熵压缩率越大, 颗粒堆积越疏松, 堵漏颗粒熵越小, 封堵层越不稳定。由图11b可知, 堵漏颗粒体积分数越大, 封堵层越致密, 堵漏颗粒熵越大, 封堵层越稳定。因此, 在设计堵漏材料时应选择合理的封端颗粒、架桥颗粒和填充颗粒粒径级配, 添加适量橡胶、凝胶等弹性颗粒, 使堵漏颗粒处于最密实状态, 堵漏颗粒熵极大化, 从而使封堵层呈现最稳定状态。
通过大量刚性颗粒优选实验, 优选核桃壳颗粒, 采用金属模拟岩样和真实裂缝岩样(直径25 mm, 长50 mm), 进行承压堵漏实验, 以揭示颗粒粒径、钻井液中堵漏颗粒加量与裂缝宽度的匹配关系。
实验所用仪器为青岛同春TCP-2高温高压堵漏仪。实验步骤为:①将岩心放置于岩心夹持器中, 加围压1~2 MPa。②将准备好的堵漏颗粒体系加入中间容器。③设置上下游压力, 调整初始压差为1 MPa, 30 s之后打开岩心夹持器下游出液口。④记录出液口的漏失量, 当漏失量为零时, 保持当前压力10 min。若在10 min之内再次发生漏失, 则记录漏失时间和漏失量, 当漏失量为零后, 再稳压10 min。⑤稳压10 min之后, 加压0.5~1.0 MPa。⑥重复步骤①— ⑤, 直至封堵失败, 结束实验。
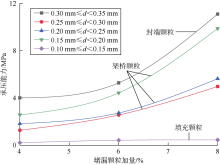
表1为颗粒加量(颗粒质量与钻井液质量之比)为8%时不同粒径堵漏颗粒承压堵漏实验结果。可以看出, 堵漏颗粒在模拟岩样和裂缝岩样中的承压能力基本吻合, 但由于裂缝岩样表面粗糙, 存在一定的迂曲度, 堵漏颗粒在裂缝岩样中的承压能力比在模拟岩样中稍大。图12为不同粒径堵漏颗粒封堵效果图。图13为不同粒径、不同加量下堵漏颗粒在模拟岩样中的承压能力。由表1、图12、图13可知, 当核桃壳颗粒粒径满足0.7 W> d≥ 0.6 W时, 容易在裂缝端口架桥封端, 裂缝内基本无封堵层, 在裂缝端口承压能力可达11.1 MPa; 当核桃壳颗粒粒径满足0.6W> d≥ 0.3 W时, 颗粒可以保持较高的浓度进入裂缝内, 形成较为致密的封堵层, 承压能力最高可达9.88 MPa; 当核桃壳颗粒粒径满足0.3W> d≥ 0.2 W时, 颗粒在裂缝内不易形成架桥堆积, 封堵层基本不承压。因此, 堵漏颗粒粒径满足2/3 W≥ d≥ 1/3 W时, 封堵效果较好, 可作为封堵层的架桥颗粒; 堵漏颗粒粒径满足d< 1/3W时, 基本无承压能力, 可作为封堵层的填充颗粒; 堵漏颗粒粒径满足W≥ d> 2/3W时, 在裂缝端口承压能力较高, 可作为封端颗粒。现场和室内实验结果表明, 在钻井液防漏堵漏体系中添加少量的封端颗粒可以保护封堵层, 提高封堵层承压能力[15, 30]。
| 表1 颗粒加量8%时不同粒径堵漏颗粒的承压堵漏能力 |
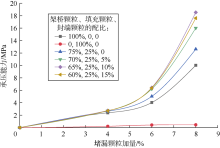
图14为不同配方、不同加量下堵漏颗粒在模拟岩样中的承压能力, 具体配方如表2所示。由图14、表2可知, 当堵漏体系中全部为填充颗粒时, 大部分钻井液漏失, 基本无承压封堵能力。当堵漏体系中全部为架桥颗粒时, 可在裂缝中形成稳定架桥, 但是封堵层不致密, 承压能力可达10.02 MPa。当堵漏体系中架桥颗粒、填充颗粒的配比为75%, 25%时, 可形成较为致密的封堵层, 承压能力可达12.61 MPa。当堵漏体系中添加封端颗粒时, 承压能力显著提高。当封端颗粒配比较低时, 其保护封堵层效果有限; 当封端颗粒配比较高时, 封端颗粒在裂缝端口堵塞, 影响架桥颗粒进入裂缝形成封堵层; 当封端颗粒配比为10%时, 封堵层承压能力最高, 可达18.53 MPa。因此, 对于模拟岩样, 当架桥颗粒、填充颗粒、封端颗粒的配比约为65%, 25%, 10%时, 堵漏颗粒体系的承压封堵能力最佳。
| 表2 颗粒总加量为8%时不同类型堵漏颗粒复配的承压堵漏能力 |
根据封堵层形成过程、堵漏颗粒组成及配比、封堵层形成机理及破坏驱动能量、承压堵漏实验的研究结果, 提出如下裂缝性地层堵漏颗粒优选规则。
①堵漏颗粒的粒径和配比。应选择10%封端颗粒(W≥ d> 2/3W)、65%架桥颗粒(2/3 W≥ d≥ 1/3 W)和25%填充颗粒(d< 1/3W), 即当颗粒粒度分布满足W≥ D90≥ 2/3 W, D25≥ 1/3 W时, 可形成具有较高承压能力的封堵层。
②堵漏颗粒物性。架桥颗粒应选择表面摩擦系数较大、形状不规则的材料, 封端颗粒和填充颗粒应选择具有一定黏弹特性的材料(橡胶或凝胶等)。
根据本文提出的裂缝性地层堵漏颗粒优选规则, 优选了架桥颗粒LCM-A, 制备了封端颗粒和填充颗粒LCM-B。LCM-A具有较大的不规则性、高摩擦系数、高抗温抗压能力。LCM-B在地层高温激活下具有较强的黏弹特性, 既可以作为填充材料提高封堵层致密性, 又可自适应封堵裂缝端口或黏结架桥颗粒。采用高温高压裂缝岩心堵漏仪, 基于不同堵漏颗粒优选规则配制颗粒总加量为8%的钻井液堵漏体系(见表3), 开展承压堵漏实验。实验结果如图15所示。
| 表3 基于不同堵漏颗粒优选规则的堵漏体系颗粒粒径 |
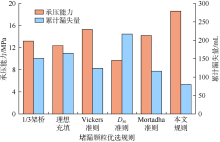
Vickers准则和Mortadha准则均选择了封端颗粒、架桥颗粒和填充颗粒作为堵漏配方, 但是3种颗粒之间配比不合理。1/3架桥规则和理想充填理论没有明确封端颗粒、架桥颗粒和填充颗粒的配比和作用, 更适合用于孔隙封堵。D50准则主要选择封端颗粒作为封堵材料, 容易在裂缝端口架桥聚集, 颗粒不易进入裂缝形成有效的封堵层。而本文提出的堵漏颗粒优选规则明确了封端颗粒、架桥颗粒和填充颗粒的配比和作用, 优选了堵漏颗粒的加量和粒径级配, 配制的堵漏体系封堵效果和封堵层承压能力明显优于其他规则, 累计漏失量可减少至80 mL, 承压能力高达18.6 MPa(见图15), 有效提高了裂缝封堵效果。
钻井液漏失通道中封堵层的形成过程经历颗粒— 力链— 体系的多尺度结构变化过程, 宏观上表现为从惯性流、弹性流到准静态流的流态变化过程。Jamming相态转变是堵漏颗粒从无相互作用的无刚性类液体体系转变为有刚性的非晶Jamming固态的非平衡转变现象, 是封堵层形成的本质特征。封堵层中颗粒对地层压力的响应由熵力驱动, 熵的极大值取决于堵漏材料的摩擦系数、配位数以及熵压缩率等。
设计钻井液堵漏体系时, 应优选封端颗粒、架桥颗粒和填充颗粒的粒径和配比, 建议颗粒粒度分布满足W≥ D90≥ 2/3 W, D25≥ 1/3 W。还应考虑堵漏颗粒物性。架桥颗粒应选择表面摩擦系数较大、形状不规则的材料, 封端颗粒和填充颗粒应选择具有一定黏弹特性的材料, 以实现快速致密封堵。
符号注释:
d— — 颗粒粒径, m; D10, D25, D50, D75, D90— — 粒度分布曲线上累计概率10%, 25%, 50%, 75%, 90%对应的粒径, m; R— — 孔隙直径, m; Rave— — 平均孔隙直径, m; Rmax— — 最大孔隙直径, m; Rmin— — 最小孔隙直径, m; S— — 堵漏颗粒熵, J/K; V— — 封堵层体积, m3; Vcs— — 封堵层中封端颗粒和架桥颗粒的总体积, m3; Vcs, J— — J点对应的封堵层中封端颗粒和架桥颗粒的总体积, m3; Vcv— — 封堵层中粗颗粒(封端颗粒和架桥颗粒)间的孔隙体积, m3; Vfs— — 封堵层中填充颗粒的体积, m3; Vfs, J— — J点对应的封堵层中填充颗粒的体积, m3; W— — 裂缝宽度, m; X— — 堵漏颗粒熵压缩率, 无因次; Z— — 力学配位数, 无因次; φ — — 封堵层中堵漏颗粒体积分数, %; φ 0— — 堵漏颗粒刚进入漏失通道时的体积分数, %; φ c— — 封堵层中封端颗粒和架桥颗粒的总体积分数, %; φ f— — 粗颗粒(封端颗粒和架桥颗粒)间孔隙中填充颗粒的体积分数, %; φ J— — J点对应的封堵层颗粒体积分数, %; φ p— — 堵漏体系中填充颗粒的配比, %。
(编辑 胡苇玮)
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|