引用本文
王强, 赵金洲, 胡永全, 任岚, 赵超能. 页岩油储集层压后焖井时间优化方法[J]. 石油勘探与开发, 2022,49(3): 586-596.
WANG Qiang, ZHAO Jinzhou, HU Yongquan, REN Lan, ZHAO Chaoneng. Shut-in time optimization after fracturing in shale oil reservoirs[J]. Petroleum Exploration & Development, 2022,49(3): 586-596.  
Doi: 10.11698/PED.20210906
Permissions
Copyright©2022, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
页岩油储集层压后焖井时间优化方法
王强, 赵金洲, 胡永全, 任岚, 赵超能
西南石油大学“油气藏地质及开发工程”国家重点实验室,成都 610500

第一作者简介：王强（1990-）,男,四川三台人,西南石油大学讲师,主要从事非常规储集层改造技术与理论等方面的研究工作。地址：四川省成都市新都区新都大道8号,西南石油大学石油与天然气工程学院,邮政编码：610500。E-mail：402038424@qq.com

收稿日期: 2021-12-18 修回日期: 2022-03-31
基金项目: 国家自然科学基金联合基金项目“致密气多相多尺度流动规律及跨尺度耦合渗流”（U1562217）; 国家自然科学基金联合基金项目“深层超深层页岩气水平井压裂缝网高效建造理论与方法研究”（U21B2701）
摘要

建立了考虑毛管压力、渗透压、膜效应以及弹性能的压裂-焖井-生产多过程多相流模型,提出了以产能最大化为目标的页岩油水平井分段多簇压裂后焖井时间优化方法,采用现场生产数据和商业软件验证了该模型的准确性。基于该模型和方法,根据现场压裂压力数据反演裂缝参数,建立物理模型,模拟了压裂、焖井以及生产阶段储集层孔隙压力、含油饱和度的变化动态,并研究了7种因素对最优焖井时间的影响规律,通过开展正交实验明确了最优焖井时间的主控因素。研究表明,随着焖井时间增加,累计产量增量先快速增加后趋于某一稳定值,变化拐点对应的焖井时间为最优焖井时间。最优焖井时间与基质渗透率、孔隙度、毛管压力倍数及裂缝长度呈非线性负相关,与膜效率、注入液体总量呈非线性正相关,与排量呈近线性正相关。对最优焖井时间的影响程度从大到小依次为注入液体总量、毛管压力倍数、基质渗透率、孔隙度、膜效率、压裂液矿化度和排量。

关键词: 页岩油; 储集层; 焖井时间; 渗吸作用; 水力压裂; 渗透压; 主控因素
中图分类号:TE345 文献标志码:A 文章编号:1000-0747(2022)03-0586-11
Shut-in time optimization after fracturing in shale oil reservoirs
WANG Qiang, ZHAO Jinzhou, HU Yongquan, REN Lan, ZHAO Chaoneng
State Key Laboratory of Oil-Gas Reservoir Geology & Exploitation, Southwest Petroleum University, Chengdu 610500, China
Abstract

A multi-process (fracturing, shut-in and production) multi-phase flow model was derived considering the osmotic pressure, membrane effect, elastic energy and capillary force, to determine the optimal shut-in time after multi-cluster staged hydraulic fracturing in shale reservoirs for the maximum production. The accuracy of the model was verified by using production data and commercial software. Based on this model and method, a physical model was made based on the inversion of fracture parameters from fracturing pressure data, to simulate the dynamic changes of pore pressure and oil saturation during fracturing, soaking and production, examine effects of 7 factors on the optimal shut-in time, and find out the main factors affecting the optimal shut-in time through orthogonal experiments. With the increase of shut-in time, the increment of cumulative production increases rapidly first and then tended to a stable value, and the shut-in time corresponding to the inflection point of the change was the optimal shut-in time. The optimal shut-in time has a nonlinear negative correlation with matrix permeability, porosity, capillary pressure multiple and fracture length, a nonlinear positive correlation with the membrane efficiency and total volume of injected fluid, and a nearly linear positive correlation with displacement. The seven factors in descending order of influence degree on optimal shut-in time are total volume of injected fluid, capillary force multiple, matrix permeability, porosity, membrane efficiency, salinity of fracturing fluid, fracturing fluid displacement.

Keyword: shale oil; reservoir; shut-in time; imbibition; hydraulic fracturing; osmotic pressure; main factors
0 引言

页岩油一般储集在渗透率小于0.1× 10-3 μ m2、孔隙度小于10%的富有机质页岩层中[1, 2]。长水平井段配合分段多簇体积压裂技术大幅度增加泄油面积的方法是目前提高页岩油采收率的主要手段之一。现场生产数据表明, 即使采用长水平井+体积压裂技术, 大量的页岩油井仍然难以达到商业开发要求[3]。压裂-焖井技术则为页岩油开发提供了新思路[4]。长庆、青海、大庆、吉林等油田先后针对页岩油区块采取了“ 压裂、焖井、再投产” 的生产管理制度, 取得了较好的增产效果。目前, 中国页岩油井压后焖井周期大多在14~60 d, 焖井时间的确定大多依赖开发人员的经验, 缺乏科学、合理的依据[5, 6]。建立压后焖井时间的优化模型及方法是当前压裂焖井措施实施的关键, 也是进一步提高页岩油采收率亟需解决的理论和工程问题。

压裂的目的是改造储集层以获得较大区域的裂缝展布, 增加油气流动的高渗体积空间; 焖井的目的则是利用大量滞留于储集层的压裂液, 基于流体流动、渗吸原理及化学反应的耦合作用, 增加地层流体流动能量, 加强油水置换的渗吸作用, 最终达到增加原油产量的目的[7]。焖井操作虽然简单, 但其内在的核心物理机制却十分复杂。Lee等[8, 9, 10, 11, 12, 13]主要从岩心尺度和矿场尺度, 利用室内实验和数值模拟手段, 研究了重力、毛管压力主导的渗吸行为, 认为岩石润湿性变化、储集层改造的复杂程度是影响焖井增产效果的重要因素。李耀华等[14, 15, 16, 17, 18, 19]除了考虑毛管压力主导的渗吸, 还考虑了化学势引起的层流以及渗透压对焖井增产效果的影响, 发现焖井过程中基质内外的矿化度差是产生渗透压、促进原油置换的根本原因。Bui等[20, 21, 22]的研究中还提到, 由于压裂液滤失到储集层中, 储集层弹性能得到补充, 也可能导致焖井后产能增加。若考虑储集层为油湿, 在压裂液中添加表面活性剂, 通过焖井过程的流体流动进一步改变储集层润湿性, 也可以达到焖井增产的效果。总的来看, 大多数学者更多的是对焖井渗吸采油的机理开展了研究, 对页岩油压后最优焖井时间的研究较少。Wang等[23]虽然对最优焖井时间开展了较为详细的研究, 但模型中未考虑渗透压对渗吸的影响, 建立的物理模型也并非完整的矿场尺度模型, 同时也未考虑水力裂缝内的多相流。

因此, 本文旨在针对页岩油储集层建立压裂-焖井- 生产一体化焖井时间优化模型, 提出一套以产能最大化为目标且同时考虑毛管压力、化学势、渗透压以及水力裂缝影响的焖井时间优化方法。结合应用实例与商业软件对模型进行验证。在压裂-焖井-生产一体化模拟过程中, 多角度分析焖井增产的关键机理, 并着重研究不同因素对页岩油开发最优焖井时间的影响规律, 以指导页岩油水平井压后焖井时间决策, 进一步为焖井制度优化提供理论依据。

1 压裂-焖井-生产一体化焖井时间优化模型
1.1 假设条件与物理模型

假设条件：①该模型包含压裂、焖井及生产3个连续的物理过程。压裂是在水力裂缝长度不变条件下短时间大排量的注入过程; 焖井是以压裂结束为初始条件, 源汇项为零, 页岩油储集层内自平衡渗吸的过程; 生产则是以焖井结束时刻为初始条件的采出过程。②物理模型为水平井多段多簇压后模型, 油水间渗吸、多相流动主要发生在水力裂缝与基质之间。③储集层中为油、水及溶质三相等温流动。④考虑裂缝、基质的压缩性, 溶质为不可压缩相。⑤考虑基质毛管压力、渗透压、膜效应及弹性能的影响。

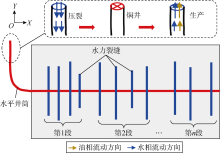
根据上述假设, 建立如图1所示页岩油水平井多段多簇压裂-焖井-生产一体化焖井时间优化模型。模型中水平井沿x轴方向, 水力裂缝垂直于水平井、与y轴平行。其中裂缝段长度、裂缝簇数及长度可通过现场压裂压力数据反演获得。压裂过程中, 压裂液在高压下通过井筒注入水力裂缝, 然后滤失进入储集层, 滤失量由基质与水力裂缝间的流量交换项来表示。压裂结束后, 源项为零, 此时水力裂缝内压裂液将在压差作用下继续流入基质, 基质中油相则在毛管压力、化学势和渗透压作用下进入水力裂缝。基于焖井结束后的物性状态, 继续进行生产模拟, 可以得到不同焖井时间下的油、水生产动态。基于焖井结束时的物性状态再进行产能模拟, 最终可以实现以产能最大化为目标的压后焖井时间优化。

图1 压裂-焖井-生产一体化焖井时间优化模型

1.2 数学模型

1.2.1 基质与裂缝中油、水连续性方程

假设溶质为不可压缩相, 仅溶于水相。基于质量守恒定律、达西定律及范特霍夫定律, 考虑静态自发渗吸中毛管压力以及渗透压影响, 可得到基质单元中油、水相的连续性方程[24, 25, 26]：

$\nabla \cdot \left[ {{K}_{\text{m}}}{{\lambda }_{\text{wm}}}\nabla \left( {{p}_{\text{wm}}}-{{\gamma }_{\text{w}}}{{D}_{\text{m}}} \right)-{{\lambda }_{\text{wm}}}\frac{{{K}_{\text{m}}}}{{{V}_{\text{w}}}}\omega R{{T}_{\text{m}}}\nabla {{c}_{\text{sm}}} \right]-{{q}_{\text{wmf}}}=\frac{\partial }{\partial t}\left[ \left( 1-{{\varepsilon }_{\text{vm}}} \right){{S}_{\text{wm}}}{{\phi }_{\text{m}}} \right]$ （1）

$\nabla \cdot \left[ {{K}_{\text{m}}}{{\lambda }_{\text{om}}}\nabla \left( {{p}_{\text{om}}}-{{\gamma }_{\text{o}}}{{D}_{\text{m}}} \right) \right]-{{q}_{\text{omf}}}=\frac{\partial }{\partial t}\left[ \left( 1-{{\varepsilon }_{\text{vm}}} \right){{S}_{\text{om}}}{{\phi }_{\text{m}}} \right]$ （2）

（1）式等号左边的第1项为水相流动项, 分别由水的达西层流项和基质孔隙中溶质浓度差导致的水相扩散项构成。第2项代表基质与裂缝间水相交换项。水力裂缝采用嵌入式离散模型表征, 引入嵌入式离散裂缝模型中基质与裂缝间传导系数（Tomf和Twmf）, 建立基质与裂缝间的质量传递关系; 考虑膜效应、渗透压对水相流动的影响, 而不考虑其对油相流动的影响, 将渗透压差$\Delta {{p}_{\text{op}}}=\frac{\omega R{{T}_{\text{m}}}}{{{V}_{\text{w}}}}\Delta {{c}_{\text{smf}}}$代入交换项中, 则交换项可以表示为[24]：

${{q}_{\text{wmf}}}=\frac{{{\lambda }_{\text{wmf}}}{{T}_{\text{wmf}}}}{{{V}_{\text{m}}}}\left( \Delta {{p}_{\text{wmf}}}+\Delta {{p}_{\text{op}}} \right)=\frac{{{\lambda }_{\text{wmf}}}{{T}_{\text{wmf}}}\Delta {{p}_{\text{wmf}}}}{{{V}_{\text{m}}}}+\frac{{{\lambda }_{\text{wmf}}}{{T}_{\text{wmf}}}}{{{V}_{\text{m}}}}\frac{\omega R{{T}_{\text{m}}}}{{{V}_{\text{w}}}}\Delta {{c}_{\text{smf}}}$ （3）

${{q}_{\text{omf}}}=\frac{{{\lambda }_{\text{omf}}}{{T}_{\text{omf}}}\Delta {{p}_{\text{omf}}}}{{{V}_{\text{m}}}}$ （4）

（3）式等号右边第1项代表压力梯度主导的流动项, 第2项代表基质与裂缝间渗透压主导的流动项。

由于裂缝具有高导流能力, 水力扩散速度快, 相比基质中浓度扩散对水相流动的影响, 裂缝内浓度扩散的影响较小。因此, 忽略溶质及毛管压力的影响。基于（1）— （4）式可以推导出水力裂缝内油、水两相一维流动方程：

$\nabla \cdot \left[ {{K}_{\text{f}}}{{\lambda }_{\text{wf}}}\nabla \left( {{p}_{\text{wf}}}-{{\gamma }_{\text{w}}}{{D}_{\text{m}}} \right) \right]+{{q}_{\text{wmf}}}+{{q}_{\text{wf}}}\text{=}\frac{\partial }{\partial t}\left( {{\phi }_{\text{f}}}{{S}_{\text{wf}}} \right)$ （5）

$\nabla \cdot \left[ {{K}_{\text{f}}}{{\lambda }_{\text{of}}}\nabla \left( {{p}_{\text{of}}}-{{\gamma }_{\text{o}}}{{D}_{\text{m}}} \right) \right]+{{q}_{\text{omf}}}+{{q}_{\text{of}}}\text{=}\frac{\partial }{\partial t}\left( {{\phi }_{\text{f}}}{{S}_{\text{of}}} \right)$ （6）

在注入过程中, 源项采用定流量注入; 在生产过程中, 汇项采用的是定井底压力采油, 此时产能计算的井指数可参考Moinfar等[25, 26]基于Peaceman井模型推导出的裂缝单元内等效井指数。

1.2.2 基质与裂缝中化学溶质连续性方程

基于质量守恒定律与范特霍夫定律, 考虑基质内水相达西流动引起的溶质扩散、溶质浓度差导致的溶质层流以及基质内外渗透压影响, 可以推导出基质单元中溶质的连续性方程[24, 27]：

$\nabla \cdot \left\{ {{c}_{\text{sm}}}{{K}_{\text{m}}}{{\lambda }_{\text{wm}}}\left( \omega +\frac{{{\rho }_{\text{w}}}}{{{\rho }_{\text{s}}}}\frac{{{c}_{\text{sm}}}}{1-{{c}_{\text{sm}}}} \right)\left[ \nabla \left( {{p}_{\text{wm}}}-{{\gamma }_{\text{w}}}{{D}_{\text{m}}} \right)-\begin{matrix} {} \\ {} \\\end{matrix} \right. \right.$$\left. \left. \frac{\omega R{{T}_{\text{m}}}}{{{V}_{\text{w}}}}\nabla {{c}_{\text{sm}}} \right]+{{\phi }_{\text{m}}}{{D}_{\text{eff}}}\nabla {{c}_{\text{sm}}} \right\}-{{q}_{\text{smf}}}=$ $\frac{\partial }{\partial t}\left[ \left( 1-{{\varepsilon }_{\text{vm}}} \right)\frac{{{\rho }_{\text{w}}}}{{{\rho }_{\text{s}}}}{{S}_{\text{wm}}}{{\phi }_{\text{m}}}\frac{{{c}_{\text{sm}}}}{1-{{c}_{\text{sm}}}} \right]$ （7）

由于岩块壁面并非完美的渗透膜, 在允许水分子通过时, 一部分离子也能通过（离子的通过能力取决于膜系数大小）。因此裂缝与基质间溶质交换项qsmf可以表示为：

${{q}_{\text{smf}}}\text{=}\frac{{{c}_{\text{swmf}}}}{1-{{c}_{\text{swmf}}}}\frac{{{\rho }_{w}}}{{{\rho }_{\text{s}}}}{{q}_{\text{wmf}}}$ （8）

将（3）式代入（8）式可得：

${{q}_{\text{smf}}}\text{=}\frac{{{c}_{\text{swmf}}}}{1-{{c}_{\text{swmf}}}}\frac{{{\rho }_{w}}}{{{\rho }_{\text{s}}}}\left( \frac{{{\lambda }_{\text{wmf}}}{{T}_{\text{wmf}}}\Delta {{p}_{\text{wmf}}}}{{{V}_{\text{m}}}}+ \right.$$\left. \frac{{{\lambda }_{\text{wmf}}}{{T}_{\text{wmf}}}}{{{V}_{\text{m}}}}\frac{\omega R{{T}_{\text{m}}}}{{{V}_{\text{w}}}}\Delta {{c}_{\text{smf}}} \right)$ （9）

对于裂缝内溶质的流动, 虽然溶质流动对油水流动的影响较小, 但由于裂缝高导流能力的影响, 较快的油水流动速度对溶质分布有很大影响。因此, 裂缝内溶质的流动需要考虑油水流动的影响。不考虑裂缝内溶质扩散的影响, 同时假设溶质不溶解于油相中, 可以得到裂缝中溶质传输的连续性方程：

$\nabla \cdot \left[ {{c}_{\text{sf}}}{{K}_{\text{f}}}{{\lambda }_{\text{wf}}}\nabla \left( {{p}_{\text{wf}}}-{{\gamma }_{\text{w}}}{{D}_{\text{m}}} \right) \right]+\frac{{{\rho }_{\text{s}}}}{{{\rho }_{\text{w}}}}{{q}_{\text{smf}}}+$$\frac{{{c}_{\text{sf, in, pro}}}}{1-{{c}_{\text{sf, in, pro}}}}{{q}_{\text{wf}}}=\frac{\partial }{\partial t}\left( {{S}_{\text{wf}}}{{\phi }_{\text{f}}}{{c}_{\text{sf}}} \right)$ （10）

1.2.3 辅助方程

要求解油水流动连续性、溶质连续性这6个非线性方程, 还需要一系列辅助方程。地层为弹性地层, 因此需要考虑裂缝和基质的压缩性, 则孔隙度和渗透率的应力敏感方程可以表示为：

$\left\{ \begin{align} & {{\phi }_{\text{m}}}={{\phi }_{0, m}}{{\text{e}}^{{{C}_{\text{m}}}\left( {{p}_{\text{om}}}-{{p}_{0}} \right)}} \\ & {{\phi }_{\text{f}}}={{\phi }_{0, \text{f}}}{{\text{e}}^{{{C}_{_{\text{f}}}}\left( {{p}_{\text{of}}}-{{p}_{0}} \right)}} \\ \end{align} \right.$ （11）

$\left\{ \begin{align} & {{K}_{\text{m}}}={{K}_{0, m}}{{\text{e}}^{{{E}_{\text{m}}}\left( {{p}_{\text{om}}}-{{p}_{0}} \right)}} \\ & {{K}_{\text{f}}}={{K}_{0, \text{f}}}{{\text{e}}^{{{E}_{_{\text{f}}}}\left( {{p}_{\text{of}}}-{{p}_{0}} \right)}} \\ \end{align} \right.$ （12）

饱和度方程为：

$\left\{ \begin{align} & {{S}_{\text{om}}}+{{S}_{\text{wm}}}=1 \\ & {{S}_{\text{of}}}+{{S}_{\text{wf}}}=1 \\ \end{align} \right.$ （13）

对于水润湿岩块, 水相为润湿相, 油相为非润湿相。于是毛管压力方程为：

${{p}_{\text{c}}}\left( {{S}_{\text{wm}}} \right)={{p}_{\text{om}}}-{{p}_{\text{wm}}}$ （14）

1.2.4 初始条件和边界条件

在模拟中, 压裂、焖井及生产为3个连续的物理过程。压裂结束时的储集层参数为焖井的初始参数, 焖井结束时的储集层参数为生产模拟的初始参数。因此, 只需要设置压裂时储集层的初始参数, 就可以通过一体化模型模拟获得一定焖井时间后的生产动态。本文假设压裂前储集层为均质二维、封闭储集层, 压裂时基质和水力裂缝的初始流体压力、初始含水饱和度、初始孔隙度、初始渗透率都相同, 其值源自页岩油井测井数据。水力裂缝长度和导流能力由现场压裂施工压力曲线反演获得。

1.3 模型求解

在保证计算精度及控制计算成本的要求下, 采用有限差分方法离散（1）式、（2）式、（5）式、（6）式、（7）式和（10）式, 结合辅助方程以及初始条件、边界条件, 采用隐式方法求解压力和饱和度, 采用显示方法求解溶质浓度分布。根据（1）式、（2）式、（5）式、（6）式的离散格式, 可以得到油相和水相的隐式求解矩阵形式[28]。同理, 对（7）式和（10）式的离散格式进行整理化简, 可以得到其矩阵形式。结合上述两个矩阵形式方程可以得到离散后的大型稀疏矩阵系统, 本文直接使用MATLAB中矩阵计算语句求解。

1.4 模型验证

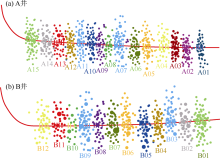
选择准噶尔盆地吉木萨尔凹陷芦草沟组页岩油储集层的两口页岩油井A和B为验证对象。两口井目的层为同一层位储集层, 假设两口井目的层物性相同, 都为均质储集层。另外, 假设裂缝导流能力均匀分布, 采用等效裂缝导流能力代替缝内非均匀分布导流能力。岩石弹性模量38 GPa、泊松比0.2、断裂韧性2 MPa· m1/2, 两口井的施工参数如表1所示, 压裂液类型相同。其中A井在压裂后采取了焖井措施, 37 d后开井生产, B井则在压裂后直接开井生产。首先根据测井数据和现场压裂压力数据, 采用商业软件进行净压力拟合获取了两口井压裂后的裂缝参数（见表2）, 然后进一步利用两口井的微地震监测数据（见表3、图2）进行校正。考虑到拟合数据可信度较高以及微地震数据偏大的特点, 校正的原则为两者取其小。将校正后的裂缝参数进行算术平均, 得到最终的基本参数为：A井水平段全长1 200 m, 井间距450 m, 压裂15段, 每段平均4簇水力裂缝, 平均裂缝半长135 m, 平均裂缝导流能力70× 10-3 μ m2· m; B井水平段全长1 200 m, 井间距400 m, 压裂12段, 每段平均4簇水力裂缝, 平均裂缝半长140 m, 平均裂缝导流能力80× 10-3 μ m2· m。另外, 模拟中两口井的油水相对渗透率曲线和毛管压力曲线为同一套数据, 由室内岩心实验测得, 如图3 所示。其余主要输入参数如表4所示。

表1 A井和B井压裂施工中的主要参数
表2 净压力拟合获得的裂缝参数
表3 微地震监测裂缝长度和方位
表4 模型验证中的主要输入参数

图2 微地震监测云图

图3 油水两相相对渗透率（a）和毛管压力（b）曲线

基于两口井的基本参数, 采用本文模型进行物理建模和模拟, 模拟结果与现场统计的生产数据具有较好的一致性（见图4）, 且针对B井参数采用Eclipse软件模拟的结果也与采用本文模型模拟的结果相匹配, 证明本文模型可以准确预测采取和未采取焖井措施时的生产动态。

图4 模拟结果与现场统计的生产数据对比

2 焖井时间优化方法

对于页岩油储集层, 渗吸采油是提高原油采收率的重要机理。除了毛管压力、重力两种源动力, 化学渗透压、基质壁面膜性质以及基质与裂缝间的流体交换面积等也是影响焖井渗吸的重要因素。在不考虑液体伤害情况下, 选择不同的焖井时间, 代表渗吸置换的原油量以及累计产量也不同。随着焖井时间增加, 累计产量或采出程度会有一定程度增加。基于建立的压裂-焖井-生产一体化模型, 本文提出了以产能最大化、最快回收成本为目标的焖井时间优化方法, 具体的操作步骤如下。

①根据建立的模型, 获得某一组工程参数及地质参数条件下和某一焖井时间下的采出动态。

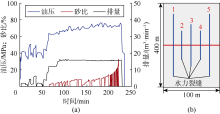
②改变焖井时间, 重复步骤①, 在相同地质参数及工程参数下, 可得到不同焖井时间下累计产量与生产时间之间的关系, 如图5a所示。

图5 焖井时间优化方法示意图

③基于步骤②的结果, 整理出某一生产时间（一般选择累计产量差异较大的时间点）下的不同焖井时间方案的累计产量与未焖井方案累计产量之间的差值, 从而得到图5b所示累计产量增量与焖井时间的关系。

④基于图5b, 找最优焖井时间。为量化选择最优焖井时间, 并保证在最短焖井时间内累计产量增量基本达到峰值, 可求累计产量增量与焖井时间关系曲线的一阶导数, 当其值为0.001 t/d, 即曲线上某点的斜率为0.001 t/d时, 认为该点对应的焖井时间为最优焖井时间。如图5b所示, A点斜率为0.001 t/d, 对应的最优焖井时间为30 d, 此时系统中油、水、溶质流动基本达到平衡状态, 累计产量增量将要达到峰值, 继续焖井累计产量增量的增加幅度较小, 选择焖井时间为30 d可达到最快回收成本的目的。

3 算例分析

最优焖井时间是压裂后地层中多相流体流动以及能量分布再次达到再平衡的时间, 是焖井决策中的关键设计参数。根据建立的压裂-焖井-生产一体化模型和焖井时间优化方法, 结合吉木萨尔凹陷页岩油井C井压裂压力数据, 建立如图6所示的单段5簇物理模型。模型中1— 5簇裂缝半长分别为142, 82, 120, 82, 142 m, 每簇平均导流能力为40× 10-3 μ m2· m。分别模拟3个连续过程, 首先进行短时间大排量注入以模拟压裂过程, 然后令源项为零开始焖井, 最后开井生产。模拟中的主要输入参数如表5所示, 相对渗透率曲线和毛管压力曲线如图3所示。

图6 压裂压力数据（a）和基于数据反演建立的压裂-焖井-生产模拟物理模型（b）

表5 模拟中的主要输入参数

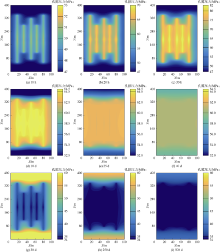
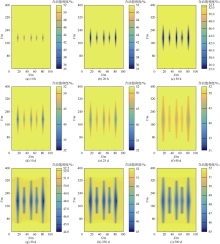
图7和图8分别为压裂、焖井、生产阶段不同时刻的孔隙压力和含油饱和度分布图。可以看出, 压裂为类似短暂水驱物理过程, 随着压裂时间的增加, 裂缝附近的含油饱和度逐渐减小, 孔隙压力逐渐增加。焖井阶段, 受毛管压力、化学势及渗透压影响, 裂缝附近的含油饱和度逐渐恢复, 基质内大量原油被置换到裂缝中, 因此焖井结束开井初期的产油量较高。随着焖井时间的增加, 孔隙压力逐渐趋于某一平衡值。在封闭边界下, 储集层孔隙压力达到平衡时的值将大于初始孔隙压力。生产阶段, 模拟孔隙压力和含油饱和度变化趋势结果与常规生产过程相同。

图7 压裂（a— c）、焖井（d— f）、生产（g— i）阶段不同时刻孔隙压力分布

图8 压裂（a— c）、焖井（d— f）、生产（g— i）阶段不同时刻含油饱和度分布

通过改变焖井时间, 模拟得到了不同焖井时间下的生产动态曲线（见图9a）。以未焖井方案第300 d的累计产量为参考, 焖井时间与累计产量增量的关系如图9b所示。图9a表明, 采取焖井措施后, 初期的日产油量和累计产量大幅度提高, 但随着生产时间的增加, 累计产量的增幅将不断减小。图9b则表明, 随着焖井时间的增加, 累计产量增量先增加, 后逐渐趋于某一稳定值。因此, 为了合理控制焖井时间, 尽快采出原油回收成本, 根据焖井时间优化方法, 找到图9b中曲线斜率等于0.001 t/d的点, 对应的50 d则为最优焖井时间。

图9 不同焖井时间下的生产动态（a）和累计产量增量（b）

4 最优焖井时间影响因素分析

基于压裂-焖井-生产一体化模型和图6b所示物理模型, 研究了基质渗透率、孔隙度、膜效率、毛管压力倍数、排量、注入液体总量和裂缝长度等参数对最优焖井时间的影响规律。在分析某一参数的影响规律时, 只对该参数取不同值, 其他参数取值与算例分析中取值相同。

4.1 基质渗透率和孔隙度对最优焖井时间的影响

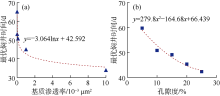
模拟得到了如图10所示最优焖井时间与基质渗透率、孔隙度的关系曲线, 并给出相应的回归关系。可以看出, 受基质中油水、溶质传输速率的影响, 最优焖井时间与基质渗透率间呈对数递减关系, 与孔隙度呈弱非线性递减关系。当基质渗透率较小时, 基质渗透率对最优焖井时间具有显著影响。

图10 最优焖井时间与基质渗透率（a）、孔隙度（b）的关系曲线

4.2 膜效率和毛管压力倍数对最优焖井时间的影响

在水润湿条件下, 膜效率和毛管压力对基质与裂缝间的渗吸作用有很大影响。研究了膜效率和毛管压力倍数（即当前毛管压力与初始毛管压力的比值）对最优焖井时间的影响, 结果如图11所示。可以看出, 最优焖井时间与膜效率非线性正相关, 与毛管压力倍数非线性负相关。随着膜效率的降低和毛管压力倍数的增加, 裂缝中水相更容易进入基质中置换出油相, 水力裂缝附近的含油饱和度更快恢复, 同时储集层将更快达到平衡态。

图11 最优焖井时间与膜效率（a）、毛管压力倍数（b）的关系曲线

4.3 排量、注入液体总量和裂缝长度对最优焖井时间的影响

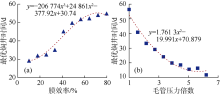
压裂中, 排量、注入液体总量及裂缝长度都是影响注入后流体分布形态的关键参数, 同时也是影响最优焖井时间的关键参数。研究了排量、裂缝长度及注入液体总量对最优焖井时间的影响, 模拟结果如图12所示。在裂缝长度影响分析中物理模型具有5簇等簇间距和等长度的裂缝。可以看出, 最优焖井时间与排量、注入液体总量分别表现出近线性正相关和非线性正相关, 与裂缝长度非线性负相关。在注入压裂液总量相同时, 排量的增加使高压注入的时间减少, 停泵后更多压裂液滞留在水力裂缝中形成局部高压区域, 此时需要更长焖井时间才能使储集层中能量和多相流体流动达到平衡。注入液体总量的增加直接增加了储集层的吸液载荷, 根据质量守恒定律及多孔介质中的传质方程可知, 在裂缝和基质传质能力不变时, 总注入量增加, 必然导致传质时间的增加。裂缝长度的减小, 使基质与裂缝间油水渗吸交换的面积减小, 从而延长最优焖井时间。

图12 排量（a）、注入液体总量（b）及裂缝长度（c）与最优焖井时间的关系曲线

4.4 最优焖井时间主控因素

为了研究最优焖井时间的主控因素, 分析了7种影响因素, 对应的参数设置如表6所示。基于正交设计思想, 对这7种影响因素进行组合, 得出共21种模拟方案。基于表5的主要输入参数, 模拟得到的多因素方差分析结果如表7所示。根据均方和F值可以看出, 对最优焖井时间的影响程度从大到小依次为注入液体总量、毛管压力倍数、基质渗透率、孔隙度、膜效率、压裂液矿化度和排量。

表6 正交实验参数设置
表7 多因素方差分析结果
5 结论

随着焖井时间增加, 页岩油井初期产量和累计产量增量都表现出先快速增加后趋于某一稳定值的变化趋势, 累计产量增量变化趋势中拐点对应的焖井时间即为最优焖井时间。

最优焖井时间与基质渗透率、孔隙度、毛管压力倍数及裂缝长度呈非线性负相关, 与膜效率、注入液体总量呈非线性正相关, 与排量呈近线性正相关。对最优焖井时间的影响程度从大到小依次为注入液体总量、毛管压力倍数、基质渗透率、孔隙度、膜效率、压裂液矿化度和排量。

符号注释：

csm, csf— — 基质、裂缝中溶质质量分数, %; csf, in, pro— — 裂缝内汇项的溶质质量分数, %; cswmf— — 裂缝与基质相交单元对应的溶质质量分数, %; Δ csmf— — 基质与裂缝中溶质质量分数之差, %; Cm, Cf— — 基质、裂缝孔隙度的压缩系数, Pa-1; Deff— — 孔隙介质中有效体积扩散系数, m2/s; Dm— — 海拔高度, m; Em, Ef— — 基质、裂缝渗透率的应力敏感系数, Pa-1; F— — 显著性差异水平; Km, Kf— — 基质、裂缝的渗透率, m2; K0, m, K0, f— — 基质、裂缝的初始渗透率, m2; n— — 压裂段数; p0— — 初始孔隙压力, Pa; pc— — 毛管压力, Pa; pof, pwf— — 裂缝中油相、水相的压力, Pa; pom, pwm— — 基质中油相、水相的压力, Pa; Δ pomf, Δ pwmf— — 基质与裂缝间油相、水相的压力差, Pa; Δ pop— — 渗透压差, Pa; P— — 检测水平; qof, qwf— — 裂缝内油相、水相的源汇项, s-1; qomf, qwmf, qsmf— — 基质与裂缝间油相、水相、溶质的交换项, s-1; R— — 气体常数, J/(mol· K); Sof, Swf— — 裂缝中油相、水相的饱和度, %; Som, Swm— — 基质中油相、水相的饱和度, %; t— — 时间, s; Tm— — 基质温度, K; Tomf, Twmf— — 基于嵌入式离散裂缝模型定义的基质与裂缝间油相、水相的传导系数, m3; Vm— — 网格单元体积, m3; Vw— — 水的偏摩尔体积, m3/mol; X, Y— — 直角坐标系, m; γ o, γ w— — 油相、水相的重度, N/m3; ε vm— — 体积应变, 无因次; λ of, λ wf— — 裂缝中油相、水相的相对流度, (Pa· s)-1; λ om, λ wm— — 基质中油相、水相的相对流度, (Pa· s)-1; λ omf, λ wmf— — 基质与裂缝相交单元对应的油相、水相的相对流度, (Pa· s)-1; ρ w, ρ s— — 水相、溶质的密度, kg/m3; ϕ m, ϕ f— — 基质、裂缝的孔隙度, %; ϕ 0, m, ϕ 0, f— — 基质、裂缝的初始孔隙度, %; ω — — 膜效率, 无因次。

（编辑 胡苇玮）

参考文献
[1] 金之钧, 朱如凯, 梁新平, 等. 当前陆相页岩油勘探开发值得关注的几个问题[J]. 石油勘探与开发, 2021, 48(6): 1276-1287.
JIN Zhijun, ZHU Rukai, LIANG Xinping, et al. Several issues worthy of attention in current lacustrine shale oil exploration and development[J]. Petroleum Exploration and Development, 2021, 48(6): 1276-1287. [本文引用:1]
[2] 胡素云, 赵文智, 侯连华, 等. 中国陆相页岩油发展潜力与技术对策[J]. 石油勘探与开发, 2020, 47(4): 819-828.
HU Suyun, ZHAO Wenzhi, HOU Lianhua, et al. Development potential and technical strategy of continental shale oil in China[J]. Petroleum Exploration and Development, 2020, 47(4): 819-828. [本文引用:1]
[3] 贾承造, 邹才能, 李建忠, 等. 中国致密油评价标准、主要类型、基本特征及资源前景[J]. 石油学报, 2012, 33(3): 343-350.
JIA Chengzao, ZOU Caineng, LI Jianzhong, et al. Assessment criteria, main types, basic features and resource prospects of the tight oil in China[J]. Acta Petrolei Sinica, 2012, 33(3): 343-350. [本文引用:1]
[4] 邹才能, 朱如凯, 白斌, 等. 致密油与页岩油内涵、特征、潜力及挑战[J]. 矿物岩石地球化学通报, 2015, 34(1): 1-17.
ZOU Caineng, ZHU Rukai, BAI Bin, et al. Significance, geologic characteristics, resource potential and future challenges of tight oil and shale oil[J]. Bulletin of Mineralogy, Petrology and Geochemistry, 2015, 34(1): 1-17. [本文引用:1]
[5] 雷群, 翁定为, 熊生春, 等. 中国石油页岩油储集层改造技术进展及发展方向[J]. 石油勘探与开发, 2021, 48(5): 1035-1042.
LEI Qun, WENG Dingwei, XIONG Shengchun, et al. Progress and development directions of shale oil reservoir stimulation technology of China National Petroleum Corporation[J]. Petroleum Exploration and Development, 2021, 48(5): 1035-1042. [本文引用:1]
[6] 王飞, 阮颖琪, 陈巧韵, 等. 考虑压裂液渗吸换油效应的压裂焖井压降模型[J]. 石油勘探与开发, 2021, 48(6): 1250-1257.
WANG Fei, RUAN Yingqi, CHEN Qiaoyun, et al. A pressure drop model of post-fracturing shut-in considering the effect of fracturing-fluid imbibition and oil replacement[J]. Petroleum Exploration and Development, 2021, 48(6): 1250-1257. [本文引用:1]
[7] ZHAO J Z, WANG Q, HU Y Q, et al. Numerical investigation of shut-in time on stress evolution and tight oil production[J]. Journal of Petroleum Science and Engineering, 2019, 179: 716-733. [本文引用:1]
[8] LEE C H, KARPYN Z T. Numerical analysis of imbibition front evolution in fractured sand stone under capillary-dominated conditions[J]. Transport in Porous Media, 2012, 94(1): 359-383. [本文引用:1]
[9] SHEN Y H, GE H K, LI C X, et al. Water imbibition of shale and its potential influence on shale gas recovery: A comparative study of marine and continental shale formations[J]. Journal of Natural Gas Science and Engineering, 2016, 35(Part A): 1121-1128. [本文引用:1]
[10] TEKLU T W, LI X P, ZHOU Z, et al. Low-salinity water and surfactants for hydraulic fracturing and EOR of shales[J]. Journal of Petroleum Science and Engineering, 2018, 162: 367-377. [本文引用:1]
[11] 李传亮, 毛万义, 吴庭新, 等. 渗吸驱油的机理研究[J]. 新疆石油地质, 2019, 40(6): 687-694.
LI Chuanliang, MAO Wanyi, WU Tingxin, et al. A study on mechanism of oil displacement by imbibition[J]. Xinjiang Petroleum Geology, 2019, 40(6): 687-694. [本文引用:1]
[12] 李士奎, 刘卫东, 张海琴, 等. 低渗透油藏自发渗吸驱油实验研究[J]. 石油学报, 2007, 28(2): 109-112.
LI Shikui, LIU Weidong, ZHANG Haiqin, et al. Experimental study of spontaneous imbibition in low-permeability reservoir[J]. Acta Petrolei Sinica, 2007, 28(2): 109-112. [本文引用:1]
[13] 王敬, 刘慧卿, 夏静, 等. 裂缝性油藏渗吸采油机理数值模拟[J]. 石油勘探与开发, 2017, 44(5): 761-770.
WANG Jing, LIU Huiqing, XIA Jing, et al. Mechanism simulation of oil displacement by imbibition in fractured reservoirs[J]. Petroleum Exploration and Development, 2017, 44(5): 761-770. [本文引用:1]
[14] 李耀华, 宋岩, 徐兴友, 等. 鄂尔多斯盆地延长组7段凝灰质页岩油层的润湿性及自发渗吸特征[J]. 石油学报, 2020, 41(10): 1229-1237.
LI Yaohua, SONG Yan, XU Xingyou, et al. Wettability and spontaneous imbibition characteristics of the tuffaceous shale reservoirs in the Member 7 of Yanchang Formation, Ordos Basin[J]. Acta Petrolei Sinica, 2020, 41(10): 1229-1237. [本文引用:1]
[15] VALLURI M K, ALVAREZ J O, SCHECHTER D S. Study of the rock/fluid interactions of sodium and calcium brines with ultra-tight rock surfaces and their impact on improving oil recovery by spontaneous imbibition[R]. SPE 180274-MS, 2016. [本文引用:1]
[16] ZHOU Z, ABASS H, LI X, et al. Mechanisms of imbibition during hydraulic fracturing in shale formations[J]. Journal of Petroleum Science and Engineering, 2016, 141: 125-132. [本文引用:1]
[17] 王飞, 潘子晴. 化学势差驱动下的页岩储集层压裂液返排数值模拟[J]. 石油勘探与开发, 2016, 43(6): 971-977.
WANG Fei, PAN Ziqing. Numerical simulation of chemical potential dominated fracturing fluid flowback in hydraulically fractured shale gas reservoirs[J]. Petroleum Exploration and Development, 2016, 43(6): 971-977. [本文引用:1]
[18] 韦青, 李治平, 王香增, 等. 裂缝性致密砂岩储层渗吸机理及影响因素: 以鄂尔多斯盆地吴起地区长8储层为例[J]. 油气地质与采收率, 2016, 23(4): 102-107.
WEI Qing, LI Zhiping, WANG Xiangzeng, et al. Mechanism and influence factors of imbibition in fractured tight sand stone reservoir: An example from Chang8 reservoir of Wuqi area in Ordos Basin[J]. Petroleum Geology and Recovery Efficiency, 2016, 23(4): 102-107. [本文引用:1]
[19] WANG Q, HU Y Q, ZHAO J Z, et al. Numerical simulation of fracture initiation, propagation and fracture complexity in the presence of multiple perforations[J]. Journal of Natural Gas Science and Engineering, 2020, 83: 103486. [本文引用:1]
[20] BUI B T, TUTUNCU A N. Contribution of osmotic transport on oil recovery from rock matrix in unconventional reservoirs[J]. Journal of Petroleum Science and Engineering, 2017, 157: 392-408. [本文引用:1]
[21] BUI B T. A multi-physics model for enhanced oil recovery in liquid- rich unconventional reservoirs[D]. Golden: Colorado School of Mines, 2016. [本文引用:1]
[22] HU Y Q, WANG Q, ZHAO J Z, et al. Numerical simulation of complex fracture geometry caused by hydrodynamics in shale with pre-existing weak planes[J]. Journal of Petroleum Science and Engineering, 2021, 199: 108306. [本文引用:1]
[23] WANG J, LIU H Q, QIAN G B, et al. Mechanisms and capacity of high-pressure soaking after hydraulic fracturing in tight/shale oil reservoirs[J]. Petroleum Science, 2021, 18(2): 546-564. [本文引用:1]
[24] MANASSERO M, DOMINIJANNI A. Modelling the osmosis effect on solute migration through porous media[J]. Géotechnique, 2003, 53(5): 481-492. [本文引用:3]
[25] MOINFAR A, VARAVEI A, SEPEHRNOORI K, et al. Development of an efficient embedded discrete fracture model for 3D compositional reservoir simulation in fractured reservoirs[J]. SPE Journal, 2014, 19(2): 289-303. [本文引用:2]
[26] PEACEMAN D W. Interpretation of well-block pressures in numerical reservoir simulation[J]. Society of Petroleum Engineers Journal, 1978, 18(3): 183-194. [本文引用:2]
[27] GEREN F, FIRINCIOGLU T, KARACAER C, et al. Modeling flow in nanoporous, membrane reservoirs and interpretation of coupled fluxes[R]. SPE 170976-MS, 2014. [本文引用:1]
[28] LI L Y, LEE S H. Efficient field-scale simulation of black oil in a naturally fractured reservoir through discrete fracture networks and homogenized media[J]. SPE Reservoir Evaluation & Engineering, 2008, 11(4): 750-758. [本文引用:1]