东河油田A区块储集层平均孔隙度15.1%, 平均渗透率68.1× 10^-3 μ m², 地质储量2 821× 10⁴ m³, 原油体积系数1.090 4。该区块1990年11月投产, 1994年5月开始注水, 2014年6月结束水驱, 水驱结束时采收率为35%。2014年7月开始注烃气, 现场预测注气可提高采收率至55%。在历史拟合基础上通过数值模拟预测了2018年5月到2026年5月的气驱生产数据, 预测期末含水气率接近90%。将以上数据作为图版讨论的数据基础。

根据实际数据并结合模拟预测数据, 对比气驱生产不同阶段新型气驱图版回归法和赋值法预测采收率。选取3个不同气驱阶段进行讨论：气驱初期（60%< f_wg≤ 70%）; 气驱中期（70%< f_wg≤ 80%）; 气驱后期（80%< f_wg≤ 90%）。

2.2.1 气驱初期数据

选取气驱初期（2014年7月— 2016年4月）的数据进行预测（60%< f_wg≤ 70%）。采用回归法绘制油藏$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}$与R交会图（见图2）, 气驱阶段$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}$与R交会图线性关系良好, 回归得bNB_o=12.22× 10⁴ m³, 代入（10）式得东河油田A区块的气驱特征曲线图版公式为：

$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}=12.22\left( R-{{E}_{\text{R}}} \right)+3.89$ （11）

图2

	Figure Option ViewDownloadNew Window
	图2 回归曲线数据选取（气驱初期）及拟合结果

根据（11）式绘制气驱特征曲线图版（见图3）, 东河油田A区块初期的生产数据与采收率为60%的曲线较吻合, 故预测采收率为60%。

图3

	Figure Option ViewDownloadNew Window
	图3 基于气驱初期数据的回归法特征曲线图版

选取相同注气阶段（2014年7月— 2016年4月）的数据绘制气驱特征曲线（见图4）, 得东河油田A区块系数b=0.002 7, 结合油田地质储量与原油体积系数计算得bNB_o=8.31× 10⁴ m³。代入（10）式得东河油田A区块的气驱特征曲线图版公式为：

$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}=8.31\left( R-{{E}_{\text{R}}} \right)+3.89$ （12）

图4

	Figure Option ViewDownloadNew Window
	图4 气驱特征曲线数据选取（气驱初期）及拟合结果

根据（12）式绘制气驱特征曲线图版（见图5）, 可以看出东河油田A区块初期的生产数据与采收率为69%的曲线比较吻合, 故得到预测采收率为69%。

图5

	Figure Option ViewDownloadNew Window
	图5 基于气驱初期数据的赋值法特征曲线图版

2.2.2 气驱中期数据

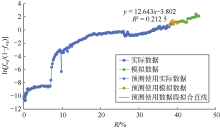
选取气驱中期（2016年5月— 2021年3月）数据进行预测（70%< f_wg≤ 80%）。采用回归法绘制油藏$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}$与R交会图（见图6）。气驱阶段$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}$与R线性关系良好, 回归得bNB_o=12.64× 10⁴ m³, 代入（10）式得东河油田A区块的气驱特征曲线图版公式为：

$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}=12.64\left( R-{{E}_{\text{R}}} \right)+3.89$ （13）

图6

	Figure Option ViewDownloadNew Window
	图6 回归曲线数据选取（气驱中期）及拟合结果

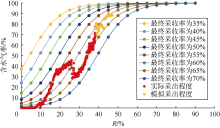
根据（13）式绘制气驱特征曲线图版（见图7）, 东河油田A区块气驱中期的生产数据与采收率为60%的曲线较吻合, 故预测采收率为60%。

图7

	Figure Option ViewDownloadNew Window
	图7 基于气驱中期数据的回归法特征曲线图版

选取相同注气阶段（2016年5月— 2021年3月）的数据, 采用赋值法绘制气驱特征曲线, 得东河油田A区块系数b=0.002 5, 结合油田地质储量与原油体积系数计算得bNB_o=7.69× 10⁴ m³。利用气驱特征图版预测得到采收率为70%。

2.2.3 气驱后期数据

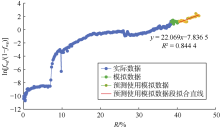
选取气驱后期阶段（2021年5月— 2026年5月）数据进行预测（80%< f_wg≤ 90%）。采用回归法绘制油藏$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}$与R交会图（见图8）, 气驱阶段$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}$与R线性关系良好, 回归得bNB_o=22.07× 10⁴ m³, 代入（10）式得东河油田A区块的气驱特征曲线图版公式为：

$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}=22.07\left( R-{{E}_{\text{R}}} \right)+3.89$ （14）

图8

	Figure Option ViewDownloadNew Window
	图8 回归曲线数据选取（气驱后期）及拟合结果

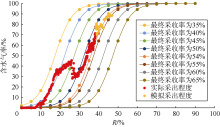
根据（14）式绘制气驱特征曲线图版（见图9）, 可以看出东河油田A区块后期的生产数据与采收率为54%的曲线较吻合, 故预测采收率为54%。

图9

	Figure Option ViewDownloadNew Window
	图9 基于气驱后期数据的回归法特征曲线图版

选取相同注气阶段（2021年5月— 2026年5月）的数据, 采用赋值法绘制气驱特征曲线, 得东河油田A区块系数b=0.004 2, 结合油田地质储量与原油体积系数计算得bNB_o=12.92× 10⁴ m³。利用气驱特征图版预测得到采收率为59%。

基于气驱生产不同阶段数据的赋值法与回归法计算结果如表1所示。已知A区块水驱结束时采收率为35%, 现场预测注气可提高采收率至55%, 通过对比回归法预测的采收率可以看出, 当60%＜f_wg≤ 80%时, 预测采收率为60%, 与现场预测接近; 当含水气率大于80%时, 回归法预测采收率与现场预测值基本一致, 说明回归法适用的含水气率范围更大。

表1

表1

表1 气驱生产不同阶段新型气驱图版预测采收率对比 预测方法 含水气率/% bNBo/104 m3 采收率/% 回归法 60＜fwg≤ 70 12.22 60 70＜fwg≤ 80 12.64 60 80＜fwg≤ 90 22.07 54 赋值法 60＜fwg≤ 70 8.31 69 70＜fwg≤ 80 7.69 70 80＜fwg≤ 90 12.92 59

表1 气驱生产不同阶段新型气驱图版预测采收率对比

对于赋值法, 选取的气驱生产数据阶段越晚, 预测采收率与现场预测采收率越接近, 分析原因认为, 气体还未突破时, 赋值法图版预测的不确定性大, 当含水气率高于80%时, 预测采收率趋于合理。

因此, 初步认为当气驱油藏含水气率为60%~80%时, 新型气驱图版回归法预测采收率适用性较好; 当气驱油藏含水气率大于80%时, 应用新型图版回归法与赋值法预测采收率皆合适。

综合回归法与赋值法得到该区块气驱图版采收率预测结果为54%~60%, 图版预测结果与现场实际预测情况相符, 说明新型气驱图版预测结果具有较好的可信度。

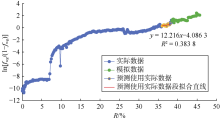
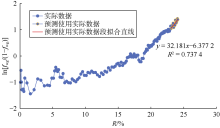
选取吉林油田B区块水驱段生产数据绘制$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}$与R交会图（见图10）, 可以看出图中黄色段线性关系良好, 回归得bNB_o=32.18× 10⁴ m³。代入（10）式得吉林油田B区块水驱特征曲线图版公式为：

$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}=32.18\left( R-{{E}_{\text{R}}} \right)+3.89$ （15）

图10

	Figure Option ViewDownloadNew Window
	图10 吉林油田B区块水驱回归曲线

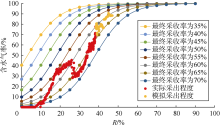
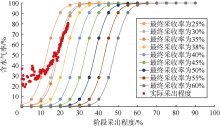
根据（15）式绘制水驱特征曲线图版（见图11）, 可以看出B区块后期生产数据与采收率为31%的曲线较吻合, 故得出预测采收率为31%。

图11

	Figure Option ViewDownloadNew Window
	图11 吉林油田B区块水驱特征曲线图版（回归法）

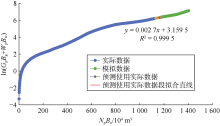
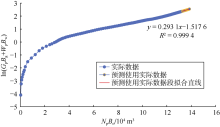
选取相同段生产数据, 采用赋值法绘制水驱特征曲线（见图12）, 回归得b=0.293 1, 已知地质储量N=49.96× 10⁴ m³, 原油体积系数B_o=1.15, 计算得bNB_o= 16.84× 10⁴ m³, 代入（10）式得吉林油田B区块水驱特征曲线图版公式为：

$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}=16.84\left( R-{{E}_{\text{R}}} \right)+3.89$ （16）

图12

	Figure Option ViewDownloadNew Window
	图12 吉林油田B区块水驱特征曲线

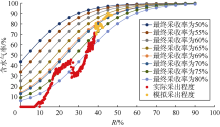
根据（16）式绘制水驱特征曲线图版（见图13）, B区块后期生产数据与采收率为40%的曲线较吻合, 由此得出预测采收率为40%。

图13

	Figure Option ViewDownloadNew Window
	图13 吉林油田B区块水驱特征曲线图版（赋值法）

此外, 据相同时间段生产数据求得童氏水驱特征曲线图版公式为：

$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}=32.18\left( R-{{E}_{\text{R}}} \right)+3.89$ （17）

采用童氏图版法预测采收率为31%, 与上述回归法预测水驱采收率一致, 说明新型气驱图版可以退化成童氏图版预测水驱采收率。童氏图版法预测采收率与赋值法预测采收率相差较大, 主要是由于含水气率低于80%, 赋值法预测采收率误差较大。

吉林油田B区块2015年12月含水气率为84%, 日产气量为13.9× 10⁴ m³, 已进入大规模产气阶段, 故选取2015年12月至2020年1月期间的生产数据进行采收率预测。

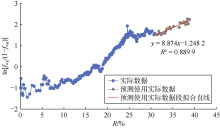
吉林油田B区块$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}$与R交会图中黄色段线性关系良好（见图14）, 回归得bNB_o=8.87× 10⁴ m³, 代入（10）式得气驱特征曲线图版公式为：

$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}=8.87\left( R-{{E}_{R}} \right)+3.89$ （18）

图14

	Figure Option ViewDownloadNew Window
	图14 吉林油田B区块气驱回归曲线

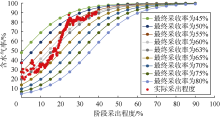
根据（18）式绘制气驱特征曲线图版（见图15）, B区块后期生产数据与采收率为58%的曲线较吻合, 因此得到预测采收率为58%。

图15

	Figure Option ViewDownloadNew Window
	图15 吉林油田B区块气驱特征曲线图版（回归法）

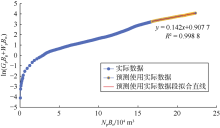
选取相同时间段生产数据, 采用赋值法绘制气驱特征曲线（见图16）, 回归得b=0.142, 代入已知地质储量与原油体积系数, 计算得bNB_o=8.16× 10⁴ m³, 代入（10）式得吉林油田B区块气驱特征曲线图版公式为：

$\ln \frac{{{f}_{\text{wg}}}}{1-{{f}_{\text{wg}}}}=8.16\left( R-{{E}_{\text{R}}} \right)+3.89$ （19）

图16

	Figure Option ViewDownloadNew Window
	图16 吉林油田B区块气驱特征曲线

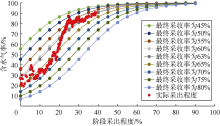
根据（19）式绘制气驱特征曲线图版（见图17）, 可以看出B区块后期生产数据与采收率为59%的曲线较吻合, 因此得到预测采收率为59%。

图17

	Figure Option ViewDownloadNew Window
	图17 吉林油田B区块气驱特征曲线图版（赋值法）

由上面分析可以看到, 回归法与赋值法预测最终采收率均相近, 说明新型气驱图版预测结果可靠。故得到吉林油田B区块预测气驱采收率为58%~59%, 水驱采收率为31%, CO₂驱提高采收率27~28个百分点, 现场预测气驱采收率提高幅度约27个百分点, 与图版预测结果一致, 说明新型图版同时适用于水驱、气驱油藏采收率预测。