引用本文
刘国强, 龚仁彬, 石玉江, 王珍珍, 米兰, 袁超, 钟吉彬. 油气层测井知识图谱构建及其智能识别方法[J]. 石油勘探与开发, 2022,49(3): 502-512.
LIU Guoqiang, GONG Renbin, SHI Yujiang, WANG Zhenzhen, MI Lan, YUAN Chao, ZHONG Jibin. Construction of well logging knowledge graph and intelligent identification method of hydrocarbon-bearing formation[J]. Petroleum Exploration & Development, 2022,49(3): 502-512.  
Doi: 10.11698/PED.20210750
Permissions
Copyright©2022, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
油气层测井知识图谱构建及其智能识别方法
刘国强1, 龚仁彬2, 石玉江3, 王珍珍2, 米兰2, 袁超2, 钟吉彬4
1.中国石油勘探与生产分公司,北京100007
2.中国石油勘探开发研究院,北京 100083
3.中国石油集团测井有限公司,西安 710077
4.中国石油长庆油田公司,西安 710018

第一作者简介：刘国强（1964-）,男,江西鄱阳人,博士,中国石油勘探与生产分公司教授级高级工程师,主要从事油气藏测井评价研究。地址：北京东城区东直门北大街9号石油大厦,中国石油勘探与生产分公司,邮政编码：100007。E-mail：lgqi@petrochina.com.cn

收稿日期: 2021-10-18 修回日期: 2022-01-18
基金项目: 国家科技重大专项“四川盆地二叠系—中三叠统天然气富集规律与目标评价”（2016ZX05007-004）
摘要

基于油气层测井知识图谱构建,提出知识驱动的神经网络油气层评价模型（KPNFE）。其功能主要包括：①多维度多尺度提取精细描述油气层的特征参数;②以图嵌入技术将这些特征参数所关联的实体、关系和属性表征为向量特征图;③实现油气层智能识别;④将专家知识有机地融入智能计算,建立潜力层推荐的评价体系与优选算法。以鄂尔多斯盆地姬塬区块所有钻遇三叠系延长组6段低孔低渗地层的547口井为研究对象,随机选取其中80%的井为训练集、20%的井为验证集,KPNFE计算结果表明,验证集的解释结果与专家解释结果吻合率达94.43%,所有试油层的解释结果符合率达84.38%,较一次解释提高了13个百分点,工作时效提高了100倍以上,并择优推荐了一批有望获得工业油流的潜力层。KPNFE模型继承了专家知识和经验并对其发扬提升,有效解决了油气层识别中存在的鲁棒性问题,且计算结果的可解释性强、准确性高,是老区老井测井再评价高效高质量工作的有效方法。

关键词: 测井; 油气层识别; 知识图谱; 图嵌入技术; 智能识别; 神经网络
中图分类号:TE122.1 文献标志码:A 文章编号:1000-0747(2022)03-0502-11
Construction of well logging knowledge graph and intelligent identification method of hydrocarbon-bearing formation
LIU Guoqiang1, GONG Renbin2, SHI Yujiang3, WANG Zhenzhen2, MI Lan2, YUAN Chao2, ZHONG Jibin4
1. PetroChina Exploration and Production Company, Beijing 100007, China
2. PetroChina Research Institute of Petroleum Exploration and Development, Beijing 100083, China
3. CNPC Logging Company, Xi’an 710077, China
4. PetroChina Changqing Oilfield Company, Xi’an 710018, China
Abstract

Based on the logging knowledge graph of hydrocarbon-bearing formation (HBF), a Knowledge-Powered Neural Network Formation Evaluation model (KPNFE) has been proposed. It has the following functions: (1) extracting characteristic parameters describing HBF in multiple dimensions and multiple scales; (2) showing the characteristic parameter-related entities, relationships, and attributes as vectors via graph embedding technique; (3) intelligently identifying HBF; (4) seamlessly integrating expertise into the intelligent computing to establish the appraising system and ranking algorithm for potential reservoir recommendation. Taking 547 wells encountered the lower porosity and lower permeability Chang 6 Member in Jiyuan Block of Ordos Basin as objects, 80% of the wells were randomly selected as the training dataset and the remainder as the validation dataset. The KPNFE prediction results on the validation dataset had a coincidence rate of 94.43% with the expert interpretations and a coincidence rate of 84.38% for all the tested layers, which is 13 percentage points higher in accuracy and over 100 times faster than the primary conventional interpretation. In addition, a number of potential reservoirs likely to produce industrial oil were recommended. The KPNFE model effectively inherits, carries forward and improves the expert knowledge, nicely solving the robustness problem in HBF identification. The KPNFE, with good interpretability and high accuracy of computation results, is a powerful technical means for efficient and high-quality well logging re-evaluation of old wells in mature oilfields.

Keyword: well logging; hydrocarbon bearing formation identification; knowledge graph; graph embedding technique; intelligent identification; neural network
0 引言

在油气勘探、生产和储气库建设等油气上游业务各个环节中, 所产生的地质、油气藏、地震、钻井、测井、录井和生产动态等资料数据既相互关联又相互独立, 涉及众多专业的海量原始数据和成果均是油公司的重要资产, 科学利用好这些多源、异构且海量数据的意义重大, 但其技术挑战非常大, 迫切需要研发新技术新方法以高效挖掘其所蕴含的巨大价值。随着现代云计算、大数据和深度学习[1]等新一代信息新技术的迅猛发展, 相继研发形成了一批基于智能计算的油气大数据应用场景, 如智能地震资料处理解释技术[2, 3, 4]、智能注水技术[5, 6]以及智能油藏分析[7, 8]等, 充分体现了数据深度挖掘的价值与潜力, 并推动了传统业务流程重构与工作方式变革[9]。

测井资料采集于钻探过程中的随钻测井、下入套管前的裸眼井测井和下套管后生产测井, 涉及电学、声学、核学和光学等井下地层的地球物理数据, 可量化表征常规油气的“ 四性关系” （岩性、物性、电性和含油气性）和非常规油气的“ 七性关系” （岩性、物性、电性、含油气性、烃源岩特性、脆性和地应力各向异性）[10], 并定量评价井筒固井质量和套管技术状况。测井数据丰富, 精度高, 存储较为规范, 是油气上游业务中数据挖掘极为重要的信息来源。近几年来, 国内外学者着手研究测井数据的智能应用以挖掘其所蕴含的价值。据统计, 2015— 2020年间国际岩石物理学家与测井分析家学会（SPWLA）年度论文中, 测井数据智能研究方面的论文数占比逐年增大, 2015— 2017年、2018年、2019年和2020年的占比分别为小于1.00%, 3.28%, 15.79%, 16.35%, 并取得了若干长足进展, 研发出一些测井解释智能评价方法及其应用场景, 如提取常规测井敏感参数并以贝叶斯（Bayes）判别分析划分地层结构[11], 构建测井深度神经网络模型识别岩性[12, 13], 基于长短期记忆神经网络设计地层识别分类器模型自动解释随钻测井的地层倾角[14], 通过机器学习算法构建含气饱和度预测模型[15], 建立随钻测井电磁波电阻率精细反演模型以改善储集层地质导向效果和地层建模精度[16], 采用井震结合机器学习方法预测油气产能[17], 以及通过深度学习提高复杂岩性的测井自动解释可靠性[18], 并且通过大数据的智能解释模型和传统专业软件的集成, 初步搭建了测井智能解释环境[19]。然而, 统观这些评价方法及其应用场景, 均存在着以下3方面的共性问题：①基于数据驱动下的机器学习未能利用地质和测井等专业专家知识, 其输出结果的可解释性和泛化能力较差; ②过度依赖已知数据信息的数量, 要求成千上万的训练样本, 显然油气层测井识别工作中难以达到此要求, 同时鲁棒性问题难以解决; ③对于测井工作中最为核心的油气层识别则研究深度不够, 公开文献检索表明, 其中采用的方法绝大多数为BP神经网络和模糊算法等机器学习方法[20, 21, 22, 23], 这些方法难以准确描述油水分布复杂的低孔低渗等复杂油气藏的测井特征以及准确识别所应采用的知识系统, 如测井、录井、岩心和地质特征等。

为解决上述问题, 应大力创新发展知识图谱驱动的油气层测井智能识别技术[24]。当前, 人工智能技术已发展进入第三代[25], 即融合第一代的知识驱动技术和第二代的数据驱动技术的人工智能, 针对知识、数据、算法和算力等4个要素建立新的可解释和鲁棒的人工智能理论与方法, 其核心是知识图谱的构建。知识图谱在大数据分析、智能推荐以及可解释人工智能等方面具有强大优势[26, 27, 28], 可以充分利用地质和测井等专业专家知识、规避鲁棒性问题、提高油气层识别准确性。总之, 基于专家知识的知识图谱技术是油气层测井智能识别和规模化老井再评价所应着重研究并尽早突破的关键技术。

1 油气层知识图谱构建

知识图谱的构建主要包括本体构建、知识获取、知识融合、知识存储及知识应用5个部分。油气层测井知识图谱的构建应遵从业务驱动设计的原则, 针对不同类型油气藏的特点, 融合油气藏勘探、评价和开发过程中所积累的大量测井、录井、试油、钻井、地震和生产动态等多源结构化数据以及研究报告、文献和多媒体等非结构化资料, 以盆地、油气田、区块和油气藏为主线而构建, 由知识体系分类、本体模型构建、命名实体识别、关系抽取、知识融合以及知识图谱生成等部分组成。本文以鄂尔多斯盆地姬塬区块三叠系延长组长6段为例构建测井知识图谱, 建立快速准确的油气层识别知识推理机制, 探索基于知识图谱的油气层智能识别方法与技术。

1.1 知识体系分类

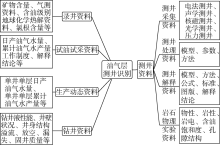
知识体系分类是构建知识图谱、实现知识管理的基础。聚焦于油气层识别, 提出了与之相关的知识体系分类（见图1）, 其中, 一级分类包括测井资料、录井资料、试油试采资料、生产动态资料和钻井资料等5个方面, 每个一级类型由若干个二级类型组成, 如测井资料可分为测井采集资料、测井处理资料、测井解释资料和岩石物理实验分析资料等4个二级类型, 二级类型还进一步细分出三级类型, 如测井采集资料包括电法测井、声学测井、核学测井、光学测井和压力测井等5个三级类型, 并可按需进一步细分出四级类型和五级类型等。

图1 油气层测井识别的知识体系分类

1.2 本体构建

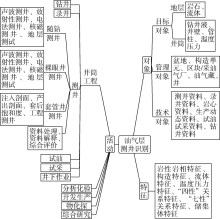
本体构建是测井知识图谱构建的基础, 由对象、活动和特征等3部分组成[29], 活动作用于对象, 特征用于描述活动和对象。最基本的本体包括概念、概念层次、属性、属性值类型、关系、关系定义域概念集以及关系值域概念集, 可采用自顶向下和自底向上相结合的方法构建。基于油气层测井识别所涉及的业务流程、数据集以及技术需求, 本文提出了以对象、活动和特征为基础的知识图谱本体构建方法（见图2）。

图2 油气层本体结构描述图

①对象。由目标、管理和技术等3类对象组成。目标对象为油气层识别的研究对象, 包括着重研究的岩石、流体及其相互作用, 以及测井作业所必须依附的井筒及其环境。管理对象为管理这些目标对象所需要的数据属性, 技术对象则是目标对象所产生的与油气层识别密切相关的数据体。

②活动。梳理油气勘探开发过程中与油气层识别相关联的主要生产活动并对其进行归纳分析, 抽象映射出衍生关系, 即“ 活动” 由井筒工程、分析化验、开发生产、物化探和综合研究等5个方面组成, 其主线活动为井筒工程中的测井, 而测井活动包括随钻测井、裸眼井测井、套管井测井、测井资料处理、测井资料解释以及测井综合评价等。

③特征。“ 特征” 是油气层的“ 生物标签” , 是测井识别不同类型油气层的根本属性。由于储集层、岩性以及油气水系统等多重复杂因素的共同作用, 测井响应特征复杂, 油气层识别并不容易。为了提高油气层识别的准确性, 应全面掌握其“ 生物标签” , 为此, 将“ 特征” 界定为岩性岩相、构造、流体、温度压力、常规油气的“ 四性关系” 或非常规油气的“ 七性关系” 等不仅仅局限于测井本身的5个方面特征。

1.3 知识图谱构建

1.3.1 信息抽取

完成测井知识本体建模后, 即可对长6段多源异构的知识成果、经验认识及结构化数据进行深度知识抽取和管理, 主要包括命名实体识别、关系抽取、属性分类和属性值提取。

命名实体识别是信息抽取的基础, 其任务是从报告文本这个非结构数据中找到命名实体, 并标记其类型。本文采用基于自然语言处理技术结合人工修正的方式进行命名实体的识别, 主要识别提取区块、井、地层、储集层和测井曲线等实体并对其命名, 例如, 识别提取的“ H278井” 、“ 姬塬区块” 、“ 延长组” 、“ 长61亚段” 和“ 自然电位” 等名词可分别命名为“ 井” 、“ 区块” 、“ 地层” 、“ 储集层” 和“ 测井曲线” 等实体。

关系抽取则需要从文本中抽取两个或多个实体之间的语义关系。语义关系通常用于连接两个实体, 并与实体一起表达文本的主要含义。常见的关系抽取结果可用主谓宾（简称SPO, 即主Subject, 谓Predication, 宾Object）三元结构表示。例如, HH278井属于姬塬区块的关系可描述为：HH278, 属于, 姬塬区块; HH278井钻遇延长组的关系可描述为：HH278, 钻遇, 延长组; 延长组包含长61亚段的关系可描述为：延长组, 包含, 长61亚段。

属性一般是指实体的属性或组成实体的成分, 需根据知识的构成以及任务的目的提取并分类。对于储集层物性评价, 孔隙度和渗透率是其敏感参数, 故主要提取孔隙度和渗透率的分布范围与平均值等4类属性, 并以自然语言处理技术从岩心物性实验分析报告等文本中提取各层段的这4类属性值。由于这些属性在文本中常为用户评价的对象, 因此, 可称之为观点评价对象抽取（opinion target extraction）。通常, 抽取后具有相同语义的属性应进行归一化处理。

1.3.2 知识融合

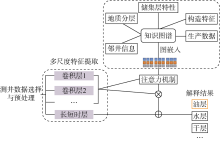
测井知识图谱的数据来源众多, 包括实验分析数据与报告、地层测试数据与报告、测井评价方法、测井处理知识（数据、方法与参数）、测井解释知识（图版、标准与报告）以及油气藏生产数据与研究报告等, 其命名规范、实体和属性的含义均存在一定差异, 为此, 在构建知识管理体系过程中, 为减小知识图谱的歧义, 参照中国石油勘探开发数据模型（EPDM）标准, 实现非结构化知识成果与结构化数据的融会贯通和深度融合。油气层测井知识的融合包括概念层和实体层的融合（见图3）, 概念层的融合主要是基于油气层测井识别本体的知识扩展, 实体层的融合则采用实体链接技术。首先, 以知识体系分类形成的测井体系知识为基础, 通过搜索引擎从各类数据源中选取候选实体; 随后, 应用有监督学习方法, 通过手工标注训练集来训练候选实体排序模型, 对候选实体进行梳理排序; 之后, 应用无监督学习方法, 基于无标签的语料库进行模型训练, 对候选实体进行修正扩展; 最后, 通过实体相似度算法完成实体层的融合。

图3 油气层测井知识融合处理框图

2 油气层智能识别新模型

考虑到油气层测井识别的样本数较少, 不足以称为大数据, 易于产生鲁棒性问题, 并且, 此项工作的专业性很强, 所用数据来源多、结构复杂, 专家知识要求高, 常用智能算法往往难以达到预期效果。为此, 本文在已构建的油气层测井知识图谱基础上, 提出了一种知识驱动的神经网络油气层识别评价模型— — KPNFE模型（Knowledge-Powered Neural Formation Evaluation Model）。KPNFE模型将测井知识图谱中实体、关系和属性（如邻井同层位的“ 四性关系” 等）以图嵌入技术（Graph Embedding）表征为向量形式, 通过所建立的神经网络模型实现油气层智能识别, 并进一步建立了潜力层推荐的指标体系与规则, 实现油气层的高效高质量识别。KPNFE模型主要由测井特征提取、图嵌入技术、网络结构和潜力层推荐方法与规则等部分组成, 具体论述如下。

2.1 测井特征参数提取

2.1.1 曲线多维特征参数提取

常规油气层“ 四性关系” 是测井数据多维特征最为专业化的描述, 结合目标区块的解释图版、解释标准、计算模型与模型参数等知识的引入, 可挖掘这些曲线多维度特征, 主要为曲线的数值特征（最大值、最小值、均值和中位数等）、形态特征（方差、标准差和基线偏移度等）及曲线之间组合关系特征（见表1）。物性参数预测曲线选择包括SP、GR、dh、Δ t、ϕ CNL和ρ , 油气层识别所用曲线还包括RLLD、RLLS、RILD和RILM等。

表1 测井曲线特征参数提取

2.1.2 知识特征参数提取

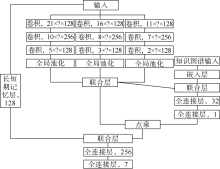
基于以下两点假设, KPNFE模型采用深度学习技术自动提取测井数据的多属性多尺度特征（见图4）。①假定同一口井同一层位的储集层特征具有相似性。基于此假设, 通过卷积神经网络自动提取测井曲线形态和数值, 通过长短期记忆神经网络学习测井曲线纵向（深度方向）上的关联特征, 最后通过联合模型实现多尺度特征的融合。②假定平面上同一层位的邻井特征（储集层特征、生产特征等）具有相似性。基于此假设, 应用已建知识图谱所包括的区块地质特征、邻井特征和储集层特性等知识, 将知识图谱与深度神经网络有机结合建立学习模型, 实现地层横向特征的提取。③基于知识图谱的分布式表征模型, 将图谱中邻井信息、地质分层、生产数据、构造特征和储集层特性等知识进行向量化, 实现知识的数值化表征。

图4 KPNFE模型的油气层多尺度特征提取原理图

2.2 图嵌入技术

图嵌入（Graph Embedding）是一种将图数据（通常为高维稠密的矩阵）映射为低维稠密向量的过程, 能够很好地解决图数据难以高效输入机器学习算法的问题。

KPNFE模型应用的数据众多, 类型多样, 包括纵向剖面上的逐深度点测井数据、逐层分层数据以及相关的录井、实验分析和地层测试等方面的数据与报告, 横向上的井筒、构造特征与油气分布等数据与报告。快捷准确地建立这些庞大且异构数据间的空间关联关系是机器学习算法研究的关键基础。

一般以图数据形式描述复杂数据间的空间关联关系, 图由边和节点组成, 可采用|V|× |V|（其中|V|表示图中节点的个数）邻接矩阵构建节点间的关联关系, 显然, KPNFE模型中图数据的节点数非常多, 如采用邻接矩阵算法则对算力要求很高。为此, KPNFE模型应用图嵌入技术实现图数据从高维特征映射为低维特征, 以达到将其高效输入至机器学习算法中的目的。

2.3 模型网络结构

KPNFE模型的神经网络结构如图5所示, 通过卷积层提取单条曲线和多条曲线的测井数值和形态特征, 长短期记忆（LSTM）层上提取曲线纵向采样点的关联特征, 然后, 通过嵌入层对知识图谱的知识特征和深度学习提取的特征进行嵌入与融合, 最后, 通过全连接层实现油气层智能识别。

图5 KPNFE模型的神经网络结构图

图5中, 卷积的操作可表示为：

${{y}^{j}}=\max \left( 0, {{b}^{j}}+\sum\nolimits_{i}{{{k}^{ij}}}* {{x}^{i}} \right)$ （1）

上式中, * 表示卷积运算。所有隐含层的单元均采用线性整流函数（ReLU）进行激活。

对每个特征图采用平均池化层进行特征降维。池化层的操作可表示为：

$y_{a, d}^{c}=\underset{0\le m, n\le s}{\mathop{\text{mean}}}\, \left\{ x_{a+s+m, d+s+n}^{c} \right\}$ （2）

嵌入层的操作可表示为：

$Y=X{{W}_{\text{emb}}}W+B$ （3）

联合（Concatenate）层的操作可表示为：

${{E}_{f, g+h}}=\text{Concatenate}\left( {{E}_{f, g}}, {{E}_{f, h}} \right)$, 即：

$\left( \begin{matrix} x_{11}^{1} \\ \vdots \\ x_{m1}^{1} \\ \end{matrix}\ \ \begin{matrix} \cdots \\ \ddots \\ \cdots \\ \end{matrix}\ \ \begin{matrix} x_{1n}^{1} \\ \vdots \\ x_{mn}^{1} \\ \end{matrix}\ \ \begin{matrix} x_{11}^{2} \\ \vdots \\ x_{m1}^{2} \\ \end{matrix}\ \ \begin{matrix} \cdots \\ \ddots \\ \cdots \\ \end{matrix}\ \ \begin{matrix} x_{1k}^{2} \\ \vdots \\ x_{mk}^{2} \\ \end{matrix} \right)=\left( \begin{matrix} x_{11}^{1} \\ \vdots \\ x_{m1}^{1} \\ \end{matrix}\ \ \begin{matrix} \cdots \\ \ddots \\ \cdots \\ \end{matrix}\ \ \begin{matrix} x_{1n}^{1} \\ \vdots \\ x_{mn}^{1} \\ \end{matrix} \right)+\left( \begin{matrix} x_{11}^{2} \\ \vdots \\ x_{m1}^{2} \\ \end{matrix}\ \ \begin{matrix} \cdots \\ \ddots \\ \cdots \\ \end{matrix}\ \ \begin{matrix} x_{1k}^{2} \\ \vdots \\ x_{mk}^{2} \\ \end{matrix} \right)$ （4）

将知识图谱的知识表征向量通过嵌入层进行编码, 然后与特征图通过联合层进行融合。

全连接层操作可表示为：

${{y}_{p}}=\max \left( 0, \sum{{{x}_{p}}* {{w}_{p, q}}+{{b}_{q}}} \right)$ （5）

最后网络的输出为n个输出的预测值：

${{y}_{s}}=\frac{\exp \left( {{{{y}'}}_{r}} \right)}{\sum\nolimits_{r=1}^{n}{\exp \left( {{{{y}'}}_{r}} \right)}}$ （6）

2.4 潜力层推荐

对区块上若干井进行油气层识别后, 可发现诸多油气层, 但这些层的置信度不尽相同。实际生产中, 需优选出其中最佳者（潜力层）作为措施作业层, 从而提高措施成功率, 提高措施作业的投入产出比。为此, 需确定潜力层的推荐规则, 即建立评价指标体系。指标体系是一个有机整体, 需全面反映潜力层的主要特征, 并能体现该系统的发展潜力和趋势。本文采用决策树分析法建立潜力层推荐综合评价模型, 计算所有油气层的期望值, 从中优选出潜力层。

2.4.1 评价指标体系构建

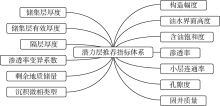
基于测井知识图谱的丰富区块知识, 可高效组织钻井、录井、测井、试油试采、生产等结构化数据以及单井测井评价报告、井史资料、井筒状况资料以及区块地质和油气藏综合研究成果等非结构化数据, 并分析这些数据间的相关性, 从中筛选潜力层评价的最优指标（见图6）, 进而构建形成完整的评价指标体系。

图6 潜力层推荐评价指标体系

2.4.2 推荐算法与规则

基于传统的层次分析法, 对采用标度法标注的数据进行计算, 并对多个业务专家所给评价指标进行两两比较, 各自得出判断矩阵, 以此为量化依据并推导出指标体系中各指标的权重, 具体步骤如下：

①通过三角模糊数构造的模糊矩阵以判断各指标重要程度, 三角模糊矩阵可表达为：

$M={{\left( {{m}_{uv}} \right)}_{n\times n}}$ （7）

其中, 三角模糊矩阵的元素计算公式如下：

${{m}_{uv}}=\left( r_{uv}^{1}+r_{uv}^{2}+\cdots +r_{uv}^{t} \right)\otimes 1/N$

②构建模糊判断因子矩阵E：

$E=\left( {{e}_{uv}} \right)=\left( \begin{matrix} 1 & 1-\frac{{{z}_{12}}-{{l}_{12}}}{2{{m}_{12}}} & \cdots & 1-\frac{{{z}_{1n}}-{{l}_{1n}}}{2{{m}_{1n}}} \\ 1-\frac{{{z}_{21}}-{{l}_{21}}}{2{{m}_{21}}} & 1 & \cdots & 1-\frac{{{z}_{2n}}-{{l}_{2n}}}{2{{m}_{2n}}} \\ \vdots & \vdots & \vdots & \vdots \\ 1-\frac{{{z}_{n1}}-{{l}_{n1}}}{2{{m}_{n1}}} & 1-\frac{{{z}_{n2}}-{{l}_{n2}}}{2{{m}_{n2}}} & \cdots & 1 \\ \end{matrix} \right)$ （8）

式中, 令：

${{s}_{uv}}={\left( {{z}_{uv}}-{{l}_{uv}} \right)}/{2{{m}_{uv}}}\; $

suv反映了专家评判的模糊程度, 数值越大, 表明该专家评判结果的模糊程度越大, 可信度越小。

③计算调整判断矩阵Q。

$Q=M\times E=\left( \begin{matrix} {{m}_{11}} & {{m}_{12}} & \cdots & {{m}_{1n}} \\ {{m}_{21}} & {{m}_{22}} & \cdots & {{m}_{2n}} \\ \vdots & \vdots & \vdots & \vdots \\ {{m}_{n1}} & {{m}_{n2}} & \cdots & {{m}_{nn}} \\ \end{matrix} \right)\left( \begin{matrix} 1 & 1-\frac{{{z}_{12}}-{{l}_{12}}}{2{{m}_{12}}} & \cdots & 1-\frac{{{z}_{1n}}-{{l}_{1n}}}{2{{m}_{1n}}} \\ 1-\frac{{{z}_{21}}-{{l}_{21}}}{2{{m}_{21}}} & 1 & \cdots & 1-\frac{{{z}_{2n}}-{{l}_{2n}}}{2{{m}_{2n}}} \\ \vdots & \vdots & \vdots & \vdots \\ 1-\frac{{{z}_{n1}}-{{l}_{n1}}}{2{{m}_{n1}}} & 1-\frac{{{z}_{n2}}-{{l}_{n2}}}{2{{m}_{n2}}} & \cdots & 1 \\ \end{matrix} \right)$ （9）

④利用方根法计算各指标的权重并进行单层排序。

⑤根据各单层的排序结果, 计算各指标的权重集合${{W}_{nb}}=\left( {{\theta }_{1}}, {{\theta }_{2}}, \cdots , {{\theta }_{m}} \right)$, 并进行综合排序。

⑥通过决策树分析法获得潜力层推荐综合评价模型, 计算所有潜力层的期望值, 从而获得最优目标。

3 应用实例及效果

以鄂尔多斯盆地姬塬区块三叠系延长组长6段低孔低渗地层为例, 通过验证样本集和试油层的油气层识别准确性以及潜力层推荐的可靠性等分析模型的生产应用效果及其适应性。

3.1 验证集的识别效果

以钻遇长6段储集层的547口井为整个数据样本集, 随机选取其中80%的井作为训练集, 20%的井作为验证集。所用数据包括测井曲线、实验分析、录井、试油、地质分层和测井解释成果等, 其中测井曲线包括Δ t、ρ 、ϕ CNL、GR、SP、dh、Rt、R10、R20、R30、R60和R90等12条, 测井解释成果为油层、差油层、油水同层、水层和干层等5类, 训练集的样本数量分别为154层、62层、18层、340层和1512层, 以此构建KPNFE模型的知识图谱。采用人工智能的准确率（Precision Rate）、召回率（Recall Rate）和F1值等3个指标量化评价KPNFE模型的训练效果。与专家解释结果对比表明, 验证集的模型预测准确率为94.4%、召回率为80.1%, F1值为86.66%, 验证效果理想, 可满足姬塬区块长6段复杂油水分布低孔低渗油层识别的生产要求。由表2和表3可知：①油水同层的准确率（33.3%）和召回率（40.0%）均较低, 这主要因为油水同层的训练样本数太少, 仅18个, 无法从这些样本中提取油水同层与油层、差油层、水层之间的差异特征, 致使这4种类型流体识别不清, 解释结论混淆, 多解性强。②差油层的准确率为90.5%, 召回率为72.0%, 相比于油水同层, 识别效果有很大提升, 表明尽管差油层的训练样本数量少（仅62个）, 仍可获得高准确率, 超出设计预期。较低的召回率主要是将部分差油层识别为干层所致, 需进一步优选小样本条件下更好地描述差油层与干层间差异的特征参数及其评价方法。③油层训练样本数为154个, 仍属于小样本范畴, 其识别准确率和召回率都很高, 分别为90.5%和92.7%。④水层和干层的识别准确率分别为91.3%和98.7%, 召回率分别为97.7%和97.9%。

表2 验证集的专家解释与智能解释对比分析表
表3 验证集的专家解释与智能解释准确率、召回率及F1值对比

由上述分析知, 尽管准确率、召回率和F1值均与训练样本数密切相关, 但是, 当训练样本数为50~100, KPNFE模型可获得较高的预测准确率; 当训练样本数为100~150, KPNFE模型即可保证高准确率和高召回率。显然, KPNFE模型所需最低样本数远低于其他深度学习算法, 可基本解决样本数为50~100、完全解决样本数为100~150的小样本所致的鲁棒性问题。另外, 由表3可知, 不同解释结论的训练样本数不均衡性十分严重, 基于数据驱动的机器学习算法对此十分棘手且难以克服, 但KPNFE模型却很好地解决了此问题。

借助于KPNFE模型, 智能解释的时效性提升显著。一般地, 目前每口探井解释需5个人天, 开发井解释需3个人天, 100口井区块的老井复查需100个人天左右的工作量。如采用KPNFE模型智能油气层识别技术, 在不降低甚至提高解释质量的前提下, 一口井的测井解释平均用时为10 min, 100口井的老井复查仅需24 h左右, 生产效率提升了百倍以上。

3.2 油层识别效果

应用所构建的测井知识图谱和KPNFE模型, 分析姬塬区块长6段验证集的所有井（109口）试油层的油层识别效果。

HX1井2 248.5~2 251.5 m井段, 一次测井解释结果为油水同层, 智能解释结果为油层（见图7）, 该井2248~2 252 m井段试油测试, 获日产油5.78 m3, 日产水1.02 m3, 含水率为15%, 对照中国石油天然气集团有限公司企业标准（以下简称企业标准）[30], 判定该层为油层, 与智能解释结论相一致。之所以出现这种情况, 是因为在智能解释中, 全局性地吸纳了井点构造特征、砂体连通性、储集层特征以及邻井H28井同一层位的测井响应特征与解释结论等知识, 并将其融入至KPNFE模型中, 综合考虑的因素多, 因而, 准确识别油层的能力强。而且, 测井曲线特征表明, 47号层与其下的48号层的“ 四性关系” 存在一定差异, 即物性较好, 岩性较纯, 电阻率较高, 专家解释也判断其含油性较好。由此可见, KPNFE模型的解释结果准确率较高, 其解释结论能够与专家测井解释结果吻合, 可解释性好。

图7 HX1井的一次解释与智能解释的结论对比图

系统分析姬塬区块长6段所有试油层, 并采用企业标准[30]的测井解释判定标准, 一次解释的符合率为71.88%, 智能解释符合率84.38%, 详见表4、表5。由表4可见, 一次解释的失误主要为油层与水层的误判, 5个水层解释为油层, 表现出高解释（解释结论较试油结论偏向含油性好或储集层物性好的方向）特点, 据此解释选择试油层段则将产生无效试油工作量; 3个油层解释为水层, 出现低解释（解释结论较试油结论偏向含油性差或储集层物性差的方向）, 漏失掉油层, 情况严重。相比而言, 表5的智能解释中, 无效试油工作量减少了2.5倍, 油层漏失率降低了1/3, 解释质量明显得到提升。

表4 验证集的试油结论与一次解释对比表
表5 验证集的试油结论与智能解释对比表
3.3 潜力层推荐

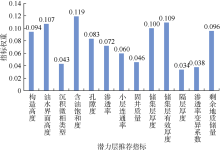
根据专家对各推荐指标重要性所给出的评价值, 以（7）— （9）式计算模糊算法的指标权重系数（见图8）。潜力层推荐评价中, 具体采用哪些指标应根据数据样本具体情况确定。由于未收集到剩余地质储量、沉积微相类型和隔层厚度等指标所对应的有效数据, 本文计算潜力层期望值时对其未做考虑。

图8 潜力层推荐的各评价指标权系数

基于油气层解释识别结果, 应用KPNFE模型的潜力层推荐评价结果, 计算验证集所有109口井潜力层（即不含已解释的、已生产动用的和已测试的油气层和可能油气层）的期望值, 对其排序优选出优先实施措施作业的层（见表6）。由表6可见, H14井和H35井的期望值最大, 为其他潜力层的对标层, 应优先实施试油, 将油气潜力转化为油气产量和储量。

表6 潜力层排序表

图9为H14井的测井解释成果图, 自然伽马曲线指示地层岩性较纯, 自然电位曲线指示储集层的渗透性较好, 3条孔隙度曲线间一致性较好, 上述均反映储集层物性较好且泥质含量低。另外, 录井（其与测井曲线间存在约2 m的深度误差）油气显示为油斑级, 因此, 其潜力层指标高, 即使专家解释结论也是很好的潜力层。由此进一步说明, KPNFE模型所推荐的潜力层可解释性好, 解释结果可信度高, 可较好地用于指导生产, 这是KPNFE模型的优势之一, 明显有别于数据驱动的人工智能技术。

图9 H14井潜力层解释成果图

4 结论

采用有别于常规数据驱动智能分析的技术方法, 在所创建的油气层测井识别知识图谱基础上, 提出了油气行业首个知识驱动的神经网络油气层评价模型（KPNFE）, 该模型既实现了专家知识的有效传承, 又可促进油气层的高效高质量识别。鄂尔多斯盆地姬塬区块长6段储集层应用实例表明, KPNFE模型的应用效果十分理想, 相比于一次解释结果, 模型解释符合率提高了13个百分点, 工作时效提高了100倍以上。另外, 基于知识图谱的油气层测井智能识别KPNFE模型还具有以下3方面的显著优势。①知识图谱集成与之密切关联的多源异构数据的实体信息, 并将其融合于一体, 借助深度学习算法、智能识别模型与知识推理机制, 实现了大批量井的油气层智能解释, 快速发现并挖掘知识的价值, 大大提高了解释工作效率, 又提高了解释质量与符合率。②借助于专家知识所构建的知识图谱可为非专家级技术人员应用, 降低了专业知识深入应用的技术门槛, 使非专家级技术人员亦可完成达到专家级工作质量的解释工作, 这对于在中国量大面广的老油气区中滚动勘探发现新储量与稳产增效均具有十分重要意义。③较好地解决了小样本问题, 识别结果鲁棒性好, 可解释性强, 为老井再评价挖潜工作, 以及评价和开发区块新井解释提供了强有力技术支撑。

需要指出的是, 尽管测井知识图谱可以广泛应用, 但目前仍然存在3方面的技术挑战。①针对不同类型油气藏以及不同资料基础, 需针对性地建立一系列知识图谱, 其中至关重要的决定因素是测井业务专家与计算机智能专家的紧密结合; ②KPNFE模型尚未在图谱与算法中考虑油藏人工研究认识过程中建立的一系列行之有效的测井油水层识别图版与解释标准; ③成像测井和扫描测井等新技术已全面推广应用, 是解决复杂油气藏测井评价疑难问题的关键资料, 而基于曲线特征提取的知识图谱构建方法如何融入这些新技术所蕴含的多维度阵列化信息还有待后续深化研究。

符号注释：

B— — 偏置矩阵; bj— — 第j个特征矩阵的偏置项; bq— — 第q个神经元的偏置; c— — 输入特征值的索引; d— — 特征值的列索引; dh— — 井径, cm; E— — 模糊判断因子矩阵; Ef, g— — f× g的输入矩阵; Ef, h— — f× h的输入矩阵; Ef, g+h— — 上一层的f× g矩阵与f× h矩阵的联合输出; euv— — 模糊判断因子矩阵E第u行、第v列元素; GR— — 自然伽马, API; i— — 输入特征矩阵的索引; j— — 输出特征矩阵的索引; k— — 联合矩阵索引; kij— — 第i个输入特征矩阵与第j个输出特征矩阵之间的卷积操作所使用的卷积核; K— — 绝对渗透率, 10-3 μ m2; luv— — 指标u与指标v之间专家评判结果的最小值; m— — 池化层矩阵的行索引; M— — 三角模糊矩阵; muv— — u行、v列三角模糊矩阵元素; n— — 池化层矩阵的列索引; N— — 专家个数; Q— — 判断矩阵; R4— — 4 m底部梯度电阻率, Ω · m; R10— — 探测深度为25.4 cm（10 in）的阵列感应电阻率, Ω · m; R20— — 探测深度为50.8 cm（20 in）的阵列感应电阻率, Ω · m; R30— — 探测深度为76.2 cm（30 in）的阵列感应电阻率, Ω · m; R60— — 探测深度为152.4 cm（60 in）的阵列感应电阻率, Ω · m; R90— — 探测深度为228.6 cm（90 in）的阵列感应电阻率, Ω · m; Rd— — 深电阻率, Ω · m; RILD— — 深感应电阻率, Ω · m; RILM— — 中感应电阻率, Ω · m; RLLD— — 深侧向电阻率, Ω · m; RLLS— — 浅侧向电阻率, Ω · m; Rs— — 浅电阻率, Ω · m; Rt— — 反演出的地层真电阻率, Ω · m; r— — 神经元的索引; rtuv— — 第t个专家的指标u与指标v的相对重要程度, 专家数为N; SP— — 自然电位, mV; s— — 池化运算的步长; suv— — 专家评判的模糊程度, 无因次; t— — 专家的索引; u— — 三角模糊矩阵行索引; v— — 三角模糊矩阵列索引; W— — 特征权重矩阵; Wemb— — 嵌入层权重矩阵; Wnb— — 权重集合; wp, q— — 第p个和第q个神经元间的权重; X— — 嵌入层的输入矩阵; xi— — 第i个输入知识特征; xp— — 第p个神经元的输入; xca+s+m, d+s+n— — 第c个输入特征矩阵的第a行、第d列特征值与维度为m× n的平均池化层矩阵进行步长为s的池化运算; Y— — 联合后输出; yj— — 第j个输出特征矩阵最大值; yp— — 全连接层第p个节点的输出; yq— — 第q个神经元的输出; ys— — 算法模型输出的第s个类别的概率值; yca, d— — 第c个输入、第a行、第d列池化后输出; y'r— — 第r个神经元的输出; zuv— — 指标u与指标v之间专家评判结果的最大值; ϕ — — 有效孔隙度, %; ϕ CNL— — 补偿中子孔隙度, %; θ i— — 第i个评价指标的权重; ρ — — 密度, g/cm3; Δ t— — 声波时差, μ s/m。

（编辑 黄昌武）

参考文献
[1] 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012.
LI Hang. Statistical method[M]. Beijing: Tsinghua University Press, 2012. [本文引用:1]
[2] 王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 421-433.
WANG Yuqing, LU Wenkai, LIU Jinlin, et al. Rand om seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 421-433. [本文引用:1]
[3] 周创, 居兴国, 李子昂, 等. 基于深度卷积生成对抗网络的地震初至拾取[J]. 石油物探, 2020, 59(5): 795-803.
ZHOU Chuang, JU Xingguo, LI Ziang, et al. A deep convolutional generative adversarial network for first-arrival pickup from seismic data[J]. Geophysical Prospecting for Petroleum, 2020, 59(5): 795-803. [本文引用:1]
[4] 陈芊澍, 文晓涛, 何健, 等. 基于极限学习机的裂缝带预测[J]. 石油物探, 2021, 60(1): 149-156, 174.
CHEN Qianshu, WEN Xiaotao, HE Jian, et al. Prediction of a fracture zone using an extreme learning machine[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 149-156, 174. [本文引用:1]
[5] 贾德利, 刘合, 张吉群, 等. 大数据驱动下的老油田精细注水优化方法[J]. 石油勘探与开发, 2020, 47(3): 629-636.
JIA Deli, LIU He, ZHANG Jiqun, et al. Data-driven optimization for fine water injection in a mature oil field[J]. Petroleum Exploration and Development, 2020, 47(3): 629-636. [本文引用:1]
[6] 刘合, 裴晓含, 贾德利, 等. 第四代分层注水技术内涵、应用与展望[J]. 石油勘探与开发, 2017, 44(4): 608-614, 637.
LIU He, PEI Xiaohan, JIA Deli, et al. Connotation, application and prospect of the fourth-generation separated layer water injection technology[J]. Petroleum Exploration and Development, 2017, 44(4): 608-614, 637. [本文引用:1]
[7] SHAHKARAMI A, MOHAGHEGH S. 智能代理在油藏建模中的应用[J]. 石油勘探与开发, 2020, 47(2): 372-382.
SHAHKARAMI A, MOHAGHEGH S. Applications of smart proxies for subsurface modeling[J]. Petroleum Exploration and Development, 2020, 47(2): 372-382. [本文引用:1]
[8] 王洪亮, 穆龙新, 时付更, 等. 基于循环神经网络的油田特高含水期产量预测方法[J]. 石油勘探与开发, 2020, 47(5): 1009-1015.
WANG Hongliang, MU Longxin, SHI Fugeng, et al. Production prediction at ultra-high water cut stage via Recurrent Neural Network[J]. Petroleum Exploration and Development, 2020, 47(5): 1009-1015. [本文引用:1]
[9] 匡立春, 刘合, 任义丽, 等. 人工智能在石油勘探开发领域的应用现状与发展趋势[J]. 石油勘探与开发, 2021, 48(1): 1-11.
KUANG Lichun, LIU He, REN Yili, et al. Application and development trend of artificial intelligence in petroleum exploration and development[J]. Petroleum Exploration and Development, 2021, 48(1): 1-11. [本文引用:1]
[10] 刘国强, 李长喜. 陆相致密油岩石物理特征与测井评价方法[M]. 北京: 科学出版社, 2019.
LIU Guoqiang, LI Changxi. Petrophysical characteristics and logging evaluation method of continental tight oil[M]. Beijing: Science Press, 2019. [本文引用:1]
[11] 石玉江, 张海涛, 周金昱, 等. 应用常规测井属性分析进行地层结构划分[J]. 测井技术, 2016, 40(4): 493-497.
SHI Yujiang, ZHANG Haitao, ZHOU Jinyu, et al. Division of formation structure using conventional logging attributes analysis[J]. Well Logging Technology, 2016, 40(4): 493-497. [本文引用:1]
[12] 安鹏, 曹丹平. 基于深度学习的测井岩性识别方法研究与应用[J]. 地球物理学进展, 2018, 33(3): 1029-1034.
AN Peng, CAO Danping. Research and application of logging lithology identification based on deep learning[J]. Progress in Geophysics, 2018, 33(3): 1029-1034. [本文引用:1]
[13] 李建国, 张卫东, 刘冠男. 深度学习在测井岩性识别中的应用[J]. 科技创新与应用, 2015(14): 21-22.
LI Jianguo, ZHANG Weidong, LIU Guannan. Application of deep learning in logging lithology identification[J]. Technology Innovation and Application, 2015(14): 21-22. [本文引用:1]
[14] 孙歧峰, 李娜, 段友祥, 等. 基于长短期记忆神经网络的随钻地层倾角解释方法[J]. 石油勘探与开发, 2021, 48(4): 843-850.
SUN Qifeng, LI Na, DUAN Youxiang, et al. Logging-while-drilling formation dip interpretation based on long short-term memory[J]. Petroleum Exploration and Development, 2021, 48(4): 843-850. [本文引用:1]
[15] ORUGANTI Y D, YUAN P, INANC F, et al. Role of machine learning in building models for gas saturation prediction[R]. Texas, USA: SPWLA, 2019. [本文引用:1]
[16] JIN Y C, WU X Q, CHEN J F, et al. Using a physics-driven deep neural network to solve inverse problems for LWD azimuthal resistivity measurements[R]. Texas, USA: SPWLA, 2019. [本文引用:1]
[17] FAROOQ U, AHMED J, ALI S, et al. Heterogeneity in the petrophysical properties of carbonate reservoirs in Tal block[R]. Texas, USA: SPWLA, 2019. [本文引用:1]
[18] PEYRET A P, AMBÍA J, TORRES-VERDÍN C, et al. Automatic interpretation of well logs with lithology-specific deep-learning methods[R]. Texas, USA: SPWLA, 2019. [本文引用:1]
[19] 石玉江, 刘国强, 钟吉彬, 等. 基于大数据的测井智能解释系统开发与应用[J]. 中国石油勘探, 2021, 26(2): 113-126.
SHI Yujiang, LIU Guoqiang, ZHONG Jibin, et al. Development and application of intelligent logging interpretation system based on big data[J]. China Petroleum Exploration, 2021, 26(2): 113-126. [本文引用:1]
[20] 邹文波. 人工智能研究现状及其在测井领域的应用[J]. 测井技术, 2020, 44(4): 323-328.
ZOU Wenbo. Artificial intelligence research status and applications in well logging[J]. Well Logging Technology, 2020, 44(4): 323-328. [本文引用:1]
[21] 陈清华, 程祥, 王晶, 等. 人工神经网络在闵北断块低阻油层识别上的应用[J]. 海洋地质前沿, 2015, 31(11): 52-57.
CHEN Qinghua, CHENG Xiang, WANG Jing, et al. Application of artificial neural network to identification of low resistivity reservoir in the north block of Minqiao oilfield[J]. Marine Geology Frontiers, 2015, 31(11): 52-57. [本文引用:1]
[22] 贺铎华. BP神经网络识别塔北低阻油气层[J]. 物探与化探, 2002, 26(2): 122-125.
HE Duohua. The application of BP neural network to recognition of the Tabei low resistivity oil and gas layers[J]. Geophysical and Geochemical Exploration, 2002, 26(2): 122-125. [本文引用:1]
[23] 王少龙, 杨斌, 赵倩, 等. BP神经网络在复杂储层流体识别中的应用[J]. 石油化工应用, 2018, 37(7): 45-48.
WANG Shaolong, YANG Bin, ZHAO Qian, et al. Application of BP neural network in recognition of complex reservoir fluids[J]. Petrochemical Industry Application, 2018, 37(7): 45-48. [本文引用:1]
[24] 刘国强. 非常规油气勘探测井评价技术的挑战与对策[J]. 石油勘探与开发, 2021, 48(5): 891-902.
LIU Guoqiang. Challenges and countermeasures of log evaluation in unconventional petroleum exploration[J]. Petroleum Exploration and Development, 2021, 48(5): 891-902. [本文引用:1]
[25] 张钹, 朱军, 苏航. 迈向第三代人工智能[J]. 中国科学(信息科学), 2020, 50(9): 1281-1302.
ZHANG Bo, ZHU Jun, SU Hang. Toward the third generation of artificial intelligence[J]. SCIENTIA SINICA Informationis, 2020, 50(9): 1281-1302. [本文引用:1]
[26] XIA L, WU B Y, LIU L X, et al. Question-answering using keyword entries in the oil & gas domain[R]. Shenyang: 2020 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), 2020. [本文引用:1]
[27] LI Z, WANG Z F, WEI Z C, et al. Cross-oilfield reservoir classification via multi-scale sensor knowledge transfer[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(5): 4215-4223. [本文引用:1]
[28] 梁琨, 任依梦, 尚余虎, 等. 深度学习驱动的知识追踪研究进展综述[J]. 计算机工程与应用, 2021, 57(21): 41-58.
LIANG Kun, REN Yimeng, SHANG Yuhu, et al. Review on research progress of deep learning driven knowledge tracking[J]. Computer Engineering and Applications, 2021, 57(21): 41-58. [本文引用:1]
[29] 周树理, 严建文, 包红林, 等. 石油勘探开发领域本体构建及应用[J]. 计算机系统应用, 2015, 24(5): 172-176.
ZHOU Shuli, YAN Jianwen, BAO Honglin, et al. Research and application of petroleum exploration and development domain-specific ontology construction[J]. Computer Systems & Applications, 2015, 24(5): 172-176. [本文引用:1]
[30] 中国石油天然气集团有限公司. 测井解释结论的认定与符合率统计规范: Q/SY 01459—2019[S]. 北京: 中国石油天然气集团有限公司标准化委员会勘探与生产专业标准化技术委员会, 2019.
China National Petroleum Corporation. Specification for defining and coincidence rate statistics of well logging interpretation conclusion: Q/SY 01459—2019[S]. Beijing: Exploration and Production Professional Stand ardization Technical Committee of Stand ardization Committee of CNPC, 2019. [本文引用:2]