第一作者简介:姜传隆(1996-),男,辽宁大连人,北京化工大学机电工程学院硕士研究生,主要从事随钻地层流体取样技术方面的研究工作。地址:北京市朝阳区北三环东路15号北京化工大学,邮政编码:100020。E-mail: 865978706@qq.com
提出以地面预充氮气方法为主、井下增压方法为辅的随钻取样保真筒的设计思路,对其工作方式、取样参数优化方法进行讨论。取样筒中氮气腔的作用相当于储能气垫,可在一定程度上补充取样过程中因温度变化带来的压力损失,井下增压则是将样品尽快地压入样品腔,并进一步提高样品压力来弥补氮气腔无法提供的压力补偿。通过对取样保真筒工作方式的分析,引入非理想气体状态方程,根据取样流体泡点压力是否已知、现场应急取样等情况,对预充氮气压力、井下增压量和取样体积等保真参数的优化取值进行了推导和计算,同时分析了地面温度对保真参数的影响并提出了相应的校正方法。研究表明,地面预充氮气与井下增压随钻取样保真筒,可有效提高样品保真程度,地层流体样品到达地面时,可基本保证样品不发生物理相变现象,进而保证其具有在地层中原有的化学组分。
A design idea of fidelity sampling cylinder while drilling based on surface nitrogen precharging and supplemented by downhole pressurization was proposed, and the working mode and optimization method of sampling parameters were explored. The nitrogen chamber in the sampling cylinder functions as an energy storage air cushion, which can supplement the pressure loss caused by temperature change in the sampling process to some extent. The downhole pressurization is to press the sample into the sample chamber as soon as possible, and further increase the pressure on sample to make up for the pressure that the nitrogen chamber cannot provide. Through analysis of the working mode of the sampling fidelity cylinder, the non-ideal gas state equation was used to deduce and calculate the optimal values of fidelity parameters such as pre-charged nitrogen pressure, downhole pressurization amount and sampling volume according to whether the bubble point pressure of the sampling fluid was known and on-site emergency sampling situation. Besides, the influences of ground temperature on fidelity parameters were analyzed, and corresponding correction methods were put forward. The research shows that the fidelity sampling cylinder while drilling can effectively improve the fidelity of the sample. When the formation fluid sample reaches the surface, it can basically ensure that the sample does not change in physical phase state and keeps the same chemical components in the underground formation.
随钻地层流体取样技术是在电缆式流体取样、随钻地层压力测试和地层流体分析等技术的基础上发展起来的, 可以在刚打开油气层时迅速收集低污染或无污染的地层流体, 获取的样品数据更贴近地层的真实情况, 可为优化完井和生产设计提供所需的关键参数[1, 2, 3, 4]。随钻地层流体取样工具中的取样筒对于实现样品“ 保真” 至关重要, 若取样筒没有采取任何保真措施, 取样筒中的地层流体样品从高温的井下环境到达地面后, 将因温度下降而体积收缩, 若样品的腔室体积不变, 则样品腔内压力会相应降低, 若下降至泡点压力以下, 样品中的溶解气将逸出, 在样品腔内形成油气两相, 相分离后整个样品将无法还原, 样品严重失真, 样品分析数据不再代表真实储集层的流体性质, 进而影响后续勘探、开发评价的准确性。
随钻地层流体取样技术研究, 国外已有20多年的历史, 而国内基本处于初级阶段[5, 6, 7, 8, 9, 10, 11, 12]。美国贝克休斯公司提出利用能量存储介质对地层流体样品增压, 其实为双活塞气垫增压法, 该方法可行且成熟。针对该种增压方法, 尤国平等[13]和谭显忠[14]在研制电缆取样器取样筒时, 提出了预充氮气的压力计算公式, 但该公式未考虑温度、压力对样品和筒体的影响; 刘健[15]在研究天然气水合物取样器的保压保真时, 提出了一种考虑温度场和压力场变化的容器内流体保压计算方法, 但这种取样器没有井下增压装置; 安莉[16]探讨了水合物保真筒的保压特性, 给出了气垫在增压情况下温度场-压力场的耦合特征, 进而描述了样品腔内流体压力的变化规律, 但保真筒在井下缺乏持续增压源, 应用受限。
目前常用的保真方法主要有井下增压泵与活塞气垫两种, 单纯用泵增压的方法因受泵容积的限制而未被业界广泛应用; 单纯用活塞气垫增压的方法虽能明显改善地层流体样品的保真度, 但现场应用时预充氮气压力依赖经验判断, 保真效果较差且使用不便。针对两种方法存在的局限性, 本文提出以地面预充氮气方法为主, 井下增压方法为辅的随钻取样保真筒设计思路, 并对其工作方式、取样参数优化方法进行讨论, 有望实现真正意义上的样品保真。
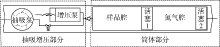
本文设计取样筒由样品腔和氮气腔构成, 中间由活塞1分隔, 同时外接抽吸泵、增压泵便于取样(见图1)。取样时, 地层流体通过抽吸泵与增压泵的共同作用从取样筒左端进入样品腔, 活塞1、活塞2的位置根据各腔室与井下压力的大小自动调节, 起压力平衡作用。
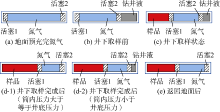
取样过程中, 样筒内各腔室的体积变化分可为5个过程(见图2):①地面预充氮气, 取样前在地面预先向氮气腔充氮气, 迫使活塞1、活塞2分别位于取样筒的两端, 此时氮气腔容积达到最大, 即筒体总容积, 筒体温度为地面温度(见图2a); ②井下取样前, 工具下至取样地层时, 钻井液柱压力高于预充氮气压力, 钻井液推动活塞2向左移动, 当氮气腔压力与钻井液柱压力达到平衡时停止移动, 此时氮气腔内压力等于此处钻井液柱压力, 温度为地层温度(见图2b); ③井下取样, 当抽吸的地层流体污染率达到取样要求时, 样品腔阀门打开, 流体通过增压泵进入样品腔推动活塞1向右移动, 此时氮气腔压力增高, 也推动活塞2向右移动, 逐步排出钻井液(见图2c); ④井下取样完成, 此时若筒内压力大于等于井底压力, 则活塞2位于筒体最右端(见图2d-1), 若筒内压力小于井底压力, 则活塞2离筒体最右端尚有一定距离(见图2d-2), 筒体右端存有钻井液; ⑤取样筒返回地面, 地面温度低于地下, 样筒到达地面后, 活塞2因失去钻井液柱压力而移动到筒体最右端, 样筒内样品压力下降, 此时活塞1向右移动, 氮气腔内压力起补偿作用, 确保取回样品不发生相变(见图2e)。
设取样筒内径为Di, 外径为D0, 取样筒体有效长度为L, 取样筒材料的弹性模量为E, 泊松比为μ , 线性膨胀系数为α , 井下取样体积为Vs; 地层压力为p, 大气压为p0, 井底增压量为pa; 地面预充氮气过程中氮气腔内状态为T1、V1、p1, 井下取样后氮气腔内状态为T2、V2、p2, 返回地面氮气腔内状态为T3、V3、p3, 返回地面时样品体积为Vs* , 对取样过程中取氧筒工况分述如下。
该过程中, 因压力变化引起取样筒容积膨胀, 可由弹性理论推导出筒体在内外压差作用下, 径向变化量为:
$\Delta {{D}_{\text{p}1-2}}=\frac{{{D}_{\text{i}}}{{p}_{\text{a}}}}{E\left( D_{0}^{2}-D_{\text{i}}^{\text{2}} \right)}\left[ D_{\text{i}}^{\text{2}}\left( 1-2\mu \right)+D_{0}^{2}\left( 1+\mu \right) \right]$ (1)
轴向变化量为:
$\Delta {{L}_{\text{p}1-2}}=\frac{D_{\text{i}}^{\text{2}}{{p}_{\text{a}}}L\left( 1-2\mu \right)}{E\left( D_{0}^{2}-D_{\text{i}}^{\text{2}} \right)}$ (2)
该过程中, 因温度变化引起取样筒容积膨胀, 可由线性膨胀系数公式可求得, 径向变化量为:
$\Delta {{D}_{\text{t}1-2}}=\alpha {{D}_{\text{i}}}\left( {{T}_{2}}-{{T}_{1}} \right)$ (3)
轴向变化量为:
$\Delta {{L}_{\text{t}1-2}}=\alpha L\left( {{T}_{2}}-{{T}_{1}} \right)$ (4)
由于温度和压力变化, 此时筒体内径为:
$D_{\text{i1}-\text{2}}^{\text{* }}={{D}_{\text{i}}}+\Delta {{D}_{\text{p}1-2}}+\Delta {{D}_{\text{t}1-2}}$ (5)
筒体外径为:
$D_{0}^{* }={{D}_{0}}+\Delta {{D}_{\text{p}1-2}}+\Delta {{D}_{\text{t}1-2}}$ (6)
筒体长度为:
$L_{1-2}^{* }=L+\Delta {{L}_{\text{p}1-2}}+\Delta {{L}_{\text{t}1-2}}$ (7)
筒体体积为:
${{V}_{1-2}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}D{{_{\text{i}1-2}^{\text{* }}}^{2}}L_{1-2}^{* }$ (8)
该过程中, 因压力变化引起取样筒容积膨胀, 同样可由弹性理论推出筒体在内外压差作用下, 径向变化量为:
$\Delta {{D}_{\text{p}2-3}}=\frac{D_{\text{i1}-\text{2}}^{\text{* }}\left( {{p}_{3}}-{{p}_{\text{a}}} \right)}{E\left( D{{_{0}^{* }}^{2}}-D{{_{\text{i1}-\text{2}}^{\text{* }}}^{2}} \right)}\left[ D{{_{\text{i1}-\text{2}}^{\text{* }}}^{2}}\left( 1-2\mu \right)+D{{_{01-2}^{* }}^{2}}\left( 1+\mu \right) \right]$ (9)
轴向变化量为:
$\Delta {{L}_{\text{p}2-3}}=\frac{D{{_{\text{i1}-\text{2}}^{\text{* }}}^{2}}\left( {{p}_{3}}-{{p}_{\text{a}}} \right){{L}^{* }}\left( 1-2\mu \right)}{E\left( D{{_{0}^{* }}^{2}}-D{{_{\text{i1}-\text{2}}^{\text{* }}}^{\text{2}}} \right)}$ (10)
该过程中, 因温度变化引起的取样筒容积收缩, 径向变化量为:
$\Delta {{D}_{\text{t}2-3}}=\alpha D_{\text{i1}-\text{2}}^{\text{* }}\left( {{T}_{3}}-{{T}_{2}} \right)$ (11)
轴向变化量为:
$\Delta {{L}_{\text{t}2-3}}=\alpha {{L}^{* }}_{1-2}\left( {{T}_{3}}-{{T}_{2}} \right)$ (12)
由于温度和压力变化, 此时筒体内径为:
$D_{\text{i2}-\text{3}}^{\text{* }}=D_{\text{i}1-2}^{* }+\Delta {{D}_{\text{p}2-3}}+\Delta {{D}_{\text{t}2-3}}$ (13)
筒体长度为:
$L_{2-3}^{* }={{L}_{1-2}}^{* }+\Delta {{L}_{\text{p}2-3}}+\Delta {{L}_{\text{t}2-3}}$ (14)
筒体体积为:
${{V}_{2-3}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}D{{_{\text{i}2-3}^{* }}^{2}}L_{2-3}^{* }$ (15)
取样筒由井下上升到地面后, 温度降低将引起取样筒容积收缩, 这个过程样品体积也由大变小, 如此地面样品的实际压力有可能小于样品地面设计压力, 故不能忽略温度对样品保真的影响; 取样筒由井下上升到地面, 取样筒外压逐步下降, 样品体积膨胀, 样品内压上升。样品到达地面的压力略高于样品地面设计压力才不影响样品保真, 故样品内压上升有利于样品保真, 故此处忽略样品内压变化对样品保真的影响。
对取样筒来说, 可跨过中间过程, 重点考虑预充好氮气的开始状态和取样完成到达地面稳定后的结束状态, 该过程中筒体径向变化量为:
$\Delta {{D}_{\text{p}1-3}}=\frac{{{D}_{\text{i}}}{{p}_{3}}}{E\left( D_{0}^{2}-D_{\text{i}}^{\text{2}} \right)}\left[ D_{\text{i}}^{\text{2}}\left( 1-2\mu \right)+D_{0}^{2}\left( 1+\mu \right) \right]$ (16)
轴向变化量为:
$\Delta {{L}_{\text{p}1-3}}=\frac{D_{\text{i}}^{\text{2}}{{p}_{\text{3}}}L\left( 1-2\mu \right)}{E\left( D_{0}^{2}-D_{\text{i}}^{\text{2}} \right)}$ (17)
通常情况T1=T3, 故有:
$\Delta {{D}_{\text{t}1-3}}=\alpha {{D}_{\text{i}}}\left( {{T}_{3}}-{{T}_{1}} \right)=0$ (18)
$\Delta {{L}_{\text{t}1-3}}=\alpha L\left( {{T}_{3}}-{{T}_{1}} \right)=0$ (19)
故样筒最终尺寸变化的结果为:
$D_{\text{i2}-\text{3}}^{\text{* }}=D_{\text{i1}-\text{3}}^{\text{* }}=D_{\text{i}}^{{}}+\Delta D_{\text{p}1-3}^{{}}$ (20)
$L_{\text{2}-\text{3}}^{\text{* }}=L_{\text{1}-\text{3}}^{\text{* }}=L+\Delta L_{\text{p}1-3}^{{}}$ (21)
(16)与(1)式两端相除并整理得:
$\Delta D_{\text{p1}-\text{3}}^{{}}=\frac{{{p}_{3}}}{{{p}_{\text{a}}}}\Delta {{D}_{\text{p}1-2}}$ (22)
(17)与(2)式两端相除并整理得:
$\Delta L_{\text{p1}-\text{3}}^{{}}=\frac{{{p}_{3}}}{{{p}_{\text{a}}}}\Delta {{L}_{\text{p}1-2}}$ (23)
将(22)式代入(20)式, 得:
$D_{\text{i2}-\text{3}}^{\text{* }}={{D}_{\text{i}}}+\frac{{{p}_{3}}}{{{p}_{\text{a}}}}\Delta {{D}_{\text{p}1-2}}$ (24)
将(23)式代入(21)式, 得:
$L_{\text{2}-\text{3}}^{\text{* }}=L+\frac{{{p}_{3}}}{{{p}_{\text{a}}}}\Delta {{L}_{\text{p}1-2}}$ (25)
将(24)、(25)式代入(15)式, 得:
${{V}_{2-3}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}{{\left( {{D}_{\text{i}}}+\frac{{{p}_{3}}}{{{p}_{\text{a}}}}\Delta {{D}_{\text{p}1-2}} \right)}^{2}}\left( L+\frac{{{p}_{3}}}{{{p}_{\text{a}}}}\Delta {{L}_{\text{p}1-2}} \right)$ (26)
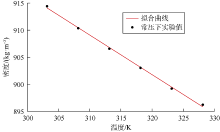
对原油样品来说, 原油密度与温度负相关[17], 如图3为常压下胜利油田某区块原油密度与温度的变化关系, 具有较好的线性关系, 经拟合可表示为:
$\rho \text{=}-A{{T}_{0}}+B$ (27)
其中A=0.73, B=1 135.66, 相关系数R2=0.998 3。
设地压力与钻井液柱压力近似相等, 钻井液密度为ρ df, 样品井下密度为ρ 2, 样品地面密度为ρ 3, 根据质量守恒, 样品腔中样品地面体积为:
$V_{\text{s}}^{* }=\frac{{{\rho }_{2}}{{V}_{\text{s}}}}{{{\rho }_{3}}}=\frac{\left( -A{{T}_{2}}+B \right){{V}_{\text{s}}}}{-A{{T}_{3}}+B}$ (28)
设地温梯度为G, 则:
${{T}_{2}}={{T}_{3}}+\frac{pG}{{{\rho }_{\text{df}}}g}$ (29)
(27)和(29)式中的A、B和G可根据取样区块的实际油藏参数确定。
当取样筒从井底返回地面, 样品体积变化量为:
$\Delta {{V}_{\text{s}}}={{V}_{\text{s}}}-V_{\text{s}}^{\text{* }}$ (30)
当没有氮气膨胀补偿时, 由样品体积收缩所致的样品腔内压差为:
$\Delta p=\frac{\Delta {{V}_{\text{s}}}}{{{V}_{\text{s}}}}{{E}_{0}}$ (31)
若无氮气膨胀补偿, 样品到达地面时样品腔内的压降较大, 引入氮气腔后, Δ Vs引起的压降基本由氮气腔来补偿。氮气非理想气体, 引入非理想气体状态方程描述氮气腔内氮气在地面预充、井下取样、取样返回地面3个时刻的状态:
$\frac{{{p}_{1}}{{V}_{1}}}{{{Z}_{1}}{{T}_{1}}}=\frac{{{p}_{2}}{{V}_{2}}}{{{Z}_{2}}{{T}_{2}}}=\frac{{{p}_{3}}{{V}_{3}}}{{{Z}_{3}}{{T}_{3}}}$ (32)
其中
${{V}_{1}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}D_{\text{i}}^{\text{2}}L$ (33)
${{V}_{2}}={{V}_{1-2}}-{{V}_{\text{s}}}-{{V}_{\text{df}}}$ (34)
${{V}_{3}}={{V}_{2-3}}-V_{\text{s}}^{\text{* }}$ (35)
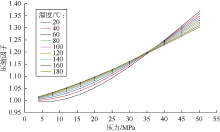
根据美国国家标准局发布的氮气在不同温度、压力下的压缩因子实验数据[18], 抽稀取99组数据绘制压缩因子与温度、压力的变化关系(见图4)。当压力大于10 MPa、温度20~180 ℃时, 压缩因子大于1; 当压力为5~35 MPa时, 温度越低, 压缩因子越低, 当压力大于35 MPa时, 温度越低, 压缩因子越高。
同样根据上述美国国家标准局发布的氮气压缩因子数据, 共取220组采用1stOpt软件进行拟合, 得氮气压缩因子与温度和压力的关系函数:
$Z=\frac{10.05{{T}^{-0.025}}{{p}^{1.512}}+9\ 998.9}{10\ 000}$ (36)
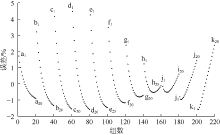
拟合公式计算值与查表值对比误差率散点分布如图5所示(图5中字母a, b, …, k分别代表压力为4, 8, 12, 16, 20, 25, 30, 35, 40, 45, 50 MPa, 共计11个; 下标1, 2, …, 20分别代表温度为10, 20, …, 200 ℃, 共20个)。可以看出, 相对于传统的查表计算, 拟合公式计算误差范围为-2%~5%, 可用于工程计算。
改写(32)式可得:
${{p}_{1}}=\frac{{{Z}_{1}}}{{{Z}_{3}}}{{p}_{3}}\frac{{{T}_{1}}{{V}_{3}}}{{{T}_{3}}{{V}_{1}}}$ (37)
${{p}_{2}}=\frac{{{Z}_{2}}}{{{Z}_{3}}}{{p}_{3}}\frac{{{T}_{2}}{{V}_{3}}}{{{T}_{3}}{{V}_{2}}}$ (38)
${{p}_{3}}=\frac{{{Z}_{3}}}{{{Z}_{1}}}{{p}_{1}}\frac{{{T}_{3}}{{V}_{1}}}{{{T}_{1}}{{V}_{3}}}$ (39)
在井底增压情况下有${{p}_{2}}=p+{{p}_{\alpha }}$, 代入(38)式得:
${{p}_{\text{a}}}=\frac{{{Z}_{2}}}{{{Z}_{3}}}{{p}_{3}}\frac{{{T}_{2}}{{V}_{3}}}{{{T}_{3}}{{V}_{2}}}-p$ (40)
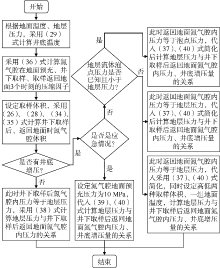
预充氮气压力(p1)与井底增压量(pa)参数的优化计算采用Matlab商业软件进行求解, 具体流程见图6。
在地层流体泡点压力未知的情况下, 最好的保真取样方式就是保证样品取到地面时的压力等于地层压力, 此时有${{p}_{3}}=p$, 该种情况下只需计算对应取样体积下的预充氮气压力和井底增压量, 由(37)、(40)式得:
${{p}_{1}}=\frac{{{Z}_{1}}}{{{Z}_{3}}}p\frac{{{T}_{1}}{{V}_{3}}}{{{T}_{3}}{{V}_{1}}}$ (41)
${{p}_{\text{a}}}=\frac{{{Z}_{2}}}{{{Z}_{3}}}p\frac{{{T}_{2}}{{V}_{3}}}{{{T}_{3}}{{V}_{2}}}-p$ (42)
下面以计算实例说明保真参数的优化过程。设取样筒内径28 mm, 外径36 mm, 保压容器原始有效长度850 mm, 取样筒材料(铍铜)弹性模量128 GPa, 泊松比0.3, 线性膨胀系数为17.6× 10-6 K-1, 井下可提供最大井底增压量20 MPa。钻井液密度1 100 kg/m3, 样品体积弹性模量1.67 GPa, 大气压力忽略不计。地面温度为293.15 K, (27)式中的线性拟合系数A=0.73, B=1 135.66, 地温梯度为3 ℃/100 m。
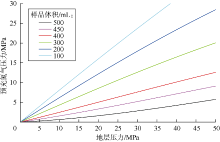
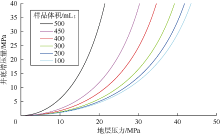
为了方便现场应用, 将取样体积分别取固定值500, 450, 400, 300, 200, 100 mL, 由(41)、(42)式计算预充氮气压力、井底增压量与地层压力关系曲线(见图7、图8)。可以看到, 相同取样体积条件下, 地层压力越高, 所需预充氮气压力越高, 所需提供的井底增压量越大。假设取样体积为400 mL, 地层压力为27.8 MPa, 查图可知, 此时预充氮气压力最大值为7 MPa, 井底增压量最小值为19 MPa。
若只预充氮气, 无井底增压, 则取样筒在井底时氮气腔压力与地层压力一致, 有p2=p, 代入(38)式可得井底样品返回地面时的压力(氮气腔压力):
${{p}_{3}}=\frac{{{Z}_{3}}}{{{Z}_{2}}}p\frac{{{T}_{3}}{{V}_{2}}}{{{T}_{2}}{{V}_{3}}}$ (43)
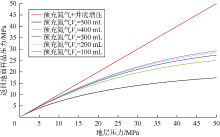
根据上式, 在不同取样体积条件下, 计算地层压力与返回地面样品压力的关系曲线, 并与相同条件下预充氮气+井底增压取样方式的计算结果对比(见图9, 图中不同取样体积条件下, 预充氮气+井底增压取样方式得到的样品腔压力与取样地层压力一致, 故图中仅以一条线代替)。可以看到, 无论取样体积为何值, 预充氮气+井底增压取样方式样品返回地面时的压力与地层压力均基本相等, 保真效果良好; 而无井底增压取样方式样品返回地面时的压力与地层压力存在较大差距, 且取样体积越大, 样品返回地面压力越小, 样品发生相变的可能越大, 说明仅预充氮气取样方式保真效果较差。
当地层压力小于泡点压力时, 取到地面的样品压力等于地层压力即可达到保真效果, 因此预充氮气压力与井底增压量的优化计算方法与地层流体泡点压力未知情况相同; 当地层压力大于泡点压力时, 则主要优化计算保证取到地面的样品压力等于泡点压力所需的预充氮气压力与井底增压量, 此时有p3=pb, 代入(37)、(40)式得:
${{p}_{1}}=\frac{{{Z}_{1}}}{{{Z}_{3}}}{{p}_{\text{b}}}\frac{{{T}_{1}}{{V}_{3}}}{{{T}_{3}}{{V}_{1}}}$ (44)
${{p}_{\text{a}}}=\frac{{{Z}_{2}}}{{{Z}_{3}}}{{p}_{\text{b}}}\frac{{{T}_{2}}{{V}_{3}}}{{{T}_{3}}{{V}_{2}}}-p$ (45)
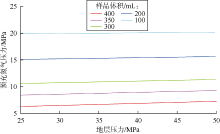
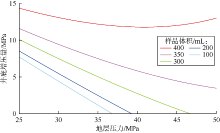
下面同样以计算实例说明保真参数的优化过程。采用前述取样筒、地层及流体等参数, 同时设地层流体泡点压力为25 MPa, 通过(44)、(45)式, 计算不同取样体积条件下预充氮气压力、井底增压量与地层压力的关系曲线(见图10、图11)。由图可知, 当地层压力大于25 MPa时, 预充氮气压力随地层压力增加而缓慢增加; 而井底增压量的变化趋势受地层压力、井下取样体积双重影响, 取样体积小于400 mL时, 井底增压量单调下调; 取样体积大于等于400 mL时, 井底增压量先下降后上升。由图10、图11, 在确定了取样体积时, 便可根据地层压力方便查得预充氮气压力、井底增压量。当取样体积为300 mL时, 如地层压力为42.5 MPa, 可查得预充氮气压力为11.1 MPa, 井底增压量为2.3 MPa; 当地层压力为50.0 MPa时, 可查得预充氮气压力为11.4 MPa, 井底增压量为0, 从曲线上可知, 当地层压力大于47.0 MPa时, 均无需井底增压, 此时取样筒右端如图2d-2所示, 存在钻井液。
向取样筒中预充定压氮气, 现场仅通过井下增压的方式来调节样品腔压力, 在一定的取样体积范围内, 若地层流体泡点压力已知, 则确保筒体中的样品压力到达地面时不小于泡点压力; 若地层流体泡点压力未知, 则确保筒体中的样品压力到达地面时不小于地层压力。
设预充氮气压力为10.0 MPa, 采用前述取样筒、地层及流体等参数, 通过(39)、(40)式计算不同取样体积条件下返回地面样品的压力、井底增压量与地层压力的关系曲线(见图12、图13)。当地层压力为25 MPa时, 如果要保证返回地面样品的压力大于或等于25 MPa, 则由图12可知取样体积必须大于等于350 mL; 由图12可知, 当井底增压能力上限为20 MPa时, 取样量为300, 350 mL可满足要求。根据图12、图13取样体积曲线的间距折算, 当取样体积为310~355 mL时, 地层样品到达地面时的压力不小于25 MPa, 可实现保真。
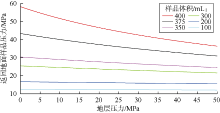
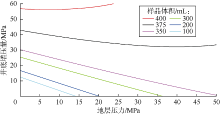
当地面温度发生变化时, 由(41)、(42)式可计算不同地面温度对预充氮气压力和井下增压量的影响。采用前述取样筒、地层及流体等参数, 分析取样体积分别为500, 100 mL时, 在不同地面温度下, 预充氮气压力、井底增压量与地层压力的关系曲线(见图14)。由图可以看出, 取样体积为500, 100 mL时, 地面温度的变化对预充氮气压力的影响甚微, 可以忽略不计。但地面温度对井底增压量有一定影响, 特别是取样体积较小时, 影响更明显, 地面温度下降, 井底增压量呈增加趋势。鉴于此, 当取样体积较大时(如大于等于500 mL), 优化计算的井底增压量误差较小, 无须校正; 当取样体积较小时(100~500 mL), 计算的井底增压量误差较大, 需适当进行较正:①地层压力小于12 MPa时, 无须校正; ②地层压力大于12 MPa时, 为保险起见, 需对优化计算的井底增压量进行校正, 可在计算值上再增加0~5 MPa。
地面预充氮气方法为主、井下增压方法为辅的随钻取样保真筒保真取样, 氮气腔相当于储能气垫, 可一定程度上补充取样过程中因温度变化带来的压力损失; 井下增压可将样品尽快地压入样品腔, 提高样品压力, 弥补氮气腔无法提供的压力补偿。
地面预充氮气与井下增压随钻取样保真筒, 可有效提高样品保真程度, 地层流体样品到达地面时, 可基本保证样品不发生物理相变现象, 进而保证其具有在地层中原有的化学组分。
符号注释:
A, B— — 线性拟合系数, 无因次; D0— — 取样筒外径, mm; Di— — 取样筒内径, mm; $D_{\text{i1-2}}^{\text{* }}$— — 地面预充氮气后到下入井下取样层段后的筒体内径, mm; $D_{\text{i1-3}}^{\text{* }}$— — 从预充好氮气到取样完成到达地面后的筒体内径, mm; $D_{\text{i2-3}}^{\text{* }}$— — 井下取样后上升到地面后的筒体内径, mm; $D_{\text{0 }}^{\text{* }}$— — 地面预充氮气后到下入井下取样层段后的筒体外径, mm; E— — 铍铜的弹性模量, MPa; E0— — 地层流体体积弹性模量, MPa; g— — 重力加速度, m/s2; G— — 地温梯度, ℃/100 m; L— — 取样筒体有效长度, mm; $L_{\text{1-2}}^{\text{* }}$— — 地面预充氮气后到下入井下取样层段时的筒体有效长度, mm; $L_{\text{1-3}}^{\text{* }}$— — 从预充好氮气到取样完成到达地面后的筒体有效长度, mm; $L_{\text{2-3}}^{\text{* }}$— — 井下取样后上升到地面后的筒体有效长度, mm; p— — 地层压力, MPa; p0— — 大气压, MPa; p1— — 预充氮气压力, MPa; p2— — 井下取样后氮气腔内压力, MPa; p3— — 返回地面氮气腔内压力, MPa; pb— — 泡点压力, MPa; pa— — 井底增压量, MPa; T— — 氮气环境温度, ℃; T0— — 原油环境温度, K; T1— — 地面温度, K; T2— — 井底温度, K; T3— — 样品返回地面温度, K; V1— — 地面预充氮气体积, mL; V1-2— — 地面预充氮气后下入到井下取样层段后的筒体体积, mL; V2— — 井下取样后氮气腔体积, mL; V2-3— — 井下取样后上升到地面时的筒体体积, mL; V3— — 返回地面时氮气腔体积, mL; Vdf— — 图2d-2所示情况下取样筒中活塞2右端进入的钻井液体积, mL; Vs— — 井下取样体积, mL; Vs* — — 返回地面时样品体积, mL; Z— — 氮气压缩因子, 无因次; Z1— — 地面预充氮气压缩因子, 无因次; Z2— — 井下取样后氮气压缩因子, 无因次; Z3— — 返回地面氮气压缩因子, 无因次; α — — 铍铜的线性膨胀系数, K-1; Δ Dp1-2— — 地面预充氮气后到下入井下取样层段过程中筒体在内外压差作用下径向变化量, mm; Δ Dp1-3— — 从预充好氮气到取样完成到达地面后的筒体在内外压差作用下径向变化量, mm; Δ Dp2-3— — 井下取样后上升到地面过程中筒体在内外压差作用下径向变化量, mm; Δ Dt1-2— — 地面预充氮气后到下入井下取样层段过程中因温度变化引起取样筒内径变化量, mm; Δ Dt1-3— — 从预充好氮气到取样完成到达地面的过程中因温度变化引起取样筒内径变化量, mm; Δ Dt2-3— — 井下取样后上升到地面过程中因温度变化引起取样筒内径变化量, mm; Δ Lp1-2— — 地面预充氮气后到下入井下取样层段过程中因压力变化引起取样筒有效长度变化量, mm; Δ Lp1-3— — 从预充好氮气到取样完成到达地面的过程中因温度变化引起取样筒有效长度变化量, mm; Δ Lp2-3— — 井下取样后上升到地面过程中筒体因压力变化引起取样筒有效长度变化量, mm; Δ Lt1-2— — 地面预充氮气后到下入井下取样层段过程中因温度变化引起取样筒有效长度变化量, mm; Δ Lt1-3— — 从预充好氮气到取样完成到达地面的过程中因温度变化引起取样筒有效长度变化量, mm; Δ Lt2-3— — 井下取样后上升到地面过程中因温度变化引起取样筒有效长度变化量, mm; Δ p— — 样品体积收缩所致的样品腔内压差, MPa; Δ Vs— — 样品体积变化量, mL; μ — — 泊松比, 无因次; ρ — — 原油密度, kg/m3; ρ 2— — 井下取样时样品密度, kg/m3; ρ 3— — 返回地面后样品密度, kg/m3; ρ df— — 钻井液密度, kg/m3。
(编辑 唐俊伟)
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|