引用本文
张东旭, 张烈辉, 唐慧莹, 赵玉龙. 致密油多级压裂水平井流-固全耦合产能数值模拟[J]. 石油勘探与开发, 2022,49(2): 338-347.
ZHANG Dongxu, ZHANG Liehui, TANG Huiying, ZHAO Yulong. Fully coupled fluid-solid productivity numerical simulation of multistage fractured horizontal well in tight oil reservoirs[J]. Petroleum Exploration & Development, 2022,49(2): 338-347.  
Doi: 10.11698/PED.2022.02.12
Permissions
Copyright©2022, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
致密油多级压裂水平井流-固全耦合产能数值模拟
张东旭, 张烈辉, 唐慧莹, 赵玉龙
西南石油大学油气藏地质及开发工程国家重点实验室,成都 610500
联系作者简介：赵玉龙（1986-）,男,湖北仙桃人,博士,西南石油大学研究员,主要从事非常规油气开发、数值模拟、试井分析等方面的教学与科研工作。地址：四川省成都市新都区新都大道8号,西南石油大学油气藏地质及开发工程国家重点实验室,邮政编码：610500。E-mail：373104686@qq.com

第一作者简介：张东旭（1992-）,男,四川宜宾人,西南石油大学在读博士研究生,主要从事非常规油气与增强型地热系统开发、数值模拟等方面的科研工作。地址：四川省成都市新都区新都大道8号,西南石油大学油气藏地质及开发工程国家重点实验室,邮政编码：610500。E-mail：ZhangDongxu1992@outlook.com

收稿日期: 2021-05-24 修回日期: 2022-02-10
基金项目: 国家科技重大专项课题“低渗-超低渗油藏提高储量动用关键工艺技术”（2017ZX05013-005）
摘要

基于多孔介质弹性理论与流-固耦合作用机理,建立了致密油储集层多重孔隙介质变形与流体流动的全耦合数学模型,采用有限元方法对模型进行数值求解并验证了模型的准确性。对致密油储集层多级压裂水平井进行产能数值模拟研究,结果表明：致密油井生产过程中近人工裂缝区域储集层物性大幅度降低,其中人工裂缝开度和人工裂缝导流能力损失幅度分别达到52.12%和89.02%;模拟致密油储集层水平井生产3 000 d,全耦合模型与未耦合模型的产能预测误差达38.30%,忽略流-固耦合效应的影响会使产能预测结果产生严重偏差;致密油储集层水平井产能对启动压力梯度最敏感,人工裂缝开度次之,提高人工裂缝初始导流能力有助于提高致密油井产能;压裂施工设计需考虑人工裂缝导流能力、间距、数量、长度的综合影响,片面追求增加裂缝条数无法取得预期的增产效果。

关键词: 致密油; 多重孔隙介质; 流-固全耦合; 水平井; 多级压裂; 油藏数值模拟; 产能预测
中图分类号:TE312 文献标志码:A
Fully coupled fluid-solid productivity numerical simulation of multistage fractured horizontal well in tight oil reservoirs
ZHANG Dongxu, ZHANG Liehui, TANG Huiying, ZHAO Yulong
State Key Laboratory of Oil & Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China
Abstract

A mathematical model, fully coupling multiple porous media deformation and fluid flow, was established based on the elastic theory of porous media and fluid-solid coupling mechanism in tight oil reservoirs. The finite element method was used to determine the numerical solution and the accuracy of the model was verified. On this basis, the model was used to simulate productivity of multistage fractured horizontal wells in tight oil reservoirs. The results show that during the production of tight oil wells, the reservoir region close to artificial fractures deteriorated in physical properties significantly, e.g. the aperture and conductivity of artificial fractures dropped by 52.12% and 89.02% respectively. The simulations of 3000-day production of a horizontal well in tight oil reservoir showed that the predicted productivity by the uncoupled model had an error of 38.30% from that by the fully-coupled model. Apparently, ignoring the influence of fluid-solid interaction effect led to serious deviations of the productivity prediction results. The productivity of horizontal well in tight oil reservoir was most sensitive to the start-up pressure gradient, and second most sensitive to the opening of artificial fractures. Enhancing the initial conductivity of artificial fractures was helpful to improve the productivity of tight oil wells. The influence of conductivity, spacing, number and length of artificial fractures should be considered comprehensively in fracturing design. Increasing the number of artificial fractures unilaterally could not achieve the expected increase in production.

Keyword: tight oil; porous media; fully coupled fluid-solid; horizontal well; multi-stage fracturing; reservoir numerical simulation; productivity prediction
0 引言

致密油资源丰富、开发潜力大, 在中国油气资源中占据十分重要的地位[1, 2, 3, 4]。与常规油气储集层相比, 致密油储集层表现为多尺度性、强非均质性, 储集层有效应力状态改变时, 具有极强的流-固耦合效应[5, 6]。传统渗流理论一般将多孔介质骨架视作刚性模型, 但致密油储集层多孔介质变形与孔隙流体流动的耦合作用不可忽略, 建立在传统渗流理论基础上的油藏数值模拟技术难以准确预测致密油储集层开发动态[7, 8]。

Terzaghi有效应力原理和Biot三维固结理论共同奠定了流-固耦合研究的基础[9], 许多学者在此基础上建立了多相饱和流体渗流和多孔介质变形耦合作用模型[10, 11, 12]。致密油储集层作为一种典型的双重介质, 包含基质孔隙系统和天然裂缝系统, 且二者通过窜流的方式进行流体交换, 具有孔喉狭小、渗透率低的特点[5, 13]。通常采用水平井水力压裂的方式改造致密油储集层, 除原有小尺度的天然裂缝外, 还出现了大尺度的导流裂缝[14, 15, 16]。随着致密油的采出, 岩石骨架有效应力重新分布, 骨架发生变形, 储集层物性发生动态变化, 这些变化又会影响流体在储集空间的流动和压力分布[17]。因此, 致密油开发过程属于多尺度、多物理过程, 且存在强非线性的力学问题, 如何建立考虑多尺度流动、多物理场耦合的模型并开展压裂井生产动态预测, 成为致密油研究的难点。本文提出一种有效的数学模型来模拟致密油储集层基质孔隙、天然裂缝及人工裂缝中的流-固耦合, 在一定程度上完善了致密油储集层多级压裂水平井多尺度多场耦合渗流理论。

油藏数值模拟技术是预测压裂水平井生产动态及其增产效果的有效方法, 目前采用的数值模型主要包括连续介质模型、离散裂缝模型和连续介质-离散裂缝混合模型, 其中连续介质-离散裂缝混合模型具有双重介质和离散裂缝模型的优点, 在裂缝储集层模拟中具有广阔的应用前景[18, 19]。流-固耦合问题的系统方程本身具有不可独立求解和无法显式消去两类独立变量（压力、位移）的特征, 根据求解方法的不同, 可分为间接耦合方法（显式迭代耦合、隐式迭代耦合）和直接求解的全耦合方法。间接耦合方法的方程积分交错进行, 耦合参数在两场间交叉迭代。Liu等[20]基于嵌入式离散裂缝模型和有限元方法建立的适用于致密油储集层多级压裂水平井流-固耦合的数值模拟, 采用迭代耦合求解渗流力学和地质力学控制方程; Zhang等[8]基于离散裂缝模型和有限元方法建立的适用于裂缝性油藏注水开发过程的流-固耦合数值模拟, 采用显式耦合求解。此类方法运算速度快, 但精度较低, 且对时间步的要求较高, 一般只能以较短的时步进行求解, 同时可能存在不收敛的情况。全耦合法可实现渗流场和应力场的同步求解, 不存在时间滞后现象, 因其计算结果稳定、误差较小, 计算结果与实际物理过程更为一致, 逐渐被国内外学者采用[21, 22]。流-固耦合问题常用的数值模拟方法包括有限差分方法、有限体积法、有限元方法等, 其中基于非结构网格的有限元方法因其能灵活处理任意边界条件和复杂的几何形状, 并且相对于其他数值方法在多物理场耦合分析方面具有优势, 被广泛应用于致密储集层生产动态模拟[5, 8, 23, 24]。

以往的研究大多集中于应力对储集层渗流能力的影响, 但对于致密油储集层压裂水平井开采的动态耦合及产能研究相对较少。因此, 本文针对致密油储集层开采的多尺度流体流动机理、多物理场耦合作用机理和多级压裂水平井渗流理论等关键问题, 建立了表征双重介质致密油储集层流体流动和储集层变形的数学模型, 构建了致密油储集层物性演化模型; 采用有限元方法全耦合求解模型, 分析多重介质变形规律以及储集层流体流动的复杂机制, 并对不同参数条件下的产能进行了研究。

1 致密油储集层流-固耦合模型

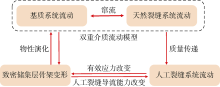
本文应用多孔介质弹性理论与流-固耦合作用机理, 描述致密油储集层人工裂缝、天然裂缝、基质系统的变形, 以及流体与固体之间的相互耦合作用。致密油储集层多尺度空间如图1所示, 模型的基本假设条件如下：①储集层由基质系统与天然裂缝系统组成, 二者之间存在拟稳态窜流; ②多孔介质视为完全饱和且各向同性的线弹性体; ③储集层为弹性变形, 满足小变形假设, 遵从Terzaghi有效应力原理; ④单相流体等温渗流, 其流动遵循达西定律, 忽略重力影响; ⑤原油从基质系统经天然裂缝流向压裂裂缝和井筒。

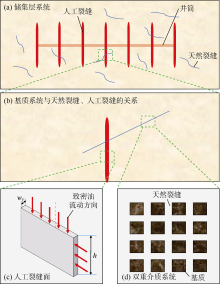图1 致密油储集层多尺度空间示意图（根据文献[16]修改）

1.1 储集层岩体变形模型

将岩体视作由岩石骨架相和流体相组成的连续多孔介质, 在小变形假设条件下, 致密油储集层的岩体力学控制方程为[25]：

$\sigma _{ij, j, \eta}^{{}}\text{+}f_{i, \eta}^{{}}\text{=}\mathbf{0}$ （1）

岩体骨架的变形主要由有效应力控制, 根据Terzaghi有效应力原理可以表示为[26]：

$\sigma _{ij, \eta}^{{}}=\sigma _{ij, \eta}^{\prime}-{{b}_{\eta}}{{p}_{\eta}}{{\delta}_{ij}}$ （2）

考虑应力平衡条件, 在双重介质系统中应力、应变满足如下关系式[27]：

${{\sigma}_{ij}}=\sigma _{ij, I}^{{}}=\sigma _{ij, II}^{{}}$ （3）

${{\varepsilon}_{ij}}=\varepsilon _{ij, I}^{{}}+\varepsilon _{ij, II}^{{}}$ （4）

基于各向同性的弹性假设, 线弹性变形状态下, 由（2）式— （4）式可得储集层弹性本构方程表达式：

${{\sigma}_{ij}}=D_{ijkl, I, II}{{\varepsilon}_{kl}}-D_{ijkl, I, II}C_{klrt, I}{{b}_{I}}{{p}_{\text{I}}}{{\delta}_{rt}}- \\ D_{ijkl, I , II}C_{klrs, II}{{b}_{\text{II}}}{{p}_{\text{II}}}{{\delta}_{rt}}$ （5）

根据（1）式和（5）式, 致密油储集层系统岩体变形的控制方程可写成以下形式：

$\left( D_{ijkl, I, II}{{\varepsilon}_{kl}}-D_{ijkl, I, II}C_{klrs, I}^{{}}{{b}_{\text{I}}}{{p}_{\text{I}}}{{\delta}_{rt}}- \right. \\ {{\left. D_{ijkl, I, II}C_{klrs, II}{{b}_{\text{II}}}{{p}_{\text{II}}}{{\delta}_{rt}} \right)}_{, j}}\text{+}{{f}_{i}}\text{=}\mathbf{0}$ （6）

在小变形假设条件下, 储集层应变分量与位移的关系为：

${{\varepsilon}_{ij}}=\frac{1}{2}\left( {{u}_{i, j}}+{{u}_{j, i}} \right)$ （7）

1.2 流体渗流模型

针对多孔介质饱和油相渗流问题, 基质系统和天然裂缝系统的连续性方程为质量守恒方程[28]：

$\left\{ \begin{align} & \frac{d{{W}_{\text{I}}}}{dt}+\nabla {{H}_{\text{I}}}-\alpha \rho \frac{{{K}_{^{I}}}}{\mu}\left( {{p}_{\text{I}}}-{{p}_{\text{II}}} \right)={{Q}_{\text{I}}} \\ & \frac{d{{W}_{\text{II}}}}{dt}+\nabla {{H}_{\text{II}}}+\alpha \rho \frac{{{K}_{^{I}}}}{\mu}\left( {{p}_{\text{I}}}-{{p}_{\text{II}}} \right)={{Q}_{\text{II}}} \\ \end{align} \right.$ （8）

根据弹性多孔介质理论, 各系统内质量的改变可以写成微分形式[25]：

$\frac{d{{W}_{\eta}}}{\rho}={{b}_{\eta}}d{{\varepsilon}_{v, \eta}}+\frac{d{{p}_{\eta}}}{{{M}_{b, \eta}}}$ （9）

由于致密油储集层的基质系统渗透率极低, 具有明显的非线性渗流特征。考虑启动压力梯度的渗流运动方程为：

${{V}_{\text{I}}}=\left\{ \begin{matrix} -\frac{{{K}_{\text{I}}}}{\mu}\left( \nabla {{p}_{\text{I}}}-G \right)\begin{matrix} {} & \left| \nabla {{p}_{\text{I}}} \right|G \\ \end{matrix} \\ \begin{matrix} \begin{matrix} {} & {} \\ \end{matrix} & 0 & {} & {} \\ \end{matrix}\begin{matrix} {} & \left| \nabla {{p}_{\text{I}}} \right|\le G \\ \end{matrix} \\ \end{matrix} \right.$ （10）

裂缝系统的运动方程由达西定律表示：

${{V}_{\text{II}}}=-\frac{{{K}_{\text{II}}}}{\mu}\nabla {{p}_{\text{II}}}$ （11）

将（9）式— （11）式代入（8）式可以得到基质系统和天然裂缝系统质量守恒方程的完整表述[29]：

$\left\{ \begin{align} & {{b}_{\text{I}}}\rho \frac{\partial {{\varepsilon}_{v, \text{I}}}}{\partial t}+\rho \frac{1}{{{M}_{b, \text{I}}}}\frac{\partial {{p}_{\text{I}}}}{\partial t}-\nabla \left[ \frac{\rho {{K}_{\text{I}}}}{\mu}\left( \nabla {{p}_{\text{I}}}-G \right) \right]- \\ & \text{ }\alpha \rho \frac{{{K}_{\text{I}}}}{\mu}\left( {{p}_{\text{I}}}-{{p}_{\text{II}}} \right)={{Q}_{\text{I}}} \\ & {{b}_{\text{II}}}\rho \frac{\partial {{\varepsilon}_{v, \text{II}}}}{\partial t}+\rho \frac{1}{{{M}_{b, \text{II}}}}\frac{\partial {{p}_{\text{II}}}}{\partial t}-\nabla \left( \frac{\rho {{K}_{\text{II}}}}{\mu}\nabla {{p}_{\text{I}}} \right)+ \\ & \text{ }\alpha \rho \frac{{{K}_{\text{I}}}}{\mu}\left( {{p}_{\text{I}}}-{{p}_{\text{II}}} \right)={{Q}_{\text{II}}} \\ \end{align} \right.$ （12）

压裂裂缝作为油相流向井筒的主要通道, 可改善致密油储集层整体的渗流能力, 裂缝作为流动内边界来处理, 缝内流体流动连续性方程为[30]：

${{s}_{^{F}}}\rho \frac{\partial {{p}_{F}}}{\partial t}-\nabla \left( \rho \frac{{{K}_{^{F}}}}{\mu}\nabla {{p}_{F}} \right)={{Q}_{F}}$ （13）

根据离散裂缝模型理论, 将水力压裂裂缝的渗流方程“ 降维” 处理后, 组装至双重介质的渗流方程中, 形成全区域渗流方程体系, 可表示为[8]：

$\int_{{{\Omega}_{\ e}}}{Q}d{{\Omega}_{\ e}}=\sum\limits_{\eta \in \left\{ I , II \right\}}{\int_{{{\Omega}_{\eta}}}{{{Q}_{\eta}}}d{{\Omega}_{\eta}}}+\sum\limits_{z}{{{w}_{F, z}}\int_{{{\Omega}_{\ F, z}}}{Q}d{{\Omega}_{\ F, z}}}$ （14）

1.3 流-固动态耦合模型

流-固耦合的过程包括：流体流动引起的压力变化会影响作用在岩石骨架上的有效应力, 导致岩体发生形变; 岩体变形使岩石孔隙空间、孔喉半径、裂缝开度等发生改变, 从而改变岩体的渗透率、孔隙度和裂缝导流能力, 同时又会影响流体的流动（见图2）。

图2 致密油储集层多物理场耦合关系示意图

基质孔隙度定义为当前基质孔隙空间体积与当前岩石总体积之比, 因此储集层发生变形后的基质孔隙度为[29]：

${{\phi}_{I}}={{\phi}_{0, I}}+{{b}_{I}}{{\varepsilon}_{v, I}}+\frac{{{b}_{^{I}}}-{{\phi}_{0, I}}}{{{M}_{s, I}}}\left( {{p}_{\text{I}}}-{{p}_{0, I}} \right)$ （15）

根据Cubic定律, 基质渗透率与孔隙度的关系满足[30]：

${{K}_{I}}={{K}_{0, I}}{{\left( \frac{{{\phi}_{I}}}{{{\phi}_{0, I}}} \right)}^{3}}$ （16）

由于天然裂缝系统孔隙度极低, 本文忽略固体变形对其孔隙度的影响, 选取Jiang等[31]考虑平均应力和地质力学参数的模型计算天然裂缝系统的渗透率：

${{K}_{II}}={{K}_{0, II}}\exp \left[ {{c}_{II}}\frac{1+\upsilon}{1-\upsilon}{{b}_{II}}\left( {{p}_{II}}-{{p}_{0, II}} \right) \right]$ （17）

压裂裂缝的开度受裂缝面有效应力控制, 裂缝面有效应力等于作用于裂缝表面的法向应力减去裂缝内流体压力, 因此压裂裂缝开度表达式如下[30]：

${{w}_{F}}={{w}_{F, 0}}exp\left[ -{{c}_{F}}\left( {{\sigma}_{\beta n}}-{{p}_{F}} \right) \right]$ （18）

采用平行板裂缝渗流公式对压裂裂缝渗透率进行计算：

${{K}_{F}}=\frac{w_{F}^{2}}{12}$ （19）

（15）式— （19）式组成了基质系统、天然裂缝系统和压裂裂缝系统的流-固动态耦合模型, 模型充分体现了渗流场和应力场之间相互影响的关系。

1.4 初始和边界条件

应力-位移条件定义为：

$u\left| {{_{\Omega}}_{_{e}}} \right.={{\bar{u}}_{s}}$ （20）

$\sigma \cdot n\left| {{_{\Omega}}_{_{e}}} \right.={{\bar{F}}_{s}}$ （21）

流动封闭外边界条件为：

$\frac{\partial {{p}_{\eta}}}{\partial n}=0$ （22）

初始边界条件为：

${{p}_{\eta}}\left| _{{{\Omega}_{\text{e}}}} \right.\left( x, y, t=0 \right)={{p}_{0, \eta}}$ （23）

$u\left| _{{{\Omega}_{\text{e}}}} \right.\left( x, y, t=0 \right)={{u}_{0}}$ （24）

$\sigma \left| _{{{\Omega}_{\text{e}}}} \right.\left( x, y, t=0 \right)={{\sigma}_{0}}$ （25）

2 模型求解与验证
2.1 离散与求解

（6）式、（12）式和（13）式构成了描述岩体变形和流体流动的控制方程, 其中每个方程均是复杂的偏微分方程, 而且多物理场耦合问题又是高度非线性化的, 只能求解其数值解。本文采用有限元法对控制方程进行离散, 将控制方程中位移和压力表示为结点变量的插值函数形式：

$\left\{ \begin{array}{* {35}{l}} u={{N}_{u}}\bar{u} \\ {{p}_{\eta}}={{N}_{p, \eta}}{{{\bar{p}}}_{\eta}} \\ {{p}_{F}}={{N}_{p, F}}{{{\bar{p}}}_{F}} \\ \end{array} \right.$ （26）

基于有限元方法与离散裂缝模型, 考虑人工裂缝内渗流以及汇-源项影响, 系统力学平衡控制方程（6）式和系统内质量守恒方程（12）式、（13）式可在空间上分别离散成如下矩阵形式[32]：

$\left[ \begin{matrix} \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & {{H}_{I}}+H_{I , \tau}^{{}} & -H_{I , \tau}^{{}} \\ \mathbf{0} & -H_{II , \tau}^{{}} & {{H}_{II}}+H_{II , \tau}^{{}} \\ \end{matrix} \right]\left[ \begin{matrix} \overline{u} \\ {{\overline{p}}_{\text{I}}} \\ {{\overline{p}}_{II}} \\ \end{matrix} \right]+ \\ \left[ \begin{matrix} {{K}_{I , II}} & -{{L}_{I}} & -{{L}_{II}} \\ {{K}_{I}} & {{S}_{I}} & 0 \\ {{K}_{II}} & 0 & {{S}_{II}} \\ \end{matrix} \right]\frac{d}{dt}\left[ \begin{matrix} \overline{u} \\ {{\overline{p}}_{\text{I}}} \\ {{\overline{p}}_{II}} \\ \end{matrix} \right]=\left[ \begin{matrix} \frac{d{{R}_{\text{u}}}}{dt} \\ {{R}_{I}} \\ {{R}_{II}} \\ \end{matrix} \right]$ （27）

其中 ${K}_{II}=\int_{{{\Omega}_{e}}}{{{B}^{T}}}{D}_{I, II}Bd{{\Omega}_{e}}$

${{L}_{\eta}}=\int_{{{\Omega}_{e}}}{{{B}^{T}}}{{D}_{I, II}}{{C}_{\eta}}{{b}_{\eta}}m{{N}_{p, \eta}}d{{\Omega}_{e}}$

${{R}_{u}}=\int_{{{\Omega}_{e}}}{N_{u}^{T}{{f}_{i}}}d{{\Omega}_{\text{e}}}+\int_{{{\Omega}_{s}}}{N_{u}^{T}{{{\bar{F}}}_{s}}}d{{\Omega}_{s}}$

${{H}_{I}}=\int_{{{\Omega}_{e}}}{\rho \frac{{{K}_{I}}}{\mu}\left[ {{\left( \nabla {{N}_{p, I}} \right)}^{T}}\nabla {{N}_{p, I}}-GN_{p, I}^{T}\nabla {{N}_{p, I}} \right]d{{\Omega}_{e}}}$

${{H}_{II}}=\int_{{{\Omega}_{e}}}{{{\left( \nabla {{N}_{p, II}} \right)}^{T}}\rho \frac{{{K}_{II}}}{\mu}}\left( \nabla {{N}_{p, II}} \right)d{{\Omega}_{e}}+$

$\int_{{{\Omega}_{F}}}{{{w}_{F}}{{\left( \nabla {{N}_{p, F}} \right)}^{T}}\rho \frac{{{K}_{F}}}{\mu}}\left( \nabla {{N}_{p, F}} \right)d{{\Omega}_{F}}$

$H_{\eta , \tau}^{{}}=\int_{{{\Omega}_{e}}}{N_{p, \eta}^{T}\alpha \rho \frac{{{K}_{I}}}{\mu}{{N}_{p, \eta}}}d{{\Omega}_{e}}$

${{K}_{\eta}}=\int_{{{\Omega}_{e}}}{N_{p, \eta}^{T}{{b}_{\eta}}\rho}{{m}^{T}}{{C}_{\eta}}{{D}_{I , II}}Bd{{\Omega}_{e}}$

${{S}_{\eta}}=\int_{{{\Omega}_{\eta}}}{N_{p, \eta}^{T}\rho \frac{1}{{{M}_{b, \eta}}}}{{N}_{p, \eta}}d{{\Omega}_{\eta}}+\int_{{{\Omega}_{F}}}{{{w}_{F}}N_{p, F}^{T}{{s}_{F}}{{N}_{p, F}}}d{{\Omega}_{F}}$

${{R}_{\text{I}}}=\int_{{{\Gamma}_{\text{m}}}}{N_{p, I}^{T}{{Q}_{\text{I}}}}d{{\Gamma}_{m}}$

${{R}_{\text{II}}}=\int_{{{\Gamma}_{\text{f}}}}{N_{p, II}^{T}{{Q}_{\text{II}}}}d{{\Gamma}_{\text{f}}}+\int_{{{\Gamma}_{F}}}{{{w}_{F}}N_{p, F}^{T}{{Q}_{F}}}d{{\Gamma}_{F}}$

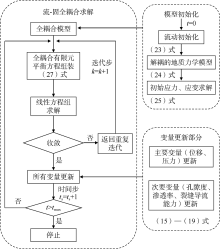
流-固全耦合有限元平衡方程在时域进行离散, 控制方程的3个主变量（储集层节点位移、基质系统压力、天然裂缝系统压力）均以隐式方式在同一时间步内联立解出; 与主变量相关的次要变量及其耦合关系在每个时间步进行迭代更新, 即可求得系统位移和压力的值。流-固耦合具体求解流程如图3所示：①模型初始化, 包括流动初始化和地质力学初始化, 得到t=0时刻空间不同位置流压场和岩体应力状态; ②流-固全耦合, 将求解过程划分成若干个时间步增量, 采用时间步推进的方法联立耦合求解压力场和位移场, 并检查其收敛性, 若不收敛, 返回重复迭代; ③利用第②步得到的位移、压力（主要变量）计算该时间步下孔隙度、渗透率、裂缝导流能力, 更新参数（次要变量）; ④重复②— ③步骤, 直至模拟时间结束。

图3 流-固全耦合求解流程图

2.2 模型验证

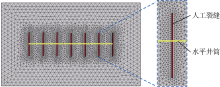
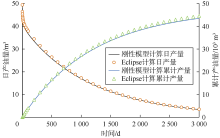
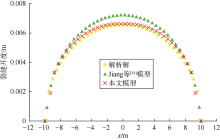
为验证上述流-固全耦合模型的正确性, 建立了致密油储集层多级压裂水平井模型, 模型基本参数如表1所示, 数值模拟参数取值主要参考文献[5]、[8]、[33]。模型采用三角形网格进行网格剖分, 其中基质系统与天然裂缝系统共用一套网格, 而压裂裂缝在网格划分过程中进行降维处理; 由于裂缝周围压力梯度较大, 所以在压裂裂缝周边进行网格加密, 由此得到整个模型储集层区域网格划分图（见图4）。由数值计算程序得到全耦合刚性模型的模拟结果, 并与商业软件Eclipse采用有限差分模型得到的日产油量和累计产油量进行对比（见图5）, 本文全耦合刚性模型数值模拟结果与Eclipse的模拟结果吻合性较好。同时, 在二维均质、线性弹性、不渗透的岩石中, 均匀受压裂缝沿裂缝长度方向的开度分布满足解析解, 则将本文模型和Jiang等[34]模型计算的裂缝开度与解析解进行对比（见图6）。可以看出, 3个模型计算的裂缝开度相近, 而本文模型与解析解更接近。从以上两个方面验证了本文流-固耦合模型的合理性与正确性。

表1 模型基本参数表

图4 储集层区域网格剖分示意图

图5 全耦合刚性模型与Eclipse模型模拟结果对比

图6 不同模型计算的裂缝开度分布与解析解对比

2.3 模型对比

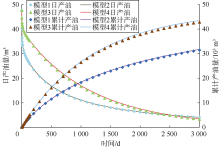
本文对比了全耦合模型（模型1）、基质+天然裂缝刚性模型（模型2）、人工裂缝刚性模型（模型3）、全刚性模型（模型4）模拟计算的多级压裂水平井产量（见图7）, 并以全耦合模型累计产油量为基数, 计算其他模型累计产油量与基数的相对误差, 结果见表2。可以看出, 全耦合与全刚性模型产量预测差异大; 开发前期, 全耦合模型计算日产油量递减快, 生产3 000 d后全耦合模型计算累计产量最小, 全刚性模型计算累计产量最高。忽略基质与天然裂缝系统的流-固耦合作用, 压裂水平井生产3 000 d产量预测误差为0.92%, 主要原因在于实际开采过程中基质与天然裂缝系统物性逐渐变差, 其向水平井筒的供给能力逐步减弱, 而模型2不考虑该因素, 因此模型2计算累计产量较模型1偏大。忽略人工裂缝系统的流-固耦合作用, 压裂水平井生产3 000 d产量预测误差为36.46%, 主要由于实际开采过程中人工裂缝导流能力强, 裂缝内压力逐渐下降、开度不断减小, 而模型3不考虑该因素, 因此模型3计算累计产量较模型1更大。对比模型2— 模型4产量预测相对误差值, 可以看出模型4产量预测相对误差（38.30%）并非模型2和模型3产量预测相对误差简单的线性叠加（37.38%）, 进一步说明基质、天然裂缝、人工裂缝之间的影响具有相互耦合特性。

图7 不同模型计算的多级压裂水平井产量

表2 不同模型计算的累计产油量对比

综上所述, 流-固耦合作用在致密油产能预测中的影响不可忽略, 未耦合模型预测的多级压裂水平井产能偏高, 流-固全耦合模型预测的产能更为精确; 人工裂缝物性是决定压裂水平井产能的重要因素, 有必要优化人工裂缝参数设计。

3 储集层物性演化规律

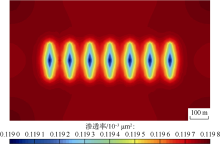
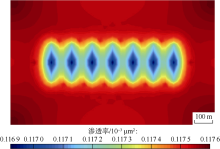
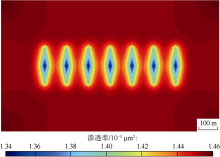
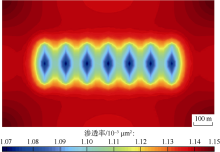
采用模型验证部分所用的数值模型, 计算致密油储集层多级压裂水平井投入生产后不同时刻基质系统的渗透率分布和不同时刻天然裂缝系统的渗透率分布（见图8— 图11）。流体经基质系统和天然裂缝系统流入人工裂缝及井筒时, 由于人工裂缝内导流能力大、流动阻力小, 近压裂裂缝区域存在较大的流体压力梯度, 储集层渗透率发生显著变化。水平井生产2 000 d后, 基质系统渗透率由0.120× 10-3μ m2最小减至约0.117× 10-3μ m2, 天然裂缝系统渗透率由1.500× 10-3μ m2最小减至约1.070× 10-3μ m2, 由于基质系统更为致密, 其渗透率变化幅度小于天然裂缝系统。储集层渗透率的最小值分布于人工裂缝周围, 随着时间的延续, 渗透率降低的范围从人工裂缝附近逐渐向储集层四周扩大。

图8 生产100 d后基质系统渗透率分布

图9 生产2 000 d后基质系统渗透率分布

图10 生产100 d后天然裂缝渗透率分布

图11 生产2 000 d后天然裂缝渗透率分布

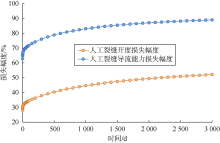
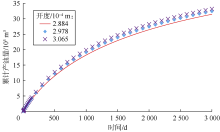
致密油储集层多级压裂水平井生产2 000 d后, 人工裂缝开度由2.884× 10-4m最小减至1.440× 10-4m左右（见图12、图13）。图14为人工裂缝开度损失幅度和导流能力损失幅度曲线。开发前期, 由于人工裂缝内流体迅速采出, 其附近压力降低较快, 导致人工裂缝开度与导流能力损失幅度大; 开发500 d后, 人工裂缝开度损失幅度为40.37%, 导流能力损失幅度为78.80%, 随后人工裂缝物性损失幅度缓慢上升; 3 000 d后, 人工裂缝开度损失幅度达52.12%, 导流能力损失幅度达89.02%。

图12 生产100 d后压裂裂缝开度分布

图13 生产2 000 d后压裂裂缝开度分布

图14 不同时刻人工裂缝开度和导流能力损失幅度曲线

4 压裂参数优化
4.1 参数敏感性

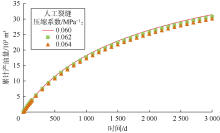
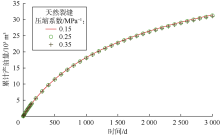
设计案例1— 案例9, 人工裂缝压缩系数分别为0.060, 0.062, 0.064 MPa-1, 人工裂缝开度分别为2.884× 10-4, 2.978× 10-4, 3.065× 10-4m, 天然裂缝压缩系数分别为0.15, 0.25, 0.35 MPa-1, 启动压力梯度分别为0, 0.05, 0.10 MPa/m, 模拟计算9个案例多级压裂水平井产量, 并以案例1的累计产油量为基数, 计算其他8个案例累计产油量与基数的相对误差, 结果见表3。图15— 图18对比了不同参数下生产3 000 d的累计产油量, 其中案例5累计产油量最大, 案例9累计产油量最小, 可见水平井产量对启动压力梯度最敏感, 人工裂缝开度次之。启动压力梯度减缓了储集层压力波的传播, 对致密油井的产量有较大的抑制作用, 提高人工裂缝初始导流能力将有助于降低产量损失, 同时水平井累计产量随人工裂缝和天然裂缝压缩系数的增加而逐渐降低。

表3 不同敏感性参数对产量的影响

图15 不同人工裂缝压缩系数下的累计产油量

图16 不同人工裂缝开度下的累计产油量

图17 不同天然裂缝压缩系数下的累计产油量

图18 不同启动压力梯度下的累计产油量

4.2 裂缝参数优化

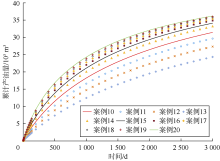
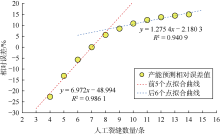
人工裂缝几何分布是影响致密油储集层产能的重要因素之一, 本文在保持压裂裂缝数量与压裂裂缝长度乘积不变的情况下, 设计了11个案例（案例10— 案例20）, 分别计算了不同压裂裂缝参数下的多级压裂水平井产量, 并以案例10的累计产油量为基数, 计算其他案例累计产油量与基数的相对误差, 案例设计与模拟结果见表4, 图19对比了不同案例生产3 000 d的累计产油量。可以看出, 案例20累计产油量最大, 案例13累计产油量最小, 随着人工裂缝数量的增多, 水平井产量不断增加; 各案例累计产油量曲线在生产后期接近平行, 因此水平井人工裂缝加密对产量的影响主要集中于生产早期。图20展示了不同人工裂缝数量与产量预测相对误差的关系。分别取产量预测相对误差曲线前5个点和后6个点, 做拟合曲线, 形成交会图, 裂缝条数为8~9条时, 产量预测相对误差曲线出现了拐点; 当裂缝数量超过10条之后, 水平井产量增幅减弱, 裂缝条数对产量的影响程度也逐渐减小。因此压裂施工优化设计需要考虑人工裂缝间距、数量、长度的综合影响, 只增加裂缝条数无法取得预期的增产效果; 在本文模拟条件下, 最佳裂缝条数为9条。

表4 不同裂缝参数对产量的影响

图19 不同案例多级压裂水平井累计产油量对比

图20 不同人工裂缝数量与产量预测相对误差关系曲线

5 结论

建立了致密油储集层多级压裂水平井多重孔隙介质变形与流体流动的全耦合数值模型, 模型综合考虑了储集层基质系统、天然裂缝和人工裂缝的变形特征与分区流体渗流规律, 能够准确模拟预测致密油储集层多级压裂水平井产能。

模型计算结果表明, 致密油储集层水平井生产过程中近人工裂缝区域储集层物性变差, 特别是人工裂缝开度和裂缝导流能力损失幅度分别达到52.12%和89.02%; 流-固耦合作用在致密油储集层产能预测中的影响不可忽略, 模拟致密油储集层水平井生产3 000 d后, 全耦合模型与未耦合模型产能预测的误差达38.30%; 参数敏感性分析表明, 致密油储集层水平井产能对启动压力梯度最敏感, 人工裂缝开度次之, 提高人工裂缝初始导流能力有助于提高致密油井产能; 致密油储集层压裂施工设计需考虑人工裂缝导流能力、间距、数量、长度的综合影响, 片面追求增加裂缝条数无法取得预期的增产效果。

符号注释：

b— — 比奥校正系数; B— — 应变矩阵; c— — 压缩系数, Р a-1; C— — 柔度矩阵; Cklrt, Ⅰ — — 基质系统柔度张量, Р a-1; Cklrt, Ⅱ — — 天然裂缝系统柔度张量, Р a-1; D— — 弹性矩阵; Dijkl, Ⅰ , Ⅱ — — 双重介质系统弹性张量, Р a; fi— — 重力项矢量, N/m3; ${{\bar{F}}_{s}}$— — 边界处已知应力, Р a; G— — 启动压力梯度, Р a/m; h— — 人工裂缝面高度, m; H— — 流体通量, kg/（m2· s）; k— — 迭代步; Κ — — 渗透率, m2; Κ 0— — 初始渗透率, m2; m— — 单位张量; Mb— — 比奥模量, Р a; Ms, Ι — — 基质系统岩石骨架体积模量, Р a; n— — 边界法线方向; n— — 边界单位法向量; Np— — 压力场的形函数; Nu— — 位移场的形函数; р — — 孔隙压力, Р a; p0— — 初始孔隙压力, Р a; $\bar{p}$— — 节点压力, Р a; Q— — 源汇项, kg/（m3· s）; Q— — 流动方程; sF— — 人工裂缝存储系数, Р a-1; t— — 时间, s; ts— — 时间步; u0— — 系统初始位移, m; u— — 位移矢量, m; ui, j— — ui对j方向求偏导数; $\bar{u}$— — 节点位移, m; ${{\bar{u}}_{s}}$— — 边界处已知位移, m; V— — 流体速度, m/s; wF— — 人工裂缝宽度, m; wF, z— — z单元压裂裂缝宽度, m; wF, 0— — 初始人工裂缝宽度, m; W— — 单位体积流体质量, kg/m3; x, y— — 储集层坐标位置, m; z— — 裂缝单元; α — — 窜流系数, m-2; — — 哈密顿算子; μ — — 流体黏度, Pa· s; υ — — 岩石泊松比; δ — — Kronecker符号; ε — — 应变张量; ε ij— — 应变分量; ε v— — 岩石体应变; ρ — — 流体密度, kg/m3; σ β n— — 作用于裂缝表面的法向应力, Р a; σ — — 总应力张量; σ 0— — 系统初始应力, Р a; σ ij— — 应力分量, Pa; σ ij, j— — σ ij对j方向求偏导数, Pa/m; ${{{\sigma }'}_{ij}}$— — 有效应力张量的分量, Pa; Γ m— — 基质系统边界; Γ f— — 天然裂缝系统边界; Γ F— — 人工裂缝系统边界; Ω e— — 整个储集层系统; Ω F— — 人工裂缝系统; Ω s— — 储集层边界; ϕ — — 孔隙度, %; ϕ 0— — 初始孔隙度, %。下标：F— — 人工裂缝; i, j, k, l, r, s— — Voigt标记方法中的指标; η — — 基质系统或天然裂缝系统; τ — — 窜流; Ⅰ — — 基质系统; Ⅱ — — 天然裂缝系统。

（编辑 刘恋）

参考文献
[1] 孙龙德, 邹才能, 贾爱林, 等. 中国致密油气发展特征与方向[J]. 石油勘探与开发, 2019, 46(6): 1015-1026.
SUN Longde, ZOU Caineng, JIA Ailin, et al. Development characteristics and orientation of tight oil and gas in China[J]. Petroleum Exploration and Development, 2019, 46(6): 1015-1026. [本文引用:1]
[2] 邹才能, 翟光明, 张光亚, 等. 全球常规-非常规油气形成分布、资源潜力及趋势预测[J]. 石油勘探与开发, 2015, 42(1): 13-25.
ZOU Caineng, ZHAI Guangming, ZHANG Guangya, et al. Formation, distribution, potential and prediction of global conventional and unconventional hydrocarbon resources[J]. Petroleum Exploration and Development, 2015, 42(1): 13-25. [本文引用:1]
[3] 胡素云, 朱如凯, 吴松涛, 等. 中国陆相致密油效益勘探开发[J]. 石油勘探与开发, 2018, 45(4): 737-748.
HU Suyun, ZHU Rukai, WU Songtao, et al. Profitable exploration and development of continental tight oil in China[J]. Petroleum Exploration and Development, 2018, 45(4): 737-748. [本文引用:1]
[4] 李国欣, 罗凯, 石德勤. 页岩油气成功开发的关键技术、先进理念与重要启示: 以加拿大都沃内项目为例[J]. 石油勘探与开发, 2020, 47(4): 739-749.
LI Guoxin, LUO Kai, SHI Deqin. Key technologies, engineering management and important suggestions of shale oil/gas development: Case study of a Duvernay shale project in Western Canada Sedimentary Basin[J]. Petroleum Exploration and Development, 2020, 47(4): 739-749. [本文引用:1]
[5] REN L, SU Y, ZHAN S, et al. Fully coupled fluid-solid numerical simulation of stimulated reservoir volume (SRV)-fractured horizontal well with multi-porosity media in tight oil reservoirs[J]. Journal of Petroleum Science and Engineering, 2019, 174: 757-775. [本文引用:4]
[6] 方文超, 姜汉桥, 李俊键, 等. 致密储集层跨尺度耦合渗流数值模拟模型[J]. 石油勘探与开发, 2017, 44(3): 415-422.
FANG Wenchao, JIANG Hanqiao, LI Junjian, et al. A numerical simulation model for multi-scale flow in tight oil reservoirs[J]. Petroleum Exploration and Development, 2017, 44(3): 415-422. [本文引用:1]
[7] 任龙, 苏玉亮, 郝永卯, 等. 基于改造模式的致密油藏体积压裂水平井动态分析[J]. 石油学报, 2015, 36(10): 1272-1279.
REN Long, SU Yuliang, HAO Yongmao, et al. Dynamic analysis of SRV-fractured horizontal wells in tight oil reservoirs based on stimulated patterns[J]. Acta Petrolei Sinica, 2015, 36(10): 1272-1279. [本文引用:1]
[8] ZHANG D, ZHANG L, TANG H, et al. A novel fluid-solid coupling model for the oil-water flow in the natural fractured reservoirs[J]. Physics of Fluids, 2021, 33(3): 036601. [本文引用:4]
[9] CRYER C W. A comparison of the three-dimensional consolidation theories of Biot and Terzaghi[J]. The Quarterly Journal of Mechanics and Applied Mathematics, 1963, 16(4): 401-412. [本文引用:1]
[10] 王自明, 杜志敏. 变温条件下弹塑性油藏中多相渗流的流固耦合数学模型与数值模拟[J]. 石油勘探与开发, 2001, 28(6): 68-72.
WANG Ziming, DU Zhimin. The coupled model and numerical simulation of multiphase flow in an elastoplastic deforming oil reservoir with transformation temperature[J]. Petroleum Exploration and Development, 2001, 28(6): 68-72. [本文引用:1]
[11] HELMIG R, FLEMISCH B, WOLFF M, et al. Model coupling for multiphase flow in porous media[J]. Advances in Water Resources, 2013, 51: 52-66. [本文引用:1]
[12] TIAN Y, XIONG Y, WANG L, et al. A compositional model for gas injection IOR/EOR in tight oil reservoirs under coupled nanopore confinement and geomechanics effects[R]. SPE-193818, 2019. [本文引用:1]
[13] 梁涛, 常毓文, 郭晓飞, 等. 巴肯致密油藏单井产能参数影响程度排序[J]. 石油勘探与开发, 2013, 40(3): 357-362.
LIANG Tao, CHANG Yuwen, GUO Xiaofei, et al. Influence factors of single well’s productivity in the Bakken tight oil reservoir[J]. Petroleum Exploration and Development, 2013, 40(3): 357-362. [本文引用:1]
[14] 雷群, 翁定为, 熊生春, 等. 中国石油页岩油储集层改造技术进展及发展方向[J]. 石油勘探与开发, 2021, 48(5): 1035-1042.
LEI Qun, WENG Dingwei, XIONG Shengchun, et al. Progress and development directions of shale oil reservoir stimulation technology of China National Petroleum Corporation[J]. Petroleum Exploration and Development, 2021, 48(5): 1035-1042. [本文引用:1]
[15] 李国欣, 覃建华, 鲜成钢, 等. 致密砾岩油田高效开发理论认识、关键技术与实践: 以准噶尔盆地玛湖油田为例[J]. 石油勘探与开发, 2020, 47(6): 1185-1197.
LI Guoxin, QIN Jianhua, XIAN Chenggang, et al. Theoretical understand ings, key technologies and practices of tight conglomerate oilfield efficient development: A case study of the Mahu oilfield, Junggar Basin, NW China[J]. Petroleum Exploration and Development, 2020, 47(6): 1185-1197. [本文引用:1]
[16] 徐建春. 多级压裂水平井产能分析及数值模拟方法研究[D]. 青岛: 中国石油大学(华东), 2017.
XU Jianchun. Production performance analysis and numerical simulation for multistage fractured horizontal well[D]. Qingdao: China University of Petroleum, 2017. [本文引用:1]
[17] 房平亮. 致密油开发流固耦合作用机理及数值模拟方法研究[D]. 北京: 中国地质大学(北京), 2017.
FANG Pingliang. Study on mechanism and numerical simulation method of multiphase flow-geomechanical deformation coupling in tight oil reservoirs[D]. Beijing: China University of Geosciences, 2017. [本文引用:1]
[18] ZHANG R, ZHANG L, WANG R, et al. Simulation of a multistage fractured horizontal well with finite conductivity in composite shale gas reservoir through finite-element method[J]. Energy & Fuels, 2016, 30(11): 9036-9049. [本文引用:1]
[19] ZHANG R, ZHANG L, WANG R, et al. Simulation of a multistage fractured horizontal well in a water-bearing tight fractured gas reservoir under non-Darcy flow[J]. Journal of Geophysics and Engineering, 2018, 15(3): 877-894. [本文引用:1]
[20] LIU Y, LIU L, LEUNG J, et al. Coupled flow/geomechanics modeling of interfracture water injection to enhance oil recovery in tight reservoirs[J]. SPE Journal, 2021, 26(1): 1-21. [本文引用:1]
[21] SETTARI A, WALTERS D A. Advances in coupled geomechanical and reservoir modeling with applications to reservoir compaction[J]. SPE Journal, 2001, 6(3): 334-342. [本文引用:1]
[22] SETTARI A, MOURITS F M. Coupling of geomechanics and reservoir simulation models[M]. Balkema: Routledge, 1994. [本文引用:1]
[23] 张芮菡. 基于多尺度渗流理论的页岩气藏多级压裂水平井数值模拟研究[D]. 成都: 西南石油大学, 2019.
ZHANG Ruihan. Numerical simulation of multi-stage fractured horizontal well in shale gas reservoir based on multi-scale flow theory[D]. Chengdu: Southwest Petroleum University, 2019. [本文引用:1]
[24] ZHANG R, WU J, ZHAO Y, et al. Numerical simulation of the feasibility of supercritical CO2 storage and enhanced shale gas recovery considering complex fracture networks[J]. Journal of Petroleum Science and Engineering, 2021, 204: 108671. [本文引用:1]
[25] COUSSY O. Poromechanics[M]. New York: John Wiley & Sons Ltd. , 2004. [本文引用:2]
[26] TERZAGHI K. Theoretical soil mechanics[M]. New York: John Wiley & Sons Ltd. , 1943. [本文引用:1]
[27] NAIR R, ABOUSLEIMAN Y, ZAMAN M. A finite element porothermoelastic model for dual-porosity media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28(9): 875-898. [本文引用:1]
[28] NAIR R S. The poromechanics of naturally fractured rock formations: A finite element approach[D]. Norman: The University of Oklahoma, 2003. [本文引用:1]
[29] LI S, LI X, ZHANG D. A fully coupled thermo-hydro-mechanical, three-dimensional model for hydraulic stimulation treatments[J]. Journal of Natural Gas Science and Engineering, 2016, 34: 64-84. [本文引用:2]
[30] FAN X, LI G, SHAH S, et al. Analysis of a fully coupled gas flow and deformation process in fractured shale gas reservoirs[J]. Journal of Natural Gas Science and Engineering, 2015, 27(Part 2): 901-913. [本文引用:3]
[31] JIANG J, YOUNIS R M. A multimechanistic multicontinuum model for simulating shale gas reservoir with complex fractured system[J]. Fuel, 2015, 161: 333-344. [本文引用:1]
[32] PENG S, ZHANG J. Engineering geology for underground rocks[M]. Berlin, Heidelberg: Springer, 2007. [本文引用:1]
[33] ZHAO Y, LIU L, ZHANG L, et al. Simulation of a multistage fractured horizontal well in a tight oil reservoir using an embedded discrete fracture model[J]. Energy Science & Engineering, 2019, 7(5): 1485-1503. [本文引用:1]
[34] JIANG J, YANG J. Coupled fluid flow and geomechanics modeling of stress-sensitive production behavior in fractured shale gas reservoirs[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 101: 1-12. [本文引用:1]