引用本文
葛新民, 薛宗安, 周军, 胡法龙, 李江涛, 张恒荣, 王烁龙, 牛深园, 赵吉儿. 核磁共振横向弛豫时间谱高斯混合聚类及应用[J]. 石油勘探与开发, 2022,49(2): 296-305.
GE Xinmin, XUE Zong’an, ZHOU Jun, HU Falong, LI Jiangtao, ZHANG Hengrong, WANG Shuolong, NIU Shenyuan, ZHAO Ji’er. An unsupervised clustering method for nuclear magnetic resonance transverse relaxation spectrums based on the Gaussian mixture model and its application[J]. Petroleum Exploration & Development, 2022,49(2): 296-305.  
Doi: 10.11698/PED.2022.02.08
Permissions
Copyright©2022, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
核磁共振横向弛豫时间谱高斯混合聚类及应用
葛新民1,2,3, 薛宗安4, 周军2,5, 胡法龙6, 李江涛7, 张恒荣8, 王烁龙9, 牛深园1, 赵吉儿1
1.中国石油大学（华东）地球科学与技术学院,山东青岛266580
2.中国石油天然气集团有限公司测井重点实验室,西安710077
3.海洋国家实验室海洋矿产资源评价与探测功能实验室,山东青岛266071
4.中国地质调查局油气资源调查中心,北京100083
5.中国石油集团测井有限公司,西安710077
6.中国石油勘探开发研究院,北京100083
7.中国石油青海油田公司,甘肃敦煌736202
8.中海石油（中国）有限公司湛江分公司,广东湛江524057
9.中国石化石油工程技术研究院,北京100101
联系作者简介：薛宗安（1975-）,男,山东高密人,博士,中国地质调查局油气资源调查中心高级工程师,主要从事油气层测井评价方法应用及研究。地址：北京市海淀区北四环中路267号奥运大厦,中国地质调查局油气资源调查中心1208室,邮政编码：100083。E-mail:xuezongan@126.com

第一作者简介：葛新民（1985-）,男,江西于都人,博士,中国石油大学（华东）副教授,主要从事测井岩石物理、核磁共振测井和复杂油气层测井评价方法等研究。地址：山东省青岛市黄岛区长江西路66号,中国石油大学（华东）工科楼C534室,邮政编码：266580。E-mail:gexinmin2002@163.com

收稿日期: 2021-08-30 修回日期: 2022-02-22
基金项目: 国家自然科学基金（42174142）; 国家科技重大专项（2017ZX05039-002）; 中国石油天然气集团有限公司测井重点实验室运行基金（2021DQ20210107-11）; 中央高校基本科研业务费专项（19CX02006A）; 中国石油天然气集团有限公司重大科技项目（ZD2019-183-006）
摘要

为使核磁共振测井横向弛豫时间（ T2）谱的定量表征结果更为直观地反映储集层类型和孔隙结构,提出基于高斯混合模型（GMM）的 T2谱无监督聚类和孔隙结构定量识别方法。首先对 T2谱数据进行主成分降维,减弱数据间的相关性;其次采用高斯混合模型概率密度函数对降维数据进行拟合,结合期望值最大化算法和赤池信息准则变化率得到模型参数和最佳聚类群集;最后分析不同聚类群集的 T2谱特征、孔隙结构类型等,并与 T2几何平均值、 T2算术平均值等进行对比,通过数值模拟和核磁共振测井资料验证算法有效性。研究表明,基于GMM方法的聚类结果与 T2谱形态、 T2谱、孔隙结构、油气产能等具有很好的对应性,为孔隙结构定量识别、储集层级别划分和产能评价等提供新的手段。

关键词: 核磁共振 T2谱; 高斯混合模型; 期望最大化算法; 赤池信息准则; 无监督聚类; 孔隙结构定量标准
中图分类号:P631 文献标志码:A
An unsupervised clustering method for nuclear magnetic resonance transverse relaxation spectrums based on the Gaussian mixture model and its application
GE Xinmin1,2,3, XUE Zong’an4, ZHOU Jun2,5, HU Falong6, LI Jiangtao7, ZHANG Hengrong8, WANG Shuolong9, NIU Shenyuan1, ZHAO Ji’er1
1. School of Geosciences, China University of Petroleum, Qingdao 266580, China
2. CNPC Key Well Logging Laboratory, Xi’an 710077, China
3. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
4. Oil and Gas Survey Center of China Geological Survey, Beijing 100083, China
5. China Petroleum Logging Co. Ltd., Xi’an 710077, China
6. PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China
7. PetroChina Qinghai Oilfield Company, Dunhuang 736202, China
8. Zhanjiang Branch of CNOOC Ltd., Zhanjiang 524057, China
9. Sinopec Research Institute of Petroleum Engineering, Beijing 100101, China
Abstract

To make the quantitative results of nuclear magnetic resonance (NMR) transversal relaxation ( T2) spectrums reflect is proposed the type and pore structure of reservoir more directly, an unsupervised clustering method was developed to obtain the quantitative pore structure information from the NMR T2 spectrums based on the Gaussian mixture model (GMM). We conducted the principal component analysis on T2 spectrums in order to reduce the dimension data and the dependence of the original variables. The dimension-reduced data was fitted using the GMM probability density function, and the model parameters and optimal clustering numbers were obtained according to the expectation-maximization algorithm and the change of the Akaike information criterion. Finally, the T2 spectrum features and pore structure types of different clustering groups were analyzed and compared with T2 geometric mean and T2 arithmetic mean. The effectiveness of the algorithm has been verified by numerical simulation and field NMR logging data. The research shows that the clustering results based on GMM method have good correlations with the shape and distribution of the T2 spectrum, pore structure, and petroleum productivity, providing a new means for quantitative identification of pore structure, reservoir grading, and oil and gas productivity evaluation.

Keyword: NMR T2 spectrum; Gaussian mixture model; expectation-maximization algorithm; Akaike information criterion; unsupervised clustering method; quantitative pore structure evaluation
0 引言

核磁共振测井在复杂及非常规油气储集层的物性参数计算、孔隙结构评价和流体识别中发挥着重要作用。由于弛豫信号仅与孔隙流体的氢核有关, 通过测量多孔介质中氢核的宏观磁化矢量随时间的衰减关系, 并将其反演成横向弛豫时间（T2）谱, 结合相关模型可计算出孔隙度、渗透率、束缚水饱和度、孔隙半径、润湿性等参数, T2谱的形态与分布可定性表征孔隙结构及储集层级别[1, 2, 3], 纵向弛豫时间、扩散系数、内部梯度等多维度数据可定量表征孔隙流体类型、含量及黏度等[4, 5, 6, 7, 8]。与自然伽马、声波时差、补偿密度等常规测井相比, 核磁共振测井T2谱中蕴含着更加丰富的地质信息。

受国外技术封锁和现场作业条件限制, 国内大部分油田的核磁共振测井资料以一维T2谱为主, 因此, 更有效地利用核磁共振测井T2谱来解决油田实际问题尤为重要。国内外学者针对核磁共振测井资料的应用开展了大量研究, 在孔隙度、渗透率、束缚水饱和度、T2截止值等参数计算和弛豫时间与孔隙半径的转换等方面取得丰硕成果[9, 10, 11, 12], 并在截止值、平均值、孔径区间占比和伪毛管压力曲线转换等传统方法基础上开展了创新研究, 提出诸如基于T2谱集中度的孔隙结构评价、基于数学形态学的T2谱量化分解、基于分形理论的T2谱分维数提取、基于多元高斯函数拟合的T2谱参数提取方法、基于自组织神经网络与独立分量分析和非负矩阵分解等机器学习的核磁共振测井T2谱定量评价技术[13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24], 为储集层孔隙结构评价提供了新的思路。但是, 上述方法仍难以描述孔隙结构与核磁共振响应的非线性映射关系, 在数据处理过程中需要人为调整参数, 需要实验数据来刻度。

为克服当前技术方法存在的局限性, 本文提出基于高斯混合模型的核磁共振测井T2谱无监督聚类算法, 并利用数值模拟和核磁共振测井资料对方法的有效性和适用性进行验证。

1 高斯混合模型聚类原理

高斯混合模型（GMM）是指有限个独立的多元高斯分布模型的线性组合, 是一元高斯分布在高维空间的扩展。GMM是学习速度最快的概率模型, 通过拟合输入数据集构建合适的混合多维高斯分布模型, 达到无监督聚类的目的, 提供合理高效的数据分布规律与划分方案。基于GMM的聚类方法在图像分割、信号处理、生物医学和地球科学等领域取得重要应用[25, 26, 27, 28, 29, 30, 31]。根据高斯混合模型的基本概念[26, 27, 28, 29], 测井数据体的概率密度函数可表示为（1）式— （3）式。

$p(X)=\sum\limits_{k=1}^{N}{{{W}_{k}}\varphi (X, {{\mathbf{M}}_{k}}}, {{\mathbf{D}}_{k}})$ （1）

$\varphi ( X, {{\mathbf{M}}_{k}}, {{\mathbf{D}}_{k}} )=\frac{1}{{\sqrt{|{\mathbf{D}}_{k}}|}( 2 \pi)^{d/2}}\exp \left[ -\frac{1}{2}{{\left( X-{{M }_{k}} \right)}^{\text{T}}}\frac{1}{{{\mathbf{D}}_{k}}}\left( X-{{M }_{k}} \right) \right]$ （2）

$\sum\limits_{k=1}^{N}{{{W}_{k}}=1}\left( 0\le {{W}_{k}}\le 1 \right)$ （3）

GMM聚类需求解出每个高斯基函数的均值、标准差和权重矩阵, 一般采用期望最大化（EM）算法。EM算法的基本思想是通过引入隐含变量求解高斯混合模型分布函数的最大似然估计, 再对隐含变量期望公式和模型分布参数重估公式进行迭代, 直至似然函数值收敛[26, 31, 32, 33]。为降低计算复杂度, 对似然函数取对数, 如（4）式。求解高斯混合模型的参数可转化为求对数似然函数的极大值, 如（5）式。

$\theta \left( \mathbf{X} \right)=\ln \underset{i=1}{\overset{M}{\mathop{\prod }}}\, p\left( {{X}_{i}}|M , \mathbf{D}, W \right)$ （4）

$\Theta \left( \mathbf{X} \right)\text{=}\arg \left\{ \max \left[ \ln \underset{i=1}{\overset{M}{\mathop{\prod }}}\, p\left( {{X}_{i}}|M , \mathbf{D}, W \right) \right] \right\}$ （5）

EM算法分两步, 第1步求期望值（称为E步）, 第2步求极大值（称为M步）, 具体迭代步骤为：①初始化模型参数, 设均值矩阵Mk为随机矩阵, 设方差矩阵Dk为单位矩阵, 模型的权重矩阵Wk为每个模型的先验概率; ②求出每个深度（或测量点）的测井数据属于各高斯模型的先验概率, 如（6）式; ③利用先验概率更新高斯混合模型中的各组参数, 如（7）式— （9）式; ④重复步骤②和步骤③, 直至满足（10）式收敛条件。

$p\left( {{X}_{i}}|{{M }_{k}}, {{\mathbf{D}}_{k}}, {{W}_{k}} \right)\text{=}\frac{{{W}_{k}}\varphi \left( {{X}_{i}}|{{M }_{k}}, {{\mathbf{D}}_{k}}, {{W}_{k}} \right)}{\sum\limits_{j=1}^{N}{{{W}_{j}}\varphi \left( {{X}_{i}}|{{M }_{j}}, {{\mathbf{D}}_{j}}, {{W}_{j}} \right)}} \\ \left( k=1, 2, \cdots , N \right)$ （6）

${{M }_{k}}=\frac{\sum\limits_{i=1}^{M}{p\left( {{X}_{i}}|{{M }_{k}}, {{\mathbf{D}}_{k}}, {{W}_{k}} \right){{X}_{i}}}}{\sum\limits_{i=1}^{M}{p\left( {{X}_{i}}|{{M }_{k}}, {{\mathbf{D}}_{k}}, {{W}_{k}} \right)}}$ （7）

${{\mathbf{D}}_{k}}=\frac{\sum\limits_{i=1}^{M}{p\left( {{X}_{i}}|{{M }_{k}}, {{\mathbf{D}}_{k}}, {{W}_{k}} \right)\left( {{X}_{i}}-{{M }_{k}} \right){{\left( {{X}_{i}}-{{M }_{k}} \right)}^{\text{T}}}}}{\sum\limits_{i=1}^{M}{p\left( {{X}_{i}}|{{M }_{k}}, {{\mathbf{D}}_{k}}, {{W}_{k}} \right)}}$ （8）

${{W}_{k}}=\frac{1}{M}\sum\limits_{i=1}^{M}{p\left( {{X}_{i}}|{{M }_{k}}, {{\mathbf{D}}_{k}}, {{W}_{k}} \right)}$ （9）

$|\theta {{\left( \mathbf{X} \right)}_{j}}-\theta {{\left( \mathbf{X} \right)}_{j-1}}|< \varepsilon $ （10）

确定合理的聚类群集数是求解高斯混合模型的关键, 聚类群集数太大会造成过拟合, 聚类群集数太小则会使模型缺乏灵活性而不能更好地拟合新数据。常用的聚类群集数确定方法是赤池信息（AIC）准则。AIC准则是基于信息熵的概念, 选择信息损失最小的模型[34, 35, 36, 37], 如（11）式。

$AIC=-2\ln (L)+2p$ （11）

可见, AIC准则是确定最佳聚类群集数的基础。前人在确定最佳聚类群集的过程中发现, 单纯依赖AIC可能会出现单调递减的现象, 因此提出采用AIC变化率来确定最佳聚类群集, 在一定程度上可反映AIC对聚类群集数目增加的敏感程度[38]。

本文采用AIC变化率确定最佳聚类群集数, 如（12）式。当聚类群集数目从p增加到p+1时, 如果AIC变化率较大, 说明聚类群集数为p描述原始数据集的聚类精度不足; 反之则说明p个聚类群集和p+1个聚类群集的聚类结果相差不大; 出于计算成本考虑, 可认为p为最佳聚类群集, 其对应的AIC变化率达到最小。

$\Delta AIC(p)=\frac{\text{ }\!\!|\!\!\text{ }AIC(p)-AIC(p+1)|}{AIC(p)}\times 100\%$ （12）

2 T2谱的高斯混合模型聚类数值模拟

鉴于T2谱是孔隙结构和流体组分等岩石物理信息的综合反映, 同一个测井深度的核磁共振T2谱可得到多个弛豫时间的占比信息, 符合高斯分布。因此, 可以通过GMM聚类算法对T2谱进行处理, 得到无监督聚类结果, 为孔隙结构评价和储集层划分提供依据。

由于T2谱数据量较大, 在进行GMM聚类之前需要通过主成分方法进行降维以减弱数据间的相关性, 并提高计算效率。首先通过数值模拟对GMM聚类方法的适用性和有效性进行测试, 在此基础上对实际的核磁共振测井数据进行处理。

2.1 T2谱主成分降维

T2谱由不同的弛豫时间所对应幅度构成, 数据维度取决于反演布点数, 不同弛豫时间对应的幅度矩阵具有一定相关性。为降低T2谱数据的冗余信息, 突出不同弛豫时间对应幅值的可分析因素, 采用主成分分析方法使多维数据信息矩阵映射到低维空间, 提取最具代表性的主成分[38, 39]。

假设核磁共振测井T2谱的布点数目为L, 某一深度段内共有M组观测数据, 则可以将这些T2谱表示为（13）式的观测矩阵。由于不同弛豫时间所对应的幅度组成的列向量存在一定的相关性, 采用主成分分析可以将其变换成少数几列线性不相关且包含最大信息量的新矩阵, 提升计算效率。利用（14）和（15）式对原始观测矩阵进行主成分变换。

$X=\left[ \begin{matrix} {{X}_{11}} & {{X}_{12}} & ... & {{X}_{1L}} \\ {{X}_{21}} & {{X}_{22}} & ... & {{X}_{2L}} \\ \vdots & \vdots & \vdots & \vdots \\ {{X}_{M1}} & {{X}_{M2}} & ... & {{X}_{ML}} \\\end{matrix} \right]$ （13）

$Y=U{{X}^{\text{T}}}$ （14）

$U=\left[ \begin{matrix} {{U}_{11}} & {{U}_{12}} & ... & {{U}_{1L}} \\ {{U}_{21}} & {{U}_{22}} & ... & {{U}_{2L}} \\ \vdots & \vdots & \vdots & \vdots \\ {{U}_{L1}} & {{U}_{L2}} & ... & {{U}_{LL}} \\ \end{matrix} \right]$ （15）

主成分分析算法的基本原理和计算方法可见相关文献[38, 39, 40], 具体步骤包括：①原始数据标准化; ②计算相关矩阵, 得到特征向量和对应的特征值; ③根据特征值的分布计算累计方差贡献率; ④设置贡献率截止值, 提取主成分信号。

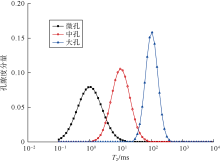
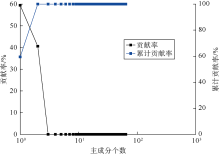
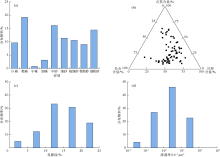
首先采用3个对数高斯函数正演400组核磁共振T2谱（见图1）, 主要控制T2谱的峰值为1, 10, 100 ms, 主要控制T2谱分布范围的方差为0.4, 0.3, 0.2, 弛豫时间为0.1~10 000.0 ms的对数均匀布点（64个点）。核磁共振T2谱数据的幅度为随机生成, 通过归一化处理降低了孔隙度对计算结果的影响。当孔隙流体均为水时, T2谱可代表微孔、小孔和中孔。统计结果显示, 微孔的T2谱区间为0.1~14.0 ms, 小孔的T2谱区间为1.3~86.0 ms, 中孔的T2谱区间为24~372 ms。为便于分析, 对每组T2谱幅度进行归一化处理。图2显示了正演模拟的核磁共振T2谱数据的主成分数与贡献率、累计贡献率的关系, 当主成分数为2时, 累计贡献率可达99.95%, 说明不同弛豫时间对应的幅度存在高度的相关性, 在进行高斯混合模型聚类时, 仅需对前2个主成分数据进行处理。

图1 对数高斯基函数T2谱

图2 正演T2谱的主成分贡献率

2.2 聚类群集数确定及结果分析

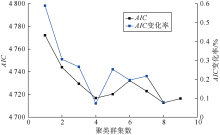
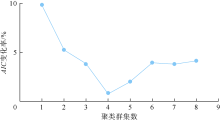
将降维后的2个主成分作为输入数据, 用EM算法进行GMM聚类, 迭代阈值为0.01, 最大迭代次数为10 000, 最大聚类群集数为9。图3显示不同聚类群集数的AIC及其变化率, 当聚类群集数为4时AIC的变化率达到最小值, 为0.073%, 说明此时拟合结果达到最优。综合考虑拟合精度和计算成本, 确定最佳聚类群集数为4。

图3 AIC及AIC变化率与聚类群集数的关系

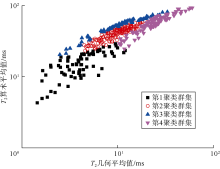
计算4个聚类群集的T2几何平均值和T2算术平均值, 并将两者进行交会（见图4）。从第1聚类群集至第4聚类群集, T2几何平均值与T2算术平均值均呈增大趋势, 但第2聚类群集至第4聚类群集的T2几何平均值和T2算术平均值的区分度低, 采用T2平均值或简单的交会图难以有效划分聚类群集。

图4 不同聚类群集的T2几何平均值与算术平均值交会图

图5是不同聚类群集的第1主成分和第2主成分交会图。与图4相比, 不同聚类群集在主成分交会中的区分度更加明显, 进一步验证了基于高斯混合模型的聚类结果的正确性。

图5 不同聚类群集的第1主成分和第2主成分交会图

聚类群集对应4个高斯模型的加权系数分布显示（见图6）, 聚类群集与高斯模型的加权系数对应较好。采用GMM聚类不仅能得到分类结果, 还能依据群集概率分配群集成员, 具有更灵活的类簇形状, 得到样本点隶属于各类的概率值, 能够有效避免硬分配, 所带信息量优于硬分配聚类[30]。

图6 不同聚类群集的高斯混合模型加权系数分布

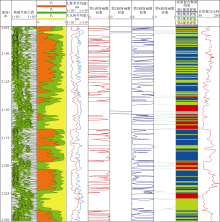
将上述算法进行整合并对核磁共振测井数据进行处理（见图7）, 与传统的核磁共振测井解释剖面相比, 本文方法可得到量化的高斯混合聚类结果及不同聚类群集的隶属度值, 可更加直观地解剖T2谱及相关地质信息。

图7 数值模拟核磁共振T2谱的GMM聚类解释成果

3 核磁共振测井T2谱的高斯混合模型聚类效果

柴达木盆地西北部阿尔金山前东段牛东地区侏罗系为辫状河三角洲平原亚相沉积, 岩性较粗, 以中— 粗砂岩为主, 成分为长石岩屑砂岩或岩屑长石砂岩, 填隙物含量低, 主要为高岭石和方解石; 储集空间主要为次生孔, 其次为粒间孔, 分布均匀且连通性较好; 储集层物性较好, 孔隙度为5%~20%, 平均值为11.3%, 渗透率为（0.1~100.0）× 10-3 μ m2, 平均值为5.0× 10-3 μ m2（见图8）。

图8 柴达木盆地牛东地区侏罗系储集层岩性和物性特征
（a）岩石粒度分布图; （b）岩石成分端元图; （c）孔隙度分布直方图; （d）渗透率分布直方图

XX-1井采用哈里伯顿公司的MRIL_P型仪器采集核磁共振信号, 采集模式为D9TW。对长等待时间（12.988 s）、短回波间隔（0.9 ms）的测量数据进行处理, 在主成分降维时贡献率阈值设为90%, 将64个横向弛豫时间对应的列向量压缩至7个主成分。对主成分矩阵进行GMM聚类, AIC变化率如图9所示, 结合AIC变化率准则得到4个聚类群集, 以0.3, 10.0, 100.0 ms为T2界限, 得到弛豫时间为0.3~10.0 ms的相对幅度占比（P1）、弛豫时间为10~100 ms的相对幅度占比（P2）、弛豫时间大于100 ms的相对幅度占比（P3）（见图10）。

图9 XX-1井侏罗系核磁共振测井T2谱AIC变化率

图10 XX-1井侏罗系核磁共振测井T2谱聚类结果

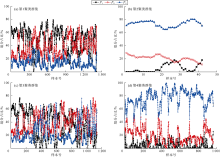
对核磁共振测井T2谱进行高斯混合聚类分析, 得到4个聚类群集的不同弛豫组分占比分布显示（见图11）, 聚类群集与不同弛豫组分占比相关性较好。第1聚类群集的P1最大、P3最小, 说明小孔隙占比较大。第2聚类群集的P3最大、P1最小, 说明大孔隙占比较大。第3聚类群集的弛豫分布较复杂, 无明显占优。第4聚类群集与第2聚类群集基本一致。

图11 XX-1井侏罗系4个聚类群集的不同弛豫区间占比

4个聚类群集的不同弛豫组分占比分布显示（见图11）, 聚类群集与不同弛豫组分占比相关性较好。第1聚类群集的P1最大、P3最小, 说明小孔隙占比较大。第2聚类群集的P3最大、P1最小, 说明大孔隙占比较大。第3聚类群集的弛豫分布较复杂, 无明显占优。第4聚类群集与第2聚类群集基本一致。

XX-1井在侏罗系总共有3个试气层位。2 074.5~2 082.5 m井段6 mm油嘴压后自喷日产气2 422 m3, 试气结论为低产气层, GMM聚类结果显示为第3聚类群集。2 146.5~2 153.5 m井段10 mm油嘴自喷日产气13 2942 m3, 日产油13.27 t, 试气结论为高产气层, 聚类结果显示为第4聚类群集。2 228.5~2 240.5 m井段5 mm油嘴压后自喷日产气22 484 m3, 日产油0.42 t, 试气结论为高产气层, 聚类结果为第4群集。2 228.5~2 240.5 m井段岩心铸体薄片照片显示岩石粒度相对较粗, 以（含砾）巨— 粗粒长石岩屑砂岩为主, 以颗粒支撑为主, 次棱磨圆度, 点接触, 孔隙式胶结类型, 石英表面干净, 具波状消光, 长石风化程度深, 岩屑以石英岩为主, 填隙物少, 孔隙较发育, 储集空间主要为粒间溶孔、粒内溶孔、基质微孔隙（见图12）。2 096~2 103 m井段自然伽马值较高的泥岩段的聚类结果为第1聚类群集。

图12 XX-1井侏罗系2 228.5~2 240.5 m试气层段岩心铸体薄片照片
（a）取样深度2 230.07 m, 含砾粗— 巨粒长石岩屑砂岩, 粗巨粒结构, 填隙物少, 孔隙较发育; （b）取样深度2 231.10 m, 巨— 粗粒岩屑砂岩, 巨粗粒结构, 填隙物少, 孔隙较发育; （c）取样深度2 233.69 m, 巨— 粗粒岩屑砂岩, 填隙物少, 孔隙较发育; （d）取样深度2 236.08 m, 含泥不等粒岩屑长石砂岩, 不等粒结构, 填隙物有泥质、方解石, 孔隙不发育

4 结语

依据核磁共振测井T2谱特征, 提出基于高斯混合模型（GMM）聚类的T2谱处理技术, 实现T2谱的无监督自动聚类。采用主成分分析对T2谱数据降维压缩, 降低输入数据之间的相关性, 提高聚类算法的计算效率。采用AIC及AIC变化率确定高斯混合模型的个数, 得到最佳聚类群集, 提升GMM聚类结果的合理性。通过数值模拟和实测资料的处理解释, 验证了方法的有效性和可行性。T2谱的聚类结果与孔隙结构、储集空间类型和储集层产能具有较好的对应性, 定量表征结果能够更为直观地反映储集层类型和孔隙结构。

值得注意的是, 数值模拟数据并未考虑流体性质差异对T2谱的影响, 而实际储集层中的核磁共振测井响应往往是由岩性、流体和孔隙结构等多种因素耦合而成。下一步将对算法进行完善, 实现复杂条件下流体信息和孔隙结构的区分。对于岩性和孔隙结构复杂的储集层, 如果能在细分岩性的基础上开展核磁共振测井T2谱的GMM聚类分析, 或者通过岩心实验、试油、生产动态数据来约束聚类数目, 在一定程度上能提升聚类效果以及解释的合理性。

符号注释：

AIC— — 赤池信息准则量; d— — 测井数据的物理维度; Dk— — 第k个高斯基函数的方差矩阵; i— — 测井观测数据的序号; j— — 迭代次数; k— — 高斯基函数的序号; L— — 核磁共振测井T2谱的布点数目; M— — 测井数据的样本数; Mk— — 第k个高斯基函数的均值矩阵; N— — 高斯基函数的个数; p— — 聚类群集个数; p（X）— — 总体概率密度函数; Wk— — 第k个高斯基函数的权重矩阵; X— — 测井数据矩阵; Y— — 测井数据对应的主成分矩阵; U— — 测井数据对应的基矩阵; θ （X）— — 对数似然函数; θ （X）j— — 第j次迭代的对数似然函数; φ （X, Mk, Dk）— — 第k个高斯基函数的概率密度函数; ε — — 对数似然函数的迭代阈值; Θ （X）— — 对数似然函数的极大值。

致谢：中国石油天然气集团有限公司测井重点实验室运行基金的资助, 中国石油青海油田公司勘探开发研究院提供核磁共振测井资料和基础地质成果, 中国石油勘探开发研究院西北分院刘建宇博士提出宝贵建议, 在此一并表示感谢。

（编辑 王晖）

参考文献
[1] 肖立志. 核磁共振成像测井与岩石核磁共振及其应用[M]. 北京: 科学出版社, 1998.
XIAO Lizhi. Nuclear magnetic resonance imaging logging and rock nuclear magnetic resonance and its application[M]. Beijing: Science Press, 1998. [本文引用:1]
[2] 肖立志, 谢然红, 廖广志. 中国复杂油气藏核磁共振测井理论与方法[M]. 北京: 科学出版社, 2012.
XIAO Lizhi, XIE Ranhong, LIAO Guangzhi. Theory and method of NMR logging for Chinese complex oil and gas reservoirs[M]. Beijing: Science Press, 2012. [本文引用:1]
[3] DUNN K J, BERGMAN D J, LATORRACA G A. Nuclear magnetic resonance petrophysical and logging applications[M]. New York: Elsevier, 2002. [本文引用:1]
[4] 胡法龙, 周灿灿, 李潮流, 等. 基于弛豫-扩散的二维核磁共振流体识别方法[J]. 石油勘探与开发, 2012, 39(5): 552-558.
HU Falong, ZHOU Cancan, LI Chaoliu, et al. Fluid identification method based on 2D diffusion-relaxation nuclear magnetic resonance (NMR)[J]. Petroleum Exploration and Development, 2012, 39(5): 552-558. [本文引用:1]
[5] MUTINA A, BACHMAN N, RENDON L. Fast multidimensional NMR logging provides advanced fluid characterization at a step change in logging speed[R]. London, UK: SPWLA 59th Annual Logging Symposium, 2018. [本文引用:1]
[6] SUN B Q. In situ fluid typing and quantification with 1D and 2D NMR logging[J]. Magnetic Resonance Imaging, 2007, 25(4): 521-524. [本文引用:1]
[7] KAUSIK R, JIANG T M, VENKATARAMANAN L, et al. Reservoir producibility index (RPI) based on 2D T1-T2 NMR logs[R]. Texas, USA: SPWLA 60th Annual Logging Symposium, 2019. [本文引用:1]
[8] ZHANG H, WANG Y, FANG T, et al. First application of new generation NMR T1-T2 logging and interpretation in unconventional reservoirs in China[R]. SPE 202261-MS, 2020. [本文引用:1]
[9] 范宜仁, 刘建宇, 葛新民, 等. 基于核磁共振双截止值的致密砂岩渗透率评价新方法[J]. 地球物理学报, 2018, 61(4): 1628-1638.
FAN Yiren, LIU Jianyu, GE Xinmin, et al. Permeability evaluation of tight sand stone based on dual T2 cutoff values measured by NMR[J]. Chinese Journal of Geophysics, 2018, 61(4): 1628-1638. [本文引用:1]
[10] 李鹏举, 谷宇峰. 核磁共振T2谱转换伪毛管压力曲线的矩阵方法[J]. 天然气地球科学, 2015, 26(4): 700-705.
LI Pengju, GU Yufeng. Matrix method of transforming NMR T2 spectrum to pseudo capillary pressure curve[J]. Natural Gas Geoscience, 2015, 26(4): 700-705. [本文引用:1]
[11] 闫建平, 温丹妮, 李尊芝, 等. 基于核磁共振测井的低渗透砂岩孔隙结构定量评价方法: 以东营凹陷南斜坡沙四段为例[J]. 地球物理学报, 2016, 59(4): 1543-1552.
YAN Jianping, WEN Danni, LI Zunzhi, et al. The quantitative evaluation method of low permeable sand stone pore structure based on nuclear magnetic resonance (NMR) logging[J]. Chinese Journal of Geophysics, 2016, 59(4): 1543-1552. [本文引用:1]
[12] GE X M, FAN Y R, ZHU X J, et al. Determination of nuclear magnetic resonance T2 cutoff value based on multifractal theory: An application in sand stone with complex pore structure[J]. Geophysics, 2015, 80(1): 11-21. [本文引用:1]
[13] 丁娱娇, 柴细元, 邵维志, 等. 基于核磁共振T2谱集中度的低孔隙度低渗透率储层饱和度参数研究[J]. 测井技术, 2017, 41(4): 405-411.
DING Yujiao, CHAI Xiyuan, SHAO Weizhi, et al. Key parameters of water saturation based on concentration of T2 spectrum distribution[J]. Well Logging Technology, 2017, 41(4): 405-411. [本文引用:1]
[14] 白松涛, 程道解, 万金彬, 等. 砂岩岩石核磁共振T2谱定量表征[J]. 石油学报, 2016, 37(3): 382-391.
BAI Songtao, CHENG Daojie, WAN Jinbin, et al. Quantitative characterization of sand stone NMR T2 spectrum[J]. Acta Petrolei Sinica, 2016, 37(3): 382-391. [本文引用:1]
[15] 张超谟, 陈振标, 张占松, 等. 基于核磁共振T2谱分布的储层岩石孔隙分形结构研究[J]. 石油天然气学报, 2007, 29(4): 80-86.
ZHANG Chaomo, CHEN Zhenbiao, ZHANG Zhansong, et al. Fractal characteristics of reservoir rock pore structure based on NMR T2 distribution[J]. Journal of Oil and Gas Technology, 2007, 29(4): 80-86. [本文引用:1]
[16] GE X M, FAN Y R, CAO Y C, et al. Reservoir pore structure classification technology of carbonate rock based on NMR T2 spectrum decomposition[J]. Applied Magnetic Resonance, 2014, 45(2): 155-167. [本文引用:1]
[17] 钟吉彬, 阎荣辉, 张海涛, 等. 核磁共振横向弛豫时间谱分解法识别流体性质[J]. 石油勘探与开发, 2020, 47(4): 691-702.
ZHONG Jibin, YAN Ronghui, ZHANG Haitao, et al. A decomposition method of nuclear magnetic resonance T2 spectrum for identifying fluid properties[J]. Petroleum Exploration and Development, 2020, 47(4): 691-702. [本文引用:1]
[18] BAUER K, KULENKAMPFF J, HENNINGES J, et al. Lithological control on gas hydrate saturation as revealed by signal classification of NMR logging data[J]. Journal of Geophysical Research. Solid Earth, 2015, 120(9): 6001-6017. [本文引用:1]
[19] ANAND V. Novel methodology for accurate resolution of fluid signatures from multi-dimensional NMR well-logging measurements[J]. Journal of Magnetic Resonance, 2017, 276: 60-68. [本文引用:1]
[20] ROJAS P A, RINCÓN M, NETTO P, et al. Application of machine learning tool to separate overlapping fluid components on NMR T2 distributions: Case studies from laboratory displacement experiment and well logs[R]. SPE 197684-MS, 2019. [本文引用:1]
[21] XU R, DENG T Q, JIANG J J, et al. Integration of NMR and conventional logs for vuggy facies classification in the Arbuckle Formation: A machine learning approach[J]. SPE Reservoir Evaluation & Engineering, 2020, 23(3): 917-929. [本文引用:1]
[22] 孟昆, 王胜建, 薛宗安, 等. 利用核磁共振资料定量评价页岩孔隙结构[J]. 波谱学杂志, 2021, 38(2): 215-226.
MENG Kun, WANG Shengjian, XUE Zong’an, et al. Quantitative evaluation of shale pore structure using nuclear magnetic resonance data[J]. Chinese Journal of Magnetic Resonance, 2021, 38(2): 215-226. [本文引用:1]
[23] 闫伟林, 张兆谦, 陈龙川, 等. 基于核磁共振技术的古龙页岩含油饱和度评价新方法[J]. 大庆石油地质与开发, 2021, 40(5): 78-86.
YAN Weilin, ZHANG Zhaoqian, CHEN Longchuan, et al. New evaluating method of oil saturation in Gulong shale based on NMR technique[J]. Petroleum Geology & Oilfield Development in Daqing, 2021, 40(5): 78-86. [本文引用:1]
[24] 陈惠, 冯春珍, 赵建鹏, 等. 基于分形与核磁共振测井的储层孔隙结构表征与分类[J]. 测井技术, 2021, 45(1): 50-55.
CHEN Hui, FENG Chunzhen, ZHAO Jianpeng, et al. Pore structure characterization and classification based on fractal theory and nuclear magnetic resonance logging[J]. Well Logging Technology, 2021, 45(1): 50-55. [本文引用:1]
[25] 高新, 靳国旺, 熊新, 等. 融合差异图与高斯混合模型相结合的SAR图像变化检测[J]. 测绘科学技术学报, 2020, 37(1): 68-73.
GAO Xin, JIN Guowang, XIONG Xin, et al. Change detection in synthetic aperture radar images based on image fusion and Gaussian mixture model[J]. Journal of Geomatics Science and Technology, 2020, 37(1): 68-73. [本文引用:1]
[26] 戚贵玲, 何冰冰, 张榆锋, 等. 基于高斯混合模型聚类的B超图像颈动脉内膜和中膜厚度检测[J]. 生物医学工程学杂志, 2020, 37(6): 1080-1088.
QI Guiling, HE Bingbing, ZHANG Yufeng, et al. Detection of carotid intima and media thicknesses based on ultrasound B-mode images clustered with Gaussian mixture model[J]. Journal of Biomedical Engineering, 2020, 37(6): 1080-1088. [本文引用:3]
[27] 张美霞, 李丽, 杨秀, 等. 基于高斯混合模型聚类和多维尺度分析的负荷分类方法[J]. 电网技术, 2020, 44(11): 4283-4293.
ZHANG Meixia, LI Li, YANG Xiu, et al. A load classification method based on Gaussian mixture model clustering and multi-dimensional scaling analysis[J]. Power System Technology, 2020, 44(11): 4283-4293. [本文引用:2]
[28] 兰志刚, 靳卫卫, 朱明亮, 等. 基于高斯混合模型的海冰图像非监督聚类分割研究[J]. 海洋科学, 2011, 35(11): 97-100.
LAN Zhigang, JIN Weiwei, ZHU Mingliang, et al. Sea ice image segmentation with unsupervised clustering based on the Gaussian mixture model[J]. Marine Sciences, 2011, 35(11): 97-100. [本文引用:2]
[29] 张宝一, 陆浩, 杨莉, 等. 顾及梯度的高斯混合模型在三维属性场空间聚类中的应用[J]. 地质找矿论丛, 2019, 34(3): 460-470.
ZHANG Baoyi, LU Hao, YANG Li, et al. Application of the gradient-based Gaussian mixture model to spatial clustering of three-dimensional attribute field[J]. Contributions to Geology and Mineral Resources Research, 2019, 34(3): 460-470. [本文引用:2]
[30] 王亚利, 都伟冰, 王双亭. 高斯混合模型自动阈值法遥感冰川信息提取[J]. 遥感学报, 2021, 25(7): 1434-1444.
WANG Yali, DU Weibing, WANG Shuangting. Extracting glacier information from remote sensing imageries by automatic threshold method of Gaussian mixture model[J]. Journal of Remote Sensing, 2021, 25(7): 1434-1444. [本文引用:2]
[31] YANG M S, LAI C Y, LIN C Y. A robust EM clustering algorithm for Gaussian mixture models[J]. Pattern Recognition, 2012, 45(11): 3950-3961. [本文引用:2]
[32] NOWAKOWSKA E, KORONACKI J, LIPOVETSKY S. Clusterability assessment for Gaussian mixture models[J]. Applied Mathematics and Computation, 2015, 256: 591-601. [本文引用:1]
[33] 王一妹, 刘辉, 宋鹏, 等. 基于高斯混合模型聚类的风电场短期功率预测方法[J]. 电力系统自动化, 2021, 45(7): 37-43.
WANG Yimei, LIU Hui, SONG Peng, et al. Short-term power forecasting method of wind farm based on Gaussian mixture model clustering[J]. Automation of Electric Power Systems, 2021, 45(7): 37-43. [本文引用:1]
[34] 柴秀俊, 王宏伟, 王林, 等. 基于高斯混合聚类的切换系统的辨识[J]. 控制理论与应用, 2021, 38(5): 634-640.
CHAI Xiujun, WANG Hongwei, WANG Lin, et al. Identification of switched systems based on Gaussian mixture clustering[J]. Control Theory & Applications, 2021, 38(5): 634-640. [本文引用:1]
[35] FRIEL N, MCKEONE J P, OATES C J, et al. Investigation of the widely applicable Bayesian information criterion[J]. Statistics and Computing, 2017, 27(3): 833-844. [本文引用:1]
[36] 张发才, 李喜旺, 樊国旗. 基于高斯混合聚类的风电出力场景划分[J]. 计算机系统应用, 2021, 30(1): 146-153.
ZHANG Facai, LI Xiwang, FAN Guoqi. Wind power output scene division based on Gaussian hybrid clustering[J]. Computer Systems & Applications, 2021, 30(1): 146-153. [本文引用:1]
[37] GE X M, WANG H, FAN Y R, et al. Joint inversion of T1-T2 spectrum combining the iterative truncated singular value decomposition and the parallel particle swarm optimization algorithms[J]. Computer Physics Communications, 2016, 198: 59-70. [本文引用:1]
[38] 周海涛, 王志刚, 刘昌明. 基于主成分分析和高斯混合模型的耐火材料损伤信号分类[J]. 武汉科技大学学报, 2014, 37(4): 269-272.
ZHOU Haitao, WANG Zhigang, LIU Changming. Classification of refractory damage signals based on the principal component analysis and Gaussian mixture model[J]. Journal of Wuhan University of Science and Technology, 2014, 37(4): 269-272. [本文引用:3]
[39] 申波, 毛志强, 樊海涛, 等. 基于主成分分析技术计算蚀变地层孔隙度的新方法[J]. 测井技术, 2012, 36(2): 130-134.
SHEN Bo, MAO Zhiqiang, FAN Haitao, et al. A new porosity calculation method based on principal component analytical technology for altered formation[J]. Well Logging Technology, 2012, 36(2): 130-134. [本文引用:2]
[40] 钟仪华, 李榕, 张志银, 等. 基于主成分分析的离散过程神经网络水淹层动态预测方法[J]. 测井技术, 2010, 34(5): 432-436.
ZHONG Yihua, LI Rong, ZHANG Zhiyin, et al. Dynamic recognition method for water-flooded layer with discrete process neural network based on the principal component analysis[J]. Well Logging Technology, 2010, 34(5): 432-436. [本文引用:1]