第一作者简介:李焕然(1994-),男,陕西扶风人,中国石油大学(华东)在读博士研究生,主要从事声波测井的理论方法和应用研究。地址:山东省青岛市黄岛区长江西路66号,中国石油大学(华东)地球科学与技术学院,邮政编码:266580。E-mail:kestrel2012@live.com
针对现有地层压裂效果评估的声波测井方法通常用压裂缝密度来评价压裂缝体积,其结果往往不能准确反映实际产能的问题,研究了压裂缝的动态渗透性能及其与测井声场的相互作用,在实验观测的压裂缝分形现象基础上建立复杂压裂缝网的渗透率模型,将该模型的动态渗流响应与描述渗透性地层声波传播的Biot-Rosenbaum理论相结合,得到斯通利波速度频散特征与压裂缝渗透性能的关系,进而提出压裂缝渗透性能的评价方法。研究结果表明:复杂压裂缝导致的斯通利波速度频散特征可以与平板缝模型等效,前提是将压裂缝模型的平均渗透率等效于平板缝的渗透率;压裂缝开启的高渗条件(缝宽为10~100 μm,渗透率为数百平方微米)和压裂缝闭合渗透率降低条件(缝宽为1~10 μm,渗透率为数十平方微米)下,斯通利波速度频散特征具有明显差异。现场应用结果表明,提出的渗透性能定量评价模型可以评价压裂缝的渗透率和压裂贯通系数。
The existing acoustic logging methods for evaluating the hydraulic fracturing effectiveness usually use the fracture density to evaluate the fracture volume, and the results often cannot accurately reflect the actual productivity. This paper studies the dynamic fluid flow through hydraulic fractures and its effect on borehole acoustic waves. Firstly, based on the fractal characteristics of fractures observed in hydraulic fracturing experiments, a permeability model of complex fracture network is established. Combining the dynamic fluid flow response of the model with the Biot-Rosenbaum theory that describes the acoustic wave propagation in permeable formations, the influence of hydraulic fractures on the velocity dispersion of borehole Stoneley-wave is then calculated and analyzed, whereby a novel hydraulic fracture fluid transport property evaluation method is proposed. The results show that the Stoneley-wave velocity dispersion characteristics caused by complex fractures can be equivalent to those of the plane fracture model, provided that the average permeability of the complex fracture model is equal to the permeability of the plane fracture. In addition, for fractures under high-permeability (fracture width 10~100 μm, permeability ~100 μm2) and reduced permeability (1~10 μm, ~10 μm2, as in fracture closure) conditions, the Stoneley-wave velocity dispersion characteristics are significantly different. The field application shows that this fluid transport property evaluation method is practical to assess the permeability and the connectivity of hydraulic fractures.
通过研究地层中裂缝(天然或人工压裂)渗透性对弹性波传播的影响, 已发展出基于微地震、VSP(垂直地震剖面)和井筒管波等多种测量技术的裂缝评价方法[1, 2, 3]。近年来中国在“ 深海、深地” 大力开展油气勘探, 勘探深度的增加, 导致成本上升和测量精度降低, 影响了这些方法的评价效果。
声波测井作为井下常用探测技术, 具有原位测量、精度高等优势。测井中的低频斯通利波在渗透性地层中产生的动态渗流效应已有大量的理论[4, 5]和实验[6, 7]研究, 利用斯通利波传播中的反射、透射以及波的频散和衰减的裂缝评价方法已有广泛应用[8, 9]。但是, 这些方法主要是针对天然裂缝, 在压裂缝中的应用鲜有报道。压裂缝的形态较为复杂, 在空间展布上具有分形特征[10], 此外其渗透性能变化巨大, 压裂缝缝宽从初期支撑开启时的百微米级(渗透率为数百平方微米)降至压实闭合时的微米级(渗透率为几个至数十平方微米)甚至更低, 这些变化导致测井声场发生复杂变化。另一个必须考虑的重要因素是, 压裂施工前普遍需要固井和射孔完井, 在射孔后的套管井条件下, 压裂缝中的渗流与井孔声场的相互作用只能通过射孔孔眼进行, 其耦合条件和裸眼井与天然裂缝的耦合条件有较大差异。
针对上述压裂缝的各种相关因素, 本文从实验压裂数据出发建立压裂缝的渗透率模型, 用有限差分方法求解动态渗流的扩散型波动方程, 再利用简化的Biot-Rosenbaum(B-R)理论[11]将压裂缝的动态渗流通过套管井壁的射孔与井孔声场耦合。据此分析斯通利波的速度频散特征与压裂缝渗透性能的关系, 得到压裂缝渗透性能的评价方法, 并用现场实例验证方法的有效性。
压裂地层是由低渗透基岩和压裂缝网组成的复杂非均匀渗透介质, 在角频率为ω 的波动激励下, 介质内部流体空间x处的动态渗流满足的扩散型波动方程[11]为:
${{\nabla }^{2}}p+\frac{\text{i}\omega }{\alpha (\omega , x)}p=0$ (1)
(1)式中, α 为流体扩散率, 其表达式为:
$\alpha (\omega , x)=\frac{K(\omega , x){{K}_{\text{f}}}}{\phi \mu (1+\xi )}$ (2)
(2)式中, ξ 为介质骨架弹性的修正量, 假设岩石骨架相对于流体不可压缩, 可取ξ =0; K(ω , x)为Johnson等描述动态渗流的动态渗透率[12], 其表达式为:
$K(\omega , x)=\frac{{{K}_{0}}(x)}{\sqrt{1-\frac{\text{i}\tau {{K}_{0}}(x)\rho \omega }{m\mu \phi }}-\frac{\text{i}\tau {{K}_{0}}(x)\rho \omega }{\mu \phi }}$ (3)
(3)式中, K0(x)是ω =0时的静态渗透率, 为空间坐标x的函数。τ 和m与孔隙或裂缝形状有关[12]:在孔隙型介质中, τ ≈ 3, m=2, ϕ 为实际孔隙度; 在裂缝型介质中, τ =1, m=3, ϕ =1。K(ω , x)随频率的变化可以使(1)式描述的流体压力传导从低频时的黏滞渗流(扩散型方程)变化到高频时的声压传播(波动型方程)[11]。
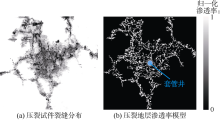
压裂地层的非均匀性导致(3)式中K0(x)在空间上的变化。假设压裂缝在井轴方向的排列具有相似的形态, 只考虑K0(x)在与井轴(z轴)垂直平面(xOy)上的变化, 即K0(x)=K0(x, y), 可将压裂地层的模拟简化为二维平面模型。研究人员对压裂缝展布的空间形态做了大量实验研究, 用等比例缩小的岩石块或水泥浇注体作为“ 基岩” 试件, 试件中心设置穿孔钢管作为射孔套管井, 对试件施以围压, 再向井孔中注入高压液体使井周地层破裂产生压裂缝网。Lee等[10]的分析表明, 这样的缝网[13]具有分形特征, 可较为真实地反映实际地层的压裂缝形态, 采用阈值分割的图像处理算法可以获取如图1a所示的压裂缝轮廓。
压裂缝面的不规则变化是造成其渗透率随空间位置变化的原因。本文采用Brown[14]提出的基于分形控制的缝面形态构型算法, 以最小缝宽(完全接触, 缝宽为零)和最大缝宽为参考值, 在压裂缝轮廓内部按分形展布赋予缝宽变化, 所生成的不规则缝宽近似于正态分布, 其平均缝宽约为最大缝宽的一半。压裂缝的渗透率变化按裂缝在各处的缝宽(d)用公式K0=d2/12转化为静态渗透率[15]。例如, 对图1a所示的压裂缝分布, 将试件尺寸等比例放大到与实际井孔模型尺寸相当, 就得到如图1b所示的压裂地层渗透率模型, 模型尺寸为4.096 m×4.096 m, 网格数为256×256。图1b中渗透率已按最大值归一化, 归一化渗透率为1和0分别指示模型中渗透率的最大值和最小值, 色调明暗的变化反映了压裂缝渗透率在井周的非均匀变化。
上述基于压裂实验和压裂缝面分形算法构建的压裂地层渗透率模型为数值模拟奠定了基础。本文数值模拟参考统计数据[16]以渗透率为1×10-3 μm2、孔隙度为8%的致密砂岩作为基岩, 基岩的弹性参数[17]及套管井介质的各项参数如表1所示, 井中和地层流体黏度取1.14 mPa· s。
| 表1 模型介质参数 |
在基岩压裂过程中, 压裂液携带支撑剂颗粒(石英砂等)进入地层, 为使支撑剂达到最佳的渗入和支撑效果, 常用颗粒粒径通常为0.15~2.00 mm(10~100目)。在地层压力作用下, 压裂缝经历了初期支撑开启、中期压实和最终趋于稳定的多个阶段, 缝宽由最初的上百微米变化到最终的几微米, 对应的渗透率也从上百平方微米降至几平方微米。
根据以上模型和参数求解(1)式。由于压裂地层渗透率在空间的非均匀变化, 必须使用数值方法求解该方程。本文采用ADI(Alternate Direction Implicit, 交替方向隐式)有限差分方法计算压裂地层中随频率变化的动态渗流, 采用ADI差分格式是因为其良好的数值稳定性[18]。
将沿套管井以波数ke传播的斯通利波作为激励源, 则(1)式中的地层渗流压力具有相同的z方向(井轴方向)传播因子$p{{\text{e}}^{i{{k}_{\text{e}}}z}}$, 由此可将(1)式转化为:
$\frac{\partial }{\partial x}\left( \alpha \frac{\partial p}{\partial x} \right)+\frac{\partial }{\partial y}\left( \alpha \frac{\partial p}{\partial y} \right)\text{+}\left( \text{i}\omega -\alpha k_{\text{e}}^{\text{2}} \right)p=0$ (4)
适用于方程(4)的井孔模型边界条件为:
$\left\{ \begin{align} & p(x, y)\left| _{{{x}^{2}}+{{y}^{2}}\le {{R}^{2}}} \right.={{p}_{0}} \\ & p(x, y)\left| _{{{x}^{2}}+{{y}^{2}}=\infty } \right.=0 \\ \end{align} \right.$ (5)
在此边界条件下用ADI差分法求解(4)式即可得到给定频率下地层中的动态流体压力p(x, y), 差分格式及计算过程详见文献[18]。
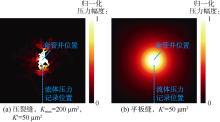
以频率为500 Hz, 最大渗透率(Kmax)为200 μm2的压裂缝为例, 该算例对应最大缝宽约为50 μm, 平均缝宽约为25 μm, 平均缝宽下渗透率(${K}'$)为50 μm2, 为方便分析, 后文以渗透率代替缝宽进行标注。该压裂缝的压力场如图2a所示, 图中压力幅度已按最大值归一化, 幅度大小由颜色显示, 所在位置颜色越亮表示流体压力越大。作为比较, 图2b给出了${K}'$=50 μm2的平板缝模型的计算结果。二者相比可以看出, 压裂缝中的动态渗流主要限于缝内, 这意味着压裂后致密地层中的渗透能力主要来自人工压裂缝网, 而基岩的渗透率很低, 对渗流的贡献可以忽略。
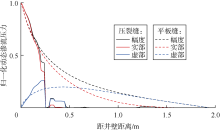
在图2计算的流体压力场中提取井壁至模型边界(蓝色虚线标记)的压力分布曲线(见图3), 不同颜色的曲线分别表示压力的幅度、实部和虚部。压裂地层的动态渗流压力场主要分布在井周0~2 m的范围内, 在声波测井频率下, 井孔声场可以激发和感知该范围内的流体动态渗流效应。压裂缝中的流体动态渗流的局部变化受缝面不规则形态控制, 无法直接与平板缝结果对比, 但与井孔声场相互作用的是缝内渗流的整体效应, 该效应变化规律可通过对井孔声场的分析体现出来。
B-R理论[19]描述了井孔声场与渗透性地层的相互作用。简化的B-R理论是该复杂理论在低频斯通利波的应用中得到的解析表达式[11], 其有效性已被理论和实验证实, 并广泛应用于地层渗透率反演, 取得了良好应用效果。然而, 压裂作业通常在套管井射孔后进行, 受套管和水泥环限制, 井孔声场与地层动态渗流只能通过套管上的射孔孔眼相互作用, 如图4所示, 假设地层中的射孔道因压裂改造而消失, 可以不考虑其影响。
结合Tang等[11]的理论推导和考虑套管射孔孔眼影响的简化B-R理论, 给出斯通利波波数表达式:
$k=\sqrt{k_{\text{e}}^{\text{2}}+\beta \frac{2R\rho {{\omega }^{2}}}{{{R}^{2}}-{{a}^{2}}}{{\left. \frac{{{U}_{\text{f}}}}{p} \right|}_{r=R}}}$ (6)
该理论的实质就是在弹性传播波数ke的基础上加上了井壁渗流的影响, 即(6)式根号中的第2项。其中β 为射孔孔眼系数, 该系数与射孔孔眼面积、射孔密度以及井径等有关, 根据常用参数计算可得β ∈ (0, 0.2), 本文中β 取0.1; R为套管内半径, 即表1井中流体外半径; a为仪器外半径, 一般小于0.05 m; ${{\left. \frac{{{U}_{\text{f}}}}{p} \right|}_{r=R}}$为裸眼井情况下井壁处动态渗流通量与其压力的比值, 即井壁导流率, 在均匀地层中可按(7)式[4]计算:
${{\left. \frac{{{U}_{\text{f}}}}{p} \right|}_{r=R}}=\frac{\text{i}K(\omega )}{\omega \mu }\sqrt{-\frac{\text{i}\omega }{\alpha }+k_{\text{e}}^{\text{2}}}\frac{{{\text{K}}_{1}}\left( \sqrt{-\frac{\text{i}\omega }{\alpha }+k_{\text{e}}^{\text{2}}} \right)}{{{\text{K}}_{0}}\left( \sqrt{-\frac{\text{i}\omega }{\alpha }+k_{\text{e}}^{\text{2}}} \right)}$ (7)
但对于复杂压裂地层的有限差分解, 需利用动态渗流的数值模拟结果计算井壁导流率。首先将直角坐标系中求解(4)式得到的压力场p(x, y)通过(8)式变换为极坐标系下的p(r, θ ), 变换过程中坐标系网格点上的压力值可通过网格插值求得。
$\left\{ \begin{align} & r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\ & \theta =\arctan \left( \frac{x}{y} \right) \\ \end{align} \right.$ (8)
再将p(r, θ )代入(9)式中的积分计算全井周上的平均导流率[18]:
${{\left. \frac{{{{\bar{U}}}_{\text{f}}}}{p} \right|}_{r=R}}=\frac{\text{i}}{2\text{ }\!\!\pi\!\!\text{ }\mu \omega }\int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{\left\{ {{\left. \frac{K(r, \theta ; \omega )}{p(r, \theta )}\frac{\text{d}p(r, \theta )}{\text{d}r} \right|}_{r=R}} \right\}}\text{d}\theta $ (9)
(9)式中的积分和微商分别通过求和与差分计算, 由此得到(6)式中的井壁导流率, 进一步得到压裂地层斯通利波波数的数值解, 再通过(10)式计算斯通利波的相速度频散:
${{v}_{\text{st}}}(\omega )=\frac{\omega }{\operatorname{Re}(k)}$ (10)
(10)式中Re表示取实部, 下文同。
地层渗流在井壁处的导流率直接反映了压裂地层的渗透性能, 可以用来验证数值解的准确性。
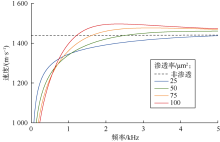
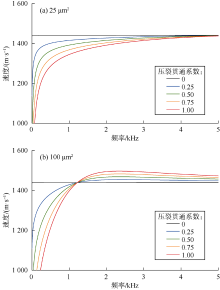
以图2模型${K}'\text{=50 }\!\!\mu\!\!\text{ }{{\text{m}}^{\text{2}}}$的情况为例, 图5a和图5b分别给出了0~5 kHz频率范围内解析解及数值解计算的压裂缝、平板缝的井壁导流率幅度值和斯通利波速度频散。利用(7)式和(9)式计算得到的平板缝井壁导流率幅值吻合良好(见图5a), 即解析解和数值解吻合良好; 将它们代入(6)式和(10)式计算得到的斯通利波速度频散也吻合良好(见图5b), 进一步验证了数值解的准确性。但是, 压裂缝与其对应平板缝的井壁导流率幅度值和斯通利波速度频散均有显著差异, 特别是在2 kHz以下的低频范围内。这种差异一方面来自压裂缝形态和缝宽的强非均匀变化; 另一方面, 渗透率与缝宽的二次方关系导致压裂缝的平均渗透率略大于平均缝宽渗透率。使用压裂缝整体的平均渗透率($\bar{K}\approx 70\text{ }\!\!\mu\!\!\text{ }{{\text{m}}^{\text{2}}}$)的计算结果(由(7)式计算得到)与压裂缝的计算结果更为贴近(见图5b等效平板缝及压裂缝斯通利波速度频散曲线), 因此可认为斯通利波速度频散曲线反映的是压裂地层中压裂缝的平均渗透率。以这一重要结论为基础, 进一步讨论不同渗透率(压裂缝缝宽状态)下的斯通利波速度频散特征, 根据表1的参数, 利用(6)式和(7)式计算了压裂缝平均渗透率分别为25, 50, 75, 100 μm2的斯通利波速度频散曲线(见图6), 不考虑仪器影响, (6)式中设a=0。鉴于B-R理论通常应用于中、低渗透地层, 有必要对此处考虑的高渗透裂缝情况进行讨论。
图6中, 在较低渗透率(25 μm2)情况下, 斯通利波速度随着频率降低单调下降, 随着渗透率升高(50 μm2), 这种下降趋势更为明显。然而, 随着渗透率进一步升高(75, 100 μm2), 斯通利波在一定频段上不降反升, 出现了1个极值。该频段以下, 波速随着频率降低迅速下降, 该频段以上, 波速随着频率升高缓慢下降并趋于1个常数。这个现象可用裂缝中渗流满足的扩散型波动方程((1)式)来解释:在动态激励下, 流体的黏滞流动仅限于界面附近一个趋肤深度的范围, 对裂缝而言, 该趋肤深度定义了裂缝的黏性趋肤深度, 例如, 1 kHz频率下, 饱含水的裂缝的黏性趋肤深度约20 μm。低频情况下, 黏性趋肤深度较大, (1)式描述的流体运动以黏滞渗流为主, 其与井孔声场的耦合降低了斯通利波速度; 而当裂缝渗透率变大和频率升高(黏性趋肤深度忽略不计)时, (1)式转化为波动方程, 这时裂缝中流体运动为Krauklis[20]、Ferrazzini和Aki[21]等讨论过的平板缝中的波动, 学界常称为Krauklis波。井壁黏滞渗流的消失对井孔声场的解耦使斯通利波波速升高并趋向于自由空间的流体声速。波速升高后随频率升高而下降是因为斯通利波波速在高频时趋于低于流体声速的Scholte波速[22]。
将压裂缝的平均渗透率与(7)式的解析解结合将为下文的评价模型提供快捷有效的正演计算方法, 同时前文的理论模拟和数值分析预示了压裂地层声波测井中的一个重要现象, 即压裂缝开启时的高渗透性使得斯通利波速度频散在1 kHz左右的频段内产生1个峰值。这个现象在渗透性储集层[16](渗透率约(0.1~2 000)×10-3 μm2)测井中未有过报道, 是压裂地层的特殊现象。因此, 这个现象的存在与否是压裂有效性的一个特征判据。
前文模拟分析了在井轴方向贯通的压裂缝地层模型中的斯通利波速度频散特征及其平均渗透率的等效关系, 但很多情况下, 在地应力控制下(如水平井情况), 每个射孔孔眼附近处裂缝沿井的开启高度小于射孔间距, 即压裂缝丛在井轴方向没有有效贯通。为此, 本文考虑更为一般的压裂缝丛模型, 如图7a所示在相邻射孔孔眼间存在垂直井轴并在基质地层中交替排列的压裂缝层, 利用图5分析得到的等效关系可将其进一步简化为图7b所示的压裂缝层状模型。考虑到压裂区间内的地应力变化较小可以忽略, 本文假定相邻压裂缝层厚度(hfrac)和基质地层厚度(hfm)相同, 并定义压裂缝沿井轴的压裂贯通系数γ =hfrac/(hfrac+hfm), 其中(hfrac+hfm)恒等于射孔间距(与射孔密度有关), γ ∈ [0, 1], kfrac和kfm分别为射孔处压裂缝层和基质地层的斯通利波波数。特别地, 当γ =1时, 压裂缝丛在井轴方向贯通, 相邻射孔间不存在未贯通的基质地层(hfm=0); 当γ =0时, 压裂缝未开启(hfrac=0), 仅有基质地层。在实际情况下射孔间距在0.02~0.06 m, 而1 kHz频率的斯通利波波长大于1 m, 因此可以采用等效介质(Effective Medium)方法将0< γ < 1条件下模型的斯通利波速度视为波在压裂缝层和基质地层速度的加权平均(权重为γ ), 如下式所示。
$v(\omega )=(1-\gamma )\frac{\omega }{\operatorname{Re}\left( {{k}_{\text{fm}}} \right)}+\gamma \frac{\omega }{\operatorname{Re}\left( {{k}_{\text{frac}}} \right)}$ (11)
上式中的kfrac按(6)式进行计算, kfm即为该式中的ke。(11)式及其对压裂缝的模拟计算提供了一个压裂缝渗透性能的评价模型。压裂贯通系数的引入, 使得该模型既适用于直井也适用于水平井。
根据前述模拟参数, 用(11)式计算了压裂贯通系数为0, 0.25, 0.50, 0.75, 1.00, 压裂缝的平均渗透率分别为25, 100 μm2时的斯通利波速度频散曲线(见图8)。压裂贯通系数小于1时的频散曲线形态与贯通时(γ =1)相似, 但压裂贯通系数趋近于0时动态渗流的作用明显变小, 斯通利波速度频散趋于弹性地层的情况。压裂贯通系数反映了压裂缝丛的连通状态, 是一个重要的评价参数。
在评价模型的实际应用中, 首先需要从压裂后地层的声波测井数据中提取斯通利波速度频散数据。此外还需要确定一些模型参数, 如流体和测井仪器参数、射孔孔眼系数和弹性斯通利波波数等。这些参数可通过测井数据直接获取, 或通过选取非压裂段进行标定。频散数据的提取和参数的标定方法参见文献[22]。射孔孔眼系数来自射孔作业所使用的工具。在以上工作的基础上, 构建以下目标函数来反演压裂缝的平均渗透率和压裂贯通系数。
$F\left( \bar{K}, \gamma \right)=\sum\limits_{f={{f}_{\min }}}^{{{f}_{\max }}}{{{\left[ {{v}_{\operatorname{m}}}\left( f, {{k}_{\text{fm}}}, \beta , \bar{K}, \gamma \right)-{{v}_{\text{d}}}\left( f \right) \right]}^{2}}}$ (12)
(12)式中, vm为按(6)式计算的理论斯通利波速度, f为频率, 在频散数据提取区间的下限fmin和上限fmax范围内取值。使目标函数达到最小的$\bar{K}$和γ 值即为地层压裂缝的平均渗透率和压裂贯通系数。
图9为某一水平生产井的应用实例。如图9a所示, 在1 183~1 187 m和1 192~1 194 m两个层段进行了压裂作业。压裂前后伽马曲线及纵波慢度曲线差异较小(见图9a), 说明压裂后岩性总体上未产生大幅变化。利用纵波径向走时层析技术[23]处理得到了压裂后纵波径向声速差异剖面(见图9a), 该技术依据不同接收器接收声波的不同径向穿透时间来反映井周地层径向声速变化, 对比压裂段与未压裂段可以观察到压裂段附近径向声速差异剖面色彩变化, 说明井周产生了裂缝, 致使径向声速降低。特别值得关注的是, 斯通利波(中心频率约为1.5 kHz)在压裂段的到时与未压裂段相比明显“ 前趋” , 这意味着压裂段内波速变快, 与前述的高渗透裂缝引起的低频斯通利波波速的峰值现象密切相关。
取上部压裂段的中点(1 185 m)和未压裂段参考点(1 177 m)的斯通利波阵列波形进行对比(见图9b), 压裂段的波形较未压裂段产生了前趋, 如图中两条指示线所指的两个波峰所示对比。进一步提取其频散数据(见图9c)进行比较, 可以看出二者具有明显的差别。图9c中未压裂段的波速随频率变化平缓, 而压裂段的数据在1 kHz时出现了明显的峰值。利用(12)式对图中的频散数据进行了反演。反演中较为敏感的裂缝流体波速和黏度分别取为1 330 m/s和1.1 mPa· s, 其余参数取自测井数据或大致设定。反演得到压裂缝区的压裂贯通系数为0.48, 压裂缝平均渗透率为330 μm2, 这一数值与常见的支撑开启裂缝API(美国石油学会)导流能力测试结果的数量级相近[24]。反演拟合的斯通利波理论速度频散曲线(见图9c)与测量数据吻合良好, 特别是在压裂段内, 实测和拟合的波速在低频段均有明显的峰值现象, 二者的形态十分一致, 证明了前文模拟分析结果的正确性。本应用实例表明, 压裂缝区斯通利波到时的“ 前趋” 及波速频散的峰值现象可以作为压裂缝开启、具有高渗透性能的特征判据。
压裂评估的另一方面是判断压裂缝的变化。压裂井在生产过程中会发生支撑剂失效、地层压力变化及生产中微粒堵塞等情况, 使压裂缝的渗透性能降低。以图10的直井为例, 其3 963~3 969 m层段进行了压裂施工。由图10a可见, 压裂后与压裂前的横波衰减包络(棕色填充)指示此处产生了裂缝; 压裂后交叉偶极横波测得的各向异性值在压裂段内明显大于压裂前, 也表明压裂在井周产生了裂缝[10]。但斯通利波(中心频率约为1.5 kHz)在压裂段的波至出现了“ 滞后” 现象, 说明压裂后波速下降, 这与图9a明显不同。
同样地, 取压裂段中点(3 966 m)和未压裂段参考点(3 979 m)的斯通利波阵列波形进行对比(见图10b), 压裂段的波形较未压裂段产生了滞后, 如图中两条指示线所指的两个波峰所示对比。进一步提取其频散数据(见图10c)进行比较, 未见图9c中所示的峰值现象, 反而压裂段的波速相对于未压裂段有明显的整体下降, 对应图10a所示的到时滞后。对图10c的数据进行反演, 得到压裂缝平均渗透率为15 μm2, 压裂贯通系数为1; 反演拟合的理论频散曲线与实测数据吻合良好。这一现象有两种可能的解释:第1种是压裂缝压开后没有充分支撑开启, 未产生良好的渗透性能; 第2种是压裂缝开启后趋于闭合, 其渗透性能降低。根据图示的压后地层的明显各向异性(压裂缝导致)来看, 第2种解释更为合理。
复杂压裂缝导致的斯通利波速度频散特征可以与平板缝模型等效, 前提是将压裂缝模型的平均渗透率等效于平板缝的渗透率。压裂后裂缝的支撑开启会导致斯通利波波速增大, 速度频散曲线出现峰值, 斯通利波波形(特别是波至)出现“ 前趋” 现象; 反之, 裂缝未有效开启或开启后闭合会导致斯通利波波速在整个频段内减小, 斯通利波波形出现“ 滞后” 现象。这两种现象都在实际测井中得到了验证, 可以作为压裂有效性评估的特征判据。
据此提出了一种基于斯通利波速度频散分析的压裂缝渗透性能定量评价模型, 可以评价压裂缝的平均渗透率和压裂贯通系数。现场数据分析结果证明了评价方法的可行性和有效性。
符号注释:
a—仪器外半径, m; d—缝宽, m; f—频率, Hz; fmin, fmax—频散数据提取频率下限和上限, Hz; F—拟合目标函数, m2/s2; hfm—基质地层厚度, m; hfrac—压裂缝层厚度, m; k—斯通利波波数, m-1; ke—纯弹性斯通利波波数, m-1; kfm—基质地层斯通利波波数, m-1; kfrac—压裂缝层斯通利波波数, m-1; K—动态渗透率, m2; Kmax—压裂缝最大(静态)渗透率, m2; K° —平均缝宽(静态)渗透率, μm2; $\overline{K}$—平均(静态)渗透率, μm2; K0—静态渗透率, m2; Kf—流体模量, Pa; K0, K1—0阶、1阶第二类修正贝塞尔函数; p—流体压力, Pa; p0—斯通利波幅度(声压), Pa; r—极坐标中半径坐标, m; R—套管内半径, m; Uf—井壁处动态流体通量, m; ${{\bar{U}}_{\text{f}}}$—井壁处平均动态流体通量, m; v—等效斯通利波速度, m/s; vm, vd—理论计算和现场提取的斯通利波速度, m/s; vst—斯通利波相速度, m/s; x, y, z—直角坐标系, m; x—空间坐标矢量, m; α —流体扩散率, m2/s; β —射孔孔眼系数; γ —压裂贯通系数; θ —极坐标系中角坐标, rad; μ—流体黏度, Pa· s; ξ —介质骨架弹性的修正量, 无因次; ρ —流体密度, kg/m3; τ , m—与孔隙或裂缝形状有关的参数, 无因次; ϕ —介质孔隙度, %; ω —角频率, rad/s。
(编辑 胡苇玮)
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|