第一作者简介:陈铭(1990-),男,山东泰安人,博士,中国石油大学(华东)师资博士后,主要从事压裂工艺理论与技术研究。地址:山东省青岛市黄岛区长江西路66号,中国石油大学(华东)石油工程学院,邮政编码:266580。E-mail: chenmingfrac@163.com
在平面三维多裂缝扩展模型基础上,构建了压裂监测井光纤应变与应变率的计算模型,提出了水平井压裂多裂缝扩展诱发光纤应变正演计算方法。基于该方法,开展了水平井压裂多裂缝扩展诱发光纤应变与应变率数值模拟分析,结果表明,裂缝扩展诱发光纤应变演化可分为应变增强、收缩汇聚和直线状汇聚3个阶段;应变率演化可分为应变率增强、收缩汇聚、直线状汇聚、停泵应变率反转4个阶段。光纤应变停泵后不变,但应变率会出现反转,光纤应变率反转可反映注入动态;根据分布式光纤应变与应变率的直线状汇聚带,可判断裂缝扩展至光纤的时刻与井间压窜,同时可依据各簇裂缝扩展到光纤监测井的时刻识别多裂缝非均匀扩展现象,评价裂缝非均匀扩展程度;光纤监测井水平段位于裂缝高度范围内时,可识别裂缝延伸至光纤的时刻,而光纤监测井水平段位于裂缝高度以外时,汇聚条带不明显;多段压裂施工中,受上一压裂段应力干扰的影响,后续压裂段的光纤应变可能不再出现压裂初期的张应变区域,但光纤应变率动态可有效呈现每一段压裂裂缝的扩展动态,单段压裂的光纤应变率演化规律适用于多段压裂。
A forward model for optical fiber strain was established based on a planar 3D multi-fracture model. Then the forward method calculating distributed fiber strain induced by multi-fracture growth was proposed. Based on this method, fiber strain evolution during fracturing of horizontal well was numerically simulated. Fiber strain evolution induced by fracture growth can be divided into three stages: strain increasing, shrinkage convergence, and straight line convergence; whereas the evolution of fiber strain rate has four stages: strain rate increasing, shrinkage convergence, straight line convergence, and strain rate reversal after pumping stop. Fiber strain does not flip after pumping stop, while the strain rate flips after pumping stop, so strain rate can reflect injection dynamics. The time when the fracture extends to the fiber and inter-well pressure channeling can be identified by the straight line convergence band of distributed fiber strain or strain rate, and the non-uniform growth of multiple fractures can be evaluated by using the instants of fractures reaching the fiber monitoring well. When the horizontal section of the fiber monitoring well is within the height range of a hydraulic fracture, the instant of the fracture reaching the fiber can be identified, otherwise, the converging band is not obvious. In multi-stage fracturing, under the influence of stress shadow from previous fracturing stages, the tensile region of fiber strain may not appear, but the fiber strain rate can effectively show the fracture growth behavior in each stage. The evolution law of fiber strain rate in single-stage fracturing can be applied to multi-stage fracturing.
近几年水平井压裂工艺发展迅速, 形成了密切割多簇压裂、多层叠置水平井立体压裂等系列技术[1, 2]。尽管工艺进步迅速、增产效果良好, 但压裂设计仍是难题, 主要根源是对裂缝扩展形态认识不清, 簇间距、压裂规模等施工参数的设计缺乏直接依据[3, 4]。裂缝实时监测是认清裂缝形态、解决压裂设计难题的关键[5]。
目前裂缝实时监测方法包括近井监测和远井监测。近井实时监测主要包括分布式光纤温度与分布式光纤声振动技术, 可评价射孔孔眼或近井地层的进液差异, 但难以实现对裂缝整体形态的诊断[6, 7]; 远井实时监测包括微地震、测斜仪、电磁监测、光纤应变监测, 前3种监测可获取裂缝整体走向或分布体积, 但难以精细诊断数米间距的多缝扩展动态[8, 9]。分布式光纤应变监测具备定位精度高、实现分布式实时监测、获取信息丰富的优势, 是当前“ 小间距” 分段多簇压裂工程背景下, 实现压裂裂缝精细诊断的有效手段[10]。
分布式光纤应变监测通过声信号的低频(小于0.05 Hz)滤波获取压裂过程中的光纤应变, 进而实现裂缝扩展动态的实时监测[11]。光纤光缆通常预先固结于监测井水泥环内, 压裂过程中在监测井入射脉冲激光, 激光由光纤传导并实时感测, 其中脉冲激光的背向散射信号返回地面解调系统, 经解调可得到裂缝扩展过程中的光纤应变和应变率实时动态, 从而进行裂缝扩展动态诊断[10, 11]。壳牌、斯伦贝谢等公司在北美页岩储集层水平井压裂中均进行了分布式光纤应变监测试验, 证实分布式光纤应变可有效识别多裂缝扩展动态、判断井间压窜等[12, 13, 14]。加拿大蒙特内页岩水平井压裂的分布式光纤应变监测发现, 水力裂缝通常为沿最大主应力方向扩展的平面裂缝[12]。分布式光纤应变展现了较大的应用前景, 但对其诊断依据“ 压裂过程中的应变及其应变率信号演化机理” 研究不足[10, 11, 12]。目前压裂过程中监测井光纤的应变解读多依据二维或拟三维模型[15, 16, 17], 但实际为三维问题, 亟需更为精细的模型研究压裂过程中光纤应变的演化机理[13], 从而为压裂裂缝扩展诱发光纤应变解释提供理论依据。
为此, 本文在耦合“ 井筒-射孔” 平面三维多裂缝扩展模型基础上, 构建了裂缝扩展诱发光纤应变和应变率的理论计算模型, 提出了裂缝扩展诱发光纤应变与应变率正演计算方法。通过对比单簇、多簇、多段多裂缝扩展过程中光纤应变信号的演化特征, 揭示多裂缝扩展诱发光纤应变与应变率的演化机理, 为利用分布式光纤应变信号诊断裂缝扩展动态提供理论依据。
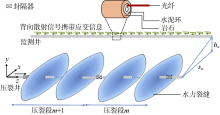
压裂裂缝变形会在地层产生诱导应力, 这种现象称为应力干扰或应力阴影。固结于监测井水泥环内的光纤可感知地层应力的变化, 根据光纤变形可推断地层应变, 进而分析裂缝扩展动态。若不考虑地层向光纤的应变传递损失, 光纤应变即为地层应变, 因此问题归结为压裂裂缝扩展诱发地层应变的演化机理。光纤应变动态的解读则需要基于裂缝扩展模拟的光纤应变正演分析。地层应变是光纤应变的来源, 地层向光纤的应变传递损失不影响裂缝扩展诱发光纤应变信号的演化规律分析[11]。裂缝扩展诱发光纤应变几何模型如图1所示, 正演模型包括:①耦合“ 井筒-射孔” 平面三维多裂缝扩展模型; ②光纤应变计算模型。光纤应变监测的直接信号是光纤的位移, 根据分布式监测点的位移可计算应变, 因此光纤应变模型需要计算光纤分布式测点的位移。
1.2.1 井筒内液体流动模型
压裂液经过井筒动态分配至各簇裂缝内。井筒内液体流动需满足流量守恒和压力一致。
首先, 总排量等于各簇裂缝的流量之和, 即:
${{Q}_{t}}=\sum\limits_{k=1}^{N}{{{Q}_{k}}}$ (1)
其次, 井筒内流动压力满足连续性条件, 即:
${p_w}=p_{in,k}+{{p}_{c,k}}+{{p}_{p,k}}\ \ \ \ (k=1,\cdots ,N)$ (2)
射孔摩阻可参考文献[18]计算。液体由跟端射孔簇流动到射孔簇k的井筒沿程摩阻为:
${{p}_{c, k}}=\int_{0}^{{{l}_{w}}}{{{f}_{c}}\left( Re, {{\varepsilon }_{\text{a}}} \right)\frac{\rho }{2{{D}_{w}}}V_{w}^{2}dz}$ (3)
压裂液沿井筒的流动包括层流、过渡流和紊流多种流态, 采用全流态模型计算沿程摩阻系数[19]:
${{f}_{c}}=8{{\left[ {{\left( \frac{8}{Re} \right)}^{12}}+\frac{1}{{{\left( {{\Theta }_{1}}+{{\Theta }_{2}} \right)}^{1.5}}} \right]}^{\frac{1}{15}}}$ (4)
(4)式中${{\Theta }_{1}}$和${{\Theta }_{2}}$计算公式[19]为:
$\left\{ \begin{align} & {{\Theta }_{1}}\text{=}-2.457\ln \left[ {{\left( \frac{7}{Re} \right)}^{0.9}}+0.27\frac{{{\varepsilon }_{\text{a}}}}{{{D}_{w}}} \right] \\ & {{\Theta }_{2}}\text{=}{{\left( \frac{37\ 530}{Re} \right)}^{16}} \\ \end{align} \right.$ (5)
1.2.2 流固耦合模型
水力裂缝形态计算需对模型进行一定程度的简化, 目前实用的裂缝扩展模型主要是拟三维(如FracproPT、Meyer、Kinetix软件)和平面三维模型(如Gohfer、StimPlan软件)[20, 21], 全三维模型由于计算耗时巨大而不利于工程设计。现场取心[22]、裂缝监测[11]和压裂裂缝历史拟合分析[23]均表明水力裂缝主要是平面裂缝, 综合考虑精度和效率问题, 采用平面三维裂缝模型计算多裂缝扩展动态。
首先基于三维位移不连续边界元计算缝内流体压力与裂缝宽度的关系[24]:
$p-{{\sigma }_{h}}=C\text{w}$ (6)
其次考虑缝内压裂液流动为层流[25], 压裂液向地层滤失, 缝内压裂液流动的控制方程为:
$\frac{\partial w}{\partial t}-\nabla \cdot \left( \frac{{{w}^{3}}}{12\mu }\nabla p \right)+\frac{2{{C}_{\text{l}}}}{\sqrt{t-{{t}_{0}}}}=\delta \left( x-{{x}_{in, k}} \right){{Q}_{k}}$ (7)
联立方程(6)和(7)式即可得到裂缝宽度和压力的流固耦合方程。采用结构化网格, 通过有限体积法进行空间项离散, 得到缝宽的微分方程:
$\frac{\text{d}w}{\text{d}t}=\left[ \theta A\left( {{\sigma }_{\text{h}}}\text{+}Cw \right)+\left( 1-\theta \right)A\left( {{\sigma }_{\text{h}}}\text{+}C{{w}_{0}} \right) \right]\text{+}S$ (8)
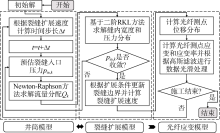
(8)式即为裂缝扩展的流固耦合方程, 隐式解法需要大量迭代求解非线性方程组, 计算量较大, 因此本文取θ =0, 即采用显式方法进行求解[26]。显式方法时间步需要满足稳定性条件, 为提高计算效率, 采用二阶精度的Runge-Kutta-Legendre(简称RKL)方法求解[26, 27]。该方法可显著提高稳定时间步长, 且避免了隐式解法中大量迭代求解非线性方程组的问题, 计算效率比隐式解法提高10倍以上[27]。
1.2.3 井筒-多裂缝扩展耦合
井筒流动与多裂缝扩展通过井底压力和流量进行迭代耦合。井筒流量方程的离散形式为:
$F\left( {{Q}_{1}}, \cdots , {{Q}_{N}}, {{p}_{w}} \right)=0$ (9)
(9)式为N+1维非线性方程组, 其分量形式为:
$\left\{ \begin{align} & {{F}_{1}}={{p}_{\text{w}}}-{{p}_{\text{p, 1}}}-{{p}_{c, 1}}-{{p}_{\text{in, 1}}}\left( {{Q}_{1}}, {{Q}_{2}}, \cdots , {{Q}_{N}}, {{p}_{\text{w}}} \right) \\ & {{F}_{2}}={{p}_{\text{w}}}-{{p}_{\text{p, 2}}}-{{p}_{c, 2}}-{{p}_{\text{in, 2}}}\left( {{Q}_{1}}, {{Q}_{2}}, \cdots , {{Q}_{N}}, {{p}_{\text{w}}} \right) \\ & \quad \quad \quad \quad \quad \quad \quad \vdots \\ & {{F}_{N}}={{p}_{\text{w}}}-{{p}_{\text{p, }N}}-{{p}_{c, N}}-{{p}_{\text{in, }N}}\left( {{Q}_{1}}, {{Q}_{2}}, \cdots , {{Q}_{N}}, {{p}_{\text{w}}} \right) \\ & {{F}_{N+1}}={{Q}_{t}}-\sum\limits_{k=1}^{N}{{{Q}_{k}}} \\ \end{align} \right.$ (10)
根据多裂缝扩展流固耦合模型计算裂缝入口压力, 然后根据(10)式计算流量分配, 再返回计算入口压力, 直至压力和流量收敛。
1.2.4 裂缝边界计算
采用网格激活方式进行裂缝边界的追踪, 当水力裂缝尖端应力强度因子达到断裂韧性条件时, 尖端激活, 新单元扩展。由于水力裂缝尖端的断裂韧性区较小[28], 断裂韧性准则方法应用于较小网格才能准确捕捉裂缝扩展条件, 为应用粗网格且不影响计算精度, 采用裂尖解析解作为扩展条件, 该解析解与断裂准则等效, 但适用范围可达10%~20%的缝长[28], 因此可显著增大空间步长, 减少存储量和计算时间。
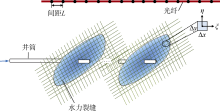
不考虑地层向光纤的应变传递损失, 光纤位移即为地层位移。光纤为细长材料, 只能发生轴向变形。分布式光纤应变监测通过监测激光相位改变得到位移变化(见图2), 再通过位移分布得到每个测点的应变。光纤每个测点的间隔距离一般为5~10 m, 因此分布式光纤监测得到的数据为5~10 m内的应变及应变率平均值。
考虑t时刻裂缝单元数量为M, 根据位移不连续基本解, 可计算每个单元产生的位移, 将M个单元的位移叠加, 即可得到光纤每个测点的(轴向)位移[24]:
${{u}_{\text{f}}}\text{=}\sum\limits_{i=1}^{M}{\frac{1}{8\pi \left( 1-v \right)}\left[ 2\left( 1-v \right){{I}_{1}}-{{I}_{2}} \right]{{w}_{i}}}$ (11)
I1和I2为核函数, 具体形式为:
$\left\{ \begin{align} & {{I}_{1}}=\left. \left[ -\arctan \frac{\left( x-\xi \right)\left( y-\eta \right)}{rz} \right] \right\| \\ & {{I}_{2}}=\left. \left\{ \frac{z\left( x-\xi \right)\left( x-\eta \right)\left[ {{\left( x-\xi \right)}^{2}}+{{r}^{2}} \right]}{r\left[ {{\left( y-\eta \right)}^{2}}+{{\left( x-\xi \right)}^{2}} \right]\left[ {{\left( y-\eta \right)}^{2}}+{{z}^{2}} \right]} \right\} \right\| \\ \end{align} \right.$ (12)
式中r和算符||分别为:
$\left\{ \begin{align} & r=\sqrt{{{\left( x-\xi \right)}^{2}}+{{\left( y-\eta \right)}^{2}}\text{+}{{z}^{2}}} \\ & \left. I\left( \xi , \eta \right) \right\|=I\left( a, b \right)-I\left( a, -b \right)-I\left( -a, b \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ I\left( -a, -b \right) \\ \end{align} \right.$ (13)
式中 $a=0.5\Delta x$, $b=0.5\Delta y$。
根据位移与应变的关系, 基于中心差分法, 由测点(轴向)位移可计算测点(轴向)应变, 即:
$\varepsilon =\frac{{{u}_{\text{f}}}\left( z+{L}/{2}\; \right)-{{u}_{\text{f}}}\left( z-{L}/{2}\; \right)}{L}$ (14)
根据相邻时刻的应变可计算应变率:
$\dot{\varepsilon }=\frac{\varepsilon \left( t+\Delta t \right)-\varepsilon \left( t \right)}{\Delta t}$ (15)
(14)和(15)式均是求离散数据变化率直接计算的结果, 具有一定粗糙度, 本文采用高斯滤波法对应变和应变率数据进行光滑化。
当分布式光纤的位移连续时, 由(14)式计算的光纤位移即为地层位移; 当分布式光纤的位移不连续时(如裂缝延伸至光纤时), 裂缝面附近位移是间断的, 间断处由光纤位移计算得到的光纤应变不等于地层应变, 而连续处仍为地层应变。
文献[26]从压裂物模实验、理论解和已发表文献结果几方面进行了裂缝扩展模型的准确性验证。光纤应变的计算依据是水力裂缝引起地层位移, 因此还需进行位移的计算验证。Sneddon等[29]给出了恒定流体内压下Penny裂缝的位移理论解:
$\left\{ \begin{align} & {{u}_{\text{n}}}=-\frac{4pR\left( 1-{{v}^{2}} \right)}{\pi E}\int_{0}^{\infty }{\left[ 1+\frac{d\zeta }{2R\left( 1-v \right)} \right]}\frac{d}{d\zeta }\left( \frac{\sin \zeta }{\zeta } \right){{\text{e}}^{-\frac{d}{R}\zeta }}{{\text{J}}_{0}}\left( \frac{{{r}_{\text{p}}}}{R}\zeta \right)d\zeta \\ & {{u}_{\text{r}}}=-\frac{2pR\left( 1+v \right)}{\pi E}\int_{0}^{\infty }{\left( 1-2v-\frac{d}{R}\zeta \right)}\frac{d}{d\zeta }\left( \frac{\sin \zeta }{\zeta } \right){{\text{e}}^{-\frac{d}{R}\zeta }}{{\text{J}}_{1}}\left( \frac{{{r}_{\text{p}}}}{R}\zeta \right)d\zeta \\ \end{align} \right.$ (16)
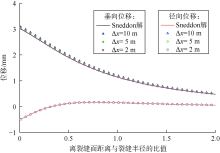
采用正方形网格进行裂缝离散。裂缝半径R=100 m, 岩石弹性模量E=35 GPa, 泊松比v=0.2, 缝内流体压力p=1 MPa。为对比网格尺寸敏感性, 取Δ x为10, 5, 2 m进行数值计算。理论解中积分通过辛普森数值积分求解。图4为rp=50 m处径向位移和轴向位移数值计算结果与理论解的对比, 结果表明, 采用以上不同网格尺寸的数值计算结果相对误差均在5%以内, 说明采用本文模型进行位移计算是准确可靠的, 可用于光纤应变计算分析。
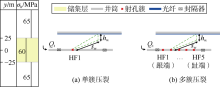
为研究裂缝扩展过程中分布式光纤的应变与应变率特征, 分别以单簇和5簇裂缝扩展为例进行分析。基本参数为:储集层厚度50 m, 层间应力差5 MPa。岩石弹性模量32.0 GPa, 泊松比0.2, 断裂韧性0.5 MPa· m0.5; 单簇压裂施工排量2.4 m3/min, 5簇压裂施工排量12 m3/min, 压裂液黏度10 mPa· s, 孔眼直径12 mm, 孔眼磨蚀系数0.8, 单簇射孔数12孔, 簇间距10 m; 施工总时间120 min, 其中泵注时间100 min, 停泵时间20 min。地应力分布及井位部署如图5所示。图中y=0 m为射孔所在深度, 两口井的水平段平行, 监测井与压裂井的井距sw=200 m, 两口井水平段的深度差hw=0; 井筒内径10.48 cm, 井筒内壁粗糙度1 μm, 监测井光纤测点间距L=5 m。需注意的是, 储集层的滤失系数是影响缝长的关键参数, 受非均质性、天然裂缝等不确定因素影响, 准确滤失系数较难确定[23], 本文滤失系数取2×10-4 m/min0.5。
裂缝扩展过程中光纤应变变化范围存在数量级差别[30]。为清晰展现应变和应变率的演化特征, 在绘制对数应变、应变率与压裂时间的关系分布图时, 采用纳应变εn(εn=109ε)与纳应变率$\ {{\dot{\varepsilon }}_{\text{n}}}$($\ {{\dot{\varepsilon }}_{\text{n}}}={{10}^{9}}\dot{\varepsilon }$)并将纳应变和纳应变率进行对数处理, 公式为:
${{\varepsilon }_{\text{L}}}\text{=}\left\{ \begin{align} & \lg \left( {{\varepsilon }_{\text{n}}} \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\varepsilon }_{\text{n}}}1 \\ & 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -1\le {{\varepsilon }_{\text{n}}}\le 1 \\ & -\lg \left( -{{\varepsilon }_{\text{n}}} \right)\ \ \ \ \ \ \ \ \ \ \ \ \ {{\varepsilon }_{\text{n}}}-1 \\ \end{align} \right.$ (17)
${{\dot{\varepsilon }}_{\text{L}}}\text{=}\left\{ \begin{align} & \lg \left( {{{\dot{\varepsilon }}}_{\text{n}}} \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{{\dot{\varepsilon }}}_{\text{n}}}1 \\ & 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -1\le {{{\dot{\varepsilon }}}_{\text{n}}}\le 1 \\ & -\lg \left( -{{{\dot{\varepsilon }}}_{\text{n}}} \right)\ \ \ \ \ \ \ \ \ \ \ \ {{{\dot{\varepsilon }}}_{\text{n}}}-1 \\ \end{align} \right.$ (18)
为方便表述, 经对数处理后的光纤应变、光纤应变率后文简称对数应变、对数应变率。
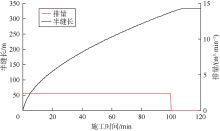
首先分析单裂缝扩展诱发的分布式光纤应变与应变率演化特征。由于层间应力差较大, 因此裂缝高度限制在产层, 由裂缝面积可计算裂缝半长(见图6)。
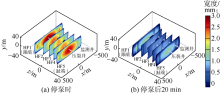
当施工时间为43 min时, 裂缝半缝长达到200 m, 该时刻缝尖到达监测井光纤所在位置; 施工时间为100 min时停泵, 裂缝继续扩展约6 min, 而后半缝长稳定在320 m。图7为当施工时间为100 min和120 min时刻的裂缝形态, 停泵后最大裂缝宽度下降约1.5 mm。
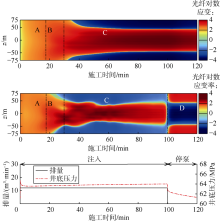
图8为单裂缝扩展过程中分布式光纤应变演化与施工井底压力动态。光纤所在位置(z坐标)的对数应变与压裂施工时间的关系分布图(简称光纤应变时间分布, 见图8a)反映了分布式光纤每个测点的信号随时间的变化, 图中“ 蓝色” 表示压应变, “ 红色” 表示张应变。可以看到, 裂缝扩展诱发的光纤应变可分为3个阶段:①应变增强阶段(图中A段), 光纤为张应变, 应变强度较弱; ②应变收缩汇聚阶段(图中B段), 光纤张应变范围缩小; ③应变直线状汇聚阶段(图中C段), 光纤张应变信号汇聚成直线状汇聚带, 汇聚带的宽度为一个测距长度(5 m), 条带外侧为压应变, 即应力阴影区域。注入100 min停泵后, 光纤应变时间分布图上没有看到明显的应变信号变化。裂缝延伸过程中井底压力有小幅度升高趋势, 符合PKN(Perkins- Kern-Nordgren)裂缝模型的井底压力动态。停泵后, 井底压力迅速降落。
为进一步分析光纤应变演化动态, 选取3个光纤测点分析应变与施工时间的关系(见图8b)。可以看到, 在裂缝到达光纤监测井前(0~43 min), 光纤发生张应变, 当裂缝延伸到光纤时, 张应变突然增大并迅速转变为压应变; 停泵之前, 压应变不断增大, 但增速逐渐减小; 停泵之后, 压应变持续增加约6 min, 继而减小, 直到120 min时仍为压应变。
图9为单裂缝扩展过程中分布式光纤应变率演化与施工压力动态。光纤所在位置(z坐标)对数应变率与压裂时间的关系分布图(简称光纤应变率时间分布, 见图9a)反映了分布式光纤每个测点的应变率信号随时间的变化, 图中“ 蓝色” 为负应变率, “ 红色” 为正应变率。由(15)式可知, 负应变率表示压应变增加或张应变减小, 正应变率表示张应变增加或压应变减小。与光纤应变演化动态不同, 裂缝扩展过程中光纤应变率包含4个阶段:①应变率增强阶段(图中A段), 该阶段光纤应变率为正; ②应变率收缩汇聚阶段(图中B段), 该阶段光纤应变率出现“ 心” 型汇聚特征, 与裂缝尖端应力特征相符, 可清晰地展现井间压窜时刻; ③应变率直线状汇聚阶段(图中C段), 直线条带由光纤两侧位移间断引起, 汇聚带两侧应变率为负, 即为应力阴影区域; ④停泵后应变率反转阶段(图中D段), 该阶段光纤正应变率转变为负应变率, 负应变率转变为正应变率。这与Ugueto等[12]通过现场光纤监测总结所得裂缝扩展过程中光纤应变率演化阶段划分结果一致, 进一步说明本文光纤应变正演模型是合理的。
同样, 选取3个光纤测点分析应变率随施工时间的关系曲线(见图9b)。裂缝在远离光纤监测井时, 应变率微弱, 且为正应变率; 裂缝延伸到光纤后, 正应变率达到峰值, 随后应变率下降转变为负应变率, 负应变率达到谷值后开始回升, 说明压应变增幅减小; 停泵后, 应变率信号迅速增加并转变为正应变率信号。由于仅有一条裂缝延伸至光纤监测井, 因此应变率只有1个明显的波峰; 同时, 距离裂缝较近的光纤测点的波峰比较明显。
总结单裂缝扩展诱发光纤应变和应变率的演化动态可知:裂缝延伸到光纤时, 光纤应变或应变率汇聚成直线状汇聚带, 汇聚带宽度理论上为光纤测点长度(本文为5 m); 汇聚条带两侧为压应变或负应变率区, 光纤应变与应变率时间分布图均可展现应力阴影区; 停泵后光纤应变的方向不变, 而应变率信号的正负方向会发生反转。根据应变或应变率汇聚的图像特征, 可识别井间压窜现象, 并可据此估算裂缝扩展速度和设计施工规模。
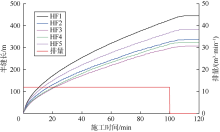
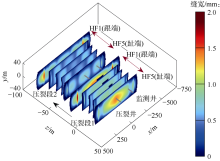
图10为1段5簇裂缝半缝长随时间的变化关系。可以看出, 5簇裂缝中跟端裂缝(HF1)长度最大, 而中间裂缝(HF3)长度最小, 表现为“ 跟端主导” 现象。现场近井光纤声监测、射孔磨蚀成像均证实存在该现象[9]。由注入结束和施工结束时刻的裂缝形态(见图11)可知, 由于流体滤失, 停泵后裂缝宽度减小, 但外侧缝宽度仍大于中间缝宽度。
图12为1段5簇裂缝扩展过程中光纤应变演化和井底压力动态。与单裂缝扩展过程中的应变演化规律类似, 1段5簇裂缝扩展过程应变时间分布图同样可划分为3个阶段(见图12a):①应变增强阶段(图中A段), 光纤发生张应变, 并在施工过程逐渐增强; ②应变收缩汇聚阶段(图中B段), 由于多条裂缝的扩展速度不同, 跟端裂缝(HF1)首先到达监测井, 因此汇聚点首先出现在HF1对应的位置; ③应变直线状汇聚阶段(图中C段), 每个汇聚条带对应一条裂缝, 且按裂缝扩展快慢依次汇聚。停泵后多簇裂缝的光纤应变方向不发生反转。由图12a可获得各簇裂缝依次扩展至光纤监测井的时间, 进而分析多裂缝非均匀扩展的规律。算例中以HF1最早扩展至光纤, HF3最晚, 扩展至光纤的时间差异为35 min; 根据HF1和HF3扩展至监测井光纤的时间, 可估算HF1和HF3扩展速度。3个光纤测点的应变曲线(见图12b)显示, 分布式光纤应变呈现多个峰值点, 与多簇裂缝不均匀扩展相一致。
1段5簇裂缝扩展过程中的应变率同样包括4个阶段(见图13a):①应变率增强阶段(图中A段)。②应变率收缩汇聚阶段(图中B段)。③直线状汇聚阶段(图中C段), 该阶段跟端裂缝(HF1)最先延伸到监测井中的光纤, 然后依次是HF5、HF2、HF4和HF3, 裂缝延伸到光纤时会出现“ 心” 型应变率。该阶段张应变率汇聚条带会出现“ 断线” (应变率正负改变), 如HF2接触到光纤时, HF1的张应变汇聚条带出现一条负应变率直线状汇聚带, 该负应变率持续时间约为15 min, 随后转变为正应变率。由图13a可知, 注入过程中并不存在停止扩展的裂缝, 因此“ 断线” 并非意味着裂缝停止扩展, 而是裂缝非均匀扩展和应力干扰引起的应变变化。Ugueto等[12]的多簇压裂现场监测也发现了较为常见的“ 断线” 现象, 本文的模拟分析为“ 断线” 形成机理提供了一种解释。④停泵后应变率反转阶段(图中D段), 该阶段每个裂缝对应的正应变率条带均转变为负应变率条带, 其他位置由负应变率转变为正应变率。由3个光纤测点的应变率变化曲线(见图13b)可知, 阶段A、B和D与单裂缝的应变率特征相同; 阶段C多裂缝非均匀扩展引起应变率出现多次峰值。当单裂缝延伸至光纤监测井时, 由于仅有一条裂缝, 因此会产生明显的应变率波峰; 而对于多簇裂缝, 由于多裂缝非均匀扩展问题, 当后续裂缝延伸至光纤监测井时, 光纤测点位置的应变不仅包括缝尖附近的张应变, 还包括已达到光纤监测井的裂缝在光纤沿程产生的压应变, 导致应变率峰值可能不明显或不出现, 因此虽然5条裂缝均延伸至光纤监测井, 但应变率峰值次数可能少于5次。
综合单裂缝和多裂缝扩展诱发的光纤应变和应变率演化动态可知, 可通过光纤应变及应变率的汇聚条带识别裂缝延伸到光纤的时刻; 停泵后缝宽减小、应变方向不变, 但应变率会发生反转, 因此光纤应变率可以反映注入动态; 由多裂缝扩展过程中的光纤应变和应变率均可依次观察到裂缝延伸到光纤的时刻, 从而可以判断裂缝非均匀扩展动态, 并可根据井间距估算裂缝扩展速度, 评价施工规模的合理性。
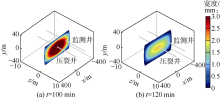
以多簇裂缝为例, 讨论监测井与压裂井存在水平段深度差时, 监测井光纤应变与应变率的演化动态。本文模拟的裂缝纵向扩展可到达y=25 m位置, 当监测井与压裂井水平段的深度差为10 m时, 即监测井位于y=10 m位置时, 裂缝仍可延伸到监测井光纤, 故裂缝延伸到光纤的时刻、整个注入过程中的应变和应变率变化仍在可观察范围内。
图14为监测井水平段深度高于压裂井10 m时的多簇裂缝扩展过程中应变、应变率时间分布与井底压力动态, 与图12a、图13a对比可以发现, 应变与应变率的直线状汇聚带、时间分布与深度差为0时基本一致。当监测井水平段深度高于压裂井30 m时, 监测井位于y=30 m位置, 而压裂井裂缝仅能到达y=25 m位置, 此时压裂过程中监测井光纤一直处于裂缝上方, 裂缝纵向并不能延伸到光纤, 因此无法监测到应变和应变率的直线状汇聚带(见图15), 汇聚带分布范围较宽, 约为60~100 m, 信号强度虽然有变化, 但难以区分各簇裂缝, 因而难以确定扩展动态, 仅可判断出裂缝纵向上未扩展到光纤所在的位置。
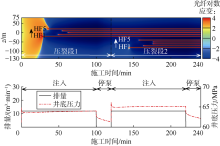
以2段5簇压裂为例, 分析多段压裂对光纤应变与应变率演化的影响。2段压裂的施工参数与单段压裂的参数相同, 第2段趾端裂缝与第1段跟端裂缝的距离为20 m, 施工结束时裂缝形态如图16所示。由图可知, 受段间应力干扰, 压裂段2的趾端裂缝(HF5)受到更大应力“ 挤压” 的干扰作用, 裂缝长度和宽度显著小于压裂段2的跟端裂缝(HF1), 该结果与现场监测结果一致[7]。
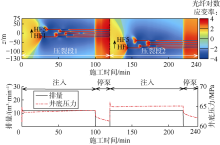
图17为2段5簇压裂过程中的光纤应变演化与井底压力动态。第1段压裂时(0~120 min), 光纤应变信号与单段压裂相同; 第1段压裂结束后, 第1段裂缝延伸位置的光纤应变仍然为张应变条带, 条带外侧为应力阴影区域; 第2段压裂时, 由于受到第1段裂缝的应力阴影影响, 未出现大范围的张应变及汇聚特征; 当第2段裂缝延伸到监测井光纤时, 出现张应变汇聚直线状汇聚带。第2段压裂的延伸压力比第1段高约1.0 MPa, 由于两个压裂段的射孔摩阻、井筒摩阻接近, 可推断第1段压裂裂缝对第2段的应力干扰约为1.0 MPa。
图18为2段5簇压裂过程中光纤应变率演化与井底压力动态。第1段压裂的光纤应变率演化与单段压裂相同; 第2段压裂时, 尽管受到上一段应力干扰作用, 但第2段的应变率特征与单段压裂相同, 即可以观察到明显的4个应变率阶段。光纤应变率对应裂缝形态的变化, 因此每一段的应变率均可反映该段的裂缝扩展动态。第1段的裂缝形态及宽度不再变化时, 其对下一段裂缝影响而产生的应变不随时间变化, 而应变率反映应变随时间的改变, 因此上一段裂缝的应变对下一段压裂过程的应变率没有影响。
综上, 对于多段压裂, 受上一压裂段应力干扰影响, 后续压裂段光纤张应变汇聚区域可能不再出现; 而光纤应变率动态可有效呈现每一段压裂裂缝扩展动态, 单段压裂的光纤应变率演化规律适用于多段压裂。
裂缝扩展诱发光纤应变演化可分为应变增强、收缩汇聚和直线状汇聚3个阶段; 应变率演化可分为应变率增强、收缩汇聚、直线状汇聚、停泵应变率反转4个阶段; 光纤应变停泵后不变, 但应变率会出现反转, 光纤应变率反转可反映注入动态。
根据分布式光纤应变与应变率的直线状汇聚带, 可判断裂缝扩展至光纤的时刻与井间压窜, 同时可依据各簇裂缝扩展到光纤监测井的时刻识别多裂缝非均匀扩展现象, 评价裂缝非均匀扩展程度。
光纤监测井水平段位于裂缝高度范围内时, 可识别裂缝延伸至光纤的时刻, 而光纤监测井水平段位于裂缝高度以外时, 直线状汇聚带不明显。
多段压裂施工中, 受上一压裂段应力干扰的影响, 后续压裂段的光纤应变可能不再出现压裂初期的张应变区域, 但光纤应变率动态可有效呈现每一段压裂裂缝的扩展动态, 单段压裂的光纤应变率演化规律适用于多段压裂。
符号注释:
a, b—网格x, y方向半长, m; A—流动方程离散后系数矩阵, m/(s· Pa); C—影响系数矩阵, Pa/m; Cl—滤失系数, m/s0.5; d—与裂缝面的距离, m; Dw—井筒内壁直径, m; E—岩石弹性模量, Pa; F—方程组; Fk—方程组F的第k个分量, 当1≤ k≤ N时, 单位为Pa, 当k=N+1时, 单位为m3/s; fc—沿程摩阻系数, 无因次; hw—监测井与压裂井水平段的深度差, m; i—网格x方向编号; I1、I2—核函数, 无因次; $I\left( \xi , \eta \right)$—核函数, 无因次; J0、J1—第一类零阶、一阶贝塞尔函数; k—裂缝簇序号; lw—与跟端射孔簇的距离, m; L—光纤测点间距, m; m—压裂段编号; M—网格数量; N—裂缝簇数量; p—缝内流体压力, Pa; p—缝内流体压力矩阵, Pa; pin, k—第k簇裂缝的裂缝入口压力, Pa; pc, k—跟端裂缝至第k簇裂缝的井筒流动摩擦阻力, Pa; pp, k—第k簇裂缝的射孔摩擦阻力, Pa; pw—跟端射孔簇位置的井底压力, Pa; Qk—第k簇裂缝的进液流量, m3/s; Qt—注入排量, m3/s; r—光纤测点与裂缝单元距离, m; rp—径向距离, m; R—裂缝半径, m; Re—雷诺数, 无因次; sw—监测井与压裂井的水平井距, m; S—源汇项系数矩阵, m/s; t—时间, s; t0—空间点发生滤失的时刻, s; ∆ t—时间步长, min; uf—光纤轴向位移, m; un, ur—圆形裂缝垂向和径向位移, m; Vw—井筒内液体速度, m/s; w—裂缝宽度, m; w—裂缝宽度矩阵, m; w0—上一时间步宽度矩阵, m; x—坐标向量, m; xin, k—注入点坐标向量, m; x, y, z—坐标, m; $\delta \left( x \right)$—狄拉克函数, m-2; ∆ x, ∆ y—空间步长, m; ε—光纤应变, 无因次; εa—井筒内壁粗糙度, m; $\dot{\varepsilon }$—光纤应变率, min-1; εL—对数应变, 无因次; ${{\dot{\varepsilon }}_{\text{L}}}$—对数应变率, 无因次; εn—纳应变, 无因次; ${{\dot{\varepsilon }}_{\text{n}}}$—纳应变率, min-1; θ —常系数, 0≤ θ ≤ 1; ${{\Theta }_{1}}$, ${{\Theta }_{2}}$—过渡变量; $\zeta $—积分变量, 无因次; μ—流体黏度, Pa· s; ν —岩石泊松比, 无因次; $\xi $, $\eta $—网格局部坐标, m; ρ —液体密度, kg/m3; σ h—最小水平主应力, Pa; σ h—最小水平主应力矩阵, Pa。
(编辑 唐俊伟)
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|