与常规气田单向开发相比, 储气库的注采运行特点如下：①注采频繁转换, 运行工况复杂。储气库要求在一个运行周期内（一般为1年）完成完整的注采作业, 注、采气时间一般约200 d和120 d; 注、采气末关井平衡期约15~20 d, 以开展地面设备和井的维护检修以及地层压力、温度等测试。特殊情况下, 如遇极端天气气温突变或管道事故, 储气库在注（采）气期需快速转采（注）或缩短平衡期进入注采作业。频繁转换的复杂工况导致地层压力、温度短期陡升陡降, 测试难度大。②单井注采流量大, 采气速度快。普遍而言, 储气库单井日均配产（注）气量是气田开发的3~5倍甚至更高, 方案设计一般要求在120 d内采出同等规模气田约50%的动态储量, 折算采气速度高达150%。单井短期大流量吞吐进一步加大储集层非均质性的影响, 地层流体渗流状态与气田开发差异较大。③储气库高速注采和频繁转换的运行工况使地层压力持续频繁震荡, 同时由于短期强注强采使天然气优先在渗流阻力较小的大孔隙中储集并被采出, 宏观表现为储气库高速注采条件下可动用的有效孔隙空间小于气田“ 低速” 开发, 拟压力曲线显示相同储量下注气时储气库拟压力高于气田开发, 而采气时拟压力低于气田开发, 储气库多周期注采拟压力曲线呈不同程度的滞后特征, 尤其扩容达产初期最为显著。注采过程地层压力的频繁震荡和滞后效应将进一步增加动态不稳定流分析难度。

气田开发现有不稳定流分析的核心基础变量为物质平衡拟时间和拟压力规整化产量, 数学定义如（1）式和（2）式所示, 其中假设初始地层压力p_i均匀分布且为常数。

${{t}_{\text{ca}}}=\frac{G{{C}_{\text{ti}}}}{q}\left( {{\psi }_{{{p}_{\text{i}}}}}-{{\psi }_{{{p}_{\text{wf}}}}} \right)$ （1）

$\frac{q}{\Delta {{\psi }_{p}}}=\frac{q}{{{\psi }_{{{p}_{\text{i}}}}}-{{\psi }_{{{p}_{\text{wf}}}}}}$ （2）

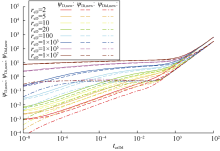
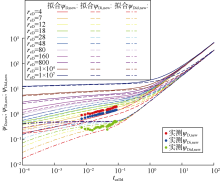
实际注采运行中, 尤其对于中国强非均质气藏型储气库, 单井高速注采进一步扩大了储集层非均质性的影响, 短期大流量快速注（采）气末地层压力处于明显的不均衡非稳定状态。同时, 由于矿场注采运行平衡期一般为15~20 d, 导致地层压力在短期内无法恢复到稳定均衡状态, 储气库随即进入下一采（注）气阶段, 使地层压力处于持续动态变化的非稳定状态。储集层非均质性越强, 储气库注采转换更快、更频繁或注采流量变化更大等现象导致地层压力非稳定特征更明显, 与现有不稳定流分析方法中数学模型假设的初始条件不一致, 产生较大的参数拟合预测误差。以现有方法对单一采气期不稳定流进行分析表明, 分析模型中初始地层压力的微小变化将引起气井不稳定流曲线形态的明显变化, 甚至出现拟合数据点脱离典型图版的现象（见图1）, 这将导致其解释的渗透率等关键地层参数误差大, 其中初始地层压力为35.5, 35.0 MPa时解释的渗透率分别为4.3×10^-3, 1.5×10^-3 μm²。

图1

	Figure Option ViewDownloadNew Window
	图1 不同初始地层压力对现有气井不稳定流分析模型拟合图版的影响

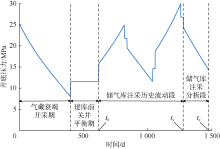
为建立适合储气库交变工况的注采动态不稳定流分析方法, 将储气库复杂工况化繁为简, 遵循每个周期的注采过程独立分析的原则; 同时为了准确获取注采分析段起始点的平均地层压力, 重新构建分析模型的初始条件, 提出适合气藏型储气库运行特点的“ 三点两段” 式分析理念。“ 三点” 是指循环注采气分析的3个时间点, 分别为建库注气起始点（t₀）、选取的注采分析段起始点（t_s）和注采分析段结束点（t_e）; “ 两段” 是指循环注采气分析的历史流动段和注采分析段（见图2）。

图2

	Figure Option ViewDownloadNew Window
	图2 储气库注采动态“ 三点两段” 式分析示意图

对于开发中后期气藏改建的储气库, 在注气建库前一般经历了10~30年的单向递减开发, 多数经历了较长时间的关井停产。因此认为在建库前地层压力已达到均衡和平稳状态, 满足现有不稳定流分析方法要求的初始时刻地层压力恒定的理论假设。本文将该时刻定义为历史流动段的初始时刻t₀, 此时的地层压力可通过现场测试较精确获取且为常数, 不考虑气藏衰竭开发时期的流量、压力变化。

t_s为注采分析段起始点, 同时也是储气库从t₀开始注气后经历的一个或多个注采周期的结束点, t₀到t_s定义为储气库注采动态分析的历史流动段。针对强非均质气藏型储气库高速注采运行工况, t_s对应的地层压力在矿场无法通过测试准确获得, 只能通过历史流动段不稳定流数学模型计算获取。

t_e为注采分析段结束点, t_s到t_e定义为储气库注采动态分析的分析预测段, 该段为需要分析的单一采气或注气期, 根据分析段不稳定流数学模型预测压力或流量。模型求解预测所需要的初始条件通过求解历史流动段数学模型获取, 而相关理论图版的制作以及对储气库注采动态数据的拟合解释均在注采分析段进行。

2.2.1 基本假设

以圆形均质封闭边界储集层中心一口直井为例, 数学模型建立的基本假设条件为：①储集层水平等厚、各向同性, 气体为单相流动、符合达西渗流规律; ②建库前地层压力分布均匀且为常数, 建库后地层压力分布不均匀, 与注采历史密切相关; ③考虑气体压缩系数和黏度随压力变化而变化, 气体压缩系数及偏差因子采用DPR（Dranchuk-Purvis-Robinson）方法计算, 气体黏度采用Lee方法计算^[25]; ④忽略重力及毛管压力的影响, 不考虑井筒储集效应、温度等其他因素对流动的影响。

2.2.2 数学模型

在上述假设条件下, 基于气体不稳定渗流理论, 引入物质平衡拟时间和拟压力处理储气库实时变井底流压、变产量及PVT（压力-体积-温度）性质随压力变化的问题, 储气库注采交变工况下的无因次注采动态不稳定流分析控制方程如下：

$\frac{{{\partial }^{2}}{{\psi }_{\text{D}}}}{\partial r_{\text{D}}^{2}}+\frac{1}{{{r}_{\text{D}}}}\frac{\partial {{\psi }_{\text{D}}}}{\partial {{r}_{\text{D}}}}=\xi \frac{\partial {{\psi }_{\text{D}}}}{\partial {{t}_{\text{caDd}}}}$ （3）

其中, 无因次变量定义式为：

${{\psi }_{\text{D}}}=\frac{Kh\left( {{\psi }_{\text{i}}}-\psi \right)}{1.842\times {{10}^{-3}}q{{\mu }_{g}}{{B}_{\text{g}}}} {{t}_{\text{caDd}}}=\xi \frac{3.6K{{t}_{\text{ca}}}}{\phi {{\mu }_{\text{g}}}{{C}_{\text{t}}}r_{\text{wa}}^{2}}$

${{t}_{\text{ca}}}=\frac{{{\mu }_{\text{gi}}}{{C}_{\text{ti}}}}{q}\int\limits_{0}^{t}{\frac{q}{{{\mu }_{\text{g}}}{{C}_{\text{t}}}}\operatorname{d}t} {{r}_{\text{D}}}=\frac{r}{{{r}_{\text{wa}}}} {{r}_{\text{eD}}}=\frac{{{r}_{\text{e}}}}{{{r}_{\text{wa}}}}$

${{r}_{\text{wa}}}={{r}_{\text{w}}}{{\text{e}}^{-S}} \psi (p)=\frac{{{\mu }_{\text{gi}}}{{Z}_{\text{i}}}}{{{p}_{\text{i}}}}\int\limits_{0}^{p}{\frac{p}{{{\mu }_{\text{g}}}Z}\operatorname{d}p}$

针对注采分析段（t_s< t< t_e）, 主要评价其运行过程中的气井压力及产量变化规律, 基于规整化压力积分产量不稳定流分析方法^[9], （3）式中的$\xi $为$\xi =1/\pi \left( r_{\text{eD}}^{2}-1 \right)$。注采分析段的初始地层压力分布不均匀（t=t_s）, 与历史流动段的注采历史密切相关, 其初始地层压力分布为储集空间的函数, 数学模型为：

${{\psi }_{\text{D}}}\left( {{r}_{\text{D}}}, {{t}_{\text{sD}}} \right)=f\left( {{r}_{\text{D}}} \right)$ （4）

从注采历史流动段（0≤ t≤ t_s）获取注采分析段的初始地层压力分布, 需要结合历史流动压力资料进行计算, 根据一般渗流方程, （3）式中$\xi $=1。同时注采历史流动段的初始地层压力分布均匀且为常数, 其初始条件如（5）式所示。由于历史流动段将建库平衡压力点作为t=0时刻条件, 该处理方法同时满足实际生产情况和模型初始条件, 且与常规气田开发的原始地层压力条件相比, 不需要考虑气田开发历史动态的影响, 极大降低了模型计算量及计算难度。

${{\psi }_{\text{D}}}\left( {{r}_{\text{D}}}, 0 \right)=0$ （5）

储气库注采动态不稳定流分析的内边界条件为：

${{r}_{\text{D}}}\frac{\partial {{\psi }_{\text{D}}}}{\partial \ {{r}_{\text{D}}}}\left| \begin{align} & \\ & {{r}_{\text{D}}}=1 \\ \end{align} \right.=-{{q}_{\text{D}}}$ （6）

其中 $~{{q}_{\text{D}}}=\frac{q\left( t \right)}{{{q}_{\text{sc}}}}$

外边界条件为：

$\frac{\partial {{\psi }_{\text{D}}}}{\partial {{r}_{\text{D}}}}\left| \begin{align} & \\ & {{r}_{\text{D}}}={{r}_{\text{eD}}} \\ \end{align} \right.=0$ （7）

考虑到模型中需要求解注采分析段的初始地层压力分布, 解析求解方法利用叠加原理可以获取地层中所有点的压力值, 但每求取一个点的压力值需要从起始点进行叠加, 计算量较大。因此, 采用数值方法进行求解, 通过迭代一次求解出地层中所有点的压力值。采用有限差分方法对模型进行求解：

${{\left( \frac{\partial u}{\partial x} \right)}_{j, n}}=\frac{u_{j}^{n+1}-u_{j}^{n}}{\Delta x}-\frac{\Delta x}{2!}{{\left( \frac{{{\partial }^{2}}u}{\partial {{x}^{2}}} \right)}_{j, n}}-\cdots $ （8）

忽略二阶导数项, 令r_D=e^x代入（3）式再转化为差分形式得到储集层控制方程的差分方程组：

$\frac{\psi _{\text{D, }\ j+2}^{n+1}-2\psi _{\text{D, }\ j+1}^{n+1}+\psi _{\text{D, }\ j}^{n+1}}{\Delta {{x}^{2}}}=\xi {{e}^{2{{x}_{j+1}}}}\frac{\psi _{\text{D, }\ j+1}^{n+1}-\psi _{\text{D, }\ j+1}^{n}}{t_{\text{caDd}}^{n+1}-t_{\text{caDd}}^{n}}$ （j=2, 3, …, m-1） （9）

将内边界条件代入控制方程差分方程组可得井网格处差分方程：

$\frac{\psi _{\text{D}, 2}^{n+1}-\psi _{\text{D, }1}^{n+1}}{\Delta x}=-q_{\text{D}}^{n+1}$ （10）

同理, 代入外边界条件可得边界处网格差分方程：

$\frac{\psi _{\text{D, }m}^{n+1}-\psi _{\text{D, }m-1}^{n+1}}{\Delta x}=0$ （11）

上述方程即为注采分析段模型的线性方程组, 结合初始条件对方程进行迭代求解, 其中初始压力分布函数f(r_D)需要根据注采历史流动段模型进行计算。历史流动段模型的差分离散过程与注采分析段模型类似, 其初始地层压力分布均匀, 根据该流动段线性方程组求解可以计算得到不同时刻的压力分布, 从而得到注采分析段模型的无因次拟压力解。

注采分析段中的无因次拟压力ψ _D是由建库平衡拟压力ψ _i变换得到的。由于储气库复杂的注采交替工况, 所选注采分析段的拟压力ψ 可能大于或小于ψ _i, 导致计算得到的ψ _D可能为正值亦可能为负值, 从而影响双对数曲线图版绘制。因此, 根据注采分析段初始压力分布f(r_D), 结合面积积分方法计算该时刻的无因次平均地层拟压力：

${{\overline{\psi }}_{\text{D}}}\left( {{t}_{\text{s}}} \right)=\iint{f\left( {{r}_{\text{D}}} \right)}\text{d}{{r}_{\text{D}}}\text{d}\theta $ （12）

在此基础上, 根据注采情况, 用计算得到的注采分析段无因次拟压力与无因次平均地层拟压力做差, 将注采分析段的${{\psi }_{\operatorname{D}}}$全部转换成正值, 从而得到新的无因次拟压力：对于注入过程,

${{\psi }_{D, \operatorname{new}}}={{\psi }_{\operatorname{D}}}-{{\bar{\psi }}_{\operatorname{D}}}({{t}_{\operatorname{sD}}})$ （13）

对于采出过程,

${{\psi }_{D, \operatorname{new}}}={{\bar{\psi }}_{\operatorname{D}}}({{t}_{\operatorname{sD}}})-{{\psi }_{\operatorname{D}}}$ （14）

同时, 对实测数据也要做类似的处理以匹配理论图版, 根据历史流量及物质平衡方程计算注采分析段起始点的平均地层压力, 并根据拟压力定义计算出对应的平均地层拟压力, 然后计算实测压力数据的规整化拟压力以及物质平衡拟时间：对于注入过程,

$\frac{\Delta \psi }{q}=\frac{\psi -\bar{\psi }({{t}_{\operatorname{s}}})}{q}$ （15）

对于采出过程,

$\frac{\Delta \psi }{q}=\frac{\bar{\psi }({{t}_{\operatorname{s}}})-\psi }{q}$ （16）

${{t}_{ca}}=\frac{G{{C}_{ti}}}{q}\left[ \bar{\psi }\left( {{t}_{\operatorname{s}}} \right)-\bar{\psi }\left( t \right) \right]$ （17）

同时, 利用产量规整化压力积分形式消除数据分散影响^[8], 分别计算修正的无因次拟压力积分及无因次拟压力积分导数曲线。

${{\psi }_{\text{Di, new}}}=\frac{1}{{{t}_{\text{caDd}}}}\int\limits_{0}^{{{t}_{\text{caDd}}}}{{{\psi }_{\text{D, new}}}d{{t}_{\text{caDd}}}}$ （18）

${{\psi }_{\text{Did, new}}}={{\psi }_{\text{D, new}}}-{{\psi }_{Di}}_{\text{, new}}$ （19）

在图版拟合和实测数据计算的基础上, 通过实测数据的拖动拟合, 结合压力拟合点及时间拟合点可得到模型中渗透率、井控半径、表皮因子以及井控储量等解释参数的计算公式。

$K=\frac{{{\mu }_{\text{gi}}}{{B}_{\text{gi}}}}{2\pi h}\frac{{{\left( {{\psi }_{\text{D, new}}} \right)}_{M}}}{{{\left( \Delta \psi /q \right)}_{M}}}$ （20）

${{r}_{\text{e}}}=\sqrt{\frac{K}{\pi \phi {{\mu }_{\text{gi}}}{{C}_{\text{ti}}}}{{\left( \frac{{{t}_{\text{ca}}}}{{{t}_{\text{caDd}}}} \right)}_{M}}}$ （21）

$S=\ln \left( \frac{{{r}_{\text{w}}}{{r}_{\text{eD}}}}{{{r}_{\text{e}}}} \right)$ （22）

$G=\frac{\pi r_{\text{e}}^{\text{2}}\phi h{{S}_{\text{g}}}}{{{B}_{\text{gi}}}}$ （23）

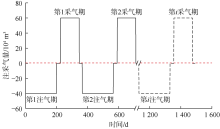
根据本文提出的“ 三点两段” 式储气库注采动态不稳定流分析模型和数值求解方法, 建立不同历史流动条件下以产量规整化压力为基础的多周期注采动态典型曲线, 包括无因次拟压力、无因次拟压力积分以及无因次拟压力积分导数。图3为储气库多周期注采运行动态曲线, 包括两个完整的注采运行周期。

图3

	Figure Option ViewDownloadNew Window
	图3 储气库多周期注采运行曲线

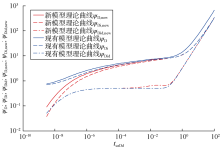
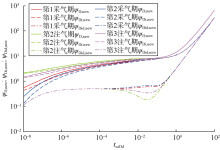
基于本文注采动态不稳定流分析模型求解得到的无因次拟压力绘制第2采气期典型曲线（见图4）, 可以看出, 其典型曲线整体形态与现有不稳定流分析方法典型曲线（见图1）类似, 但在具体曲线特征上存在一定差异; 利用平均地层拟压力值做差, 一定程度上消除了由于计算得到的负值导致双对数图无法绘制的问题。与现有不稳定流分析方法曲线对比（见图5）, 注采动态不稳定流分析新模型的典型曲线中无因次拟压力曲线及无因次拟压力积分曲线前端出现下掉现象, 无因次拟压力积分导数曲线中期呈上凸形态。

图4

	Figure Option ViewDownloadNew Window
	图4 注采动态不稳定流分析新模型典型曲线

图5

	Figure Option ViewDownloadNew Window
	图5 新模型与现有不稳定流分析典型曲线对比（reD=5 000）

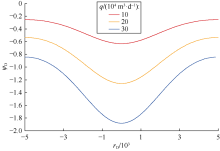
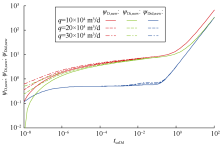
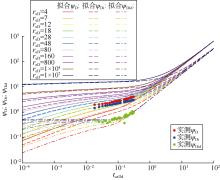
进一步对比不同注采流动期的理论曲线（见图6）, 可以看出不同流动期曲线整体趋势一致, 但无因次拟压力曲线及无因次拟压力积分曲线前端在不同注采周期出现上下偏移; 在压力积分导数曲线中期阶段, 两个采气期曲线出现上凸特征, 两个注气期曲线出现下凹特征。积分导数曲线中期的上凸下凹现象, 主要是由于注采分析段初始地层压力分布不均匀所致。考虑第1注气期流量不同, 分别绘制第1采气期初始时刻无因次地层拟压力分布及典型曲线（见图7—图8）。

图6

	Figure Option ViewDownloadNew Window
	图6 不同注采周期典型曲线对比

图7

	Figure Option ViewDownloadNew Window
	图7 不同流量下注采分析段初始无因次地层拟压力分布

图8

	Figure Option ViewDownloadNew Window
	图8 不同流量下注采分析段典型曲线对比

从无因次地层拟压力分布曲线可以看出, 第1注气期不同流量下的压力分布均处于不平衡状态, 且各流量下的压力之间有较大差异, 结合典型曲线对比图可以看出, 地层压力分布越不平衡, 其曲线中期凸起程度相对越大; 而注气期由于压力分布随距离r_D的变化趋势与采气期相反, 从而导致曲线下凹。

综合上述分析可知, 对于不同注采分析段, 在注采流动历史的影响下, 典型曲线具有差异性, 即不同的注采分析段具有不同的典型图版, 因此储气库井交变工况下的注采动态分析图版具有非典型性, 使得解释分析结果更符合储气库特殊工况。

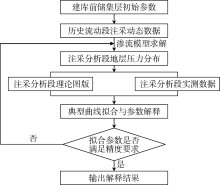
注采动态不稳定流新模型的分析流程如图9所示, 首先以t₀时刻地层平均压力、气井渗透率及表皮因子测试结果作为初始参数值, 根据历史流动注采动态数据, 计算t_s时刻注采分析段地层压力分布; 然后绘制注采分析段理论图版和实测数据曲线, 通过实测曲线与理论图版拖动拟合, 解释得到储集层参数; 对比分析解释参数与初始参数, 若不满足精度要求, 需要将拟合的储集层参数作为迭代值, 循环开展理论图版绘制、实测曲线拟合解释, 直至达到精度要求即得到最终的解释结果。注采动态不稳定流分析模型的解释参数包括储集层渗透率、表皮因子、井控半径以及井控库存量等, 在后续储气库优化运行中可以应用于产能评价、库容量分析、注采动态预测等。

图9

	Figure Option ViewDownloadNew Window
	图9 注采动态不稳定流新模型的计算流程图

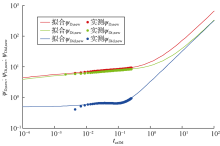
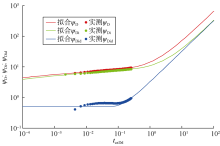
通过给定的流量、渗透率、井控半径等参数, 利用天然气不稳定渗流方程计算压力, 根据井底压力与流量数据绘制典型曲线并与本文建立的理论曲线拟合解释, 对比解释结果与给定参数的精度从而验证本文新模型。在先注后采两个流动期中, 选择采气期分别应用本文新模型及现有不稳定流分析模型进行解释分析, 两种方法的拟合效果如图10和图11所示。

图10

	Figure Option ViewDownloadNew Window
	图10 本文不稳定流分析模型模拟实例曲线拟合

图11

	Figure Option ViewDownloadNew Window
	图11 现有不稳定流分析模型模拟实例曲线拟合

相对于现有不稳定流分析模型中积分导数曲线拟合效果较差的现象, 本文新模型拟合效果图中理论曲线与实测数据拟合效果较好, 能够很好拟合数据凸起的特征, 实测数据前端出现下掉主要是由于积分及积分导数差分求解方法所致。两种方法拟合结果见表1, 注采动态不稳定流分析方法的拟合结果与给定的渗透率及井控库存等参数基本完全一致, 而现有不稳定流分析方法的拟合结果与给定参数存在一定误差, 综合图版拟合效果及解释参数, 初步验证了本文构建的注采动态不稳定流分析方法的准确性。

表1

表1

表1 模拟实例拟合结果对比 拟合参数 渗透率/ 10-3 μm2 表皮 因子 井控半径/ m 井控库存/ 108 m3 注采动态不稳定流分析拟合结果 3.01 0 500.002 2.73 现有不稳定流 分析拟合结果 2.91 0.13 481.000 2.93 给定初始参数 3.00 0 500.000 2.73

表1 模拟实例拟合结果对比

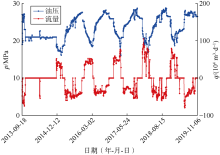
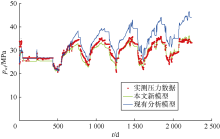
采用本文适用于储气库交变工况的注采不稳定流分析模型, 对呼图壁储气库H14井进行注采动态分析, 并与现有模型的拟合结果进行对比说明新模型的可靠性与实用性。H14井储集层中深3 553.8 m, 有效厚度35 m, 孔隙度15.5%, 地层温度84.78 ℃, 建库前静压24 MPa, 油管内径0.076 2 m, 天然气相对密度0.6; 在改建储气库前, 主力生产层测试的平均地层压力约14.4 MPa, 其原始地层压力约34.0 MPa。5个注采周期的日注采气量、油压数据如图12所示, 注入时流量为负, 采出时流量为正。以最后一个采气期作为分析段, 现有不稳定流分析方法中此阶段初始地层压力取32.4 MPa, 该方法和本文新方法的拟合图分别如图13和图14所示, 两种方法多周期全历史流量曲线的拟合效果如图15所示。

图12

	Figure Option ViewDownloadNew Window
	图12 H14井多周期注采流量及油压历史图

图13

	Figure Option ViewDownloadNew Window
	图13 H14井现有不稳定流分析模型曲线拟合

图14

	Figure Option ViewDownloadNew Window
	图14 H14井本文不稳定流分析模型曲线拟合

图15

	Figure Option ViewDownloadNew Window
	图15 H14井多周期全历史流量曲线拟合图

在现有不稳定流分析方法拟合过程中, 通常只进行图版拟合和所选分析段的压力历史拟合, 不进行储气库全注采周期的全压力历史拟合; 从分析结果可以看出, 图版能够进行一定程度的拟合, 但对于整个注采周期压力历史的拟合效果较差, 压力曲线整体向上偏移, 导致解释结果的可靠性较差。对比现有模型拟合图和本文新建模型拟合图可以看出, 无因次拟压力积分导数曲线更早（中期）出现上翘现象, 与理论曲线形态（见图5）完全一致。通过精细拟合该上翘段的无因次距离, 整体曲线簇得到较好的拟合, 且整个注采周期压力的拟合程度更高, 同时不需要调整初始地层压力值。

两种方法的拟合结果见表2, 注采动态不稳定流分析模型和现有不稳定流分析方法拟合的井控库存、渗透率及表皮均有一定差异。

表2

表2

表2 呼图壁H14井注采动态不稳定流分析结果表 拟合参数 渗透率/ 10-3 μm2 表皮 因子 井控半径/ m 井控库存/ 108 m3 注采动态不稳定流分析方法 7.37 -2.50 353 4.55 现有不稳定流 分析方法 9.35 -1.25 264 3.17

表2 呼图壁H14井注采动态不稳定流分析结果表

对H14井不同注采周期采用注采动态不稳定流分析模型进行拟合解释（见表3）。从分析结果中可以看出, 随注采周期的进行, 解释参数中渗透率、井控半径、井控库存整体呈上升趋势, 表明该井在注采过程中由于强注强采一定程度改善了储集层渗透性以及扩容效果等, 扩大了井控范围; 同时表皮因子整体呈减小的趋势, 表明该井在注采过程中, 对近井储集层有一定的改善作用, 说明注采动态分析优势体现在分段分析的相关性显著提高。

表3

表3

表3 注采动态不稳定流分析模型拟合结果 注采周期 分析期 渗透率/ 10-3 μm2 表皮 因子 井控半径/ m 井控库存/ 108m3 第1周期 注气期 4.09 -2.28 285 2.97 采气期 5.34 -2.30 291 3.08 第2周期 注气期 5.95 -2.36 309 3.49 采气期 6.46 -2.38 314 3.59 第3周期 注气期 7.18 -2.40 320 3.74 采气期 7.01 -2.43 332 4.02 第4周期 注气期 7.33 -2.50 354 4.57 采气期 7.37 -2.50 353 4.55

表3 注采动态不稳定流分析模型拟合结果