基于LWR理论, 传统的孔隙油-水渗吸方程（标记为LWR模型）^[8]如下：

${{p}_{\text{ce, b}}}=-{{p}_{\text{v, w, b}}}-{{p}_{\text{v, nw, b}}}-{{p}_{\text{g, b}}}$ （1）

考虑纳米限域效应、入口端效应和惯性效应, 则渗吸方程（标记为ND模型）可表示为^[15]：

${{p}_{\text{in, e}}}={{p}_{\text{ce, e}}}-{{p}_{\text{v, w, e}}}-{{p}_{\text{v, nw, e}}}-{{p}_{\text{en, e}}}-{{p}_{\text{g, e}}}$ （2）

ND模型忽略动态接触角效应（即假设接触角不随渗吸速度改变而改变）, 但事实上, 由于接触线处具有摩擦效应, 接触角将随着渗吸速度的变化而改变, 是动态变化的。如考虑动态接触角效应, 则纳米孔隙渗吸方程（标记为CD模型）可表示为：

${{p}_{\text{in, e}}}={{p}_{\text{ce, e}}}-{{p}_{\text{v, w, e}}}-{{p}_{\text{v, nw, e}}}-{{p}_{\text{en, e}}}-{{p}_{\text{g, e}}}-{{p}_{\text{fl, e}}}$ （3）

（3）式中惯性力为：

${{p}_{\text{in, e}}}=\frac{\text{d}\left[ {{\rho }_{\text{w, e}}}xv\text{+}{{\rho }_{\text{nw, e}}}\left( L-x \right)v \right]}{\text{d}t}$ （4）

基于平衡接触角计算的毛细管力为^[15]：

${{p}_{\text{ce, e}}}=\frac{2{{\gamma }_{\text{e}}}\cos {{\theta }_{\text{eq}}}}{R}$ （5）

基于考虑滑脱的泊肃叶方程, 黏性力可表示为^[6]：

${{p}_{\text{v, w, e}}}=\frac{8{{\mu }_{\text{w, e}}}x}{{{R}^{2}}+4R{{l}_{\text{s, w}}}}v$ （6）

${{p}_{\text{v, nw, e}}}=\frac{8{{\mu }_{\text{nw, e}}}\left( L-x \right)}{{{R}^{2}}+4R{{l}_{\text{s, nw}}}}v$ （7）

滑脱长度可表示为^{[6, 16]}：

${{l}_{\text{s, w}}}\text{=}\frac{{{C}_{\text{sw}}}}{{{\left( 1+\cos {{\theta }_{\text{eq}}} \right)}^{2}}}$ （8）

${{l}_{\text{s, nw}}}\text{=}\delta \left\{ \frac{{{\tau }_{\text{t, b}}}}{{{\tau }_{\text{t, i}}}}\text{exp}\left[ \frac{\alpha S{{\sigma }_{1}}\left( 1+\cos {{\theta }_{\text{eq}}} \right)}{{{k}_{\text{B}}}T} \right]-1 \right\}$ （9）

入口端效应可以表示为^[17]：

${{p}_{\text{en, e}}}=\frac{1}{6}{{\rho }_{\text{w, e}}}{{v}^{2}}$ （10）

重力作用为^[15]：

${{p}_{\text{g, e}}}\text{=}\left( {{\rho }_{\text{w, e}}}-{{\rho }_{\text{nw, e}}} \right)gx\sin \varphi $ （11）

三相接触线摩擦力为^[15]：

${{p}_{\text{fl, e}}}=\frac{2\zeta v}{R}$ （12）

（12）式中三相接触线摩擦系数表征了动态接触角效应的强弱。

根据分子动力学理论, 动态接触角和速度的关系为^{[18, 19]}：

$v\text{=}\frac{{{\gamma }_{\text{i}}}}{\zeta }\left( \cos {{\theta }_{\text{eq}}}-\cos {{\theta }_{\text{d}}} \right)$ （13）

$\zeta \text{=}\frac{{{k}_{\text{B}}}T}{K{{\lambda }^{3}}}$ （14）

$K=\frac{{{k}_{\text{B}}}T}{h}\exp \left( \frac{-\Delta {{G}_{\text{wet}}}}{{{N}_{\text{A}}}{{k}_{\text{B}}}T} \right)$ （15）

考虑到三相接触区中固相、润湿相和非润湿相分子以混合形式存在, 在此提出权重法计算润湿活化自由能：

$\Delta {{G}_{\text{wet}}}\text{=}{{\omega }_{\text{w}}}(\Delta {{G}_{\text{v, w}}}+\Delta {{G}_{\text{s-w}}})+{{\omega }_{\text{nw}}}(\Delta {{G}_{\text{v, nw}}}+\Delta {{G}_{\text{s-nw}}})$ （16）

式中权重系数为单相流体黏度占总黏度的比值。

黏度效应的活化自由能通过Eyring理论表征^[20]：

$\mu =\frac{h}{V}\exp \left( \frac{\Delta {{G}_{\text{v}}}}{{{N}_{\text{A}}}{{k}_{\text{B}}}T} \right)$ （17）

岩石-流体相互作用的活化自由能为^{[21, 22]}：

$\Delta {{G}_{\text{s-w}}}\text{=}\frac{{{N}_{\text{A}}}}{{{n}_{\text{w}}}}{{\gamma }_{\text{i}}}\left( 1+\cos {{\theta }_{\text{eq}}} \right)$ （18）

$\Delta {{G}_{\text{s-nw}}}\text{=}\frac{{{N}_{\text{A}}}}{{{n}_{\text{nw}}}}{{\gamma }_{\text{i}}}\left( 1-\cos {{\theta }_{\text{eq}}} \right)$ （19）

由（14）—（19）式可知, 三相接触线的摩擦系数为：

$\zeta \text{=}\frac{{{\left( {{\mu }_{\text{w, b}}}{{V}_{\text{w, b}}} \right)}^{{{\omega }_{\text{w}}}}}{{\left( {{\mu }_{\text{nw, b}}}{{V}_{\text{nw, b}}} \right)}^{{{\omega }_{\text{nw}}}}}}{{{\lambda }^{3}}}\times \\ \exp \left\{ \frac{{{\gamma }_{\text{i}}}}{{{k}_{\text{B}}}T}\left[ \frac{{{\omega }_{\text{w}}}}{{{n}_{\text{w}}}}\left( 1+\cos {{\theta }_{\text{eq}}} \right)+\frac{{{\omega }_{\text{nw}}}}{{{n}_{\text{nw}}}}\left( 1-\cos {{\theta }_{\text{eq}}} \right) \right] \right\}$ （20）

考虑多层黏附效应, 固-液界面区黏度为：

${{\mu }_{\text{i}}}=\frac{h}{V}\exp \left( \frac{\Delta {{G}_{\text{v}}}+\Delta {{G}_{\text{s-l}}}}{{{N}_{\text{A}}}{{k}_{\text{B}}}T} \right)$ （21）

结合（18）、（19）式, 界面区流体黏度为：

${{\mu }_{\text{w, i}}}\text{=}{{\mu }_{\text{w, b}}}\exp \left[ \frac{{{\gamma }_{\text{i}}}\left( 1+\cos {{\theta }_{\text{eq}}} \right)}{{{n}_{\text{w}}}{{k}_{\text{B}}}T} \right]$ （22）

${{\mu }_{\text{nw, i}}}={{\mu }_{\text{nw, b}}}\exp \left[ \frac{{{\gamma }_{\text{i}}}\left( 1-\cos {{\theta }_{\text{eq}}} \right)}{{{n}_{\text{nw}}}{{k}_{\text{B}}}T} \right]$ （23）

综合（20）、（22）和（23）式, 可得接触线摩擦系数和界面区域流体黏度的关系：

$\zeta \text{=}\frac{1}{{{\lambda }^{3}}}{{\left( {{\mu }_{\text{w, i}}}{{V}_{\text{w, b}}} \right)}^{{{\omega }_{\text{w}}}}}{{\left( {{\mu }_{\text{nw, i}}}{{V}_{\text{nw, b}}} \right)}^{{{\omega }_{\text{nw}}}}}$ （24）

此外, 流体有效黏度可通过面积权重法计算^[6]。

Wang等^[23]研究了纳米孔隙介质中分子相互作用、动态接触角效应与入口端效应对水渗吸动态的影响, 获得了较为可靠的渗吸动态数据（经过Lattice Boltzmann验证的模拟数据）。为讨论多层黏附、滑脱、入口端、惯性等效应对渗吸动态的影响程度, 在此采用该文献中渗吸模型参数作为本文CD模型的基础参数（见表1）, 其渗吸动态数据作为验证数据, 模拟分析忽略多层黏附、滑脱、入口端、惯性等效应对渗吸结果的影响。

表1

表1

表1 孔隙渗吸模型验证所需基础参数 参数名称 参数值 参数名称 参数值 参数名称 参数值 参数名称 参数值 润湿相 水 非润湿相 正辛烷 油水界面张力 0.05 N/m 孔隙半径 5.0 nm 水相密度 998 kg/m3 油相密度 698.3 kg/m3 水相润湿角 30° 孔隙长度 100 nm 水相黏度 0.001 Pa· s 油相黏度 0.000 45 Pa· s 岩石-水相界面区域厚度 0.70 nm 孔隙倾角 0° 水相滑脱长度 0.12 nm 油相滑脱长度 0.19 nm 岩石-油相界面区域厚度 0.98 nm 温度 298 K

表1 孔隙渗吸模型验证所需基础参数

其中有效界面张力计算公式为^[24]：

${{\gamma }_{\text{e}}}\text{=}{{\gamma }_{\text{b}}}{{\left( 1+\frac{2{{\delta }_{\text{l}}}}{R} \right)}^{-1}}$ （25）

界面区域的厚度取两层流体分子厚度之和^[6], 润湿相界面区域密度计算公式为^[25]：

${{\rho }_{\text{i}}}\text{=}{{\rho }_{\text{b}}}+f\left( {{\theta }_{\text{eq}}} \right)$ （26）

假设润湿相界面区域密度与流体常规密度的比值和非润湿相界面区域密度与流体常规密度的比值相同, 非润湿相界面区域密度同样采用（26）式计算。

有效密度采用权重法计算：

${{\rho }_{\text{e}}}\left( d \right)\text{=}{{\rho }_{\text{b}}}\left[ 1-\frac{{{A}_{\text{i}}}\left( d \right)}{{{A}_{\text{t}}}\left( d \right)} \right]+{{\rho }_{\text{i}}}\frac{{{A}_{\text{i}}}\left( d \right)}{{{A}_{\text{t}}}\left( d \right)}$ （27）

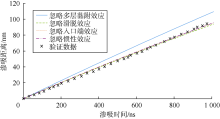
CD模型忽略多层黏附、滑脱、入口端、惯性等效应时, 模拟结果与验证数据的对比曲线如图1所示。可以看到, 当忽略入口端与惯性效应时, 模拟曲线与验证数据曲线基本重合, 说明入口端与惯性效应对渗吸的影响很小, 可以忽略。而忽略多层黏附效应时, 模拟曲线偏离验证数据曲线较远, 误差较大, 该项不能忽略。

图1

	Figure Option ViewDownloadNew Window
	图1 CD模型忽略多层黏附等效应时的模拟结果

经计算, 亲水性储集层的水滑脱长度较小, 为0.10~0.41 nm; 油滑脱长度与孔隙壁面性质、油的组分相关, 计算参数中油的主要组分为正辛烷, 油滑脱长度亦较小, 为0.19 nm, 该种情况下滑脱效应对渗吸动态的影响可以忽略。但是当油组分改变时, 油滑脱长度将发生改变, 如已知表面能为61.2 mN/m的砂岩中, 正十二烷烃和正十四烷烃在其表面的滑脱长度分别为5.7 nm和28.0 nm^[16], 此时滑脱效应对渗吸的影响将较为显著, 该种情况下滑脱效应对渗吸动态的影响不能忽略。

基于上述分析, 如忽略入口端与惯性效应的影响, 此时由（3）、（5）—（7）和（12）式整理得：

$\left( \frac{4{{\mu }_{\text{w, e}}}}{R+4{{l}_{\text{s, w}}}}-\frac{4{{\mu }_{\text{nw, e}}}}{R+4{{l}_{\text{s, nw}}}} \right)xv+\left( \frac{4{{\mu }_{\text{nw, e}}}L}{R+4{{l}_{\text{s, nw}}}}+\zeta \right)v\text{=}{{\gamma }_{\text{e}}}\cos {{\theta }_{\text{eq}}}$ （28）

为方便表征和计算, 上式可表示为：

${{A}_{1}}xv+Bv=C$ （29）

则渗吸距离和体积分别为：

$x=\frac{1}{{{A}_{1}}}\left[ {{\left( {{B}^{2}}+2{{A}_{1}}Ct \right)}^{0.5}}-B \right]$ （30）

$Q=\text{ }\!\!\pi\!\!\text{ }{{R}^{2}}x\left( R, t \right)$ （31）

考虑初始含水饱和度和渗吸后残余油饱和度的影响, 岩心中可发生流体流动的孔隙体积为：

${{V}_{\text{m}}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}\phi {{D}_{\text{c}}}^{2}{{L}_{\text{c}}}\left( 1-{{S}_{\text{wc}}}-{{S}_{\text{or}}} \right)$ （32）

而基于毛细管束的岩心可流动孔隙体积为：

${{V}_{\text{m}}}=\int\limits_{{{R}_{\min }}}^{{{R}_{\max }}}{\text{ }\!\!\pi\!\!\text{ }{{N}_{\text{m}}}{{R}^{2}}Lf\left( R \right)\text{d}R}$ （33）

结合（32）和（33）式, 岩心中可发生流体流动的毛细管总数量为：

${{N}_{\text{m}}}=\frac{\phi {{D}_{\text{c}}}^{2}\left( 1-{{S}_{\text{wc}}}-{{S}_{\text{or}}} \right)}{4\tau \int\limits_{{{R}_{\min }}}^{{{R}_{\max }}}{{{R}^{2}}f\left( R \right)\text{d}R}}$ （34）

则岩心渗吸体积、油相采出程度可表示为：

${{Q}_{\text{c}}}={{N}_{\text{m}}}\int\limits_{{{R}_{\min }}}^{{{R}_{\text{max}}}}{Qf\left( R \right)\text{d}R}$ （35）

${{R}_{\text{o}}}=\frac{4{{Q}_{\text{c}}}}{\text{ }\!\!\pi\!\!\text{ }\phi {{D}_{\text{c}}}^{2}{{L}_{\text{c}}}\left( 1-{{S}_{\text{wc}}} \right)}\times 100$ （36）

岩心孔隙尺寸可通过对数正态分布模型表征^[26]：

$f\left( R \right)=\frac{1}{R{{f}_{1}}\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}\exp \left[ -\frac{1}{2}{{\left( \frac{\ln R-{{f}_{2}}}{{{f}_{1}}} \right)}^{2}} \right]$ （37）

${{R}_{\text{ave}}}={{C}_{\text{f1}}}\exp ({{f}_{2}}-{{f}_{1}}^{2})$ （38）

采用表1中的基础数据, 验证动态接触角模型、孔隙渗吸模型的可靠性, 具体计算流程如图2所示。

图2

	Figure Option ViewDownloadNew Window
	图2 模型验证计算流程

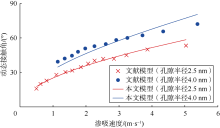
Stroberg等^[27]首次开展了纳米尺度渗吸分子动态模拟研究, 选取其研究结果对本文模型进行验证。首先计算界面区域的流体黏度, 然后计算接触线摩擦系数（其中分子跳跃长度作为拟合参数）, 最后通过（13）式计算动态接触角与速度的关系。由图3可见, 本文提出的动态接触角模型与文献模型（分子动态模型）模拟结果吻合度较高（模拟孔隙半径分别为2.5 nm、4.0 nm）, 说明本文模型可以较好地表征渗吸过程中接触角的动态变化。

图3

	Figure Option ViewDownloadNew Window
	图3 纳米尺度动态接触角模型验证

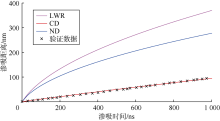
采用表1中的基础数据, 分别采用LWR、ND、CD模型模拟渗吸时间与渗吸距离的关系, 并将模拟结果与验证数据曲线进行对比（见图4）。可以看到, 传统LWR模型未考虑纳米限域效应、入口端效应、惯性效应、动态接触角效应, 模拟曲线离验证数据曲线最远, 误差最大, 不能表征纳米尺度孔隙的渗吸过程; ND模型虽然考虑了纳米限域、入口端、惯性等效应, 但未考虑动态接触角效应, 其模拟曲线虽然比LWR模型更接近验证数据曲线, 但误差仍然很大; 在ND模型基础上, CD模型修正了动态接触角效应的影响, 模拟效果较好, 拟合优度为0.99。可见, 动态接触角效应对渗吸的影响最为显著, 纳米限域效应（多层黏附效应和滑脱效应）次之, 惯性效应和入口端效应影响最小。

图4

	Figure Option ViewDownloadNew Window
	图4 孔隙渗吸模型模拟结果对比曲线

Ren等^[28]开展了渗透率和黏度对致密岩心渗吸的影响研究, 结果表明采出程度随渗透率增大而升高, 随油相黏度增大而减小。王秀宇等^[29]研究了温度、压力对致密岩心渗吸的影响, 证实温度越高, 采出程度越高, 而压力存在一个最佳范围。Kathel等^[30]探讨了润湿性对致密岩心渗吸的影响, 发现表面活性剂可以使岩心发生润湿反转, 自发渗吸采出程度约为68%。上述文献共选用5块实验岩心, 岩心编号分别为岩心A-5^[28]、岩心R4-2^[29]、岩心R4-4^[29]、岩心2^[30]、岩心7^[30], 均为致密砂岩, 岩心基础参数如表2所示^{[28, 29, 30]}, 通过实验获取了岩心渗吸采出程度随渗吸时间变化的5组数据。

表2

表2

表2 文献中实验岩心基础参数 岩心编号 渗透率/ 10-3 μm2 孔隙度/% 长度/cm 孔隙半径 分布/nm A-5 0.251 12.8 5.522 1~350 R4-2 0.053 10.3 5.530 1~100 R4-4 0.474 10.9 4.980 1~250 2 0.236 13.3 5.584 1~200 7 0.239 13.4 5.573 1~200

表2 文献中实验岩心基础参数

根据表2中的基础数据, 采用CD模型模拟渗吸采出程度与渗吸时间的关系曲线, 并与5组实验数据进行对比（见图5）。由图可知, CD模型模拟结果与文献实验结果吻合较好, 可较好地模拟致密岩心中的油-水渗吸过程。但CD模型忽略了重力影响, 因此当毛细管力较弱时, 重力作用对渗吸动态存在一定影响, 导致模拟曲线与实验数据存在一定的偏差。

图5

	Figure Option ViewDownloadNew Window
	图5 渗吸采出程度与渗吸时间的关系曲线

渗吸过程中的主要阻力为惯性力、接触线摩擦力、湿相（水）黏滞力和非湿相（油）黏滞力, 其中单项阻力与这4项阻力之和的比定义为单项阻力比。不同半径孔隙渗吸过程中单项阻力比随渗吸时间的变化如图6所示。由图可知：①渗吸初期, 以惯性力为主导, 以半径为50.0 nm的孔隙模拟为例, 当渗吸时间小于0.100 ns时, 随着时间增加, 惯性阻力比逐渐减小, 接触线摩擦阻力比逐渐增加。当渗吸时间为0.1~100.0 ns, 接触线摩擦阻力比最高、油相黏滞阻力比次之, 接触线摩擦力占主导地位, 且接触线摩擦阻力、油相黏滞力基本保持不变; 渗吸时间大于100 ns时, 接触线摩擦阻力比和油相黏滞阻力比逐渐减小, 而水相黏滞阻力比逐渐增加。②接触线摩擦力不仅作用于渗吸后期, 呈下降趋势, 也作用渗吸初期, 且阻力比呈上升趋势。③随着孔隙半径减小, 惯性阻力比曲线左移, 惯性力作用时间缩短; 渗吸初期接触线摩擦阻力比曲线向左移动（对应孔隙半径从50.0 nm到20.0 nm再到10.0 nm的模拟曲线变化。由于本文最小模拟时间为0.001 ns, 因此孔隙半径为5.0 nm和2.5 nm的模拟曲线未能完整显示该过程）, 动态接触角效应增强, 渗吸中后期接触线摩擦阻力比曲线向下移动, 动态接触角效应减弱; 油相黏滞阻力比曲线向上移动, 油相黏滞力的影响增加; 水相黏滞阻力比曲线向左移动, 水相黏滞力初始作用时间提前。

图6

	Figure Option ViewDownloadNew Window
	图6 不同孔隙半径条件下渗吸时间与单项阻力比的关系

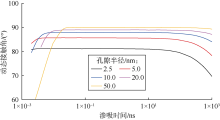
图7为不同渗吸模型在不同孔隙半径条件下渗吸时间与渗吸距离、渗吸距离增强因子（CD模型渗吸距离与ND模型渗吸距离的比值）的关系, 可以看到, 孔隙半径减小, CD、ND模型的模拟曲线位置下降, 相同渗吸时间内渗吸距离减小。随着渗吸时间的延长, 渗吸距离增强因子曲线呈“ U” 形, 早期下降, 中期趋于平稳, 后期上升, 因渗吸距离与动态接触角效应负相关, 故动态接触角效应表现为早期上升, 中期趋于平稳, 后期下降, 与图6b中的接触线摩擦阻力比变化一致。同时还可以看到, 孔隙半径减小, 渗吸初期曲线向左移动, 动态接触角效应的影响增强, 渗吸中后期曲线向上移动, 动态接触角效应的影响减弱, 仍与图6b中的接触线摩擦阻力比变化一致。

图7

	Figure Option ViewDownloadNew Window
	图7 不同渗吸模型在不同孔隙半径条件下渗吸时间与渗吸距离、渗吸距离增强因子关系曲线

图8为不同孔隙半径下, 渗吸时间与动态接触角的关系曲线。渗吸初始, 水相刚接触孔隙内壁面时渗吸速度近似为零, 根据（13）式可知, 此时的接触角为平衡接触角（初始时间接近于零, 远小于本文最小模拟时间0.001 ns, 因此图中未显示该过程）; 随着渗吸时间增加, 渗吸速度增大, 接触角逐渐增加至最大, 并在一定时间内保持稳定, 如图8所示; 随着渗吸时间进一步增加, 渗吸速度减小, 动态接触角逐渐减小, 如图8所示。根据（13）式可以预计, 当渗吸时间增大至渗吸速度减小趋近于零时, 接触角将最终趋近平衡接触角（趋近时间远大于本文最大模拟时间1 000 ns）。

图8

	Figure Option ViewDownloadNew Window
	图8 不同孔隙半径下渗吸时间与动态接触角的关系曲线

油水界面张力越大, 渗吸动力越大, 然而流体与岩石之间的黏附功也会增加。图9为不同界面张力条件下渗吸时间与接触线摩擦阻力比的关系曲线, 可以看到, 界面张力增加, 曲线上移, 接触线摩擦阻力比增加, 动态接触角效应增强。

图9

	Figure Option ViewDownloadNew Window
	图9 不同界面张力下渗吸时间与接触线摩擦阻力比的关系曲线

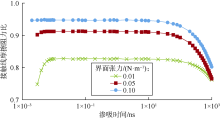
图10为不同界面张力条件下渗吸时间与渗吸距离、渗吸距离增强因子的关系曲线。可以看到, 界面张力由0.01 N/m增大至0.05 N/m, CD、ND模型的模拟曲线位置上升, 相同渗吸时间内渗吸距离增加; 但当界面张力由0.05 N/m增大至0.10 N/m时, CD模型的模拟曲线位置下降, ND模型的模拟曲线先上升后下降, 可见界面张力存在临界值（本算例位于0.05~0.10 N/m）。因此, 致密储集层渗吸提高采收率, 过低的界面张力并不能获得更好的渗吸效果, 而应该通过优化获得最佳的界面张力。图10c渗吸后期的结果同样显示界面张力存在临界值。

图10

	Figure Option ViewDownloadNew Window
	图10 不同界面张力条件下渗吸时间与渗吸距离、渗吸距离增强因子的关系曲线

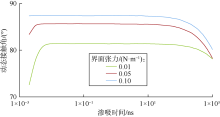
图11为采用CD模型模拟的不同界面张力条件下渗吸时间与动态接触角的关系曲线。随着渗吸时间的延长, 动态接触角从最初的平衡接触角逐渐增加至最大, 并在一定时间内保持稳定, 随后动态接触角将逐渐减小并趋近于平衡接触角。同时最大动态接触角随着界面张力增加而增大, 即界面张力增加, 接触角的变化范围增大, 动态接触角效应增强。

图11

	Figure Option ViewDownloadNew Window
	图11 界面张力对动态接触角的影响