引用本文
朱海燕, 宋宇家, 雷征东, 唐煊赫. 致密油水平井注采储集层四维地应力演化规律—以鄂尔多斯盆地元284区块为例[J]. 石油勘探与开发, 2022,49(1): 136-147.
ZHU Haiyan, SONG Yujia, LEI Zhengdong, TANG Xuanhe. 4D-stress evolution of tight sandstone reservoir during horizontal wells injection and production: A case study of Yuan 284 block, Ordos Basin, NW China[J]. Petroleum Exploration & Development, 2022,49(1): 136-147.  
Doi: 10.11698/PED.2022.01.12
Permissions
Copyright©2022, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
致密油水平井注采储集层四维地应力演化规律—以鄂尔多斯盆地元284区块为例
朱海燕1,2, 宋宇家2, 雷征东3, 唐煊赫1
1.成都理工大学油气藏地质及开发工程国家重点实验室,成都 610059
2.西南石油大学油气藏地质及开发工程国家重点实验室,成都 610500
3.中国石油勘探开发研究院,北京 100083

第一作者简介：朱海燕（1984-）,男,安徽亳州人,博士,成都理工大学能源学院教授,主要从事石油钻采岩石力学方面的教学和科研工作。地址：四川省成都市成华区二仙桥东三路1号,成都理工大学能源学院,邮政编码：610059。E-mail：zhuhaiyan040129@163.com

收稿日期: 2021-05-28 修回日期: 2021-12-07
基金项目: 国家自然科学基金面上项目“页岩储层射孔簇内复杂三维多裂缝起裂与竞争扩展机理研究”（51874253）; 国家自然科学基金联合基金重点项目“四川深层页岩智能传控靶向复合压裂基础研究”（U20A20265）
摘要

综合考虑储集层物性和力学参数的非均质性、初次压裂裂缝以及实际注采制度影响,提出了一套致密砂岩油注采开发过程中储集层多物理场四维地应力演化数值模拟方法,建立了致密砂岩油储集层渗流-地质力学耦合的四维地应力演化模型,以鄂尔多斯盆地华庆油田元284区块为例,开展了水平井注采开发过程中四维地应力演化规律研究。研究表明：①受注采关系影响,注水井处三向应力增大,生产井处三向应力减小,但平面上水平两向主应力沿各自应力方向呈明显的条带状分布。②注采开发过程中,水平两向主应力差在注水井所对应的水平井井筒处最大,而在注水井之间的未动用区域则最小;在注水井处最大水平主应力方向变化最大,且呈径向汇聚状分布。③注采井网中,水平井重复压裂时,水力裂缝受地应力影响会出现非对称扩展和方向偏转。研究结果有效指导了致密砂岩油水平井注采井网调整和重复压裂设计。

关键词: 致密油; 致密砂岩储集层; 注采井网; 地应力演化; 渗流-地质力学耦合; 鄂尔多斯盆地
中图分类号:TE357.1 文献标志码:A 文章编号:1000-0747(2022)01-0136-12
4D-stress evolution of tight sandstone reservoir during horizontal wells injection and production: A case study of Yuan 284 block, Ordos Basin, NW China
ZHU Haiyan1,2, SONG Yujia2, LEI Zhengdong3, TANG Xuanhe1
1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu 610059, China
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China
3. PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China
Abstract

To investigate the 4D stress change during injection and production in tight sandstone reservoirs, a multi-physical fields modeling method is proposed considering the reservoir heterogeneity, hydraulic fracture and complex injection-production system. The 4D stress evolution of tight sandstone reservoir in Yuan 284 block of Huaqing oilfield, Ordos Basin, during injection-production in horizontal wells is investigated by modeling coupled flow and geomechanics. Results show: (1) Induced by injection and production, the 3D stress increases near the injectors but decreases near the producers, and the horizontal stresses are distributed in obvious strips along their respective stress directions. (2) The horizontal stress difference is the highest at the horizontal wellbore beside injectors during injection and production, while it is the lowest in undeveloped zone between the injectors, and the orientation of maximum horizontal principal stress changes the most near the injectors, which is distributed radially. (3) The hydraulic fracture in re-fracturing well was observed to be asymmetrical in geometry and deflected as the stress changed. The results provide theoretical guidance for horizantal well network modification and re-fracturing optimization design in tight sandstone reservoir.

Keyword: tight oil; tight sandstone reservoir; injection-production well network; stress evolution; flow and geomechanical coupling; Ordos Basin
0 引言

中国致密油储量丰富, 开发潜力巨大, 鄂尔多斯盆地是中国致密油的主要生产基地, 其产量超过中国致密油总产量的50%[1, 2]。致密油储集层普遍具有物性差、非均质性强、孔隙连通性差等特征, 导致油井产量递减快、注水能量补充困难, 调整开发思路、增加泄油面积、减小渗流距离是致密油开发的重点和难点, 而注采井网调整和老井重复压裂是保证致密油稳产增产的有效措施[3, 4, 5, 6, 7]。

在致密油注水开发过程中, 流体的注入和采出会引起地层孔隙压力变化, 从而导致地应力场随开发时间动态变化, 即四维（常规的三维加上时间维度）地应力演化。Wright等[8, 9]、Kristiansen等[10]、Dons等[11]、Zhang等[12]和Minner等[13]通过分析压裂监测数据和地震测试数据等, 证实了油藏注采过程会引起地层应力场大小和方向变化从而改变老井重复压裂和加密井压裂裂缝扩展形态。同时应力场变化还会引起地层形变, 激活断层[14, 15, 16, 17], 使套管发生变形[18], 给生产作业带来极大的安全隐患。王友净等[19]、赵向原等[20, 21]、范天一等[22]和Li等[23]结合现场数据和数值模拟结果, 发现储集层长期注水会激活天然裂缝或引起新裂缝起裂及动态扩展。因此, 研究注采过程中地应力演化对致密砂岩油高效开发具有重要意义。

长期以来, 考虑油气藏开发过程中地应力演化的多物理场耦合模拟, 一直是国内外学者研究的热点。早在1980年, Hagoort等[24]和Settari[25]首次考虑油藏渗流引起的储集层孔隙压力和地应力变化, 建立了油藏渗流与压裂裂缝扩展耦合的数值模型。岳迎春等[26]和董光等[27]结合理论模型, 研究了均质地层压裂井生产过程中应力转向问题及其对重复压裂裂缝扩展的影响。Roussel等[28]结合位移不连续法和有限元法, 研究了压裂井注入和生产引起的地层应力变化及其对加密井压裂裂缝扩展的影响。Abou-Sayed等[29]考虑热弹性效应, 研究了均质地层注采过程中井筒周围地应力场变化。Hwang等[30]综合考虑岩石热弹性和孔隙弹性, 系统研究了均质油藏模型注采过程中地层应力场变化及井间干扰。现有研究主要针对均质油藏, 研究了注采开发过程中单井井周及注采井井间的地应力变化规律, 但对于非均质致密油储集层复杂井网注采开发过程中的地应力演化未见详细研究。

本文综合考虑储集层物性和地质力学非均质性特征, 以及水力压裂裂缝和注采开发复杂性, 以鄂尔多斯盆地华庆油田元284区块重复压裂注采先导试验区为例, 通过储集层三维地质和力学模型建立、水力压裂裂缝模拟和储集层四维地应力动态演化模拟, 构建水平井注采井网注采开发过程中致密油储集层渗流-地质力学耦合模型, 结合现场测压数据、微地震监测结果及重复压裂井施工数据等验证模型准确性, 研究长期注采过程中地层应力场动态演化规律, 为注采井网调整及重复压裂方案设计提供理论指导。

1 致密砂岩储集层渗流-地质力学耦合的地应力演化模型
1.1 地应力演化数值模拟方法

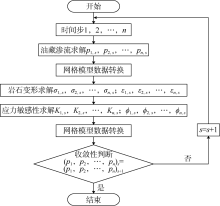
本文提出的致密砂岩储集层长期注采过程中地应力动态演化数值模拟方法, 综合考虑了储集层非均质性、井网实际注采制度, 利用井层数据、地震数据、测井数据、实验数据等, 分别构建储集层地质模型和力学模型。其次, 该方法考虑水力压裂裂缝的导流增产效果, 采用水力压裂裂缝扩展模型, 根据压裂施工数据模拟计算水力裂缝参数, 结合压裂微地震监测数据进行校正。为了保证现场适用性和计算时效性, 本方法采用迭代耦合计算方法。根据地质模型建立基于有限差分方法的储集层渗流模型, 并利用等效算法将水力裂缝转换为地层单元等效渗透率, 参与渗流计算。同时, 以初始孔隙压力及地应力作为基于有限元方法的地质力学模型初始条件, 以渗流模型计算所得储集层注采过程中孔隙压力变化数据作为边界条件, 进行致密砂岩储集层注采过程中渗流-地质力学耦合模拟。该方法考虑应力变化对地层孔渗参数的影响, 加入了应力敏感性计算模型。由于渗流模型和地质力学模型的网格数据结构存在差异, 采用自主编制的网格映射策略程序, 实现不同网格数据之间的转化。该方法充分发挥储集层渗流模型、地质力学模型及水力裂缝扩展模型的计算优势, 实现各模型的有机结合, 具有较好的兼容性和灵活性。

1.2 渗流-地质力学耦合模型

1.2.1 储集层渗流方程

根据目标区域致密油储集层特征, 本文采用单孔单渗油水两相渗流模型, 假设孔隙介质中油、水两相为弱可压缩性流体, 渗流过程中遵循达西定律, 多孔介质为水湿性, 油、水两相不相溶, 且不考虑温度变化影响, 则模型满足连续性方程：

$\nabla \cdot \left[ \frac{{{K}_{i}}{{K}_{\text{ro}}}}{{{\mu }_{\text{o}}}{{B}_{\text{o}}}}\left( \nabla {{p}_{\text{o}}}-{{\rho }_{\text{o}}}g\nabla H \right) \right]+\frac{{{q}_{\text{o}}}}{V}=\frac{\partial }{\partial t}\left( \frac{\beta \phi {{S}_{\text{o}}}}{{{B}_{\text{o}}}} \right)$ （1）

$\nabla \cdot \left[ \frac{{{K}_{i}}{{K}_{\text{rw}}}}{{{\mu }_{\text{w}}}{{B}_{\text{w}}}}\left( \nabla {{p}_{\text{w}}}-{{\rho }_{\text{w}}}g\nabla H \right) \right]+\frac{{{q}_{\text{w}}}}{V}=\frac{\partial }{\partial t}\left( \frac{\beta \phi {{S}_{\text{w}}}}{{{B}_{\text{w}}}} \right)$ （2）

其中饱和度满足：

${{S}_{\text{o}}}+{{S}_{\text{w}}}=1$ （3）

孔隙压力可视为油、水相平均压力：

$p={{p}_{\text{o}}}{{S}_{\text{o}}}+{{p}_{\text{w}}}{{S}_{\text{w}}}$ （4）

同时, 油、水相压力与毛管压力关系满足：

${{p}_{\text{cow}}}={{p}_{\text{o}}}-{{p}_{\text{w}}}$ （5）

模型外边界Г 采用封闭边界, 满足：

${{\left. \nabla p \right|}_{\Gamma }}=0$ （6）

内边界（井筒处）油、水两相分别满足：

${{\left. \frac{\partial {{p}_{\text{o}}}}{\partial r} \right|}_{r={{r}_{\text{w}}}}}=-\frac{{{\mu }_{\text{o}}}}{2\text{ }\!\!\pi\!\!\text{ }h{{K}_{\text{o}}}{{r}_{\text{w}}}}{{q}_{\operatorname{o}}}$ （7）

${{\left. \frac{\partial {{p}_{\text{w}}}}{\partial r} \right|}_{r={{r}_{\text{w}}}}}=-\frac{{{\mu }_{\text{w}}}}{2\text{ }\!\!\pi\!\!\text{ }h{{K}_{\text{w}}}{{r}_{\text{w}}}}{{q}_{\text{w}}}$ （8）

1.2.2 岩体形变方程

对于线弹性固体材料, 其满足平衡方程：

${{\sigma }_{ij, j}}+{{F}_{i}}=0$ （9）

地层多孔介质形变基于Biot有效应力理论[31]计算, 即：

${{{\sigma }'}_{ij}}={{\sigma }_{ij}}-\alpha p{{\delta }_{ij}}$ （10）

饱和油水的油藏开发过程中, 假设岩体发生微小弹性形变, 并且具有一定的变形速度, 此时, 岩体处于动态平衡状态, 因此, （9）式可表示为：

${{\sigma }_{ij, j}}+{{F}_{i}}-{{\left( \alpha p{{\delta }_{ij}} \right)}_{, j}}=0$ （11）

岩体位移和应变关系满足几何方程：

${{\varepsilon }_{ij}}=\frac{1}{2}\left( {{u}_{i, j}}+{{u}_{j, i}} \right)$ （12）

通常地层岩体力学形变特征表现为各向异性, 因此, 岩体应力与应变关系可表示为[32]：

$\left[ \begin{matrix} {{\varepsilon }_{11}} \\ {{\varepsilon }_{22}} \\ {{\varepsilon }_{33}} \\ {{\varepsilon }_{23}} \\ {{\varepsilon }_{31}} \\ {{\varepsilon }_{12}} \\ \end{matrix} \right]=\left[ \begin{matrix} \frac{1}{{{E}_{1}}} & -\frac{{{\upsilon }_{21}}}{{{E}_{2}}} & -\frac{{{\upsilon }_{31}}}{{{E}_{3}}} & {} & {} & {} \\ -\frac{{{\upsilon }_{12}}}{{{E}_{1}}} & \frac{1}{{{E}_{2}}} & -\frac{{{\upsilon }_{32}}}{{{E}_{3}}} & {} & {} & {} \\ -\frac{{{\upsilon }_{13}}}{{{E}_{1}}} & -\frac{{{\upsilon }_{23}}}{{{E}_{2}}} & \frac{1}{{{E}_{3}}} & {} & {} & {} \\ {} & {} & {} & \frac{1}{{{G}_{23}}} & {} & {} \\ {} & {} & {} & {} & \frac{1}{{{G}_{31}}} & {} \\ {} & {} & {} & {} & {} & \frac{1}{{{G}_{12}}} \\ \end{matrix} \right]\left[ \begin{matrix} {{\sigma }_{11}} \\ {{\sigma }_{22}} \\ {{\sigma }_{33}} \\ {{\sigma }_{23}} \\ {{\sigma }_{31}} \\ {{\sigma }_{12}} \\ \end{matrix} \right]$ （13）

边界条件包含位移边界和应力边界, 其分别为：

${{\left. {{u}_{i}}\left( r \right) \right|}_{\Gamma }}={{g}_{1}}\left( r \right)$ （14）

${{\left. {{\sigma }_{ij}}\left( r \right) \right|}_{\Gamma }}={{g}_{2}}\left( r \right)$ （15）

1.2.3 应力敏感性方程

对于孔弹性介质, 孔隙压力及应力条件的变化会使地层岩体发生变形, 从而导致孔隙度变化。根据Carman-Kozeny公式, 渗透率与孔隙度密切相关, 因此, 孔隙度、渗透率应力敏感性模型可表示为[33]：

$\phi \text{=1}-\frac{{{\phi }_{\text{0}}}}{{{\text{e}}^{{{\varepsilon }_{\text{v}}}}}}$ （16）

$K={{K}_{0}}\left[ \frac{1}{{{\phi }_{0}}}{{\left( 1+{{\varepsilon }_{\text{v}}} \right)}^{3}}-\frac{1-{{\phi }_{0}}}{{{\phi }_{0}}}{{\left( 1+{{\varepsilon }_{\text{v}}} \right)}^{-\frac{1}{3}}} \right]$ （17）

1.2.4 渗流-地质力学耦合方法

渗流-地质力学耦合的数值方法按照耦合求解形式可划分为全耦合、迭代耦合和单向耦合3种。通常全耦合方法计算精度较高, 但计算效率较低, 计算结果不易收敛, 且难以体现地层非均质性特征, 而单向耦合计算效率较高, 但计算精度较低[34, 35]。迭代耦合能满足地层非均质性要求, 同时计算效率和计算精度较高[36]。因此, 本文采用迭代耦合方法开展致密砂岩储集层的渗流-地质力学耦合模拟。

常规的迭代耦合方法需在某一时间步内, 采用渗流模型完成孔隙压力计算, 将其传递给地质力学模型, 作为模型边界条件, 完成应力形变计算, 根据应力敏感性模型更新孔渗数据, 将其传递给渗流模型, 开始下一时间步计算。但该方法需要在每个时间步内至少完成1次迭代, 之后才可进入下一时间步的计算, 计算步骤较为繁琐, 影响计算效率。与常规迭代耦合方法不同, 渗流-地质力学迭代耦合模拟需要在1次迭代中完成所有时间点的储集层孔隙压力、应力、应变以及渗透率、孔隙度的数据计算。基于计算结果, 需要检验当前迭代步计算所得各时间步孔隙压力数据与前一迭代步相比是否收敛, 若不收敛, 则增加迭代次数, 若收敛, 模拟结束（见图1）。渗流-地质力学迭代耦合模拟可通过减小计算时间步长及调整网格尺寸来缩小迭代步内地层孔隙体积变化率, 从而控制迭代收敛性。该方法通过全时间步多次迭代, 实现模拟计算精度要求, 同时方便渗流模型、地质力学模型以及应力敏感性模型各自操作和计算, 以及各模型之间的数据转换[37]。

图1 油藏渗流-地质力学迭代耦合模拟过程

1.3 网格数据转化方法

渗流-地质力学迭代耦合模拟中, 渗流模型采用有限差分方法, 地质力学模型则采用有限元方法, 两者的网格数据存在差异。因此, 本文采用笔者自主编制的网格映射策略子程序, 通过球形自适应搜索算法, 以赋值数据点为中心进行搜索, 并利用邻近点法实现密集节点向赋值数据点插值, 利用线性插值法实现稀疏节点向赋值数据点插值, 从而实现有限差分角点网格中心数据与有限元网格节点数据之间的转换, 详见文献[38, 39]。

1.4 水力裂缝模拟及裂缝数据转化方法

可根据地层特征及压裂施工工艺选择适当的模型（如解析模型、离散裂缝模型等）进行水力裂缝模拟, 计算水力裂缝扩展形态及裂缝导流能力、渗透率等参数。采用Oda法[40, 41], 将每条裂缝的渗透率投影到对应的地质网格各方向上, 形成二阶裂缝渗透率张量, 并将其作为油藏模型中裂缝渗透率, 或附加在基质渗透率中, 参与油藏渗流模拟。

2 模型建立与验证
2.1 区域概况

本文以元284区块重复压裂注采先导试验区为例, 该区块位于鄂尔多斯盆地伊陕斜坡西南部。该区块以三叠系延长组长63层为主要产层, 包含9个小层, 其中主力层长631顶界埋深2 092~2 134 m（海拔-682~-640 m）, 长63储集层厚度55~90 m, 平均约70 m。该地区储集层物性普遍较差, 属于致密油储集层。孔隙度主要介于10.0%~15.0%, 平均为12.4%, 渗透率主要介于（0.20~0.50）×10-3 μm2, 平均为0.37×10-3 μm2。但由于部分区域发育天然裂缝, 局部地层渗透率大于1.00×10-3 μm2, 储集层具有较强的层内和层间非均质性。目标区域长63储集层最大水平主应力方向约为NE75° , 垂向主应力（σ v）、最大水平主应力（σ H）和最小水平主应力（σ h）大小关系为σ v> σ H> σ h, 符合正断层机制。针对储集层特征, 该区块开展了水平井注采井网开发试验, 并取得较好的效果[3, 42]。

2.2 油藏模型及地质力学模型建立

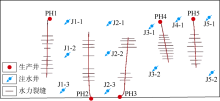
根据注采井分布特征和模拟计算需求, 本文选取水平井注采区长63储集层进行地应力演化模拟。该区平面范围为3 800 m×1 740 m, 其中包含5口水平井, 11口定向井。采用水平井采油、定向井注水的井网模式, 生产井井距平均约720 m, 注水井井距平均约650 m。其中生产井采用常规胍胶压裂后投产, 而注水井则采用燃爆压裂后进行近平衡注水驱替, 即注水压力接近地层最小水平主应力。

结合区域地层特征、储集层改造工艺及开发方案, 分别建立渗流模型及地质力学模型, 模型主要参数如表1所示。模型假设：①储集层属于致密储集层, 暂不考虑边底水作用; ②地质力学模型外边界位移为零; ③注水作用使注水井周围储集层渗透率条件得到改善, 模型根据生产历史拟合, 调整注水井周围储集层渗透率; ④储集层为连续介质。

表1 目标区域模型主要参数

考虑模型运算精度及计算效率, 油藏模型中网格平面尺寸为20 m×15 m, 垂向尺寸根据各层位厚度进行划分, 网格高度平均为2 m, 地质力学模型中网格平面尺寸为10 m×10 m, 网格高度平均为5 m。本文基于该区域的实际地质条件、水力压裂参数和生产数据, 开展特定井网条件下长期注采过程中储集层四维地应力演化规律研究。

2.3 生产井初次水力压裂裂缝模拟

目标区域内共5口生产井, 均为水平井, 井深约为2 770~3 120 m, 水平段长度约为450~840 m。各井均采用分段多簇水力喷射压裂工艺, 选用常规胍胶压裂液, 压裂施工段数为7~10段, 每段约2簇, 平均每段施工液量约160 m3, 平均每段支撑剂用量约27.5 m3。鉴于区块储集层宏观天然裂缝发育情况及微地震监测结果, 目标区域生产井初次压裂以简单两翼裂缝扩展为主。本文结合储集层物性参数、岩石力学参数、地应力数据、实际压裂施工数据及微地震监测结果, 通过净压力拟合的方式, 反演得到区块内各井水力压裂裂缝几何参数及其导流能力。以PH2井为例, 各段施工参数及裂缝反演结果如表2所示。可以看出, PH2井模拟裂缝长度约200~220 m, 裂缝高度约35~38 m, 裂缝导流能力约（180~220）×10-3 μm2· m。研究区域水平井水力裂缝扩展分布结果如图2所示, 为了降低注水突进风险, 水平井采用纺锤状布缝设计, 靠近注水井处裂缝较短, 远离注水井处裂缝较长, 各井水力压裂裂缝长度主要为170~250 m, 导流能力主要为（130~280）×10-3 μm2· m。采用Oda法将水力裂缝进行渗透率等效处理, 并映射到渗流网格中, 形成致密砂岩基质-水力裂缝渗流系统。

表2 PH2井水力压裂施工参数及水力裂缝模拟结果

图2 研究区域井位及水力裂缝扩展分布

2.4 油藏渗流-地质力学迭代耦合模拟结果及验证

为了研究水平井注采井网条件下长63储集层长期注采过程中地应力动态演化规律及其对重复压裂裂缝扩展的影响, 本文利用Eclipse油藏模拟软件建立单孔单渗油水两相渗流模型。利用Abaqus有限元软件平台建立储集层地质力学模型, 以孔隙压力为边界条件, 结合应力敏感性理论模型, 以该区各井压裂投产至重复压裂前（2011年12月至2016年12月）的实际生产数据为基础, 进行渗流-地质力学耦合模拟。

2.4.1 渗流历史拟合结果

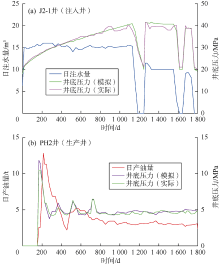
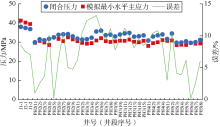
本文采用定产量、拟合井底压力方式进行渗流模拟计算, 图3为J2-1井（注入井）和PH2井（生产井）渗流模型历史拟合结果。可以看出, 注入井日注水量较为稳定; 生产井稳产效果较好, 后期产量约为3.0 t/d, 井底压力约为5 MPa。与实际井底压力相比, 模拟结果误差在8%以内, 吻合程度较好。

图3 注采井开发历史拟合结果对比

2.4.2 渗流-地质力学迭代耦合结果

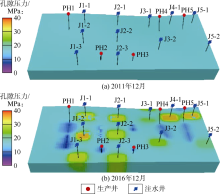
模型区域内注采井自2011年12月开始相继投产, 2016年12月之后开始进行重复压裂改造试验, 在此期间注水井平均累计注水量约21 880 m3, 平均日注水量13.98 m3, 生产井平均累计产液量约7 580 m3, 平均日产液量5.08 m3, 平均累计产油量5 172 t, 平均日产油量3.46 t。图4为渗流-地质力学耦合模拟孔隙压力变化情况, 受生产注入影响, 注水井处孔隙压力逐渐升高, 生产井处孔隙压力逐渐降低。地层初始孔隙压力为15.5~16.2 MPa, 截至2016年12月（注采开发60个月）, 注水井处孔隙压力约为30~38 MPa, 生产井处约7~10 MPa。

图4 注采过程中孔隙压力变化

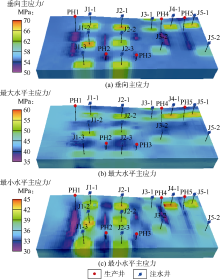
该区域储集层初始垂向主应力约55~58 MPa, 初始最大水平主应力约41~45 MPa, 初始最小水平主应力约33~36 MPa。受孔隙压力变化影响, 注入井处三向应力升高, 生产井处三向应力降低, 但三向应力平面分布变化规律略有不同。截至2016年12月, 注水井处垂向主应力约60~68 MPa, 生产井处约51~54 MPa; 注水井处最大水平主应力约48~52 MPa, 生产井处约39~45 MPa; 注水井处最小水平主应力约40~43 MPa, 生产井处约29~32 MPa, 如图5所示。

图5 2016年12月储集层三向主应力分布

2.4.3 最小水平主应力模拟结果及验证

重复压裂井水力裂缝闭合压力能一定程度上反映储集层最小水平主应力变化。图6为重复压裂井各施工段裂缝闭合压力与最小水平主应力模拟结果对比。可以看出, 受注水作用和各段产量贡献差异影响, PH2井趾端（第1—4段）和PH3井趾端（第2—4段）最小水平主应力较低, PH4及PH5井各段最小水平主应力较为稳定。最小水平主应力计算结果与重复压裂井裂缝闭合压力对比误差为0.2%~13.2%, 平均误差7.6%, 验证了本文模型的正确性。

图6 重复压裂井压裂裂缝闭合压力与最小水平主应力模拟结果对比

3 元284区块长期注采过程中储集层四维地应力演化规律
3.1 孔隙压力变化规律

受生产和注入影响, 注入井井周附近孔隙压力明显增大, 生产井压裂改造区域则减小, 如图4所示。但由于注水井间距过大且储集层致密, 井间仍存在较大范围的压力未波及区。而水平井各段储集层物性参数、水力裂缝位置及扩展情况不同, 生产过程中各段渗流条件及产量贡献存在差异, 因此, 水平井井筒方向上各段孔隙压力变化有所不同。本文孔隙压力变化规律与常规认识区别不大, 因此仅作简单阐述。

3.2 地应力动态演化规律

3.2.1 垂向应力演化规律

垂向应力变化集中分布在各井井筒及裂缝波及范围内, 随孔隙压力增大（或减小）则增大（或减小）, 但垂向应力变化幅度略有差异, 如图5a所示。垂向应力主要受压实作用影响, 其他各向应力变化对其影响较小, 因此, 变化区域范围和变化规律与孔隙压力基本保持一致。本文垂向应力变化规律与常规认识区别不大, 且垂向地应力变化对本文中所论述的开发方案指导作用不明显, 因此仅作简单阐述。

3.2.2 水平主应力演化规律

在井筒和裂缝波及范围内, 水平两向主应力与孔隙压力变化规律相同, 但其分别沿各自应力方向呈条带状变化, 如图5b和图5c所示。孔隙压力变化会引起有效应力变化, 使储集层岩体产生形变, 但由于水平两向主应力差异, 使未受孔隙压力影响的位置产生水平两向主应力变化, 或在部分位置孔隙压力变化与水平两向主应力变化规律出现明显差异[28, 30]。以J1-2注水井为例, 注水过程中, 其井周储集层孔隙压力增大, 有效应力减小, 地层岩体膨胀, 从而挤压周边岩体。J1-2井与J1-1井之间区域主要受最小水平主应力方向挤压, 使得最小水平主应力明显增大, 同理, J1-2井与J2-2井之间主要受最大水平主应力方向挤压, 因此, 该方向水平主应力增长明显, 从而造成水平两向主应力分布变化与孔隙压力的差异。

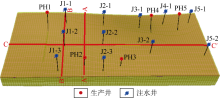
针对主力开发层位长631小层, 以AA° （PH2井水平井筒方向）、BB° （J1-1、J1-2和J1-3井所在纵向井排）和CC° （J1-2井所在横向井排）3个截面（见图7）为例, 进一步分析和对比注采过程中水平两向主应力随时间变化规律。

图7 模型研究截面分布

对比PH2井井筒方向上（AA° 剖面）水平两向主应力变化（见图8a、图9a）, 自2013年以后最小水平主应力在3口注水井对应位置并无明显变化, 但最大水平主应力则逐年增大。该位置注水作用会削弱生产引起的最大水平主应力降低, 甚至会使其超过初始值。对比注水井井排方向上（BB° 剖面）水平两向主应力变化（见图8b、图9b）, 在注水井之间的孔隙压力未波及区域最大水平主应力逐年减小, 而最小水平主应力逐年增大, 且明显高于初始值。对比CC° 剖面水平两向主应力变化（见图8c、图9c）, 生产井PH1和PH2处受邻井注水作用影响较为明显, 水平两向主应力变化规律存在差异, 其压裂改造范围内最小水平主应力随孔隙压力的减小而降低, 但改造区外变化不明显。而PH1和PH2井压裂改造区内最大水平主应力自2013年开始呈明显上升趋势。与之相比, PH4和PH5井距离注水井相对较远, 注水作用对生产井处水平两向主应力变化影响较小。水平两向主应力变化主要受孔隙压力梯度影响, 孔隙压力梯度越大, 应力变化越明显, 甚至可能发生应力反转[28, 43, 44]。但本文中, 储集层水平两向主应力差较大, 且受水力裂缝对基质渗透率的改善作用影响, 在生产井处未形成足够大的孔隙压力梯度变化, 因此, 未出现应力反转现象[30]。

图8 注采过程中最大水平主应力变化

图9 注采过程中最小水平主应力变化

图10为2016年12月储集层水平两向主应力方向的平面分布情况。可以看出, 水平两向主应力方向保证正交, 截至2016年12月, 井区水平主应力方向发生0~30° 偏转, 注水井处尤为明显, 其中最大水平主应力呈近似径向汇聚状分布。在注采开发过程中, 地层应力变化主要受孔弹性、热弹性及压裂裂缝张开引起的位移作用影响[8, 28, 29, 30]。对于多孔介质, 孔隙压力增大使其有效应力减小, 岩石发生膨胀变形, 其正应力和切向应力减小, 应力方向受挤压发生偏转。同时孔隙压力变化越剧烈, 孔隙压力梯度越大, 应力变化越明显, 方向偏转越明显, 该结果也在其他文章中得到证实[28, 30, 45, 46, 47, 48]。

图10 2016年12月储集层水平两向应力方向平面分布

3.2.3 水平两向主应力差动态变化规律

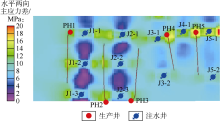
图11为目标区域注采开发60个月后长631储集层水平两向主应力差分布情况。该区域初始水平两向主应力差约7~9 MPa, 受水平两向主应力变化规律影响, 注水井所对应的水平井段水平两向主应力差上升幅度最大, 截至2016年12月, 该位置水平两向主应力差约12.4~13.8 MPa, 而其余水平井段处则变化较小。注水井之间的孔隙压力未波及区水平两向主应力差下降幅度最大, 截至2016年12月, 该位置水平两向主应力差约1.2~5.8 MPa, 为可能发生应力反转的最佳区域, 而注水井处应力差变化不明显。

图11 2016年12月储集层水平两向主应力差大小平面分布

4 四维地应力演化规律在元284区块的应用
4.1 元284区块水平井注采开发方案优化

元284区块致密砂岩储集层在长达5年的注采开发过程中, 生产井孔隙压力下降幅度最高达9.0 MPa, 水平两向主应力差最大升高了52.7%; 注水井孔隙压力增大幅度最高达22.8 MPa, 水平两向主应力差最大降低了84.6%。可见, 长期注采显著改变了储集层的地应力场, 致使部分注水井组“ 水窜” 和注水不见效现象日益突出, 必须采取增产措施。长期注采过程中, 地应力方向变化会改变裂缝扩展方向, 而最小水平主应力大小直接影响水力压裂施工压力大小, 同时当井筒两侧最小水平主应力分布不均时会产生“ 压裂冲击” （Frac-hit）效应, 使得水力裂缝呈现非对称分布[46, 47, 49, 50, 51]。此外, 该区块地应力符合正断层机制, 水平两向主应力差会影响压裂分支裂缝扩展形态。为了弥补产量递减损失, 结合储集层四维地应力演化规律, 本文提出了水平生产井重复压裂和注水定向井压裂转采的优化方案。

4.1.1 水平生产井重复压裂方案优化

元284区块水平井初次压裂排量为3.2 m3/min左右, 液量约160 m3, 压裂规模较小。储集层开发过程中, 在注水井之间区域存在大面积未动用区, 且该区域水平两向主应力差较小, 是压裂改造的有利区域。因此, 对水平井进行重复压裂改造时, 可优先改造该区域, 增大该层段改造规模, 力求在该区域产生复杂分支裂缝。同时, 受注水影响, 注水井处应力方向发生变化, 最大水平主应力呈明显的径向汇聚状分布, 这将使靠近注水井的部分水平井段重复压裂裂缝向注水井位置偏转[45, 52]。基于演化后的储集层非均匀地应力场, 采用压裂模拟软件计算水力裂缝扩展形态, 优化出压裂排量3.5 m3/min, 注水井之间区域所对应的水平井压裂井段液量800~900 m3, 靠近注水井的井段则控制在700 m3以内, 结合微地震监测数据, 适当控制该井段改造规模, 防止压窜。

4.1.2 注水定向井压裂转采方案优化

元284区块长期注采开发, 储集层四维地应力演化显著改变了储集层的应力环境, 可对驱替效果不明显或发生“ 水窜” 的注水井采用体积压裂, 增大注水井周围的有效渗流体积, 压裂后将该注水井转变成生产井, 反向调整注采关系和应力分布, 抑制前期开采引起的“ 水窜” , 增加区块原油产量。由于注水井所对应的水平井处水平两向主应力差较大, 基于四维地应力演化结果, 优化出压裂排量6.0 m3/min, 液量控制在700 m3以内, 充分改造储集层, 同时防止裂缝扩展到高应力差区域时发生突进、连通甚至压窜水平井。

4.2 元284区块水平井注采井网重复压裂现场试验

采用上述优化方案, 从2016年12月开始对研究区域内5口水平井相继进行了重复压裂试验, 对8口注水定向井进行了压裂后转采试验。试验采用体积压裂工艺, 选用双封单卡油管注入分段压裂工具、滑溜水+胍胶压裂体系, 其中部分水平井在原压裂段基础上进行了补孔压裂, 每段平均施工排量3.4 m3/min, 每段压裂液用量600~860 m3, 平均约760 m3, 每段支撑剂用量30~60 m3, 平均约54 m3。注水井平均每段施工排量5.5 m3/min, 平均每段压裂液用量约675 m3, 平均每段支撑剂用量约66 m3, 施工液量明显小于水平井重复压裂。

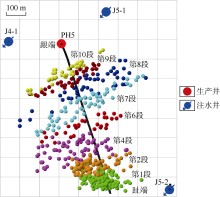
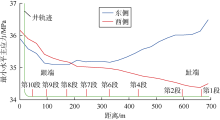
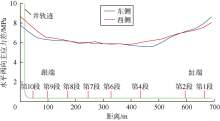
研究区域地层地应力演化会影响水平井重复压裂裂缝扩展方向和扩展形态。以PH5井为例, 该井于2017年4月20日至5月13日进行重复水力压裂, 压裂施工10段, 其中第5段和第10段进行了补孔作业。根据地层应力分布情况, 该井压裂过程中跟端和趾端压裂段压裂液用量较小, 而中部井段则较多。各压裂段施工参数及微地震监测结果如表3所示, 水力压裂微地震事件点分布如图12所示。该井第1段至第6段西侧裂缝扩展长度明显大于东侧, 而第7段至第10段两侧裂缝则基本呈对称分布。结合PH5井井筒两侧裂缝扩展中部最小水平主应力分布情况（见图13）, 该井趾端东侧最小水平主应力明显大于西侧, 相差约2.0 MPa; 跟端东西两侧大小相近, 相差约0.3 MPa。该井井筒两侧最小水平主应力差大于1.0 MPa时, 水力裂缝呈明显非对称扩展, 因此, 该井趾端水力裂缝更偏向井筒西侧, 而跟端裂缝则呈对称扩展。对比水平两向主应力差（见图14）, PH5井井筒两侧差异较小, 但跟端和趾端水平两向主应力差约8 MPa, 明显大于中部的6 MPa。而该井中部压裂微地震事件点分布宽度约65~90 m, 大于跟端和趾端的30~50 m。当该井水平两向主应力差小于6.5 MPa时, 水力裂缝扩展宽度明显增大。另外, 该井第1、2段重复压裂水力裂缝方位约NE83° ~NE93° , 第7—10段裂缝方位约NE62° ~NE66° 。而井区最大水平主应力初始方向约为NE75° , 受地应力方向变化影响, 该井趾端和跟端裂缝明显向其东侧注水井（J5-1和J5-2）位置偏转, 最大偏转达18° 。

表3 PH5井重复压裂施工参数及微地震监测结果

图12 PH5井重复体积压裂微地震事件点分布

图13 PH5井井筒两侧最小水平主应力对比

图14 PH5井两侧水平两向主应力差对比

区域内其他水平井重复压裂过程中, 注水井间区域对应的井段水力裂缝扩展总长度约280~560 m, 平均约440 m, 两侧裂缝半长差异约30~250 m。而PH1井、PH2井及PH3井两侧水平主应力差较低, 约1.2~3.8 MPa, 导致其裂缝扩展宽度达80~250 m, 明显大于PH4井和PH5井。而水平井重复压裂裂缝方向在注水井对应井段偏转约8° ~21° 。

该区域注水井由于未进行压裂微地震监测, 无法确定裂缝扩展情况, 但其压裂过程中施工压力未见明显降低, 且邻井压力未见升高, 表明压裂裂缝与生产井未窜通, 压裂改造满足设计要求。

4.3 开发效果对比

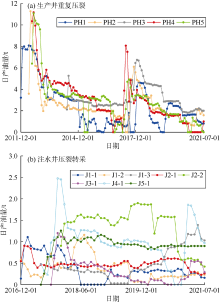
该区水平井重复压裂前后（2011年12月至2021年7月）日产油量变化如图15a所示, 各水平井重复压裂后初期产量约为初次压裂后的45%~135%, 平均约60%, 与重复压裂前相比, 产油量平均提高了3倍。稳定期产量平均约1.78 t/d, 增产有效期均大于1 200 d, 增产效果明显, 有效地缓解了油井生产后期产量递减趋势。该区注水井压裂转采后（2016年12月至2021年7月）日产油量变化如图15b所示, 注水井转采后, 初期平均产油量为1.07 t/d, 稳定期平均产量约0.57 t/d, 与相邻区块定向生产井产量相当, 且各井压裂后日产油量相对稳定, 个别井还出现稳步回升趋势, 如J2-1井等。生产井重复压裂和注水井转采不仅有效提高区块产量, 同时缓解了水平井“ 水窜” 风险, 该试验方案整体效果较好。

图15 生产井重复压裂及注水井压裂转采效果对比

5 结论

鄂尔多斯盆地华庆油田元284区块重复压裂注采先导试验区注采开发5年, 受水平井注采关系影响, 注水井处三向应力增大6~13 MPa, 生产井处三向应力减小2~6 MPa, 但水平两向主应力沿各自应力方向呈明显的条带状分布; 在注水井井排方向上, 注水井之间水平两向主应力差减小2~8 MPa, 同时, 水平主应力方向发生了约0~30° 的偏转, 在注水井处偏转尤为明显, 该处最大水平主应力方向呈近似径向汇聚状分布。

研究区域注采开发过程中地应力变化会影响水平井重复压裂裂缝扩展方向和形态, 当井筒两侧最小水平主应力差大于1 MPa时, 水力裂缝偏向最小水平主应力较小的一侧, 出现明显非对称扩展; 在水平两向应力差小于6.5 MPa的区域, 水力裂缝扩展宽度较大, 约65~250 m; 受施工井段相邻注水井影响, 水平井水力裂缝扩展方向发生偏转并指向注水井, 最大偏转达21° 。

结合目标井区注采过程中地应力变化规律, 优化了水平井重复压裂及注水井压裂后转采试验方案：①增大注水井间区域对应的水平井段改造规模, 平均压裂改造范围总长度由210 m提高到440 m; ②控制水力裂缝扩展方向上注水井对应位置处水平井段及注水井压裂液量在700 m3以内。该方案使区块水平井重复压裂后产量提高了3倍, 注水井压裂转采产量与相邻区块定向生产井产量相当且产量稳定, 同时缓解了水平井“ 水窜” 风险。

符号注释：

Bo, Bw—油相和水相体积系数, m3/m3; Ei—地层岩体各向弹性模量, i=1, 2, 3, Pa; Fi—地层岩体各向体积力, i=1, 2, 3, N/m3; g—重力加速度, m/s2; g1, g2—边界函数; Gij—地层岩体剪切模量张量, i=1, 2, 3, j=1, 2, 3, Pa; h—储集层厚度, m; H—垂向深度, m; Ki—储集层各向渗透率, i=1, 2, 3, m2; K—基质渗透率, m2; K0—初始基质渗透率, m2; Ko, Kw—油相和水相渗透率, m2; Kro, Krw—油相和水相相对渗透率; n—时间步序号; p—平均孔隙压力, Pa; pcow—毛管压力, Pa; po, pw—油相和水相压力, Pa; qo, qw—油相和水相流量, m3/s; r—任意变量; rw—井筒半径, m; s—迭代步序号; So, Sw—含油饱和度和含水饱和度, %; t—时间, s; V—网格体积, m3; ui, uj—地层岩体各向位移, i=1, 2, 3, j=1, 2, 3, m; α —Biot有效应力系数; β —转换系数; δ ij—克罗内克函数; εij—地层岩体应变张量, i=1, 2, 3, j=1, 2, 3; εv—地层岩体体积应变; μo, μw—油相和水相黏度, Pa· s; ρ o, ρ w—油相和水相密度, kg/m3; σ ij, ${{{\sigma }'}_{ij}}$—地层岩体总应力张量和有效应力张量, i=1, 2, 3, j=1, 2, 3, Pa; υ ij—地层岩体泊松比张量, i=1, 2, 3, j=1, 2, 3; ϕ —基质孔隙度, m3/m3; ϕ 0—初始基质孔隙度, m3/m3。

（编辑 胡苇玮）

参考文献
[1] 孙龙德, 邹才能, 贾爱林, 等. 中国致密油气发展特征与方向[J]. 石油勘探与开发, 2019, 46(6): 1015-1026.
SUN Longde, ZOU Caineng, JIA Ailin, et al. Development characteristics and orientation of tight oil and gas in China[J]. Petroleum Exploration and Development, 2019, 46(6): 1015-1026. [本文引用:1]
[2] 朱如凯, 邹才能, 吴松涛, 等. 中国陆相致密油形成机理与富集规律[J]. 石油与天然气地质, 2019, 40(6): 1168-1184.
ZHU Rukai, ZOU Caineng, WU Songtao, et al. Mechanism for generation and accumulation of continental tight oil in China[J]. Oil & Gas Geology, 2019, 40(6): 1168-1184. [本文引用:1]
[3] 胡文瑞, 魏漪, 鲍敬伟. 中国低渗透油气藏开发理论与技术进展[J]. 石油勘探与开发, 2018, 45(4): 646-656.
HU Wenrui, WEI Yi, BAO Jingwei. Development of the theory and technology for low permeability reservoirs in China[J]. Petroleum Exploration and Development, 2018, 45(4): 646-656. [本文引用:2]
[4] 朱维耀, 岳明, 刘昀枫, 等. 中国致密油藏开发理论研究进展[J]. 工程科学学报, 2019, 41(9): 1103-1114.
ZHU Weiyao, YUE Ming, LIU Yunfeng, et al. Research progress on tight oil exploration in China[J]. Chinese Journal of Engineering, 2019, 41(9): 1103-1114. [本文引用:1]
[5] 王晶, 刘俊刚, 李兆国, 等. 超低渗透砂岩油藏水平井同井同步注采补能方法: 以鄂尔多斯盆地长庆油田为例[J]. 石油勘探与开发, 2020, 47(4): 772-779.
WANG Jing, LIU Jungang, LI Zhaoguo, et al. Synchronous injection-production energy replenishment for a horizontal well in an ultra-low permeability sand stone reservoir: A case study of Changqing oilfield in Ordos Basin, NW China[J]. Petroleum Exploration and Development, 2020, 47(4): 772-779. [本文引用:1]
[6] 张安顺, 杨正明, 李晓山, 等. 低渗透油藏直井体积压裂改造效果评价方法[J]. 石油勘探与开发, 2020, 47(2): 409-415.
ZHANG Anshun, YANG Zhengming, LI Xiaoshan, et al. An evaluation method of volume fracturing effects for vertical wells in low permeability reservoirs[J]. Petroleum Exploration and Development, 2020, 47(2): 409-415. [本文引用:1]
[7] LIU S, CAO L, HE H, et al. An improved interwell connectivity model to obtain interwell connectivity information by using complex well data[J]. Simulation, 2021, 97(2): 135-143. [本文引用:1]
[8] WRIGHT C A, CONANT R A, GOLICH G M, et al. Hydraulic fracture orientation and production/injection induced reservoir stress changes in diatomite waterfloods[R]. SPE 29625-MS, 1995. [本文引用:2]
[9] WRIGHT C A. Reorientation of propped refracture treatments in the lost hills field[R]. SPE 27896-MS, 1994. [本文引用:1]
[10] KRISTIANSEN T G, BARKVED O I, BUER K, et al. Production-induced deformations outside the reservoir and their impact on 4D seismic[R]. IPTC 10818-MS, 2005. [本文引用:1]
[11] DONS T, JØRGENSEN O, GOMMESEN L. Observations and quantitative analyses of waterflood patterns in a chalk reservoir using seismic data, Halfdan Field, Danish North Sea[R]. SPE 108531-MS, 2007. [本文引用:1]
[12] ZHANG F S, DAMJANAC B, MAXWELL S. Investigating hydraulic fracturing complexity in naturally fractured rock masses using fully coupled multiscale numerical modeling[J]. Rock Mechanics and Rock Engineering, 2019, 52(12): 5137-5160. [本文引用:1]
[13] MINNER W A, WRIGHT C A, STANLEY G R, et al. Waterflood and production-induced stress changes dramatically affect hydraulic fracture behavior in lost hills infill wells[R]. SPE 77536-MS, 2002. [本文引用:1]
[14] ALTMANN J B, MÜLLER B I R, MÜLLER T M, et al. Pore pressure stress coupling in 3D and consequences for reservoir stress states and fault reactivation[J]. Geothermics, 2014, 52: 195-205. [本文引用:1]
[15] HADDAD M, EICHHUBL P. Poroelastic models for fault reactivation in response to concurrent injection and production in stacked reservoirs[J]. Geomechanics for Energy and the Environment, 2020, 24: 100181. [本文引用:1]
[16] SOLTANZADEH H, HAWKES C D. Assessing fault reactivation tendency within and surrounding porous reservoirs during fluid production or injection[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(1): 1-7. [本文引用:1]
[17] ZHANG F S, YIN Z R, CHEN Z W, et al. Fault reactivation and induced seismicity during multistage hydraulic fracturing: Microseismic analysis and geomechanical modeling[J]. SPE Journal, 2020, 25(2): 692-711. [本文引用:1]
[18] HAN L H, YIN F, YANG S Y, et al. Coupled seepage-mechanical modeling to evaluate formation deformation and casing failure in waterflooding oilfields[J]. Journal of Petroleum Science and Engineering, 2019, 180: 124-129. [本文引用:1]
[19] 王友净, 宋新民, 田昌炳, 等. 动态裂缝是特低渗透油藏注水开发中出现的新的开发地质属性[J]. 石油勘探与开发, 2015, 42(2): 222-228.
WANG Youjing, SONG Xinmin, TIAN Changbing, et al. Dynamic fractures are an emerging new development geological attribute in water-flooding development of ultra-low permeability reservoirs[J]. Petroleum Exploration and Development, 2015, 42(2): 222-228. [本文引用:1]
[20] 赵向原, 曾联波, 胡向阳, 等. 低渗透砂岩油藏注水诱导裂缝特征及其识别方法: 以鄂尔多斯盆地安塞油田W区长6油藏为例[J]. 石油与天然气地质, 2017, 38(6): 1187-1197.
ZHAO Xiangyuan, ZENG Lianbo, HU Xiangyang, et al. Characteristics of waterflood induced fracture in low-permeability sand stone reservoirs and its identification methods: A case study from Chang 6 reservoir in W area in Ansai oilfield, Ordos Basin[J]. Oil & Gas Geology, 2017, 38(6): 1187-1197. [本文引用:1]
[21] 赵向原, 曾联波, 靳宝光, 等. 低渗透油藏注水诱导裂缝特征及形成机理: 以鄂尔多斯盆地安塞油田长6油藏为例[J]. 石油与天然气地质, 2018, 39(4): 696-705.
ZHAO Xiangyuan, ZENG Lianbo, JIN Baoguang, et al. Characteristics and formation mechanisms of waterflood induced fractures in low-permeability reservoirs: A case study from Chang 6 reservoir in Ansai oilfield, Ordos Basin[J]. Oil & Gas Geology, 2018, 39(4): 696-705. [本文引用:1]
[22] 范天一, 宋新民, 吴淑红, 等. 低渗透油藏水驱动态裂缝数学模型及数值模拟[J]. 石油勘探与开发, 2015, 42(4): 496-501.
FAN Tianyi, SONG Xinmin, WU Shuhong, et al. A mathematical model and numerical simulation of waterflood induced dynamic fractures of low permeability reservoirs[J]. Petroleum Exploration and Development, 2015, 42(4): 496-501. [本文引用:1]
[23] LI Z J, HOU B, XIAO Y. Study on mechanism of dynamic fracture propagation induced by long-term water injection of low permeability reservoir[R]. ARMA 2018-492, 2018. [本文引用:1]
[24] HAGOORT J, WEATHERILL B D, SETTARI A. Modeling the propagation of waterflood-induced hydraulic fractures[J]. Society of Petroleum Engineers Journal, 1980, 20(4): 293-303. [本文引用:1]
[25] SETTARI A. Simulation of hydraulic fracturing processes[J]. Society of Petroleum Engineers Journal, 1980, 20(6): 487-500. [本文引用:1]
[26] 岳迎春, 郭建春. 重复压裂转向机制流-固耦合分析[J]. 岩土力学, 2012, 33(10): 3189-3193.
YUE Yingchun, GUO Jianchun. Fluid-solid coupling analysis of reorientation mechanism of refracturing[J]. Rock and Soil Mechanics, 2012, 33(10): 3189-3193. [本文引用:1]
[27] 董光, 邓金根, 朱海燕, 等. 重复压裂前的地应力场分析[J]. 断块油气田, 2012, 19(4): 485-488, 492.
DONG Guang, DENG Jingen, ZHU Haiyan, et al. Analysis of stress field before refracture treatment[J]. Fault-Block Oil and Gas Field, 2012, 19(4): 485-488, 492. [本文引用:1]
[28] ROUSSEL N P, FLOREZ H A, RODRIGUEZ A A. Hydraulic fracture propagation from infill horizontal wells[R]. SPE 166503-MS, 2013. [本文引用:5]
[29] ABOU-SAYED A S, ZHAI Z Y. Thermal-poro elastic stress effect on stress reorientation in production and injection wells[R]. SPE 140949-MS, 2011. [本文引用:2]
[30] HWANG J, BRYANT E C, SHARMA M M. Stress reorientation in waterflooded reservoirs[R]. SPE 173220-MS, 2015. [本文引用:5]
[31] BIOT M A. General solutions of the equations of elasticity and consolidation for a porous material[J]. Journal of Applied Mechanics, 1956, 23(1): 91-96. [本文引用:1]
[32] LEKHNITSKII S G. Theory of elasticity of an anisotropic body[M]. Moscow: Mir Publishers, 1981. [本文引用:1]
[33] ZHU H Y, ZHAO X, GUO J C, et al. Coupled flow-stress-damage simulation of deviated-wellbore fracturing in hard-rock[J]. Journal of Natural Gas Science and Engineering, 2015, 26: 711-724. [本文引用:1]
[34] CHIN L Y, THOMAS L K, SYLTE J E, et al. Iterative coupled analysis of geomechanics and fluid flow for rock compaction in reservoir simulation[J]. Oil & Gas Science and Technology, 2002, 57(5): 485-497. [本文引用:1]
[35] DEAN R H, GAI X L, STONE C M, et al. A comparison of techniques for coupling porous flow and geomechanics[J]. SPE Journal, 2006, 11(1): 132-140. [本文引用:1]
[36] SETTARI A T, WALTERS D A. Advances in coupled geomechanical and reservoir modeling with applications to reservoir compaction[R]. SPE 51927-MS, 1999. [本文引用:1]
[37] SAMIER P, ONAISI A, DE GENNARO S. A practical iterative scheme for coupling geomechanics with reservoir simulation[J]. SPE Reservoir Evaluation & Engineering, 2008, 11(5): 892-901. [本文引用:1]
[38] ZHU H Y, TANG X H, LIU Q Y, et al. 4D multi-physical stress modelling during shale gas production: A case study of Sichuan Basin shale gas reservoir, China[J]. Journal of Petroleum Science and Engineering, 2018, 167: 929-943. [本文引用:1]
[39] TANG X H, ZHU H Y, LIU Q Y, et al. A reservoir and geomechanical coupling simulation method: Case studies in shale gas and CBM reservoir[R]. IPTC 19288-MS, 2019. [本文引用:1]
[40] ODA M. Permeability tensor for discontinuous rock masses[J]. Géotechnique, 1985, 35(4): 483-495. [本文引用:1]
[41] GHAHFAROKHI P K. The structured gridding implications for upscaling model discrete fracture networks (DFN) using corrected Oda’s method[J]. Journal of Petroleum Science and Engineering, 2017, 153: 70-80. [本文引用:1]
[42] 赵继勇, 安小平, 王晶, 等. 超低渗油藏井网适应性定量评价方法: 以鄂尔多斯盆地三叠系长6、长8油藏为例[J]. 石油勘探与开发, 2018, 45(3): 482-488.
ZHAO Jiyong, AN Xiaoping, WANG Jing, et al. A quantitative evaluation for well pattern adaptability in ultra-low permeability oil reservoirs: A case study of Triassic Chang 6 and Chang 8 reservoirs in Ordos Basin[J]. Petroleum Exploration and Development, 2018, 45(3): 482-488. [本文引用:1]
[43] ZHAI Z Y, SHARMA M M. Estimating fracture reorientation due to long term fluid injection/production[R]. SPE 106387-MS, 2007. [本文引用:1]
[44] GUPTA J K, ZIELONKA M G, ALBERT R A, et al. Integrated methodology for optimizing development of unconventional gas resources[R]. SPE 152224-MS, 2012. [本文引用:1]
[45] GAO Q, CHENG Y F, HAN S C, et al. Numerical modeling of hydraulic fracture propagation behaviors influenced by pre-existing injection and production wells[J]. Journal of Petroleum Science and Engineering, 2019, 172: 976-987. [本文引用:]
[46] ROUSSEL N P, SHARMA M M. Role of stress reorientation in the success of refracture treatments in tight gas sand s[J]. SPE Production & Operations, 2012, 27(4): 346-355. [本文引用:]
[47] ROUSSEL N P, SHARMA M M. Quantifying transient effects in altered-stress refracturing of vertical wells[J]. SPE Journal, 2010, 15(3): 770-782. [本文引用:]
[48] LIU H, LAN Z X, ZHANG G L, et al. Evaluation of refracture reorientation in both laboratory and field scales[R]. SPE 112445-MS, 2008. [本文引用:]
[49] YADAV H, MOTEALLEH S. Improving quantitative analysis of frac-hits and refracs in unconventional plays using RTA[R]. SPE 184812-MS, 2017. [本文引用:]
[50] YANG Y T, TANG X H, ZHENG H, et al. Hydraulic fracturing modeling using the enriched numerical manifold method[J]. Applied Mathematical Modelling, 2018, 53: 462-486. [本文引用:]
[51] YANG Y T, TANG X H, ZHENG H, et al. Three-dimensional fracture propagation with numerical manifold method[J]. Engineering Analysis with Boundary Elements, 2016, 72: 65-77. [本文引用:]
[52] BRUNO M S, NAKAGAWA F M. Pore pressure influence on tensile fracture propagation in sedimentary rock[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1991, 28(4): 261-273. [本文引用:]