引用本文
范继林, 张锋, 田立立, 梁启轩, 张笑瑒, 方群伟, 鲁保平, 李向辉. 二氧化碳气驱稠油层脉冲中子含气量监测方法[J]. 石油勘探与开发, 2021,48(6): 1232-1240.
FAN Jilin, ZHANG Feng, TIAN Lili, LIANG Qixuan, ZHANG Xiaoyang, FANG Qunwei, LU Baoping, LI Xianghui. A method of monitoring gas saturation in carbon dioxide injection heavy oil reservoirs by pulsed neutron logging technology[J]. Petroleum Exploration & Development, 2021,48(6): 1232-1240.  
Doi: 10.11698/PED.2021.06.15
Permissions
Copyright©2021, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
二氧化碳气驱稠油层脉冲中子含气量监测方法
范继林1, 张锋1,2, 田立立1, 梁启轩1, 张笑瑒1, 方群伟1, 鲁保平3, 李向辉4
1.中国石油大学（华东）地球科学与技术学院,山东青岛 266580
2.山东省深层油气重点实验室,山东青岛 266580
3.中国石油集团测井有限公司技术中心,西安 710000
4.河南省科学院同位素研究所有限责任公司,郑州 450000
联系作者简介：张锋（1970-）,男,山东莒南人,博士,中国石油大学（华东）教授,主要从事核测井理论、方法与技术研究。地址：山东省青岛市黄岛区长江西路66号,中国石油大学（华东）地球科学与技术学院,邮政编码：266580。E-mail: zhfxy_cn@upc.edu.cn

第一作者简介：范继林（1996-）,男,河南济源人,中国石油大学（华东）在读博士研究生,主要从事核测井理论、方法与技术研究。地址：山东省青岛市黄岛区长江西路66号,中国石油大学（华东）地球科学与技术学院,邮政编码：266580。E-mail: fanjl1996@163.com

收稿日期: 2021-01-25 修回日期: 2021-09-23
基金项目: 国家自然科学基金（41974127,41974155）; 中国石油大学（华东）研究生创新工程资助项目（YCX2020008）
摘要

提出了一种利用非弹性伽马射线与俘获伽马射线组合定量表征快中子散射截面（ σf）的方法,从而基于三探测器脉冲中子测井技术实现了注CO2稠油储集层含气饱和度的评价,分析了评价效果的影响因素并利用模拟实例验证了方法的有效性。利用蒙特卡罗模拟方法结合岩石体积物理模型,研究了 σf与CO2饱和度的响应关系,并建立饱和度解释模型,分析了地层温度压力、稠油密度、井眼流体及储集层CH4含量对CO2饱和度评价效果的影响。研究表明,通过次生伽马信息组合对 σf进行表征可以消除地层岩性的影响;井眼流体与储集层CH4含量是影响CO2饱和度定量监测的主要因素,地层温度压力和稠油密度的影响可以忽略。模拟实例进一步验证了使用该方法进行注CO2稠油储集层含气饱和度评价的可行性。图10表4参25

关键词: 二氧化碳驱; 含气饱和度; 稠油储集层; 脉冲中子测井; 快中子散射截面; 次生伽马射线; 蒙特卡罗模拟
中图分类号:P618.13 文献标志码:A
A method of monitoring gas saturation in carbon dioxide injection heavy oil reservoirs by pulsed neutron logging technology
FAN Jilin1, ZHANG Feng1,2, TIAN Lili1, LIANG Qixuan1, ZHANG Xiaoyang1, FANG Qunwei1, LU Baoping3, LI Xianghui4
1. School of Geosciences, China University of Petroleum, Qingdao 266580, China
2. Shandong Provincial Key Laboratory of Deep Oil and Gas, Qingdao 266580, China
3. CNPC Well Logging Technology Research Center, Xi’an 710000, China
4. Isotope Research Institute of Henan Academy of Sciences Co., Ltd., Zhengzhou 450000, China
Abstract

A method is proposed to characterize the fast neutron scattering cross-section ( σf) quantitatively by the combination of inelastic gamma rays and captured gamma rays, so as to realize the gas saturation evaluation of CO2-injected heavy oil reservoirs based on the three-detector pulsed neutron logging technology. Factors influencing of the evaluation effect of this method are analyzed and the effectiveness of this method is verified by a simulation example. By using the Monte Carlo simulation method and the physical model of bulk-volume rock, the relationship between σf and CO2 saturation is studied, and the saturation interpretation model is established. The influences of formation temperature and pressure, heavy oil density, borehole fluid and reservoir methane content on the evaluation results of CO2 saturation are analyzed. The results show that the characterization of σf by the combination of secondary gamma information can eliminate the influence of formation lithology, borehole fluid and methane content are the main factors affecting the quantitative monitoring of CO2 saturation, and the effects of formation temperature and pressure and heavy oil density are negligible. The simulation example verified the feasibility of the method for evaluating the CO2 saturation of CO2-injected heavy oil reservoirs.

Keyword: CO2 flooding; gas saturation; heavy oil reservoir; pulsed neutron logging; fast neutron scattering cross-section; secondary gamma-ray; Monte Carlo simulation
0 引言

CO2是最常见的温室气体之一, 世界各国都希望找到消除其对环境危害的解决方案[1, 2]。集中工业排放CO2并将其注入到深部地层中进行长期储存是一种有前景的解决温室效应的方法[3]。CO2驱提高采收率（CO2-EOR）技术满足这一要求, 同时间接实现了油层的二次开采, 可增加油气产量, 提高经济效益。阿尔及利亚的In Salah项目在5年内成功向裂缝性砂岩地层注入超过300× 104 t的CO2, 证明了该方法的可行性和可观的经济价值[4]。

目前, 许多监测CO2储存状态的方法已经成功地应用于世界各地[5], 如地震[6, 7, 8]、CT[9]、井温测井[10, 11]等。在CO2-EOR技术中, CO2饱和度是表征其分布和运移的关键参数。脉冲中子测井技术作为核地球物理勘探中评价含气饱和度的重要方法, 在注CO2油藏含气饱和度评价中发挥着不可或缺的作用[12, 13, 14, 15, 16, 17]。近几年, 斯伦贝谢设计了一支多功能脉冲中子测井仪, 利用长源距YAP（铝酸钇）晶体探测器结合脉冲中子产额监测器探测实现快中子散射截面（σf）的测量, 用于储集层含气饱和度的定量监测[18]。但是直接利用非弹伽马信息表征14 MeV快中子散射截面一定程度上会受到地层岩性影响, 导致含气饱和度解释结果存在误差。

本文针对CO2、水和稠油对快中子减速能力的差异, 基于快中子散射及次生伽马分布理论, 以三探测器脉冲中子测井技术为基准, 提出一种利用次生非弹和俘获伽马信息组合表征σf的方法, 克服地层岩性对σf表征的影响。针对实际地层中存在泥质的情况, 给出相对应的CO2饱和度解释模型, 并阐述储集层各种因素对σf关于地层孔隙度响应的影响, 建立更完善的注CO2稠油储集层含气饱和度定量评价方法。

1 理论与方法

稠油储集层孔隙一般被高密度、高黏度的稠油充填, 部分储集层存在一定的孔隙水。CO2气驱过程中, 孔隙流体逐渐被CO2所驱替, 形成稠油-气双相或稠油- 气-水三相流体。CO2的含氢指数为零, 其密度、热中子俘获截面、快中子散射截面等参数与地层水、稠油相差较大。因此, 注入地层的CO2气体会导致地层的热中子俘获截面和快中子散射截面发生极大变化。作为一种独立于其他中子测量信息的参数[18], 快中子散射截面对定量监测注CO2稠油储集层含气饱和度有较好的效果。

1.1 地层介质的快中子散射截面

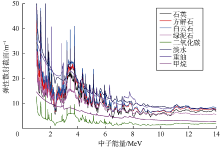
根据ENDF/B-VII.0核数据库获取地层常见元素的微观截面, 再根据相关公式求取介质的宏观弹性散射截面[19]。图1展示了不同地层骨架矿物和孔隙流体的弹性散射截面与中子能量的关系。可以看出, 气体的弹性散射截面明显小于地层骨架矿物和孔隙液相流体, CO2的这一特征尤其明显。本文基于地层介质弹性散射截面的差异, 将弹性散射截面作为σf, 用于定量评价CO2饱和度。

图1 不同介质的弹性散射截面与中子能量关系曲线

利用数值积分方法计算常见地层骨架矿物与孔隙流体的σf值, 如表1所示。可以看出, 气体σf值相对较低, 尤其是CO2, 地层骨架矿物σf值总体较大且略有差异, 淡水和稠油的σf值更大且较为接近。因此, 基于CO2的超低弹性散射截面的特性, 将注CO2稠油储集层油水气三相流体视作气液两相流体。

表1 一定密度下不同介质的σf值
1.2 利用非弹和俘获伽马信息组合表征快中子散射截面的方法

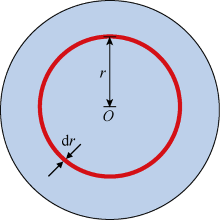
快中子进入地层与地层原子核相互碰撞而慢化。在此过程中, 次生非弹伽马射线产生于快中子与地层元素作用的非弹性散射过程。图2所示的球状模型中, 氘-氚中子源（D-T）位于图示中心位置O点, 向四周均匀发射能量为14 MeV的快中子, 半径为r的球面用于记录来自地层的非弹伽马射线。

图2 无限大均匀球状介质模型

根据快中子散射理论[20], 发生非弹性散射的快中子通量分布如下式所示：

${{\phi }_{\text{f}}}\left( r \right)=\frac{{{\phi }_{0}}}{4\text{ }\!\!\pi\!\!\text{ }{{r}^{2}}}{{\text{e}}^{-\frac{r}{{{\lambda }_{\text{s}}}}}}=\frac{{{\phi }_{0}}}{4\text{ }\!\!\pi\!\!\text{ }{{r}^{2}}}{{\text{e}}^{-r{{\sigma }_{\text{f}}}}}$ （1）

非弹伽马射线的强度取决于地层元素的类型及其微观非弹性散射截面。元素k在一次碰撞中产生的伽马光子数为ik, 对应的微观非弹性散射截面为σ k, 在半径为r、厚度为dr的球壳中产生的伽马射线数为：

$\text{d}I=\sum{{{i}_{k}}{{\sigma }_{k}}4\text{ }\!\!\pi\!\!\text{ }{{r}^{2}}{{\phi }_{\text{f}}}\left( r \right)\text{d}r}$ （2）

整个球体模型中的非弹伽马光子数等于dI从r=0到r=+∞ 的积分。考虑伽马衰减的影响, 假设地层各处的σf值相等, 其质量衰减系数（μm）和一个快中子与地层元素碰撞发生非弹性散射产生的平均伽马光子数（i）为定值, 忽略探测器外的伽马光子贡献, 根据中子伽马耦合场理论[21], 非弹性伽马通量为：

${{\phi }_{\text{in}}}\left( R \right)=\int_{0}^{R}{{{\text{e}}^{-\rho {{\mu }_{\text{m}}}\left| r-R \right|}}\text{d}I}=\frac{i{{\sigma }_{\text{in}}}{{\phi }_{\text{0}}}}{4\text{ }\!\!\pi\!\!\text{ }{{R}^{2}}}\frac{{{\text{e}}^{-R{{\sigma }_{\text{f}}}}}-{{\text{e}}^{-\rho {{\mu }_{\text{m}}}R}}}{\rho {{\mu }_{\text{m}}}-{{\sigma }_{\text{f}}}}$ （3）

利用拉格朗日中值定理, 将（3）式简化为：

${{\phi }_{\text{in}}}\left( R \right)=\frac{i{{\sigma }_{\text{in}}}{{\phi }_{\text{0}}}}{4\text{ }\!\!\pi\!\!\text{ }R}{{\text{e}}^{-R\left[ \left( 1-\alpha \right){{\sigma }_{\text{f}}}+\alpha \rho {{\mu }_{\text{m}}} \right]}}$ （4）

（4）式中, α 为与源距有关的比例因子, 对于给定仪器为定值。由（4）式可知, 非弹性伽马通量不仅与σf值有关, 还与地层密度有关。因此, 可以将σf视作非弹性伽马计数和地层密度的函数。基于多探测器脉冲中子测井仪, 用组合双探测器非弹、俘获伽马计数比表征地层密度[22]：

$\rho =A\ln \frac{{{\phi }_{\text{in1}}}}{{{\phi }_{\text{in3}}}}+B\ln \frac{{{\phi }_{\text{cap1}}}}{{{\phi }_{\text{cap3}}}}+C$ （5）

（5）式中, A、B、C为常数, 通过模拟或刻度井实测数据拟合获得。

将（4）式和（5）式相结合, 使用近、远探测器的非弹和俘获伽马计数实现σf的定量表征：

${{\sigma }_{\text{f}}}=K\ln {{\phi }_{\text{in3}}}+L\ln \frac{{{\phi }_{\text{in1}}}}{{{\phi }_{\text{in3}}}}+M\ln \frac{{{\phi }_{\text{cap1}}}}{{{\phi }_{\text{cap3}}}}+N$ （6）

其中 $K=\frac{1}{R\left( \alpha -1 \right)}$ $L=\frac{A\alpha {{\mu }_{\text{m}}}}{\alpha -1}$

$M=\frac{B\alpha {{\mu }_{\text{m}}}}{\alpha -1}$ $N=\frac{C\alpha {{\mu }_{\text{m}}}}{\alpha -1}+\ln \frac{4\text{ }\!\!\pi\!\!\text{ }R}{i{{\sigma }_{\text{in}}}{{\phi }_{\text{0}}}}$

（6）式表明地层σf可以通过双源距探测器的非弹和俘获伽马信息组合表征得到, 其中系数K、L、M、N可以通过模拟或刻度井实测数据拟合得出。

1.3 注CO2稠油储集层含气饱和度解释模型

σf是储集层的宏观物理特性, 遵循岩石体积物理模型。利用（6）式获取储集层σf值, 针对孔隙中充填CO2和稠油的砂岩储集层, 宏观σf满足以下岩石体积物理模型：

${{\sigma }_{\text{f}}}={{\sigma }_{\text{f, mat}}}\left( 1-\phi \right)+{{\sigma }_{\text{f, gas}}}\phi {{S}_{\text{g}}}+{{\sigma }_{\text{f, oil}}}\phi \left( 1-{{S}_{\text{g}}} \right)$ （7）

则储集层含气饱和度解释模型为：

${{S}_{\text{g}}}=\frac{{{\sigma }_{\text{f}}}-{{\sigma }_{\text{f, mat}}}\left( 1-\phi \right)-{{\sigma }_{\text{f, oil}}}\phi }{{{\sigma }_{\text{f, gas}}}\phi -{{\sigma }_{\text{f, oil}}}\phi }$ （8）

纯砂岩储集层骨架为理想地层条件, 实际地层骨架组分常含有一定比例的泥质或其他固体矿物。以含泥质的地层为研究对象, 基于地层泥质与砂岩骨架σf值的差异, 根据岩石体积物理模型, 当地层存在泥质时, σf满足下式：

${{\sigma }_{\text{f}}}={{\sigma }_{\text{f, mat}}}\left( 1-\phi \right)\left( 1-{{V}_{\text{sh}}} \right)+{{\sigma }_{\text{f, gas}}}\phi {{S}_{\text{g}}}+{{\sigma }_{\text{f, oil}}}\phi \left( 1-{{S}_{\text{g}}} \right)+$ ${{\sigma }_{\text{f, sh}}}\left( 1-\phi \right){{V}_{\text{sh}}}$ （9）

由（9）式可知, 泥质的存在会引起岩石体积物理模型的改变。当地层中存在泥质时, 需要结合测量点的泥质含量及地层孔隙度来校正（7）式所示砂岩地层模型。因此, 含泥质储集层含气饱和度解释模型为：

${{S}_{\text{g}}}=\frac{{{\sigma }_{\text{f}}}-{{\sigma }_{\text{f, mat}}}\left( 1-\phi \right)\left( 1-{{V}_{\text{sh}}} \right)-{{\sigma }_{\text{f, sh}}}\left( 1-\phi \right){{V}_{\text{sh}}}-{{\sigma }_{\text{f, oil}}}\phi }{{{\sigma }_{\text{f, gas}}}\phi -{{\sigma }_{\text{f, oil}}}\phi }$ （10）

相比于（8）式所示纯砂岩地层条件下的含气饱和度计算公式, （10）式考虑了含泥质的地层条件。当地层含有其他固体矿物时, 同样需要对含气饱和度解释模型进行修正, 以满足实际地层骨架条件。

2 蒙特卡罗模拟

蒙特卡罗模拟（MCNP）属于随机抽样或统计实验方法, 可用于中子、光子、电子及其耦合输运过程的模拟, 在放射性测井模拟、仪器制造和响应等方面得到了广泛的应用[23]。本文利用MCNP建立仪器地层模型, 模拟计算快中子输运的所有过程, 包括快中子慢化产生非弹伽马、热中子俘获产生俘获伽马以及伽马射线的衰减。基于MCNP模拟结果, 分析σf的表征及含气响应, 从而实现注CO2稠油储集层含气饱和度的定量监测。

2.1 仪器地层模型建立

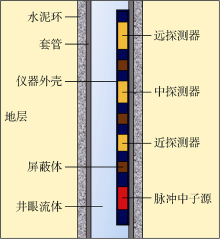
图3所示为本文所建立的数值计算模型。地层模型整体设置为高150 cm、直径120 cm套管井地层条件, 井眼直径20 cm且充填淡水, 地层骨架为砂岩、石灰岩或白云岩。套管为0.7 cm厚的不锈钢材料, 套管与地层之间充填厚度为3 cm的CaSiO3材料水泥环。储集层孔隙度从0变化到40%, 间隔5%; CO2饱和度设置为0~100%, 地层压力设置为35, 50, 65 MPa, 地层温度设置为363.15, 393.15, 423.15 K。在地层压力和温度分别为35 MPa和363.15 K时, CO2气体、淡水与稠油的密度分别为0.50, 1.00, 0.95 g/cm3。

图3 仪器地层模型示意图

采用三探测器脉冲中子测井仪进行CO2气体饱和度监测。设计中子脉冲发射的时间为40 μ s, 非弹和俘获伽马射线的测量时间分别为0~40 μ s和50~1 000 μ s。测井仪器的近、中、远3个探测器分别编号为1, 2, 3, 同时记录非弹和俘获伽马计数。源与探测器之间以及相邻探测器之间加屏蔽。采用17-4PH钢作为仪器外壳材料, 厚度0.5 cm。源为D-T脉冲中子源, 向地层均匀发射高能快中子（14 MeV）。探测器材料为LaBr3晶体, 3个探测器的源距分别为27.5, 40.0, 60.0 cm。3个探测器的晶体直径为5 cm, 长度分别为5, 10, 10 cm。

2.2 快中子散射截面表征方法

通过对含稠油和CO2的砂岩、石灰岩和白云岩等不同岩性储集层的研究分析, 模拟得到了在不同地层岩性（砂岩、石灰岩和白云岩）、孔隙度（0~30%, 间隔5%）、含油气性（饱含稠油和饱含CO2）条件下的三探测器非弹、俘获伽马计数。（5）式所示非弹、俘获伽马计数比组合的目的是消除地层密度的影响, 因此综合考虑计数统计性与σf表征的准确性, 选用近、远探测器信息进行σf的定量表征。利用（6）式, 采用多元线性回归方法, 建立了非弹、俘获伽马信息向σf转换的表征公式：

${{\sigma }_{\text{f}}}=-6.567\ln {{\phi }_{\text{in3}}}-1.964\ln \frac{{{\phi }_{\text{in1}}}}{{{\phi }_{\text{in3}}}}+1.416\ln \frac{{{\phi }_{\text{cap1}}}}{{{\phi }_{\text{cap3}}}}-74.808$ （11）

为了验证该公式的适用性, 对其计算所得的σf值与地层模型设置的σf理论值进行对比分析, σf计算值与理论值的误差表达式为：

$\varepsilon =\frac{{{\sigma }_{\text{f, cal}}}-{{\sigma }_{\text{f, real}}}}{{{\sigma }_{\text{f, real}}}}\times 100%$ （12）

表2给出了不同孔隙度下饱含稠油与饱含CO2砂岩储集层σf计算值与理论值误差分析结果, 表3给出了不同孔隙度下饱含CO2砂岩、灰岩以及白云岩储集层σf计算值与理论值误差分析结果, 以验证在不同含油气性、不同岩性条件下表征公式的准确性。可以看出, （11）式能够较为精准地表征地层σf, 计算得到的σf值与地层模型设置的σf理论值的误差可控制在± 2%以内。因此, 利用脉冲中子测井仪非弹、俘获伽马信息组合可以实现对注CO2气驱稠油储集层σf的定量表征。

表2 砂岩储集层σf计算值与理论值误差分析
表3 饱含CO2的3种岩性储集层σf计算值与理论值误差分析

实际稠油储集层中, 在地层泥质含量、稠油密度、地层温度和压力以及气体类型等因素的影响下, 利用（11）式进行储集层σf的表征可能存在误差。因此, 在不同井眼-地层因素的影响下, 应首先对（11）式获取的σf值进行校正, 保证σf值的准确性, 实现利用σf评价稠油储集层CO2气驱效果的普适性。

2.3 快中子散射截面与CO2饱和度响应

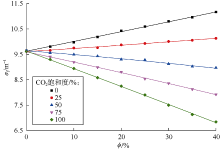
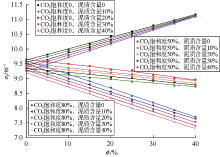
基于蒙特卡罗数值计算方法建立图3所示仪器地层模型, 在孔隙含稠油和CO2混合流体的砂岩储集层条件下, 设置地层孔隙度为0~40%, 间隔5%, CO2饱和度分别为0, 25%, 50%, 75%, 100%。利用给出的储集层σf表征公式, 得到不同CO2饱和度条件下σf与地层孔隙度响应关系, 如图4所示。可以看出, 储集层CO2饱和度对σf随孔隙度的变化规律影响极大。在低CO2饱和度情况下, 稠油为孔隙流体的主要成分, 除地层骨架外, 稠油对中子的减速作用占主导地位; 随着CO2饱和度的增大, 孔隙逐渐被CO2气体填充, CO2对中子的减速作用逐渐明显直至占主导地位。相对于地层骨架, 稠油具有较高的σf值, CO2具有超低σf特性, 因此, 在CO2饱和度较低时（0, 25%）, σf随着地层孔隙度的增大呈现上升趋势; 在CO2饱和度较高时（50%, 75%, 100%）, σf随着地层孔隙度的增大呈现明显的下降趋势。基于以上分析可知, 在注CO2稠油储集层中, 地层宏观σf是由孔隙度、含气饱和度综合决定的。在已知地层孔隙度条件下, 利用多探测器信息表征地层宏观σf, 结合岩石体积物理模型即可进行注CO2稠油储集层含气饱和度的定量监测。

图4 σf与地层孔隙度响应关系

在实际储集层中, 常含有不同类型的泥质组分, 影响整个储集层介质对快中子的减速能力。因此, 需要根据（10）式进行含泥质储集层CO2饱和度计算。以绿泥石为泥质组分研究对象, 基于图3所示仪器地层模型, 设置砂岩地层中泥质含量为10%, 20%, 30%, 40%, 地层孔隙度为0~40%, 间隔5%, CO2饱和度分别为0, 50%, 80%, 模拟地层含泥质条件下σf与地层孔隙度的响应关系, 如图5所示。总体来说, 泥质类型为绿泥石时, 泥质的存在导致地层σf的计算值明显小于纯砂岩地层。在高CO2饱和度条件下, 不同泥质含量下σf随地层孔隙度呈近似平行变化, 在低CO2饱和度条件下, 随着孔隙度的增加, 泥质含量对σf的影响逐渐减小。这说明泥质引起的σf值变化量由地层孔隙度和泥质含量共同决定, 同时表明在实际储集层中, 利用σf结合含泥质岩石体积物理模型进行CO2饱和度解释较为合理。

图5 泥质含量对σf与孔隙度响应的影响

3 影响因素分析

本文提出了利用σf评价注CO2稠油储集层含气饱和度的定量解释方法。但在实际注CO2稠油储集层中, 由于测井环境影响因素的不确定性, 含气饱和度评价方法有时可能失效。因此, 对地层影响因素（如温度、压力、井眼环境等）进行分析和校正是十分必要的, 这是保证利用σf定量监测CO2含气饱和度的适用性的基础。

3.1 储集层温度、压力的影响

对于CO2气驱储集层, 地层温度和压力改变是导致CO2溶于稠油形成混相油的主要因素。由于溶解度的不同, 混相油密度在不同温压条件下存在一定的差异。根据Marra等[24]的研究, 地层压力、温度改变引起的混相油密度变化按照以下两个公式计算：

$\begin{align} & \Delta {{\rho }_{\text{p}}}=0.016\ 02\left[ 0.145p\left( 0.167+16.181\times {{10}^{-2.652\ 93{{\rho }_{0}}}} \right) \right.- \\ & \ \ \ \ \ \ \ \ \ \left. 0.01\left( 0.299+263\times {{10}^{-3.764{{\rho }_{0}}}} \right){{\left( 0.145p \right)}^{2}} \right] \\ \end{align}$ （13）

$\begin{align} & \Delta {{\rho }_{\text{t}}}=0.016\ 02\left[ 0.013\ 3+0.006\ 087{{\left( {{\rho }_{0}}+\Delta {{\rho }_{\text{p}}} \right)}^{-2.45}}{{-}^{^{^{{}}}}} \right. \\ & \left. \ \ \ \ \ \ \ \ 8.1\times {{10}^{-6}}\text{+}0.062\ 2\times {{10}^{4.769\left( {{\rho }_{0}}+\Delta {{\rho }_{\text{p}}} \right)}} \right]\left( 1.8T-519.67 \right) \\ \end{align}$ （14）

基于图3所示仪器地层模型, 在砂岩地层条件下, 设置地层孔隙度为0~40%, 间隔5%, CO2含气饱和度为0, 50%, 80%。固定地层温度为363.15 K, 依次改变地层压力为35, 50, 65 MPa, 研究地层压力的影响; 固定地层压力为35 MPa, 依次改变地层温度为363.15, 393.15, 423.15 K, 研究地层温度的影响。由图6可知, 地层温压条件对利用σf计算CO2含气饱和度的效果影响不大。由（13）式和（14）式计算得到, 地层温度为363.15 K, 稠油地层压力从35 MPa增加到65 MPa时, 混相油的密度变化范围为0.950~0.963 g/cm3; 地层压力为35 MPa, 地层温度从363.15 K增加到423.15 K时, 混相油的密度从0.950 g/cm3增加到0.983 g/cm3。地层温压变化引起的混相油密度变化范围较小, 对快中子的减速能力基本不变, 加之地层骨架因素, 整个储集层对快中子的减速能力不变。在所研究的地层温度和压力范围内, 混相油的密度不会发生剧烈变化, 稠油储集层温度和压力引起的稠油密度变化并不足以影响整个地层的快中子减速能力。因此, 在注CO2稠油储集层中采用σf评价CO2含气饱和度时, 可以忽略地层温度和压力的影响。

图6 地层温压条件对σf与孔隙度响应的影响

3.2 稠油密度的影响

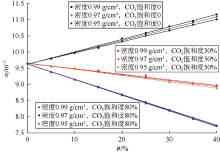
在CO2气驱稠油储集层过程中, 由于CO2溶解度的变化, 稠油密度在一定的温度和压力范围内发生变化[25]。当压力从35 MPa增加到65 MPa, 温度为333.15 K时, 稠油的密度变化范围为0.94~1.00 g/cm3。基于图3所示仪器地层模型, 改变稠油密度为0.95, 0.97, 0.99 g/cm3, 研究在3种稠油密度情况下σf与孔隙度的响应关系。由图7可知, 在低CO2饱和度（0）地层条件下, 稠油密度对σf有一定的影响, 随着稠油密度的增加, σf计算值有一定的增大趋势。然而, 在高CO2饱和度（80%）储集层中, 稠油密度影响并不明显, 这是由于此时储集层流体已经大部分被CO2驱替。对于实际注CO2稠油油藏, 多次注入CO2气体后稠油密度的变化范围远小于本文所研究的稠油密度变化范围。因此, 注CO2气驱后稠油密度的变化对CO2饱和度的测量影响可以忽略。

图7 稠油密度对σf与孔隙度响应的影响

3.3 井眼流体性质的影响

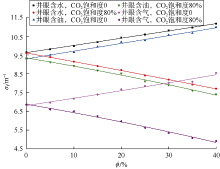
稠油储集层CO2气驱提高采收率技术常采用连续多次注入或水、CO2气体交替注入的形式, 因此井筒环境会由钻井液充填改变为稠油、CO2或水等多种流体充填的情况。为了研究井眼流体对利用σf评价储集层CO2含气饱和度的影响, 基于图3所示仪器地层模型, 分别将井眼流体类型设置为水、气与稠油, 得到不同井眼流体以及储集层含气饱和度条件下σf与地层孔隙度的响应关系, 如图8所示。可以看出, 在任意储集层CO2饱和度条件下, 不同井眼流体使得σf关于地层孔隙度呈现平行变化。水和油对快中子的减速能力差异较小, 井眼含油条件下σf值略小于井眼含水条件下σf值; 与水和油相比, 气对快中子的减速能力明显减弱, σf值显著减小。因此, 在用σf判断注CO2稠油储集层气驱效果时, 需要区分井内流体类型, 对井眼含气性进行校正。

图8 井眼流体性质对σf与孔隙度响应的影响

3.4 储集层CH4含量的影响

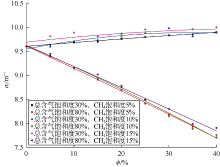
稠油储集层多次注入CO2过程中, 在储集层孔隙中存在CH4的条件下, 由于注入的CO2气体与一定比例的CH4气体混合, CH4气体将在CO2驱替过程中积聚, 对CO2饱和度的测量会产生一定的影响。基于图3所示仪器地层模型, 设置地层总含气饱和度（CO2和CH4）分别为30%和80%, 改变其中CH4含气饱和度分别为5%, 10%, 15%, 得到两种气体不同混合比例条件下σf与地层孔隙度的响应关系, 如图9所示。可以看出, 当总含气饱和度较高时, CH4含量的影响较小。总气饱和度较低时（30%）, 尽管CH4含量的影响增大, 但仍不明显。因此, 利用σf进行储集层CO2饱和度评价难以区分CH4和CO2两种气体类型。相对于地层骨架、稠油和水, CH4和CO2的σf均为低值, 尽管CH4的σf值略大于CO2, 但实际地层中两种气体相对地层总体积占比较小, 孔隙CO2中存在少量CH4并不影响地层对快中子的宏观减速能力, CO2饱和度的计算结果更加接近于CO2和CH4的总饱和度。因此, 利用σf评价储集层含气饱和度的方法难以消除CH4气体的存在引起的CO2饱和度计算误差。为了确保在CO2-EOR技术实施期间CO2饱和度监测的准确性, 必须严格控制CO2多次注入后的CH4含量。

图9 储集层CH4含量对σf与孔隙度响应的影响

4 模拟实例验证

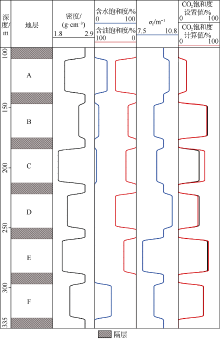
利用模拟实例验证本文方法的有效性。地层总厚度234 m, 地层之间被黏土层隔开, 地层孔隙流体均为稠油、淡水以及CO2气体的不同组合。表4给出了各个储集层的岩性、孔隙度、密度、泥质含量以及流体性质及饱和度参数。模拟测井过程中, 仪器由下至上沿井壁滑动, 记录仪器多探测器的非弹、俘获伽马信息, 转化为σf, 并结合饱和度计算方法和校正方法, 得到储集层CO2气体饱和度。

表4 模拟实例各储集层基本参数

由图10所示解释结果可知, A— F层CO2饱和度计算误差分别为0.3%, 1.7%, 13.5%, 2.9%, 2.4%, 0.6%。地层岩性及泥质含量不影响该方法评价CO2饱和度的误差, 无论地层含泥质与否, CO2饱和度的计算误差可控制在3%以内。因此, 对于含稠油砂岩地层, 利用σf实现CO2饱和度监测是一种有效的方法。当地层存在CH4气体时（C层）, CO2饱和度的计算误差偏大, 为13.5%, 这一现象也印证了该方法存在难以区分CO2和CH4气体的缺点。

图10 模拟实例解释结果

5 结论

CO2与油、水对快中子减速能力存在极大差异, 本文将快中子散射截面应用于注CO2稠油储集层含气饱和度的定量监测中, 建立CO2含气饱和度评价模型以实现饱和度的定量计算, 为注CO2稠油储集层剩余油勘探开发中含气饱和度监测提供了技术支持。

基于三探测器脉冲中子测井技术, 利用近远探测器的非弹和俘获伽马组合可以实现储集层快中子散射截面的定量表征。含泥质储集层的快中子散射截面与纯岩性地层存在差异, 利用储集层泥质含量结合含泥质岩石体积物理模型进行CO2饱和度评价较为合理。地层温度和压力变化引起的混相油密度变化范围较小, 不影响孔隙中稠油和CO2混相流体对快中子的减速能力, 可以忽略地层温度压力以及稠油密度的影响。相对于地层骨架, CH4和CO2的快中子散射截面均为低值, CH4的存在容易造成CO2含气饱和度评价的误差, 因此进行CO2饱和度监测时需要严格控制CH4含量。此外, 井眼流体类型极大影响了快中子散射截面的测量, 在利用快中子散射截面判断注CO2稠油储集层气驱效果时, 需要区分井内流体类型, 对井眼含气性进行校正。

模拟测井实例结果表明, 在储集层孔隙中不含CH4气体时, 该方法可以将CO2饱和度计算误差控制在3%以内, 验证了方法的有效性。

符号注释：

A, B, C— — 常数, g/cm3; i— — 一个快中子与地层元素碰撞发生非弹性散射产生的平均伽马光子数; ik— — 元素k在一次碰撞中产生的伽马光子数; p— — 地层压力, MPa; I— — 伽马射线数; r— — 以中子源为中心的球形半径, m; dr— — 半径为r的球壳的厚度, m; R— — 探测器的源距, m; Sg— — CO2饱和度, %; T— — 地层温度, K; Vsh— — 泥质含量, %; α — — 与源距有关的比例因子; ε — — σf计算值与理论值的误差, %; λs— — 快中子散射自由程, m; μm— — 质量衰减系数, m2/kg; ρ — — 地层密度, kg/m3; ∆ ρ p, ∆ ρ t— — 由地层压力和温度改变引起的混相油密度的变化量, g/cm3; ρ 0— — 0.1 MPa和288.7 K地层温压条件下的混相油密度, g/cm3; σf— — 快中子散射截面, m-1; σf, cal— — σf计算值, m-1; σf, gas, σf, mat, σf, oil, σf, sh— — CO2气体、地层骨架、原油、泥质组分的快中子散射截面, m-1; σf, real— — 地层模型设置的σf理论值, m-1; σ k— — 元素k在一次碰撞中对应的微观非弹性散射截面, m-1; σin— — 地层的非弹性散射截面, m-1; ϕ— — 储集层孔隙度, %; ϕ0— — 中子源强度; ϕf(r)— — 快中子通量, m-2; ϕin(R)— — 非弹性伽马通量, m-2; ϕcap1, ϕcap3— — 近、远探测器俘获伽马计数; ϕin1, ϕin3— — 近、远探测器非弹伽马计数。

（编辑 胡苇玮）

参考文献
[1] DE FIGUEIREDO M, BACANSKAS L, KOLIAN M. Greenhouse gas reporting for geologic sequestration of carbon dioxide[R]. Orland o, Florida, USA: Carbon Management Technology Conference, 2012. [本文引用:1]
[2] LEYRIS J, JANSEN B O, FOLLUM O A, et al. Greenhouse gas emissions along the Norwegian gas value chain[R]. SPE 190587-MS, 2018. [本文引用:1]
[3] 胡永乐, 郝明强, 陈国利, 等. 中国CO2驱油与埋存技术及实践[J]. 石油勘探与开发, 2019, 46(4): 716-727.
HU Yongle, HAO Mingqiang, CHEN Guoli, et al. Technologies and practice of CO2 flooding and sequestration in China[J]. Petroleum Exploration and Development, 2019, 46(4): 716-727. [本文引用:1]
[4] MATHIESON A, MIDGELY J, WRIGHT I, et al. In Salah CO2 storage JIP: CO2 sequestration monitoring and verification technologies applied at Krechba, Algeria[J]. Energy Procedia, 2011, 4: 3596-3603. [本文引用:1]
[5] FU K, RONGWONG W, LIANG Z, et al. Experimental analyses of mass transfer and heat transfer of post-combustion CO2 absorption using hybrid solvent MEA-MeOH in an absorber[J]. Chemical Engineering Journal, 2015, 260: 11-19. [本文引用:1]
[6] CHEN S, LIU Y. DoReMi: A passive, geophysical monitoring technique for CO2 injection[R]. SPE 149265-MS, 2011. [本文引用:1]
[7] KAZEMEINI S H, JUHLIN C, FOMEL S. Monitoring CO2 response on surface seismic data; a rock physics and seismic modeling feasibility study at the CO2 sequestration site, Ketzin, Germany[J]. Journal of Applied Geophysics, 2010, 71(4): 109-124. [本文引用:1]
[8] LI H G, ZHANG X G, GUO H Z, et al. 4D seismic or CO2 in formation-fast neutron cross section[C]//SPWLA 25th Formation Evaluation Symposium of Japan. Chiba, Japan: Society of Petrophysicists and Well-Log Analysts, 2019. [本文引用:1]
[9] IZGEC O, DEMIRAL B, BERTIN H J, et al. CO2 injection in carbonates[R]. SPE 93773-MS, 2005. [本文引用:1]
[10] WITTERHOLT E J, TIXIER M R. Temperature logging in injection wells[R]. SPE 4022-MS, 1972. [本文引用:1]
[11] HURTER S, GARNETT A A, BIELINSKI A, et al. Thermal signature of free-phase CO2 in porous rocks: Detectability of CO2 by temperature logging[R]. SPE 109007-MS, 2007. [本文引用:1]
[12] RAEESI B, CEDILLO G, HAN X, et al. Expand ing application of multi-detector pulsed neutron instrumentation for quantitative gas saturation monitoring in gas-filled boreholes[C]//SPWLA 58th Annual Logging Symposium. Oklahoma City, Oklahoma, USA: Society of Petrophysicists and Well-Log Analysts, 2017. [本文引用:1]
[13] ZHANG F, LIU J, YUAN C. Monte Carlo simulation for determining gas saturation using three-detector pulsed neutron logging technology in tight gas reservoir and its application[J]. Applied Radiation and Isotopes, 2013, 78: 51-56. [本文引用:1]
[14] MURRAY D R, YANG X W, HORIE T, et al. CO2 sequestration monitoring in a low salinity reservoir[R]. SPE 130773-MS, 2010. [本文引用:1]
[15] MÜLLER N, RAMAKRISHNAN T S, BOYD A, et al. Time-lapse carbon dioxide monitoring with pulsed neutron logging[J]. International Journal of Greenhouse Gas Control, 2007, 1(4): 456-472. [本文引用:1]
[16] ARYANI A, MOHAMED F, OBEIDI A, et al. Pulsed neutron monitoring of the first CO2 EOR pilot in the Middle East[R]. SPE 141490-MS, 2011. [本文引用:1]
[17] ZHANG F, ZHANG Q, TIAN L, et al. Monitoring CO2 saturation using three-detector PNC logging technique for CO2-EOR in heavy oil reservoir[C]//SPWLA 60th Annual Logging Symposium. The Woodland s, Texas, USA: Society of Petrophysicists and Well-Log Analysts, 2019. [本文引用:1]
[18] ZHOU T, ROSE D, QUINLAN T, et al. Fast neutron cross-section measurement physics and applications[C]//SPWLA 57th Annual Logging Symposium. Reykjavik, Iceland : Society of Petrophysicists and Well-Log Analysts, 2016. [本文引用:2]
[19] CHADWICK M B, OBLOŽINSKÝ P, HERMAN M, et al. ENDF/B-VII. 0: Next generation evaluated nuclear data library for nuclear science and technology[J]. Nuclear Data Sheets, 2006, 107(12): 2931-3060. [本文引用:1]
[20] TITTLE C W. Theory of neutron logging I[J]. Geophysics, 1961, 26(1): 27-39. [本文引用:1]
[21] ZHANG F, ZHANG Q, LIU J, et al. A method to describe inelastic gamma field distribution in neutron gamma density logging[J]. Applied Radiation and Isotopes, 2017, 129: 189-195. [本文引用:1]
[22] 张泉滢, 张锋, 王玉伟, 等. 随钻中子伽马密度测井的双源距含氢指数校正方法[J]. 中国石油大学学报(自然科学版), 2017, 41(4): 78-84.
ZHANG Quanying, ZHANG Feng, WANG Yuwei, et al. Dual-spacing hydrogen index correction method for neutron gamma density measuring in LWD[J]. Journal of China University of Petroleum (Edition of Natural Science), 2017, 41(4): 78-84. [本文引用:1]
[23] Los Alamos National Laboratory. MCNP: A general Monte Carlo n-particle transport code, version 5[R]. LA-UR-03-1987, 2003. [本文引用:1]
[24] MARRA R K, POETTMANN F H, THOMPSON R S. Density of crude oil saturated with CO2[J]. SPE Reservoir Engineering, 1988, 3(3): 815-821. [本文引用:1]
[25] 席长丰, 齐宗耀, 张运军, 等. 稠油油藏蒸汽驱后期CO2辅助蒸汽驱技术[J]. 石油勘探与开发, 2019, 46(6): 1169-1177.
XI Changfeng, QI Zongyao, ZHANG Yunjun, et al. CO2 assisted steam flooding in late steam flooding in heavy oil reservoirs[J]. Petroleum Exploration and Development, 2019, 46(6): 1169-1177. [本文引用:1]