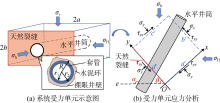
四川盆地南部地区页岩储集层中普遍发育高角度天然裂缝^{[11, 19, 20, 21]}, 页岩储集层压裂过程中, 由于裂缝扩展或固井水泥空隙等流动通道的存在, 压裂液可能沿某条通道进入与井筒相交的天然裂缝, 使裂缝内流体压力升高^[5]。当缝内压力增加达到临界值时, 裂缝面摩擦力与井筒剪力（井筒抵抗裂缝滑移的剪力）的合力将小于地层滑移的剪力, 天然裂缝发生滑移并导致套变。基于上述物理过程, 本文建立了地层-裂缝-套管系统受力模型（见图1）, 并以此为基础研究裂缝滑移套变中的力学机理。图中最大水平主应力方向（Oe方向）沿顺时针方向与裂缝面的夹角（简称裂缝逼近角）为θ , 其与水平井筒的夹角（简称井筒逼近角）为α 。模型假设：①水平井筒（全部处于同一水平面内）贯穿一垂直天然裂缝, 压裂液通过某流动通道由井筒进入天然裂缝; ②水平井筒由一层生产套管和水泥环组成, 完整的水泥环与套管共同承受剪应力, 破坏的水泥环无法承受剪应力; ③天然裂缝未被充填胶结, 流体进入即充满天然裂缝; ④压裂液不滤失、裂缝不扩展, 流体压力在天然裂缝内处处相等。

图1

	Figure Option ViewDownloadNew Window
	图1 地层-裂缝-套管系统受力模型

由于天然裂缝假设为垂直缝, 地层垂向应力在裂缝面上无剪应力分量, 主要考虑水平主应力对于裂缝面的作用。因此, 在水平方向上选取系统受力单元（见图1a）中套管与地层组合的正方形截面开展受力分析（见图1b）, 受力单元4个侧面由a'、b'、c'、d' 4条虚线表示, 边长等于裂缝长度, 图中x轴垂直于裂缝面, y轴平行于裂缝面。由平面应力分析可知, 压裂施工前受力单元在x方向的正应力与y方向的剪应力可表示为：

$\left\{ \begin{align} & {{\sigma }_{x}}=0.5({{\sigma }_{\text{H}}}+{{\sigma }_{\text{h}}})-0.5({{\sigma }_{\text{H}}}-{{\sigma }_{\text{h}}})\cos \ 2\theta \\ & {{\tau }_{xy}}=0.5({{\sigma }_{H}}-{{\sigma }_{\text{h}}})\sin \ 2\theta \\ \end{align} \right.$ （1）

1.1.1 裂缝未完全撑开模型

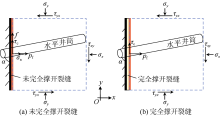
压裂施工时, 压裂液进入并支撑天然裂缝。当裂缝未被完全撑开时, 如图2a所示, 裂缝面在x方向上主要受力为岩体接触压力与压裂液流体压力, 在y方向上主要受力为裂缝面摩擦力与井筒剪力。假设受力单元静止, x方向上可建立受力平衡关系为：

${{\sigma }_{x}}{{A}_{\text{f}}}+{{\tau }_{yx}}{{A}_{\text{f}}}={{p}_{\text{f}}}{{A}_{\text{f}}}+{{\sigma }_{\text{n}}}{{A}_{\text{f}}}+{{\tau }_{yx}}{{A}_{\text{f}}}$ （2）

图2

	Figure Option ViewDownloadNew Window
	图2 正方形受力单元应力分析示意图

y方向上可建立受力平衡关系为：

${{\sigma }_{y}}{{A}_{\text{f}}}+{{\tau }_{xy}}{{A}_{\text{f}}}={{\sigma }_{y}}{{A}_{\text{f}}}+f+{{\tau }_{c}}{{A}_{c}}$ （3）

由于固井前井眼周围应力已经释放, 同时忽略固井水泥凝固时的附加应力, 则当裂缝面摩擦力大于地层在y方向（b'面）上所受剪力时, 由（3）式可知, 裂缝面实际摩擦力等于地层所受剪力, 井筒剪力为零。

当裂缝面摩擦力小于地层在y方向上所受的剪力时, 若地层内无井筒存在, 地层会沿裂缝面发生滑移。当井筒存在时, 井筒会承受一部分剪力以抵抗地层滑移, 此时裂缝面实际摩擦力为最大静摩擦力。因此, 由（3）式可以计算当前条件下井筒抵抗裂缝滑移的剪应力（以下简称井筒剪应力）：

${{\tau }_{\text{c}}}=({{\tau }_{xy}}{{A}_{\text{f}}}-{{f}_{\max }})/{{A}_{\text{c}}}$ （4）

f_max可以采用裂缝面摩擦系数计算, 裂缝面摩擦系数μ 取值为0.6~1.0^[5]：

${{f}_{\max }}\text{=}\mu {{\sigma }_{\text{n}}}{{A}_{\text{f}}}$ （5）

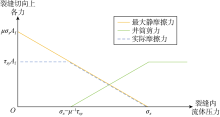
当裂缝几何参数一定时, 假设受力分析单元不发生移动, 可以建立裂缝内流体压力与裂缝切向上所受各力的关系。由图3可知, 随着p_f增加, f_max线性递减, 裂缝面实际摩擦力等于地层在y方向上所受的剪力${{\tau }_{xy}}{{A}_{\text{f}}}$, 此时井筒需要承受的剪力为零; 当f_max递减至等于${{\tau }_{xy}}{{A}_{\text{f}}}$后, 井筒需要承担一部分剪力（${{\tau }_{\text{c}}}{{A}_{\text{c}}}$）以保持受力单元静止, 此时f等于f_max; 当p_f增加至等于${{\sigma }_{x}}$后, 裂缝被压裂液完全撑开, 裂缝两侧岩体不再接触, f为零, 此时井筒需要承受的剪力等于${{\tau }_{xy}}{{A}_{\text{f}}}$。

图3

	Figure Option ViewDownloadNew Window
	图3 裂缝内流体压力与裂缝切向上所受各力的关系

1.1.2 裂缝完全撑开模型

当天然裂缝被压裂液完全撑开时, 裂缝两侧岩体不再接触（见图2b）, 裂缝面在x方向上只受p_f作用, 在y方向上f为零, y方向上的剪力由井筒承受。因此, 由（3）式可以计算当前条件下井筒剪应力为：

${{\tau }_{\text{c}}}={{\tau }_{xy}}\frac{{{A}_{\text{f}}}}{{{A}_{\text{c}}}}$ （6）

A_c为井筒与裂缝截面上水泥环围成的圆环面积：

${{A}_{c}}=\frac{\text{ }\!\!\pi\!\!\text{ }({{R}^{2}}-r_{1}^{2})}{\left| \sin \left( \alpha -\theta \right) \right|}$ （7）

水泥环破坏后, A_c为仅由套管围成的圆环面积${{{A}'}_{\text{c}}}$：

${{{A}'}_{\text{c}}}=\frac{\text{ }\!\!\pi\!\!\text{ }(r_{\text{2}}^{2}-r_{1}^{2})}{\left| \sin \left( \alpha -\theta \right) \right|}$ （8）

威远地区某区块页岩储集层改造井筒基础参数如表1所示, 地质工程参数如表2所示。该区块地应力方向约为东西向, 最大水平主应力约为75 MPa, 最小水平主应力约为65 MPa, 水平井筒方向与最小水平主应力方向近似平行。蚂蚁体和测井数据综合解释成果显示该区块天然裂缝走向以北东向为主, 平均长度约为150 m。采用上述数据分析逼近角、裂缝面积、缝内流体压力、裂缝摩擦系数等因素对井筒剪应力的影响。

表1

表1

表1 威远某区块储集层水平井改造井筒基础参数 参数 取值 参数 取值 裸眼井筒直径 215.9 mm 套管（P125钢）抗剪强度 178 MPa 套管直径 139.7 mm 水泥环抗剪强度 11.5 MPa 套管（厚壁）壁厚 12.7 mm

表1 威远某区块储集层水平井改造井筒基础参数

表2

表2

表2 威远某区块储集层水平井改造地质工程参数 井号 弹性模量/ MPa 泊松比 最小水平 主应力/MPa 最大水平 主应力/MPa 最大水平主应力 方位角/（° ） 井筒逼近角/ （° ） 天然裂缝 条数/条 天然裂缝 方位角/（° ） 天然裂缝 平均长度/m 套变 次数/次 套变位置裂缝 逼近角/（° ） A1 33 210 0.24 61.6 74.3 100 110 5 36.8~46.0 125 2 53.2 A2 34 103 0.22 60.7 71.6 100 90 4 25.8~44.0 180 2 45.5 A3 36 104 0.24 62.8 74.1 100 90 2 25.0 64 A4 34 136 0.23 62.0 73.5 100 90 2 68.0 31 B1 37 334 0.27 70.5 82.4 95 85 6 35.0~60.0 120 3 38.0~52.0 B2 30 804 0.22 65.9 78.6 95 90 4 0~10.0 130 C1 35 154 0.22 69.5 83.8 90 90 6 30.0~65.0 300 3 35.0~56.0 C2 40 852 0.21 65.0 78.8 90 90 8 20.0~50.0 220 1 50.0

表2 威远某区块储集层水平井改造地质工程参数

1.2.1 逼近角

图4为A_f=10 m², p_f=75 MPa, 水泥环完整与破坏两种井况条件下, 裂缝逼近角（θ ）、井筒逼近角（α ）与井筒剪应力（τ _c）的关系曲线。可以看到, 当裂缝走向与最大水平主应力（σ _H）方向平行或垂直时, 井筒剪应力计算值为零, 与α 值无关。其他情况下, τ _c值由θ 值和α 值共同决定。目前, 威远气田现场通常沿最小水平应力方向（α 近90° ）布置水平井筒, 本算例中α =90° 时的高剪应力区（τ _c≥ 1 GPa）所对应的θ 值范围为20° ~55° （或补角）, 与表2中套变位置天然裂缝逼近角吻合程度较高。因此, θ 值一定时, 可根据图版适当调整α 值以避免井筒受到高剪应力的影响。

图4

	Figure Option ViewDownloadNew Window
	图4 不同井筒逼近角条件下裂缝逼近角对井筒剪应力的影响

水泥环完整性对井筒剪应力影响明显, 本例中水泥环破坏条件下的井筒最大剪应力（α =135° , θ =45° ）是水泥环完整条件下的5.97倍。图4a显示水泥环完整条件下, τ _c计算值远高于水泥环的抗剪强度（S_s）, 可以认为当地层沿着裂缝面发生滑移时, 水泥环完整性将很难保持, 因此水泥环破坏条件下的套管剪切变形将是下一步的分析重点。同时本例采用了高钢级厚壁套管, 在此情况下对比水泥环破坏条件下的τ _c值与套管抗剪强度（S_c）发现, τ _c值同样远高于套管的抗剪强度（见图4b）, 这说明提高套管强度或固井质量对降低套变风险作用有限^[22]。

1.2.2 裂缝面积

图5为裂缝被压裂液完全撑开, θ =30° , 不同α 值条件下裂缝面积（A_f）与井筒剪应力的关系。可以看到, A_f值越大, τ _c值越大; τ _c值随着α 值的增大先增大后减小。由（6）式可知, 在τ _xy、A_c值一定时, τ _c值受A_f值控制, 即天然裂缝面积越大, 井筒剪切破坏的风险越高。

图5

	Figure Option ViewDownloadNew Window
	图5 裂缝面积对井筒剪应力的影响

1.2.3 缝内流体压力

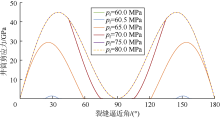
当裂缝未被压裂液完全撑开时, 缝内流体压力（p_f）会对裂缝滑移产生影响。图6为α =90° , μ =0.6, A_f=50 m²时, 不同p_f值条件下, θ 与τ _c的关系曲线。当p_f值高于σ _x时, τ _c值最大。当p_f值低于σ _x-μ ^-1τ _xy时, τ _c在任意θ 下为零。以θ =30° 为例, 计算σ _x为67.5 MPa, σ _x-μ ^-1τ _xy为60.3 MPa。如图所示, 随着p_f值的增加, τ _c值增加, 当p_f值高于67.5 MPa时, p_f值为70, 75, 80 MPa的3条曲线在θ =30° 处重合, τ _c达到最大值。而p_f值低于60.3 MPa时, 井筒剪应力为零。

图6

	Figure Option ViewDownloadNew Window
	图6 缝内流体压力对井筒剪应力的影响

1.2.4 裂缝摩擦系数

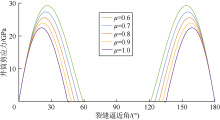
图7为裂缝未被压裂液完全撑开, α =90° , p_f=65 MPa, A_f=50 m²时, 不同裂缝摩擦系数（μ ）条件下, θ 与τ _c的关系曲线。可以看到地应力与裂缝几何参数一定时, μ 值增加, 裂缝面最大静摩擦力增加, ${{\tau }_{\text{c}}}$值减小。因μ 取值范围有限, 故μ 的变化对剪应力的影响不及p_f的影响显著。

图7

	Figure Option ViewDownloadNew Window
	图7 裂缝面摩擦系数对井筒剪应力的影响

综合上述分析认为天然裂缝是诱发水平井套变的主要因素, 加强区块内天然裂缝的监测和识别有利于工程上预防套变发生：①在深刻认识区块地质条件的基础上, 尽量使井筒方位与天然裂缝走向平行或垂直、避开大型天然裂缝有利于减小井筒剪力, 降低套变风险; ②通过工程措施降低缝内净压力是降低套变风险的有效方法^[9]。

威远地区在水平井压裂过程中采用“ 多簇射孔+暂堵转向” 工艺在降低套变风险方面取得了较好效果, 套变井比例为21%, 远小于常规工艺的48%。在地质工程参数明确的工区, 可以采用本文提出的方法, 建立图版并快速分析套变风险程度, 通过优化井筒方位、控制排量、实施暂堵等技术措施合理控制缝内流体压力降低套变风险。

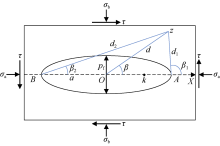
套变量的快速确定对套变后续工程设计意义重大。由于裂缝滑移的剪应力远大于井筒抗剪强度, 因此可假设套变量近似等于裂缝切向滑移量, 同时假设：①天然裂缝为Ⅰ +Ⅱ 复合型（张开型裂缝定义为Ⅰ 型, 滑移型裂缝定义为Ⅱ 型）叠加裂缝^[23]（见图8）, 缝内流体压力为p_f; ②裂缝在p_f作用下被完全撑开, 流体压力在裂缝内处处相等, 压裂液不滤失, 裂缝不扩展。基于上述假设, 采用复变函数建立套变量快速计算模型。

Ⅰ +Ⅱ 复合型叠加裂缝Westergaard应力函数为^[23]：

$\left\{ \begin{align} & Z\left( z \right)=\sqrt{\frac{{{d}^{2}}}{{{d}_{1}}{{d}_{2}}}}\left( {{\sigma }_{\text{b}}}\cos \ \psi +\tau \sin \ \psi \right)+\frac{{{\sigma }_{\text{a}}}-{{\sigma }_{\text{b}}}}{2}+ \\ & \ \ \ \ \ \ \ \ \ \text{i}\sqrt{\frac{{{d}^{2}}}{{{d}_{1}}{{d}_{2}}}}\left( {{\sigma }_{\text{b}}}\sin \ \psi -\tau \cos \ \psi \right) \\ & \psi =\beta -\frac{{{\beta }_{1}}+{{\beta }_{2}}}{2} \\ \end{align} \right.$ （9）

图8

	Figure Option ViewDownloadNew Window
	图8 Ⅰ +Ⅱ 复合型叠加裂缝平面应变模型

基于Muskhelishvili等推导的裂缝位移计算方法^[23], Ⅰ +Ⅱ 复合型叠加裂缝位移场可以表示为：

$\left\{ \begin{align} & u=\frac{1}{{{E}'}}\left\{ 2\operatorname{Re}\widetilde{Z}\left( z \right)-\left( 1+{\upsilon }' \right)\left[ \frac{1}{2}\operatorname{Re}\bar{z}Z\left( z \right)-\begin{matrix} {} \\ {} \\\end{matrix} \right. \right. \\ & \ \ \ \left. \left. \begin{matrix} {} \\ {} \\\end{matrix}\frac{1}{2}\operatorname{Re}zZ\left( z \right)+\operatorname{Re}\widetilde{{{Z}_{\text{I}}}}\left( z \right) \right] \right\} \\ & v=\frac{1}{{{E}'}}\left\{ 2\operatorname{Im}\widetilde{Z}\left( z \right)-\left( 1+{\upsilon }' \right)\left[ \operatorname{Im}\widetilde{Z}\left( z \right)-\begin{matrix} {} \\ {} \\\end{matrix} \right. \right. \\ & \ \ \ \left. \left. \begin{matrix} {} \\ {} \\\end{matrix}\frac{1}{2}\operatorname{Im}\bar{z}Z\left( z \right)-\frac{1}{2}\operatorname{Im}zZ\left( z \right)-\operatorname{Im}\widetilde{{{Z}_{\text{I}}}}\left( z \right) \right] \right\} \\\end{align} \right.$ （10）

由（9）式、（10）式可推导出裂缝面相对位移为：

$\left\{ \begin{align} & \Delta u=4\left( 1-{{\upsilon }^{2}} \right)\frac{\tau }{E}a\sqrt{1-{{\left( \frac{{{k}'}}{a} \right)}^{2}}} \\ & \Delta v=4\left( 1-{{\upsilon }^{2}} \right)\frac{{{\sigma }_{\text{b}}}}{E}a\sqrt{1-{{\left( \frac{{{k}'}}{a} \right)}^{2}}} \\ \end{align} \right.$ （11）

同理, 可推导出在附加流体压力作用下裂缝面的相对位移表达式为：

$\left\{ \begin{align} & \Delta {{u}_{\text{p}}}=0 \\ & \Delta {{v}_{\text{p}}}=4\left( 1-{{\upsilon }^{2}} \right)\frac{{{p}_{\text{f}}}}{E}a\sqrt{1-{{\left( \frac{{{k}'}}{a} \right)}^{2}}} \\ \end{align} \right.$ （12）

综合（11）、（12）式, 可得Ⅰ +Ⅱ 复合型叠加裂缝相对位移量为：

$\left\{ \begin{align} & \Delta {{u}_{\text{f}}}=4\left( 1-{{\upsilon }^{2}} \right)\frac{\tau a}{E}\sqrt{1-{{\left( \frac{{{k}'}}{a} \right)}^{2}}} \\ & \Delta {{v}_{\text{f}}}=4\left( 1-{{\upsilon }^{2}} \right)a\frac{{{\sigma }_{\text{b}}}-{{p}_{\text{f}}}}{E}\sqrt{1-{{\left( \frac{{{k}'}}{a} \right)}^{2}}} \\ \end{align} \right.$ （13）

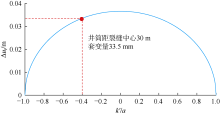
威202井区HX-1井射孔联作过程中, 桥塞泵送至3 090 m时遇阻。蚂蚁体解释结果显示遇阻点天然裂缝贯穿井筒（缝长150 m, 方位北偏东50° ）, 井筒距裂缝中心约30 m, 井温测井显示遇阻点有明显温度下降, 井径测井显示遇阻点发生三级套变（见表3、表4）。基于上述数据, 计算HX-1井Δ u_f（Ⅰ +Ⅱ 复合型叠加裂缝的切向相对位移量, 简称套变量）值为33.5 mm（见图9）, 井径测井结果显示本井套管最大变形量为31.8 mm, 相对误差5.3%, 说明本模型计算结果可靠。

表3

表3

表3 HX-1井工程地质基础参数 参数 取值 参数 取值 天然裂缝长度 150 m 泊松比 0.22 裸眼井筒直径 215.9 mm 弹性模量 43.5 GPa 套管直径 139.7 mm 最小水平主应力 60 MPa 套管壁厚 12.7 mm 最大水平主应力 72 MPa

表3 HX-1井工程地质基础参数

表4

表4

表4 HX-1井套管损伤检测测井参数 参数 取值 参数 取值 变形长度 10 m 最大变形量 31.8 mm 平均内径 112.7 mm 变形级别 三级 最大内径 141.4 mm

表4 HX-1井套管损伤检测测井参数

图9

	Figure Option ViewDownloadNew Window
	图9 HX-1井套变量计算结果

2.3.1 岩石力学参数

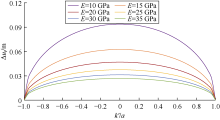
图10为θ =45° , $\upsilon $=0.25, a=50 m时, 不同岩石弹性模量条件下k'/a与Δ u_f的关系曲线。由图可知, 套变量呈抛物线型变化, 最大值出现在裂缝中心处; 相同应力作用下, 弹性模量越高的岩石应变越小, 故弹性模量越大, 套变量越小。

图10

	Figure Option ViewDownloadNew Window
	图10 地层岩石弹性模量对套变量的影响

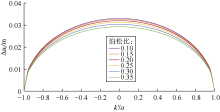
保持θ 、a不变, 取E=30 GPa, 计算不同地层岩石泊松比条件下k'/a与Δ u_f的关系曲线（见图11）。可以看到岩石套变量与泊松比负相关, 但泊松比对套变量的影响较小。

图11

	Figure Option ViewDownloadNew Window
	图11 地层岩石泊松比对套变量的影响

2.3.2 裂缝几何参数

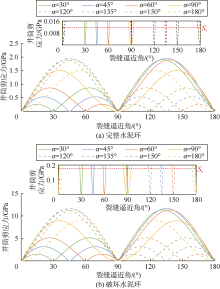
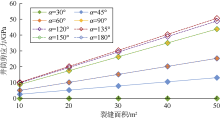
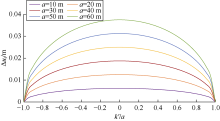
保持θ 、$\upsilon $不变, 取E=30 GPa, 计算不同裂缝半长条件下k'/a与Δ u_f的关系曲线（见图12）。由图可知, 裂缝半长对套变量影响显著, a越大, 套变量越大。这是因为a越大, 则裂缝面积越大, 地层所受剪应力越大, 位移量越大。

图12

	Figure Option ViewDownloadNew Window
	图12 裂缝半长对套变量的影响

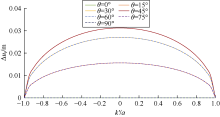
保持$\upsilon $、a不变, 取E=30 GPa, 计算不同裂缝逼近角条件下k'/a与Δ u_f的关系曲线（见图13）。由于剪应力是$\theta $的正弦函数, 故仅讨论θ ∈ [0° , 90° ]时的套变量变化情况。计算结果显示, 套变量随$\theta $的增大先增大后减小, 在θ =45° 时, 套变量最大。

图13

	Figure Option ViewDownloadNew Window
	图13 裂缝逼近角对套变量的影响