四川盆地致密砂岩和碳酸盐岩的岩心薄片、扫描电镜和微CT扫描图像如图1所示。其中, 图1a— 图1b为致密砂岩薄片鉴定图像, 图1c— 图1d为碳酸盐岩薄片鉴定图像, 图1e— 图1h为致密砂岩扫描电镜图像, 图1i— 图1j为分辨率为0.62 μ m的致密砂岩微CT扫描图像, 图1k— 图1l为分辨率为14.10 μ m的碳酸盐岩微CT扫描图像。致密砂岩岩样孔隙度4.1%~7.3%, 渗透率0.05× 10^-3~0.14× 10^-3μ m²; 碳酸盐岩岩样孔隙度3.2%~7.5%, 渗透率0.03× 10^-3~1.50× 10^-3μ m²。如图所示, 致密砂岩和碳酸盐岩中均发育形态复杂的微裂缝, 包括构造缝、粒间缝、层间缝、溶蚀缝等; 部分微裂缝相交, 形成微裂缝网络。致密砂岩微裂缝开度为0.002~0.050 mm; 碳酸盐岩微裂缝开度为0.002~0.100 mm, 与王璐等^[27]的认识一致。

图1

	Figure Option ViewDownloadNew Window
	图1 致密砂岩和碳酸盐岩中的微裂缝

微观图像和三维数字岩心直观展示了岩石中的微裂缝网络形态, 可获取微裂缝开度和数量等信息。但受限于观测尺度, 部分微裂缝延伸至薄片范围外, 难以准确获取长度^[2]。而裂缝长度影响微裂缝网络的连通性, 对岩石渗流起着重要作用; 同时受分辨率限制, 三维数字岩心未能捕获岩石中大部分基质孔隙。若直接基于数字岩心开展模拟, 会高估岩石微裂缝网络连通性、低估基质孔隙渗流能力。

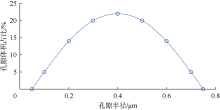
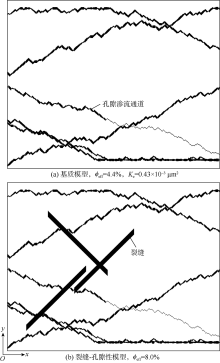
高压压汞实验可准确测量岩石微观孔隙性质, 以四川盆地某气藏储集层岩石为例, 测得其基质孔隙半径主要为0.1~0.7 μ m, 近似满足正态分布（见图2）。本文结合该气藏储集层岩石数字岩心和高压压汞实验结果, 采用数值算法构建裂缝性多孔介质和裂缝-孔隙性多孔介质模型。其中, 裂缝性多孔介质模型（简称裂缝性模型）含有贯穿性微裂缝网络（忽略基质孔隙影响）, 裂缝-孔隙性多孔介质模型（简称裂缝-孔隙性模型）含有孔隙和未贯穿性微裂缝网络。裂缝-孔隙性模型构建过程如下：①设定多孔介质区域, 将整个区域均设为固相; ②结合高压压汞实验结果, 设定多孔介质基质孔隙孔径满足图2所示正态分布, 确定不同尺寸孔隙所占节点数量, 在多孔介质内随机指定孔隙的半径; 当生成孔隙的节点数量达到预期, 停止孔隙生长, 确保孔隙连通（见图3a）; ③基于微观图像和数字岩心分析结果, 设置微裂缝开度和长度, 并将其随机分布于多孔介质; ④设置不同裂缝数量, 重复步骤①— ③, 即可生成含不同微裂缝网络的裂缝-孔隙性模型（见图3b）。只需执行步骤③和④即可生成不同裂缝性模型。

图2

	Figure Option ViewDownloadNew Window
	图2 四川盆地某气藏储集层岩石基质孔隙半径分布

图3

	Figure Option ViewDownloadNew Window
	图3 多孔介质模型

岩石渗流能力只与相互连通的孔隙和微裂缝有关, 采用四连通区域标记算法^[23]进一步去除多孔介质中的孤立孔隙和裂缝。基于形态学原理^[28], 按一定线条间隔沿多孔介质x、y方向分别插入多条直线, 单位长度直线所遇到平均裂缝数的比值定义为裂缝网络走向因子（A）：

$A\text{=}\frac{{{n}_{y}}}{{{n}_{x}}}$ （1）

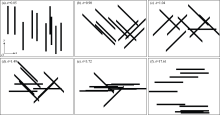
图4为6个由10条长400格子, 开度20格子的微裂缝组成的微裂缝网络示意图。将线条间隔设置为5格子, 沿多孔介质x和y方向插入直线得到n_x和n_y。运用（1）式计算得到6个微裂缝网络的A值为0.05~17.61, 不同走向的微裂缝网络A取值不同。当倾向于y方向的微裂缝数量多于倾向于x方向时, A值小于1; 当倾向于x方向的微裂缝数量多于倾向于y方向时, A值大于1; 当倾向于x方向的微裂缝数量等于y方向时, A值等于1。当微裂缝走向均为y方向时, A值最小（A=0.05）; 当微裂缝走向均为x方向时, A值最大（A=17.61）。随着倾向于x方向微裂缝数量的增加, A值增大, 因此A值可以定量表征微裂缝网络整体走向。

图4

	Figure Option ViewDownloadNew Window
	图4 不同走向的微裂缝网络示意图

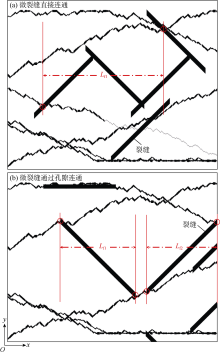
微裂缝网络在多孔介质中形成新的渗流通道, 微裂缝间可能直接连通, 也可能通过基质孔隙间接连通。以往裂缝网络连通性的评价方法未能兼顾裂缝网络局部与多孔介质整体的关系, 适用性较差^[15]。本文将某一流动路径上与基质孔隙相连通的微裂缝水平长度之和的最大值（L_{f, max}）与多孔介质长度（L）的比值定义为微裂缝网络连通系数（f）, 表征流体渗流路径上微裂缝的最大占比, f取值0~1, f值越大, 多孔介质中微裂缝网络整体连通性越好。当f< 1时, 微裂缝网络处于多孔介质内部, 为裂缝-孔隙性模型; 当f=1时, 微裂缝网络连通多孔介质出入口端, 为裂缝性模型。运用数值算法筛选多孔介质中与孔隙连通的裂缝, 并判断裂缝间连通情况, 便可求得L_{f, max}（见图5, 红色圆圈表示选择的起始点和终止点）。通过（2）式计算得到图5a和图5b中f分别为0.58和0.70。

$f\text{=}\frac{{{L}_{f, \max }}}{L}\text{=}\frac{{{L}_{f1}}+{{L}_{f2}}+\cdots +{{L}_{fn}}}{L}$ （2）

图5

	Figure Option ViewDownloadNew Window
	图5 微裂缝网络连通系数计算示意图

MRT-LBM由Boltzmann方程直接推导, 可表示为^[23]：

${{f}_{i}}(\text{x}+{{\text{e}}_{i}}{{\delta }_{t}}, t+{{\delta }_{t}})-{{f}_{i}}(\text{x}, t)=-\mathbf{\Omega }[{{f}_{i}}(\text{x}, t)-{{f}_{eq, i}}(\text{x}, t)]$ （3）

其中 Ω =M^-1SM

M为分布函数f_i的变换矩阵^[29], （3）式可写为：

${{f}_{i}}(\text{x}+{{\text{e}}_{i}}{{\delta }_{t}}, t+{{\delta }_{t}})-{{f}_{i}}(\text{x}, t)=-{{\text{M}}^{-1}}\text{S}[{{\text{m}}_{i}}(\text{x}, t)-{{\text{m}}_{eq, i}}(\text{x}, t)]$ （4）

其中 m=Mf_i m_eq=Mf_{eq, i}

二维9个离散速度方向（D2Q9）模型中平衡态分布函数为：

${{f}_{eq, i}}=\rho {{w}_{i}}\left[ 1+\frac{({{\mathbf{e}}_{i}}\cdot \mathbf{u})}{c_{s}^{2}}+\frac{{{({{\mathbf{e}}_{i}}\cdot \mathbf{u})}^{2}}}{2c_{s}^{4}}-\frac{{{\mathbf{u}}^{2}}}{2c_{s}^{2}} \right]$ （5）

其中 ${{c}_{s}}={c}/{\sqrt{3}}\; $

离散速度c_i定义为：c₀=（0, 0）, c₁=– c₃=（c, 0）, c₂=-c₄=（0, c）, c₅=-c₇=（c, c）, c₆=-c₈=（-c, c）。对角矩阵S定义为：

$S=diag({{s}_{\rho }}, {{s}_{e}}, {{s}_{\varepsilon }}, {{s}_{j}}, {{s}_{q}}, {{s}_{j}}, {{s}_{q}}, {{s}_{v}}, {{s}_{v}})$ （6）

本文选取s_ρ =s_j=1.0, s_e=1.19, s_ε =1.4, s_q=8(2-s_v)/(8- s_v)^[29], s_v与运动黏度有关。宏观流体的密度、速度和运动黏度如（7）式所示。

$\left\{ \begin{align} & \rho =\sum\limits_{i}{{{f}_{i}}} \\ & u=\frac{1}{\rho }\sum\limits_{i}{{{e}_{i}}}{{f}_{i}} \\ & \nu =c_{\text{s}}^{2}\left( \frac{1}{{{s}_{\text{v}}}}-0.5 \right){{\delta }_{t}} \\\end{align} \right.$ （7）

多孔介质孔隙表面不规则, 可直接应用经典的LBM边界条件^[28]。本文中多孔介质出入口端均采用压力边界^{[25, 30]}, 上下边界采用标准反弹边界。

采用Fortran语言编写MRT-LBM模拟程序, 并验证其模拟多孔介质流体渗流的准确性。

2.2.1 裂缝性模型流体渗流模拟

结合储集层岩石微裂缝的开度、数量、长度等数据, 采用数值算法构建28个裂缝性模型, 通过MRT-LBM模拟裂缝开度分别为30, 60, 120 μ m时多孔介质中的流体（水）连续流动。裂缝性模型构建参数及模拟条件如表1所示, 模拟中流体流动均为层流（Re值较小）。模拟偏差用（8）式计算, 模拟偏差小于1× 10^-6时, 模拟结果不再变化, 结束迭代过程^{[30, 31]}。

${{\delta }_{\text{E}}}\text{ =}\sqrt{\frac{\sum\nolimits_{x, y}{{{\left[ u\left( x, y, t+{{\delta }_{t}} \right)-u\left( x, y, t \right) \right]}^{2}}}}{\sum\nolimits_{x, y}{u{{\left( x, y, t+{{\delta }_{t}} \right)}^{2}}}}}$ （8）

表1

表1

表1 裂缝性模型构建参数及MRT-LBM模拟参数 参数名称 参数值 参数名称 参数值 裂缝开度 30, 60, 120 μ m 温度 333 K 裂缝长度 2 000, 4 000, 8 000 μ m 入口压力 20 MPa 裂缝数量 8 入口密度 983.1 kg/m3 网格数 500× 400 出口密度 980 kg/m3 网格步长 5, 10, 20 μ m 动力黏度 4.699× 10-4 Pa· s

表1 裂缝性模型构建参数及MRT-LBM模拟参数

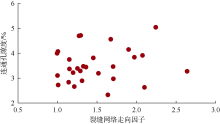
图6所示为微裂缝开度为60 μ m的裂缝性模型的模拟结果, 可见裂缝网络显著影响多孔介质中流体渗流路径以及速度场分布。基于模拟结果, 进一步删除模型中未参与流动的微裂缝, 得到裂缝性模型的连通孔隙度（即多孔介质中相互连通孔隙的体积与多孔介质总体积之比）。将线条间隔设置为5个格子, 采用（1）式计算裂缝性模型的裂缝网络走向因子。裂缝性模型的裂缝网络走向因子为0.99~2.70, 连通孔隙度为2.3%~5.0%, 二者无明显相关性（见图7）。

图6

	Figure Option ViewDownloadNew Window
	图6 开度60 μ m的裂缝性模型模拟结果

图7

	Figure Option ViewDownloadNew Window
	图7 裂缝性模型连通孔隙度与裂缝网络走向因子的关系

2.2.2 裂缝-孔隙性模型流体渗流模拟

结合对储集层岩石性质的认识, 设定裂缝-孔隙性模型的基质孔隙度为5%, 且孔隙半径满足正态分布（见图2）, 微裂缝孔隙度为5%。考虑到岩石中微裂缝尺度普遍大于基质孔隙, 将微裂缝开度分别设为2 μ m和4 μ m。微裂缝分布于裂缝-孔隙性模型内部, 随机设定其走向和长度, 微裂缝起止点均与基质孔隙连通。模型详细构建参数见表2。为考虑随机性影响, 不同开度下均生成20个裂缝-孔隙性模型, 共计40个。

表2

表2

表2 裂缝-孔隙性模型构建参数及MRT-LBM模拟参数 参数名称 参数值 参数名称 参数值 裂缝开度 2, 4 μ m 温度 333 K 裂缝长度 40 μ m 入口压力 20 MPa 裂缝孔隙度 5% 入口密度 983.100 kg/m3 网格数 1 000× 800 出口密度 983.063 kg/m3 网格步长 0.1 μ m 动力黏度 4.699× 10-4 Pa· s 基质孔隙度 5% 压力梯度 0.1 MPa/m

表2 裂缝-孔隙性模型构建参数及MRT-LBM模拟参数

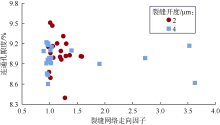
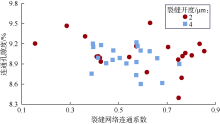
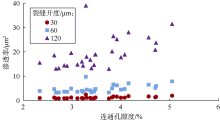
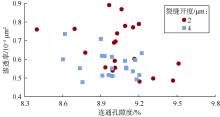
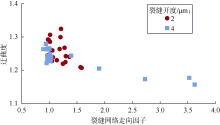
结合（2）式计算裂缝-孔隙性模型的裂缝网络连通系数, 采用D2Q9 MRT-LBM模拟其中流体（水）连续流动, 模拟条件如表2所示。图8对比了基质模型和裂缝网络连通系数分别为0.36, 0.70, 0.80时裂缝-孔隙性模型（裂缝开度2 μ m）的模拟结果。可以看出, 裂缝网络显著影响裂缝-孔隙性模型中流体渗流路径以及速度场分布, 部分渗流通道中的流体渗流速度显著增加（见图8c、图8d）, 优势通道效应显著。随后, 删除裂缝-孔隙性模型中未参与流动的微裂缝, 将线条间隔设置为5个格子, 采用（1）式计算裂缝-孔隙性模型的裂缝网络走向因子, 得到模型的连通孔隙度与裂缝网络走向因子和裂缝网络连通系数的关系（见图9、图10）。当裂缝开度为2 μ m时, 裂缝-孔隙性模型的连通孔隙度为8.4%~9.5%, 裂缝网络走向因子为0.99~1.58, 裂缝网络连通系数为0.11~0.80; 裂缝开度为4 μ m时, 裂缝-孔隙性模型的连通孔隙度为8.6%~9.2%, 裂缝网络走向因子为0.89~3.63, 裂缝网络连通系数为0.34~0.70。裂缝-孔隙性模型的连通孔隙度与裂缝网络走向因子和裂缝网络连通系数均无明显相关性。

图8

	Figure Option ViewDownloadNew Window
	图8 基质模型和裂缝-孔隙性模型模拟结果

图9

	Figure Option ViewDownloadNew Window
	图9 裂缝-孔隙性模型连通孔隙度与裂缝网络走向因子的关系

图10

	Figure Option ViewDownloadNew Window
	图10 裂缝-孔隙性模型连通孔隙度与裂缝网络连通系数的关系

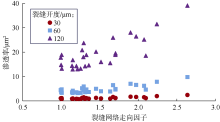
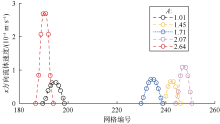
裂缝性模型渗透率与裂缝网络走向因子呈较好的正相关性（见图13）, 当裂缝网络走向因子由1.0增加至2.7时, 不同裂缝开度下的裂缝性模型渗透率增加幅度均超过160%; 而其迂曲度与裂缝网络走向因子呈负相关性（见图14）, 二者的多项式拟合效果最好, 拟合相关系数平方达0.953（见表3）。裂缝-孔隙性模型的渗透率和迂曲度与裂缝网络走向因子均无明显相关性（见图15、图16）。进一步分析裂缝性模型出口端速度剖面, 发现微裂缝网络走向因子越大, 多孔介质出口端流体渗流速度越大（见图17）。从微观角度分析, 裂缝网络走向因子越大, 裂缝性模型的迂曲度越小, 渗流路径越平直, 渗透率就越大。但对于裂缝-孔隙性模型（f< 1）, 基质孔隙与微裂缝尺寸普遍存在数量级差异, 基质孔隙是制约裂缝-孔隙性模型渗流能力的关键因素^[32]。因此, 微裂缝网络走向对裂缝性模型渗流能力的影响显著大于裂缝-孔隙性模型。

图13

	Figure Option ViewDownloadNew Window
	图13 裂缝性模型渗透率与裂缝网络走向因子的关系

图14

	Figure Option ViewDownloadNew Window
	图14 裂缝性模型迂曲度与裂缝网络走向因子的关系

表3

表3

表3 裂缝性模型迂曲度-裂缝网络走向因子拟合函数及裂缝-孔隙性模型渗透率-裂缝网络连通系数拟合函数 裂缝性模型 裂缝-孔隙性模型 拟合关系式 R2 拟合关系式 R2 $\tau \text{=1}\text{.682}{{\text{e}}^{-0.189A}}$ 0.948 ${{K}_{0}}\text{=0}\text{.93}{{K}_{\text{e}}}{{\text{e}}^{0.886f}}$ 0.832 $\tau \text{=}-0.233A\text{+}1.620$ 0.941 ${{K}_{0}}\text{=1}\text{.395}{{K}_{\text{e}}}(f+0.667)$ 0.795 $\tau \text{=}-0.372\ln A\text{+}1.408$ 0.950 ${{K}_{0}}\text{=0}\text{.465}{{K}_{\text{e}}}\ln f+4$ 0.667 $\tau \text{=0}\text{.056}{{A}^{2}}-0.422A\text{+}1.767$ 0.953 ${{K}_{0}}\text{=0}\text{.93}{{K}_{\text{e}}}({{f}^{2}}\text{+}0.5f\text{+}1)$ 0.807 $\tau \text{=1}\text{.415}{{A}^{-0.3}}$ 0.948 ${{K}_{0}}\text{=1}\text{.86}{{K}_{\text{e}}}{{f}^{0.324}}$ 0.717

表3 裂缝性模型迂曲度-裂缝网络走向因子拟合函数及裂缝-孔隙性模型渗透率-裂缝网络连通系数拟合函数

图15

	Figure Option ViewDownloadNew Window
	图15 裂缝-孔隙性模型渗透率与裂缝网络走向因子的关系

图16

	Figure Option ViewDownloadNew Window
	图16 裂缝-孔隙性模型迂曲度与裂缝网络走向因子的关系

图17

	Figure Option ViewDownloadNew Window
	图17 裂缝性模型速度剖面与裂缝网络走向因子的关系

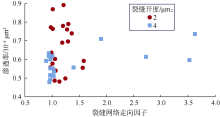
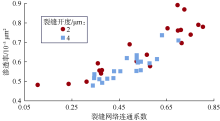
裂缝-孔隙性模型的渗透率与裂缝网络连通系数呈较好的正相关关系（见图18）。当裂缝开度为2 μ m且裂缝网络连通系数由0.11增至0.80时, 裂缝-孔隙性模型的渗透率增加幅度达61.83%; 当裂缝开度为4 μ m且裂缝网络连通系数由0.34增至0.70时, 裂缝-孔隙性模型的渗透率增加幅度达48.43%。裂缝-孔隙性模型渗透率与裂缝网络连通系数的指数式拟合效果最好（以开度2 μ m为例）, 拟合相关系数平方为0.832（见表3）。

图18

	Figure Option ViewDownloadNew Window
	图18 裂缝-孔隙性模型渗透率与裂缝网络连通系数的关系

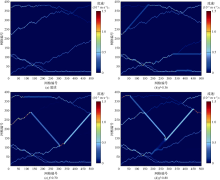
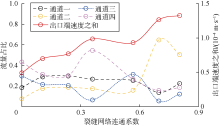
随后分析了模型（f=0为基质模型, 0< f< 1为裂缝-孔隙性模型）出口端各流动通道流体速度之和以及不同孔隙渗流通道流量占比（即通过该通道的流体流量与通过多孔介质总流体流量的比值）与裂缝网络连通系数的关系（见图19）。随着裂缝网络连通系数的增加, 裂缝-孔隙性模型出口端各流动通道流体流速之和总体增加, 局部差异由多孔介质结构随机性造成; 各通道流量占比随裂缝网络连通系数的变化而变化, 但二者无明显相关性。说明裂缝网络连通系数越大, 流体渗流路径上的裂缝占比越大, 流体流过裂缝-孔隙性模型消耗的能量越少, 模型渗透率越大。因此, 裂缝网络连通系数对裂缝-孔隙性模型渗流能力的影响大于裂缝网络走向。

图19

	Figure Option ViewDownloadNew Window
	图19 模型出口端各通道流量占比与裂缝网络连通系数的关系

此外, 部分裂缝-孔隙性模型中优势通道效应显著, 通道二在裂缝网络连通系数为0.70和0.80时, 以及通道四在裂缝网络连通系数为0.36时, 其流量占比均超过0.5（见图19）。总体来看裂缝网络连通系数越大, 多孔介质中越易出现优势通道效应（f≥ 0.7时尤为显著）。优势通道效应存在时, 多孔介质中其余通道的流量占比减小, 而通过这些通道的流体流量大多增加, 少数情况下也存在个别通道传输流体流量减少的现象。

裂缝开度为60 μ m和120 μ m时的裂缝性模型渗透率分别约为裂缝开度为30 μ m时裂缝性模型的4倍和16倍, 其连通孔隙度、渗透率、迂曲度与裂缝网络走向因子的相关性均与裂缝开度为30 μ m的裂缝性模型一致（见图13、图14）。即对于裂缝性模型, 其渗流能力主要取决于裂缝网络走向和裂缝开度, 而裂缝开度的影响更显著。裂缝-孔隙性模型的基质孔隙特征长度为0.344 μ m^[31], 当裂缝开度与基质特征长度的比值由5.814增加至11.628时（微裂缝开度由2 μ m增加至4 μ m）, 裂缝-孔隙性模型的渗透率变化幅度小于10%（见图18）。所以, 裂缝开度对裂缝-孔隙性模型渗流能力的影响远小于裂缝网络连通性。

目前气藏储量可动性评价方法主要包括实验法和数值模拟法, 综合考虑经济因素、实验结果和现场测试数据求取储集层可动储量孔隙度下限的方法取得了较好效果。但由前文可知, 含微裂缝网络多孔介质的渗流能力与孔隙度无明显相关性, 因此采用孔隙度划分储集层储量可动下限的方法未考虑微裂缝网络对岩石渗流能力的影响。以本文得到的多孔介质渗透率与微裂缝网络连通性指数关系式为例, 基质孔隙度和裂缝开度相同时, 当裂缝网络连通系数由0增至1, 多孔介质渗透性增加120.98%, 储量可动性差异显著。因此针对不同气藏, 需要结合微观实验分析岩石微裂缝性质（裂缝开度、数量和连通性等）, 评价微裂缝网络对岩石渗透性的影响程度。对于微裂缝网络影响较弱的气藏, 直接使用实验法等得到的孔隙度下限评价储量动用情况; 而对于微裂缝网络影响显著且水体能量较弱的气藏, 根据影响程度不同幅度地下调实验法得到的储量动用孔隙度下限, 提升储集层评价的准确性; 对于微裂缝网络影响显著且水体能量较强的气藏, 岩石中存在水驱时, 优势通道效应的存在会导致波及效率下降^[33], 加剧水封气现象, 降低储集层储量可动性。

准确获取储集层渗透性是气井产能评价的关键。试井分析得到的近井区和远井区储集层渗透性通常差异较大, 非均质性显著。由本研究可知, 近井区和远井区储集层渗流能力的差异可能是由不同的裂缝网络走向导致的。裂缝开度和数量相同时, 当裂缝网络走向因子由1.00增加至2.64, 裂缝性多孔介质的迂曲度减小幅度超过25%, 渗透率增加幅度超过160%。考虑裂缝网络走向的影响可进一步提升对气井产能的认识程度。