引用本文
李宁, 王克文, 刘鹏, 武宏亮, 冯周, 范华军, SMEULDERS David. 不同裂缝条件下斯通利波幅度衰减实验[J]. 石油勘探与开发, 2021,48(2): 258-265.
LI Ning, WANG Kewen, LIU Peng, WU Hongliang, FENG Zhou, FAN Huajun, SMEULDERS David. Experimental study on attenuation of Stoneley wave under different fracture factors[J]. Petroleum Exploration & Development, 2021,48(2): 258-265.  
Doi: 10.11698/PED.2021.02.03
Permissions
Copyright©2021, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
不同裂缝条件下斯通利波幅度衰减实验
李宁1, 王克文1, 刘鹏1, 武宏亮1, 冯周1, 范华军2, SMEULDERS David3
1.中国石油勘探开发研究院,北京 100083
2.中国石油大学（北京）地球物理学院,北京 102249
3.埃因霍温理工大学,埃因霍温 5600MB,荷兰

第一作者简介：李宁（1958-）,男,北京市人,博士,中国工程院院士,中国石油勘探开发研究院教授级高级工程师,主要从事测井理论方法和处理软件研究工作。地址：北京市海淀区学院路20号,中国石油勘探开发研究院,邮政编码：100083。E-mail：ln@petrochina.com.cn

收稿日期: 2020-06-24 修回日期: 2021-01-30
基金项目: 中国石油“十三五”测井基础研究项目“储层基质-裂缝组合渗透率测井计算新方法研究”（2019A-3609）
摘要

为了定量确定裂缝宽度、倾角、延伸长度及填充物等不同因素对斯通利波幅度衰减的影响,将原先岩心样品固定、中部钻孔移动探头的激波管斯通利波测量方法,改进为岩心样品不钻孔垂直升降、沿激波管管壁固定分置多探头的测量方法进行实验分析。通过对斯通利波信号进行时间校正和幅度校正,有效改善了斯通利波首波信噪比,提高了测量精度。同时,利用全直径碳酸盐岩岩心,针对此测量方法加工了21组裂缝参数相异（裂缝宽度为毫米级）的岩心模型,并定义相对幅度表征斯通利波衰减。实验结果表明,斯通利波相对幅度随裂缝宽度增加呈指数衰减、随裂缝倾角增加线性降低、随裂缝深度增大呈指数衰减、随填充物渗透率增加而降低。在上述4种情况中,裂缝宽度对斯通利波幅度衰减的影响最大,其次是裂缝延伸长度和填充物渗透率,最后是裂缝倾角。图11表2参20

关键词: 斯通利波; 幅度衰减; 激波管实验; 裂缝宽度; 裂缝倾角; 裂缝延伸长度; 裂缝填充物
中图分类号:P631.4 文献标志码:A
Experimental study on attenuation of Stoneley wave under different fracture factors
LI Ning1, WANG Kewen1, LIU Peng1, WU Hongliang1, FENG Zhou1, FAN Huajun2, SMEULDERS David3
1. Research Institute of Petroleum Exploration & Development, PetroChina, Beijing 100083, China
2. College of Geophysics, China University of Petroleum (Beijing), Beijing 102249, China
3. Eindhoven University of Technology, Eindhoven 5600 MB, the Netherlands
Abstract

To quantitatively determine the effect of different factors such as fracture width, dip angle, extension and filling material on Stoneley wave amplitude decreasing, the shock tube experiment method was changed from fixing the sample and vertically moving the sensor in the borehole to fixing the sensors along the shock tube wall and vertically moving the sample without drilling the borehole in it. The measurement accuracy and the signal-to-noise ratio of the first Stoneley wave were improved by the time corrections and amplitude corrections of Stoneley wave signals. At the same time, 21 sets of core models with different fracture parameters were processed for this measurement method by using full-diameter carbonate core, and relative amplitudes were defined to characterize Stoneley wave amplitude decreasing. The experimental results show that the relative amplitude of Stoneley wave exponentially decreases with increasing fracture width. The relative amplitude of Stoneley wave linearly decreases with increasing fracture dip angle. The relative amplitude of Stoneley wave exponentially decreases with increasing fracture extension. The relative amplitude of Stoneley wave decreases with increasing the permeability of filling material in the fracture. Under the above four conditions, the fracture width has the greatest effect on the decreasing of Stoneley wave amplitude, followed by the fracture extension and the permeability of filling material, and finally the fracture dip angle.

Keyword: Stoneley wave; amplitude decreasing; shock tube experiment; fracture width; fracture dip angle; fracture extension; filling material permeability
0 引言

中国深层复杂碳酸盐岩、火山岩及致密碎屑岩储集层的基质渗透率普遍较低, 裂缝对油气流动起主导作用, 因此裂缝的准确识别及定量评价对油气勘探具有重要意义[1, 2, 3, 4]。目前裂缝评价方法主要有双侧向电阻率差异法、高分辨率电成像法和斯通利波衰减法等[5, 6, 7, 8, 9, 10, 11]。针对含裂缝储集层的双侧向测井响应特征, 国内外学者开展了大量理论及数值模拟研究, 提出了基于双侧向电阻率差异的裂缝定量评价方法[5, 6, 7]。由于双侧向电阻率差异除受裂缝影响之外, 还与地层水矿化度、钻井液电阻率和基质渗透率等因素有关, 故其定量评价裂缝精度较低。近年来, 高分辨率电成像测井被广泛应用于储集层裂缝评价[8, 9, 10], 但当存在泥质夹层或裂缝被低电阻率物质充填时, 电成像测井难以甄别真假裂缝及裂缝的有效性。此外, 电成像测井在微裂缝及裂缝径向延伸情况评价中也面临挑战。斯通利波衰减法是储集层裂缝定量评价的重要方法, 1989年, 李宁通过全波测量实验研究了不同模式波首波的相位关系, 发现斯通利波首波相位与纵波首波相位相同, 而与横波首波相位相反[11]。这为斯通利波首波幅度提取以及进一步的斯通利波裂缝评价奠定了基础。Hornby等基于简化的平板状裂缝模型, 提出了斯通利波裂缝宽度评价方法[12]。Kostek等进一步研究了井眼扩径条件下, 斯通利波反射波对不同宽度裂缝的响应特征[13, 14]。Tang等提出了一种斯通利波波场分离方法, 并分析了储集层渗透率对直达斯通利波衰减幅度的影响[15, 16]。尽管如此, 由于低频斯通利波的激发相对困难, 对斯通利波衰减规律的实验研究还非常有限。

激波管是一种通过激励冲击波来测量管内全直径岩心声学性质的实验装置, 该装置激励的声波频率范围宽（0.5~160.0 kHz）, 测量波形中包含声波测井的主要井孔模式波, 特别是低频斯通利波, 为斯通利波衰减规律研究提供了一种可靠的实验手段[17]。利用激波管装置, Smeulders等研究了部分及完全饱和水岩样的声波特性[18], Fan等研究了饱和水岩心中裂缝对斯通利波的影响[19], 但他们使用的均为人造岩心。Li等首先开展了井下真实碳酸盐岩岩心激波管实验及其理论分析, 研究不同宽度水平裂缝对斯通利波的影响[20]。为了进一步模拟井下真实地层情况, 本文提出了一种改进的激波管实验装置及复杂裂缝模型制作方法, 并通过对不同裂缝条件下斯通利波激波管实验测量, 研究了裂缝宽度、倾角、延伸长度及填充物对斯通利波幅度衰减的影响。

1 实验方法
1.1 实验装置

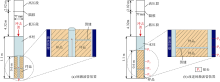
原激波管实验装置如图1a所示, 岩心中间钻孔并置于激波管底部, 通过钻孔中心接收探头的上下移动进行斯通利波测量。这种装置存在两个问题：①当采用真实碳酸盐岩岩心实验时, 中间钻孔难度大, 容易导致岩心破碎; ②钻孔中仅有单个测量探头, 无法对测量数据进行刻度和校正, 误差较大。对此, 本文提出一种改进的激波管实验装置（见图1b）, 在岩心底部安装螺距精度为0.1 mm的螺旋齿轮, 用于精确控制岩心上下移动; 在激波管管壁安装P1、P2、P3和P4共4个固定探头, P2、P3和P4用于测量岩心不同位置斯通利波信号。探头P1与P2间距为30 cm, P2与P3、P3和P4间距均为20 cm。测量过程中, 探头P1始终位于岩心上端管壁, 而探头P2、P3和P4则位于岩心侧面管壁, 因此可利用探头P1的测量信号对探头P2、P3和P4测量的斯通利波进行时间校正和幅度校正, 从而有效改善斯通利波首波信噪比, 提高测量精度。改进装置利用螺旋齿轮实现岩心测量位置的变动, 因此无需在岩心中间钻孔, 实验模型制作方便, 有利于真实岩心斯通利波测量。为了确保实验过程中, 探头P3能够测量到裂缝上、下的斯通利波波形, 将模型高度设定为60 cm, 裂缝中心距模型上端距离设定为40 cm。

图1 激波管实验装置示意图

实验时先往激波管内注水形成高度为1.1 m的水柱, 并在水面上部4.32 m处安装一个PET（polyethlene telephthalate）薄膜（见图1）, 用于封隔上部的高压气段和下部的常压气段。然后静置2~5 d, 待岩心完全饱和水后开始实验测量。测量时, 薄膜下部的通电金属环切割开薄膜, 使高压气段与常压气段瞬时连通, 产生冲击波。该冲击波作用于上部水柱, 产生均匀、稳定的平面波。平面波向下传播, 一部分在岩心上表面发生反射, 另一部分进入岩心与激波管壁之间的环形流体区域（见图1b）, 产生斯通利波。探头P1、P2、P3和P4记录了4个不同位置随时间变化的声压信号。然后旋转底部的螺旋齿轮, 使岩心向上移动5 mm, 更换激波管顶部的薄膜, 重复上述测量过程, 4个探头记录另外4组测量信号。多次移动岩心, 可使模型中的裂缝逐渐经过探头P3, 并获得多组测量信号。岩心向上移动的次数取决于岩心尺寸, 本文所有模型均向上移动15次。另外, 由于测量探头P3可在裂缝的下部、上部获得测量信号, 从而完整记录到斯通利波经过裂缝前后的波形, 因此P3接收波形是本文分析重点。

1.2 裂缝模型制作

1.2.1 不同宽度裂缝模型

叠合法是裂缝模型制作的重要方法, 但利用该方法制作的模型, 支撑物占据裂缝空间比例较大, 支撑物本身对斯通利波测量结果具有较大影响。对此, 本文提出利用点状支撑物制作不同宽度裂缝模型的方法, 若裂缝宽度较小, 选用小球作为支撑物, 小球直径等于裂缝宽度（见图2a）; 若裂缝宽度较大, 则采用中间为圆柱、两端为半球状的支撑物, 通过调整中间圆柱的高度制作具有特定宽度的裂缝模型（见图2b）。当裂缝中间无任何支撑物时, 裂缝处于闭合状态, 裂缝宽度近似为零。本文利用碳酸盐岩全直径岩心制作了宽度分为0, 2, 4, 6, 10, 30 mm的6个不同宽度水平裂缝模型。上述不同宽度裂缝模型制作方法, 不仅能够确保支撑物与裂缝两端面点接触, 最大限度降低支撑物体积及其对实验结果的影响, 而且还能通过合理确定支撑物的数量、位置, 维持模型稳定性及不同位置裂缝宽度的一致性。

图2 利用点状支撑物制作不同宽度裂缝模型

1.2.2 不同倾角裂缝模型

为了定量确定裂缝倾角对斯通利波幅度衰减的影响, 制作了0° 、16° 和70° 的3种不同倾角裂缝模型, 其中0° 、16° 裂缝模型正好利用了被测碳酸盐岩全直径岩心上的两条天然裂缝, 倾角为70° 的裂缝则是在同一岩心上人为加工形成。

对低角度裂缝模型, 利用前述不同宽度裂缝模型制作方法, 选用3个小球作为支撑物, 小球的直径为裂缝宽度。图3a展示了利用被测碳酸盐岩全直径岩心上的一条天然裂缝制作而成的倾角为16° 、宽度为6 mm的低角度裂缝模型。对高角度裂缝模型, 若采用小球作为支撑物则模型难以固定, 为此提出了一种高角度裂缝模型制作方法, 在裂缝中间用两个圆形垫片支撑裂缝, 垫片的厚度等于裂缝宽度, 垫片直径为5 mm。图3b展示了利用被测碳酸盐岩全直径岩心人为加工的倾角为70° 、宽度为6 mm的高角度裂缝模型。

图3 相同宽度不同倾角裂缝模型

1.2.3 不同延伸长度裂缝模型

不同裂缝在地层中的延伸长度存在差异。为了确定裂缝延伸长度对斯通利波幅度衰减的影响, 利用全直径碳酸盐岩岩心制作了裂缝宽度为2 mm, 延伸长度分别为4, 14, 24 mm的3个裂缝模型。图4展示了裂缝宽度为2 mm, 延伸长度为14 mm的裂缝模型。由于本文所述全直径岩心的直径为68 mm, 所以数据分析时可将前述宽度为2 mm水平贯通裂缝模型看作宽度为2 mm、延伸长度为34 mm的裂缝模型。

图4 宽度为2 mm、延伸长度为14 mm裂缝模型

1.2.4 不同填充物裂缝模型

储集层中裂缝往往被泥质、钙质或其他矿物成分不同程度地充填。不同填充物对裂缝有效性影响差异显著, 为了研究裂缝中不同填充情况对斯通利波幅度的衰减特征, 本文利用全直径碳酸盐岩岩心制作了不同填充物裂缝模型, 并开展了激波管实验。

为精确测量填充物对斯通利波幅度的衰减, 需确保不同裂缝模型的基质及其他裂缝参数一致。为此, 提出如下模型制作方法：首先, 制作内径为44 mm、外径为68 mm、宽度为6 mm的环形填充物（见图5a）; 然后, 利用被测碳酸盐岩岩心制作直径为44 mm、宽度为6 mm的圆柱形垫片, 并将其置于环形填充物中心形成组合体; 最后, 将上述组合体嵌入被测碳酸盐岩岩心裂缝中, 形成如图5b所示的特定填充物裂缝模型。本次试验利用Bentheimer砂岩、Felser砂岩和PVC（聚氯乙烯）材料制作了3种不同填充物裂缝模型。为了考查填充物渗透率单因素的影响, 所选的两种砂岩孔隙度均为21%, 但渗透率相差3个数量级, 即Bentheimer砂岩的渗透率为1 001.3× 10-3 µ m2, 而Felser砂岩的渗透率仅为1.802× 10-3 µ m2。

图5 填充裂缝模型

采用上述模型制作方法, 利用全直径碳酸盐岩岩心加工了21组不同参数裂缝模型（见表1）。表1中A1— A6模型代表不同宽度水平裂缝模型, B1— B3模型代表宽度为2 mm不同倾角裂缝模型, C1— C3模型代表宽度为6 mm不同倾角裂缝模型, D1— D5模型代表不同延伸长度裂缝模型, E1— E4模型代表不同填充物裂缝模型。

表1 21组裂缝模型及主要参数
2 数据处理

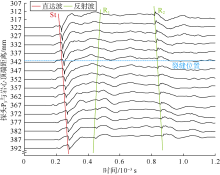
利用图1b改进的激波管实验装置, 对表1中21组碳酸盐岩裂缝模型开展了斯通利波测量。图6展示了探头P3针对模型A4记录的15道波形。所有测量波形均已经过时间校正, 即均以声波首次到达岩心顶端的时间为零时刻。根据到达时间的先后, 从图中可依次观察到斯通利波直达波（St）、斯通利波反射波（R1、R2）。斯通利波反射波R1为直达斯通利波在岩心底端的反射信号, 斯通利波反射波R2为样品顶端反射声波在水层上界面再次反射向下传播形成的斯通利波[20], 本文重点讨论的是直达斯通利波St。

图6 宽度6 mm水平裂缝模型P3探头测量波形

由图6可观察到, 斯通利波经过裂缝之后幅度明显降低。本文将斯通利波幅度定义为斯通利波峰峰值, 即斯通利波波包峰值和谷值的差值。图6中15道波形对应的斯通利波幅度如图7所示。图7中红色虚线左侧区域的数据点为接收探头P3位于裂缝上部（即经过裂缝前）不同位置的斯通利波幅度, 其右侧区域的数据点为接收探头P3位于裂缝下部（即经过裂缝后）不同位置的斯通利波幅度。图7表明, 斯通利波幅度并非到达裂缝才开始衰减, 在到达裂缝之前、经过裂缝之后的一定范围内均存在衰减, 即裂缝对斯通利波的影响并非局限于裂缝所在位置, 而是存在于裂缝附近一段区域内。

图7 不同距离条件下斯通利波幅度衰减变化

为了定量描述斯通利波的衰减规律, 定义斯通利波相对幅度为：

${{R}_{\text{st}}}=\frac{{{A}_{\text{st2}}}}{{{A}_{\text{st1}}}}$ （1）

相对幅度Rst有效消除了岩心基质物性差异等干扰因素, 能更准确地反映裂缝对斯通利波影响的强弱。Rst的数值越接近1, 裂缝对斯通利波的衰减越小; Rst数值越接近0, 裂缝对斯通利波的衰减越大。

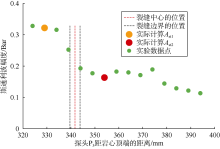
准确确定经过裂缝前后斯通利波的幅度Ast1和Ast2是利用（1）式定量计算斯通利波相对幅度Rst的关键。实验数据分析表明, 对于水平裂缝, 以距裂缝上、下两端面10 mm位置处的斯通利波幅度作为斯通利波经过裂缝前、后的幅度比较合适。图7中, 红色虚线为裂缝中心的位置, 两侧蓝色虚线为裂缝边界的位置, 裂缝左右两侧的橙、红色数据点分别为按上述方法确定的Ast1和Ast2。

对于倾斜裂缝, 仍以距裂缝上端面10 mm处的幅度为斯通利波经过裂缝前的幅度Ast1, 但由于经过裂缝后斯通利波幅度衰减的范围与裂缝倾角有关, 因此不能统一以距裂缝下端面10 mm位置处的幅度作为Ast2。实验数据分析表明, 当Ast2的取值点与裂缝下端面的距离L满足如下关系式时Ast2的计算最为合理：

$L=0.33\theta +10$ （2）

需要指出的是, 若在距裂缝下端面L位置处没有实际测量点, 则选取与该位置最邻近测量点斯通利波幅度值作为Ast2。

3 数据分析
3.1 裂缝宽度的影响

图8展示了不同裂缝宽度下斯通利波相对幅度的变化规律, 由图可见, 随着裂缝宽度的增大, 经过裂缝后斯通利波相对幅度降低, 但降低的速度逐渐减慢。例如, 当裂缝宽度从零增加到10 mm时, 斯通利波相对幅度降低0.648, 即增加单位裂缝宽度（1 mm）相对幅度降低0.064; 当裂缝宽度从10 mm增加到30 mm时, 斯通利波相对幅度降低0.266, 即增加单位裂缝宽度（1 mm）相对幅度降低仅为0.013。

图8 不同裂缝宽度下斯通利波相对幅度变化

实验数据分析表明, 斯通利波相对幅度与裂缝宽度之间满足如下关系：

${{R}_{\text{st}}}={{a}_{1}}{{\text{e}}^{{{b}_{1}}\left( {{w}^{{{n}_{1}}}}+{{w}^{{{n}_{2}}}} \right)}}$ （3）

本实验中常数a1为1.021, b1为-0.143, n1为0.810, n2为0.170。图8中红色实线即（3）式, 可以看出, 实验数据点基本都落在红色曲线上, 说明（3）式准确刻画了裂缝宽度对斯通利波幅度的影响规律。由于（3）式中的指数部分存在两项, 可进一步变形为：

${{R}_{\text{st}}}={{f}_{1}}\left( w \right){{f}_{2}}\left( w \right)$ （4）

（4）式表明, 裂缝宽度对斯通利波的衰减由两部分${{f}_{1}}\left( w \right)$与${{f}_{2}}\left( w \right)$组成。对本文裂缝模型, ${{f}_{1}}\left( w \right)=$ ${{a}_{1}}{{\text{e}}^{-0.143{{w}^{0.81}}}}$, ${{f}_{2}}\left( w \right)={{\text{e}}^{-0.143{{w}^{0.17}}}}$, 它们随裂缝宽度衰减的变化规律分别如图8中绿色、蓝色实线所示。由图8可见, ${{f}_{1}}\left( w \right)$为裂缝对斯通利波影响的主体, 随着裂缝宽度的增加呈指数衰减; ${{f}_{2}}\left( w \right)$为裂缝对斯通利波影响的次要部分, 其值相对较小, 在裂缝宽度逐渐增大过程中其数值趋于稳定。

3.2 裂缝倾角的影响

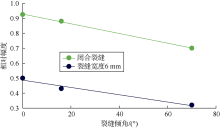
图9展示了闭合裂缝、宽度为6 mm的裂缝分别在0° 、16° 和70° 共3种不同倾角条件下斯通利波经过裂缝后的相对幅度。可以看出, 无论是闭合裂缝还是宽度为6 mm的裂缝, 随倾角的增大, 斯通利波经过裂缝后相对幅度均呈线性降低。这是因为, 随着裂缝倾角增大, 裂缝截面积增大, 斯通利波因裂缝而发生的能量扩散增多, 衰减变强, 相对幅度降低。

图9 不同裂缝倾角条件下斯通利波相对幅度变化

实验数据分析表明, 斯通利波相对幅度与裂缝倾角满足如下线性关系：

${{R}_{\text{st}}}={{a}_{2}}\theta +{{c}_{2}}$ （5）

对本文的全直径碳酸盐岩岩心裂缝模型, 当裂缝自然闭合（宽度为0）时, （5）式中a2为-0.003, c2为0.928; 当裂缝宽度为6 mm时, （5）式中a2为-0.002, c2为0.487。这表明, 当基质相同时, 不同宽度裂缝模型a2的数值非常相近, 即随着裂缝倾角的增大, 相对幅度线性降低的斜率基本相同; c2的数值则与斯通利波经过相同宽度水平裂缝后的相对幅度相同。

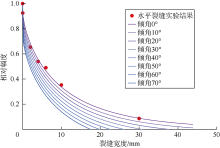
利用（5）式, 可对图8中不同宽度水平裂缝斯通利波相对幅度实验结果进行插值, 进而得到斯通利波经过不同宽度、不同倾角裂缝后的相对幅度。插值结果如图10所示, 图中横坐标为裂缝宽度、纵坐标为斯通利波相对幅度, 不同颜色的曲线代表不同裂缝倾角。

图10 不同宽度、不同倾角裂缝对斯通利波相对幅度的影响

3.3 裂缝延伸长度的影响

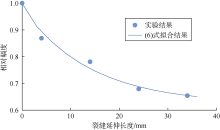
受地层岩性、地应力等因素的影响, 储层中不同裂缝的径向延伸长度存在差异。裂缝延伸长度对斯通利波衰减影响的实验结果如图11所示, 从图中可以看出：①随着裂缝延伸长度的增加, 斯通利波相对幅度降低, 衰减程度增大; ②随着裂缝延伸长度的增加, 斯通利波相对幅度降低的速度逐渐减慢。实验数据分析表明, 斯通利波相对幅度与裂缝延伸长度满足如下定量关系：

${{R}_{\text{st}}}={{a}_{3}}{{\text{e}}^{{{b}_{3}}d}}+{{c}_{3}}$ （6）

图11 不同裂缝延伸长度条件下斯通利波相对幅度变化

由于裂缝延伸长度d为零时, 斯通利波相对幅度Rst为1.0, 因此参数a3、c3不独立, 二者之和为1.0。对本文的不同延伸长度裂缝模型而言, 参数a3为0.364, b3为-0.072, c3为0.636。

3.4 裂缝填充物的影响

为了研究裂缝填充物对斯通利波幅度衰减的影响, 对表1中4种不同填充物裂缝模型开展了斯通利波测量。在上述4个模型中, 模型E1代表裂缝内无固体填充物, 完全被水充填, 这种情况下裂缝渗透率最高; 模型E2、E3分别代表裂缝被渗透率为1 001.305× 10-3 µ m2的Bentheimer砂岩、渗透率为1.802× 10-3 µ m2的Felser砂岩所充填; 模型E4代表裂缝被无孔实心PVC材料充填, 填充物渗透率趋于零。表2给出了4种不同情况下, 斯通利波经过裂缝之后的相对幅度。由表2可见, 随着填充物渗透率的增大, 经过裂缝后斯通利波相对幅度逐渐降低, 衰减逐渐增大。这是因为, 随着填充物渗透率的增大, 斯通利波经过裂缝时产生的能量扩散增加, 裂缝对斯通利波的衰减增大。因此, 在实际地层中, 若裂缝未填充或部分填充, 裂缝渗透率高, 其对斯通利波影响非常显著; 若裂缝被致密物质（如钙质）完全填充, 则其对斯通利波幅度的影响很小。

表2 裂缝不同填充物下斯通利波实验结果
3.5 不同裂缝条件影响强度

实验结果表明, 裂缝宽度和延伸长度增大均会引起斯通利波相对幅度Rst指数降低, 它们之间的定量关系分别满足（3）式和（6）式, （3）式中参数b1体现了裂缝宽度对相对幅度的影响强度, 而（6）式中参数b3体现了裂缝延伸长度对相对幅度的影响强度。实验结果分析表明, 参数b1的绝对值远大于参数b3的绝对值, 因此裂缝宽度对斯通利波的影响比延伸长度更显著。

为了比较裂缝填充物和裂缝延伸长度影响的相对强弱, 假设模型中存在单条裂缝, 当裂缝延伸长度最大且无填充物时, 斯通利波经过裂缝后的相对幅度为Rst。若该裂缝延伸长度变为零或该裂缝被非渗透物质完全填充, 则斯通利波相对幅度均为1。因此, 对该裂缝而言, 延伸长度、填充物可引起的斯通利波相对幅度最大变化量均为（1-Rst）, 二者的影响强度相当。

随着裂缝倾角增加, 斯通利波相对幅度按（5）式线性降低, 且线性降低的斜率（参数a2）不受裂缝宽度的影响。对本文研究的全直径碳酸盐岩岩心而言, 若裂缝倾角从0° 变为90° , 斯通利波相对幅度最大变化量仅为0.27。因此, 相对于其他影响因素而言, 裂缝倾角的影响强度较低。

综合上述分析, 在裂缝宽度、倾角、延伸长度及填充物4种影响因素中, 裂缝宽度对斯通利波相对幅度的影响最大, 其次是裂缝延伸长度和填充物的渗透率, 最后是裂缝倾角。

4 结论

利用改进的激波管装置, 可进行不同裂缝条件全直径岩心斯通利波测量, 并有效改善斯通利波首波信噪比, 提高测量精度。裂缝对斯通利波的影响在斯通利波到达裂缝前、经过裂缝后一定范围内均存在, 利用本文定义的相对幅度能够准确表征斯通利波经过不同裂缝后的衰减。斯通利波相对幅度随裂缝宽度增加呈指数衰减, 裂缝宽度对斯通利波相对幅度的影响可表述为两部分, 其中第1部分是裂缝对斯通利波影响的主体, 第2部分对斯通利波的影响较小。随裂缝倾角的增大, 斯通利波相对幅度线性降低。随裂缝延伸长度增大, 斯通利波相对幅度呈指数衰减。随填充物渗透率的增大, 斯通利波相对幅度逐渐降低。在裂缝宽度、倾角、延伸长度及填充物4种情况中, 裂缝宽度对斯通利波相对幅度的影响最大, 其次是裂缝延伸长度和填充物的渗透率, 最后是裂缝倾角。

致谢：感谢荷兰代尔夫特大学ETIENNE J在激波管实验中提供的帮助。

符号注释：

a1、a2、a3、b1、b3、c2、c3、n1、n2— — 常量, 无因次; Ast1— — 斯通利波经过裂缝之前的幅度, Bar; Ast2— — 斯通利波经过裂缝之后的幅度, Bar; d— — 裂缝延伸长度, mm; f1(w)— — 裂缝对斯通利波影响的主要部分; f2(w)— — 裂缝对斯通利波影响的次要部分; L— — 斯通利波经过裂缝之后的取值点与裂缝下端面的距离, mm; Rst— — 斯通利波相对幅度, 无因次; w— — 裂缝宽度, mm; θ — — 裂缝倾角, (° )。

（编辑 黄昌武）

参考文献
[1] 李宁. 中国海相碳酸盐岩测井解释概论[M]. 北京: 科学出版社, 2013.
LI Ning. Well logging interpretation outline of carbonate reservoir in China[M]. Beijing: Science Press, 2013. [本文引用:1]
[2] 谢芳, 张承森, 刘瑞林, 等. 碳酸盐岩缝洞储集层电成像测井产量预测[J]. 石油勘探与开发, 2018, 45(2): 349-356.
XIE Fang, ZHANG Chengsen, LIU Ruilin, et al. Production prediction for fracture-vug carbonate reservoirs using electric imaging logging data[J]. Petroleum Exploration and Development, 2018, 45(2): 349-356. [本文引用:1]
[3] 王蓓, 刘向君, 司马立强. 四川盆地磨溪地区寒武系龙王庙组缝洞型储集层分级评价及预测[J]. 石油勘探与开发, 2019, 46(2): 290-301.
WANG Bei, LIU Xiangjun, SIMA Liqiang. Grading evaluation and prediction of fracture-cavity reservoirs in Cambrian Longwangmiao Formation of Moxi Area, Sichuan Basin, SW China[J]. Petroleum Exploration and Development, 2019, 46(2): 290-301. [本文引用:1]
[4] 李宁, 王克文, 张宫, 等. 应用CT分析及核磁测井预测碳酸盐岩产气量[J]. 石油勘探与开发, 2015, 42(2): 150-157.
LI Ning, WANG Kewen, ZHANG Gong, et al. Prediction of gas production in carbonates based on CT analysis and nuclear magnetic resonance (NMR) logging[J]. Petroleum Exploration and Development, 2015, 42(2): 150-157. [本文引用:1]
[5] SIBBIT A M, FAIVRE Q. The dual laterolog response in fractured rocks[R]. Dallas, Texas: SPWLA 26th Annual Logging Symposium, 1985. [本文引用:2]
[6] 葛新民, 范宜仁, 李军, 等. 井旁裂缝的双侧向测井物理模拟及特征分析[J]. 地球物理学报, 2019, 62(1): 354-360.
GE Xinmin, FAN Yiren, LI Jun, et al. Experimental studies and investigations on the dual lateral log response of near borehole fractures[J]. Chinese Journal of Geophysics, 2019, 62(1): 354-360. [本文引用:2]
[7] 南泽宇, 李军, 贾丽华, 等. 低阻碳酸盐岩储层双侧向裂缝响应模拟及定量评价[J]. 地球物理学进展, 2014, 29(5): 2224-2230.
NAN Zeyu, LI Jun, JIA Lihua, et al. Simulation and quantitative evaluation of dul-laterolog responces of fracture in low resistivity carbonate reservoir[J]. Progress in Geophysics, 2014, 29(5): 2224-2230. [本文引用:2]
[8] 张兆辉, 杜社宽, 陈华勇, 等. 基于电成像测井的火山岩裂缝分布定量表征: 以准噶尔盆地滴西地区石炭系为例[J]. 石油学报, 2018, 39(10): 1130-1140.
ZHANG Zhaohui, DU Shekuan, CHEN Huayong, et al. Quantitative characterization of volcanic fracture distribution based on electrical imaging logging: A case study of Carboniferous in Dixi Area, Junggar Basin[J]. Acta Petrolei Sinica, 2018, 39(10): 1130-1140. [本文引用:2]
[9] 屈海洲, 张福祥, 王振宇, 等. 基于岩心-电成像测井的裂缝定量表征方法: 以库车坳陷ks2区块白垩系巴什基奇克组砂岩为例[J]. 石油勘探与开发, 2016, 43(3): 425-432.
QU Haizhou, ZHANG Fuxiang, WANG Zhenyu, et al. Quantitative fracture evaluation method based on core-image logging: A case study of Cretaceous Bashijiqike Formation in KS2 well area, Kuqa Depression, Tarim Basin, NW China[J]. Petroleum Exploration and Development, 2016, 43(3): 425-432. [本文引用:2]
[10] 刘瑞林, 谢芳, 肖承文, 等. 基于小波变换图像分割技术的电成像测井资料裂缝、孔洞面孔率提取方法[J]. 地球物理学报, 2017, 60(12): 4945-4955.
LIU Ruilin, XIE Fang, XIAO Chengwen, et al. Extracting fracture-vug plane porosity from electrical imaging logging data using dissection of wavelet-transform-based image[J]. Chinese Journal of Geophysics, 2017, 60(12): 4945-4955. [本文引用:2]
[11] 李宁. 纵、横波首波相位关系实验现象的解释及其对全波测井的意义[J]. 地球物理测井, 1989, 13(4): 14-20.
LI Ning. Interpretation of the experimental phenomena about the P and S head wave phase relations, and its significance to full wave logging[J]. Geophysical Well Logging, 1989, 13(4): 14-20. [本文引用:2]
[12] HORNBY B E, JOHNSON D L, WINKLER K W, et al. Fracture evaluation using reflected Stoneley-wave arrivals[J]. Geophysics, 1989, 54(10): 1274-1288. [本文引用:1]
[13] KOSTEK S, JOHNSAON D L, RANDALL C J. The interaction of tube waves with borehole fractures, Part I: Numerical models[J]. Geophysics, 1998, 63(3): 800-808. [本文引用:1]
[14] KOSTEK S, JOHNSAON D L, WINKELER K W, et al. The interaction of tube waves with borehole fractures, Part II: Analytical models[J]. Geophysics, 1998, 63(3): 809-815. [本文引用:1]
[15] TANG X M, CHENG C H. Quantitative borehole acoustic methods[M]. San Diego: Elsevier, 2004. [本文引用:1]
[16] TANG X M, CHENG C H. Fast inversion of formation permeability from Stoneley wave logs using a simplified Biot Rosenbaum Model[J]. Geophysics, 1996, 61(3): 639-645. [本文引用:1]
[17] CHAO G E, SMEULDERS D M J, VAN DONGEN M E H. Measurement of shock-induced guided and surface acoustic waves along boreholes in poroelastic materials[J]. Journal of Applied Physics, 2006, 99(9): 094904-1-094904-6. [本文引用:1]
[18] SMEULDERS D M J, VAN DONGEN M E H. Wave propagation in porous media containing a dilute gas-liquid mixture: Theory and experiments[J]. Journal of Fluid Mechanism, 1997, 343: 351-373. [本文引用:1]
[19] FAN H J, SMEULDERS D M J. Shock-induced borehole waves and fracture effects[J]. Transport in Porous Media, 2012, 93(2): 263-270. [本文引用:1]
[20] LI Ning, WANG Kewen, WU Hongliang, et al. Shock-induced Stoneley waves in carbonate rock samples[J]. Geophysics, 2019, 84(5): D2009-D2016. [本文引用:2]