引用本文
刘静, 夏军勇, 刘玺, 吴飞鹏, 蒲春生. 人工地震波强化泡沫稳定性微观动力学模型[J]. 石油勘探与开发, 2021,48(1): 185-192.
LIU Jing, XIA Junyong, LIU Xi, WU Feipeng, PU Chunsheng. A micro-kinetic model of enhanced foam stability under artificial seismic wave[J]. Petroleum Exploration & Development, 2021,48(1): 185-192.  
Doi: 10.11698/PED.2021.01.17
Permissions
Copyright©2021, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
人工地震波强化泡沫稳定性微观动力学模型
刘静1,2, 夏军勇1,3, 刘玺4, 吴飞鹏1,2, 蒲春生1,2
1.中国石油大学（华东）石油工程学院,山东青岛 266580
2.中国石油大学（华东）非常规油气开发教育部重点实验室,山东青岛 266580
3.大庆油田采油工程研究院,黑龙江大庆 163453
4.陕西延长油田股份有限公司志丹采油厂,陕西延安 717500

第一作者简介：刘静（1982-）,女,河南商丘人,博士,中国石油大学（华东）讲师,主要从事非常规油气物理化学强化开采理论与技术方面的研究工作。地址：山东省青岛市黄岛区长江西路66号,中国石油大学（华东）石油工程学院,邮政编码：266580。E-mail: liujing4522009@163.com

收稿日期: 2020-04-13 修回日期: 2020-10-20
基金项目: 国家自然科学基金（51904320,51874339）; 中央高校基本科研业务费专项资金（18CX02095A）
摘要

针对低频人工地震波对泡沫稳定性的协同强化效应,基于垂直液膜排液模型和波动理论,建立了低频人工地震波激励下泡沫稳定性微观动力学模型;采用高阶偏微分方程组无因次变换、隐式和显式差分方法对该模型进行复合求解并验证了模型的可靠性,对低频人工地震波作用下的泡沫液膜厚度、表面活性剂浓度分布及排液速度等进行了定量化分析。研究表明,低频振动可降低排液后期泡沫液膜中表面活性剂浓度最大值与最小值之差,强化Marangoni效应的作用效果,提高了泡沫液膜的稳定性。当振动频率接近泡沫液膜固有频率时振动效果最佳,最佳振动频率约为50 Hz。振动加速度越大,泡沫液膜中表面活性剂浓度的恢复速度越快,Marangoni效应延缓泡沫液膜排液的能力越强,稳泡性能越好,但振动加速度并非越大越好,最佳振动加速度约为0.5倍重力加速度。合理的振动参数会大幅提高Marangoni效应的作用效果,表面活性剂初始浓度越小,振动提高Marangoni效应效果越好。图11表2参19

关键词: 人工地震波; 泡沫稳定性; 液膜排液; 波动理论; 动力学模型; 振动参数
中图分类号:TE357 文献标志码:A
A micro-kinetic model of enhanced foam stability under artificial seismic wave
LIU Jing1,2, XIA Junyong1,3, LIU Xi4, WU Feipeng1,2, PU Chunsheng1,2
1. School of Petroleum Engineering, China University of Petroleum, Qingdao 266580, China
2. Key Laboratory of Unconventional Oil & Gas Development, China University of Petroleum, Qingdao 266580, China
3. Daqing Oilfield Production Technology Institute, Daqing 163453, China
4. Zhidan Oil Production Plant, Shaanxi Yanchang Petroleum (Group) Co., LTD, Yan’an 717500, China
Abstract

To get a deeper understanding on the synergistic enhancement effect of low frequency artificial seismic wave on foam stability, a micro-kinetic model of enhanced foam stability under low frequency artificial seismic wave is established based on a vertical liquid film drainage model and elastic wave theory. The model is solved by non-dimensional transformation of the high order partial differential equations and a compound solution of implicit and explicit differences and is verified to be accurate. The foam film thickness, surfactant concentration distribution and drainage velocity under the action of low frequency artificial seismic wave are quantitatively analyzed. The research shows that low-frequency vibration can reduce the difference between the maximum and minimum concentrations of surfactant in the foam liquid film at the later stage of drainage, enhance the effect of Marangoni effect, and improve the stability of the foam liquid film. When the vibration frequency is close to the natural frequency of the foam liquid film, the vibration effect is the best, and the best vibration frequency is about 50 Hz. The higher the vibration acceleration, the faster the recovery rate of surfactant concentration in the foam liquid film is. The higher the vibration acceleration, the stronger the ability of Marangoni effect to delay the drainage of foam liquid film and the better the foam stability is. It is not the higher the vibration acceleration, the better. The best vibration acceleration is about 0.5 times of gravity acceleration. Reasonable vibration parameters would greatly enhance the effect of Marangoni effect. The smaller the initial concentration of surfactant, the better the vibration works in enhancing Marangoni effect.

Keyword: artificial seismic wave; foam stability; liquid film drainage; wave theory; kinetic model; optimum vibration parameters
0 引言

泡沫调驱技术是裂缝性低渗透油藏水窜调控和提高采收率的有效途径, 泡沫的稳定性及见效时间是影响其施工效果的重要因素[1, 2]。因此, 提高泡沫在油藏深部的稳定性是改善泡沫调驱效果的关键[3]。目前主要通过化学剂复配、合成、添加剂使用等降低表面张力、改变界面层结构、增强扩张黏弹性等相关实验及机理分析研究泡沫稳定性[4, 5, 6, 7]。Marangoni效应是指表面活性剂在液膜上不均匀分布所产生的表面张力梯度使表面活性剂分子自高浓度区域向低浓度区域流动的现象, 是影响泡沫稳定性的内在机理之一。Schwartz等[8]、Mysels等[9]建立了垂直液膜及多尺度液膜的排液及演化模型, 其中以两端固定的垂直液膜排液模型为代表的泡沫排液过程简化模型较好地模拟了垂直液膜排液的全过程, 并解释了Marangoni 现象。随着研究的深入, 叶学民等[10, 11]、杨少东等[12]在垂直液膜排液模型的基础上研究了活性剂浓度、分离压及表面黏度变化对垂直液膜排液过程的影响规律, 揭示了泡沫排液过程中的Marangoni效应、泡沫衰变演化规律与控制因素。

低频人工地震波复合泡沫驱技术是利用低频地震波对泡沫进行动态物理干预, 提高泡沫在油藏深部稳定性的新方法。该复合技术曾在鄂尔多斯盆地开展了单井组矿场试验, 并取得了显著效果[13, 14], 后续相关研究也表明低频振动确实可延长不同孔隙介质中泡沫的半衰期, 降低泡沫Plateau边界流体的渗流速度[15]。然而, 低频人工地震波激励下的泡沫排液演化过程、稳定性微观动力学机制与作用特征尚待深入研究。鉴于此, 本文将低频人工地震波扰动作用力引入垂直液膜排液模型[16], 建立了低频波激励下泡沫垂直液膜排液演化模型, 探索了低频波对垂直液膜排液过程中Marangoni效应的强化作用以及降低液膜排液速度的影响规律。

1 模型建立

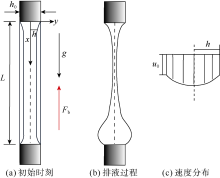
泡沫液膜由金属线框形成, 侧面平视如图1所示, 为了使模型简化, 提出如下假设：①泡沫为垂直泡沫液膜; ②表面活性剂溶液为不可压缩流体, 且流体的密度与黏度为定值; ③忽略液膜排液过程中表面活性剂溶液的蒸发现象; ④泡沫液膜的顶部与底部都被固定在金属线框上, 满足泡沫液膜无滑移的边界条件; ⑤泡沫液膜的厚度关于y=0对称, 并且满足$y=\pm h\left( x, t \right)$, 所以仅考虑y≥ 0时泡沫液膜的变化; ⑥泡沫液膜的初始厚度（h0）与泡沫液膜特征长度（L）的比值很小, 即$\varepsilon ={{h}_{0}}/L$远远小于1, 保证其适用润滑理论[17]; ⑦波动力为正弦作用力且假设波动力的初始方向与重力方向相反, 文中引入波动力的表达式为$\rho a{{\text{e}}^{-\alpha \kappa t}}\sin \left( 2\text{ }\!\!\pi\!\!\text{ }ft \right)$。

图1 低频波作用下垂直液膜排液过程示意图

1.1 低频波作用下的控制方程

根据质量守恒方程和动量守恒方程, 将低频波产生的作用力引入运动方程, 得到低频波激励下液膜中流体流动的连续方程和运动方程为：

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$ （1）

$-\frac{\partial p}{\partial x}+\mu \left( \frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{y}^{2}}} \right)+\rho g-\rho a{{\text{e}}^{-\alpha \kappa t}}\sin \left( 2\text{ }\!\!\pi\!\!\text{ }ft \right)=0$ （2）

$-\frac{\partial p}{\partial y}+\mu \left( \frac{{{\partial }^{2}}v}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}v}{\partial {{y}^{2}}} \right)=0$ （3）

边界条件如下：

当y=0时,

$\left\{ \begin{align} & v=0 \\ & \frac{\partial u}{\partial y}=0 \\ \end{align} \right.$ （4）

当y=h时,

$\frac{\partial h}{\partial t}=v-u\frac{\partial h}{\partial x}$ （5）

当y=h时, 液膜所受切向应力和表面压力分别为：

$\tau \left( x, t \right)=\mu \left[ 1-{{\left( \frac{\partial h}{\partial x} \right)}^{2}} \right]\left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \right)+$$2\mu \frac{\partial h}{\partial x}\left( \frac{\partial v}{\partial y}-\frac{\partial u}{\partial x} \right)$ （6）

${{p}_{\text{S}}}=p-\frac{2\mu }{1+{{\left( \frac{\partial h}{\partial x} \right)}^{2}}}\left[ {{\left( \frac{\partial h}{\partial x} \right)}^{2}}\frac{\partial u}{\partial x}- \right.$$\left. \frac{\partial h}{\partial x}\left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \right)+\frac{\partial v}{\partial y} \right]$ （7）

x方向上泡沫液膜排液速度可以分解为滑移速度和剪切速度[8], 即：

$u={{u}_{0}}\left( x, t \right)+{{u}_{1}}\left( x, y, t \right)$ （8）

（7）式中液膜表面压力由毛管压力和分离压组成, 即：

${{p}_{\text{S}}}=-\sigma \lambda -{{p}_{\text{se}}}\approx -\sigma \frac{{{\partial }^{2}}h}{\partial {{x}^{2}}}-{{p}_{\text{se}}}$ （9）

分离压的计算模型采用双项分离压模型[11], 表达式为：

${{p}_{\text{se}}}=A\left[ {{\left( \frac{{{h}_{\text{eq}}}}{h} \right)}^{4}}-{{\left( \frac{{{h}_{\text{eq}}}}{h} \right)}^{3}} \right]$ （10）

表面活性剂溶液的表面张力随表面活性剂浓度的变化关系为：

$\sigma ={{\sigma }_{0}}-K\left( {{C}_{\text{S}}}-{{C}_{\text{S}}}_{0} \right)$ （11）

在泡沫液膜表面, 剪切应力可简单近似等于泡沫液膜的表面张力梯度, 即：

$\tau \approx \frac{\partial \sigma }{\partial x}=-K\frac{\partial {{C}_{\text{S}}}}{\partial x}$ （12）

由于Marangoni现象的存在, 在确定滑移速度${{u}_{0}}$时需要考虑表面活性剂浓度变化对滑移速度的影响。表面活性剂的对流-扩散演化方程为：

$\frac{\partial {{C}_{\text{S}}}}{\partial t}=-\frac{\partial \left( {{u}_{0}}{{C}_{\text{S}}} \right)}{\partial x}+D\frac{{{\partial }^{2}}{{C}_{\text{S}}}}{\partial {{x}^{2}}}$ （13）

1.2 无因次化方程推导

定义一组特征项：

$\begin{align} & {{p}_{\text{f}}}=\frac{\mu {{U}_{0}}}{L}\ \ \ \ \text{ }T=\frac{3\mu {{L}^{4}}}{{{\sigma }_{0}}{{h}_{0}}^{3}}\ \ \ \ \ \ \ \ \ \\ & {{U}_{0}}=\frac{{{\sigma }_{0}}{{h}_{0}}^{3}}{3\mu {{L}^{3}}}\ \ \ \text{ }{{U}_{1}}={{\varepsilon }^{2}}{{U}_{0}}\ \ \ \ \text{ }V=\varepsilon {{U}_{0}} \\ \end{align}$

对前文变量进行无因次化：

$\begin{align} & {{A}_{\text{D}}}=\frac{A}{{{\varepsilon }^{2}}{{{\sigma }_{0}}}/{{{h}_{0}}}\; }\ \ \ \ {{C}_{\text{SD}}}=\frac{K{{C}_{\text{S}}}}{{{\sigma }_{0}}{{\varepsilon }^{2}}}\ \ \text{ }\ \ {{D}_{\text{D}}}=\frac{DT}{{{L}^{2}}}\text{ }{{f}_{\text{D}}}=Tf \\ & \ {{h}_{\text{D}}}=\frac{h}{\varepsilon L}\ \ \ \text{ }\ {{p}_{\text{D}}}=\frac{p}{{{p}_{\text{f}}}}\ \ \ \text{ }\ {{p}_{\text{SD}}}=\frac{{{p}_{\text{S}}}}{{{p}_{\text{f}}}} \\ \end{align}$${{p}_{\text{seD}}}=\text{ }{{A}_{\text{D}}}\left[ {{\left( \frac{{{h}_{\text{eq}}}}{h} \right)}^{4}}-{{\left( \frac{{{h}_{\text{eq}}}}{h} \right)}^{3}} \right]\ \ \ \ \text{ }{{t}_{\text{D}}}=\frac{t}{T}\ \ $$\begin{align} & {{u}_{0}}_{\text{D}}=\frac{{{u}_{0}}}{{{U}_{0}}}\text{ }{{u}_{1}}_{\text{D}}=\frac{{{u}_{1}}}{{{U}_{1}}}\text{ }{{v}_{\text{D}}}=\frac{v}{V} \\ & {{x}_{\text{D}}}=\frac{x}{L}\text{ }{{y}_{\text{D}}}=\frac{y}{\varepsilon L}\text{ }\ \ \ \ \ {{\tau }_{\text{D}}}=\frac{\tau }{\varepsilon \mu \frac{{{U}_{0}}}{L}} \\ \end{align}$

将特征项和无因次变量代入（1）— （8）式得无因次切应力方程：

${{\tau }_{\text{D}}}\left( {{x}_{\text{D}}}, {{t}_{\text{D}}} \right)=-4\frac{\partial \left( {{h}_{\text{D}}}\frac{\partial {{u}_{0\text{D}}}}{\partial {{x}_{\text{D}}}} \right)}{\partial {{x}_{\text{D}}}}-{{h}_{\text{D}}}\left( -\frac{\partial {{p}_{\text{SD}}}}{\partial {{x}_{\text{D}}}}+\frac{\rho {{L}^{2}}g}{\mu {{U}_{0}}} \right)+$ ${{h}_{\text{D}}}\frac{\rho {{L}^{2}}}{\mu {{U}_{0}}}a{{\text{e}}^{-\alpha \kappa {{t}_{\text{D}}}}}\sin \left( 2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{D}}}{{t}_{\text{D}}} \right)$ （14）

结合润滑理论和质量守恒积分表达式可得无因次液膜厚度方程为：

$\frac{\partial {{h}_{\text{D}}}}{\partial {{t}_{\text{D}}}}=-\frac{\partial \left( {{Q}_{0\text{D}}}+{{\varepsilon }^{2}}{{Q}_{1\text{D}}} \right)}{\partial {{x}_{\text{D}}}}$ （15）

无因次排液量方程为：

${{Q}_{0\text{D}}}={{u}_{0\text{D}}}{{h}_{\text{D}}}$ （16）

${{Q}_{1\text{D}}}=\int_{0}^{{{h}_{\text{D}}}}{{{u}_{\text{1D}}}^{\left( 0 \right)}\text{d}{{y}_{\text{D}}}}=\frac{h_{\text{D}}^{3}}{3}\left[ 3\frac{{{\partial }^{2}}{{u}_{0\text{D}}}}{\partial x_{\text{D}}^{2}}-\frac{\partial {{p}_{\text{SD}}}}{\partial {{x}_{\text{D}}}}+\frac{\rho {{L}^{2}}g}{\mu {{U}_{0}}} \right]-$ $\frac{h_{\text{D}}^{3}}{3}\frac{\rho {{L}^{2}}a}{\mu {{U}_{0}}}{{\text{e}}^{-\alpha \kappa {{t}_{\text{D}}}}}\sin \left( 2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{D}}}{{t}_{\text{D}}} \right)$ （17）

将（11）、（12）式无因次化后与（14）式联立求解得无因次方程式：

$\frac{\partial \left( {{h}_{\text{D}}}\frac{\partial {{u}_{\text{0D}}}}{\partial {{x}_{\text{D}}}} \right)}{\partial {{x}_{\text{D}}}}=\frac{3}{4{{\varepsilon }^{2}}}\left[ \frac{\partial {{C}_{\text{SD}}}}{\partial {{x}_{\text{D}}}}-{{h}_{\text{D}}}\left( \frac{\rho {{L}^{2}}g}{{{\sigma }_{0}}\varepsilon }+\frac{{{\partial }^{3}}{{h}_{\text{D}}}}{\partial x_{\text{D}}^{3}}+{{A}_{\text{D}}}\frac{\partial {{p}_{\text{seD}}}}{\partial {{x}_{\text{D}}}} \right) \right]+$ $\frac{3}{4{{\varepsilon }^{2}}}\left\{ {{h}_{\text{D}}}\left[ \frac{\rho {{L}^{2}}}{{{\sigma }_{0}}\varepsilon }a{{\text{e}}^{-\alpha \kappa {{t}_{\text{D}}}}}\sin \left( 2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{D}}}{{t}_{\text{D}}} \right) \right] \right\}$ （18）

将（9）、（10）式无因次化后与（16）、（17）式一起代入（15）式得到无因次方程式：

$\frac{\partial {{h}_{\text{D}}}}{\partial {{t}_{\text{D}}}}=-\frac{\partial \left[ {{u}_{\text{0D}}}{{h}_{\text{D}}}+h_{\text{D}}^{3}\left( \frac{\rho {{L}^{2}}g}{{{\sigma }_{0}}\varepsilon }+\frac{{{\partial }^{3}}{{h}_{\text{D}}}}{\partial x_{\text{D}}^{3}}+{{A}_{\text{D}}}\frac{\partial {{p}_{\text{seD}}}}{\partial {{x}_{\text{D}}}} \right) \right]}{\partial {{x}_{\text{D}}}}+$ $\frac{\partial \left\{ h_{\text{D}}^{3}\left[ \frac{\rho {{L}^{2}}}{{{\sigma }_{0}}\varepsilon }a{{\text{e}}^{-\alpha \kappa {{t}_{\text{D}}}}}\sin \left( 2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{D}}}{{t}_{\text{D}}} \right) \right] \right\}}{\partial {{x}_{\text{D}}}}$ （19）

将（13）式无因次化得：

$\frac{\partial {{C}_{\text{SD}}}}{\partial {{t}_{\text{D}}}}=-\frac{\partial \left( {{u}_{\text{0D}}}{{C}_{\text{SD}}} \right)}{\partial {{x}_{\text{D}}}}+{{D}_{\text{D}}}\frac{{{\partial }^{2}}\left( {{u}_{\text{0D}}}{{C}_{\text{SD}}} \right)}{\partial x_{\text{D}}^{2}}$ （20）

（18）— （20）式即为低频人工地震波作用下表示液膜表面活性剂浓度、液膜厚度、排液速度演化的主控方程。

1.3 方程边界、初始条件

假设液膜上端和液膜下端的厚度为定值, 即：

${{h}_{\text{D}}}\left( 0, {{t}_{\text{D}}} \right)={{h}_{\text{D}}}\left( 1, {{t}_{\text{D}}} \right)=1$ （21）

顶部和底部流体、表面活性剂不流动, 即：

${{u}_{\text{0D}}}\left( 0, {{t}_{\text{D}}} \right)={{u}_{\text{0D}}}\left( 1, {{t}_{\text{D}}} \right)=\frac{\partial {{C}_{\text{SD}}}\left( 0, {{t}_{\text{D}}} \right)}{\partial {{x}_{\text{D}}}}=$$\frac{\partial {{C}_{\text{SD}}}\left( 1, {{t}_{\text{D}}} \right)}{\partial {{x}_{\text{D}}}}=0$ （22）

泡沫液膜的无因次初始厚度为：

${{h}_{\text{D}}}\left( {{x}_{\text{D}}}, 0 \right)=\frac{1}{\text{ }\!\!\pi\!\!\text{ }}\left[ \arctan \left( \frac{{{x}_{\text{D}}}-1}{0.01} \right) \right.-$$\left. \frac{1}{\text{ }\!\!\pi\!\!\text{ }}\arctan \left( \frac{{{x}_{\text{D}}}}{0.01} \right) \right]+1.5$ （23）

泡沫液膜中无因次表面活性剂初始浓度为：

${{C}_{\text{SD}}}\left( {{x}_{\text{D}}}, 0 \right)={{C}_{\text{S0D}}}=500$ （24）

2 模型求解与验证
2.1 模型求解

将主控方程（18）— （20）式、边界条件方程（21）— （22）式、初始条件方程（23）— （24）式写成差分格式。为计算方便, 将泡沫液膜的厚度和泡沫液膜中表面活性剂的浓度取整点差分, 泡沫液膜的排液速度取半点差分, 采用隐式和显式结合进行差分求解。在求解过程中, 根据流动尺度选取0< xD< 1内的一维区域进行计算, 在保证满足精确度和缩短计算时间的条件下, 将计算区域划分为100等份进行计算, 可得无因次模拟结果。

2.2 模型验证

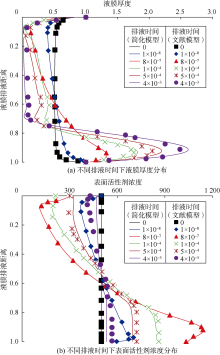
为了验证本模型求解结果的准确性, 将本模型（18）— （20）式中加速度设为0（波动力为0）, 得到波动条件的简化模型（简称简化模型）, 参照文献模型中的基础参数取值（见表1）, 分别计算简化模型中不同无因次排液时间条件下无因次液膜表面活性剂浓度、无因次液膜厚度与无因次液膜排液距离（为表述方便, 后面将省略“ 无因次” , 如无特别说明, 文中、图中所涉及物理量均为无因次量）间的关系曲线并分别与文献[8, 11]中模型（简称文献模型）的计算结果进行对比（见图2）, 由图2可知, 两种模型计算所得液膜表面活性剂浓度和液膜厚度具有一致的分布规律, 进而验证了模型的正确性。

表1 模型对比计算基础参数表

图2 本文简化模型与文献模型解对比

3 Marangoni效应影响因素
3.1 振动频率的影响

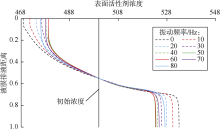
根据叶学民等[11]的研究成果可知, 液膜排液过程中液膜顶部形成半月形区, 底部因液体累积形成不断膨胀的球形凸起, 中间部分为液膜曲率较小、形状近乎直线的区域。随着排液时间的增加, 在半月形区域末端液膜厚度出现最小值, 且当液膜排液时间tD=4× 10-3时, 中间部分有较长区域液膜厚度与最小液膜厚度非常接近, 这与实验中的黑膜区域相对应, 因此将与最小液膜厚度非常接近的区域称为“ 黑膜” , 且此时Marangoni效应最强。因此, 当tD=4× 10-3时泡沫液膜排液达到排液后期阶段。设置振动加速度为0.5倍重力加速度, 计算不同振动频率下泡沫液膜中表面活性剂的浓度分布（见图3）。由图3可知, 泡沫液膜中表面活性剂浓度自上而下呈现逐渐增加的趋势。无振动时, 泡沫液膜中表面活性剂浓度最大值与最小值之差为64; 有振动后, 表面活性剂浓度最大值与最小值之差明显降低, 且该差值随着振动频率的增加呈现先降低后增加的趋势, 当振动频率为50 Hz和60 Hz时最大值与最小值之差达到最小（约为44）, 比无振动时降低了31.3%。当振动频率与物体固有频率接近时, 物体易产生共振效应, 振动效果最佳[18, 19], 由前述分析可知50 Hz和60 Hz与泡沫液膜的固有频率较为接近。

图3 不同振动频率下表面活性剂浓度分布

图4为无振动和振动频率为50 Hz时, 不同时间泡沫液膜中表面活性剂的浓度分布（图中tD=8× 10-7与tD=1× 10-8时无振动和有振动数据线重合）。无论有、无振动, 当0< tD≤ 8× 10-7时, 随着时间增加, 液膜上部区域表面活性剂浓度逐渐降低, 底部表面活性剂浓度逐渐增加; 当1× 10-4≤ tD≤ 4× 10-3时, 随着时间增加泡沫液膜上部表面活性剂浓度增加、下部液膜表面活性剂浓度逐渐降低。这表明从tD=1× 10-4时刻开始表面活性剂分子在Marangoni效应作用下逆流而上, 使表面活性剂浓度最大值与最小值之差逐渐降低, 同时Marangoni效应的存在迟滞了泡沫液膜的排液速度, 泡沫液膜稳定性得到提高。当tD=4× 10-3时, 泡沫液膜排液趋于稳定, 表面活性剂浓度最大值与最小值之差达到最小。

图4 有振动与无振动条件下表面活性剂浓度分布

对比振动频率为50 Hz和无振动两种情况下的整个排液过程发现：早期tD=1× 10-8与tD=8× 10-7两种情况下的表面活性剂分布曲线重合, 说明在泡沫排液早期低频波动对排液没有影响; 随着排液的进行, Marangoni效应从tD=1× 10-4时出现, 此时低频振动对液膜中Marangoni效应的影响开始显现; 当tD=4× 10-3时, 低频振动对Marangoni效应的影响达到最大, 泡沫液膜中表面活性剂浓度最大值与最小值之差最小。低频振动有利于排液后期泡沫液膜中表面活性剂浓度的恢复, 进而强化Marangoni效应, 提高泡沫液膜的稳定性。

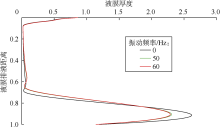
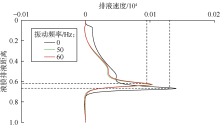
图5、图6分别为无振动、振动频率为50 Hz和60 Hz, tD=4× 10-3时不同位置液膜厚度和液膜排液速度分布。可以看出, 当tD=4× 10-3时, 与无振动相比, 振动能显著降低液膜排液速度和液膜底部因液体积累而形成的凸起半径; 振动频率为50、60 Hz时液膜排液速度和底部凸起半径基本相同, 进一步说明低频振动可改变液膜厚度分布, 减缓排液速度, 提高泡沫稳定性, 这与前期实验和理论研究结果一致[15], 进一步证实模型是可靠的。

图5 不同振动频率下液膜厚度分布

图6 不同振动频率下液膜排液速度分布

由于液膜初始厚度相同, 与无振动相比, 振动时液膜底部形成的凸起半径较小, 因此在排液方向上, 当0.65< xD< 0.80时, 振动时泡沫液膜厚度更大, 最小厚度液膜的长度更短。这主要是因为振动延缓了液膜的排液速度, 相同时间内泡沫液膜的厚度变化小, 达到与无振动相同的最小液膜厚度对应的长度需要更长时间, 即振动提高了泡沫的稳定性。由图6还可看到, 与无振动相比, 有振动时液膜排液速度最大值对应的排液位置靠上, 这是因为出现最大液膜排液速度的位置与最小液膜厚度结束时的位置相对应。

当振动频率为50 Hz与60 Hz时, 泡沫液膜中表面活性剂浓度、液膜厚度和排液速度相差不大, 结合现场的实际情况, 选择50 Hz作为最佳振动频率。

3.2 振动加速度的影响

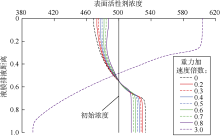
在最佳振动频率下, 改变振动加速度, 结合表1中的参数取值, 计算tD=4× 10-3时, 不同振动加速度下泡沫液膜中表面活性剂的浓度分布（见图7）。可以看到：振动加速度小于等于0.8倍重力加速度时, 泡沫液膜中表面活性剂浓度自上而下逐渐步增加, 达到一定值后保持不变; 活性剂浓度最大值与最小值之差随振动加速度的增加而降低, 且均小于无振动时的差值, 说明振动加速度越大越能提高泡沫液膜中表面活性剂浓度的恢复速度, Marangoni效应延缓泡沫液膜排液的能力就越强, 稳泡性能越好; 当振动加速度等于3.0倍重力加速度时, 泡沫液膜顶部的表面活性剂浓度远远大于液膜底部, 表现为表面活性剂逆流而上在液膜顶部聚集, 这与液膜向下排液的事实相悖。表面活性剂在Marangoni效应的作用下发生逆向扩散, 在一定程度上能恢复液膜局部表面活性剂浓度, 延缓液膜排液的速度, 但Marangoni效应的作用能力有限, 只能延缓液膜排液, 并不能逆转排液流动方向。因此, 振动加速度并非越大越好。

图7 不同振动加速度下液膜中表面活性剂浓度分布

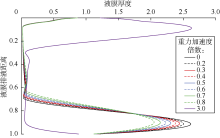
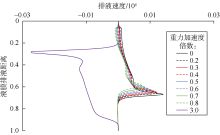
图8、图9分别为tD=4× 10-3时, 不同振动加速度下液膜厚度、排液速度的分布。由图可知, 当振动加速度小于0.8倍重力加速度时, 因液膜排液累积而形成的凸起半径、液膜排液速度随振动加速度的增加而降低; 当振动加速度等于3.0倍重力加速度时, 泡沫液膜的排液方向向上, 且最大液膜排液速度约为无振动时的2倍, 这导致泡沫液膜逆向积累在液膜顶部形成凸起, 这明显与事实不符。

图8 不同振动加速度下液膜厚度分布

图9 不同振动加速度下液膜排液速度分布

振动加速度、振动频率和振动位移满足：

$a={{f}^{2}}z$ （25）

可见对于同一台振动设备而言, 其振动位移的范围是确定的, 最佳振动频率确定后, 最大振动加速度也随之确定。李星红等[14]研究表明, 振动加速度过大或过小均对起泡效果有抑制作用, 结合本文的认识, 最佳振动加速度可取0.5倍重力加速度。

3.3 表面活性剂初始浓度的影响

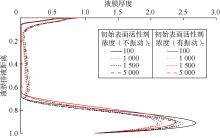
在最佳振动参数下, 改变表面活性剂初始浓度分别为100, 1 000, 1 500和5 000, 计算排液时间为tD=4× 10-3时不同初始表面活性剂浓度下液膜厚度分布（见图10）。可以看到, 在相同条件下, 液膜底部凸起半径随着初始表面活性剂浓度的增大而降低, 这是因为当液膜中表面活性剂浓度较低时, 活性剂浓度差相对较小, Marangoni效应相对较弱, 难以长久保持液膜稳定存在; 当表面活性剂初始浓度不断增加时, 液膜中活性剂浓度差相应增大, Marangoni效应逐渐增强, 表面活性剂初始浓度高的液膜底部形成的凸起半径相对较小。

图10 不同初始浓度条件下两种排液方式的液膜厚度分布

此外, 当表面活性剂初始浓度不同时, 在相同的振动参数下, 振动对液膜底部凸起半径的影响程度也不相同（见表2）, 随着液膜中表面活性剂初始浓度的增加, 振动与无振动对应的液膜底部凸起半径之差逐渐降低, 说明表面活性剂初始浓度越小, 振动效果越好。这是因为表面活性剂初始浓度较低时, 液膜中Marangoni效应相对较弱, 对延缓液膜排液速度的能力有限, 振动会大幅提高Marangoni效应的作用效果。

表2 不同初始浓度下两种排液方式底部凸起参数统计

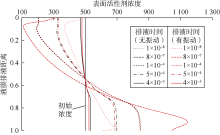
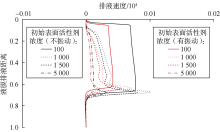
改变不同初始表面活性剂浓度参数, 计算排液时间为tD=4× 10-3时不同初始活性剂浓度下液膜的排液速度分布（见图11）。可以看出, 无振动时液膜的排液速度随液膜中表面活性剂初始浓度的增加而降低; 相同表面活性剂初始浓度下, 无振动与有振动时液膜的排液速度的差值随表面活性剂初始浓度的增加而降低, 说明表面活性剂初始浓度越小振动效果越好。

图11 不同初始浓度条件下两种排液方式的排液速度分布

图中还可看到, 在无振动情况下, xD约为0.65处, 表面活性剂初始浓度为1 000时的最大液膜排液速度比初始浓度为100时大, 该现象较为反常。分析认为表面活性剂初始浓度为100的液膜率先达到“ 黑膜” 阶段, 该阶段液膜排液速度很小; 表面活性剂初始浓度为1 000的液膜厚度相对较厚, 且最大速度出现在液膜下端凸起附近, 与液膜重力相比, 此时Marangoni效应的影响较小, 因而液膜排液速度较大; 表面活性剂初始浓度为1 500的液膜排液速度最大值与初始浓度为100的液膜基本相同, 说明该浓度下Marangoni效应逐渐增强, 液膜排液速度降低; 表面活性剂初始浓度进一步增大为5 000, Marangoni效应进一步增强, 液膜排液速度大幅降低。

4 结论

低频振动可降低排液后期泡沫液膜中表面活性剂浓度最大值与最小值之差, 强化Marangoni效应的作用效果, 提高泡沫液膜的稳定性; 当振动频率接近泡沫液膜固有频率时振动效果最佳, 最佳振动频率约为50 Hz。

振动加速度越大, 泡沫液膜中表面活性剂浓度的恢复速度越快, Marangoni效应延缓泡沫液膜排液的能力越强, 稳泡性能越好; 但振动加速度并非越大越好, 最佳振动加速度约为0.5倍重力加速度。

合理的振动参数会大幅提高Marangoni效应的作用效果, 表面活性剂初始浓度越小, 振动提高Marangoni效应的效果越好。

符号注释：

a— — 振动加速度, m/s2; A— — 分离压强度系数, Pa; AD— — 无因次分离压强度系数; BD— — 无量纲修正邦德数, 表示重力和毛细管力之比; CD— — 无量纲毛细管数; CS— — 表面活性剂浓度, mol/L; CS0— — 初始表面活性剂浓度, mol/L; CSD— — 无因次表面活性剂浓度; CS0D— — 无量纲初始表面活性剂浓度; ${{C}_{\text{SD}}}\left( 0, {{t}_{\text{D}}} \right)$— — 液膜上端无因次表面活性剂浓度; ${{C}_{\text{SD}}}\left( 1, {{t}_{\text{D}}} \right)$— — 液膜下端无因次表面活性剂浓度; ${{C}_{\text{SD}}}\left( {{x}_{\text{D}}}, 0 \right)$— — 液膜初始时刻无因次表面活性剂浓度; D— — 扩散系数, m2/s; DD— — 无因次扩散系数; f— — 振动频率, Hz; fD— — 无因次振动频率; Fb— — 波动力, N/m3; g— — 重力加速度, m/s2; h— — 液膜厚度, m; h0— — 液膜初始厚度, m; hD— — 无因次液膜厚度; heq— — 平衡液膜厚度, m; ${{h}_{\text{D}}}\left( 0, {{t}_{\text{D}}} \right)$— — 液膜上端无因次厚度; ${{h}_{\text{D}}}\left( 1, {{t}_{\text{D}}} \right)$— — 液膜下端无因次厚度; ${{h}_{\text{D}}}\left( {{x}_{\text{D}}}, 0 \right)$— — 液膜初始时刻无因次厚度; K— — 与表面活性剂浓度相关的系数, N· L/（mol· m）; L— — 液膜特征长度, m; p— — 液膜所受压力, Pa; pD— — 无因次液膜所受压力; pf— — 特征压力, Pa; pse— — 分离压, Pa; pseD— — 无因次分离压; pS— — 液膜表面压力, Pa; pSD— — 无因次液膜表面压力; Q0D— — 无因次滑移流量; Q1D— — 无因次剪切流量; t— — 排液时间, s; tD— — 无因次排液时间; T— — 特征时间, s; u— — 泡沫液膜排液速度, m/s; u0— — 滑移速度, m/s; u0D— — 无因次滑移速度; u1— — 剪切速度, m/s; u1D— — 无因次剪切速度; ${{u}_{\text{1D}}}^{\left( 0 \right)}$— — 无因次剪切速度级数展开式首项; U0— — 特征滑移速度, m/s; U1— — 特征剪切速度, m/s; v— — 泡沫液膜厚度变化速度, m/s; V— — 泡沫液膜厚度特征变化速度, m/s; vD— — 无因次泡沫液膜厚度变化速度; x— — 泡沫液膜排液距离, m; xD— — 无因次泡沫液膜排液距离; y— — 垂直于x的泡沫液膜排液距离, m; yD— — 垂直于x的无因次泡沫液膜排液距离; z— — 振动位移, m; α — — 衰减系数, s-1; ε — — 泡沫液膜初始厚度与泡沫液膜特征长度的比值, 无因次; κ — — 修正系数, 无因次; λ — — 液膜表面曲率, m-1; μ — — 泡沫液黏度, Pa· s; ρ — — 起泡剂溶液密度, kg/m3; σ — — 表面张力, N/m; σ 0— — 初始表面张力, N/m; τ — — 切应力, Pa; τ D— — 无因次切应力。

（编辑 唐俊伟）

参考文献
[1] 李松岩, 王麟, 韩瑞, 等. 裂缝性致密油藏超临界CO2泡沫驱规律实验研究[J]. 油气地质与采收率, 2020, 27(1): 29-35.
LI Songyan, WANG Lin, HAN Rui, et al. Experimental study on supercritical CO2 foam flooding in fractured tight reservoirs[J]. Petroleum Geology and Recovery Efficiency, 2020, 27(1): 29-35. [本文引用:1]
[2] 袁士义, 王强. 中国油田开发主体技术新进展与展望[J]. 石油勘探与开发, 2018, 45(4): 657-668.
YUAN Shiyi, WANG Qiang. New progress and prospect of oilfields development technologies in China[J]. Petroleum Exploration and Development, 2018, 45(4): 657-668. [本文引用:1]
[3] 李兆敏, 徐正晓, 李宾飞, 等. 泡沫驱技术研究与应用进展[J]. 中国石油大学学报(自然科学版), 2019, 43(5): 118-127.
LI Zhaomin, XU Zhengxiao, LI Binfei, et al. Advances in research and application of foam flooding technology[J]. Journal of China University of Petroleum (Natural Science Edition), 2019, 43(5): 118-127. [本文引用:1]
[4] 刘珑, 范洪富, 孙江河, 等. 纳米颗粒稳定泡沫驱油研究进展[J]. 油田化学, 2019, 36(4): 748-754.
LIU Long, FAN Hongfu, SUN Jianghe, et al. Research progress of nanoparticles-stabilized foam for EOR[J]. Oilfield Chemistry, 2019, 36(4): 748-754. [本文引用:1]
[5] 付亚峰, 印万忠, 姚金, 等. 绿泥石颗粒效应对泡沫稳定性的影响[J]. 中南大学学报(自然科学版), 2018, 49(8): 1857-1862.
FU Yafeng, YIN Wanzhong, YAO Jin, et al. Study on stability of flotation foam influenced by particle effect of chlorite[J]. Journal of Central South University (Natural Science Edition), 2018, 49(8): 1857-1862. [本文引用:1]
[6] 张景楠, 狄勤丰, 华帅, 等. 泡沫驱油核磁共振实验及泡沫动态稳定性评价[J]. 石油勘探与开发, 2018, 45(5): 853-860.
ZHANG Jingnan, DI Qinfeng, HUA Shuai, et al. Nuclear magnetic resonance experiments on foam flooding and evaluation of foam dynamic stability[J]. Petroleum Exploration and Development, 2018, 45(5): 853-860. [本文引用:1]
[7] 熊春明, 曹光强, 张建军, 等. 适应中国主要气田的纳米粒子泡排剂系列[J]. 石油勘探与开发, 2019, 46(5): 966-973.
XIONG Chunming, CAO Guangqiang, ZHANG Jianjun, et al. Nanoparticle foaming agents for major gas fields in China[J]. Petroleum Exploration and Development, 2019, 46(5): 966-973. [本文引用:1]
[8] SCHWARTZ L W, ROY R V. Modeling draining flow in mobile and immobile soap films[J]. Journal of Colloid and Interface Science, 1999, 218(1): 309-323. [本文引用:2]
[9] MYSELS K J, SHINODA K, FRANKEL S. Soap films: Studies of their thinning and a bibliography[M]. New York: Pergamon Press, 1959. [本文引用:1]
[10] 叶学民, 杨少东, 李春曦. 随活性剂浓度变化的分离压对垂直液膜排液过程的影响[J]. 物理学报, 2017, 66(18): 147-159.
YE Xuemin, YANG Shaodong, LI Chunxi. Effect of concentration- dependent disjoining pressure on drainage process of vertical liquid film[J]. Acta Physica Sinica, 2017, 66(18): 147-159. [本文引用:1]
[11] 叶学民, 杨少东, 李春曦. 分离压和表面黏度的协同作用对液膜排液过程的影响[J]. 物理学报, 2017, 66(19): 178-190.
YE Xuemin, YANG Shaodong, LI Chunxi. Synergistic effects of disjoining pressure and surface viscosity on film drainage process[J]. Acta Physica Sinica, 2017, 66(19): 178-190. [本文引用:3]
[12] 杨少东, 叶学民, 李春曦. 活性剂浓度分布对液膜排液过程的影响[J]. 计算物理, 2018, 35(5): 577-586.
YANG Shaodong, YE Xuemin, LI Chunxi. Effect of surfactant concentration distribution on film drainage[J]. Chinese Journal of Computational Physics, 2018, 35(5): 577-586. [本文引用:1]
[13] 张磊. 低频谐振波对N2泡沫复合驱油效果影响规律实验研究[D]. 西安: 西安石油大学, 2012.
ZHANG Lei. Low-frequency resonant wave on N2 foam flooding effect of the influence of experimental study[D]. Xi’an: Xi’an Petroleum University, 2012. [本文引用:1]
[14] 李星红, 徐加祥, 刘玺, 等. 振动-空气泡沫驱封堵性能评价与矿场试验研究[J]. 西安石油大学学报(自然科学版), 2017, 32(1): 83-88.
LI Xinghong, XU Jiaxiang, LIU Xi, et al. Plugging performance evaluation and field test of vibration-air foam flooding[J]. Journal of Xi’an Shiyou University (Natural Science Edition), 2017, 32(1): 83-88. [本文引用:2]
[15] 刘静, 夏军勇, 刘玺, 等. 低频波对泡沫稳定性协同强化效应[J]. 石油学报, 2020, 41(5): 584-591.
LIU Jing, XIA Junyong, LIU Xi, et al. Synergistic reinforcement effect of low-frequency waves for foam stability[J]. Acta Petrolei Sinica, 2020, 41(5): 584-591. [本文引用:2]
[16] 刘静, 蒲春生, 林承焰, 等. 低频振动单相不可压缩流体细管流动微观动力学数学模型研究[J]. 天然气地球科学, 2014, 25(10): 1610-1613.
LIU Jing, PU Chunsheng, LIN Chengyan, et al. Mathematical model of microscopic dynamics about single-phrase incompressible fluid flows in thin tube under low frequency vibration[J]. Science Technology and Engineering, 2014, 25(10): 1610-1613. [本文引用:1]
[17] 杨少东. 分离压和表面粘度对液膜排液过程影响研究[D]. 保定: 华北电力大学, 2018.
YANG Shaodong. Investigation of effect of disjoining pressure and surface viscosity on film drainage process[D]. Baoding: North China Electric Power University, 2018. [本文引用:1]
[18] 牟静, 陶超, 朱哲民, 等. 液体中包膜气泡的非线性振动特性[R]. 济南: 中国声学学会2003年青年学术会议, 2003.
MU Jing, TAO Chao, ZHU Zhemin, et al. The nonlinear oscillation characteristics of gas bubble with an elastic solid layer in liquid[R]. Jinan: 2003 Youth Academic Conference of Chinese acoustic Society, 2003. [本文引用:1]
[19] 吴化勇. 考虑残余应力影响的谐振式生化传感器微膜动态特性研究[D]. 济南: 山东大学, 2015.
WU Huayong. Dynamic characteristics of micro-diaphragm of resonant biochemical sensors considering the effect of residual stress[D]. Jinan: Shand ong University, 2015. [本文引用:1]