水侵气藏型储气库注采相渗滞后数值模拟修正方法
[朱思南1, 2, 3, 4 
, 孙军昌3, 4 , 魏国齐1, 2, 3, 4 , 郑得文1, 2, 3, 4 , 王皆明3, 4 , 石磊3, 4 , 刘先山3, 4 ]
, 孙军昌, 王皆明引用本文
朱思南, 孙军昌, 魏国齐, 郑得文, 王皆明, 石磊, 刘先山. 水侵气藏型储气库注采相渗滞后数值模拟修正方法[J]. 石油勘探与开发, 2021,48(1): 166-174.
ZHU Sinan, SUN Junchang, WEI Guoqi, ZHENG Dewen, WANG Jieming, SHI Lei, LIU Xianshan. Numerical simulation-based correction of relative permeability hysteresis in water- invaded underground gas storage during multi-cycle injection and production[J]. Petroleum Exploration & Development, 2021,48(1): 166-174.
Doi: 10.11698/PED.2021.01.15ZHU Sinan, SUN Junchang, WEI Guoqi, ZHENG Dewen, WANG Jieming, SHI Lei, LIU Xianshan. Numerical simulation-based correction of relative permeability hysteresis in water- invaded underground gas storage during multi-cycle injection and production[J]. Petroleum Exploration & Development, 2021,48(1): 166-174.
Permissions
Copyright©2021, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
水侵气藏型储气库注采相渗滞后数值模拟修正方法
第一作者简介：朱思南（1986-）,男,浙江杭州人,现为中国科学院大学博士研究生,主要从事油气田开发/地下储气库数值模拟及地质力学方面的研究工作。地址：河北省廊坊市广阳区万庄石油分院地下储库研究中心,邮政编码：065007。E-mail: zsntiancai@163.com
摘要
以天然岩心气水多周期互驱相渗测定实验为基础,揭示了储气库多周期注采相渗滞后效应,结合Carlson和Killough经典相渗滞后理论,建立了水侵气藏型储气库多周期注采相渗滞后数值模拟修正方法,并通过建立的中低渗透砂岩水侵气藏型储气库地质模型,系统研究了多周期注采相渗滞后效应对储气库流体宏观分布规律和生产运行指标的影响。研究表明：水侵气藏型储气库高速注采运行过程中存在相渗滞后效应,该效应的存在使储气库气水过渡区宽度、厚度增加,高效储气区不断收缩,含气孔隙体积峰值变化幅度减小,进而降低储气库的库容、工作气量及高效运行寿命等;数值模拟中若不考虑相渗滞后效应的影响,预测的储气库运行指标将存在较大误差,采用Killough和Carlson方法可对储气库相渗滞后效应进行修正,提高预测精度,其中Killough方法对实例模型的适应性更好。图20表3参25
关键词:
水侵气藏; 储气库; 多周期注采; 相渗滞后; 模型修正; 指标预测
中图分类号:TE82
文献标志码:A
Numerical simulation-based correction of relative permeability hysteresis in water- invaded underground gas storage during multi-cycle injection and production
ZHU Sinan1, 2, 3, 4 , SUN Junchang3, 4 , WEI Guoqi1, 2, 3, 4 , ZHENG Dewen1, 2, 3, 4 , WANG Jieming3, 4 , SHI Lei3, 4 , LIU Xianshan3, 4
, SUN Junchang, WANG Jieming
Abstract
By conducting relative permeability experiments of multi-cycle gas-water displacement and imbibition on natural cores, we discuss relative permeability hysteresis effect in underground gas storage during multi-cycle injection and production. A correction method for relative permeability hysteresis in numerical simulation of water-invaded gas storage has been worked out using the Carlson and Killough models. A geologic model of water-invaded sandstone gas storage with medium-low permeability is built to investigate the impacts of relative permeability hysteresis on fluid distribution and production performance during multi-cycle injection and production of the gas storage. The study shows that relative permeability hysteresis effect occurs during high-speed injection and production in gas storage converted from water-invaded gas reservoir, and leads to increase of gas-water transition zone width and thickness, shrinkage of the area of high-efficiency gas storage, and decrease of the peak value variation of pore volume containing gas, and then reduces the storage capacity, working gas volume, and high-efficiency operation span of the gas storage. Numerical simulations exhibit large prediction errors of performance indexes if this hysteresis effect is not considered. Killough and Carlson methods can be used to correct the relative permeability hysteresis effect in water-invaded underground gas storage to improve the prediction accuracy. The Killough method has better adaptability to the example model.
Keyword:
water-invaded gas reservoir; underground gas storage; multicycle injection-production; relative permeability hysteresis; model-based correction; index prediction
0 引言
气藏型地下储气库工作气量大, 便于集中管理, 多由枯竭气藏改建而成[1, 2], 属于废旧气藏二次利用, 经济效益较好。而部分可利用的气藏在流体封存和地质演化过程中形成边、底水, 随着建库需求量增加, 水侵气藏不可避免地成为建库目标。气藏改建储气库后, 单井运行工况从“ 衰竭式低速开发” 变为“ 多周期高速注采” [3, 4], 这种“ 呼吸式” 注采运行方式, 加剧了多相流体在储集层孔隙中流动与共存状态的复杂性[5, 6]。“ 相渗滞后” 效应多见于单次渗吸或驱替后流体相对渗流能力的变化, 这既取决于岩石的润湿性, 又和流体的物理属性及流动方式息息相关[7]; 而“ 多周期注采相渗滞后” 效应源于储气库特有的“ 双向” 注采过程, 驱替与渗吸在同区域内多次交互发生, 该过程因流体渗流特征发生改变, 影响储气库的库容、单井注采能力、扩容达产周期、井型井网设计及注采运行管理[8, 9]。因此, 在储气库数值模拟研究中, 多周期注采相渗滞后效应的客观描述是数值模型可靠性的基础, 是准确刻画流体分布、预测建库运行指标的前提。
针对“ 相渗滞后” 现象, 国内外学者开展了大量研究。1951年Osoba等[10]通过实验证实气顶油藏使用驱替相渗曲线、底水油藏使用渗吸相渗曲线开展研究较为合适; 1968年Land[11]建立了非润湿相渗吸后饱和度与初始饱和度的函数关系式; 1976年Killough[12]通过实验中毛细管力和相对渗透率的滞后现象建立了结合饱和历史重现滞后曲线的数学模型。随着实验技术的进步, 近年来Kadet等[13]获取了相对准确的油水两相流体相渗滞后曲线; Carlson[14]、Ranaee等[15]进一步完善了“ 滞后” 理论。目前部分油气藏数值模拟器中已集成并可追加滞后理论模型, Kossack[16]对比了不同经典滞后模型在数值模拟器中的应用差别; Mahzari等[17]针对水湿和混合润湿系统改进了实验方法并校准滞后模型, 提高了数值模型历史拟合精度。实际应用中, Ismail等[18]结合实际生产数据分析了滞后效应对气藏开发历史拟合的影响; Juanes等[19]评价了相渗滞后效应对二氧化碳埋存的影响; Spiteri等[20]利用数值模拟研究了相渗滞后对气水交互驱替提高石油采收率的影响。
目前相渗滞后效应的物理实验主要针对油-水、气- 油、CO2-卤水等流体系统, 仅Shi等[21]初步完成了多周期气水互驱相渗测定实验; 数值模拟方面, 多为气水两相流中气水交互单方向驱替提高石油采收率及二氧化碳埋存等方面的研究, 而气藏型储气库气-水“ 双向” 多周期交互驱替工况下相渗滞后数值模拟研究相对欠缺。本文以气藏型储气库天然岩心气-水多周期互驱相对渗透率测定为基础, 评价气、水两相流体相渗变化的规律, 建立储气库多周期注采相渗滞后数值模拟修正方法, 并分析多周期注采相渗滞后效应对储气库流体分布规律及运行指标的影响。
1 多周期注采相渗滞后机理
1.1 相渗滞后概述
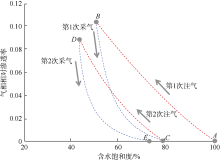
气水两相流体在岩石内的渗流过程中相对渗透率会产生变化, 并与岩石润湿性[22]、毛细管数、流体饱和度及岩石孔隙结构等[23]相关。一般认为气、水、岩石三相界面的润湿角变化会产生润湿滞后, 而润湿滞后、岩石孔隙内表面不平整及喉道半径变化等因素又会引起毛管压力滞后[24], 这些“ 滞后” 效应对多相流体在岩石孔隙中的渗流能力有较大影响。同时, 亲水岩石渗吸过程中润湿相（水相）的饱和度快速升高时, 非润湿相（气相）会被润湿相分散, 变成非连续相, 以段塞与气泡等多种形式存在, 这将导致非润湿相渗流能力发生变化。水侵气藏型储气库在运行过程中, 气体通过单井被多次高速注入和采出, 储集层内的气水两相流体完全符合相互驱替-渗吸行为机制, 形成储气库多周期注采相渗滞后效应（见图1）。第1次气驱水后（驱替）获得曲线段AB, 代表气藏成藏过程; 再进行第1次水驱气（渗吸）获得曲线段BC, 含水饱和度C无法达到初始含水饱和度A; 第2次气驱水获得曲线段CD; 第2次水驱气获得曲线DE, 点E的含水饱和度低于点C。在此气水交互驱替过程中, 除了端点值的变化, 相渗曲线依赖于注采路径, 整个过程中气相相对渗透率下降, 表现出“ 滞后” 效应。
 | 图1 气相相对渗透率滞后曲线示意图 |
1.2 气水多周期互驱相渗测定实验
利用水侵砂岩储气库全直径天然岩心, 制备24块直径2.5 cm, 长度5.0 cm的实验样品, 烘干后进行基础物性测试, 挑选3块典型样品, 渗透率分别为1.65× 10-3 μ m2, 19.34× 10-3 μ m2和49.00× 10-3 μ m2, 孔隙度分别为4.6%, 13.8%和16.5%, 分别代表该储气库低、中、高渗3类储集层。参照国家标准（GB/T 28912— 2012 岩石中两相流体相对渗透率测定方法[25]）测定气水两相流体相对渗透率, 模拟储气库多周期运行气水驱替-渗吸过程。具体实验步骤为：①岩心样品抽真空, 饱和模拟地层水; ②从岩心一端气驱水（模拟注气）, 优化驱替压差, 记录各时刻驱替压力、产气量、产水量, 驱替至岩心达到束缚水状态（产水量小于0.1 mL/h）时, 测定束缚水状态下气相有效渗透率, 结束气驱水; ③随后从岩心另一端水驱气（模拟采气）, 水驱替量大于20倍孔隙体积, 测定残余气状态下水相有效渗透率, 结束水驱气; ④连续重复第②、③步, 直到相同含水饱和度下相渗变化率小于3%时结束实验。
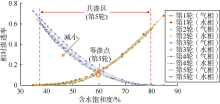
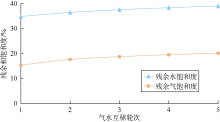
从实验结果看出, 随注采轮次增加, 该组岩心的相渗曲线均出现等渗点下移, 共渗区缩小的特点。以渗透率为19.34× 10-3 μ m2的岩心为例, 气相相对渗透率在前3个注采周期降低明显（见图2）, 到第5周期时气相相对渗透率与上一周期相比下降幅度变缓, 残余气饱和度随多轮次气水互驱呈增加趋势, 且整个过程逐渐趋于稳定（见图3）。而水相作为润湿相在此实验过程中相对渗透率虽然有所减小, 但变化幅度不大, “ 滞后” 效应不明显。
 | 图2 多周期气水互驱相渗滞后曲线 |
 | 图3 多周期气驱残余水与水驱残余气饱和度变化曲线 |
2 注采相渗滞后数值模拟修正方法
2.1 相渗滞后数值模拟原理
储气库数值模拟研究中描述非润湿相与润湿相间驱替-渗吸过程的相渗滞后, 采用室内物理实验获得所有周期的相渗曲线效率低、成本高, 因此需根据实验结论, 结合数学模型计算相渗滞后曲线。
Killough方法[12]基于Land数学模型[11]发展而来, 根据“ 历史最大非润湿相饱和度” 与“ 润湿相完全再饱和后的束缚非润湿相饱和度” 之间的关系：
${{S}_{\text{gt}}}=\frac{{{S}_{\text{gi}}}}{1+C{{S}_{\text{gi}}}}$ （1）
$C=\frac{1}{{{S}_{\text{gtm}}}}-\frac{1}{{{S}_{\text{gm}}}}$ （2）
引入驱替过程中非润湿相开始流动时的临界饱和度Sgc, 可建立：
${{S}_{\text{gt}}}={{S}_{\text{gc}}}+\frac{{{S}_{\text{ghy}}}-{{S}_{\text{gc}}}}{1+C\left( {{S}_{\text{ghy}}}-{{S}_{\text{gc}}} \right)}$ （3）
$C=\frac{1}{{{S}_{\text{gtm}}}-{{S}_{\text{gc}}}}-\frac{1}{{{S}_{\text{gm}}}-{{S}_{\text{gc}}}}$ （4）
相对渗透率变量关系式为：
${{K}_{\text{rgi}}}\left( {{S}_{\text{g}}} \right)=\frac{{{K}_{\text{rgi}}}\left( {{S}_{\text{gn}}} \right){{K}_{\text{rgd}}}\left( {{S}_{\text{ghy}}} \right)}{{{K}_{\text{rgd}}}\left( {{S}_{\text{gm}}} \right)}$ （5）
${{S}_{\text{gn}}}={{S}_{\text{gtm}}}+\frac{\left( {{S}_{\text{g}}}-{{S}_{\text{gt}}} \right)\left( {{S}_{\text{gm}}}-{{S}_{\text{gtm}}} \right)}{{{S}_{\text{ghy}}}-{{S}_{\text{gt}}}}$ （6）
此方法可计算渗吸过程中的残余非润湿相饱和度, 并获得渗吸过程的“ 滞后” 曲线和端点值。
Carlson方法[14]获得储气库多周期注采渗吸曲线更高效、方便, 该方法省去了复杂的取值和计算过程, 其计算原理见图4。根据实验室中测得的非润湿相渗吸过程相渗包络线FG及不同运行周期驱替相渗曲线端点B、D, 绘制非润湿相渗吸平行线相交于含水饱和度坐标轴得到DE、BC等曲线, 从而获得多轮次驱替-渗吸中间过程的相渗曲线。此方法的使用前提是在实验室中测得渗吸过程相渗曲线[14], 且在含水饱和度相同时, 非润湿相渗吸过程的相对渗透率应低于驱替过程的相对渗透率。
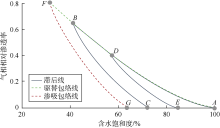 | 图4 Carlson相渗滞后数学模型原理图（据文献[14]修改） |
储气库多周期注采相渗滞后数值模拟的实现流程为：①确定驱替与渗吸过程相渗包络线, 数据取自岩心实验中模拟成藏后的第2次驱替相渗曲线, 以及气水两相流体多周期互驱至稳定时的渗吸相渗曲线; ②计算包络线间的相渗曲线, 包络线间的“ 滞后曲线” 代表了储气库在多周期运行过程中多相流体渗流能力的变化, 用以还原数值模拟时储气库每次注采过程的流体渗流状态。相渗滞后数学模型的确定应根据储气库生产数据历史拟合结果判断其适应性, 或结合新的机理认识优化理论模型; ③建立准确的储气库数值模拟模型并进行方案设计与结果预测。
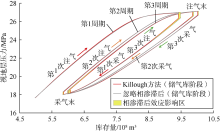
本次研究所用的相渗包络线取自气水互驱相渗实验测定结果, 因实验中水相流体相渗滞后效应不明显, 计算中设定水相驱替线与渗吸线重合。相渗滞后对模拟结果影响较大（见图5）, 不考虑相渗滞后模拟所得气相相对渗透率（图中红点）分布在驱替包络线上, 而考虑相渗滞后模拟所得气相相对渗透率主要分布在渗吸与驱替包络线间。
 | 图5 数值模型中使用的相对渗透率曲线 |
2.2 数值模拟模型
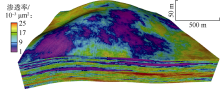
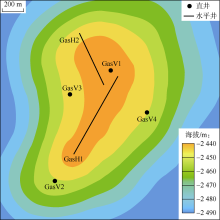
采用表1中的基础参数建立多周期注采相渗滞后三维精细地质模型（见图6）。模型网格总数为124× 104; 模型构造平缓, 重力对流体分布影响较小, 储集层具有平面非均质性, 存在局部优势通道; 层间分布低渗隔层, 设置网格水体表征边、底水, 模型边界处定义解析水体作为补充, 初始状态具有统一的气水界面。
 | 表1 储气库三维精细地质模型基础参数 |
 | 图6 储气库三维地质模型渗透率分布图 |
3 数值模拟结果
3.1 数值模拟方案设计
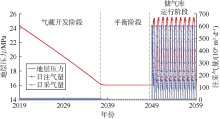
方案模拟气藏开发到改建地下储气库运行的完整历程, 设置有气藏开发阶段、平衡阶段和储气库运行阶段（见图7）。
 | 图7 不同阶段压力与日注采气量模拟曲线 |
气藏开发阶段布置1口直井与1口水平井（GasV1井、GasH1井）。设定气藏年开采速度为2.5%（地质储量）开发20年, 并在剩余地质储量为50%时停止开发, 转为储气库垫底气, 随后关井10年, 使地层流体充分平衡。储气库运行阶段, 在现有开发井基础上新增3口直井和1口水平井（见图8）, 实现井网对含气区的整体控制。新增直井位于含气区边翼部, 最低完井层位距初始气水界面10 m; 水平井水平段距初始气水界面30 m。
 | 图8 储气库井位部署图 |
通过模拟单井短期试注试采, 调整地质模型中每口气井的动态参数, 设定单井合理的最大注采气能力、限制注采气时最大井底流压, 利用井组优化配产控制储气库全区注、采气总量（见表2）。设计采用Carlson、Killough滞后修正方法及忽略滞后效应3个研究方案, 每个方案分为定流压与定气量运行两类。为恢复地层压力, 储气库采用先注后采的运行顺序, 并设置10个注采运行周期（见表3）。
| 表2 储气库注采阶段约束条件 |
| 表3 方案设计参数 |
3.2 相渗滞后对储气库注采气水分布的影响
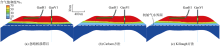
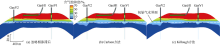
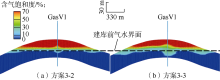
对比储气库建库前含气饱和度的分布, 发现气藏低速开发阶段若忽略相渗滞后效应, 纵向上气水界面抬升平缓（见图9a）, 考虑相渗滞后效应, 两种方法计算得到的气水过渡带下部边缘与开发前初始气水界面基本一致, 但气水过渡带厚度均明显增大（见图9b、图9c）。
 | 图9 建库前含气饱和度分布图 |
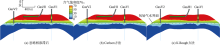
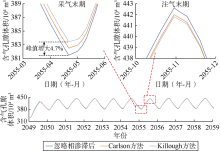
储气库注采运行阶段, 两种相渗滞后方法计算的气水过渡区与忽略相渗滞后效应相比, 纵向上采气末期均增厚8 m、注气末期均增厚4 m, 气顶厚度平均损失2 m（见图10、图11）; 平面上气水过渡区采气末期均增宽80 m、注气末期均增宽60 m, 气顶长、短轴平均收缩120 m（见图12）; 含气孔隙体积峰值随多周期注采变化幅度减小, 采气末期Killough方案平均增大4.7%（见图13）, 可动气量相应降低, 说明采气时水侵加剧, 随后注气时, 部分气体通过优势通道运移到原始气水界面以下, 气水过渡区逐渐变宽、变厚, 可利用的孔隙空间减少。
 | 图10 第10周期注气末期含气饱和度分布图 |
 | 图11 第10周期采气末期含气饱和度分布图 |
 | 图12 第10周期“ 采气末期” 储集层中部含气饱和度分布图 |
 | 图13 含气孔隙体积变化多方案对比图 |
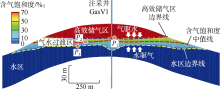
若根据以上研究定义储气库流体动态分区, 从纵向上可将储气库划分为高效储气区、气水过渡区和水区, 分区边界线会随多周期注采气产生变化。选择气水过渡区最宽的Killough方案第10周期计算结果, 过GasV1井沿含气饱和度剖面进行分区（见图14）, 并选高效储气区边界线处网格P1、含气饱和度中值分界线处网格P2及水区边界线处网格P3为研究对象。
 | 图14 储气库运行第10周期流体分区剖面图 |
网格P1处, 相渗滞后方案计算的含气饱和度（见图15a）在第2注采周期开始降低, 含气饱和度“ 振幅” 较大, 下降幅度也较大, 说明该区域随着注采运行发生水侵且滞后效应明显, 注采过程中该网格内更多的气体流动困难。随多周期注采的运行, 高效储气区边界线处网格的含气饱和度不断下降, 说明当前工况条件下, 高效储气区未达到平衡并不断“ 收缩” , 考虑相渗滞后的方案“ 收缩” 速度更快。
 | 图15 网格P1、P2、P3含气饱和度多方案对比曲线 |
网格P2距GasV1井200 m, 在储气库运行阶段含气饱和度变化总体相对稳定, 只是随注采运行周期性上下波动（见图15b）, 考虑相渗滞后方案的波动幅度较大。含气饱和度周期性变化说明随着储气库的运行, 此区域的气水两相流体不断相互驱替, 当高效储气区收缩部分变为气水过渡区后, 库容空间减少, 气水过渡区可以部分利用。设计运行方案时, 需对气水过渡区进行优化, 将该区设计成“ 缓冲带” , 保护上部的高效库容空间。
网格P3, 若忽略相渗滞后效应, 在气藏开发末期气体被地层水完全驱替, 并在储气库多周期注采运行后没有变化, 气水界面整体位于此网格之上。考虑相渗滞后效应的影响后发现, 此网格处的含气饱和度比忽略相渗滞后要高（见图15c）, 说明地层水捕集了部分天然气, 但因气相流动能力差, 在有限时间内无法被水完全驱出。
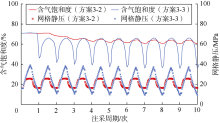
表3中方案3-2、方案3-3模拟结果（见图16）表明, 网格P1处含气饱和度随储气库多周期注采不断下降, 方案3-2至第6周期后峰值趋于平稳, 方案3-3至第2周期后峰值趋于平稳。但方案3-3含气饱和度波动幅度较大, 第5周期前波谷逐步降低, 随后趋于平稳。这说明在相同时间内, 注采压差增大, 气体波及效率提高, 但每周期注气末的残余水饱和度无法恢复至初始状态; 同时在较高的注采压差作用下, 气体沿高渗通道运移, 形成更为复杂的气水两相过渡区（见图17）。
 | 图16 不同运行压力区间P1网格含气饱和度变化 |
 | 图17 不同方案气水分布关系对比 |
以上分析说明储气库的高效储气区一旦有地层水侵入, 在相同运行周期内通过提高注气压差无法将地层水完全驱出, 反而会在原来的水区中产生一定的注入气损失。在储气库实际注采运行中, 可通过优化布井及注采运行方案综合控制气水过渡区, 提高库容空间利用率, 延长储气库高效注采运行的生命周期。
3.3 相渗滞后对储气库数值模拟预测指标的影响
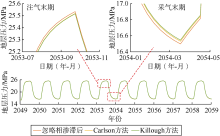
限定井底注采流压运行, 考虑相渗滞后效应发现, 与不考虑相渗滞后效应相比：①注气末期地层平均压力较低, 采气末期地层平均压力较高（见图18）; ②多周期库存分析曲线（见图19）表明采气末期库存剩余量增多、注气末库存量减少, Carlson和Killough方法模拟工作气量分别减少1.2%和1.8%。
 | 图18 定流压注采方案地层压力变化对比 |
 | 图19 定流压注采方案库存量变化对比（前3个注采周期） |
由上述分析可知：①多周期注采相渗滞后效应较大程度降低了气相渗流能力, 气体供给量降低。采气时气体动用效率降低, 注气时气体扩散运移能力变差, 气水过渡区增大, 可动气体减少, 可高效利用的储气空间减少, 储气库工作气量降低; ②注气时气体在高压驱动下进入水层, 近井区易气窜, 采气时地层水侵入储集层并汇集到近井区域, 直井易形成局部水锥, 再注气时侵入地层水难以被完全驱替, 部分滞留并占据孔隙空间, 多周期交替注采后气水过渡区增大; 完井层位位于气水过渡区附近或储气库边翼部的井, 若忽略相渗滞后效应将影响单井运行指标预测结果。
4 实例验证
实例验证采用由低渗透水驱气藏改建而成的地下储气库。该库储集层非均质性较强, 平均孔隙度10%, 平均渗透率2× 10-3 μ m2, 储集层连通性较好, 开发前具有统一的气水界面, 开发后由于部分生产井存在局部水锥, 气水界面平面上差异明显, 建库前气藏采出程度40%, 目前该储气库已投运6个注采运行周期。
建立并粗化该储气库三维精细地质模型, 粗化模型的网格步长为100 m× 100 m× 20 m、网格数量为50× 70× 75。模型中赋设的相关流体参数均来自天然岩心室内实验综合分析, 且通过拟合气藏开发至储气库运行的全过程历史对该数值模拟模型的地质参数进行综合修正。
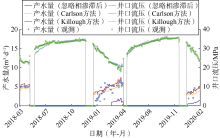
对比完井层位在储气库气水过渡区边界处A井的注采运行指标拟合曲线（见图20）, 可看出考虑相渗滞后效应的拟合结果与观测数据吻合度较高, 两种相渗滞后方法计算的流压非常接近（图上基本重合）, Killough方法计算的产水量更准确, 对此模型的适应性更好。故在水侵气藏型储气库数值模拟研究中考虑相渗滞后效应, 可提高储气库多周期注采运行后的气水分布关系刻画与运行指标预测精度。
 | 图20 A井生产运行数据不同方法拟合曲线 |
5 结论
水侵气藏型储气库高速注采运行过程中存在相渗滞后效应, 该效应的存在使储气库气水过渡区宽度、厚度增加, 高效储气区不断收缩, 含气孔隙体积峰值变化幅度减小, 进而降低储气库的库容、工作气量及高效运行寿命等。
数值模拟中若不考虑相渗滞后效应的影响, 预测的储气库运行指标将存在较大误差, 采用Killough和Carlson方法可对储气库相渗滞后效应进行修正, 提高预测精度, 其中Killough方法对实例模型的适应性更好。
符号注释：
C— — Land常数, 无因次; Krgd— — 驱替包络线对应的相对渗透率, 无因次; Krgi— — 渗吸包络线对应的相对渗透率, 无因次; Sg— — 含气饱和度, %; Sgc— — 驱替过程中非润湿相临界流动饱和度, %; Sghy— — 驱替过程非润湿相所达到的某中间饱和度, %; Sgi— — 驱替时初始非润湿相饱和度, %; Sgm— — 驱替过程中最大非润湿相饱和度, %; Sgn— — 归一化含气饱和度, %; Sgt— — 开始渗吸时达到的非润湿相残余饱和度, %; Sgtm— — 渗吸时最大残余非润湿相饱和度, %。
（编辑 唐俊伟）
参考文献
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|