引用本文
ALAROUJ Mutlaq, ALOMAIR Osamah, ELSHARKAWY Adel. 凝析气藏露点压力计算方法[J]. 石油勘探与开发, 2020,47(5): 1016-1026.
ALAROUJ Mutlaq, ALOMAIR Osamah, ELSHARKAWY Adel. A calculation method of dew-point pressure of gas condensate reservoir[J]. Petroleum Exploration & Development, 2020,47(5): 1016-1026.  
Doi: 10.11698/PED.2020.05.16
Permissions
Copyright©2020, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
凝析气藏露点压力计算方法
ALAROUJ Mutlaq, ALOMAIR Osamah, ELSHARKAWY Adel
科威特大学石油工程系,萨法特 13060,科威特

联系作者简介：ALOMAIR Osamah（1971-）,男,科威特人,博士,科威特大学石油工程系副教授,主要从事提高采收率和油气藏工程等方面的研究工作。地址：Petroleum Engineering Department, College of Engineering & Petroleum, Kuwait University, PO Box 5956, Safat 13060, Kuwait。E-mail：dr.alomair@ku.edu.kw

第一作者简介：ALAROUJ Mutlaq（1989-）,男,科威特人,博士,科威特石油公司工程师,主要从事油藏工程和遥感技术等方面的研究。地址：Petroleum Engineering Department, College of Engineering & Petroleum, Kuwait University, PO Box 5956, Safat 13060, Kuwait。E-mail：mutlaalaroj@gmail.com

收稿日期: 2020-03-04
基金项目: 科威特大学石油流体研究中心（PFRC）科研基金（GE 01/17）
摘要

基于实验测量和文献调研建立了包含700多个样本的凝析气藏数据集,对常用的计算露点压力的经验关系式和状态方程进行了评估,并新建了一个经验关系式,对各种关系式及Peng-Robinson状态方程进行了对比评估和参数敏感性分析。研究表明,目前常用的凝析气判别标准不够准确;Peng-Robinson状态方程不具有唯一解,受C7+组分的表征关系式和分割方案等多种因素的影响;应用于建立的数据集时,Nemeth-Kennedy关系式准确度最高,其次为Elsharkawy关系式和Godwin关系式,Shokir关系式由于无法用于不含C7+组分的样本,准确度最低;新建关系式的平均绝对误差、均方根误差和决定系数分别为7.6%,588和0.87,在统计学意义上优于前人4种关系式。通过与实验数据和Peng-Robinson状态方程模拟结果进行对比验证了新建关系式的准确性和有效性。图13表16参36

关键词: 凝析气藏; 露点压力; 经验关系式; 状态方程
中图分类号:TE372 文献标志码:A 文章编号:1000-0747(2020)05-1016-11
A calculation method of dew-point pressure of gas condensate reservoir
ALAROUJ Mutlaq, ALOMAIR Osamah, ELSHARKAWY Adel
Petroleum Engineering Department, College of Engineering & Petroleum, Kuwait University, PO Box 5956, Safat 13060, Kuwait
Abstract

A large data bank of more than 700 gas-condensate samples collected from literatures and experiments was established. On this basis, empirical correlations equations of state commonly used to calculate dew-point pressure (DDP) were evaluated, a new model for estimating DPP was proposed, all the empirical correlations and Peng-Robinson state equation were compared, and sensitivity of parameters was analyzed. The current standard used to identify gas condensate isn’t accurate enough. The Peng-Robinson state equation has no unique solution and is affected by multiple factors such as the characterization relation of C7+ components and the splitting scheme. The Nemeth-Kennedy correlation has the highest accuracy when applied to the data bank established in this study, followed by Elsharkawy correlation and Godwin correlation, Shokir correlation can’t be used to samples without C7+ components and thus is the lowest in accuracy. The newly proposed model has an average absolute error, root mean square error and coefficient of determination of 7.5%, 588, and 0.87, respectively, and is better than the above four correlations statistically. The proposed model was proved accurate and valid by comparing its results with experimental data and the results of simulation with Peng-Robinson state equation.

Keyword: gas condensate reservoir; dew-point pressure; empirical relation; equation of state
0 引言

在凝析气藏中, 当地层压力下降至低于露点压力时就会出现反凝析现象, 形成凝析油并聚集于近井带。聚集的凝析油阻碍天然气的流动, 导致天然气的有效渗透率降低。在地层压力低于露点压力的情况下, 天然气的产量会迅速下降[1]。同时, 储集层中仍存在大量凝析油, 难以开采。因此, 准确计算露点压力对于凝析气藏的高效开发十分重要。

开展等组分膨胀实验测量凝析气藏露点压力, 可以得到最准确的值。但实验花费高、耗时长, 实验效果取决于是否有足够的样本, 并且在对采自分离器的油、气样本进行重组时容易出现人为失误。因此, 需要寻找一个简单、准确的露点压力计算方法。前人曾提出过一些数学模型, 用于在无法获取可靠样本或难以进行压力-体积-温度（PVT）实验时进行露点压力预测[1, 2], 主要包括状态方程和经验关系式。为将状态方程应用于凝析气藏流体特性表征, 前人进行了大量研究[3, 4, 5, 6, 7]。其中Peng-Robinson状态方程（简称PR状态方程）[5]以及Soave状态方程[7]被认为是最可靠的计算储集层流体性质的方法[8, 9]。由于受到选用的状态方程、“ +” 馏分的分割方案、“ +” 馏分的表征方法以及二元相互作用系数等多种因素的影响, 使用状态方程预测出的露点压力值并不唯一[1]。经验关系式的应用受限于建立关系式时所使用的数据范围。两种常用的经验关系式中, 一种取决于C7+馏分的组分和性质, 另一种则依赖生产数据。第1种关系式中, 露点压力为流体组分和地层温度的函数[1, 10, 11, 12, 13, 14, 15], 而在第2种关系式中, 露点压力为生产数据和地层温度的函数[16, 17, 18, 19, 20]。

本文对前人多种凝析气藏露点压力计算方法的精度和适用范围进行了评估, 并建立了一个新的露点压力计算模型, 将新建模型与前人关系式和状态方程进行对比。

1 方法和数据
1.1 工作流程

本文收集了大量不同来源的数据, 建立了一个大型数据库。在此基础上, 对状态方程和前人经验关系式进行评估, 还提出了一种新的关系式, 用于在缺乏可靠样本或实验工作无法进行的情况下估算露点压力。

1.2 样本露点压力的实验室测定

本文用科威特大学石油流体研究中心的全自动无汞PVT细胞液评价分析仪（VINCI）对6个凝析气样本的露点压力进行了测定, 这些样本部分在井底采集, 部分在地面分离器采集。利用恒组分膨胀（即恒重衰竭（CMD））测试和零压闪蒸法测定井底样本的露点压力、初始组分和气油比。根据初始气油比对采自分离器的油、气样本进行重组, 并与井底样本进行组分核对。使用Macro软件进行CMD测试, 在地层温度下, 将压力调整至初始地层压力。随后逐渐降低压力, 直到反凝析液形成, 此时测定露点压力。利用气相色谱仪（Agilent 7890B）测定用于重组的采自分离器的油、气样本的组分, 并结合现场的气油比, 计算储集层流体组分。井筒流体组分及其摩尔分数、C7+相对分子质量、C7+相对密度和露点压力的测定结果如表1所示。

表1 6个凝析气样本的实验室测定数据
2 数据采集与筛选

本文数据主要来自于文献。从前人的研究中一共收集到了925个样本, 包括Nemeth和Kennedy[13]的579个样本和Elsharkawy[1]的340个样本。另外, 笔者在科威特大学石油流体研究中心对6个样本进行了实验测量。对采集的数据进行筛选, 去除重复和有缺陷的样本。在筛选过程中需要注意检查样本的摩尔分数总和（应为1）、相对分子质量、C7+摩尔分数和C1摩尔分数。

2.1 凝析气判别

对于凝析气的判别, 目前还没有达成共识。McCain[21]、Danesh[22]、Lake和Holstein[23]、Beggs[24]以及Ahmed[25]提出了不同的凝析气判别标准, 如表2、表3所示。

表2 基于气油比、相对密度、C7+摩尔分数的凝析气判别标准
表3 基于相对分子质量和C7+摩尔分数的流体判别标准[23]

从表2可以看出, 不同学者提出的判别标准中, 气油比和相对密度有明显差异。而根据Lake和Holstein[23]提出的基于组分和相对分子质量的判别方案（见表3）, 表2中的判别标准可能会将其他类型储集层流体错误地判定为凝析气。需要指出的是, 大多数已发表文献数据中没有气油比和相对密度数据。

2.2 重复及错误样本剔除

首先, 剔除重复的样本, 然后, 剔除摩尔分数总和不等于1的样本。这些异常的样本可能是前人测量错误或输入错误导致的。

2.3 相对分子质量检查

根据表3, 典型凝析气相对分子质量在23~40。使用PVTi软件绘制每个样本的相包络线, 发现相对分子质量大于40的样本都表现出挥发油特征, 所以被剔除。然后, 逐个检查相对分子质量小于40的样本的相包络线, 发现相对分子质量在35~40的样本有的表现出凝析气特征, 有的表现出挥发油特征。因此, 对于相对分子质量在23~40的样本, 如果其相包络线表现出挥发油特征, 也应该被剔除。随后用相同的方法检查相对分子质量小于23的样本。按相对分子质量标准及相包络线筛选样本的过程如表4和图1所示。

表4 按相对分子质量标准筛选样本示例

图1 根据相对分子质量筛选的样本的相包络线示例

2.4 C7+摩尔分数检查

在根据相对分子质量对样本进行筛选、过滤后, 再根据C7+摩尔分数对样本进行过滤。根据表3, 凝析气的C7+摩尔分数在1%~6%, 而挥发油的C7+摩尔分数在10%~30%。而根据表2, 凝析气的C7+摩尔分数通常小于12.5%, 特殊情况下可达15%。由于C7+摩尔分数大于11%的样本的相包络线均表现出挥发油的特征, 所以被剔除。C7+摩尔分数在6%~11%的样本的相包络线有的表现出凝析气特征, 有的表现出挥发油特征。当C7+摩尔分数小于1%时, 大多数样本表现出凝析气的特征, 仅有少数样本表现出湿气的特征。例如, 样本9的C7+摩尔分数为0.4%, 在给定的储集层温度下相包络线表现出湿气特征, 而样本10中C7+摩尔分数为零, 其相包络线仍表现出凝析气特征。剔除相包络线不具有凝析气特征的样本。按C7+摩尔分数标准及相包络线筛选样本的过程如表5和图2所示。

表5 按C7+摩尔分数标准筛选样本示例

图2 根据C7+摩尔分数筛选样本的相包络线示例

2.5 C1摩尔分数检查

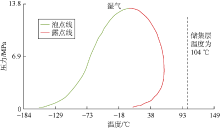
最后, 根据C1摩尔分数对样本进行筛选。气体样本的C1含量通常较高, 因此, 检查C1摩尔分数大于90%的样本的相包络线。例如, 样本11的C1摩尔分数和C7+摩尔分数分别为94.5%和1.6%（见表6）, 储集层温度为104 ℃, 高于临界凝析温度（49 ℃）, 该样本相包络线呈现出湿气的特征（见图3）; 样本7相包络线亦呈现出湿气的特征。然而, C1摩尔分数较低的样本也可表现出凝析气的相态特征。例如, 样本10的C1摩尔分数为58.3%, C7+摩尔分数为零, 其相包络线仍具凝析气的特征（见图2c）。

表6 按C1摩尔分数标准筛选样本示例

图3 样本11的相包络线

应用上述方法对样本进行筛选、过滤后, 样本个数从925个缩减到715个。对715个样本进行了统计分析（见表7）。样本筛选结果表明表2和表3中的数值范围并不一定准确。因此, 本文认为储集层流体的分类不应该依据气油比和相对密度等生产数据, 也不应该依据C7+摩尔分数, 而应该依据流体的相包络线。

表7 本文使用的数据集的统计分析
3 前人经验关系式和状态方程评估

本文对以组分数据为输入项的经验关系式和未修正的PR状态方程进行评估。常用的此类经验关系式有Elsharkawy关系式[1], Godwin关系式[11], Nemeth- Kennedy关系式[13]以及Shokir关系式[26]。这些关系式都将C7+组分归为一组（即集总C7+）, 所以将这些关系式与未修正的状态方程进行对比具有合理性。

3.1 前人经验关系式和状态方程的准确度统计评估

利用平均绝对误差（AAE）、平均相对误差（ARE）、均方根误差（RMSE）和决定系数（R2）等对上述关系式和未修正的PR状态方程进行统计评估[5]。结果如表8所示, 可以看出, 在本次评估的所有经验关系式中, Nemeth-Kennedy关系式的准确度最高。这个结论在意料之中, 因为本文使用的大部分数据是建立Nemeth- Kennedy关系式时使用的数据。一般来说, Nemeth- Kennedy关系式应适用于输入参数的整个范围。但是, 对于一些中间组分（C2、C3、C4和C5）摩尔分数较小的样本, Nemeth-Kennedy关系式预测出的露点压力偏低。样本的中间组分摩尔分数较小则C1或非烃组分摩尔分数较大。从统计学的观点看, Elsharkawy关系式的准确度位列第2, 除C1摩尔分数极大和极小以及N2和H2S摩尔分数较大的样本外, 它能很好地预测大部分样本的露点压力。Godwin关系式的准确度位列第3, 但对于C1摩尔分数极小和不含C7+组分的样本, 它估算出的露点压力值会偏低。此外, 对于非烃和（或）中间组分摩尔分数较大（同时C1含量相对较低）的样本, Godwin关系式预测的露点压力误差较大。Shokir关系式的准确度最差。负的R2值代表模型的预测结果非常不可靠, 预测结果无效。本文认为Shokir关系式误差较大是因为它不能预测不含C7+组分的样本的露点压力。对于这类不含C7+组分的样本, Shokir关系式计算出的露点压力为负值, 与实际不符。除了这4种关系式之外, 还基于PVTi软件利用PR状态方程估算露点压力, 求解PR状态方程时使用的分割方案为集总C7+, 使用的临界压力和温度关系式以及偏差因子关系式均为Kesler-Lee关系式。从表8可以看出, 对于本文使用的数据, Nemeth-Kennedy关系式和Elsharkawy关系式比PR状态方程的准确度更高。表8所示的6个统计指标中, 平均绝对误差是判断每种方法准确度最有力的指标。

表8 前人经验关系式与PR状态方程的统计评估结果
3.2 状态方程应用分析

已有研究表明, 状态方程计算的露点压力值并不唯一, 与拟组分的数量和划分方式等因素有关。本文将三参数PR状态方程应用于样本12, 对此进行分析。可变参数是C7+组分的表征关系式和分割方案（见表9）, 而二元相互作用系数保持不变。除了集总C7+之外, 每种分割方案都考虑在C7+组分中分割出C12+组分和C16+组分这两种情况。用PVTi软件运行三参数PR状态方程, 并考虑软件内置的“ +” 馏分的表征关系式。样本12中C1、C2、C3、C4、C5、C6、C7+、N2、CO2、H2S的摩尔分数分别为81.3%, 4.8%, 2.3%, 1.7%, 1.3%, 1.4%, 4.3%, 1.9%, 1.1%和0。样本12的C7+相对密度为0.74, C7+相对分子质量为139.9, 储集层温度为54 ℃, 露点压力为27.0 MPa。

表9 C7+组分的分割方案和表征关系式

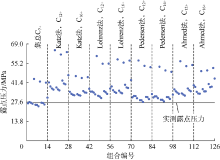
通过改变C7+组分的表征关系式和分割方案, 总共得出126个可能的组合, 计算出了126个露点压力值（见图4）。每个组合设置1个编号。例如, 组合25是指使用的分割方案为Katz法且分割出C12+组分, 使用的临界压力和温度关系式为Winn关系式, 使用的偏差因子关系式为Edmister关系式; 组合121是指使用的分割方案为Ahmed法且分割出C16+组分, 使用的临界压力和温度关系式为Riazi-Daubert关系式, 使用的偏差因子关系式为Pedersen关系式。由图4可知, 状态方程不具有唯一解, 在本算例中有126个计算结果。如果再改变二元相互作用系数就更加复杂。此外, 为某一样本调整匹配的状态方程也很复杂、耗时, 且计算结果不一定准确。

图4 状态方程的计算结果

4 新经验关系式建立

首先, 通过重新拟合参数对前人经验关系式进行改进。然后, 建立一个新的估算凝析气藏露点压力的经验关系式。

4.1 前人关系式的改进

Nemeth-Kennedy、Elsharkawy、Shokir和Godwin等关系式中含有多个常系数, 这些常系数是根据建立每个关系式时使用的数据推导出来的。利用本文采集的数据库, 通过修改系数、最小化误差来对这4种关系式进行改进。

表10对比了各关系式改进前与改进后的准确度。改进后的Nemeth-Kennedy关系式的准确度提升程度最小, 这是因为本文使用的大部分数据是建立Nemeth- Kennedy关系式时使用的数据。改进后的Elsharkawy关系式的准确度稍有提升, 因为本文使用的部分数据是建立Elsharkawy关系式时使用的数据。Shokir和Godwin关系式经改进后准确度得到了显著提升。

表10 改进前和改进后各关系式的统计参数
4.2 新关系式的建立

首先, 对输入和输出参数进行分析, 以明确参数间的关系以及对这些参数进行分组的可行性。露点压力与各参数之间的相关系数如表11所示。可以看出, 露点压力随中间组分摩尔分数的增加而下降, 但与C7+摩尔分数、C7+相对分子质量、C7+相对密度之间呈正相关; 与其他参数相比, 非烃组分含量的影响较小。这与Elsharkawy[1]和Shokir等[26]的观点一致。表11中体现的露点压力与C1摩尔分数的相关性也与Shokir关系式相符。

表11 露点压力与各参数之间的相关系数

根据表11, C2— C6摩尔分数均与露点压力呈负相关, 因此将C2— C6组分分为一组。将表11所示的相关性转化为数学式（见（1）式）, 该式是一个简单的线性方程, 可通过多元线性回归求解。

${{p}_{\text{d}}}={{A}_{1}}+{{A}_{2}}T+{{A}_{3}}{{F}_{{{\text{C}}_{\text{1}}}}}+{{A}_{4}}\left( {{F}_{{{\text{C}}_{\text{2}}}}}+{{F}_{{{\text{C}}_{\text{3}}}}}+{{F}_{{{\text{C}}_{\text{4}}}}}+{{F}_{{{\text{C}}_{\text{5}}}}}+{{F}_{{{\text{C}}_{\text{6}}}}} \right)+ {{A}_{5}}{{F}_{{{\text{C}}_{\text{7+}}}}}+{{A}_{6}}{{\gamma }_{{{\text{C}}_{\text{7+}}}}}+{{A}_{7}}{{M}_{{{\text{C}}_{\text{7+}}}}}+{{A}_{8}}{{F}_{\text{C}{{\text{O}}_{\text{2}}}}}+{{A}_{9}}{{F}_{{{\text{H}}_{\text{2}}}\text{S}}}+{{A}_{10}}{{F}_{{{\text{N}}_{\text{2}}}}}$ （1）

通过改变组分分组和（或）添加新参数对（1）式进行调整, 得到最终关系式, 如（2）式所示。

${{p}_{\text{d}}}=\left( {{I}_{1}}+{{I}_{2}}+{{I}_{3}}+{{I}_{4}}+{{I}_{5}} \right)/145.038$ （2）

其中

${{I}_{1}}={{B}_{1}}+{{B}_{2}}\left( 1.8T+32 \right) {{I}_{2}}={{B}_{3}}{{F}_{{{\text{C}}_{\text{1}}}}}+{{B}_{4}}\left( {{F}_{{{\text{C}}_{\text{2}}}}}+{{F}_{{{\text{C}}_{\text{3}}}}} \right)+{{B}_{5}}{{F}_{{{\text{C}}_{\text{4}}}}}+{{B}_{6}}\left( {{F}_{{{\text{C}}_{\text{5}}}}}+{{F}_{{{\text{C}}_{\text{6}}}}} \right) {{I}_{3}}\\={{B}_{7}}{{F}_{\text{C}{{\text{O}}_{\text{2}}}}}+{{B}_{8}}{{F}_{{{\text{H}}_{\text{2}}}\text{S}}}+{{B}_{9}}{{F}_{{{\text{N}}_{\text{2}}}}} {{I}_{4}}={{B}_{10}}\left( {{\gamma }_{{{\text{C}}_{\text{7+}}}}}{{M}_{{{\text{C}}_{\text{7+}}}}} \right)+{{B}_{11}}\left( {{F}_{{{\text{C}}_{\text{7+}}}}}{{\gamma }_{{{\text{C}}_{\text{7+}}}}}{{M}_{{{\text{C}}_{\text{7+}}}}} \right)+{{B}_{12}}\frac{{{M}_{{{\text{C}}_{\text{7+}}}}}}{{{\gamma }_{{{\text{C}}_{\text{7+}}}}}+0.000\ 01}+{{B}_{13}}{{\left( \frac{{{M}_{{{\text{C}}_{\text{7+}}}}}}{{{\gamma }_{{{\text{C}}_{\text{7+}}}}}+0.000\ 01} \right)}^{2}} {{I}_{\text{5}}}\\={{B}_{\text{14}}}\frac{{{F}_{{{\text{C}}_{\text{1}}}}}}{{{F}_{{{\text{C}}_{\text{7+}}}}}\text{+0}\text{.000}\ \text{01}}+{{B}_{\text{15}}}\frac{{{F}_{{{\text{C}}_{\text{1}}}}}}{{{I}_{2}}-{{B}_{3}}{{F}_{{{\text{C}}_{\text{1}}}}}}+ {{B}_{\text{16}}}\frac{{{M}_{{{\text{C}}_{\text{7+}}}}}}{{{F}_{{{\text{C}}_{\text{2}}}}}+{{F}_{{{\text{C}}_{\text{3}}}}}+{{F}_{{{\text{C}}_{\text{5}}}}}+{{F}_{{{\text{C}}_{\text{6}}}}}}$

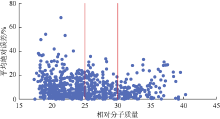
由图5可知, 除了一些分散的异常点以外, 误差总体上随着相对分子质量的增加而减小; 相对分子质量小于25以及相对分子质量大于30的样本误差分散程度较高。因此, 将数据集按照相对分子质量小于25、相对分子质量在25~30、相对分子质量大于30分为3组。

图5 数据集分组前新关系式平均绝对误差-相对分子质量散点图

由表12和图6可知, 将数据集分为3组后新建关系式的准确度显著提高。数据集分组后, 平均绝对误差从10.03%降低到7.58%, 均方根误差从705降低到588, 决定系数从0.81提高到0.87。数据集分组后关系式的结构与（2）式相同, 只是重新拟合了系数（见表13）。

表12 数据集分组前后新建关系式的统计参数
表13 数据集分组后根据各组数据拟合的新建关系式的系数

图6 数据集分组前后露点压力计算值与测量值的交会图

5 新建关系式与前人关系式对比
5.1 统计对比

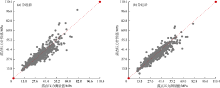
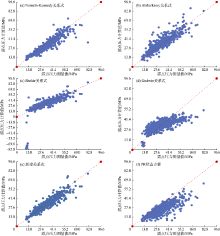
将表10中前人4个关系式的统计参数与表12中数据集分组后新建关系式的统计参数进行对比可知, 新建关系式的准确度最高。通过绘制露点压力计算值与测量值交会图（见图7）也可以发现, 新建关系式的计算值与实验测量值吻合度最高。

图7 露点压力计算值与测量值交会图

由于新建关系式根据相对分子质量将数据集分为了3组, 因此有必要针对每组数据进行新建关系式与前人关系式的统计对比。由表14可知, 对于第1组数据（相对分子质量小于25）, 新建关系式的平均绝对误差最低, 决定系数最高; 对于第2组数据（相对分子质量在25~30）, 新建关系式的平均绝对误差最低, 而Nemeth-Kennedy关系式的决定系数最高。对于第3组数据（相对分子质量大于30）, 新建关系式的平均绝对误差最低, 决定系数最高。

表14 数据集分组后新建关系式与前人关系式统计对比
5.2 参数敏感性分析

完成统计评估之后, 对前人关系式和新建关系式进行参数敏感性分析, 包括温度、C1摩尔分数、C7+摩尔分数和C7+相对分子质量。

5.2.1 对温度的敏感性

本文使用的数据集中, 许多样本在不同温度下进行了实验测定。将关系式和未修正的PR状态方程应用于这些样本, 并对比计算的露点压力与实验测定的露点压力随温度的变化趋势。选用样本13和样本14来说明关系式对温度的敏感性。这两个样本的组成如表15所示。

表15 用于温度敏感性分析的样本

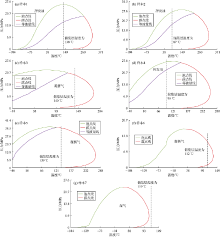
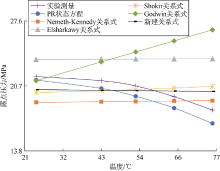
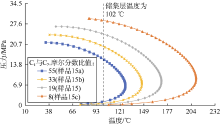
典型的凝析气藏相包络线上, 露点压力随着温度的升高而持续升高, 在升至临界凝析压力值后开始下降。图8中, 随着温度的升高, 实验测定的露点压力和未修正的PR状态方程计算的露点压力均呈现出明显的下降趋势; 新建关系式计算的露点压力略有下降; Nemeth-Kennedy关系式、Elsharkawy关系式和Shokir关系式计算的露点压力略有升高; Godwin关系式计算的露点压力显著升高。由此可见, 所有的关系式都未能反映露点压力随温度变化的实际趋势。

图8 样本13的温度敏感性分析结果

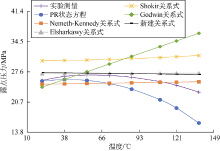
图9中, 随着温度的升高, 实验测定的露点压力和未修正的PR状态方程计算的露点压力先逐渐升高到最大值再开始下降。而所有的关系式都不能反映露点压力随温度变化的实际趋势。因此, 不建议使用任何计算露点压力的经验关系式来构建凝析气藏的相包络线。

图9 样本14的温度敏感性分析结果

图8和图9都显示, 新建关系式计算的露点压力随着温度的升高略有下降, 这是符合预期的, 因为对于某些样本, 露点压力与温度可能呈负相关, 如（2）式和表13所示（B2为负值）。虽然图中这个下降趋势较微弱, 但新建关系式是唯一能反映这一趋势的关系式。

5.2.2 对C1和C7+摩尔分数的敏感性

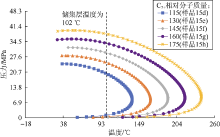
数据集中没有实验数据能够用于分析露点压力对C1和C7+摩尔分数的敏感性。本文通过改变C1与C7+摩尔分数比值, 在原始样本的基础上生成多个合成样本。选择样本15来分析关系式对C1和C7+摩尔分数的敏感性。表16显示了作为原始样本的样本15及其合成样本（样本15a、15b、15c）的组成。由于只有原始样本有实验室测定的露点压力值, 则将PR状态方程预测的露点压力随C1与C7+摩尔分数比值的变化趋势作为参照。用PVTi软件为表16中的样本绘制了相包络线, 这些样本的露点线如图10所示。可以看出, 储集层温度线与所有样本的露点线相交; 随着C1与C7+摩尔分数比值的增大, 相包络线收缩并向左移动。

表16 用于C1和C7+摩尔分数敏感性分析的样本

图10 不同C1与C7+摩尔分数比值样本的露点线

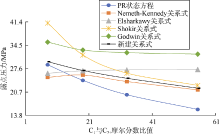
图11中, 随着C1与C7+摩尔分数比值的增加, PR状态方程计算的露点压力下降。Nemeth-Kennedy关系式、Shokir关系式和Godwin关系式及新建关系式均反映了这种趋势, 而Elsharkawy关系式则得出相反的趋势。

图11 C1和C7+摩尔分数敏感性分析结果

5.2.3 对C7+相对分子质量的敏感性

通过改变样本15的C7+相对分子质量（样本组成不变）生成5个合成样本, 各样本的露点线如图12所示。可以看出, 随着C7+相对分子质量的增加, 相包络线逐渐扩张并向右移动。

图12 不同C7+相对分子质量样本的露点线

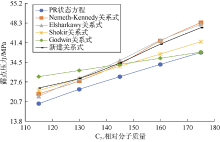
图13中, 前人4种关系式、新建关系式和状态方程计算的露点压力均随着C7+相对分子质量的增加呈上升趋势。

图13 C7+相对分子质量敏感性分析结果

6 结论

通过对实验测定和来自文献的凝析气藏数据样本进行深入过滤和筛选, 去除了有缺陷和不可靠的样本。筛选过程中发现基于相对分子质量和C7+组分含量的凝析气藏判别标准不准确。将Nemeth-Kennedy, Elsharkawy, Shokir和Godwin这4个经验关系式及未修正的Peng-Robinson状态方程应用于过滤后的数据集, 发现Nemeth-Kennedy关系式准确度最高, 其次为Elsharkawy关系式和Godwin关系式, Shokir关系式由于无法用于不含C7+组分的样本, 准确度最低; 状态方程不具有唯一解, 且计算结果不一定准确。对前人4种关系式进行了改进, 并基于收集到的大型数据库新建了一个经验关系式。新建关系式在统计学意义上优于前人4种关系式。

参数敏感性分析结果表明, Peng-Robinson状态方程能反映露点压力随储集层温度的实际变化趋势, 而所有关系式都不能; Peng-Robinson状态方程、Nemeth- Kennedy关系式、Shokir关系式和Godwin关系式及新建关系式均能反映露点压力随着C1与C7+摩尔分数比值的增加而下降的趋势, 而Elsharkawy关系式不能; Peng-Robinson状态方程和所有关系式均能反映露点压力随着C7+相对分子质量增加而上升的趋势。

符号注释：

A1— A10, B1— B16— — 系数; FC1— FC6— — C1— C6的摩尔分数, %; FC7+— — C7+的摩尔分数, %; FCO2— — CO2的摩尔分数, %; FH2S— — H2S的摩尔分数, %; FN2— — N2的摩尔分数, %; MC7+— — C7+的相对分子质量; pd— — 露点压力, MPa; T— — 温度, ℃; γ C7+— — C7+的相对密度。

编辑 胡苇玮

参考文献
[1] ELSHARKAWY A. Predicting the dew point pressure for gas condensate reservoirs: Empirical models and equations of state[J]. Fluid Phase Equilibria, 2002, 193(1/2): 147-165. [本文引用:7]
[2] ELSHARKAWY A M, FODA S G. EOS simulation and GRNN modeling of the constant volume depletion behavior of gas condensate reservoirs[J]. Energy Fuels, 1998, 12(2): 353-364. [本文引用:1]
[3] ESMAEILZADEH F, ROSHANFEKR M. A new cubic equation of state for reservoir fluids[J]. Fluid Phase Equilibria, 2006, 239(1): 83-90. [本文引用:1]
[4] PATEL N C, TEJA A S. A new cubic equation of state for fluids and fluids mixtures[J]. Chemical Engineering Science, 1982, 37(3): 463-473. [本文引用:1]
[5] PENG D, ROBINSON D B. A new two constants equation of state[J]. Industrial and Engineering Chemistry Fundamentals, 1976, 15(1): 59-64. [本文引用:3]
[6] REDLICH O, KWONG J N S. On the thermodynamics of solutions. V: An equation of state. Fugacities of gaseous solutions[J]. Chemical Reviews, 1949, 44(1): 233-244. [本文引用:1]
[7] SOAVE G. Equilibrium constants from a modified Redlich Kwong equation of state[J]. Chemical Engineering Science, 1972, 27(6): 1197-1203. [本文引用:2]
[8] ASHOUR I, AL-RAWAHI N, FATEMI A, et al. Applications of equations of state in the oil and gas industry[M]//MORENO J C. Thermodynamics-kinetics of dynamic systems. London: InTech, 2011. [本文引用:1]
[9] BONYADI M, ESMAEILZADEH F. Prediction of gas condensate properties by Esmaeilzadeh-Roshanfekr equation of state[J]. Fluid Phase Equilibria, 2007, 260(2): 326-334. [本文引用:1]
[10] EILERTS K, SMITH R V. Specific volumes and phase boundary- properties of separator-gas and liquid-hydrocarbon mixtures[R]. BM-RI-3642, 1942. [本文引用:1]
[11] GODWIN O N. A new analytical method for predicting dew point pressures for gas condensate reservoirs[R]. SPE 162985, 2012. [本文引用:2]
[12] KURATA F, KATZ D L. Critical properties of volatile hydrocarbon mixtures[J]. Trans. AIChE, 1942, 38: 995-1021. [本文引用:1]
[13] NEMETH L K, KENNEDY H T. A correlation of dewpoint pressures with fluid composition and temperature[J]. Society of Petroleum Engineers Journal, 1967, 7(2): 99-104. [本文引用:3]
[14] OLDS R H, SAGE B H, LACEY W N. Volumetric and phase behavior of oil and gas from Paloma Field[J]. Transactions of the AIME, 1945, 160(1): 77-99. [本文引用:1]
[15] ORGANICK E I, GOLDING B H. Prediction of saturation pressures for condensate-gas and volatile oil mixtures[J]. Journal of Petroleum Technology, 1952, 4(5): 135-148. [本文引用:1]
[16] HUMOUD A A, AL-MARHOUN M A. A new correlation for gas condensate dew point pressure prediction[R]. SPE 68230, 2001. [本文引用:1]
[17] MARRUFFO I, MAITA J, HIM J, et al. Correlations to determine retrograde dew pressure and C7+ percentage of gas condensate reservoirs on basis of production test data of eastern Venezuelan fields[R]. SPE 75686, 2002. [本文引用:1]
[18] OLDS R H, SAGE B H, LACEY W N. Volumetric and viscosity studies of oil and gas from a San Joaquin valley Field[J]. Transactions of the AIME, 1949: 179(1): 287-302. [本文引用:1]
[19] POTSCH K T, BRAEUER L. A novel graphical method for determining dewpoint pressures of gas condensates[R]. SPE 36919, 1996. [本文引用:1]
[20] REAMER H H, SAGE B H. Volumetric behavior of oil and gas from Louisiana Field[J]. International Journal of Petroleum Technology, 1950, 2(9): 261-268. [本文引用:1]
[21] MCCAIN W. Properties of petroleum fluids[M]. Tulsa, Oklahoma: PennWell Publishing Company, 1990. [本文引用:1]
[22] DANESH A. PVT and phase behavior of petroleum reservoir fluids[M]. London: Elsevier Science B. V. , 1998. [本文引用:1]
[23] LAKE L W, HOLSTEIN E D. Petroleum engineering hand book[M]. Houston, Texas: Gulf Publishing Company, 2007. [本文引用:2]
[24] BEGGS H D. Gas production operations[M]. 5th ed. Tulsa, Oklahoma: Oil and Gas Consultants International, Inc. , 2002. [本文引用:1]
[25] AHMED T. Equations of state and PVT analysis: Applications for improved reservoir modeling[M]. Houston, Texas: Gulf Publishing Company, 2016. [本文引用:1]
[26] SHOKIR E, EL-M M. Dewpoint pressure model for gas condensate reservoirs based on genetic programming[J]. Energy Fuels, 2008, 2(5): 3194-3200. [本文引用:2]
[27] KATZ D. Overview of the phase behavior of oil and gas production[R]. SPE 9995-PA, 1983. [本文引用:1]
[28] LOHRENZ J, BRAY B G, CLARK C R. Calculating viscosities of reservoir fluids from their compositions[J]. Journal of Petroleum Technology, 1964, 16(10): 1171-1176. [本文引用:1]
[29] PEDERSEN K, THOMASSEN P, FREDENSLUND A. Phase equilibria and separation process[R]. Lyngby, Denmark: Institute for Kemiteknik, Denmark Tekniske Hojeskole, 1982. [本文引用:1]
[30] AHMED T, CADY G, STORY A. A generalized correlation for characterizing the hydrocarbon heavy fraction[R]. SPE 14266, 1985. [本文引用:1]
[31] KESLER M G, LEE B I. Improved prediction of enthalpy of fractions[J]. Hydrocarbon Processing, 1976, 55(3): 153-158. [本文引用:1]
[32] RIAZI M R, DAUBERT T E. Characterization parameters for petroleum fractions[J]. Industrial and Engineering Chemical Research, 1987, 26(4): 755-759. [本文引用:1]
[33] CAVETT R H. Physical data for distillation correlations: Vapor-liquid equilibrium[C]//Proceedings of the 27th Meeting. San Francisco, CA: API, 1962. [本文引用:1]
[34] WINN F W. Simplified monographic presentation, characterization of petroleum fractions[J]. Petroleum Refiner, 1957, 36: 157. [本文引用:1]
[35] THOMASSEN P, PEDERSEN K S, FREDENSLUND A. Adjustments of C7+ molecular weights in the characterization of petroleum mixtures containing heavy hydrocarbons[R]. SPE 8617, 1986. [本文引用:1]
[36] EDMISTER W C. Applied hydrocarbon thermodynamics. Part 4. Compressibility factors and equations of state[J]. Petroleum Refiner, 1958, 37: 173-179. [本文引用:1]