引用本文
王洪亮, 穆龙新, 时付更, 窦宏恩. 基于循环神经网络的油田特高含水期产量预测方法[J]. 石油勘探与开发, 2020,47(5): 1009-1015.
WANG Hongliang, MU Longxin, SHI Fugeng, DOU Hongen. Production prediction at ultra-high water cut stage via Recurrent Neural Network[J]. Petroleum Exploration & Development, 2020,47(5): 1009-1015.  
Doi: 10.11698/PED.2020.05.15
Permissions
Copyright©2020, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
基于循环神经网络的油田特高含水期产量预测方法
王洪亮, 穆龙新, 时付更, 窦宏恩
中国石油勘探开发研究院,北京 100083

第一作者简介：王洪亮（1984-）,男,黑龙江哈尔滨人,中国石油勘探开发研究院在读博士研究生,主要从事统计建模、油气领域大数据与人工智能研究。地址：北京市海淀区学院路20号,中国石油勘探开发研究院计算机应用技术研究所,邮政编码：100083。E-mail：whldqpi@126.com

收稿日期: 2019-09-20
基金项目: 国家科技重大专项“大型油气田及煤层气开发”（2016ZX05016-006）
摘要

根据油田生产历史数据利用深度学习方法预测油田特高含水期产量,并进行了实验验证和应用效果分析。考虑到传统全连接神经网络（FCNN）无法描述时间序列数据的相关性,基于一种循环神经网络（RNN）即长短期记忆神经网络（LSTM）来构建油田产量预测模型。该模型不仅考虑了产量指标与其影响因素之间的联系,还兼顾了产量随时间变化的趋势和前后关联。利用国内某中高渗透砂岩水驱开发油田生产历史数据进行特高含水期产量预测,并与传统水驱曲线方法和FCNN的预测结果比较,发现基于深度学习的LSTM预测精度更高,针对油田生产中复杂时间序列的预测结果更准确。利用LSTM模型预测了另外两个油田的月产油量,预测结果较好,验证了方法的通用性。图3表3参40

关键词: 产量预测; 特高含水期; 机器学习; 长短期记忆神经网络; 人工智能
中图分类号:TP392 文献标志码:A 文章编号:1000-0747(2020)05-1009-07
Production prediction at ultra-high water cut stage via Recurrent Neural Network
WANG Hongliang, MU Longxin, SHI Fugeng, DOU Hongen
PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China
Abstract

A deep learning method for predicting oil field production at ultra-high water cut stage from the existing oil field production data was presented, and the experimental verification and application effect analysis were carried out. Since the traditional Fully Connected Neural Network (FCNN) is incapable of preserving the correlation of time series data, the Long Short-Term Memory (LSTM) network, which is a kind of Recurrent Neural Network (RNN), was utilized to establish a model for oil field production prediction. By this model, oil field production can be predicted from the relationship between oil production index and its influencing factors and the trend and correlation of oil production over time. Production data of a medium and high permeability sandstone oilfield in China developed by water flooding was used to predict its production at ultra-high water cut stage, and the results were compared with the results from the traditional FCNN and water drive characteristic curves. The LSTM based on deep learning has higher precision, and gives more accurate production prediction for complex time series in oil field production. The LSTM model was used to predict the monthly oil production of another two oil fields. The prediction results are good, which verifies the versatility of the method.

Keyword: production prediction; ultra-high water cut; machine learning; Long Short-Term Memory; artificial intelligence
0 引言

油田开发指标预测是评价油田开采状况、编制油田开发规划、进行油田开发方案设计与调整等决策问题的基础和依据, 只有对油田开发指标进行科学可靠的预测, 才能实现对各项措施工作的科学安排部署和工作量的合理匹配, 确保规划目标的实现。

油田进入特高含水（含水率大于90%）阶段, 利用水驱特征曲线预测特高含水期产量, 水驱特征曲线发生上翘, 预测结果误差较大, 已不适于描述特高含水期产量递减规律[1, 2, 3]。一些学者对水驱特征曲线进行了改造, 在不同程度上都可以对特高含水期的实际生产数据进行拟合, 但所得水驱特征曲线多为非线性曲线, 不便于应用且外推预测的误差较大。此外, 油田地质条件复杂, 进入特高含水期, 地层物性变化多样, 常规油藏工程方法考虑的影响因素少, 一般只能进行平滑预测[4, 5]; 油藏数值模拟等方法的时效性不强, 费用高。因此, 需要一种能够提高工作效率、提高预测精度的开发指标预测方法。

近年来, 随着人工智能在科学和工程领域的广泛应用, 数字化转型、大数据、人工智能已经成为石油和天然气工业的热点[6, 7, 8, 9, 10, 11, 12]。石油工业上游领域的学术期刊中频繁出现人工智能应用的相关报道[13, 14, 15, 16, 17, 18]。很多学者利用支持向量机（Support Vector Machine, 简称SVM）、自回归（Autoregressive, 简称AR）和人工神经网络（Artificial Neural Network, 简称ANN）等方法来进行地质特征预测[19]、岩性判别[20]、油井产量主控因素分析[21, 22, 23]等。其中, 用于油井产量预测的人工神经网络以全连接神经网络（Fully Connected Neural Network, 简称FCNN）为主[24, 25, 26, 27, 28]。由于FCNN无法保存、利用之前时刻的信息, 无法预测时间序列数据, 一些学者通过组合模型来预测油井产量[29, 30]。为了生成油田高含水阶段产量时间序列数据, 更加合理的选择是利用循环神经网络（Recurrent Neural Network, 简称RNN）。在RNN中, 每个神经单元内存在一个能够重复使用该单元的自循环结构, 这一循环结构使得先前的信息可以保留并在之后被使用。由于信息可以在循环神经网络中自由流动, 基于该方法预测的产量综合考虑了时间因素, 更加符合实际生产情况。

本文使用深度学习算法的长短期记忆神经网络（Long Short-Term Memory, 简称LSTM）[31]预测油田特高含水期产量, 其也适用于预测其他阶段的油田与油井产量[32, 33]。该网络在每个自循环结构内引入门结构, 进一步模仿生物神经元信息传导模式, 不需任何额外的调整即可储存更加长期的序列信息。这一优点使其在人工智能和深度学习领域获得了极大关注, 在自然语言处理[34]、语音识别[35]、机器翻译[36]等领域都得到了广泛应用。另外, LSTM也被应用于水文学、金融等领域来处理包含时间序列数据的问题[37, 38]。

本文旨在根据油田生产历史数据, 通过使用LSTM预测油田特高含水期的产量。首先, 阐述LSTM的理论基础以及相应的网络结构设计和特殊设置。其次, 分析LSTM在油田特高含水期产量预测中的应用效果, 并与传统水驱曲线方法和FCNN模型的预测结果进行对比。

1 原理与方法
1.1 长短期记忆神经网络

和回归预测不同, 时间序列预测在时间上具有复杂的序列依赖关系。FCNN无法根据序列数据中先前步骤的预测结果来预测当前步骤中的计算结果, 无法分析序列数据中前后数据之间的相互关系。RNN的结构可以让之前步骤中的信息持续保留并影响后续步骤的运算, 然而, 如果先前的相关信息所在的位置与当前计算步骤之间距离非常远, 因为不断输入数据的影响, 模型中的记忆模块（单一的tanh层或sigmoid层）无法长期有效地保存历史信息, 容易产生梯度消失或者梯度爆炸等问题[39]。LSTM是一种特殊的RNN, 它改进了传统RNN中的记忆模块。通过门结构和记忆单元状态的设计, 使得LSTM可以让时间序列中的关键信息有效地更新和传递, 有效地将长距离信息保存在隐藏层中。LSTM中隐藏层的循环网络包含遗忘门、输入门、输出门和1个tanh层。处理器状态有选择地保存先前步骤中的有用信息并贯穿整个LSTM。交互层中的门可以根据上一步的隐状态和当前步骤的输入对处理器状态中的信息进行增加、删除和更新操作, 更新后的处理器状态和隐状态向后传递[27]。LSTM模型支持端到端预测, 可以实现单因素预测单指标、多因素预测单指标和多因素预测多指标。

1.2 特征选择

在机器学习问题上, 不相关变量可能对模型预测精度产生负面影响。特征选择可以消除不相关的变量, 改进模型精度, 规避过拟合现象。

递归特征消除（Recursive feature elimination）[40]算法是特征选择方法之一, 其主要思想是使用一个基模型（本文利用支持向量机模型）来进行多轮训练。首先基于全部特征进行训练, 针对训练结果对每个特征进行打分, 每个特征的打分规则如（1）式所示。去掉得分最小的特征, 即最不重要的特征。利用剩余的特征进行第2轮训练, 递归此过程直至剩余最后1个特征。特征消除顺序即特征的重要性排序, 最先消除的特征重要程度最低, 最后消除的特征重要程度最高。

$c_i=\omega^2_i$ （1）

2 数据预处理与模型训练

本文以国内某油田产量数据为例, 建立产量预测模型。该油田为中高渗透砂岩水驱开发油田, 2005年进入特高含水阶段。目前采油井1.4× 104口, 年产油800多万吨, 含水率大于95%。本文采用该油田2001年1月至2018年12月的生产数据开展模型验证实验。依据砂岩油田水驱开发特征以及油田开发生产历史, 筛选出产量影响因素包括新井数、新井产量、前1年投产采油井数、前1年投产采油井产量贡献、前2年投产采油井数、前2年投产采油井产量贡献、…、前9年投产采油井数、前9年投产采油井产量贡献、前10年及以前投产采油井数、前10年及以前投产采油井产量贡献、注水井数、月注入量、含水率、生产天数、剩余可采储量、新区动用可采储量、老区新增可采储量、措施井次、措施增油量及原油价格, 共计32项。需要说明的是, 以2018年为例, 前1年为2017年, 前2年为2016年, 以此类推。实验的主要目的是：①评价LSTM根据产量影响因素以及历史产量数据预测未来产量的能力; ②比较LSTM、传统水驱曲线方法和FCNN的预测结果。

2.1 影响因素分析

使用全部32个产量影响因素对数据质量要求高, 相关性较小的因素会对模型精度造成干扰。只使用主控因素可以增加模型灵活性, 降低模型复杂度, 提高模型精度。因此, 本文利用基于支持向量机的递归特征消除方法进行特征选择, 将各影响因素按重要程度排序。经交叉验证得到最优的特征数量为17, 所以选择重要程度排前17的影响因素, 即生产天数、前10年及以前投产采油井产量贡献、前1年投产采油井产量贡献、前9年投产采油井产量贡献、前7年投产采油井产量贡献、前6年投产采油井产量贡献、前4年投产采油井产量贡献、前3年投产采油井产量贡献、前8年投产采油井产量贡献、前5年投产采油井产量贡献、前2年投产采油井产量贡献、前10年及以前投产采油井数、当年投产采油井产量贡献、措施增油量、措施井次、当年投产采油井数、月注入量。

2.2 数据标准化

为了提高模型的预测精度和消除指标之间量纲的影响, 需要对输入和输出数据进行预处理。由于数据较稳定, 不存在极端的最大、最小值, 本文采用归一化处理方法, 将其映射到[0, 1]区间, 线性变换式为：

$X_{norm}=\frac{X-X_{min}}{X_{max}-X_{min}}$ （2）

2.3 样本集构造

2.3.1 特征向量构造

假设Xt为t时刻的产量影响因素特征向量, 目标是预测未来N个月的产量。每个特征向量包含17个特征, 编号为F1— F17。其中, F1— F9为前1— 9年投产采油井产量贡献, F10为前10年及以前投产采油井产量贡献, F11为前10年及以前投产采油井数, F12为当年投产采油井产量贡献, F13为措施增油量, F14为生产天数, F15为当年投产采油井数, F16为月注入量, F17为措施井次。特征F1— F13采用t时刻的数据。特征F14— F17采用t+N时刻的数据, 如果有实际的生产数据则使用生产数据, 否则使用计划数据。也就是说, 后4个特征的时间比前13个特征的时间滞后N个月。

2.3.2 时间序列化数据构造

LSTM的特殊结构要求其输入是特征向量的序列, 而序列是由连续的M个特征向量组成, M为时间序列步长。所以, 在进行训练之前, 需要构造LSTM的输入序列。假设Xt为t时刻的特征向量, 则本文构造的输入序列形式为{Xt– M+1, Xt– M+2, …, Xt}。第1个序列为{X1, X2, …, XM}, 第2个序列为{X2, X3, …, XM+1}, 并以此类推得到其他序列。

2.3.3 样本数据集构造

本文利用LSTM模型的多对多预测功能, 即用历史上多个月的生产数据预测未来多个月的产量。样本由输入时间序列和输出时间序列构成。假设生产时间为T, 即记录了T个月的生产数据, 时间步长为M, 预测产量滞后N个月, Yt为t时刻的月产油量。则输入时间序列包括SI1={X1, X2, …, XM}, SI2={X2, X3, …, XM+1}, …, SIZ={XZ, XZ+1, …, XZ+M– 1}; 输出时间序列包括SO1={YM+1, YM+2, …, YM+N}, SO2={YM+2, YM+3, …, YM+N+1}, …, SOZ={YM+Z, YM+Z+1, …, YM+Z+N– 1}, 共组成Z个监督学习样本, 则Z=T– N– M+1。模型要求的输入样本为形如（Z, M, F）的三维张量, 其中F为特征向量的维度。在输入时间序列中, 将输入数据划分为A、B两个部分：A部分包含特征F1— F13, 代表第1个月到第T– N个月的实际生产数据; B部分包含特征F14— F17, 代表第T– N+1个月到第T个月的计划数据。

2.3.4 数据集划分

本文选取2001年1月至2018年12月的生产数据为实验数据, 总共有18× 12=216个月的生产数据。结合前文的时间滞后和序列化方法组装成算法需要的样本数据集。其中2001年1月至2016年12月的数据作为训练集, 2017年1月至2017年12月的数据为验证集, 2018年1月至2018年12月的数据作为测试集。

2.4 评价指标

为了评估LSTM模型在产量预测上的准确度, 本文采用相关系数和平均绝对百分误差（Mean Absolute Percentage Error, MAPE）这两个评价指标。

2.5 模型训练与自动调优

本文实验验证采用Tensorflow开源平台作为深度学习平台, 采用Python 3.3编写实验程序, 同时使用了一些第三方库, 如使用Sklearn、Numpy计算技术指标, 使用Keras搭建网络结构。

2.5.1 模型训练

首先随机初始化LSTM神经网络参数。设置神经网络层数（layers）为1、时间序列步长（timesteps）为12个月、神经元个数（neurons）为55、训练循环次数（epochs）为60、批量大小（batchsize）为3。然后使用训练数据进行模型训练, 模型训练完成后准备验证模型。

以预测2018年12个月的产量为例, 输入数据为时间步长为12的序列数据, A部分为2017年1月至2017年12月的实际生产数据, B部分为2018年1月至2018年12月的计划数据; 输出数据为2018年1月至2018年12月的月产油量数据序列。模型预测结果的相关系数为0.83, 平均绝对百分误差为25%。

2.5.2 参数自动调优

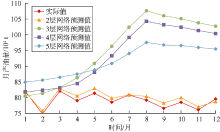
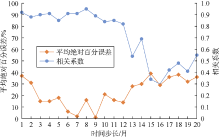
随机初始化神经网络参数, 模型的预测结果不一定理想, 而神经网络模型参数非常多, 每个参数又有较宽的取值范围, 因此本文采用手动确定参数范围, 计算机自动寻找最优解的方式来训练模型。首先通过手动尝试的方法来开发过拟合的模型, 如添加更多的隐层、每层设置更多的神经元节点, 同时监控训练误差和验证误差的变化情况, 通过寻找验证数据集上性能开始下降（过拟合）的位置, 确定参数范围。以网络层数和时间序列步长为例。如图1所示, 当网络层数为2时, 预测值与实际值的相关系数为0.94, 平均绝对百分误差为2%; 当网络层数继续增加时, 发生过拟合, 预测结果与实际值偏差较大, 所以设置网络层数范围为[1, 2]。如图2所示, 当时间序列步长小于13个月时, 相关系数大于0.80, 平均绝对百分误差小于20%, 所以确定时间步长参数范围为[1, 12]。

图1 不同层数神经网络产量预测值与实际值对比

图2 不同时间序列步长下的相关系数、平均绝对百分误差

确定所有参数的范围后, 采用计算机自动调优的方法寻找最优参数组合。自动调优的参数包括网络层数、时间步长、神经元个数、训练循环次数、批量大小。依据确定的参数范围, 结合油田开发生产经验, 设置每个参数的步长, 各参数及其取值如表1所示。

表1 神经网络模型参数组合

LSTM的损失函数（loss function）使用均方误差（Mean Square Error, MSE）。

优化器（optimizer）使用“ adam” , 用来计算神经网络每个参数的自适应学习率。采用Dropout（按照一定的比例将神经元暂时从网络中丢弃）方法防止过拟合, Dropout的比例为30%。

这里共有34 848个参数组合, 程序采用分布式技术将每组参数生成对应的模型文件和预测结果进行存储。待所有参数训练完成后, 选用相关系数高且平均绝对百分误差小的模型为最优模型。

3 结果与讨论
3.1 实验结果

利用最优模型预测该油田2018年的产量, 通过与实际产量对比, 相关系数为0.93, 平均绝对百分误差为1%（见表2）。LSTM最优参数组合为：隐藏层层数为2, 隐藏层神经元个数分别为55和25, 时间步长为9个月, 即用过去9个月的信息来预测未来1个月的产量, 批量大小为2, 即用每2个样本更新1次网络参数, 训练循环次数为60。

表2 水驱曲线、FCNN及LSTM预测结果指标对比

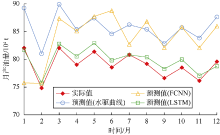
通过模型在测试集上的预测结果可知（见图3）, LSTM模型的预测结果与实际产量的趋势基本相同, 并且数值也较为接近, 比传统水驱曲线和FCNN模型预测得更准确。实验结果表明LSTM模型能较好地用于油气产量时间序列的预测。

图3 水驱曲线、FCNN和LSTM预测结果

利用LSTM模型预测了另外两个油田2018年的月产油量（见表3）, 显示了较好的预测结果, 验证了本文方法的通用性。

表3 应用LSTM模型对两个油田进行产量预测的结果
3.2 讨论

本文将机器学习中的LSTM应用于油田特高含水期的产量预测。LSTM能够有效建立在时间上具有长期相关性的产量序列的模式, 并基于这些模式对产量进行预测。

在模型训练过程中, 模型考虑因素的多少影响预测精度。LSTM模型既考虑了产量指标与影响因素之间的关系, 又考虑了产量指标自身的变化趋势, 预测准确度和相关性都较高; FCNN只考虑了产量指标与影响因素之间的关系, 预测结果高于实际值; 水驱曲线模型只考虑了产量自身的变化趋势, 预测结果高于实际值。特征工程对模型预测精度也有重要影响。针对同样的模型结构, 进行特征工程操作后的预测结果明显优于未进行特征工程操作的预测结果。根据特征工程分析, 历年投产井在当年的产量、生产天数、新投产井数、措施井次、措施增油量、月注入量等对产量的影响较大。根据预测结果分析, LSTM针对时间序列数据的特征提取能力较强, 可以提取历年投产井在当年的产量剖面数据, 并依靠神经网络记忆单元中储存的历史生产信息, 模拟出历年投产井的产量随时间变化的趋势, 相当于预测老井产量; 利用新投产井数和新井产量的历史数据, 挖掘二者之间的关系, 并预测新井产量; 利用措施井次和措施增油量历史数据能够反映措施工作量带来的增油量情况。

4 结语

利用LSTM实现了基于数据驱动方法预测油田特高含水期产量, 并与传统水驱曲线方法进行对比, 显示出良好的趋势和较小的误差, 可以快速预测新井、老井产量变化情况。与数值模拟相比, 该方法不需要建立物理模型, 可实现快速预测。虽然物理意义缺失, 但可以丰富产量预测方法, 支撑油田开发调整工作。

LSTM具有强大的非线性拟合和时间记忆能力, 从训练数据中提取信息的能力较强。既能考虑产量指标与影响因素之间的关系, 又能考虑产量指标自身的变化趋势。LSTM是基于历史数据建立目标和影响因素之间的非线性映射关系。要利用LSTM建立特高含水期产量预测模型, 需要获取一定时间段的特高含水期生产数据。本文所选择油田具备10年以上特高含水期生产历史, 并选择了特高含水之前的4年生产数据参加了模型训练。针对生产历史较短的油田, 可以考虑迁移学习的方法, 利用其他具备较长生产历史的油田训练获得的模型进行预测分析。特征工程操作有助于提高模型精度。特征选择可以过滤掉非主控因素; 标准化操作可以消除量纲的影响。网络的深度要适应数据的复杂情况, 从浅层网络开始尝试, 通过观察模型精度变化曲线确定模型参数的取值范围, 再采用分布式技术针对不同模型参数组合并行训练, 有助于提高模型训练效率。

符号注释：

ci— — 第i个特征的得分; F— — 特征向量维度; M— — 时间步长, 月; N— — 滞后时间, 月; t— — 时间, 月; T— — 生产时间, 月; X— — 生产指标的特征值; Xmax— — 生产指标的最大值; Xmin— — 生产指标的最小值; Xnorm— — 标准化处理后的值; Xt— — t时刻的特征向量; Yt— — t时刻的月产油量预测结果, t; Z— — 组装的样本总数; ω i— — 支持向量机模型中最优超平面第i个特征的权重。

编辑 胡苇玮

参考文献
[1] 黄广庆. 特高含水期产量递减分析及递减率表征公式[J]. 科学技术与工程, 2019, 19(15): 99-104.
HUANG Guangqing. Production decline analysis and characterization formula of decline rate at the ultra-high water cut stage[J]. Science Technology and Engineering, 2019, 19(15): 99-104. [本文引用:1]
[2] 王继强, 石成方, 纪淑红, 等. 特高含水期新型水驱特征曲线[J]. 石油勘探与开发, 2017, 44(6): 955-960.
WANG Jiqiang, SHI Chengfang, JI Shuhong, et al. New water drive characteristic curves at ultra-high water cut stage[J]. Petroleum Exploration and Development, 2017, 44(6): 955-960. [本文引用:1]
[3] 陈元千, 陶自强. 高含水期水驱曲线的推导及上翘问题的分析[J]. 断块油气田, 1997, 4(3): 19-24.
CHEN Yuanqian, TAO Ziqiang. Derivation of water drive curve at high water-cut stage and its analysis of upwarding problem[J]. Fault-Block Oil & Gas Field, 1997, 4(3): 19-24. [本文引用:1]
[4] 刘晓华, 邹春梅, 姜艳东, 等. 现代产量递减分析基本原理与应用[J]. 天然气工业, 2010, 30(5): 50-54.
LIU Xiaohua, ZOU Chunmei, JIANG Yand ong, et al. Basic principle and application of modern production decline analysis[J]. Natural Gas Industry, 2010, 30(5): 50-54. [本文引用:1]
[5] 张倩倩. 产量递减分析方法简评[J]. 油气地球物理, 2013, 11(3): 41-44.
ZHANG Qianqian. A brief review of production decline analysis methods[J]. Oil and Gas Geophysics, 2013, 11(3): 41-44. [本文引用:1]
[6] CRNKOVIC-FRIIS L, ERLANDSON M. Geology driven EUR prediction using deep learning[R]. SPE 174799-MS, 2015. [本文引用:1]
[7] GU M, GOKARAJU D, CHEN D, et al. Shale fracturing characterization and optimization by using anisotropic acoustic interpretation, 3D fracture modeling, and supervised machine learning[J]. Petrophysics, 2016, 57(6): 573-587. [本文引用:1]
[8] SIDAHMED M, ROY A, SAYED A. Streamline rock facies classification with deep learning cognitive process[R]. SPE 187436-MS, 2017. [本文引用:1]
[9] WU P, JAIN V, KULKARNI M S, et al. Machine learning-based method for automated well-log processing and interpretation[M]//ALUMBAUGH D, BEVC D. SEG technical program expand ed abstracts 2018. Tulsa: Society of Exploration Geophysicists, 2018: 2041-2045. [本文引用:1]
[10] NOSHI C I, ASSEM A I, SCHUBERT J J. The role of big data analytics in exploration and production: A review of benefits and applications[R]. SPE 193776-MS, 2018. [本文引用:1]
[11] PHAM N, FOMEL S, DUNLAP D. Automatic channel detection using deep learning[M]//ALUMBAUGH D, BEVC D. SEG technical program expand ed abstracts 2018. Tulsa: Society of Exploration Geophysicists, 2018: 2026-2030. [本文引用:1]
[12] LI W. Classifying geological structure elements from seismic images using deep learning[M]//ALUMBAUGH D, BEVC D. SEG technical program expand ed abstracts 2018. Tulsa: Society of Exploration Geophysicists, 2018: 4643-4648. [本文引用:1]
[13] MEHTA A. Tapping the value from big data analytics[J]. Journal of Petroleum Technology, 2016, 68(12): 40-41. [本文引用:1]
[14] HALL B. Facies classification using machine learning[J]. The Leading Edge, 2016, 35(10): 906-909. [本文引用:1]
[15] CARPENTER C. Geology-driven estimated-ultimate-recovery prediction with deep learning[J]. Journal of Petroleum Technology, 2016, 68(5): 74-75. [本文引用:1]
[16] MA S M. Technology focus: Formation evaluation (August 2018)[J]. Journal of Petroleum Technology, 2018, 70(8): 50. [本文引用:1]
[17] SAPUTELLI L. Technology focus: Petroleum data analytics[J]. Journal of Petroleum Technology, 2016, 68(10): 66. [本文引用:1]
[18] LI H, MISRA S. Long short-term memory and variational autoencoder with convolutional neural networks for generating NMR T2 distributions[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 16(2): 192-195. [本文引用:1]
[19] JOBE T D, VITAL-BRAZIL E, KHAIF M. Geological feature prediction using image-based machine learning[J]. Petrophysics, 2018, 59(6): 750-760. [本文引用:1]
[20] SILVA A A, LIMA NETO I A, MISSÁGIA R M, et al. Artificial neural networks to support petrographic classification of carbonate-siliciclastic rocks using well logs and textural information[J]. Journal of Applied Geophysics, 2015, 117: 118-125. [本文引用:1]
[21] 柴艳军. 基于灰色关联法的页岩气水平井产量主控因素分析[J]. 重庆科技学院学报(自然科学版), 2018, 20(2): 32-34.
CHAI Yanjun. Analysis of main controlling factors of shale gas horizontal well production based on grey correlation method[J]. Journal of Chongqing University of Science and Technology (Natural Science Edition), 2018, 20(2): 32-34. [本文引用:1]
[22] 王忠东, 王业博, 董红, 等. 页岩气水平井产量主控因素分析及产能预测[J]. 测井技术, 2017, 41(5): 577-582.
WANG Zhongdong, WANG Yebo, DONG Hong, et al. Analysis of production control factors and productivity prediction of horizontal wells in shale gas[J]. Journal of Well Logging Technology, 2017, 41(5): 577-582. [本文引用:1]
[23] 李亚林. 基于机器学习方法研究煤层气单井产量主控因素及产量预测[D]. 北京: 中国石油大学(北京), 2017.
LI Yalin. Study on main control factors and production prediction of single well production of coalbed methane based on machine learning[D]. Beijing: China University of Petroleum (Beijing), 2017. [本文引用:1]
[24] 李春生, 谭民浠, 张可佳. 基于改进型BP神经网络的油井产量预测研究[J]. 科学技术与工程, 2011, 11(31): 7766-7769.
LI Chunsheng, TAN Minxi, ZHANG Kejia. Oil well production prediction based on improved BP neural network[J]. Science and Technology and Engineering, 2011, 11(31): 7766-7769. [本文引用:1]
[25] 田亚鹏, 鞠斌山. 基于遗传算法改进BP神经网络的页岩气产量递减预测模型[J]. 中国科技论文, 2016, 11(15): 1710-1715.
TIAN Yapeng, JU Binshan. Shale gas production decline prediction model based on improved BP neural network based on genetic algorithm[J]. Chinese Science and Technology Paper, 2016, 11(15): 1710-1715. [本文引用:1]
[26] 马林茂, 李德富, 郭海湘, 等. 基于遗传算法优化BP神经网络在原油产量预测中的应用: 以大庆油田BED试验区为例[J]. 数学的实践与认识, 2015, 45(24): 117-128.
MA Linmao, LI Defu, GUO Haixiang, et al. Application of BP neural network optimization based on genetic algorithm in crude oil production prediction: Take BED test area of Daqing Oilfield as an example[J]. Practice and Understand ing of Mathematics, 2015, 45(24): 117-128. [本文引用:1]
[27] 樊灵, 赵孟孟, 殷川, 等. 基于BP神经网络的油田生产动态分析方法[J]. 断块油气田, 2013, 20(2): 204-206.
FAN Ling, ZHAO Mengmeng, YIN Chuan, et al. Dynamic analysis method of oil field production based on BP neural network[J]. Fault Block Oil and Gas Field, 2013, 20(2): 204-206. [本文引用:2]
[28] 杨婷婷. 基于人工神经网络的油田开发指标预测模型及算法研究[D]. 大庆: 东北石油大学, 2013.
YANG Tingting. Research on prediction model and algorithm of oilfield development index based on artificial neural network[D]. Daqing: Northeast Petroleum University, 2013. [本文引用:1]
[29] 谷建伟, 隋顾磊, 李志涛, 等. 基于ARIMA-Kalman滤波器数据挖掘模型的油井产量预测[J]. 深圳大学学报(理工版), 2018, 35(6): 575-581.
GU Jianwei, SUI Gulei, LI Zhitao, et al. Oil well production prediction based on ARIMA-Kalman filter data mining model[J]. Journal of Shenzhen University (Science and Technology Edition), 2018, 35(6): 575-581. [本文引用:1]
[30] 李达. 基于时间序列分析方法的油田产量预测与应用[D]. 兰州: 兰州理工大学, 2018.
LI Da. Oilfield production prediction and application based on time series analysis method[D]. Lanzhou: Lanzhou University of Technology, 2018. [本文引用:1]
[31] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. [本文引用:1]
[32] 谷建伟, 周梅, 李志涛, 等. 基于数据挖掘的长短期记忆网络模型油井产量预测方法[J]. 特种油气藏, 2019, 26(2): 77-81.
GU Jianwei, ZHOU Mei, LI Zhitao, et al. Prediction method of oil well production based on data mining based on long-term and short-term memory network model[J]. Special Oil and Gas Reservoirs, 2019, 26(2): 77-81. [本文引用:1]
[33] 侯春华. 基于长短期记忆神经网络的油田新井产油量预测方法[J]. 油气地质与采收率, 2019, 26(3): 105-110.
HOU Chunhua. Prediction method of oil production in new wells based on long and short term memory neural network[J]. Oil and Gas Geology and Recovery, 2019, 26(3): 105-110. [本文引用:1]
[34] MIKOLOV T, KARAFIÁT M, BURGET L, et al. Recurrent neural network based language model[R]. Makuhari, Chiba, Japan: 11th Annual Conference of the International Speech Communication Association, 2010. [本文引用:1]
[35] GRAVES A, JAITLY N. Towards end-to-end speech recognition with recurrent neural networks[C]//Proceedings of the 31st International Conference on Machine Learning. Washington D. C. : IEEE Computer Society Press, 2014: 1764-1772. [本文引用:1]
[36] SUTSKEVER I, VINYALS O, LE Q V. Sequence to sequence learning with neural networks[R]. Montreal, Canada: Advances in Neural Information Processing Systems 27 (NIPS 2014), 2014. [本文引用:1]
[37] 杨祎玥, 伏潜, 万定生. 基于深度循环神经网络的时间序列预测模型[J]. 计算机技术与发展, 2017, 27(3): 35-38.
YANG Yiyue, FU Qian, WAN Dingsheng. A prediction model for time series based on deep recurrent neural network[J]. Computer Technology and Development, 2017, 27(3): 35-38. [本文引用:1]
[38] 黄婷婷, 余磊. SDAE-LSTM模型在金融时间序列预测中的应用[J]. 计算机工程与应用, 2019, 55(1): 142-148.
HUANG Tingting, YU Lei. Application of SDAE-LSTM model in financial time series forecasting[J]. Computer Engineering and Application, 2019, 55(1): 142-148. [本文引用:1]
[39] DAS S, GILES C L, SUN G. Learning context-free grammars: Capabilities and limitations of a recurrent neural network with an external stack memory[C]//Proceedings of the Fourteenth Annual Conference of the Cognitive Science Society. New York: Cognitive Science Society, 1992. [本文引用:1]
[40] GUYON I, WESTON J, BARNHILL S, et al. Gene selection for cancer classification using support vector machines[J]. Machine Learning, 2002, 46(1/2/3): 389-422. [本文引用:1]