低渗透油藏直井体积压裂改造效果评价方法

引用本文

张安顺, 杨正明, 李晓山, 夏德斌, 张亚蒲, 骆雨田, 何英, 陈挺, 赵新礼. 低渗透油藏直井体积压裂改造效果评价方法[J]. 石油勘探与开发, 2020,47(2): 409-415.
ZHANG Anshun, YANG Zhengming, LI Xiaoshan, XIA Debin, ZHANG Yapu, LUO Yutian, HE Ying, CHEN Ting, ZHAO Xinli. An evaluation method of volume fracturing effects for vertical wells in low permeability reservoirs[J]. Petroleum Exploration & Development, 2020,47(2): 409-415. 复制到剪切板

Doi: 10.11698/PED.2020.02.20
Permissions

低渗透油藏直井体积压裂改造效果评价方法

张安顺¹, 杨正明^1,², 李晓山³, 夏德斌^1,², 张亚蒲^1,², 骆雨田^1,², 何英^1,², 陈挺^1,², 赵新礼^1,²

1. 中国石油勘探开发研究院渗流流体力学研究所,北京 100083

2. 中国科学院渗流流体力学研究所,河北廊坊 065007

3. 新疆油田公司勘探开发研究院,新疆克拉玛依 834000

第一作者简介：张安顺（1994-）,男,新疆克拉玛依人,中国石油勘探开发研究院在读硕士研究生,主要从事数值模拟及压裂效果评价研究。地址：北京市海淀区学院路20号,中国石油勘探开发研究院渗流流体力学研究所,邮政编码：100083。E-mail：zhanganshun@petrochina.com.cn

收稿日期: 2019-06-26

基金项目: 国家科技重大专项（2017ZX05013-001）; 中国石油天然气集团有限公司重大基础科技攻关课题“致密油藏物理模拟方法与开采机理研究”（2018B-4907）

摘要

为评价低渗透油藏直井体积压裂改造效果及其动态变化过程,建立了油水两相渗流模型和井模型,在此基础上提出了基于生产数据及压裂液返排数据的改造效果评价方法,并进行了矿场实例分析。将压裂后主裂缝附近区域划分为不同的改造区域,用改造区域渗透率和面积分别表征压裂后缝网的改造强度和规模,并将改造区域导流能力定义为改造区域渗透率与面积的乘积。进行了参数敏感性分析,发现裂缝半长和核心区域渗透率主要影响近井端流体流动规律,即生产早期规律,基质渗透率主要影响裂缝远端流体流动规律。以长庆油田典型老井为例,评价了该井两轮次体积压裂后的压裂改造效果及其变化,发现第1次体积压裂后随着生产时间的增加,改造区域渗透率和导流能力逐渐降低,压裂效果逐渐变小直至消失;第2次体积压裂后,改造区域渗透率及导流能力又大幅增加。图12表2参30

关键词: 体积压裂; 压裂效果评价; 压裂改造区域; 导流能力; 低渗透油藏; 直井

中图分类号:TE357 文献标志码:A

An evaluation method of volume fracturing effects for vertical wells in low permeability reservoirs

ZHANG Anshun¹, YANG Zhengming^1,², LI Xiaoshan³, XIA Debin^1,², ZHANG Yapu^1,², LUO Yutian^1,², HE Ying^1,², CHEN Ting^1,², ZHAO Xinli^1,²

1. Research Institute of Petroleum Exploration & Development, PetroChina, Beijing 100083, China;

2. Institute of Porous Flow and Fluid Mechanics, University of Chinese Academy of Sciences, Langfang 065007, China

3. Research Institute of Petroleum Exploration and Development, PetroChina Xinjiang Oilfield Company, Karamay 834000, China

Abstract

To evaluate the fracturing effect and dynamic change process after volume fracturing with vertical wells in low permeability oil reservoirs, an oil-water two-phase flow model and a well model are built. On this basis, an evaluation method of fracturing effect based on production data and fracturing fluid backflow data is established, and the method is used to analyze some field cases. The vicinity area of main fracture after fracturing is divided into different stimulated regions. The permeability and area of different regions are used to characterize the stimulation strength and scale of the fracture network. The conductivity of stimulated region is defined as the product of the permeability and area of the stimulated region. Through parameter sensitivity analysis, it is found that half-length of the fracture and the permeability of the core area mainly affect the flow law near the well, that is, the early stage of production; while matrix permeability mainly affects the flow law at the far end of the fracture. Taking a typical old well in Changqing Oilfield as an example, the fracturing effect and its changes after two rounds of volume fracturing in this well are evaluated. It is found that with the increase of production time after the first volume fracturing, the permeability and conductivity of stimulated area gradually decreased, and the fracturing effect gradually decreased until disappeared; after the second volume fracturing, the permeability and conductivity of stimulated area increased significantly again.

Keyword: volume fracturing; fracturing effect evaluation; fracturing area; conductivity; low permeability reservoir; vertical well

文章图片

0 引言

近年来低渗透油气藏已经逐渐成为国内油气勘探开发的主体, 低渗透油藏储量已占探明石油储量的70%以上^[1]。由于低渗透油藏喉道细小^{[2, 3, 4]}, 补充能量较难, 导致产量逐年递减, 油井逐渐变成低产低效井。中国石油天然气集团有限公司（以下简称中国石油）有该类低产低效直井8万多口, 用常规压裂方法难以达到增产目的。近年来, 中国石油借鉴页岩气储集层体积压裂的理念, 在长庆、吉林、大庆等油田开展老井（直井）重复体积压裂矿场试验, 取得了显著成效。

目前评价体积压裂效果的方法主要有两种。一种是直接法, 即通过一些裂缝监测技术来评价体积压裂后的储集层改造区域, 如微地震、测斜仪、分布式光纤等技术。有些学者利用微地震监测结果校正了体积压裂后地质模型, 并针对不同压裂方案进行开发指标预测^{[5, 6]}。有些学者基于微地震数据及成像结果对储集层改造区域进行了大量研究^{[7, 8, 9]}。有些学者基于微地震等裂缝监测技术对复杂缝网进行分区, 给定不同区域的渗透率, 并进行产能预测及敏感性分析^{[10, 11, 12]}。测斜仪主要通过测量裂缝引起的地层倾斜量来反演地层参数, 进而描述体积压裂后裂缝的复杂程度^{[13, 14]}。分布式光纤通过测量产液剖面、各层段产量的贡献来对裂缝进行监测^{[15, 16, 17]}。这些直接法只能评价体积压裂后某一时刻的压裂效果。另一种为间接法, 即利用数学方法来进行体积压裂效果评价。有些学者^{[5, 18, 19, 20, 21]}主要考虑体积压裂后近井地带裂缝条数或表皮因子的变化, 通过模拟体积压裂后产量的变化评估体积压裂改造效果。但这些研究没有涉及体积压裂后压裂改造区域的范围、主裂缝半长等关键问题。Xu等^{[22, 23, 24, 25]}和Meyer等^{[26, 27]}针对油井在体积压裂后会形成高导流的复杂缝网结构的特点, 基于物质平衡和动量守恒方程, 分别提出线网模型和离散裂缝模型。然而, 两种模型在计算裂缝缝网参数时需结合压裂施工参数和地应力参数, 不能给出油井在压裂后生产阶段渗流场的变化规律。一般常用裂缝渗透率与缝宽的乘积来表示导流能力^{[28, 29]}, 但用该方法来表征直井体积压裂改造后导流能力存在很多不足。因此, 本文建立可以评价低渗透油藏直井体积压裂改造效果及其动态变化过程的数值方法, 提出体积压裂改造区域导流能力表征方法, 并应用于矿场实际。

1 体积压裂数值模拟模型

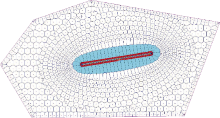
采用混合网格对油藏进行剖分（见图1）, 针对体积压裂后流体流动特征和油藏复杂地质特征采用不同类型网格。在井筒附近采用径向网格, 在远离近井地带采用非结构PEBI（perpendicular bisection）网格。这样既可以反映井眼附近流体流动特征, 又能精确描述压裂后地层的裂缝形态, 同时以较少的网格数目得到了较高的模拟精度^[30]。

	Figure Option View Download New Window
	图1 油藏体积压裂模型及网格划分示意图

1.1 流体渗流模型

储集层中流体流动符合油水两相渗流规律, 本文数值分析基于有限体积方法, 对于油相, 有如下方程：

$\underset{V_{i}}{∭} \nabla \cdot [\frac{K K_{ro}}{μ_{o} B_{o}} (\nabla p_{o} - γ_{o} \nabla Z)] d Ω = \underset{V_{i}}{∭} \frac{\partial}{\partial t} (\frac{φ S_{o}}{B_{o}}) d Ω + q_{osc}$ （1）

记网格i相邻网格的编号为j, 用 $\sum_{j}$ 表示对网格i的所有相邻网格求和。应用高斯定理, 通过一系列变形, 采用隐式格式对（1）式进行离散后可得：

$\sum_{j} {[T_{ij, o} (Δ p_{o} - γ_{o} Δ Z)]}^{n + 1} = \frac{V_{i}}{Δ t} [{(\frac{φ S_{o}}{B_{o}})}_{i}^{n + 1} - {(\frac{φ S_{o}}{B_{o}})}_{i}^{n}] + q_{osc}^{n + 1}$ （2）

其中 $T_{ij, o} = λ_{ij, o} G_{ij}$

$G_{ij} = \frac{K_{i} ω_{ij}}{d_{ij}}$ $λ_{ij, o} = {(\frac{K_{ro}}{μ_{o} B_{o}})}_{ij}$

同理, 对于水相有：

$\sum_{j} {[T_{ij, w} (Δ p_{o} - Δ p_{cow} - γ_{w} Δ Z)]}^{n + 1} = \frac{V_{i}}{Δ t} [{(\frac{φ S_{w}}{B_{w}})}_{i}^{n + 1} - {(\frac{φ S_{w}}{B_{w}})}_{i}^{n}] + q_{wsc}^{n + 1}$ （3）

1.2 井模型

油井实际生产中产液量会发生变化。将生产历史按时间段划分, 在产液量恒定的情况下, 把该时间段设定为定液量生产。

对于多层压裂的直井, 对第m个生产层, 井底流量可以表示为：

$q_{b, m}^{n + 1} = \sum_{x} (J_{o, m}^{n + 1} + J_{w, m}^{n + 1}) (p_{x, m}^{n + 1} - p_{wf, m}^{n + 1})$ （4）

其中 $J_{o, m} = \frac{θK K_{ro} h}{μ_{o} B_{o} [S + \ln \ln (r_{o} / r_{w})]}$

$J_{w, m} = \frac{θK K_{rw} h}{μ_{w} B_{w} [S + \ln \ln (r_{o} / r_{w})]}$

假设无层间窜流, 则第m层产液量所占比例为：

$β = \frac{q_{b, m}}{q_{b}} = \frac{\sum_{x} (J_{o, m} + J_{w, m}) (p_{x, m} - p_{wf, m})}{\sum_{m}^{=} \sum_{x} (J_{o, m} + J_{w, m}) (p_{x, m} - p_{wf, m})}$ （5）

考虑井底储集效应, 则：

$Q_{s, m}^{n + 1} = Q_{p, m}^{n + 1} - q_{b, m}^{n + 1} = - \frac{βC}{Δ t} (p_{wf, m}^{n + 1} - p_{wf, m}^{n})$ （6）

联立（4）— （6）式, 可得第m层的井底流压为：

$p_{wf, m}^{n + 1} = \frac{\sum_{x} (J_{o, m}^{n + 1} + J_{w, m}^{n + 1}) p_{x, m}^{n + 1} + \frac{βC}{Δ t} p_{wf, m}^{n} - {Q_{p,}}_{m}}{\sum_{x} (J_{o, m}^{n + 1} + J_{w, m}^{n + 1}) + \frac{βC}{Δ t}}$ （7）

则第m层产油量为：

$q_{o, m}^{n + 1} = J_{o, m}^{n + 1} (p_{x, m}^{n + 1} - p_{wf, m}^{n + 1})$ （8）

同理可求出第m层产水量。

以上为油水两相渗流模型和井模型。对（2）式、（3）式、（4）式和（7）式进行线性化处理, 结合边界条件, 可计算出相应的压力场分布及井底流压。将井底流压的计算值与实测值进行拟合得到相关的拟合参数, 进而进行压裂效果评价。

2 体积压裂效果评价方法

在体积压裂数值模拟模型基础上, 要形成体积压裂效果评价的数值方法, 需要解决数值方法中的参数多解性问题, 这就需要进行直井体积压裂区域划分、参数敏感性分析以及体积压裂导流能力表征。

2.1 数值模拟模型验证

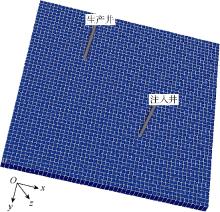
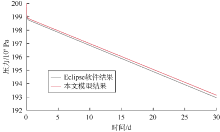
为了验证数值模拟模型的正确性, 建立一注一采地层地质模型（见图2）, 利用数值模拟模型计算压力曲线, 并与Eclipse软件模拟结果进行对比。模型平面大小为200 m× 200 m, 单个网格大小为4 m× 4 m, 模型基本参数如表1所示。定液量生产30 d, 日产液量为10 m³。由图3可知, 本文建立的数值模拟模型计算结果与Eclipse软件结果相符, 模型可靠。

	Figure Option View Download New Window
	图2 地质模型示意图

表1 模型基本参数

	Figure Option View Download New Window
	图3 本文模型与Eclipse软件计算生产井压力曲线对比

2.2 直井体积压裂区域划分及导流能力表征

以一矩形封闭边界油藏中的一口体积压裂直井为例来说明不同体积压裂区域的划分（见图4）。体积压裂主要改造区即主裂缝区或核心区域, 该区域改造强度大, 因此裂缝渗透率大, 导流能力高; 体积压裂改造影响区即次级裂缝区或外部改造区域, 与核心区域相比, 该区域裂缝渗透率较小, 导流能力较低; 改造影响区的外部为未改造区域。通过体积压裂区域划分可有效解决在数值模拟过程中渗透率和压裂改造范围存在多解性的问题。

	Figure Option View Download New Window
	图4 封闭边界油藏直井体积压裂区域划分示意图

本文用新定义的体积压裂改造区域导流能力来描述体积压裂改造效果, 用改造区域渗透率和面积分别表征压裂后缝网的改造强度和规模。将体积压裂改造区域导流能力定义为改造区域渗透率与改造区域面积的乘积。由于压裂改造区域内的渗透率非均质, 采用下式计算改造区域导流能力：

$SRC = \sum_{k}^{=} K_{k} A_{k}$ （9）

2.3 参数敏感性分析

利用开发生产数据和压裂液返排数据进行压裂效果评价, 主要是通过分析体积压裂后各参数对压力变化曲线的影响而反求出体积压裂参数和储集层参数。为了消除影响因素的多解性, 进行了参数敏感性分析。

假定油藏中有一体积压裂改造直井, 体积压裂改造区域的大小恒定, 研究裂缝半长、核心区域渗透率、基质渗透率的变化对井底流压的影响。基本参数如表2所示。

表2 封闭边界油藏体积压裂改造直井基本参数

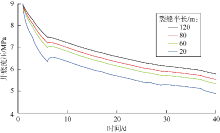
图5为不同裂缝半长下的井底流压曲线, 计算时核心区域渗透率取15× 10^-3 μ m², 基质渗透率取0.5× 10^-3 μ m²。由图5可知, 裂缝半长主要影响井底流压曲线的前期段, 而后期不同裂缝半长下井底流压曲线几乎平行。因此, 当井底流压曲线前期拟合不上时, 要调整裂缝半长。

	Figure Option View Download New Window
	图5 不同裂缝半长下的井底流压曲线

图6为不同核心区域渗透率下的井底流压曲线, 计算时裂缝半长取120 m, 基质渗透率取0.5× 10^-3 μ m²。由图6可知, 不同核心区域渗透率下井底流压曲线的前期段几乎重合, 说明该阶段相对于裂缝半长, 核心区域渗透率对井底流压曲线影响较小; 后期不同核心区域渗透率下井底流压曲线几乎平行, 表明该阶段核心区域渗透率不影响流体流动规律。结合图5和图6可以发现裂缝半长和核心区域渗透率主要影响近井端流体流动规律, 即生产早期流体流动规律, 且裂缝半长的影响更大。

	Figure Option View Download New Window
	图6 不同核心区域渗透率下的井底流压曲线

图7为不同基质渗透率下的井底流压曲线, 计算时裂缝半长取120 m, 核心区域渗透率取15× 10^-3 μ m²。由图7可知, 基质渗透率影响整条井底流压曲线形态。基质渗透率主要影响裂缝远端的流体流动规律, 基质渗透率越低, 裂缝远端流体流动能力越弱, 即流体从基质向裂缝的流动能力越弱。一般来说, 不考虑应力敏感性的情况下, 基质渗透率由前期地质资料确定且不作调整。

	Figure Option View Download New Window
	图7 不同基质渗透率下的井底流压曲线

3 矿场应用实例

3.1 实例井地质、开发概况

选取鄂尔多斯盆地长庆油田1口典型老井（Y井）, 该井为直井, 目的层位为延长组长6₂和长6₃储集层, 储集层分布相对连续。油层厚度为24 m, 孔隙度为12%, 渗透率为（0.2~0.3）× 10^-3 μ m², 含油饱和度为56%。由于储集层渗透率极低, 该井于2007年压裂投产, 初期有一定产量, 但产量下降较快, 很快成为低产井。借鉴页岩气体积压裂理念, 于2016年和2018年分别对该井进行体积压裂改造。

3.2 体积压裂效果评价

本文采用Y井2016年第1次体积压裂后至2018年第2次体积压裂前的开发生产数据对该井2016年第1次体积压裂效果进行评价; 对于2018年第2次体积压裂, 由于生产时间较短, 因此进行体积压裂效果评价时采用压裂液返排数据。

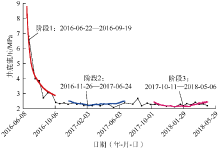
通过对第1次体积压裂后的生产数据进行处理, 拟合得到井底流压随时间变化曲线, 根据拟合结果将该井的生产过程分为3个阶段, 如图8所示。

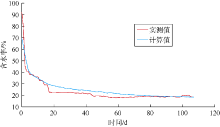
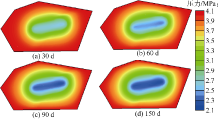
	Figure Option View Download New Window
	图8 Y井生产动态曲线拟合结果

第1阶段为2016年6月22日到2016年9月19日。该阶段计算的核心区域渗透率为15× 10^-3 μ m², 改造面积为3 687.5 m², 导流能力为55 312.5× 10^-3 μ m²· m²; 外部改造区域渗透率为1.5× 10^-3 μ m², 改造面积为13 382.52 m², 导流能力为20 073.78× 10^-3 μ m²· m²。则该阶段体积压裂改造区域导流能力为75 386.28× 10^-3 μ m²· m²。由图9可知, 随着生产时间的增加, 核心区域和外部改造区域的压力急剧降低。生产到第38天时, 核心区域的压力下降到初始压力的46.96%, 而外部改造区域的压力下降到初始压力的61.19%, 核心区域的压力下降幅度比外部改造区域的压力下降幅度大。生产到第110天时, 地层压力呈现整体下降的趋势, 而外部能量补充作用不明显。由于第1阶段的含水率变化较为明显, 采用油水两相模型对该阶段含水率进行拟合, 拟合结果如图10所示。结合该阶段含水饱和度分布拟合结果可知, 压裂后裂缝周围的含水饱和度较高。

	Figure Option View Download New Window
	图9 第1阶段地层压力分布图

	Figure Option View Download New Window
	图10 第1阶段含水率拟合结果

第2阶段为2016年11月26日到2017年6月24日。该阶段计算的核心区域渗透率为8× 10^-3 μ m², 改造面积为3 687.5 m², 导流能力为29 500× 10^-3 μ m²· m²; 外部改造区域渗透率为1× 10^-3 μ m², 改造面积为12 904.06 m², 导流能力为12 904.06× 10^-3 μ m²· m²。则该阶段体积压裂改造区域导流能力为42 404.06× 10^-3 μ m²· m²。与第1阶段相比, 第2阶段体积压裂改造区域渗透率和导流能力下降了近50%。由图11可知, 第2阶段油藏压力较为稳定, 外部能量补充作用明显, 拟合的油藏边界为定压边界。该阶段井底流压较为稳定, 后期井底流压略有上升, 也说明在边界有一定能量补充。这与该井附近有注水井相吻合。

	Figure Option View Download New Window
	图11 第2阶段地层压力分布图

第3阶段为2017年10月11日到2018年5月6日。该阶段计算的核心区域渗透率为0.8× 10^-3 μ m², 改造面积为3 687.50 m², 导流能力为2 950× 10^-3 μ m²· m²; 外部改造区域渗透率为0.5× 10^-3 μ m², 改造面积为4 832.19 m², 导流能力为2 416.1× 10^-3 μ m²· m²。则该阶段体积压裂改造区域导流能力为5 493.48× 10^-3 μ m²· m²。该阶段核心区域渗透率和导流能力下降到第2阶段的1/10, 核心区域和外部改造区域的渗透率与基质渗透率已相差不大, 表明压裂改造已逐渐失效。该阶段井底流压较为稳定, 表明在边界有一定能量补充, 但能量补充作用较弱。

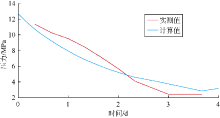
由于第1次体积压裂改造失效, Y井于2018年8月又进行了第2次体积压裂改造。由于生产时间较短, 用压裂液返排数据进行压裂效果评价, 返排压力曲线如图12所示。由于压裂液返排时间较短, 相关数据只能反映核心区域的压裂改造效果。根据压裂液返排数据计算的核心区域渗透率为90× 10^-3 μ m², 改造面积为7 241.89 m², 导流能力为651 770.1× 10^-3 μ m²· m²。与第1次体积压裂第1阶段相比, 核心区域渗透率提高了5倍, 改造面积增大了近1倍, 导流能力增加了10倍以上。

	Figure Option View Download New Window
	图12 压裂液返排阶段压力随时间变化曲线

分析体积压裂改造区域导流能力的动态变化过程可以发现, 随着生产时间的增加, 压裂效果逐渐变小, 直至消失。

4 结论

建立了低渗透油藏直井体积压裂数值模拟模型, 并通过体积压裂区域划分、参数敏感性分析以及体积压裂导流能力表征解决了数值计算中的参数多解性问题, 形成了新的低渗透油藏直井体积压裂改造效果评价方法。将体积压裂改造区域划分为核心区域和外部改造区域。将改造区域导流能力定义为改造区域渗透率与改造区域面积的乘积。分别计算核心区域和外部改造区域导流能力, 两者之和即为体积压裂改造区域导流能力。参数敏感性分析结果表明, 裂缝半长及核心区域渗透率主要影响近井端流体流动规律, 即生产早期流体流动规律, 且裂缝半长的影响更大, 基质渗透率主要影响裂缝远端流体流动规律。

建立的方法可以评价体积压裂后不同生产阶段的压裂改造效果, 反映其动态变化。矿场应用实例表明, 压裂效果随着生产时间的增加逐渐变小, 直至消失。

符号注释：

A_k— — 第k个区域面积, m²; B_o, B_w— — 油、水体积系数, m³/m³; C— — 井储系数, m³/Pa; d_ij— — 网格i与网格j中心点的距离, m; dΩ — — 体积微元, m³; h— — 油层厚度, m; i— — 网格编号; j— — 网格i相邻网格的编号; J_o, J_w— — 油井的油、水生产指数, m³/(Pa· s); k— — 区域编号; K— — 绝对渗透率, m²; K_i— — 网格i的绝对渗透率, m²; K_k— — 第k个区域渗透率, 10^-3 μ m²; K_ro, K_rw— — 油相、水相相对渗透率, f; m— — 生产层编号; M— — 区域数; n— — 时间步序号; N— — 总生产层数; p_cow— — 毛管压力, Pa; p_o— — 油相压力, Pa; p_wf— — 井底流压, Pa; p_x_,_m— — 第m层网格x压力, Pa; q_b— — 井底流量, m³/s; q_b,_m— — 第m层产液量, m³/s; q_o,_m— — 第m层产油量, m³/s; q_osc, q_wsc— — 标况下油、水的源汇项, m³/s; Q_p— — 总产量, m³/s; Q_s— — 井储效应引起的产量, m³/s; r_w— — 井筒半径, m; r_o— — 油藏半径, m; S— — 表皮因子, f; S_o, S_w— — 含油、含水饱和度, f; SRC— — 体积压裂改造区域导流能力, 10^-3 μ m²· m²; T_ij_{, o}, T_ij_{, w}— — 油相、水相传导系数, m³/(Pa· s); V_i— — 网格i的体积, m³; x— — 第m层井所在网格的编号; Z— — 深度, m; β — — 第m层液量在总液量中所占比例; γ _o, γ _w— — 油、水重度, N/m³; Δ t— — 时间微元, s; θ — — 网格的某一边所对应的角度, rad; μ _o, μ _w— — 油、水黏度, Pa· s; ϕ — — 孔隙度, f; ω _ij— — 网格i与网格j相邻面的面积, m²。

参考文献

文献选项

[1]	侯启军, 何海清, 李建忠, 等. 中国石油天然气股份有限公司近期油气勘探进展及前景展望[J]. 中国石油勘探, 2018, 23(1): 1-13. HOU Qijun, HE Haiqing, LI Jianzhong, et al. Recent progress and prospect of oil and gas exploration by PetroChina Company Limited[J]. China Petroleum Exploration, 2018, 23(1): 1-13. [本文引用:1]
[2]	邹才能, 朱如凯, 吴松涛, 等. 常规与非常规油气聚集类型、特征、机理及展望: 以中国致密油和致密气为例[J]. 石油学报, 2012, 33(2): 173-187. ZOU Caineng, ZHU Rukai, WU Songtao, et al. Types, characteristics, genesis and prospects of conventional and unconventional hydrocarbon accumulations: Taking tight oil and tight gas in China as an instance[J]. Acta Petrolei Sinica, 2012, 33(2): 173-187. [本文引用:1]
[3]	邹才能, 张国生, 杨智, 等. 非常规油气概念、特征、潜力及技术: 兼论非常规油气地质学[J]. 石油勘探与开发, 2013, 40(4): 385-399, 454. ZOU Caineng, ZHANG Guosheng, YANG Zhi, et al. Geological concepts, characteristics, resource potential and key techniques of unconventional hydrocarbon: On unconventional petroleum geology[J]. Petroleum Exploration and Development, 2013, 40(4): 385-399, 454. [本文引用:1]
[4]	ZHAO X, YANG Z, LIN W, et al. Study on pore structures of tight sand stone reservoirs based on nitrogen adsorption, high-pressure mercury intrusion, and rate-controlled mercury intrusion[J]. Journal of Energy Resources Technology, 2019, 141(11): 112903. [本文引用:1]
[5]	XU T, LINDSAY G. Unique multidisciplinary approach to model and optimize pad refracturing in the Haynesville shale[C]//Proceedings of the 5th Unconventional Resources Technology Conference. Austin, Texas, USA: American Association of Petroleum Geologists, 2017. [本文引用:2]
[6]	XU T, LINDSAY G, BAIHLY J, et al. Proposed refracturing methodology in the Haynesville shale[R]. SPE 187236-MS, 2017. [本文引用:1]
[7]	MAYERHOFER M J, LOLON E P, YOUNGBLOOD J E, et al. Integration of microseismic-fracture-mapping results with numerical fracture network production modeling in the Barnett shale[R]. SPE 102103-MS, 2006. [本文引用:1]
[8]	MAYERHOFER M J, LOLON E, WARPINSKI N R, et al. What is stimulated reservoir volume?[J]. SPE Production & Operations, 2010, 25(1): 89-98. [本文引用:1]
[9]	LOLON E, CIPOLLA C, WEIJERS L, et al. Evaluating horizontal well placement and hydraulic fracture spacing/conductivity in the Bakken Formation, North Dakota[R]. SPE 124905-MS, 2009. [本文引用:1]
[10]	CIPOLLA C L, LOLON E, MAYERHOFER M J. Reservoir modeling and production evaluation in shale-gas reservoirs[R]. IPTC 13185-MS, 2009. [本文引用:1]
[11]	HARIKESAVANALLUR A K, DEIMBACHER F, CRICK M V, et al. Volumetric fracture modeling approach (VFMA): Incorporating microseismic data in the simulation of shale gas reservoirs[R]. SPE 134683-MS, 2010. [本文引用:1]
[12]	MORIDIS G J, BLASINGAME T A, FREEMAN C M. Analysis of mechanisms of flow in fractured tight-gas and shale-gas reservoirs[R]. SPE 139250-MS, 2010. [本文引用:1]
[13]	WRIGHT C A, DAVIS E J, MINNER W A, et al. Surface tiltmeter fracture mapping reaches new depths: 10000 feet and beyond?[R]. SPE 39919-MS, 1998. [本文引用:1]
[14]	WRIGHT C A, DAVIS E J, WEIJERS L, et al. Downhole tiltmeter fracture mapping: A new tool for directly measuring hydraulic fracture dimensions[R]. SPE 49193, 1998. [本文引用:1]
[15]	HAUSTVEIT K, DAHLGREN K, GREENWOOD H, et al. New age fracture mapping diagnostic tools: A STACK case study[R]. SPE 184862-MS, 2017. [本文引用:1]
[16]	UGUETO G A, EHIWARIO M, GRAE A, et al. Application of integrated advanced diagnostics and modeling to improve hydraulic fracture stimulation analysis and optimization[R]. SPE 168603-MS, 2014. [本文引用:1]
[17]	WHEATON B, HAUSTVEIT K, DEEG W, et al. A case study of completion effectiveness in the Eagle Ford Shale using DAS/DTS observations and hydraulic fracture modeling[R]. SPE 179149-MS, 2016. [本文引用:1]
[18]	DAHL J, DHULDHOYA K, VAIDYA R, et al. An evaluation of completion effectiveness in hydraulically fractured wells and the assessment of refracturing scenarios[R]. SPE 179136-MS, 2016. [本文引用:1]
[19]	ASALKHUZINA G F, DAVLETBAEV A Y, FEDOROV A I, et al. Identification of refracturing reorientation using decline-analysis and geomechanical simulator[R]. SPE 187750, 2017. [本文引用:1]
[20]	LI Y, HE Y, XIAO J, et al. Optimal selection and effect evaluation of re-fracturing intervals in shale gas horizontal wells[J]. Natural Gas Industry B, 2019, 6(1): 79-85. [本文引用:1]
[21]	郭建春, 陶亮, 曾凡辉. 致密油储集层水平井重复压裂时机优化: 以松辽盆地白垩系青山口组为例[J]. 石油勘探与开发, 2019, 46(1): 146-154. GUO Jianchun, TAO Liang, ZENG Fanhui. Optimization of refracturing timing for horizontal wells in tight oil reservoirs: A case study of Cretaceous Qingshankou Formation, Songliao Basin, NE China[J]. Petroleum Exploration and Development, 2019, 46(1): 146-154. [本文引用:1]
[22]	XU W, LE CALVEZ J H, THIERCELIN M J. Characterization of hydraulically-induced fracture network using treatment and microseismic data in a tight-gas sand formation: A geomechanical approach[R]. SPE 125237-MS, 2009. [本文引用:1]
[23]	XU W, THIERCELIN M J, WALTON I C. Characterization of hydraulically-induced shale fracture network using an analytical/semi-analytical model[R]. SPE 124697-MS, 2009. [本文引用:1]
[24]	XU W, THIERCELIN M J, GANGULY U, et al. Wiremesh: A novel shale fracturing simulator[R]. SPE 132218-MS, 2010. [本文引用:1]
[25]	XU W, THIERCELIN M J, LE CALVEZ J, et al. Fracture network development and proppant placement during slickwater fracturing treatment of Barnett shale laterals[R]. SPE 135484-MS, 2010. [本文引用:1]
[26]	MEYER B R, BAZAN L W, JACOT R H, et al. Optimization of multiple transverse hydraulic fractures in horizontal wellbores[R]. SPE 131732, 2010. [本文引用:1]
[27]	MEYER B R, BAZAN L W. A discrete fracture network model for hydraulically induced fractures: Theory, parametric and case studies[R]. SPE 140514, 2011. [本文引用:1]
[28]	温庆志, 王淑婷, 高金剑, 等. 复杂缝网导流能力实验研究[J]. 油气地质与采收率, 2016, 23(5): 116-121. WEN Qingzhi, WANG Shuting, GAO Jinjian, et al. Research on flow conductivity experiment in complex fracture network[J]. Petroleum Geology and Recovery Efficiency, 2016, 23(5): 116-121. [本文引用:1]
[29]	GU M, KULKARNI P, RAFIEE M, et al. Optimum fracture conductivity for naturally fractured shale and tight reservoirs[J]. SPE Production & Operations, 2016, 31(4): 289-299. [本文引用:1]
[30]	LI D, YANG J, LU D. Thief zone identification based on transient pressure analysis: A field case study[J]. Journal of Petroleum Exploration and Production Technology, 2016, 6(1): 63-72. [本文引用:1]

2018

0.0

... 0 引言近年来低渗透油气藏已经逐渐成为国内油气勘探开发的主体,低渗透油藏储量已占探明石油储量的70%以上^[1] ...

2012

0.0

... 由于低渗透油藏喉道细小^[2,3,4],补充能量较难,导致产量逐年递减,油井逐渐变成低产低效井 ...

2013

0.0

... 由于低渗透油藏喉道细小^[2,3,4],补充能量较难,导致产量逐年递减,油井逐渐变成低产低效井 ...

2019

0.0

... 由于低渗透油藏喉道细小^[2,3,4],补充能量较难,导致产量逐年递减,油井逐渐变成低产低效井 ...

2017

0.0

... 有些学者利用微地震监测结果校正了体积压裂后地质模型,并针对不同压裂方案进行开发指标预测^[5,6] ...

... 有些学者^{[5, 18,19,20,21]}主要考虑体积压裂后近井地带裂缝条数或表皮因子的变化,通过模拟体积压裂后产量的变化评估体积压裂改造效果 ...

2017

0.0

... 有些学者利用微地震监测结果校正了体积压裂后地质模型,并针对不同压裂方案进行开发指标预测^[5,6] ...

2006

0.0

... 有些学者基于微地震数据及成像结果对储集层改造区域进行了大量研究^[7,8,9] ...

2010

0.0

... 有些学者基于微地震数据及成像结果对储集层改造区域进行了大量研究^[7,8,9] ...

2009

0.0

... 有些学者基于微地震数据及成像结果对储集层改造区域进行了大量研究^[7,8,9] ...

2009

0.0

... 有些学者基于微地震等裂缝监测技术对复杂缝网进行分区,给定不同区域的渗透率,并进行产能预测及敏感性分析^[10,11,12] ...

2010

0.0

... 有些学者基于微地震等裂缝监测技术对复杂缝网进行分区,给定不同区域的渗透率,并进行产能预测及敏感性分析^[10,11,12] ...

2010

0.0

... 有些学者基于微地震等裂缝监测技术对复杂缝网进行分区,给定不同区域的渗透率,并进行产能预测及敏感性分析^[10,11,12] ...

1998

0.0

... 测斜仪主要通过测量裂缝引起的地层倾斜量来反演地层参数,进而描述体积压裂后裂缝的复杂程度^[13,14] ...

1998

0.0

... 测斜仪主要通过测量裂缝引起的地层倾斜量来反演地层参数,进而描述体积压裂后裂缝的复杂程度^[13,14] ...

2017

0.0

... 分布式光纤通过测量产液剖面、各层段产量的贡献来对裂缝进行监测^[15,16,17] ...

2014

0.0

... 分布式光纤通过测量产液剖面、各层段产量的贡献来对裂缝进行监测^[15,16,17] ...

2016

0.0

... 分布式光纤通过测量产液剖面、各层段产量的贡献来对裂缝进行监测^[15,16,17] ...

2016

0.0

... 有些学者^{[5, 18,19,20,21]}主要考虑体积压裂后近井地带裂缝条数或表皮因子的变化,通过模拟体积压裂后产量的变化评估体积压裂改造效果 ...

2017

0.0

... 有些学者^{[5, 18,19,20,21]}主要考虑体积压裂后近井地带裂缝条数或表皮因子的变化,通过模拟体积压裂后产量的变化评估体积压裂改造效果 ...

2019

0.0

... 有些学者^{[5, 18,19,20,21]}主要考虑体积压裂后近井地带裂缝条数或表皮因子的变化,通过模拟体积压裂后产量的变化评估体积压裂改造效果 ...

2019

0.0

... 有些学者^{[5, 18,19,20,21]}主要考虑体积压裂后近井地带裂缝条数或表皮因子的变化,通过模拟体积压裂后产量的变化评估体积压裂改造效果 ...

2009

0.0

... Xu等^{[22,23,24,25]}和Meyer等^[26,27]针对油井在体积压裂后会形成高导流的复杂缝网结构的特点,基于物质平衡和动量守恒方程,分别提出线网模型和离散裂缝模型 ...

2009

0.0

2010

0.0

2010

0.0

2010

0.0

2011

0.0

2016

0.0

... 一般常用裂缝渗透率与缝宽的乘积来表示导流能力^[28,29],但用该方法来表征直井体积压裂改造后导流能力存在很多不足 ...

2016

0.0

... 一般常用裂缝渗透率与缝宽的乘积来表示导流能力^[28,29],但用该方法来表征直井体积压裂改造后导流能力存在很多不足 ...

2016

0.0

... 这样既可以反映井眼附近流体流动特征,又能精确描述压裂后地层的裂缝形态,同时以较少的网格数目得到了较高的模拟精度^[30] ...