引用本文
张佳佳, 印兴耀, 张广智, 谷一鹏, 樊祥刚. 基于线性化岩石物理反演的物性参数预测方法[J]. 石油勘探与开发, 2020,47(1): 57-64.
ZHANG Jiajia, YIN Xingyao, ZHANG Guangzhi, GU Yipeng, FAN Xianggang. Prediction method of physical parameters based on linearized rock physics inversion[J]. Petroleum Exploration & Development, 2020,47(1): 57-64.  
Doi: 10.11698/PED.2020.01.05
Permissions
Copyright©2020, 石油勘探与开发》编辑部
石油勘探与开发》编辑部 所有
基于线性化岩石物理反演的物性参数预测方法
张佳佳1,2,3, 印兴耀1,2,3, 张广智1,2,3, 谷一鹏1,2,3, 樊祥刚1,2,3
1. 中国石油大学（华东）地球科学与技术学院,山东青岛 266580
2. 深层油气地质与勘探教育部重点实验室,山东青岛 266580
3. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266071

第一作者简介：张佳佳（1986-）,男,湖北随州人,博士,中国石油大学（华东）讲师,主要从事地震岩石物理和地震储集层预测研究。地址：山东省青岛市长江西路66号,中国石油大学（华东）地球科学与技术学院,邮政编码：266580。E-mail：zhangjj@upc.edu.cn

收稿日期: 2019-04-10
基金项目: 国家油气重大专项（2017ZX05049-002,2016ZX05027004-001）; 国家自然科学基金（41874146,41674130）; 中央高校基础研究业务费专项基金（18CX02061A）; 中国石油科技创新基金（2016D-5007-0301）; 中国石油科学研究与技术开发项目（2017D-3504）
摘要

针对制约岩石物理反演精度的两个关键问题：岩石物理模型和反演算法,提出了一种线性化岩石物理反演方法。首先,对复杂岩石物理模型进行泰勒展开,得到岩石物理反演问题的一阶近似表达式;然后,利用阻尼最小二乘算法直接求解线性化的岩石物理反演问题,获得岩石物理反演问题的解析解。该方法不需要全局寻优或者随机抽样,而是直接求逆运算,计算效率高。理论模型分析表明,线性化岩石物理模型可以用来近似表示复杂岩石物理模型。实际测井数据和地震数据应用表明,线性化岩石物理反演方法可以获得较为准确的物性参数。该方法适用于线性或轻微非线性的岩石物理模型,对于高度非线性岩石物理模型可能不适应。图8参31

关键词: 岩石物理反演; 线性化; 物性参数; 岩石物理模型; 泰勒展开
中图分类号:TE631.4 文献标志码:A 文章编号:1000-0747(2020)01-0057-08
Prediction method of physical parameters based on linearized rock physics inversion
ZHANG Jiajia1,2,3, YIN Xingyao1,2,3, ZHANG Guangzhi1,2,3, GU Yipeng1,2,3, FAN Xianggang1,2,3
1. School of Geosciences, China University of Petroleum (East China), Qingdao 266580, China
2. Key Laboratory of Deep Oil and Gas Geology and Exploration, Ministry of Education, Qingdao 266580, China
3. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
Abstract

A linearized rock physics inversion method is proposed to deal with two important issues, rock physical model and inversion algorithm, which restrict the accuracy of rock physics inversion. In this method, first, the complex rock physics model is expanded into Taylor series to get the first-order approximate expression of the inverse problem of rock physics; then the damped least square method is used to solve the linearized rock physics inverse problem directly to get the analytical solution of the rock physics inverse problem. This method does not need global optimization or random sampling, but directly calculates the inverse operation, with high computational efficiency. The theoretical model analysis shows that the linearized rock physical model can be used to approximate the complex rock physics model. The application of actual logging data and seismic data shows that the linearized rock physics inversion method can obtain more accurate physical parameters. This method is suitable for linear or slightly non-linear rock physics model, but may not be suitable for highly non-linear rock physics model.

Keyword: rock physics inversion; linearization; physical parameters; rock physics model; Taylor expansion
0 引言

地震数据中蕴含着丰富的地震弹性参数和储集层物性参数信息[1], 储集层物性参数预测主要分两步：第1步是利用常规地震反演方法由地震数据获取地震弹性参数, 现有的地震反演技术已经非常成熟[2, 3, 4, 5], 能够反演得到较为准确的弹性参数, 例如纵横波速度、密度等; 第2步是利用岩石物理反演由地震弹性参数预测储集层参数, 如孔隙度、饱和度、泥质含量等[6, 7, 8]。岩石物理反演首先需要构建一个理论的或经验的岩石物理模型, 即建立地震弹性参数与储集层物性参数之间的关系[9, 10]。其次就是岩石物理反演采用的反演算法, 现阶段绝大多数采用了概率统计学反演方法等[11, 12]。

岩石物理模型和岩石物理反演算法都直接影响储集层物性参数反演的精度。例如在许多岩石物理模型中, 接触胶结模型[13]数学形式相对简单, 被广泛应用于岩石物理反演中[14, 15]。但是实际生产中弹性参数与物性参数之间的关系非常复杂, 例如利用等效介质理论[16]来构建岩石物理模型。如果选择复杂岩石物理模型则需要采用概率统计学反演算法, 如贝叶斯方法或蒙特卡洛算法等。国内外很多学者在这两方面开展了大量研究工作, 如Bachrach等建立了物性参数与弹性参数之间的统计关系, 采用贝叶斯反演方法实现了孔隙度和含水饱和度的联合反演[17]。Spikes等利用接触胶结模型建立了物性参数与弹性参数之间的关系, 采用贝叶斯反演方法实现了孔隙度、泥质含量和含水饱和度的预测[18]。Bosch利用Wyllie时间平均方程[14]对岩石进行建模, 采用马尔可夫链蒙特卡洛抽样方法和最小二乘迭代反演物性参数[19]。邓继新等提出了基于随机岩石物理模型的贝叶斯反演方法, 实现对孔隙度与含水饱和度进行联合反演[20]。Grana和Rossa利用接触胶结模型[13]进行岩石物理建模, 在贝叶斯理论框架下进行储集层参数后验概率分布估计, 实现储集层参数反演[21]。印兴耀等建立了弹性阻抗与储集层物性参数之间的统计关系, 利用贝叶斯理论估计物性参数的后验概率分布, 实现储集层物性参数反演[11]。Grana提出了对胶结接触模型线性近似的方法, 利用贝叶斯理论求解岩石物理反演问题, 估计储集层物性参数[22]。林恬等利用包含物模型构建岩石物理模型, 提出了约束最小二乘法与信赖域的储集层参数地震反演方法[12]。Li等利用等效介质理论[23]构建三维岩石物理模版, 采用最小二乘原理寻找三维模版网格点的方法预测物性参数。杨培杰建立了砂泥岩储集层物性参数和地震弹性参数之间的定量关系, 基于贝叶斯理论同步反演储集层孔隙度和含水饱和度[24]。上述岩石物理反演方法选用的岩石物理模型比较简单, 例如统计经验关系和胶结接触模型, 另一个问题就是很多反演算法利用的是概率统计学反演算法, 需要进行全局寻优或者随机抽样, 求解岩石物理反演问题的计算效率较低。因此, 本文提出了一种岩石物理模型线性化方法, 对岩石物理模型进行泰勒展开, 得到岩石物理反演问题的一阶近似表达式。然后再利用阻尼最小二乘算法直接求解岩石物理反演问题, 获得岩石物理反演问题的解析解, 不需要全局寻优或者随机抽样, 而是直接求逆运算, 计算效率较高。本文利用Gassmann方程[25]和临界孔隙度模型[26]对含泥质砂岩储集层进行岩石物理建模, 建模过程比较复杂, 构建的地震弹性参数和储集层物性参数之间的关系是非线性的。实际测井数据和地震数据验证表明, 线性化岩石物理反演方法可以获得较为准确的物性参数, 可以用来近似实际岩石物理模型。

1 方法原理
1.1 线性化岩石物理反演

岩石物理反演问题一般可写为：

$d=f(m)$ （1）

（1）式中, d为弹性参数, m为待预测的物性参数, f为弹性参数与物性参数之间的关系式, 即岩石物理模型。为简单起见, 首先假设（1）式中所有变量均为单一参数的标量, 然后再把它们推广到多参数, 例如d为纵波速度, m为孔隙度, f为Wyllie时间平均方程[19]或者Raymer改进公式[27]。

实际生产中, 岩石物理模型f并不像Wyllie时间平均方程或者Raymer改进公式这样简单, 往往是非常复杂而且是非线性的。地球物理中经常利用泰勒展开来近似复杂的非线性函数, 特别是在地震成像中[28]。为了求解岩石物理反演问题, 本文也采用了基于泰勒展开的线性化岩石物理反演方法[22]。

利用泰勒展开对岩石物理反演问题进行线性化, 这里使用一阶泰勒展开, 那么（1）式可以改写为：

$d\cong f({{m}_{0}})+{f}'({{m}_{0}})(m-{{m}_{0}})$ （2）

对（2）式中的多项式进行展开和合并, 岩石物理反演问题可以改写为线性形式：

$d\cong {f}'({{m}_{0}})m+\left[ f({{m}_{0}})-{{m}_{0}}{f}'({{m}_{0}}) \right]$ （3）

再把这种线性化岩石物理反演方法推广到多个参数, 那么弹性参数d和物性参数m为包含多参数变量的矢量形式。例如, d为纵波速度vp、横波速度vs和密度ρ 等弹性参数组成的向量, m为孔隙度ϕ 、含水饱和度Sw和泥质含量C等物性参数组成的向量。同样岩石物理模型f也写成矢量形式, 那么岩石物理反演问题可以写为：

$\mathbf{d}=\mathbf{f}\text{(}\mathbf{m}\text{)}$ （4）

对公式（4）进行一阶泰勒展开, 变为

$\mathbf{d}\cong \mathbf{f}\text{(}{{\mathbf{m}}_{0}}\text{)}\mathbf{+}{{\mathbf{J}}_{{{\mathbf{m}}_{\text{0}}}}}(\mathbf{m}-{{\mathbf{m}}_{\text{0}}})$ （5）

其中, ${{\mathbf{J}}_{{{\mathbf{m}}_{\text{0}}}}}$为函数f在自变量${{\mathbf{m}}_{\text{0}}}$处的Jacobian矩阵。再将其改写成线性化形式则变为：

$\mathbf{d}\cong {{\mathbf{J}}_{{{\mathbf{m}}_{\text{0}}}}}\mathbf{m}+(\mathbf{f}({{\mathbf{m}}_{0}})-{{\mathbf{J}}_{{{\mathbf{m}}_{\text{0}}}}}{{\mathbf{m}}_{\text{0}}})$ （6）

1.2 岩石物理模型建模

本文选用Gassmann方程[25]和临界孔隙度模型[26]对含泥质砂岩进行岩石物理建模, 具体建模过程如下：

①岩石基质的体积模量${{K}_{\text{m}}}$、剪切模量${{\mu }_{\text{m}}}$和密度${{\rho }_{\text{m}}}$可以利用Voigt-Reuss-Hill平均方法[29]计算：

${{K}_{\text{m}}}=\frac{\left[ C{{K}_{\text{c}}}+(1-C){{K}_{\text{q}}} \right]+\frac{1}{C/{{K}_{\text{c}}}+(1-C)/{{K}_{\text{q}}}}}{2}$ （7）

${{\mu }_{\text{m}}}=\frac{\left[ C{{\mu }_{\text{c}}}+(1-C){{\mu }_{\text{q}}} \right]+\frac{1}{C/{{\mu }_{\text{c}}}+(1-C)/{{\mu }_{\text{q}}}}}{2}$ （8）

${{\rho }_{\text{m}}}=C{{\rho }_{\text{c}}}+(1-C){{\rho }_{\text{q}}}$ （9）

②饱和流体的体积模量${{K}_{\text{fl}}}$和密度${{\rho }_{\text{fl}}}$计算公式为：

${{K}_{\text{fl}}}={{\left( \frac{1-{{S}_{\text{w}}}}{{{K}_{\text{hc}}}}+\frac{{{S}_{\text{w}}}}{{{K}_{\text{w}}}} \right)}^{-1}}$ （10）

${{\rho }_{\text{fl}}}=\left( 1-{{S}_{\text{w}}} \right){{\rho }_{\text{hc}}}+{{S}_{\text{w}}}{{\rho }_{\text{w}}}$ （11）

这里利用流体均匀混合公式[9]来计算饱和流体的体积模量。

③岩石骨架的体积模量${{K}_{\text{dry}}}$和剪切模量${{\mu }_{\text{dry}}}$可以利用临界孔隙度模型[26]计算：

${{K}_{\text{dry}}}={{K}_{\text{m}}}\left( 1-\frac{\phi }{{{\phi }_{\text{c}}}} \right)$ （12）

${{\mu }_{\text{dry}}}={{\mu }_{\text{m}}}\left( 1-\frac{\phi }{{{\phi }_{\text{c}}}} \right)$ （13）

这里临界孔隙度值${{\phi }_{\text{c}}}$虽然是经验值, 譬如砂岩取40%、灰岩取60%等, 但是临界孔隙度值包含了岩石的孔隙类型或者孔隙形状对纵横波速度的影响[30]。

④饱和岩石的体积模量${{K}_{\text{sat}}}$和剪切模量${{\mu }_{\text{sat}}}$可以用Gassmann方程[25]计算：

$K_{\text{sat}}^{{}}={{K}_{\text{dry}}}+\frac{{{\left( 1-\frac{{{K}_{\text{dry}}}}{{{K}_{\text{m}}}} \right)}^{2}}}{\frac{\phi }{{{K}_{\text{fl}}}}+\frac{1-\phi }{{{K}_{\text{m}}}}-\frac{{{K}_{\text{dry}}}}{K_{\text{m}}^{2}}}$ （14）

$\mu _{\text{sat}}^{{}}={{\mu }_{\text{dry}}}$ （15）

⑤饱和岩石的纵波速度${{v}_{\text{P}}}$、横波速度${{v}_{\text{s}}}$和密度$\rho $计算公式为：

$\rho ={{\rho }_{\text{m}}}(1-\phi )+{{\rho }_{\text{fl}}}\phi $ （16）

${{v}_{\text{P}}}=\sqrt{\frac{{{K}_{\text{sat}}}+\frac{4}{3}{{\mu }_{\text{sat}}}}{\rho }}$ （17）

${{v}_{\operatorname{S}}}=\sqrt{\frac{{{\mu }_{\text{sat}}}}{\rho }}$ （18）

由于上述岩石物理建模过程即（7）— （18）式是非线性的, 所以可以对其进行线性化处理。将弹性参数d（即纵波速度${{v}_{\text{P}}}$、横波速度${{v}_{\operatorname{S}}}$和密度$\rho $）分别对物性参数m（孔隙度$\phi $、泥质含量$C$和含水饱和度${{S}_{\text{w}}}$）求导, 计算其对应的Jacobian矩阵：

$\mathbf{J}(\phi , C, {{S}_{\text{w}}})=\left( \begin{align} & \frac{\partial {{v}_{\text{P}}}}{\partial \phi }\quad \frac{\partial {{v}_{\text{P}}}}{\partial C}\quad \frac{\partial {{v}_{\text{P}}}}{\partial {{S}_{\text{w}}}} \\ & \frac{\partial {{v}_{\text{S}}}}{\partial \phi }\quad \frac{\partial {{v}_{\text{S}}}}{\partial C}\quad \frac{\partial {{v}_{\text{S}}}}{\partial {{S}_{\text{w}}}} \\ & \frac{\partial \rho }{\partial \phi }\quad \ \frac{\partial \rho }{\partial C}\quad \ \frac{\partial \rho }{\partial {{S}_{\text{w}}}} \\ \end{align} \right) $ （19）

上式中, 纵波速度${{v}_{\text{P}}}$对孔隙度$\phi $的偏导数为：

$\frac{\partial {{v}_{\text{P}}}}{\partial \phi }\text{=}\frac{1}{2\rho }{{\left( \frac{{{K}_{\text{sat}}}+\frac{4}{3}{{\mu }_{\text{sat}}}}{\rho } \right)}^{-\frac{1}{2}}}\frac{\left( \frac{1}{{{K}_{\text{m}}}}-\frac{1}{{{K}_{\text{fl}}}} \right){{\left( 1-\frac{{{K}_{\text{dry}}}}{{{K}_{\text{m}}}} \right)}^{2}}}{{{\left( \frac{\phi }{{{K}_{\text{fl}}}}+\frac{1-\phi }{{{K}_{\text{m}}}}-\frac{{{K}_{\text{dry}}}}{{{K}_{\text{m}}}} \right)}^{2}}}-\frac{1}{2\rho }{{\left( \frac{{{K}_{\text{sat}}}+\frac{4}{3}{{\mu }_{\text{sat}}}}{\rho } \right)}^{-\frac{1}{2}}}\frac{\frac{2\left( {{K}_{\text{dry}}}-{{K}_{\text{m}}} \right)}{{{\phi }_{c}}{{K}_{\text{m}}}}}{\frac{\phi }{{{K}_{\text{fl}}}}+\frac{1-\phi }{{{K}_{\text{m}}}}-\frac{{{K}_{\text{dry}}}}{K_{\text{m}}^{2}}}\ -\frac{1}{2\rho }{{\left( \frac{{{K}_{\text{sat}}}+\frac{4}{3}{{\mu }_{\text{sat}}}}{\rho } \right)}^{-\frac{1}{2}}}\times \\\frac{\frac{1}{{{\phi }_{c}}{{K}_{\text{m}}}}{{\left( 1-\frac{{{K}_{\text{dry}}}}{{{K}_{\text{m}}}} \right)}^{2}}}{{{\left( \frac{\phi }{{{K}_{\text{fl}}}}+\frac{1-\phi }{{{K}_{\text{m}}}}-\frac{{{K}_{\text{dry}}}}{{{K}_{\text{m}}}} \right)}^{2}}}\ -{{\left( \frac{{{K}_{\text{sat}}}+\frac{4}{3}{{\mu }_{\text{sat}}}}{\rho } \right)}^{-\frac{1}{2}}}\left( \frac{2{{\mu }_{\text{m}}}}{3{{\phi }_{c}}\rho }+\frac{1}{2\rho }\frac{{{K}_{\text{m}}}}{{{\phi }_{c}}} \right)+{{\left( \frac{{{K}_{\text{sat}}}+\frac{4}{3}{{\mu }_{\text{sat}}}}{\rho } \right)}^{-\frac{1}{2}}}\frac{{{\rho }_{\text{m}}}-{{\rho }_{\text{fl}}}}{2\rho }$ （20）

横波速度${{v}_{\text{s}}}$对孔隙度$\phi $的偏导数为：

$\frac{\partial {{v}_{\text{s}}}}{\partial \phi }\text{=}\frac{-1}{2\rho }{{\left[ \frac{{{\mu }_{\text{m}}}\left( 1-\frac{\phi }{{{\phi }_{\text{c}}}} \right)}{\rho } \right]}^{-\frac{1}{2}}}\frac{{{\mu }_{\text{m}}}}{{{\phi }_{c}}}+\\ \frac{{{\mu }_{\text{m}}}\left( 1-\frac{\phi }{{{\phi }_{\text{c}}}} \right)\left( {{\rho }_{\text{m}}}-{{\rho }_{\text{fl}}} \right)}{2\rho _{{}}^{2}}{{\left( \frac{{{\mu }_{\text{dry}}}}{\rho } \right)}^{-\frac{1}{2}}}$ （21）

密度$\rho $对孔隙度$\phi $的偏导数为：

$\frac{\partial \rho }{\partial \phi }\text{=}{{\rho }_{\text{hc}}}-{{\rho }_{\text{m}}}+{{S}_{\text{w}}}\left( {{\rho }_{\text{w}}}-{{\rho }_{\text{hc}}} \right) $ （22）

纵波速度${{v}_{\text{P}}}$对含水饱和度${{S}_{\text{w}}}$的偏导数为：

$\frac{\partial {{v}_{\text{P}}}}{\partial {{S}_{\text{w}}}}\text{=}\frac{{{K}_{\text{w}}}-{{K}_{\text{hc}}}}{2\rho }\frac{\phi }{K_{\text{fl}}^{\text{2}}}\frac{{{\left( 1-\frac{{{K}_{\text{dry}}}}{{{K}_{\text{mat}}}} \right)}^{2}}}{{{\left( \frac{\phi }{{{K}_{\text{fl}}}}+\frac{1-\phi }{{{K}_{\text{m}}}}-\frac{{{K}_{\text{dry}}}}{{{K}_{\text{m}}}} \right)}^{2}}}{{\left( \frac{{{K}_{\text{sat}}}+\frac{4}{3}{{\mu }_{\text{sat}}}}{\rho } \right)}^{-\frac{1}{2}}}\text{+}\\ \frac{\phi \left( {{\rho }_{\text{hc}}}-{{\rho }_{\text{w}}} \right)}{2\rho }{{\left( \frac{{{K}_{\text{sat}}}+\frac{4}{3}{{\mu }_{\text{sat}}}}{\rho } \right)}^{-\frac{1}{2}}}$ （23）

横波速度${{v}_{\text{s}}}$对含水饱和度${{S}_{\text{w}}}$的偏导数为：

$\frac{\partial {{v}_{\text{s}}}}{\partial {{S}_{\text{w}}}}\text{=}\frac{{{\mu }_{\text{m}}}\left( 1-\frac{\phi }{{{\phi }_{\text{c}}}} \right)\phi \left( {{\rho }_{\text{hc}}}-{{\rho }_{\text{w}}} \right)}{2\rho _{{}}^{2}}{{\left[ \frac{\left( 1-\frac{\phi }{{{\phi }_{\text{c}}}} \right)}{\rho } \right]}^{-\frac{1}{2}}}$ （24）

密度$\rho $对含水饱和度${{S}_{\text{w}}}$的偏导数为：

$\frac{\partial \rho }{\partial {{S}_{\text{w}}}}\text{=}\phi \left( {{\rho }_{\text{w}}}-{{\rho }_{\text{hc}}} \right)$ （25）

纵波速度${{v}_{\text{P}}}$、横波速度${{v}_{\text{s}}}$和密度$\rho $对泥质含量$C$的偏导数太复杂, 故本文没有给出具体表达式。

再将Jacobian矩阵代入到线性化岩石物理反演问题（6）式中。求解线性化之后的岩石物理反演问题可以有很多方法, 例如最小二乘算法, 阻尼最小二乘算法或者贝叶斯方法。这里选用阻尼最小二乘方法来求解, 可得：

$\mathbf{m}={{\left( {{\mathbf{J}}_{{{\mathbf{m}}_{\text{0}}}}}^{\text{T}}{{\mathbf{J}}_{{{\mathbf{m}}_{\text{0}}}}}+\mathbf{\varepsilon }\cdot \mathbf{I} \right)}^{-1}}{{\mathbf{J}}_{{{\mathbf{m}}_{\text{0}}}}}^{\text{T}}\left\{ \mathbf{d}-\left[ \mathbf{f}\left( {{\mathbf{m}}_{0}} \right)-{{\mathbf{J}}_{{{\mathbf{m}}_{\text{0}}}}}{{\mathbf{m}}_{\text{0}}} \right] \right\}$ （26）

1.3 线性化岩石物理模型精度分析

为了检验线性化岩石物理反演的精度, 分别利用实际岩石物理模型以及线性化岩石物理模型进行含泥质砂岩的岩石物理正演模拟分析。假设含泥质砂岩的矿物成分为石英和黏土, 孔隙流体为水和气混合, 相应的弹性模量和密度分别为：${{K}_{\text{q}}}={{36}_{{}}}\text{GPa}$, ${{\mu }_{\text{q}}}={{36}_{{}}}\text{GPa}$, ${{\rho }_{\text{q}}}={{2.65}_{{}}}\text{g/c}{{\text{m}}^{\text{3}}}$, ${{K}_{\text{c}}}={{21}_{{}}}\text{GPa}$, ${{\mu }_{\text{c}}}={{15}_{{}}}\text{GPa}$, ${{\rho }_{\text{c}}}=$ 2.45 g/cm3, ${{K}_{\text{hc}}}={{0.020}_{{}}}{{8}_{{}}}\text{GPa}$, ${{\rho }_{\text{hc}}}={{0.001}_{{}}}\text{g/c}{{\text{m}}^{\text{3}}}$, ${{K}_{\text{w}}}=$ 2.25 GPa, ${{\rho }_{\text{w}}}={{1.03}_{{}}}\text{g/c}{{\text{m}}^{\text{3}}}$。线性化岩石物理模型均在孔隙度、泥质含量和饱和度的均值处进行一阶泰勒展开。

图1分别展示了弹性参数（纵波速度、横波速度及密度）与孔隙度之间的变化关系, 图中含泥质砂岩的泥质含量$C$以10%为间隔从0到50%变化, 含水饱和度${{S}_{\text{w}}}$为常数30%, 孔隙度$\phi $从0到30%均匀变化。由图1a和1b可以看出, 线性化岩石物理模型与实际岩石物理模型在孔隙度为15%左右处吻合最好, 在孔隙度较低和较高时有一定的误差, 这是因为在孔隙度均值15%处进行的一阶泰勒展开。由图1c可以看出, 线性化岩石物理模型与实际岩石物理模型的密度完全一样, 这是因为密度计算公式本身就是线性的, 线性化岩石物理模型与实际岩石物理模型是完全相同的。

图1 实际岩石物理模型及线性化岩石物理模型计算的弹性参数与孔隙度之间的变化关系

图2分别展示了弹性参数（纵波速度、横波速度及密度）与泥质含量之间的变化关系。图中含泥质砂岩的孔隙度$\phi $从以10%间隔从0到30%变化, 含水饱和度${{S}_{\text{w}}}$为常数50%, 泥质含量$C$从0到50%均匀变化。由图2a和2b可以看出, 线性化岩石物理模型与实际岩石物理模型在25%处吻合最好, 在泥质含量较低和较高时有一定的误差, 这是因为在泥质含量均值处（25%）进行的一阶泰勒展开。由图2c同样可以看出, 线性化岩石物理模型与实际岩石物理模型的密度是完全一样的, 这是因为密度计算公式本身就是线性的, 线性化岩石物理模型与实际岩石物理模型是完全相同的。

图2 实际岩石物理模型及线性化岩石物理模型计算的弹性参数与泥质含量之间的变化关系

图3分别展示了弹性参数（纵波速度、横波速度及密度）与含水饱和度之间的变化关系。图中含泥质砂岩的孔隙度$\phi $以10%间隔从0到30%变化, 泥质含量$C$为常数25%, 含水饱和度${{S}_{\text{w}}}$从0到100%均匀变化。由图3a和3b可以看到, 利用均匀饱和方式计算饱和流体的体积模量, 实际岩石物理模型和线性化岩石物理模型计算的纵波速度吻合很好, 仅在含水饱和度${{S}_{\text{w}}}$接近100%左右误差较大, 是符合近似要求的。由图3c同样可以看出, 线性化岩石物理模型与实际岩石物理模型的密度是完全一样的, 这是因为密度计算公式本身就是线性的, 线性化岩石物理模型与实际岩石物理模型是完全相同的。

图3 实际岩石物理模型及线性化岩石物理模型计算的弹性参数与含水饱和度之间的变化关系

2 实际应用对比
2.1 测井数据结果对比

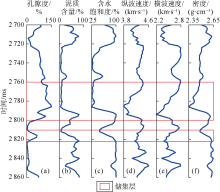
首先将线性化岩石物理反演方法应用于实际测井数据。A井位于中国东部海上油田, 储集层为含气砂岩, 测井曲线包括孔隙度、泥质含量和含水饱和度等物性参数, 以及纵波速度、横波速度和密度等弹性参数（见图4）。测井数据经过井震标定后由深度域转换成时间域, 并按照2 ms进行重采样。主力产气层为时间深度为2 760~2 800 ms的一套厚砂岩储集层, 其上覆2 718 ms左右有一层较薄的泥岩层, 2 810~2 822 ms有一套较薄的砂岩储集层, 其下覆为一套较厚泥岩层。

图4 A井实际测井数据

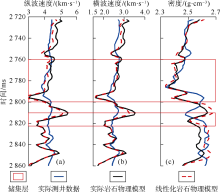
在进行线性化岩石物理反演之前, 首先进行正演模拟分析。含泥质砂岩的矿物成分为石英和黏土, 孔隙流体为水和气混合, 相应的弹性模量和密度分别：${{K}_{\text{q}}}={{38}_{{}}}\text{GPa}$, ${{\mu }_{\text{q}}}={{40}_{{}}}\text{GPa}$, ${{\rho }_{\text{q}}}={{2.65}_{{}}}\text{g/c}{{\text{m}}^{\text{3}}}$, ${{K}_{\text{c}}}=$ 15 GPa, ${{\mu }_{\text{c}}}={{7}_{{}}}\text{GPa}$, ${{\rho }_{\text{c}}}={{2.55}_{{}}}\text{g/c}{{\text{m}}^{\text{3}}}$, ${{K}_{\text{hc}}}={{0.020}_{{}}}{{8}_{{}}}\text{GPa}$, ${{\rho }_{\text{hc}}}={{0.001}_{{}}}\text{g/c}{{\text{m}}^{\text{3}}}$, ${{K}_{\text{w}}}={{2.25}_{{}}}\text{GPa}$, ${{\rho }_{\text{w}}}={{1.03}_{{}}}\text{g/c}{{\text{m}}^{\text{3}}}$。利用精确岩石物理模型以及线性化岩石物理模型, 由图4中的孔隙度、泥质含量和含水饱和度等物性参数来计算纵波速度、横波速度和密度, 如图5所示。图中蓝色实线代表实际测井数据, 黑色实线代表实际岩石物理模型正演计算结果, 红色虚线代表线性化岩石物理模型正演计算结果。由图5可见, 线性化岩石物理模型与实际岩石物理模型正演计算结果基本一致, 与实际测井曲线有一定误差, 但整体变化趋势相同。线性化岩石物理模型与实际弹性参数之间的平均误差, 纵波速度约为4.0%, 横波速度约为3.0%, 密度约为1.2%。在2 820~2 860 ms泥岩段误差较大, 主要是由于泥岩的弹性模量变化较大, 很难获取精确值。

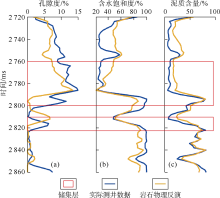
图5 实际岩石物理模型与线性化岩石物理模型正演计算的弹性参数以及实际测井弹性参数

其次, 再对测井曲线进行线性化岩石物理反演, 即利用图4d— 4f中纵波速度、横波速度和密度来反演图4a— 4c中的孔隙度、泥质含量和含水饱和度。使用的弹性模量和密度等参数与图5中一致, 反演结果如图6所示。由图6可见, 线性化岩石物理模型反演结果与实际测井曲线基本一致, 虽然幅值没有完全吻合, 但整体变化趋势是相同的。这里给出了线性化岩石物理模型反演结果与实际测井曲线之间的相关系数和平均误差, 其中孔隙度的相关系数为64.8%, 平均误差约为28%, 含水饱和度的相关系数为85.4%, 平均误差约为17%, 泥质含量的相关系数为90.2%, 平均误差约为10%。

图6 线性化岩石物理模型反演与实际测井物性参数

2.2 地震数据结果对比

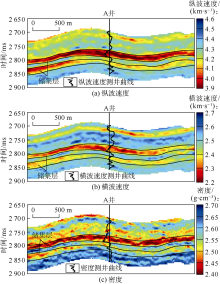
在进行测井曲线的岩石物理反演之后, 再对地震数据进行线性化岩石物理反演。选择一条过A井的二维地震剖面, 由叠前同时反演[31]分别获得了纵波速度、横波速度和密度等弹性参数的二维剖面（见图7）。由二维弹性参数剖面上可以看到, 无论是纵波速度、横波速度还是密度在2 800 ms左右都有一套较厚的低值区域, 这是主要的目的层段。再利用图7中的弹性参数进行物性参数反演（见图8）, 图8a— 8c分别展示了线性化岩石物理反演得到的孔隙度、泥质含量和含气饱和度, 图8d— 8f分别展示了利用弹性参数与物性参数之间的经验关系拟合得到的孔隙度、泥质含量和含气饱和度。由反演结果可见, 两种反演结果得到的主要目的层段物性参数与A井上的物性参数吻合较好, 并且能够获取主要目的层段的物性参数空间展布情况, 特别是线性化岩石物理反演含气饱和度效果要优于经验关系拟合结果。

图7 地震弹性参数反演剖面

图8 线性化岩石物理反演的物性参数

3 讨论

本文提出了一种线性化岩石物理反演方法, 由于岩石物理模型一般并不是线性的, 所以本文方法较适用于非线性化不是特别强的岩石物理模型, 尤其适用于孔隙结构较简单的储集层, 如碎屑岩储集层; 对于孔隙结构复杂的储集层, 如碳酸盐岩储集层并不太适用。另外值得注意的是, 不同的岩石类型应该选用不同的岩石物理模型。本文是针对含泥质砂岩储集层进行建模, 选择了临界孔隙度模型和Gassmann方程是合理的, 如果针对其他类型储集层则需要选用其他的岩石物理模型。文中给出的岩石物理正演模型表明, 实际岩石物理模型与线性化岩石物理模型是可以近似的。利用线性化岩石物理模型的优势就是可以获取岩石物理反演问题的解析解。本文中选择阻尼最小二乘方法来求解线性反演问题, 求解速度较快, 但对岩石物理建模中使用的弹性模量和密度等参数较为敏感。另外, 不同于其他岩石物理反演方法, 线性化岩石物理反演方法获得的泥质含量和饱和度反演精度要优于孔隙度的反演精度。主要是由于在Jacobian矩阵的逆矩阵中与泥质含量以及饱和度有关的系数项较大, 而与孔隙度有关的系数项较小, 所以导致泥质含量与饱和度的反演效果要优于孔隙度反演效果。当然, 本文中的弹性参数是由AVO叠前地震反演获得, 下一步还可以直接利用地震数据进行岩石物理反演。

4 结论

提出了一种线性化岩石物理反演方法, 即通过对实际岩石物理模型进行泰勒级数展开, 得到一阶近似的线性化岩石物理模型, 再利用阻尼最小二乘方法求解线性化后的岩石物理反演问题, 获得精确的解析解。利用了Gassmann方程和临界孔隙度模型对含泥质砂岩进行实际岩石物理建模, 并且给出了其线性化岩石物理模型表达式。本方法适用于线性或轻微非线性的岩石物理模型, 对于高度非线性岩石物理模型可能不适应。实际测井数据和地震数据应用表明, 线性化岩石物理反演方法能够反演得到比较好的物性参数结果。

符号注释：

C— — 泥质含量, %; C0— — 泥质含量均值, %; d— — 弹性参数; d— — 弹性参数矢量形式; f— — 岩石物理模型; ${f}'$— — 岩石物理模型$f$的一阶导数; $\mathbf{f}$— — 岩石物理模型矢量形式; $\mathbf{f}\left( {{\mathbf{m}}_{0}} \right)$— — 岩石物理模型在${{\mathbf{m}}_{0}}$（即${{\phi }_{0}}$、${{C}_{0}}$和${{S}_{\text{w0}}}$）处的值; $\mathbf{I}$— — 单位矩阵; ${{\mathbf{J}}_{{{\mathbf{m}}_{\text{0}}}}}$— — Jacobian矩阵在${{\mathbf{m}}_{0}}$（即${{\phi }_{0}}$、${{C}_{0}}$和${{S}_{\text{w0}}}$）处的值; ${{K}_{\text{c}}}$— — 泥质矿物的体积模量, GPa; ${{K}_{\text{dry}}}$— — 岩石骨架的体积模量, GPa; ${{K}_{\text{fl}}}$— — 饱和流体的体积模量, GPa; ${{K}_{\text{m}}}$— — 岩石基质的体积模量, GPa; ${{K}_{\text{hc}}}$— — 油或气等碳氢化合物的体积模量, GPa; ${{K}_{\text{q}}}$— — 砂质矿物的体积模量, GPa; ${{K}_{\text{sat}}}$— — 饱和岩石的体积模量, GPa; ${{K}_{\text{w}}}$— — 水的体积模量, GPa; m— — 待预测的物性参数; ${{m}_{0}}$— — 物性参数$m$某一具体值, 一般选择${{m}_{0}}$为待预测模型参数的均值; $\mathbf{m}$— — 待预测的物性参数矢量形式; ${{\mathbf{m}}_{\text{0}}}$— — 物性参数矢量形式$\mathbf{m}$某一具体值, 即${{\phi }_{0}}$、${{C}_{0}}$和${{S}_{\text{w0}}}$; ${{S}_{\text{w}}}$— — 含水饱和度, %; ${{S}_{\text{w0}}}$— — 饱和度均值, %; ${{v}_{\text{P}}}$— — 饱和岩石的纵波速度, km/s; ${{v}_{\text{s}}}$— — 饱和岩石的横波速度, km/s; $\rho $— — 饱和岩石的密度, g/cm3; ${{\rho }_{\text{c}}}$— — 矿物的密度, g/cm3; ${{\rho }_{\text{fl}}}$— — 饱和流体的密度, g/cm3; ${{\rho }_{\text{hc}}}$— — 油或气等碳氢化合物的密度, g/cm3; ${{\rho }_{\text{m}}}$— — 岩石基质的密度, g/cm3; ${{\rho }_{\text{q}}}$— — 砂质矿物的密度, g/cm3; ${{\rho }_{\operatorname{w}}}$— — 水的密度, g/cm3; $\phi $— — 孔隙度, %; ${{\phi }_{0}}$— — 孔隙度均值, %; ${{\phi }_{\text{c}}}$— — 岩石的临界孔隙度, %; ${{\mu }_{\text{c}}}$— — 泥质矿物的剪切模量, GPa; ${{\mu }_{\text{dry}}}$— — 岩石骨架的剪切模量, GPa; ${{\mu }_{\text{m}}}$— — 岩石基质的剪切模量, GPa; ${{\mu }_{\text{q}}}$— — 砂质矿物的剪切模量, GPa; ${{\mu }_{\text{sat}}}$— — 饱和岩石的剪切模量, GPa; $\mathbf{\varepsilon }$— — 阻尼因子。

（编辑 黄昌武）

参考文献
[1] 甘利灯, 王峣钧, 罗贤哲, 等. 基于孔隙结构参数的相控渗透率地震预测方法[J]. 石油勘探与开发, 2019, 46(5): 883-890.
GAN Lideng, WANG Yaojun, LUO Xianzhe, et al. A permeability prediction method based on pore structure and lithofacies[J]. Petroleum Exploration and Development, 2019, 46(5): 883-890. [本文引用:1]
[2] CONNOLLY P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. [本文引用:1]
[3] RUSSELL B. Introduction to seismic inversion methods[R]. Tulsa: SEG, 1988. [本文引用:1]
[4] 杨华, 王大兴, 张盟勃, 等. 鄂尔多斯盆地致密气储集层孔隙流体地震预测方法[J]. 石油勘探与开发, 2017, 44(4): 513-520.
YANG Hua, WANG Daxing, ZHANG Mengbo, et al. Seismic prediction method of pore fluid in tight gas reservoirs, Ordos Basin, NW China[J]. Petroleum Exploration and Development, 2017, 44(4): 513-520. [本文引用:1]
[5] 曾庆才, 陈胜, 贺佩, 等. 四川盆地威远龙马溪组页岩气甜点区地震定量预测[J]. 石油勘探与开发, 2018, 45(3): 406-414.
ZENG Qingcai, CHEN Sheng, HE Pei, et al. Quantitative seismic prediction of shale gas sweet spots in Lower Silurian Longmaxi Formation, Weiyuan area, Sichuan Basin, SW China[J]. Petroleum Exploration and Development, 2018, 45(3): 406-414. [本文引用:1]
[6] SALTZER R, FINN C, BURTZ O. Predicting shale and porosity using cascaded seismic and rock physics inversion[R]. SEG Technical Program Expand ed Abstracts, 2005: 732-736. [本文引用:1]
[7] DOYEN P. Seismic reservoir characterization: An earth modelling perspective[R]. Houten: EAGE, 2007. [本文引用:1]
[8] 胡华锋, 印兴耀, 吴国忱. 基于贝叶斯分类的储层物性参数联合反演方法[J]. 石油物探, 2012, 52(3): 225-232.
HU Huafeng, YIN Xingyao, WU Guochen. Joint inversion of petrophysical parameters based on Bayesian classification[J]. Geophysical Prospecting for Petroleum, 2012, 52(3): 225-232. [本文引用:1]
[9] MAVKO G, MUKERJI T, DVORKIN J. The rock physics hand book[M]. London: Cambridge University Press, 2009. [本文引用:2]
[10] AVSETH P, MUKERJI T, MAVKO G. Quantitative seismic interpretation[M]. London: Cambridge University Press, 2005. [本文引用:1]
[11] 印兴耀, 崔维, 宗兆云, 等. 基于弹性阻抗的储层物性参数预测方法[J]. 地球物理学报, 2014, 57(12): 4132-4140.
YIN Xingyao, CUI Wei, ZONG Zhaoyun et al. Petrophysical property inversion of reservoirs based on elastic impedance[J]. Chinese Journal of Geophysics, 2014, 57(12): 4132-4140. [本文引用:2]
[12] 林恬, 孟小红, 张致付. 基于约束最小二乘与信赖域的储层参数反演方法[J]. 地球物理学报, 2017, 60(10): 3969-3983.
LIN Tian, MENG Xiaohong, ZHANG Zhifu. The petrophysical parameter inversion method based on constrained least squares and trust region approach[J]. Chinese Journal of Geophysics, 2017, 60(10): 3969-3983. [本文引用:2]
[13] DVORKIN J, NUR A, YIN H. Effective properties of cemented granular materials[J]. Mechanics of Materials, 1994, 18: 351-366. [本文引用:2]
[14] BOSCH M, CARVAJAL C, RODRIGUES J, et al. Petrophysical seismic inversion conditioned to well-log data: Methods and application to a gas reservoir[J]. Geophysics, 2009, 74(2): O1-O15. [本文引用:2]
[15] GRANA D. Bayesian inversion methods for seismic reservoir characterization and time-lapse studies[D]. Stanford: Stanford University, 2013. [本文引用:1]
[16] 李宏兵, 张佳佳. 多重孔岩石微分等效介质模型及其干燥情形下的解析近似式[J]. 地球物理学报, 2014, 57(10): 3422-3430.
LI Hongbing, ZHANG Jiajia. A differential effective medium model of multiple-porosity rock and its analytical approximations for dry rock[J]. Chinese Journal of Geophysics, 2014, 57(10): 3422-3430. [本文引用:1]
[17] BACHRACH R, DUTTA N. Joint estimation of porosity and saturation using stochastic rock-physics modeling[J]. SPE 89991, 2006. [本文引用:1]
[18] SPIKES K, MUKERJI T, DVORKIN J, et al. Probabilistic seismic inversion based on rock-physics models[J]. Geophysics, 2007, 72(5): R87-R97. [本文引用:1]
[19] WYLLIE M R J, GREGORY A R, GARDNER L W. Elastic wave velocities in heterogeneous and porous media[J]. Geophysics, 1956, 21(1): 41-70. [本文引用:2]
[20] 邓继新, 王尚旭. 基于统计岩石物理的含气储层饱和度与孔隙度联合反演[J]. 石油天然气学报, 2009, 31(1): 48-52.
DENG Jixin, WANG Shangxu. Joint inversion of saturation and porosity in gas reservoirs based on statistical rock physics[J]. Journal of Oil and Gas Technology, 2009, 31(1): 48-52. [本文引用:1]
[21] GRANA D, ROSSA E D. Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion[J]. Geophysics, 2010, 75(3): O21-O37. [本文引用:1]
[22] GRANA D. Bayesian linearized rock-physics inversion[J]. Geophysics, 2016, 81(6): D625-D641. [本文引用:2]
[23] LI Hongbing, ZHANG Jiajia. Well log and seismic data analysis for complex pore-structure carbonate reservoir using 3D rock physics templates[J]. Journal of Applied Geophysics, 2018, 151: 175-183. [本文引用:1]
[24] 杨培杰. 泥岩储层孔隙度和含水饱和度同步反演[J]. 地球物理学报, 2018, 61(2): 673-682.
YANG Peijie. Porosity and water saturation simultaneous inversion for sand -mudstone reservoir[J]. Chinese Journal of Geophysics, 2018, 61(2): 673-682. [本文引用:1]
[25] GASSMANN F. Über die elastizität poröser medien[J]. Vier der Natur Gesellschaft Zürich, 1951, 96: 1-23. [本文引用:3]
[26] NUR A. Critical porosity and the seismic velocities in rocks[J]. EOS, Transactions American Geophysical Union, 1992, 73: 43-66. [本文引用:3]
[27] RAYMER L L, HUNT E R, GARDNER J S. An improved sonic transit time-to-porosity transform[R]. Tulsa: SPWLA, 1980. [本文引用:1]
[28] URSIN B, STOVAS A. Travel time approximations for a layered transversely isotropic medium[J]. Geophysics, 2006, 71(2): D23-D33. [本文引用:1]
[29] HILL R. The elastic behavior of crystalline aggregate[J]. Proceedings of the Physical Society, 1952, 65(5): 349-354. [本文引用:1]
[30] ZHANG Jiajia, LI Hongbing, YAO Fengchang. Rock critical porosity inversion and S-wave velocity prediction[J]. Applied Geophysics, 2012, 9(1): 57-64. [本文引用:1]
[31] HAMPSON D P, RUSSELL B H. Simultaneous inversion of pre-stack seismic data[R]. Houston: SEG Technical Program Expand ed Abstracts, 2005: 1633-1637. [本文引用:1]