和声搜索优化算法在油藏工程辅助历史拟合中的应用
[SHAMS Mohamed1 
, EL-BANBI Ahmed2 , SAYYOUH Helmy2 ]
, EL-BANBI Ahmed引用本文
SHAMS Mohamed, EL-BANBI Ahmed, SAYYOUH Helmy. 和声搜索优化算法在油藏工程辅助历史拟合中的应用[J]. 石油勘探与开发, 2020,47(1): 148-154.
SHAMS Mohamed, EL-BANBI Ahmed, SAYYOUH Helmy. Harmony search optimization applied to reservoir engineering assisted history matching[J]. Petroleum Exploration & Development, 2020,47(1): 148-154.
Doi: 10.11698/PED.2020.01.14SHAMS Mohamed, EL-BANBI Ahmed, SAYYOUH Helmy. Harmony search optimization applied to reservoir engineering assisted history matching[J]. Petroleum Exploration & Development, 2020,47(1): 148-154.
Permissions
Copyright©2020, 石油勘探与开发》编辑部
石油勘探与开发》编辑部 所有
和声搜索优化算法在油藏工程辅助历史拟合中的应用
第一作者简介：SHAMS Mohamed（1986-）,男,埃及人,高级油藏工程师,主要从事油藏工程和油藏模拟方面的研究。地址：Plot 188, City Center, 5th Settlement, New Cairo, 11835 Egypt。E-mail: mohamed.shams@danagas.com
摘要
基于对和声搜索优化算法（HSO）特点及其优越性的分析,将其应用于埃及苏伊士湾Amal油田Kareem油藏油藏工程辅助历史拟合中。HSO算法具有如下优越性：对解空间探索和开发能力之间的良好平衡使得算法具有鲁棒性和高效性;生成解的多样性由两个组件有效控制,更适用于油藏工程历史拟合这样的高度非线性问题;和声记忆库取值、微调和随机化3个组件之间的配合有助于找到无偏性解;算法实现过程简单。将HSO算法与油藏工程辅助历史拟合中2种常用的优化技术（遗传算法和粒子群算法）应用于3个不同复杂程度的油藏工程历史拟合问题——2个不同尺度的物质平衡历史拟合和1个油藏历史拟合,通过对比3种算法拟合效果验证了HSO算法的正确性和优越性。Kareem油藏历史拟合结果表明,在辅助历史拟合工作流中采用HSO算法作为优化方法可以显著提高拟合质量,缩短求解时间。图7表2参44
关键词:
油藏工程; 辅助历史拟合; 优化算法; 和声搜索优化算法
中图分类号:TE319
文献标志码:A
文章编号:1000-0747(2020)01-0148-07
Harmony search optimization applied to reservoir engineering assisted history matching
Abstract
Based on the analysis of characteristics and advantages of HSO (harmony search optimization) algorithm, HSO was used in reservoir engineering assisted history matching of Kareem reservoir in Amal field in the Gulf of Suez, Egypt. HSO algorithm has the following advantages: (1) The good balance between exploration and exploitation techniques during searching for optimal solutions makes the HSO algorithm robust and efficient. (2) The diversity of generated solutions is more effectively controlled by two components, making it suitable for highly non-linear problems in reservoir engineering history matching. (3) The integration between the three components (harmony memory values, pitch adjusting and randomization) of the HSO helps in finding unbiased solutions. (4) The implementation process of the HSO algorithm is much easier. The HSO algorithm and two other commonly used algorithms (genetic and particle swarm optimization algorithms) were used in three reservoir engineering history match questions of different complex degrees, which are two material balance history matches of different scales and one reservoir history matching. The results were compared, which proves the superiority and validity of HSO. The results of Kareem reservoir history matching show that using the HSO algorithm as the optimization method in the assisted history matching workflow improves the simulation quality and saves solution time significantly.
Keyword:
reservoir engineering; assisted history matching; optimization algorithm; harmony search optimization algorithm
0 引言
人工历史拟合过程十分耗时且经常无法得到满意的结果[1, 2, 3, 4, 5], 近年来研究者引入多种方法以实现拟合过程中部分任务的自动化。辅助历史拟合即将历史拟合问题转换为优化问题, 其目标是将实际数据（如压力、产量和饱和度分布）与模拟数据之间的差值降至最小, 其工作流通常包括实验设计、代理建模和优化。Shams等[6]详细描述了辅助历史拟合过程并提出了新的工作流。
和声搜索优化算法（HSO）是由Geem等[7]开发的一种随机优化算法, 其灵感来自乐师在持续的排练中通过反复调整乐队中各乐器的音调, 寻找和声即兴表演里最佳和声的过程[8]。优化问题的最优解是在给定目标下, 受约束条件限制的最佳解。利用上述两个过程追求目标的相似性, 提出了新的优化算法即HSO算法, 该算法尚未在油藏工程问题中得到应用。
本文将HSO算法用于辅助历史拟合流程中的优化部分。分析了该算法相较于其他两种常用算法（遗传算法和粒子群算法）的优越性, 其中遗传算法（GA）是辅助历史拟合商业软件中应用最为广泛的优化方法, 粒子群算法（PSO）是最新的高效全局优化技术之一。将HSO算法与GA算法、PSO算法应用于不同复杂程度的3个油藏工程历史拟合问题, 以验证HSO算法的有效性; 最后将HSO算法应用于具有28年开发历史的带气顶老油藏的数值模拟中, 将其拟合效果与人工拟合及GA算法辅助历史拟合进行了对比。
1 优化技术
优化算法有确定性算法和随机算法两大类[8], 确定性优化算法是完全依赖线性代数优化方法的经典算法, 通过计算数学模型的梯度来优化参数, 将目标函数最小化, 该算法的解为局部最优解而非全局最优解, 局部的极大或极小最优值不是真正的最优解。由于历史拟合问题解的非唯一性, 研究者通常期望得到若干个局部最小值, 所以确定性算法无法有效解决问题[9]。随机优化算法则是在搜索过程中采用随机化方法[10], 模拟退火[11, 12, 13]、热浴算法[14]、遗传算法[15, 16, 17, 18]、进化策略[19, 20, 21, 22]、散点搜索优化[23]、随机扰动近似算法[24, 25, 26]、集合卡尔曼滤波[27, 28, 29, 30, 31, 32, 33, 34]、粒子群算法[35]、蚁群优化算法[36]等在油藏工程辅助历史拟合中都得到了应用[37, 38, 39, 40]。本文将HSO算法引入油藏工程辅助历史拟合问题中, 并将其性能与油藏工程应用中常用的两种优化算法（遗传算法和粒子群算法）进行对比。
1.1 和声搜索优化算法
如前所述, HSO算法的灵感来自于乐师通过反复调整乐队中各乐器的音调寻求最佳和声状态的过程。音乐和声即兴创作过程中和声搜索分为3个步骤：①从乐师的记忆库中选择一个满意的音调; ②选择一个与满意音调相似的音调, 然后由乐师进行调整; ③创作新的或随机的音调, 存储更好的和声, 舍弃相对较差的和声, 和声集合不断更新, 直到得到最佳和声。为了模拟和声即兴创作的优化过程, Geem等[7]提出了HSO算法, 确定了和声搜索优化的步骤：首先初始化和声记忆库; 然后产生新的解向量, 其分量可通过3种机理产生, 即①保留和声记忆库中的某些解分量, 和声记忆库保留概率为HMCR, ②随机生成, 概率为1-HMCR, ③对①和②得到的新的解分量进行微调; 若新的解向量评价函数优于和声记忆库中的最差解, 则用新的解向量替换最差解; 达到终止条件后停止计算（如达到最大迭代次数）。HSO算法的主要控制参数为和声记忆库大小、和声记忆库保留概率（HMCR）及微调概率（PAR）。
①和声记忆库大小。和声记忆库为表示HSO算法基本结构的简单矩阵, 由最佳解向量组成。和声记忆矩阵中的每一行表示一个解向量, 最后一列表示向量的适应度值。在优化过程开始之前, 和声记忆库以随机生成的解向量进行初始化。解向量可以围绕着一个点随机选择, 该点代表搜索设计空间内最有可能找到最优值的区域。在油藏工程辅助历史拟合中, 可以使用历史拟合目标参数最可能值的解向量初始化和声记忆矩阵。历史拟合目标参数最可能值可由油藏工程师根据经验确定, 也可以简单取每个目标参数取值范围的中值。在M维优化问题中, 和声记忆矩阵可以表示为：
$\left[ \begin{array}{* {35}{l}} A_{1, 1}^{{}} & \cdots & A_{1, M}^{{}} & \left| {{}_{1}} \right. \\ \text{ }\vdots & {} & \text{ }\vdots & \text{ }\vdots \\ A_{S\text{, 1}}^{{}} & \cdots & A_{S, M}^{{}} & \left| {{}_{S}} \right. \\ \end{array} \right] $ （1）
②和声记忆库保留概率（HMCR）。和声记忆库取值是一个类似于乐师选择满意音调的过程, 并以此确保产生出好的音乐作品。在HSO算法中, HMCR值为每个解分量选择最佳拟合解, 确保将最佳的和声传递给新的和声记忆库。HMCR为概率参数, 取值范围为0~1, 如果设定的HMCR值太低, 只选择少数最佳和声, 可能会导致收敛缓慢; 如果指定的HMCR值太高（接近1）, 则几乎所有的和声都会出现在和声记忆库中, 则无法得到很好的搜索过程, 导致产生错误解。因此大多数应用中, HMCR值设为0.70~0.95[7]。
③微调概率（PAR）。音调微调过程类似于演奏与满意音调相似的音调。在HSO算法中, 音调微调对应于创作略微不同解的过程。通过对音调进行微小的随机调整, 在已有合适解附近产生一个新解。通过PAR值（0~1）来控制音调调整程度。如果设定一个窄带宽低微调概率值, 搜索将仅限于整个搜索空间的一个子空间内, 则和声搜索的收敛性降低。反之, 如果设定带宽较宽的高微调概率值, 围绕最优解产生分散解的概率会增加。因此, 大多实际应用中使用的PAR值为0.1~0.5[7]。
1.2 和声搜索优化算法的优越性
HSO算法应用于油藏工程辅助历史拟合问题中优于其他优化技术的原因如下：①在寻找最优解的过程中, 对解空间探索和开发能力之间的良好平衡使得HSO算法具有鲁棒性和高效性。探索意味着该算法能够产生包括潜在最优解在内的多种解, 并且探索整个搜索空间, 避免产生局部极小解; 而开发则意味着算法将围绕最优或近似最优解进行搜索, 以找到更好的解。②在HSO算法中, 与其他几乎只由单个组件控制的优化算法相比, 生成解的多样性由两个组件（微调和随机化）有效控制。随机化组件可以使HSO算法至少具有与其他优化方法相同的效率; 探索组件（微调）通过小幅度增加现有音调或和声记忆库中解向量的随机性来强化生成的解向量, 换言之, 微调组件代表了局部解的改进过程。油藏工程历史拟合问题具有高度的非线性, 通常采用大量的优化参数, 采用HSO算法的探索功能可获得更好的效果。③HSO算法3个组件（和声记忆库取值、微调和随机化）之间的配合有助于找到无偏性解。和声记忆库取值和音调微调过程之间的相互作用确保了潜在最优局部解存在。同时, 和声记忆库取值与随机化过程相互作用, 高效探索全局搜索空间, 提供良好解附近的受控多样化解。随机化更有效地探索搜索空间, 而音调微调确保新生成解与现有良好解之间的距离不会太远。④HSO算法的实现过程比其他优化算法容易得多。这是因为HSO算法对优化参数不敏感, 为了获得更高质量的解, 无需对优化参数进行微调。
GA算法优化结果的质量很大程度上取决于遗传算子（交叉、选择、变异）的概率, 这些参数的调试方式对优化结果影响很大。此外, GA算法参数的调试是纯随机过程, 依赖于试验和误差。如果GA算法优化中种群规模太小, 将没有足够的进化次数维持算法的进行, 很可能产生少数个体控制整个种群的风险, 导致过早收敛或产生无意义的解[41]。Clerc和Kennedy[42]指出PSO算法的理论数学基础不够, 他们分析PSO算法传输矩阵的稳定性时发现粒子稳定运动的条件有限。此外, 根据Shailendra[43]的研究, 一旦粒子过早地收敛到搜索空间任一特定区域, PSO算法就会陷入停滞。PSO算法在粒子数较少时计算效率高, 当粒子数增加时算法的性能会变差, 而油藏数值模拟历史拟合问题中通常包含多个待优化参数, 因此这将成为一大问题。
2 和声搜索优化算法在油藏工程辅助历史拟合中的应用
2.1 辅助历史拟合测试
针对3个不同复杂程度的油藏工程历史拟合问题（即2个不同尺度模型的物质平衡拟合和1个油藏模拟辅助历史拟合）进行测试, 验证HSO算法的正确性和通用性。
2.1.1 单储集层物质平衡拟合
利用Hurst-van Eversdingen修正水侵方程建立简单的水层单储集层物质平衡模型。选取3个不确定性参数（石油地质储量、水层侵入角和水层渗透率）作为历史拟合参数, 对HSO优化技术进行测试。
2.1.2 多储集层物质平衡拟合
多储集层物质平衡拟合模型由3个断块组成, 每个断块2层, 每个断块/层均采用其自身的物质平衡模型进行建模, 总共形成6个区, 断块间相互连通, 具有传导性。模型共有8口井, 采用合采方式。选取不同断块的20个不确定性参数（包括原油地质储量、储集层厚度、含水层侵入角、初始气顶体积、储集层间的传导率等）作为历史拟合参数。
2.1.3 油藏历史拟合
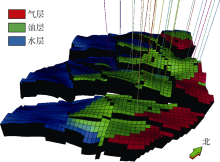
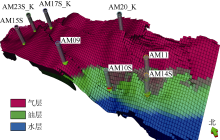
油藏地质模型如图1所示, 该模型包括3个具有不同初始油水界面和油气界面的断块, 模型尺寸为50× 49× 199, 单元总数为487 750。模型中共有20口生产井和3口注水井。
 | 图1 油藏历史拟合地质模型 |
为了实现辅助历史拟合, 选择了50个历史拟合参数, 包括不同断块的油水界面和油气界面、渗透率乘子、水层孔隙度、水层渗透率、水层厚度、水层侵入角、断层传导率乘子、不同岩石的Corey指数、不同岩石的临界含水饱和度、油井表皮系数等。
2.2 不同优化技术拟合结果对比
将本文辅助历史拟合优化技术应用于上述3个历史拟合问题, 并且保持选择样本点的实验方法、历史拟合参数的搜索空间大小以及建模技术在HSO、GA、PSO算法中一致, 从而确保所得结果的任何改进均仅由优化方法引起。其中, 实验设计技术采用Sobol序列, 建模技术采用人工神经网络（ANN）。
按以下步骤进行辅助历史拟合测试：①利用MBAL、Eclipse和Petrel软件工具, 采用3个测试中已知的储集层参数预测10年的生产数据。MBAL用于物质平衡历史拟合; Eclipse用于油藏历史拟合, 其中水层采用Petrel软件中的Carter Tracy模型进行拟合。②将生成的生产数据作为测试中的已知历史数据。③改变原始储集层参数以获得未拟合的生产数据。④使用Sobol序列实验设计技术选择历史拟合参数的样本, 用于启动运行。⑤使用（2）式计算每次运行的目标函数。⑥利用实验设计选择的储集层参数样本, 采用ANN建立目标函数的代理模型。由隐神经元的S型传递函数和输出神经元的线性传递函数组成的双层前馈神经网络来拟合多维数据。该网络采用Levenberg- Marquardt反向传播算法进行训练, 当神经网络均方误差停止修正时, 训练自动停止。输入向量和目标向量随机分为3组：70%训练网络, 15%验证网络, 15%测试网络。⑦使用优化算法将创建的代理模型最小化, 最小化过程运行5次来选择更具代表性的解。⑧使用（3）式计算的性能指标量化历史拟合参数估计值和精确值之间的误差。
$f\left( x \right)=\mathop{\sum }^{}\frac{1}{n}\left\{ \underset{i=1}{\overset{n}{\mathop \sum }}\, {{\left[ {{w}_{i}}{{\left( y_{i}^{\text{*}}-{{y}_{i}} \right)}^{2}} \right]}_{\text{WC}}}+ \right.\\ \underset{i=1}{\overset{n}{\mathop \sum }}\, {{\left[ {{w}_{i}}{{\left( y_{i}^{\text{*}}\text{ }\!\!~\!\!\text{ }-{{y}_{i}} \right)}^{2}} \right]}_{\text{GOR}}}+\left. \underset{i=1}{\overset{n}{\mathop \sum }}\, {{\left[ {{w}_{i}}{{\left( y_{i}^{\text{*}}\text{ }\!\!~\!\!\text{ }-{{y}_{i}} \right)}^{2}} \right]}_{\text{P}}} \right\}$ （2）
$PI\text{=}\frac{1}{N}\sum\limits_{j=1}^{N}{\left| \frac{{{H}_{\text{est, }j}}-{{H}_{\text{exa, }j}}}{{{H}_{\text{exa, }j}}} \right|}$ （3）
性能指标值越小, 历史拟合参数的估计值与精确值越接近。为了公平对比3种优化算法, 种群中的个体数、每次运行的迭代次数和运行次数均保持不变。在采用GA算法时, 设置适应度为路径长度的倒数, 使用轮盘赌选择法、概率为95%的部分匹配交叉算子和概率为0.1%的互换变异算子。对PSO算法采用相同适应度设置。性能指标值如表1所示, 与GA算法和PSO算法相比, HSO算法对前述3个历史拟合测试始终保持较低的性能指标值, 表明该优化算法具有较好的性能。
 | 表1 3个历史拟合测试中不同算法的性能指标值 |
3 Kareem油藏模拟辅助历史拟合
3.1 辅助历史拟合测试
Kareem油藏是一个带气顶的老油藏, 1988年12月投入开发, 生产过程中表现出弱底水强气顶的驱动机制。该油藏由3个断块组成, 发育6条连通断层, 3个断块具有相同的初始油水和油气界面, 并且表现出相同的压力枯竭趋势。Kareem油藏共钻井23口, 目前有9口井生产。地质模型如图2所示, 模型尺寸为44× 119× 72, 单元总数为376 992, 其中包括116 676个活动单元。对Kareem油藏进行的最新油藏模拟研究成功地实现了28年历史数据的人工拟合, 综合油藏研究大约历时5个月, 其中包括人工历史拟合90 d。本文将HSO技术应用于Kareem油藏辅助历史拟合, 并与人工历史拟合及GA技术辅助历史拟合进行对比。
 | 图2 Kareem油藏三维地质模型 |
辅助历史拟合和人工历史拟合采用的15个历史拟合参数如表2所示。辅助历史拟合工作流步骤如下：①使用Sobol序列实验设计技术在历史拟合参数范围内取值开展25次运行。②运行域包含26次运行（其中25次运行参数值由实验设计方法选择, 剩余1次运行代表历史拟合参数的最接近值）, 遵循JUTILA的经验法则[44], 其中规定运行次数不少于（2N+1）, 上限为26次。③对前14年的历史数据进行模拟, 每次运行过程都使用（2）式计算多目标函数。④在通过ANN建立的代理模型中插入目标函数和实验设计的油藏参数样本。⑤采用HSO和GA算法将建立的ANN代理模型最小化。每个最小化过程运行5次, 以获得更具代表性的解, 且两种优化算法的运行次数保持一致。⑥将通过2个工作流获得的历史拟合参数值作为输入参数, 在预测模式下对后14年数据进行模拟。⑦使用（4）式计算误差指标, 对各工作流在预测模式下得到的模拟数据和实际数据进行对比。⑧应用Petrel和Eclipse软件进行油藏模拟, 然后使用Matlab运行编码辅助历史拟合工作流。
$EI\text{=}\frac{1}{n}\underset{i=1}{\overset{n}{\mathop \sum }}\, \left[ {{\left( \frac{y_{i}^{\text{* }}-{{y}_{i}}}{{{y}_{i}}} \right)}_{\text{WC}}} \right.+\\ \left. {{\left( \frac{y_{i}^{\text{* }}-{{y}_{i}}}{{{y}_{i}}} \right)}_{\text{GOR}}}\text{+}{{\left( \frac{y_{i}^{\text{* }}-{{y}_{i}}}{{{y}_{i}}} \right)}_{\text{P}}} \right] $ （4）
| 表2 基于不同工作流模型的历史拟合参数值 |
3.2 辅助历史拟合结果
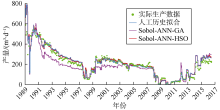
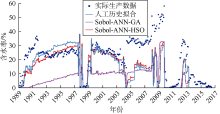
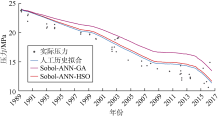
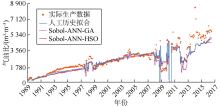
基于拟合质量和拟合时间, 对比HSO算法优化、人工历史拟合以及应用最为广泛的辅助历史拟合优化技术（GA）的结果。产量、含水率、平均储集层压力和气油比的拟合效果如图3— 图6所示。由图3可见, Sobol-ANN-HSO工作流产量历史拟合结果与人工历史拟合结果接近, 两者都与实际数据拟合良好。Sobol- ANN-GA工作流历史拟合效果相对较差, 尤其是在1991— 2004年。含水率的历史拟合效果与产量类似（见图4）, Sobol-ANN-GA工作流拟合的油藏整个寿命期内的含水率均较低, 人工历史拟合及Sobol-ANN- HSO工作流拟合的含水率非常接近, 对实际数据拟合效果更好。对于油藏平均压力, 人工历史拟合和Sobol- ANN-HSO工作流的拟合结果接近, 与Sobol-ANN-GA工作流相比表现出更好的拟合效果（见图5）。在气油比的拟合结果中, 3个工作流未表现出明显差异（见图6）。
 | 图3 Kareem油藏产量历史拟合结果 |
 | 图4 Kareem油藏含水率历史拟合结果 |
 | 图5 Kareem油藏平均压力历史拟合结果 |
 | 图6 Kareem油藏气油比历史拟合结果 |
计算每个历史拟合模型的误差指标以进行定量对比：人工拟合模型、Sobol-ANN-GA模型、Sobol-ANN- HSO模型的误差指标值分别为0.698, 1.035, 0.691; 3种模型的运行次数分别为200, 26, 26次, 运行时间分别为90, 2, 2 d。Sobol-ANN-HSO工作流辅助历史拟合模型具有最低的误差指标, 表现出最好的拟合质量和效率。
以油井为对象, 计算每口井的拟合目标函数, Sobol-ANN-GA和Sobol-ANN-HSO工作流的历史拟合质量对比如图7所示。可以看出, 与Sobol-ANN-GA工作流相比, 本文工作流Sobol-ANN-HSO在6口井中表现更佳, 1口井中拟合质量相当, 2口井中表现更差。
 | 图7 Sobol-ANN-HSO和Sobol-ANN-GA工作流历史拟合质量对比 |
4 结语
基于3个油藏工程历史拟合测试和Kareem油藏实际历史拟合的研究结果认为, 和声搜索优化算法优于辅助历史拟合工作流中的常用优化技术遗传算法和粒子群算法; 在辅助历史拟合工作流中引入和声搜索优化算法, 可明显节省油藏研究所花费的时间; 本文优化算法拟合效果接近人工历史拟合效果, 且所用时间明显缩短。
符号注释：
A— — 和声分量; EI— — 误差指标; f(x)— — 使用一组历史拟合参数x获得的目标函数; Hest— — 历史拟合参数估计值; Hexa— — 历史拟合参数精确值; i— — 实际数据点序号; j— — 历史拟合参数序号; Krow— — 油水相对渗透率; Krog— — 油气相对渗透率; M— — 优化问题维数; n— — 实际数据点的个数; N— — 历史拟合参数个数; PI— — 性能指标, %; S— — 和声记忆库大小; wi— — 分配给目标函数中每个数据集的权重; $y_{i}^{\text{* }}$— — 使用一组历史拟合参数x计算得到的模拟数据; yi— — 实际数据; Φ — — 适应度。下标：GOR— — 气油比; WC— — 含水率; P— — 压力。
（编辑 刘恋）
参考文献
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|