引用本文
时新磊, 崔云江, 许万坤, 张建升, 关叶钦. 基于随钻测压流度的地层渗透率评价方法及产能预测[J]. 石油勘探与开发, 2020,47(1): 140-147.
SHI Xinlei, CUI Yunjiang, XU Wankun, ZHANG Jiansheng, GUAN Yeqin. Formation permeability evaluation and productivity prediction based on mobility from pressure measurement while drilling[J]. Petroleum Exploration & Development, 2020,47(1): 140-147.  
Doi: 10.11698/PED.2020.01.13
Permissions
Copyright©2020, 石油勘探与开发》编辑部
石油勘探与开发》编辑部 所有
基于随钻测压流度的地层渗透率评价方法及产能预测
时新磊, 崔云江, 许万坤, 张建升, 关叶钦
中海石油（中国）有限公司天津分公司,天津300459

第一作者简介：时新磊（1982-）,男,河南南阳人,硕士,中海石油（中国）有限公司天津分公司渤海石油研究院高级工程师,主要从事测井资料综合解释与储量评价研究。地址：天津市滨海新区海川路2121号,渤海石油管理局B座,邮政编码：300459。E-mail: shixl3@cnooc.com.cn

收稿日期: 2019-03-26
基金项目: “十三五”国家科技重大专项“渤海油田加密调整及提高采收率油藏工程技术示范”（2016ZX05058-001）; 中海石油（中国）有限公司科技项目“渤海油田3 000×104 t持续稳产关键技术研究”（CNOOC-KJ135-ZDXM36-TJ）
摘要

基于随钻测压过程中流度的测量机理,通过大量的测压流度数据分析发现,水基钻井液钻井条件下（水基钻井液滤液）的随钻测压流度与钻井液滤液黏度乘积无限接近于相渗实验过程中残余油饱和度下的水相渗透率,据此提出一种随钻测压流度到岩心渗透率的转换方法,并建立基于Timur公式刻度的渗透率评价模型。该方法在渤海蓬莱19-9油田应用效果表明：①与借用相邻油田模型计算的渗透率相比,该模型计算的渗透率与岩心分析渗透率吻合程度更高;②基于新模型建立了测井计算流度与实钻比采油指数的相关关系,与借用相邻油田渗透率模型建立的关系对比,新模型相关性相对更好;③对4口生产井进行了产能预测,预测结果与钻后实际产量吻合较好。图11表4参20

关键词: 随钻测压流度; 渗透率; 束缚水饱和度; Timur公式; 产能预测; 蓬莱19-9油田
中图分类号:TE271 文献标志码:A 文章编号:1000-0747(2020)01-0140-08
Formation permeability evaluation and productivity prediction based on mobility from pressure measurement while drilling
SHI Xinlei, CUI Yunjiang, XU Wankun, ZHANG Jiansheng, GUAN Yeqin
CNOOC China Limited, Tianjin Branch, Tianjin 300459, China
Abstract

Based on the measurement mechanism of mobility in pressure measurement while drilling, through analyzing a large number of mobility data, it is found that under the condition of water-based mud drilling, the product of mobility from pressure measurement while drilling and the viscosity of mud filtrate is infinitely close to the water phase permeability under the residual oil in relative permeability experiment. Based on this, a method converting the mobility from pressure measurement while drilling to core permeability is proposed, and the permeability based on Timur formula has been established. Application of this method in Penglai 19-9 oilfield of Bohai Sea shows: (1) Compared with the permeability calculated by the model of adjacent oilfields, the permeability calculated by this model is more consistent with the permeability calculated by core analysis. (2) Based on the new model, the correlation between the calculated mobility of well logging and the actual drilling specific productivity index bas been established. Compared with the relationship established by using the permeability model of an adjacent oilfield, the correlation of the new model is better. (3) Productivity of four directional wells was predicted, and the prediction results are in good agreement with the actual production after drilling.

Keyword: mobility from pressure measurement while drilling; permeability; irreducible water saturation; Timur formula; productivity prediction; Penglai 19-9 oilfield
1 研究背景与问题的提出

渗透率的测量精度直接影响产能预测及储集层非均质性研究的准确性[1]。目前, 尚未有直接通过测井手段来测量地层连续渗透率曲线的方法, 渗透率的求取主要通过实验室岩心分析获得[2, 3, 4]。由于海上油田取心成本昂贵, 如何在缺乏岩心分析资料情况下, 精确计算储集层渗透率成为油气田开发阶段迫切需要解决的难题。刘堂晏等[5]提出钻井液滤液转换法将MDT（模块地层动态测试）测压流度转换为储集层有效渗透率; 鹿克峰等[6]、杨冬等[7]均提出利用岩心相渗实验相关关系将低渗气藏电缆地层测试流度转换为气相渗透率的方法, 但以上方法转换后的渗透率仍为离散的单点渗透率, 无法获取连续的渗透率曲线。

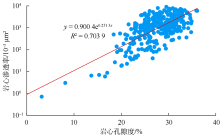
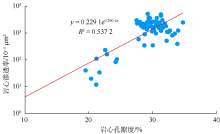
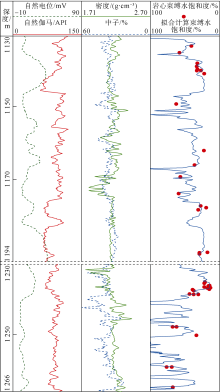
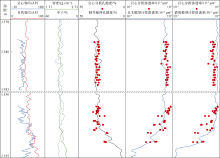
渤海蓬莱19-9油田位于渤海湾盆地东北部, 发育在郯庐断裂带上, 构造类型为古隆起背景上发育的断背斜。主力油层发育于新近系明化镇组下段和馆陶组, 储集层岩性为河流相陆源碎屑岩, 以长石砂岩为主[8, 9], 储集层物性以高孔、高渗为主, 孔隙度为21.5%~38.4%, 渗透率为（13.9~6 049.8）× 10-3 μ m2。该油田油藏埋藏浅, 岩性疏松, 储集层胶结程度差、非均质性强, 如何精确计算地层渗透率给测井解释人员带来了巨大的挑战。勘探阶段认为蓬莱19-9油田与相邻油田具有相同的沉积环境、相近的油藏埋深、相同的矿物成分、相似的测井响应特征及相近的储集物性, 因此勘探阶段蓬莱19-9油田并未进行钻井取心, 渗透率评价模型借用相邻油田储量评价阶段所建立的模型（见图1）。开发阶段蓬莱19-9油田在渗透率评价方面主要存在以下两方面问题：①随着整体开发方案随钻实施的逐步深入, 发现开发取心井岩心分析渗透率与借用相邻油田模型计算的渗透率之间存在较大误差; ②开发阶段蓬莱19-9油田由于工程需求进行了2筒钻井取心, 收获率为70%, 从岩心描述及岩心分析孔渗数据来看, 储集层孔隙结构复杂, 非均质性强。由于该井岩心分析样品较少（74块）且孔渗关系较差（见图2）, 不能满足油田渗透率评价的需求。以上问题给开发阶段钻后产能预测带来一定的不确定性, 因此建立适合本油田自身的渗透率评价模型对开发阶段合理的产能预测尤为重要。

图1 相邻油田岩心孔渗关系模型

图2 蓬莱19-9油田开发井岩心分析孔渗关系模型

在前人研究基础上, 本文通过调研目前常用的随钻测压仪器参数范围, 分析蓬莱19-9油田21口井330余个随钻测压资料点及油田实际生产数据, 基于随钻测压流度的测量机理, 结合岩心相渗实验数据, 建立随钻测压流度到岩心渗透率的转化方法, 进而建立基于Timur公式刻度的渗透率评价模型, 以期为开发阶段产能预测提供更可靠的依据。

2 基于随钻测压流度的地层渗透率评价方法

目前利用随钻测压流度评价渗透率的方法仅能通过钻井液滤液黏度将各测压点流度转换为单点的渗透率, 尚无利用随钻测压流度资料进行连续渗透率评价的方法。本文基于纵向上分布范围较大的随钻测压流度资料, 结合测井解释孔隙度及束缚水饱和度建立连续的渗透率评价模型。

2.1 随钻测压流度与水相渗透率相关关系

流度表征了流体在多孔介质中的渗流能力, 流度值越大, 渗流能力越强。随钻测压的主要目的是通过求取地层压力来评价地层的连通性、确定油水界面及地层超压或亏空等情况。随钻测压过程中可利用流体压力的变化通过（1）式求取地层流度[10]。

${{\lambda }_{\text{Mb}}}=\frac{GV}{10.2{{r}_{\text{p}}}\int_{{{t}_{1}}}^{{{t}_{2}}}{0.006\text{ }895\text{ }\left[ {{p}_{\text{sf}}}-p\left( t \right) \right]\text{d}t}}$ （1）

本文调研了目前常用的随钻测压系统, 统计了3家公司的抽吸流体参数范围（见表1）, 发现随钻测压仪器均存在抽吸速率低、测试时间短、取样体积范围小的特点, 说明随钻测压压力波及范围比较小, 且抽吸流体仅为近井眼地带的钻井液滤液[11, 12, 13]。

表1 随钻测压系统抽吸流体参数范围统计表

通过以上统计分析可知, 随钻测压提供的压降流度为近井眼地带钻井液滤液的流度。由于水基钻井液钻井条件下冲洗带钻井液侵入过程与相渗实验中水驱油机理相似[6, 7, 8], 因此与DST（钻杆测试）及MDT测试相比, 随钻测压流度与钻井液滤液黏度的乘积更接近于相渗实验中残余油饱和度下的水相渗透率（见图3）。据统计, 渤海地区钻井液滤液黏度为0.40~0.85 mPa· s[5], 根据现场化验分析结果, 蓬莱19-9油田钻井液滤液黏度为0.5 mPa· s。

图3 油水相对渗透率曲线

确定钻井液滤液黏度后, 利用（2）式可将随钻测压流度数据转换为残余油饱和度下的水相渗透率, 由此明确了随钻测压流度与钻井液滤液黏度乘积为相渗实验中残余油饱和度下的水相渗透率。

${{K}_{\text{w}({{S}_{\text{or}}})}}={{\lambda }_{\text{Mb}}}{{\mu }_{\text{mf}}}$ （2）

2.2 随钻测压流度到岩心渗透率的转换方法

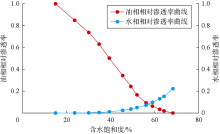
油水相对渗透率曲线反映了油水两相在多孔介质中的流动规律, 是油田开发设计及油藏工程中的重要资料。理论与实验表明, 相对渗透率与流体饱和度有密切关系[14], 通过相渗实验可以确定束缚水饱和度下的油相渗透率及残余油饱和度下的水相渗透率。

利用蓬莱19-9及周边油田46块岩心样品设计了4组油水相渗对比实验, 实验用油选取4种白油（黏度分别为10.1, 39.6, 50.8, 141.8 mPa· s）; 实验用水为氯化钾溶液, 黏度为0.738 5 mPa· s, 矿化度为72 924 mg/L, 具体实验相关参数及结果见表2。其中白油黏度为39.6 mPa· s及50.8 mPa· s的2组实验岩心取自蓬莱19-9油田, 为地层温度、压力及原油黏度条件下的模拟实验; 由于蓬莱19-9油田平面及纵向上地层原油黏度变化较大且取心资料覆盖深度范围有限, 因此另2组实验岩心取自蓬莱19-9周边油田, 取心段物性与蓬莱19-9油田取心段类似而地层原油黏度不同。

表2 蓬莱19-9及周边油田相渗实验参数及实验结果统计表

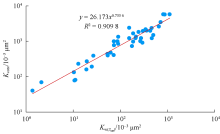
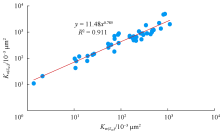
基于以上46块岩心相渗实验数据, 分别建立了残余油饱和度下的水相渗透率与岩心渗透率（见（3）式、图4）、残余油饱和度下的水相渗透率与束缚水饱和度下的油相渗透率（见（4）式、图5）相关关系, 相关性均较好。

${{K}_{\text{core}}}=26.173{{K}_{\text{w}({{S}_{\text{or}}})}}^{0.733\text{ 6}}$ （3）

${{K}_{\text{o}({{S}_{\text{wi}}})}}=11.48{{K}_{\text{w}({{S}_{\text{or}}})}}^{0.785\text{ 0}}$ （4）

图4 残余油饱和度下的水相渗透率与岩心渗透率关系

图5 残余油饱和度下的水相渗透率与束缚水饱和度下的油相渗透率关系

因此, 在确定钻井液滤液黏度后, 将由（2）式计算得到的残余油饱和度下的水相渗透率代入（3）式或（4）式, 便可以将随钻测压点流度数据转换为岩心渗透率或束缚水饱和度下的油相渗透率。为了后续利用岩心渗透率验证该方法的有效性, 本文利用（3）式将随钻测压流度数据转换为岩心渗透率。

2.3 基于Timur公式刻度建立渗透率模型

将随钻测压流度转换为岩心渗透率后, 如何利用转换后的离散点建立连续渗透率评价模型是本文研究的重点。由于蓬莱19-9油田具有丰富的随钻测压资料且测压点在纵向上可覆盖整个主力砂体, 因此建立基于Timur公式刻度的连续渗透率模型具有一定的可行性。

Timur[15]利用北美3个油田155块砂岩岩心样品相渗分析数据及岩心分析孔隙度和渗透率, 建立了经典的Timur经验公式（5）, 其通用公式为公式（6）。

${{K}_{\text{core}}}=0.136\frac{\phi _{\text{core}}^{4.4}}{S_{\text{wi }\!\!\_\!\!\text{ core}}^{2}}$ （5）

${{K}_{\text{core}}}=A\frac{\phi _{\text{core}}^{B}}{S_{\text{wi }\!\!\_\!\!\text{ core}}^{C}}$ （6）

由于蓬莱19-9油田岩心分析样品少且代表性差, 因此利用随钻测压流度转换后的岩心渗透率, 结合测井解释孔隙度和束缚水饱和度这2个参数来刻度Timur公式建立连续渗透率评价模型。将（6）式中的岩心渗透率由随钻测压流度转换后的岩心渗透率替代; 一般情况下, 测井解释的孔隙度精度较高, 因此（6）式中的岩心孔隙度由测井解释孔隙度替代; 岩心束缚水饱和度由常规测井资料及核磁共振测井拟合求取。

2.3.1 束缚水饱和度计算

目前确定束缚水饱和度的方法主要有岩心实验法和测井资料预测法。岩心实验法为直接测量方法, 得到的束缚水饱和度较为准确, 但取心价格昂贵且无法获得连续的束缚水饱和度曲线[16]。本文采用测井资料预测法, 主要利用核磁共振测井结合常规测井资料确定束缚水饱和度。

束缚水饱和度是刻度Timur公式的关键参数。本文利用8口评价井的核磁共振测井束缚水饱和度、核磁共振测井有效孔隙度及密度中子曲线计算的泥质含量等数据, 基于经典的束缚水饱和度计算公式（7）[17], 拟合得到适合于蓬莱19-9油田的束缚水饱和度计算模型公式（8）。

${{S}_{\text{wi }\!\!\_\!\!\text{ Nmr}}}=\frac{100}{c}\left[ a-\lg \left( \frac{{{\phi }_{\text{Nmr}}}}{{{V}_{\text{sh}}}-b} \right) \right] $ （7）

${{S}_{\text{wi }\!\!\_\!\!\text{ Nmr}}}=\frac{100}{3.497}\left[ 0.632-\lg \left( \frac{{{\phi }_{\text{Nmr}}}}{{{V}_{\text{sh}}}+39.53} \right) \right] $ （8）

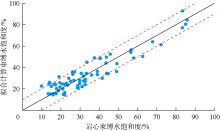
利用（8）式计算得到的束缚水饱和度与岩心束缚水饱和度吻合效果较好（见图6）。图7显示, 拟合计算束缚水饱和度与岩心束缚水饱和度的绝对误差基本在± 10%以内, 表明计算的束缚水饱和度精度能够满足拟合Timur公式的要求。

图6 拟合计算束缚水饱和度与岩心束缚水饱和度对比图

图7 拟合计算束缚水饱和度精度分析

2.3.2 渗透率模型建立

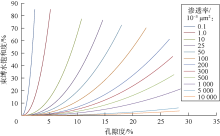
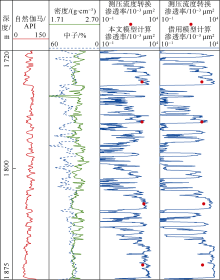
利用蓬莱19-9油田21口井330余个随钻测压流度资料点转换得到的岩心渗透率及其所对应深度的测井解释有效孔隙度和束缚水饱和度来刻度Timur通用公式（6）, 建立蓬莱19-9油田地层渗透率评价模型。通过刻度得到（6）式中的A、B、C参数分别为2.60, 2.98, 1.32, 拟合关系如（9）式, 拟合相关系数为0.89, 具有较高的拟合精度。利用（9）式建立蓬莱19-9油田不同孔隙度及束缚水饱和度条件下的渗透率拟合图版（见图8）, 能够实现地层渗透率的快速定量评价。

${{K}_{\text{core }\!\!\_\!\!\text{ Mb}}}=2.60\frac{\phi _{\log }^{2.98}}{S_{\text{wi }\!\!\_\!\!\text{ log}}^{1.32}}$ （9）

图8 蓬莱19-9油田渗透率拟合图版

3 应用实例
3.1 基于Timur公式刻度的渗透率模型应用实例

开发取心井A35井的渗透率计算结果显示, 本文模型得到的渗透率比借用相邻油田模型得到的渗透率更接近岩心实测值（见图9）。借用相邻油田模型计算渗透率的相对误差为112.5%~135.2%, 而本文模型计算误差为17.0%~35.5%（见表3）。为了进一步验证本文模型的计算精度, 选取了1口未参与本文渗透率模型建立的井, 将其由随钻测压流度转换后的岩心渗透率分别与本文模型和借用相邻油田模型计算的渗透率进行对比（见图10）, 结果显示本文模型的吻合效果更好、计算精度更高。

图9 本文模型和借用相邻油田模型计算渗透率与岩心分析渗透率对比图

表3 A35井取心井段平均渗透率计算精度对比表

图10 本文模型和借用相邻油田模型计算渗透率与随钻测压流度转换后的渗透率对比图

3.2 渗透率模型在产能预测中的应用

储集层渗透率及油藏条件下流体物性参数是影响产能计算精度最敏感的参数[18, 19]。理论上可以根据裘比公式（10）计算比采油指数, 一般在井网参数（re、rw）及流体物性参数（μ o、Bo）变化不大的情况下, 比采油指数与渗透率呈线性关系[20]。因此在油田实际配产过程中通常利用渗透率或测井计算流度来确定比采油指数, 利用（11）式进行产能预测。

${{J}_{\text{os}}}=\frac{0.236{{K}_{\text{o}}}}{\text{ln}\left( {{{r}_{\text{e}}}}/{{{r}_{\text{w}}}}\; \right){{\mu }_{\text{o}}}{{B}_{\text{o}}}}$（10）

${{Q}_{\text{o}}}=h\left( {{p}_{\text{r}}}-{{p}_{\text{wf}}} \right){{J}_{\text{os}}}$ （11）

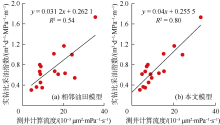
由于蓬莱19-9油田在横向上流体性质差异较大, 需要考虑地层原油黏度对产能的影响。基于本文模型及相邻油田模型建立蓬莱19-9油田已投产16口井的实钻比采油指数与测井计算流度的相关关系（12）和（13）式。与相邻油田模型相比（见图11a）, 本文模型拟合的实钻比采油指数与测井计算流度的相关关系更好（见图11b）, 明显提高了比采油指数的预测精度。

${{J}_{\text{os}}}_{\text{ }\!\!\_\!\!\text{ p}}=0.04\frac{{{K}_{\text{n}}}}{{{\mu }_{\text{o}}}}+0.255\text{ }5$ （12）

${{J}_{\text{os}}}_{\text{ }\!\!\_\!\!\text{ p}}=0.0312\frac{{{K}_{\text{b}}}}{{{\mu }_{\text{o}}}}+0.262\text{ }1$ （13）

图11 借用相邻油田模型和本文模型计算流度与实钻比采油指数相关关系图

利用（11）式和（12）式对蓬莱19-9油田4口生产井进行产能预测, 由表4可见, 基于本文模型预测的比采油指数、日产油量与钻后实际生产数据更为接近, 明显提高了产能预测的精度, 对油田整体开发方案部署的开发井产能预测具有重要的指导意义。

表4 本文模型和借用相邻油田模型产能预测结果与实际生产数据对比
4 结论

随钻测压流度与钻井液滤液黏度的乘积无限接近相渗实验中残余油饱和度下水相渗透率, 据此提出一种随钻测压流度到岩心渗透率的转换方法, 并建立基于Timur公式刻度的渗透率评价模型。

与借用相邻油田模型计算的渗透率相比, 本文模型计算的渗透率与岩心分析渗透率吻合程度更高, 提高了渗透率的评价精度, 解决了缺乏岩心分析孔渗数据情况下渗透率评价的难题。

基于本文模型建立的测井计算流度与实钻比采油指数相关关系精度更高, 利用该关系对蓬莱19-9油田4口井进行产能预测, 预测结果与钻后实际产量吻合较好, 提高了产能预测精度, 具有一定的推广意义。

符号注释：

a, b, c— — 与岩性有关的相关系数; A, B, C— — 与孔隙结构相关的拟合系数; Bo— — 地层原油体积系数; G— — 形状因子; h— — 油层射开厚度, m; Jos— — 比采油指数, m3/（d· MPa· m）; Jos_p— — 已投产井实钻比采油指数, m3/（d· MPa· m）; Kb— — 借用模型计算渗透率, 10-3 μ m2; ${{K}_{\text{core}}}$— — 岩心渗透率, 10-3 μ m2; ${{K}_{\text{core }\!\!\_\!\!\text{ Mb}}}$— — 随钻测压流度转换得到的岩心渗透率, 10-3 μ m2; Kn— — 本文模型计算渗透率, 10-3 μ m2; Ko— — 油相渗透率, 10-3 μ m2; ${{K}_{\text{o}\left( {{S}_{\text{wi}}} \right)}} $— — 束缚水饱和度下的油相渗透率, 10-3 μ m2; ${{K}_{\text{w}({{S}_{\text{or}}})}}$— — 残余油饱和度下的水相渗透率, 10-3 μ m2; psf— — 井筒附近地层压力, MPa; pr— — 地层压力, MPa; pwf— — 井底流压, MPa; p（t）— — 压力计在t时刻测量的压力, MPa; Qo— — 预测油产量, m3/d; re— — 供油半径, m; rp— — 探针半径, cm; rw— — 井筒半径, m; Sor— — 残余油饱和度, %; Swi_core— — 岩心束缚水饱和度, %; Swi_log— — 测井解释束缚水饱和度, %; Swi_Nmr— — 核磁共振测井束缚水饱和度, %; t1— — 测试压力下降开始时刻, s; t2— — 测试压力恢复结束时刻, s; t— — 测试时间, s; V— — 预测试抽取流体体积, cm3; Vsh— — 泥质含量, %; μ mf— — 钻井液滤液黏度, mPa· s; μ o— — 地层原油黏度, mPa· s; ϕ core— — 岩心孔隙度, %; ϕ log— — 测井解释有效孔隙度, %; ϕ Nmr— — 核磁共振测井有效孔隙度, %; λ Mb— — 随钻测压流度, 10-3 μ m2/（mPa· s）。

（编辑 王晖）

参考文献
[1] 时新磊, 吕洪志, 崔云江, 等. 基于图论多分辨率聚类法的测井相划分及渗透率评价: 以渤海P油田W井区馆陶组为例[J]. 中国海上油气, 2018, 30(1): 81-88.
SHI Xinlei, LYU Hongzhi, CUI Yunjiang, et al. Logging facies division and permeability evaluation based on graph theory multi resolution clustering: A case study of Guantao Formation in Well W block of P oilfield in Bohai Sea[J]. China Offshore Oil and Gas, 2018, 30(1): 81-88. [本文引用:1]
[2] SHI X L, CUI Y J, GUO X Y, et al. Logging facies classification and permeability evaluation: Multi-resolution graph based clustering[R]. SPE 187030, 2017. [本文引用:1]
[3] CUI Y J, SHI X L. Accurate permeability estimation in a heterogeneous middle east carbonate field through facies classification and core-log integration[R]. OTC 28651, 2018. [本文引用:1]
[4] 袁新涛, 彭仕宓, 林承焰, 等. 分流动单元精确求取储层渗透率的方法[J]. 石油学报, 2005, 26(6): 78-81.
YUAN Xintao, PENG Shimi, LIN Chengyan, et al. An interpretation method for permeability based on flow units and its applicability[J]. Acta Petrolei Sinica, 2005, 26(6): 78-81. [本文引用:1]
[5] 刘晏堂, 吕洪志, 王绍民, 等. 用MDT压降流度计算地层渗透率的新方法[J]. 中国海上油气, 2003, 17(3): 211-214.
LIU Yantang, LYU Hongzhi, WANG Shaomin, et al. New calculating methods of formation permeability from MDT mobility[J]. China Offshore Oil and Gas, 2003, 17(3): 211-214. [本文引用:2]
[6] 鹿克峰, 简洁, 朱文娟, 等. 利用MDT压降流度求取低渗气藏气相渗透率的方法[J]. 中国海上油气, 2015, 27(6): 53-56.
LU Kefeng, JIAN Jie, ZHU Wenjuan, et al. Calculating gas phase permeability with drawdown fluidity tested by MDT for low permeability gas reservoir[J]. China Offshore Oil and Gas, 2015, 27(6): 53-56. [本文引用:2]
[7] 杨冬, 张海荣, 吴一雄, 等. 电缆地层测试资料在低渗气藏产能预测中的应用[J]. 中国海上油气, 2018, 30(6): 109-114.
YANG Dong, ZHANG Hairong, WU Yixiong, et al. Application of cable formation test data in productivity prediction of low permeability gas reservoirs[J]. China Offshore Oil and Gas, 2018, 30(6): 109-114. [本文引用:2]
[8] 郭太现, 刘春成, 吕洪志, 等. 蓬莱19-3油田地质特征[J]. 石油勘探与开发, 2001, 28(2): 26-28.
GUO Taixian, LIU Chuncheng, LYU Hongzhi, et al. Geological characteristics and hydrocarbon accumulation pattern of Penglai 19-3 oilfield[J]. Petroleum Exploration and Development, 2001, 28(2): 26-28. [本文引用:2]
[9] 刘彦成, 罗宪波, 康凯, 等. 陆相多层砂岩油藏渗透率表征与定向井初期产能预测: 以蓬莱19-3 油田为例[J]. 石油勘探与开发, 2017, 44(1): 1-7.
LIU Yancheng, LUO Xianbo, KANG Kai, et al. Permeability characterization and directional wells initial productivity prediction in the continental multilayer sand stone reservoirs: A case from Penglai 19-3 oil field, Bohai Bay Basin[J]. Petroleum Exploration and Development, 2017, 44(1): 1-7. [本文引用:1]
[10] 陈鸣, 聂桂萍, 谭舜, 等. Stethoscope随钻测压技术在南海Z油田的应用[J]. 录井工程, 2016, 27(3): 67-71.
CHEN Ming, NIE Guiping, TAN Shun, et al. Application of Stethoscope pressure while drilling in Z Oilfield of South China Sea[J]. Mud Logging Engineering, 2016, 27(3): 67-71. [本文引用:1]
[11] 邸德家, 陶果, 孙华峰, 等. 随钻地层测试技术的分析与思考[J]. 测井技术, 2012, 36(3): 294-298.
DI Dejia, TAO Guo, SUN Huafeng, et al. Analysis and consideration of formation testing while drilling technology[J]. Well Logging Technology, 2012, 36(3): 294-298. [本文引用:1]
[12] 刘鹏飞, 刘良跃, 司念亭, 等. 随钻测压工具Geo-Tap在渤中25-1油田E3S井的应用[J]. 石油钻探技术, 2009, 37(3): 42-44.
LIU Pengfei, LIU Liangyao, SI Nianting, et al. Application of Geo-Tap in well E3S of Bozhong25-1 Oilfield[J]. Petroleum Drilling Techniques, 2009, 37(3): 42-44. [本文引用:1]
[13] 邸德家, 陶果, 张同义, 等. 随钻地层测试器Geo-Tap数据实时处理方法分析[J]. 测井技术, 2015, 39(5): 555-560.
DI Dejia, TAO Guo, ZHANG Tongyi, et al. On real time data processing method of formation tester while drilling (Geo-Tap)[J]. Well Logging Technology, 2015, 39(5): 555-560. [本文引用:1]
[14] 杨胜来, 魏俊之. 油层物理学[M]. 北京: 石油工业出版社, 2004: 239-243.
YNAG Shenglai, WEI Junzhi. Reservoir physics[M]. Beijing: Petroleum Industry Press, 2004: 239-243. [本文引用:1]
[15] TIMUR A. An investigation of permeability, porosity, and residual water saturation relationships[J]. Log Analyst, 1968, 9(4): 8-17. [本文引用:1]
[16] 朱林奇, 张冲, 石文睿, 等. 核磁共振测井评价致密砂岩储层孔隙结构与渗透率方法研究[J]. 科学技术与工程, 2017, 16(15): 22-27.
ZHU Linqi, ZHANG Chong, SHI Wenrui, et al. Study on the method of prediction of irreducible water saturation by combining mercury intrusion and NMR logging data[J]. Science Technology and Engineering, 2017, 16(15): 22-27. [本文引用:1]
[17] 雍世和, 张超谟. 测井数据处理与综合解释[M]. 北京: 中国石油大学出版社, 1996: 459-467.
YONG Shihe, ZHANG Chaomo. Logging data processing and comprehensive interpretation[M]. Beijing: China University of Petroleum Press, 1996: 459-467. [本文引用:1]
[18] 赵立新, 廖新维. 电缆地层测试油气层产能预测技术研究及应用[J]. 测井技术, 2009, 33(3): 92-96.
ZHAO Lixin, LIAO Xinwei. An approach for reservoir yield prediction using WFT and its applications[J]. Well Logging Technology, 2009, 33(3): 92-96. [本文引用:1]
[19] SHI X L, CHEN H B, LI R J, et al. Improving permeability and productivity estimation with electrofacies classification and core data collected in multiple oilfields[R]. OTC 29214, 2019. [本文引用:1]
[20] 杨思玉, 胡永乐, 蒋漫旗, 等. 新油田生产能力确定方法[J]. 石油勘探与开发, 2008, 35(6): 115-119.
YANG Siyu, HU Yongle, JIANG Manqi, et al. Methodology for determining productivity of new oilfields[J]. Petroleum Exploration and Development, 2008, 35(6): 115-119. [本文引用:1]