引用本文
董长银, 周玉刚, 陈强, 朱春明, 李彦龙, 李效波, 刘亚宾. 流体黏速物性对砾石层堵塞影响机制及充填防砂井工作制度优化实验[J]. 石油勘探与开发, 2019,46(6): 1178-1186.
DONG Changyin, ZHOU Yugang, CHEN Qiang, ZHU Chunming, LI Yanlong, LI Xiaobo, LIU Yabin. Effects of fluid flow rate and viscosity on gravel-pack plugging and the optimization of sand-control wells production[J]. Petroleum Exploration & Development, 2019,46(6): 1178-1186.  
Doi: 10.11698/PED.2019.06.15
Permissions
Copyright©2019, 石油勘探与开发》编辑部
石油勘探与开发》编辑部 所有
流体黏速物性对砾石层堵塞影响机制及充填防砂井工作制度优化实验
董长银1, 周玉刚1, 陈强2, 朱春明3, 李彦龙2, 李效波3, 刘亚宾1
1. 非常规油气开发教育部重点实验室（中国石油大学（华东））,山东青岛 266580
2. 青岛海洋地质研究所,山东青岛 266073
3. 中海油服油田生产事业部,天津 300459

第一作者简介：董长银（1976-）,男,河南卫辉人,博士,中国石油大学（华东）教授,主要从事岩石力学、出砂模拟、防砂完井与油气田开发工程方面的教学与研究工作。地址：山东省青岛市黄岛区长江西路66号,中国石油大学（华东）石油工程学院,邮政编码：266580。E-mail: dongcy@upc.edu.cn

收稿日期: 2019-03-11
基金项目: 国家自然科学基金项目“深水储层微观出砂机理与过程模拟技术研究”（51774307）; 国家重点研发计划课题“水合物开采过程气-液-固多相流动规律与泥砂控制机理”（2017YFC0307304）; 国家海洋地质调查二级项目（DD20190231）
摘要

选用粒度中值0.10 mm和0.16 mm的2种地层砂、粒径0.6~1.2 mm的石英砂和陶粒,开展不同流体黏度与流体流速组合条件下的砾石层挡砂堵塞模拟实验,提出采用黏速指数（流体黏度与流速的乘积）表征流体物性和流动条件对砾石层堵塞的影响机制和规律,同时提出了砾石充填防砂井投产工作制度优化方法。研究表明地层砂侵入交混带渗透率、砾石层最终堵塞渗透率与携砂流体流速、黏度负相关,流速越高、黏度越大,地层砂侵入交混带渗透率、砾石层最终堵塞渗透率越低。流体流速、黏度是影响砾石层堵塞程度的关键参数,黏速指数可以很好地表征流体的流动特征,同时也便于分析砾石层堵塞机理;不同黏度和流速组合,只要最终的黏速指数相同（近）,其对砾石层总体渗透率的影响基本一致;砾石层渗透率随着黏速指数增加首先迅速下降,然后降速变缓直至基本稳定。最优配产量与阶梯提产相结合的砾石充填防砂井投产工作制度优化方法,可以有效降低携砂流体对砾石层渗透率的损害,提高油井生产效益。图14表3参25

关键词: 砾石充填; 挡砂实验; 堵塞规律; 黏速指数; 工作制度; 优化方法; 堵塞模拟
中图分类号:TE355 文献标志码:A 文章编号:1000-0747(2019)06-1178-09
Effects of fluid flow rate and viscosity on gravel-pack plugging and the optimization of sand-control wells production
DONG Changyin1, ZHOU Yugang1, CHEN Qiang2, ZHU Chunming3, LI Yanlong2, LI Xiaobo3, LIU Yabin1
1. Key Laboratory of Unconventional Oil & Gas Development (China University of Petroleum (East China)), Ministry of Education, Qingdao 266580, China;
2. Qingdao Institute of Marine Geology, Qingdao 266073, China
3. Production Optimization-COSL, Tianjin 300459, China
Abstract

Series of experiments were performed to simulate the invasion of formation sand into and the plugging process of gravel-pack at different viscosities and flowing rates of fluid. Two types of formation sands with the medium size of 0.10 mm and 0.16 mm and the gravel and ceramicite of 0.6-1.2 mm were used in the experiments. A new viscosity-velocity index (the product of fluid viscosity and velocity) was put forward to characterize the influencing mechanism and law of physical property and flow condition of formation fluid on gravel-pack plugging, and a new method to optimize the production rate of wells controlling sand production with gravel-packing was proposed. The results show that the permeability of formation sand invaded zone and final permeability of plugged gravel-pack have negative correlations with viscosity and flow velocity of fluid, the higher the flow velocity and viscosity, the lower the permeability of formation sand invaded zone and final permeability of plugged gravel-pack will be. The flow velocity and viscosity of fluid are key factors affecting plugging degree of the gravel zone. The velocity-viscosity index (v-v index) can reflect the flow characteristics of fluid very well and make it easier to analyze the plugging mechanism of gravel zone. For different combinations of fluid viscosity and flow velocity, if the v-v index is the same or close, their impact on the final gravel permeability would be the same or close. With the increase of the v-v index, the permeability of plugged gravel zone decreases first, then the reduction rate slows down till the permeability stabilizes. By optimizing production and increasing production step by step, the optimal working scheme for sand-control well can reduce the damage to gravel-pack zone permeability caused by sand-carrying fluid effectively, and increase well productivity and extend the sand control life.

Keyword: gravel-pack; sand retention experiment; plugging law; viscosity-velocity index; working scheme; optimization method; plugging simulation
0 引言

砾石充填防砂井投产后地层砂侵入砾石层造成渗透率下降, 进而导致油井大幅降产及防砂有效期缩短[1, 2]。研究表明, 挡砂介质挡砂过程实质是被流体携带的地层砂逐步堵塞的过程, 堵塞过程中挡砂介质渗透率逐渐降低最终达到平衡状态, 挡砂介质渗透率下降直接影响防砂后油井产量[3, 4, 5, 6, 7]。砾石层多孔介质堵塞机制除了与砾石-地层砂粒度中值比（GSR）等参数有关外, 还与流体流速和黏度等流动参数直接相关[8, 9, 10, 11]。目前针对砾石层堵塞机制的研究主要集中在GSR对挡砂效果的影响以及砾石尺寸优化[8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]。早期Saucier[12]通过实验考虑GSR的影响提出了经典的砾石尺寸设计方法; 众多研究者通过数值和实验模拟探究了GSR、地层砂均匀系数、泥质含量、流速、黏度以及砾石充实程度等对砾石层堵塞的影响规律[8, 9, 10, 11, 12, 13, 14, 15, 16], 但基本是单因素的定性分析。董长银[18]拟合得到了预测砾石层堵塞程度随生产时间变化的定量模型, 但未重点考察流体流速与黏度的共同影响。有研究者基于地层砂-砾石尺寸的配比优化进行了砾石尺寸的优化研究[19, 20, 21, 22, 23], 但依然对流体流动因素考虑较少。综上所述, 现有相关研究对不同油井的生产条件如原油黏度、采液强度及流速等因素考虑不足, 或者仅定性分析了各单因素的影响规律。

由于流体物性和油井产量对地层砂侵入砾石层的影响机制和定量规律尚不明确, 砾石充填防砂井投产后的工作制度优化尚无直接依据和具体方法。本文针对上述问题开展不同地层砂、流体黏度和流速条件下的砾石层挡砂堵塞过程模拟实验。基于实验规律分析, 提出采用黏速指数表征流体物性和流动条件对砾石层堵塞的影响机制和规律, 同时也提出一种油井防砂后最优配产量测算和阶梯式提高产量的砾石充填防砂井投产工作制度优化方法。

1 实验原理与实验条件
1.1 实验原理与方法

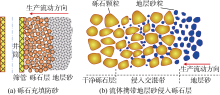
砾石充填防砂井施工完成后形成如图1a所示的筛管-砾石层-地层砂桥架结构。投产后地层流体携带地层砂侵入砾石层, 形成如图1b所示的侵入交混带, 造成砾石层渗透率和油井产量严重降低, 其降低幅度取决于侵入交混带的深度以及渗透率的降低幅度[2, 9, 10]。

图1 砾石充填防砂原理及地层砂侵入砾石层示意图

根据图1b, 地层砂侵入砾石层的过程, 实质是流体携带地层砂粒在砾石层孔喉空间中的运移和堵塞; 地层砂侵入的深度和数量首先与GSR密切相关, 其次是流体密度、黏度以及流速。

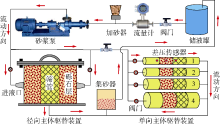
为了模拟地层流体携带地层砂侵入砾石层的挡砂和堵塞过程, 构建了砾石充填挡砂模拟实验装置（见图2）。该装置由储液罐、泵、加砂器、集砂器、径向和单向主体驱替装置、数据采集传感器与控制系统等组成。本次实验主要使用的单向主体驱替装置由一组不同直径的透明圆柱短节组合而成, 短节中可以灵活预充填砾石层。

图2 砾石充填挡砂模拟实验装置图

实验时, 通过加砂器向流体中掺入一定比例的地层砂, 流体携带地层砂冲击砾石层, 模拟地层砂对砾石层的侵入和堵塞过程。由于本次实验的要点是砾石充填层的挡砂堵塞规律, 主要模拟储集层产出砂对砾石层的冲击、侵入和堵塞作用, 所以采用来流携砂方式模拟地层砂的产出。流体黏度、流量、地层砂粒径、含砂率等参数均可人为控制。实验过程中, 通过集砂器测量通过砾石层的地层砂量以及粒径; 通过测量流量、砾石充填层两端压差以及充填几何参数可以计算砾石层渗透率随时间的变化, 并可实时观测地层砂侵入砾石层的深度。单向流条件下的砾石层渗透率可由实验测试数据用下式计算：

${{K}_{s}}=\frac{Q\mu {{L}_{s}}}{A\Delta p}$ （1）

1.2 实验材料与实验条件

实验流体使用清水（黏度约1 mPa· s）和胍胶溶液（黏度1~20 mPa· s）配制; 实验使用模拟地层砂根据胜利油田2种典型地层砂筛析曲线由不同粒径石英砂配制而成, 其粒度中值为0.10 mm和0.16 mm, 泥质含量分别为15%和25%, 泥质使用高岭石、伊利石、蒙脱粉按1∶ 3∶ 1比例配制而成; 固相充填材料为普通石英砂和陶粒, 粒径范围为0.6~1.2 mm, 与地层砂匹配得到的GSR范围约为5.4~8.6, 基本代表了油田现场常用的GSR范围。模拟地层砂和固相充填材料粒径及其编号如表1、表2所示。需要指出的是, 2种固相充填材料的粒度中值差异是分选加工工艺不同造成的; 另外本实验忽略了2种固相材料物性参数不同导致的挡砂堵塞效果差异, 重点研究其随流体参数的变化规律。

表1 实验使用地层砂基础参数
表2 实验使用固相充填材料基础参数
2 侵入堵塞规律及黏速指数敏感性
2.1 地层砂侵入砾石层交混带

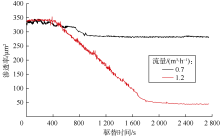
使用S1号地层砂和T1号陶粒以及黏度约1.0 mPa· s的清水进行挡砂实验。主体装置使用图2中的2号单向驱替装置, 内径50 mm, 砾石充填段长度150 mm; 驱替流量设置为0.7 m3/h和1.2 m3/h, 驱替时间约46 min。实验过程中测量砾石层两端流动压差和流量随时间的变化, 可计算得到如图3所示的两次实验的渗透率变化曲线。

图3 实验过程中砾石层总体渗透率变化曲线

由图3可见, 实验测试砾石层渗透率从初始值逐步下降并达到平稳状态, 体现了文献[23]提到的堵塞开始、堵塞加剧和堵塞平衡3个阶段。砾石层堵塞平衡后, 侵入交混带的深度和渗透率基本不再变化。实验中T1号陶粒初始渗透率约为335 μ m2, 流量1.2 m3/h和0.7 m3/h条件下达到的最终堵塞渗透率分别约为45 μ m2和275 μ m2, 渗透率比分别为13.4%和82.1%, 两者相差较大; 驱替流量（流速）对地层砂侵入砾石层的堵塞动态有明显影响, 相同条件下, 流体流速越大, 地层砂对砾石层的侵入堵塞越严重。

实验完毕后, 从主体装置中取出局部样品观察地层砂侵入砾石层形成的交混带形态。图4为2种不同流量实验条件下地层砂侵入形成交混带的对比照片, 图5为地层砂侵入砾石层形成的交混带微观照片。由于地层砂粒径的分布规律以及砾石颗粒形成孔喉尺寸的非均质性, 即使在合理的GSR下, 地层砂侵入砾石层的现象也是不可避免的。砾石充填层内部形成具有一定随机尺度分布的孔喉[21], 地层砂颗粒中较小粒径部分在流体携带作用下会侵入砾石层, 形成一定长度的地层砂与砾石层侵入交混带。

图4 不同驱替流量下地层砂侵入形成交混带区域照片

图5 地层砂侵入砾石层形成交混带微观照片（驱替流量为1.2 m3/h）

砾石层堵塞程度由最终堵塞渗透率（整个砾石层的表观渗透率）和渗透率比（最终堵塞渗透率与干净砾石层初始渗透率的比值）表示。砾石层堵塞程度取决于地层砂侵入交混带的深度和砾石层渗透率。流量为1.2 m3/h时目测可见侵入交混带长度约为1.2 cm（见图4a）; 根据充填层长度、初始渗透率和最终堵塞渗透率, 可计算得到交混带实际渗透率约为4.2 μ m2。流量为0.7 m3/h时目测可见交混带长度约为4.2 cm（见图4b）, 计算得到交混带实际渗透率约为192.1 μ m2。

一个值得注意的现象是, 虽然较高流量（1.2 m3/h）导致较低的最终堵塞渗透率, 但其目测可见交混带深度（1.2 cm）却明显低于较低流量（0.7 m3/h）下的值（4.2 cm）。探析其原因, 在相同的含砂率条件下, 高流量意味着较快的来砂速度, 由于砾石层的复杂孔喉结构, 地层砂在砾石孔喉中的运移速度往往较慢, 这导致地层砂来不及被携带到砾石层深部, 而是堆积在砾石层的表层或浅层内部形成沉积堵塞, 占据地层砂侵入的空间和通道, 最终形成深度（长度）较小但渗透率较低的交混带, 且与干净砾石层的界面清晰（见图5b）。

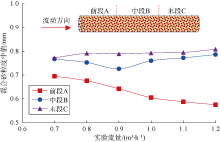
为了探究地层砂粒在砾石层内部的运移情况, 将砾石充填段按来流方向分为3段（前段A、中段B、末段C）, 根据不同流量的实验结果, 分析得到如图6所示的各段砾石和地层砂混合物的砂粒粒度中值分布。

图6 不同流量实验结束各段混合砂粒度中值测试结果

前段A是最容易受流体和地层砂冲击造成侵入堵塞的位置。随着驱替流量的增加, 前段A的混合砂粒度中值明显降低（这是由于砾石中混入了较细的地层砂所致）, 表明砾石层中混入的地层砂量明显增加; 中段B混合砂粒度中值略有降低, 但变化不大, 这表明从入口侵入到砾石层中段的地层砂量不多。相类似, 在末段C处, 混合砂粒度中值基本保持不变, 说明地层砂侵入基本未到达或穿透整个砾石层, 到达末段的地层砂量非常少, 砾石层起到很好的挡砂效果。

2.2 流体流速和黏度对堵塞程度的影响规律

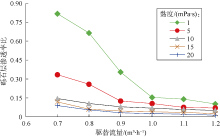
为了研究流体流动条件参数对砾石层堵塞程度的影响规律, 选择泥质含量25%的S2号地层砂、T1号陶粒材料和黏度为1.0 mPa· s的驱替流体, 采用不同流量进行实验, 得到堵塞平衡后的最终堵塞渗透率（或渗透率比）、交混带渗透率、交混带深度的变化情况（见图7）。

图7 驱替流量对砾石层堵塞程度参数的影响

图7表明了不同流量（流速）对砾石层堵塞程度的影响规律。相同条件下, 流体流速越高, 由地层砂侵入砾石层形成的交混带渗透率越低, 堵塞平衡后砾石层最终堵塞渗透率及渗透率比也越低; 驱替流量从0.7 m3/h上升到1.0 m3/h后, 砾石层渗透率比从0.818下降至0.154, 降幅高达81.2%。需要注意的是, 随着驱替流量增加, 最终交混带深度（长度）却变小, 主要原因如前所述。

使用泥质含量25%的S2号地层砂和T1号陶粒, 设置流量0.8 m3/h、5种流体黏度（1, 5, 10, 15, 20 mPa· s）进行挡砂模拟实验, 以考察流体黏度对砾石层堵塞程度的影响, 得到如图8所示的结果。

图8 流体黏度对砾石层堵塞程度参数的影响

相同条件下, 携砂流体黏度越高, 地层砂侵入后交混带渗透率降低越明显, 堵塞平衡后砾石层最终堵塞渗透率及渗透率比越低。同时, 随着黏度增加, 堵塞平衡后的最终交混带深度越来越浅, 这一点与驱替流量（流速）对砾石层堵塞程度的影响规律基本相似。

为进一步探究流速及黏度对砾石层堵塞的影响, 使用S1号地层砂和G1号石英砂, 采用不同黏度的流体进行多种驱替流量的挡砂模拟实验, 结果如图9所示。可以发现, 驱替流量（流速）和黏度均对砾石层堵塞程度有直接影响, 流体流速越高、黏度越大, 则流体对地层砂粒的携带能力越强, 会导致更多的地层砂侵入砾石层内部, 最终渗透率越低。

图9 驱替流量和流体黏度对砾石层堵塞程度的影响

对比图7— 图9的实验结果, 可以看到不同实验条件下驱替流量和流体黏度两种参数对堵塞程度的影响规律基本一致。

2.3 堵塞程度与流体黏速指数的关系

研究表明, 对于液固两相携砂流动, 流体对固相颗粒的携带能力与流体和固相颗粒的相对运动速度、流体黏度均近似呈线性正相关[24, 25]。由于实际油井产出流体的黏度存在差异, 为了更加全面地表征流体黏度、流量（速）对挡砂介质堵塞的影响规律, 避免流量或黏度单因素分析给结果带来的不确定性, 提出使用“ 黏速指数” 来表征流体的黏度与流速条件, 定义为流体流速与黏度的乘积：

$\beta \text{=}\mu v$ （2）

为证明驱替液流速和黏度对砾石层堵塞的综合影响, 并考察黏速指数表征流体流动条件的合理性, 使用S1号地层砂和G1号石英砂, 设定黏速指数3.33× 10-4 N/m和10.00× 10-4 N/m为目标, 组合不同的流体黏度和流速, 使其乘积等于目标黏速指数, 形成多套实验方案（见表3）进行模拟实验, 考察砾石层堵塞程度在不同的黏度和流速组合且保持黏速指数相同（相近）条件下的变化规律。

表3 相同（近）黏速指数下的流速和黏度配比实验方案

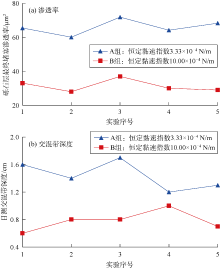
按照表3的参数组合进行挡砂模拟实验, 并计算砾石层最终堵塞渗透率, 记录目测交混带深度并绘制曲线（见图10）。分析图10a发现, 无论是A组实验还是B组实验, 黏速指数相同条件下, 尽管黏度和流速的组合不同, 但砾石层最终堵塞渗透率基本接近, 波动范围小于15%。同样观察图10b, 相同黏速指数下, 交混带深度的变化也不大, 波动范围小于18%。该现象表明, 流体携带地层砂侵入砾石层, 最终砾石层的侵入和堵塞程度与流体黏度和驱替流速有关, 且与黏速指数具有更好的相关性。在不同黏度和流速组合下, 如果其乘积即黏速指数不变, 则其堵塞程度也其本一致。这表明黏速指数可以很好地表征流体的流动特征, 且是影响砾石层堵塞程度的关键参数。

图10 恒定黏速指数条件下不同参数组合实验结果对比

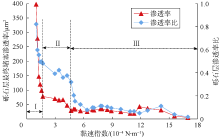
为进一步探究黏速指数对砾石层堵塞的影响规律, 通过调节驱替液流速和黏度, 设定黏速指数为（1.0~17.0）× 10-4 N/m进行实验, 对比砾石层的挡砂性能与堵塞后的渗流能力。实验中流量调节范围为0.7~1.2 m3/h, 相应流体流速为0.099~0.170 m/s, 流体黏度为1~10 mPa· s。使用S1号地层砂和T1号陶粒, 共进行了60组驱替模拟实验, 得到砾石层最终堵塞渗透和渗透率比随黏速指数的变化规律（见图11）。

图11 黏速指数对砾石层堵塞程度的影响

总体而言, 流体黏速指数越大, 砾石层最终堵塞渗透率越低, 随着黏速指数增大, 最终堵塞渗透率表现出不同的变化规律：①阶段Ⅰ （黏速指数低于1.7× 10-4 N/m）, 随着黏速指数增加, 砾石层最终堵塞渗透率从初始值约400 μ m2下降到70 μ m2左右, 渗透率比从0.8下降到0.5左右, 下降速度非常快; ②阶段Ⅱ （黏速指数（1.7~4.5）× 10-4 N/m）, 随着黏速指数增加, 砾石层最终堵塞渗透率和渗透率比下降趋势减缓, 渗透率由70 μ m2下降到40 μ m2, 渗透率比由0.5下降到0.3左右; ③阶段Ⅲ （黏速指数超过4.5× 10-4 N/m）, 砾石层最终堵塞渗透率和渗透率比随着黏速指数增加呈极缓慢降低或水平波动趋势, 平均值分别为约28 μ m2和0.105。

3 砾石充填防砂井工作制度优化

砾石层堵塞程度受地层产出流体黏速指数的直接影响, 油井防砂后的合理产能大小可利用等效原则（实验与油井实际条件等效）确定, 通过流体黏速指数可确定防砂井投产后的合理工作制度。

3.1 阶梯式流量驱替实验

根据图11, 流体黏速指数越高, 砾石层最终堵塞渗透率越低。对于给定的油井, 流体黏度基本不变, 决定黏速指数的可控因素就是流速, 即油井产液量。产液量的大小是影响砾石充填防砂油井投产后砾石层最终堵塞渗透率的主要因素, 适当控制产液量可获得较高的砾石层最终堵塞渗透率, 但该方法与单井配产追求高产存在一定矛盾。针对该问题, 本文提出一种既可以控制砾石层最终堵塞渗透率降低幅度又可以满足配产要求的砾石充填防砂井工作制度优化方法— — 阶梯式逐步提高产量配产法。

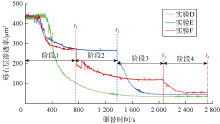
为了验证其有效性, 使用S1号地层砂、T1号陶粒和黏度1.0 mPa· s的驱替流体, 设定最高驱替流量为1.2 m3/h, 分别以3种流量组合方式（D、E、F）进行驱替实验, 得到砾石层渗透率随时间的变化规律（见图12）。

图12 阶梯流量驱替时砾石层渗透率变化曲线

实验D在整个驱替中采用最高恒定流量（目标流量1.2 m3/h）直接恒速驱替。实验E采用2级阶梯流量驱替：时间从0到t2（约1 360 s）采用流量0.8 m3/h驱替, t2之后, 提高到目标流量。实验F采用3级阶梯流量驱替：时间从0到t1（约750 s）, 驱替流量为0.8 m3/h, t1到t3（约2 080 s）驱替流量提高到1.0 m3/h, t3之后提高到目标流量。

3个实验的最终驱替流量均为目标流量1.2 m3/h, 因流量组合方式不同, 最终驱替过程中的渗透率变化规律以及驱替结束时砾石层的最终堵塞渗透率也差异较大：①直接以最高流量进行驱替（实验D）, 砾石层渗透率在驱替早期迅速下降, 驱替结束时砾石层最终堵塞渗透率相对最低（33 μ m2）; ②2级阶梯式驱替, 以较低流量开始驱替一段时间, 然后提高到目标流量, 不仅在驱替过程中可以保持较高的渗透率, 而且在驱替结束时砾石层最终堵塞渗透率也明显高于恒定流量驱替方式; ③3级阶梯式流量驱替, 驱替过程中砾石层渗透率要高于恒定流量驱替, 驱替结束时砾石层的最终堵塞渗透率也明显高于恒定流量和2级阶梯流量驱替。

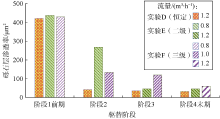
图13为3种流量阶梯组合方式驱替实验中不同驱替阶段砾石层渗透率值的对比：①阶段1, 该段前期, 驱替对砾石层渗透率的影响尚未体现, 因此砾石层渗透率比较接近, 该段后期, 随驱替时间延长, 砾石层渗透率开始下降, 流量越大, 下降的幅度越大; ②阶段2, 实验D流量较高, 与实验E（流量为0.8 m3/h）和实验F（1.0 m3/h）相比, 渗透率降低幅度也较大, 总体表现为流量越大, 渗透率下降幅度越大; ③阶段3, 实验F流量最低, 渗透率下降幅度最小, 渗透率值最高; ④阶段4末期, 3次实验的流量均达到目标流量1.2 m3/h, 但驱替结束时砾石层最终堵塞渗透率差异却十分明显, 实验D、E、F的值分别为33、46、60 μ m2。与实验D相比, 采用2级阶梯流量和3级阶梯流量驱替结束时, 砾石层的最终堵塞渗透率高出39%和82%; 3级阶梯驱替比2级阶梯驱替渗透率高出约30%。

图13 阶梯流量驱替不同阶段砾石层渗透率对比

3.2 防砂后最高配产量优化方法

砾石层是砾石充填防砂井的油气入井通道, 其渗透率决定了油井防砂投产后的产能。除了产量提升方式对井底防砂介质渗透率和产量有明显影响外, 目标配产量也是决定砾石层最终堵塞渗透率和实际产量的重要因素。上述实验及分析为砾石充填防砂井防砂后投产工作制度优化提供了思路。基于实验与实际油井的黏速指数等效原则, 对于确定了目标配产量的油井, 采用阶梯式逐步提高产量达到配产量, 井底挡砂介质最终堵塞渗透率比直接以配产量生产高, 最终产量收益更好。具体推荐方法：根据配产量将产量分为3个等级（产量逐步设置为配产量的40%~50%、70%~80%和100%）, 按3个阶梯逐步提高产量, 前2个阶段生产时间推荐12~24 h。考虑到现场实施和操作的复杂性, 对超过3个阶梯的提产模式不进行深入探讨。

根据图11中砾石层最终堵塞渗透率和渗透率比与地层产出流体黏速指数的关系, 结合防砂井对砾石层的最低渗透率要求, 可确定临界黏速指数, 进而根据油井流体黏度折算对应的油井产量, 该值即为避免砾石层过度堵塞的最优配产量。

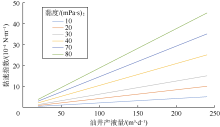
以油层厚度10 m、垂直射孔井为例说明合理配产的具体优化方法。假设射孔密度为36孔/m, 孔径14 mm。根据产量和射孔孔眼流速折算得到不同产出流体黏度条件下黏速指数与油井产液量的关系（见图14）; 以砾石层渗透率不低于40 μ m2为基本要求, 根据图11得到对应的最高黏速指数约为5.0× 10-4 N/m; 设定产出流体黏度30 mPa· s, 根据图14可得对应黏度与黏速指数条件下的产液量约为100 m3/d, 此产量即为避免投产后砾石层过度堵塞的最优配产量。确定出最优配产量后, 根据该产量采用阶梯提产方法即可得到合理的工作制度。

图14 产出液黏度、黏速指数与油井产液量的关系

4 结论

地层砂侵入交混带深度、交混带渗透率、砾石层最终堵塞渗透率与携砂流体流速、黏度负相关, 流速越高、黏度越大, 地层砂侵入交混带渗透率、砾石层最终堵塞渗透率越低, 交混带深度越小。

流体流速、黏度是影响砾石层堵塞程度的关键参数, 黏速指数可以很好地表征流体的流动特征, 同时也便于分析砾石层堵塞机理; 不同黏度和流速组合, 只要最终的黏速指数相同（近）, 其对砾石层总体渗透率的影响基本一致; 砾石层渗透率随着黏速指数增加首先迅速下降, 然后降速变缓直至基本稳定。

最优配产量与阶梯提产相结合的砾石充填防砂井投产工作制度优化方法, 可以有效降低携砂流体对砾石层渗透率的损伤, 提高油井生产效益。

符号注释：

A— — 流通面积, m2; Ks— — 砾石层堵塞渗透率, m2; Ls— — 砾石层厚度, m; Q— — 采集流体流量, m3/s; v— — 流体流速, m/s; β — — 黏速指数, N/m; Δ p— — 砾石层两侧压差, Pa; μ — — 流体黏度, Pa· s。

参考文献
[1] 司连收, 李自安, 张健. 砾石充填防砂对稠油井产能影响研究[J]. 西南石油大学学报(自然科学版), 2013, 35(5): 135-140.
SI Lianshou, LI Zi’an, ZHANG Jian. Influence of gravel packing sand control on the productivity of heavy oil well[J]. Journal of Southwest Petroleum University (Edition of Natural Science), 2013, 35(5): 135-140. [本文引用:1]
[2] 高凯歌, 董长银. 防砂井投产初期砾石层渗透率损害规律[J]. 石油钻采工艺, 2016, 38(6): 876-881.
GAO Kaige, DONG Changyin. Regularity of permeability loss in gravel-packing layer for sand control during initial production[J]. Oil Drilling & Production Technology, 2016, 38(6): 876-881. [本文引用:2]
[3] 李爱芬, 姚军, 寇永强. 砾石充填防砂井产能预测方法[J]. 石油勘探与开发, 2004, 31(1): 103-105.
LI Aifen, YAO Jun, KOU Yongqiang. Productivity prediction method for gravel-packing sand control well[J]. Petroleum Exploration and Development, 2004, 31(1): 103-105. [本文引用:1]
[4] MIRSHEKARI B, DADVAR M, MODARES H, et al. Modeling and simulation of gravel-pack damage due to particle transport by single phase flow in cased hole completion[J]. International Journal of Oil Gas & Coal Technology, 2014, 7(2): 152-168. [本文引用:1]
[5] KAMPEL G, GOLDSZTEIN G H. Transport of non-brownian particles in porous media[J]. Siam Journal on Applied Mathematics, 2011, 71(3): 773-790. [本文引用:1]
[6] 董长银, 张清华, 郑华安, 等. 稠油热采防砂井动态产能评价方法及其应用[J]. 特种油气藏, 2016, 23(6): 123-127.
DONG Changyin, ZHANG Qinghua, ZHENG Hua’an, et al. Dynamic productivity evaluation and application of sand -control well in thermal recovery of heavy oil reservoir[J]. Special Oil and Gas Reservoirs, 2016, 23(6): 123-127. [本文引用:1]
[7] PERERA M S A, RANJITH P G, RATHNAWEERA T D, 等. 未固结流砂地层采油过程中出砂情况模拟实验[J]. 石油勘探与开发, 2017, 44(5): 811-816.
PERERA M S A, RANJITH P G, RATHNAWEERA T D, et al. An experimental study to quantify sand production during oil recovery from unconsolidated quicksand formations[J]. Petroleum Exploration and Development, 2017, 44(5): 811-816. [本文引用:1]
[8] 董长银, 贾碧霞, 刘春苗, 等. 机械防砂筛管挡砂介质堵塞机制及堵塞规律试验[J]. 中国石油大学学报(自然科学版), 2011, 35(5): 82-88.
DONG Changyin, JIA Bixia, LIU Chunmiao, et al. Blocking mechanism and blocking laws experiments of sand retention media in mechanical screens[J]. Journal of China University of Petroleum (Edition of Natural Science), 2011, 35(5): 82-88. [本文引用:3]
[9] 王志刚, 李爱芬. 砾石充填防砂井砾石层堵塞机理实验研究[J]. 石油大学学报(自然科学版), 2000, 24(5): 49-53.
WANG Zhigang, LI Aifen. Experimental study on the mechanism of gravel packing for gravel packing[J]. Journal of China University of Petroleum (Edition of Natural Science), 2000, 24(5): 49-53. [本文引用:4]
[10] 董长银, 高凯歌, 王静, 等. 注聚驱防砂井挡砂介质物理化学复合堵塞机制试验[J]. 中国石油大学学报(自然科学版), 2016, 40(5): 104-111.
DONG Changyin, GAO Kaige, WANG Jing, et al. Experimental study on mechanical and chemical combined plugging mechanism of sand control media in heavy oil reservoirs with polymer flooding[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016, 40(5): 104-111. [本文引用:4]
[11] YUAN H, SHAPIRO A. Induced migration of fines during water flooding in communicating layer-cake reservoirs[J]. Journal of Petroleum Science & Engineering, 2011, 78(3): 618-626. [本文引用:3]
[12] SAUCIER R J. Consideration in gravel pack design[J]. JPT, 1974, 26(2): 205-206. [本文引用:3]
[13] BOUHROUM A, LIU X, CIVAN F. Predictive model and verification for sand particulates migration in gravel packs[R]. SPE 28534, 1994. [本文引用:2]
[14] YANN B. Investigation of pore-blocking mechanism in gravel packs in the management and control of fines migration[R]. SPE 27342, 1994. [本文引用:2]
[15] 董长银, 高凯歌, 徐鸿志, 等. 充填密实程度对砾石层挡砂效果及稳定性影响实验[J]. 石油钻采工艺, 2018, 40(1): 123-130.
DONG Changyin, GAO Kaige, XU Hongzhi, et al. Experimental study on the influence of filling density on the sand blocking effect and stability of gravel[J]. Oil Drilling & Production Technology, 2018, 40(1): 123-130. [本文引用:2]
[16] MOGHADASI J, MÜLLER-STEINHAGEN H, JAMIALAHMADI M, et al. Theoretical and experimental study of particle movement and deposition in porous media during water injection[J]. Journal of Petroleum Science & Engineering, 2004, 43(3): 163-181. [本文引用:2]
[17] DONG C Y, GAO K G, DONG S X, et al. A new integrated method for comprehensive performance of mechanical sand control screens testing and evaluation[J]. Journal of Petroleum Science and Engineering, 2017, 158: 775-783. [本文引用:1]
[18] 董长银. 防砂井挡砂介质堵塞规律实验及堵塞程度定量预测模型[J]. 实验力学, 2017, 32(3): 351-360.
DONG Changyin. Experimental study of sand retaining media plugging pattern in sand control well and quantitative prediction model for plugging degree[J]. Journal of Experiment Mechanics, 2017, 32(3): 351-360. [本文引用:2]
[19] 李彦龙, 胡高伟, 刘昌岭, 等. 天然气水合物开采井防砂充填层砾石尺寸设计方法[J]. 石油勘探与开发, 2017, 44(6): 129-134.
LI Yanlong, HU Gaowei, LIU Changling, et al. Gravel sizing method for sand control packing in hydrate production test wells[J]. Petroleum Exploration and Development, 2017, 44(6): 129-134. [本文引用:2]
[20] 董长银, 张琪, 孙炜. 砾石充填防砂工艺参数优化设计方法[J]. 中国石油大学学报(自然科学版), 2006, 30(5): 57-61.
DONG Changyin, ZHANG Qi, SUN Wei. New considerations in optimization design of sand control methods concerning gravel pack[J]. Journal of China University of Petroleum (Edition of Natural Science), 2006, 30(5): 57-61. [本文引用:1]
[21] 薄启炜, 董长银, 张琪, 等. 砾石充填层孔喉结构可视化模拟[J]. 石油勘探与开发, 2003, 30(4): 108-110.
BO Qiwei, DONG Changyin, ZHANG Qi, et al. Visual simulation of porous structure in packed gravels[J]. Petroleum Exploration and Development, 2003, 30(4): 108-110. [本文引用:2]
[22] 董长银, 张清华, 高凯歌, 等. 机械筛管挡砂精度优化实验及设计模型[J]. 石油勘探与开发, 2016, 43(6): 991-996.
DONG Changyin, ZHANG Qinghua, GAO Kaige, et al. Screen sand retaining precision optimization experiment and a new empirical design model[J]. Petroleum Exploration and Development, 2016, 43(6): 991-996. [本文引用:1]
[23] 董长银, 钟奕昕, 武延鑫, 等. 水合物储层高泥质细粉砂筛管挡砂机制及控砂可行性评价试验[J]. 中国石油大学学报(自然科学版), 2018, 42(6): 79-87.
DONG Changyin, ZHONG Yixin, WU Yanxin, et al. Experimental study on sand retention mechanisms and feasibility evaluation of sand control for gas hydrate reservoirs with highly clayey fine sand s[J]. Journal of China University of Petroleum (Edition of Natural Science), 2018, 42(6): 79-87. [本文引用:2]
[24] 焦艳红, 李萍, 王利华, 等. 高黏度流体垂直井筒携砂临界流速实验与计算[J]. 石油学报, 2018, 39(5): 604-608.
JIAO Yanhong, LI Ping, WANG Lihua, et al. Experiment and calculation of critical sand -carrying velocity for high-viscosity fluid in vertical wellbore[J]. Acta Petrolei Sinica, 2018, 39(5): 604-608. [本文引用:1]
[25] 隋冰, 刘刚, 李博, 等. 颗粒在起伏成品油管道中的沉积运移规律[J]. 石油学报, 2016, 37(4): 523-530.
SUI Bing, LIU Gang, LI Bo, et al. Deposition and movement laws of particles in fluctuating oil product pipelines[J]. Acta Petrolei Sinica, 2016, 37(4): 523-530. [本文引用:1]