引用本文
牛博, 赵家宏, 付平, 李军建, 鲍志东, 胡勇, 苏进昌, 高兴军, 张弛, 于登飞, 臧东升, 李敏. 曲流河废弃河道走向判定与单砂体构型表征——以渤海湾盆地埕宁隆起石臼坨凸起西部新近系明化镇组下段为例[J]. 石油勘探与开发, 2019,46(5): 891-901.
NIU Bo, ZHAO Jiahong, FU Ping, LI Junjian, BAO Zhidong, HU Yong, SU Jinchang, GAO Xingjun, ZHANG Chi, YU Dengfei, ZANG Dongsheng, LI Min. Trend judgment of abandoned channels and fine architecture characterization in meandering river reservoirs: A case study of Neogene Minhuazhen Formation NmⅢ2 layer in Shijiutuo bulge, Chengning uplift, Bohai Bay Basin, East China [J]. Petroleum Exploration & Development, 2019,46(5): 891-901.  
Doi: 10.11698/PED.2019.05.08
Permissions
Copyright©2019, 石油勘探与开发》编辑部
曲流河废弃河道走向判定与单砂体构型表征——以渤海湾盆地埕宁隆起石臼坨凸起西部新近系明化镇组下段为例
牛博1, 赵家宏2, 付平2, 李军建3, 鲍志东1, 胡勇4, 苏进昌4, 高兴军5, 张弛4, 于登飞4, 臧东升1, 李敏1
1. 中国石油大学（北京）地球科学学院,北京 102249
2. 中国石油吉林油田公司勘探开发研究院,吉林松原 138001
3. 中国石油长庆油田公司第五采油厂,西安 710200
4. 中海石油（中国）有限公司天津分公司,天津 300452
5. 中国石油勘探开发研究院,北京 100083
联系作者简介：鲍志东（1964-）,男,安徽巢湖人,博士,中国石油大学（北京）地球科学学院教授,主要从事储集层地质与油藏描述、沉积学及岩相古地理等方面的研究。地址：北京市昌平区府学路18号,中国石油大学（北京）地球科学学院,邮政编码：102249。E-mail: baozhd@cup.edu.cn

第一作者简介：牛博（1988-）,男,河北任丘人,现为中国石油大学（北京）在读博士研究生,主要从事沉积学、储集层地质学、油藏描述与建模等方面的研究。地址：北京市昌平区府学路18号,中国石油大学（北京）地球科学学院,邮政编码：102249。E-mail: niubo2012@foxmail.com

收稿日期: 2018-08-10
基金项目: 国家科技重大专项（2008ZX05030-005-01,2011ZX05004-004-007）
摘要

基于测井响应特征,结合沉积模式与砂体厚度,对渤海湾盆地埕宁隆起石臼坨凸起西部新近系明化镇组下段明三油层组第2小层古曲流河沉积砂体分布特征开展研究。针对目前废弃河道形态存在多解性的问题,探索出一种利用水平井电阻率曲线计算砂泥岩界面产状的方法,该方法利用随钻探测半径、界面倾角、曲线变化段长度之间的三角函数关系对砂泥岩界面产状进行定性—定量计算,以确定废弃河道的真实走向,是对现有曲流河砂体构型解剖技术的补充与完善。利用经验公式、水平井等方法对研究区点坝内部侧积层倾角与侧积体规模进行定量研究,确定点坝内部侧积层的空间分布。利用界面搭建相关构型要素,采用非均匀粗化对侧积层、侧积体分别施加不同的网格密度,对研究区多点坝复合曲流河砂体进行精细三维构建,实现构型级别数值模拟的工业化应用。研究结果对油田剩余油分布预测和挖潜以及油田优化注水具有指导意义。图13参31

关键词: 渤海湾盆地; 曲流河; 水平井电阻率曲线; 侧积层; 侧积体; 构型建模; 剩余油分布
中图分类号:TE122.1 文献标志码:A 文章编号:1000-0747(2019)05-0891-11
Trend judgment of abandoned channels and fine architecture characterization in meandering river reservoirs: A case study of Neogene Minhuazhen Formation NmⅢ2 layer in Shijiutuo bulge, Chengning uplift, Bohai Bay Basin, East China
NIU Bo1, ZHAO Jiahong2, FU Ping2, LI Junjian3, BAO Zhidong1, HU Yong4, SU Jinchang4, GAO Xingjun5, ZHANG Chi4, YU Dengfei4, ZANG Dongsheng1, LI Min1
1. College of Geosciences, China University of Petroleum, Beijing 102249, China
2. Research Institute of Exploration and Development, PetroChina Jilin Oilfield Company, Songyuan 138001, China
3. No.5 Oil Production Plant, PetroChina Changqing Oilfield Company, Xi’an 710020, China;
4. Bohai Oilfield Research Institute, CNOOC Tianjin Company, Tianjin 300452, China
5. PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China;
Abstract

Based on well logging responses, sedimentary patterns and sandstone thickness, the distribution characteristics of meandering river sedimentary sand body of Neogene Minghuazhen Formation NmⅢ2 layer in the west of Shijiutuo Bulge, Chengning Uplift, Bohai Bay Basin were investigated. A new approach to calculate the occurrence of the sand-mudstone interfaces using resistivity log of horizontal well was advanced to solve the multiple solution problem of abandoned channel’s orientation. This method uses the trigonometric function relationship between radius, dip and length of the resistivity log to calculate the occurrence qualitatively - quantitatively to help determine the true direction of the abandoned channels. This method can supplement and improve the architecture dissection technique for meandering river sandbodies. This method was used to study the dip angle and scale of the lateral accretion layers in point bar quantitatively to help determine the spatial distribution of lateral accretion layers. The fine architecture model of underground meandering river reservoir in the study area has been established. Different from traditional grids, different grid densities for lateral accretion layers and bodies were used in this model by non-uniform upscaling to establish the inner architecture model of point-bars and realize industrial numerical simulation of the whole study area. The research results can help us predict the distribution of remaining oil, tap remaining oil, and optimize the waterflooding in oilfields.

Keyword: Bohai Bay Basin; meandering river; horizontal well resistivity curve; lateral accretion layers; lateral accretion bodies; architecture modeling; remaining oil distribution
1 研究背景及地质概况

目前, 中国东部油田已经进入高含水开发阶段, 传统的沉积微相刻画已经不能满足生产需求, 单砂体精细刻画及内部构型定量表征成为储集层研究的热点[1, 2]。中国东部新生代含油盆地中河流相储集层的储量占已开发油田的40%以上[3]。曲流河作为重要的河流相储集类型, 其单砂体及内部构型的刻画对高含水油田后期剩余油研究有着重要意义。为此, 前人进行了大量研究并形成了一套较为完善的曲流河点坝单砂体构型分析方法[4, 5, 6]。但是由于曲流河点坝砂体切割叠置复杂, 分析结果往往具有多解性, 如何准确判定废弃河道走向, 精确预测点坝及内部构型, 目前仍存在一定的不确定性[7]。本文结合油田实际, 利用水平井、定向井等资料, 综合废弃河道走向判定、砂体平面组合、经验公式分析等技术, 对曲流河点坝单砂体及其内部构型进行定量化表征, 并以此为基础建立基于三级构型界面的三维原型模型, 并对曲流河点坝构型空间展布及其剩余油分布特征进行研究。

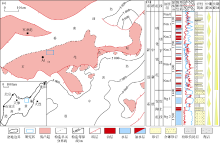
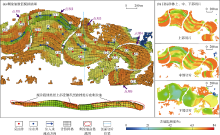
本文研究区位于渤海湾盆地埕宁隆起石臼坨凸起西部, 是在前第三系古隆起背景上发育并被断层复杂化的大型披覆构造。含油层系主要发育在新近系明化镇组（Nm）下段（简称明下段）和馆陶组（Ng）上段（简称馆上段）, 目的层位于明化镇组下段明三油层组第2小层（NmⅢ 2）, 发育曲流河沉积环境, 平面上河道呈带状分布, 单砂层厚度为6~12 m（见图1）。由于储集层埋深较浅, 处于欠压实阶段, 成岩作用较弱, 因此物性较好, 平均孔隙度为35%, 平均渗透率为1 750× 10-3 μ m2。研究区目前已进入高含水开发阶段, 采出程度仅为21%, 而局部含水率却超过90%, 存在大量可动剩余油。前人研究表明, 在高含水时期, 储集层内部隔夹层已经成为影响流体运动和剩余油分布的重要因素[5, 6]。因此, 对研究区开展曲流河单砂体构型精细解剖, 建立相关点坝构型模型, 有助于进一步认识储集层非均质性, 为厘清地下剩余油分布及后期调整挖潜提供依据。

图1 研究区位置（a）及地层柱状图（b）

2 点坝与废弃河道识别及刻画

曲流河储集层内部构型解剖主要分为两个级次：①在曲流河内部识别出单一成因砂体; ②对点坝内部三级构型要素的产状、规模进行研究[5, 8]。前者是曲流河储集层构型解剖的基础, 具体包括点坝识别和废弃河道刻画这两个方面的内容。尤其是废河道刻画直接关系到点坝侧积层倾向的判定, 需要重点予以关注。

2.1 点坝与废弃河道识别

由于废弃河道是点坝最后一次侧向迁移的边界, 其在平面上与点坝形成“ 镶边” 的位置形态。因此, 目前国内主要采用“ 废弃河道定边、厚度定位” 的方法对曲流河内部单砂体的平面展布形态进行刻画[9]。

点坝是曲流河的基本单元, 是构成曲流河“ 二元结构” 的主体, 单井垂向呈现正韵律是其最主要的特征。测井曲线主要表现为自然电位曲线呈钟形或箱形, 电阻率曲线呈较大幅度差。

废弃河道通常围绕点坝发育, 是点坝边界的重要识别标志。根据废弃方式的不同, 废弃河道可以分为渐弃型和突弃型。渐弃型废弃河道反映水动力逐级减弱的过程, 测井曲线形态由底部的高幅度向上逐渐减弱为小型齿状形态。突弃型废弃河道则形成于水动力突然减弱的沉积环境, 测井曲线形态由底部的高幅度快速突变为接近泥岩基线的小型锯齿状[10, 11, 12]。研究区废弃河道主要以突弃型或快速废弃型为主, 反映水动力突然改变的沉积环境特征。

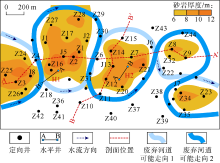
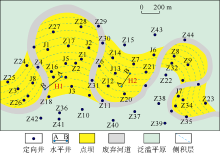
点坝的形成过程为一个明显的“ 凹蚀增凸” 的过程, 点坝砂体在复合河道内部呈透镜状与周围废弃河道加以区分。因此, 通过砂岩厚度图可有效识别出点坝及其周围废弃河道的分布形态。研究区可以识别出5个点坝, 整体呈由东向西的方向排列, 废弃河道围绕点坝发育, 是不同点坝间隔的重要识别标志（见图2）。

2.2 点坝与废弃河道平面组合

曲流河单砂体平面分析的关键与难点在于点坝与废弃河道的平面组合。目前主流组合方法是在密井网条件下, 根据废弃河道的废弃模式, 结合废弃河道和点坝的平面分布状况, 确定不同废弃河道归属, 最终组合出曲流河砂体的展布形态[9]。但是, 该方法存在一定的局限性, 由于废弃河道宽度往往接近或者小于井距, 一般井网难以对其走向和弯曲幅度进行有效判定; 虽有学者提出“ 初-末期流线包络线” 的方法进行辅助判断, 但由于曲流河砂体演化复杂, 最终的平面预测结果仍具有很强的多解性。如本文存在两种不同的废弃河道走向解释方案（见图2）, 哪种代表真实的废弃河道流向尚不甚明确, 该问题在较长时间内一直限制着曲流河单砂体解剖的进一步发展[7]。

图2 研究区砂岩厚度及点坝分布图

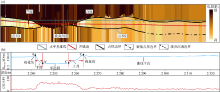
相比定向井而言, 水平井可以在平面上更为准确地揭示储集层的横向变化, 随着地质导向探边技术的发展, 可以对水平井轨迹上下边界数米范围内的岩性边界进行有效识别, 为储集层砂体及废弃河道的组合关系提供了新的判定依据[13, 14, 15, 16, 17]。如A1水平井地质导向探边解释成果显示（见图3a）, 在两个砂体之间夹有泥岩, 通过对比两侧砂体尖灭形态及泥岩组成的半月形河道发育特征, 结合研究区沉积特征, 综合判定在两点坝之间夹有废弃河道。废弃河道左侧界面比右侧有着更大的倾斜角度, 根据废弃河道的地质形态, 综合判定左侧为废弃河道凹岸, 右侧为废弃河道凸岸。

图3 A1水平井地质导向探边解释成果与测井曲线响应特征

水平井地质导向探边成果直观、可靠, 是废弃河道走向判定的直接证据, 但该方法成本高昂, 资料稀少。本文基于水平井地质导向原理, 探索一种利用水平井普通电阻率曲线计算砂泥岩界面倾角的方法, 进而确定废弃河道的弯曲方式, 是对现有曲流河单砂体-构型解剖技术的一种补充与完善。

3 利用水平井电阻率曲线确定砂泥岩界面产状
3.1 方法及原理

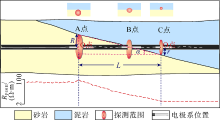
在水平井电阻率测井过程中, 随着推进器的移动, 测井电极系对储集层电性进行测量。在均质砂岩地层中, 测井电阻率曲线为一条水平线（见图4）; 当电极系探测半径的上边缘由砂岩进入泥岩时（A点）, 探测半径内地层岩性由砂岩变为砂泥岩, 电阻率曲线开始下降; 当电极系探测半径的下边缘开始离开砂岩时（C点）, 探测半径内地层岩性由砂泥岩变为泥岩, 电阻率曲线停止下降并达到最低值。因此, 可以利用电极系径向探测半径、砂泥岩界面倾角、电阻率曲线下降段长度之间的三角函数关系, 对砂泥岩界面的视倾角进行定量化表征。考虑到测井电阻率电极系的探测半径会随着介质电阻率的降低而减小, 因此其在砂岩和泥岩中具有不同的探测半径。在电阻率测井过程中, 电极系在A点为对应砂岩电性下的探测半径R, 在C点为对应泥岩电性下的探测半径r, 在A点与C点之间的探测半径受多种因素影响而呈现为一个类椭圆结构。当井轨迹保持水平时, 可以利用（1）式计算砂泥岩界面视倾角。当井轨迹不是水平时, 需要根据水平井轨迹与砂泥岩界面的组合关系进行校正（见图5）。当砂泥岩界面倾向与井轨迹倾向一致时（见图5a— 图5d）, 利用（2）式对（1）式进行校正; 当砂泥岩界面倾向与井轨迹倾向相向时（见图5e— 图5h）, 利用（3）式对（1）式进行校正。

图4 水平井电极系探测砂泥岩界面电阻率曲线变化示意图

图5 水平井轨迹与砂泥岩界面的不同组合关系模式图
（a）井轨迹上升段由砂岩进入泥岩, 砂泥岩界面倾向与井轨迹倾向一致; （b）井轨迹下降段由砂岩进入泥岩, 砂泥岩界面倾向与井轨迹倾向一致; （c）井轨迹上升段由泥岩进入砂岩, 砂泥岩界面倾向与井轨迹倾向一致; （d）井轨迹下降段由泥岩进入砂岩, 砂泥岩界面倾向与井轨迹倾向一致; （e）井轨迹上升段由砂岩进入泥岩, 砂泥岩界面倾向与井轨迹倾向相向; （f）井轨迹下降段由砂岩进入泥岩, 砂泥岩界面倾向与井轨迹倾向相向; （g）井轨迹下降段由泥岩进入砂岩, 砂泥岩界面倾向与井轨迹倾向相向; （h）井轨迹上升段由泥岩进入砂岩, 砂泥岩界面倾向与井轨迹倾向相向

\[\alpha =\arctan \left[ {\left( R+r \right)}/{L}\; \right]\ \ （1）\]

\[\theta =\arctan \left[ {\left( R+r \right)}/{L}\; \right]+\left| 90{}^\circ -\beta \right|\ \ （2）\]

\[\theta =\arctan \left[ {\left( R+r \right)}/{L}\; \right]-\left| 90{}^\circ -\beta \right|\ （3）\]

上述方法的适用条件为：①砂泥岩分界面为突变或者快速渐变地层; ②界面两侧为均质地层; ③地层砂体要有一定厚度, 不能突然尖灭或者复杂叠置。

本文研究区主要采用P16H、P40H、A40H这3类随钻测井电阻率曲线, 对应在电阻率为25 Ω · m砂岩中的探测半径分别为0.3 m, 0.9 m, 1.8 m。其中, P16H电极系探测半径过小, 受冲洗带影响较大; 考虑到研究区水平井主要沿着砂体中上部钻进, A40H曲线的探测半径相对于储集层厚度过大; 因此, 本文主要采用探测距离较为适中的P40H电阻率曲线进行计算, 从而降低探测范围超出砂体的可能。

3.2 水平井应用实例分析

3.2.1 定性快速判定A1井钻遇废弃河道凹岸、凸岸

由（1）式可知, 单一电极系在砂泥岩均质地层, 在R、r等值变化幅度有限的前提下, θ 值与L值呈负相关关系, 即L值越大、θ 值越小。因此, 可以通过L值对废弃河道凹岸、凸岸进行快速定性识别。

以A1水平井为例, 电阻率曲线在A点突然降低（钻遇泥岩）, 在A° 点达到最低, 在A° — C° 段保持平直, 在C° 点迅速上升（钻遇砂岩）, 最终在C点恢复平直（见图3b）, 研究表明A1井在A— C段钻遇了废弃河道, 通过对比发现左侧（A— A° ）电阻率曲线比右侧（C° — C）电阻率曲线的斜率更大、L值更大, 可定性判定废弃河道左侧产状大于右侧, 进而推断左侧为凹岸、右侧为凸岸。上述结果已得到A1井探边解释成果的验证（见图3）。

3.2.2 定量判定H1井钻遇废弃河道凹岸、凸岸

H1水平井主体位于点坝2, 尾部钻遇点坝1与点坝2之间的泥岩（见图2）, 属于废弃河道的有利发育位置。该井水平段钻遇180 m砂岩后进入泥岩段, 测井曲线由平稳快速下降, 疑似钻遇废弃河道。电阻率曲线（见图6）在D点达到最高值25 Ω · m, 在D° 点达到最低值3 Ω · m, L值为7.8 m, R值为0.9 m, r值为0.5 m, β 值为89.97° , 考虑到水平井主要沿砂岩中上部钻进, 更易向上钻出储集层, 故利用（2）式计算得到θ 值为10.2° 。由于H1井倾斜插入泥岩中, 砂泥岩界面的真实倾角会更大, 其倾角不仅远超该处地层产状, 也大大超过了研究区5° ~6° 的侧积层产状。H1井在砂岩段曲线平直, 电阻率变化幅度极小, 排除了中途经点坝钻遇溢岸砂等较差砂体的可能, 说明水平井在该处从点坝直接钻出到泥岩。点坝以大倾角与泥岩接触, 应为与点坝两侧发育的废弃河道侧向接触, 水平井方向为垂直侧积层方向。综上所述, 最终判断H1井在水平段尾部泥岩段钻遇废弃河道, 并在废弃河道内部完钻。由于其左侧界面产状远大于侧积层产状, 结合废弃河道的地质形态, 综合判定其左侧为废弃河道凹岸, 右侧为废弃河道凸岸, 进而最终确定图2中废弃河道可能走向2为研究区废弃河道的真实发育方向。由于点坝4比点坝3和点坝5的位置更加突出, 利用“ 初-末期流线包络线” 方法亦可得出相同结论[7], 进一步验证上述结果。

图6 H1水平井水平段测井曲线响应特征（井位见图2）

3.3 砂体解剖成果

采用“ 废弃河道定边、砂体厚度定位” 的研究思路, 首先根据单井分析砂体厚度及曲线特征圈定出每个点坝的范围, 再根据废弃河道的废弃模式, 结合废弃河道和点坝的平面分布状况, 对废弃河道沿着点坝边缘进行平面组合, 并辅以剖面作为验证, 最终得到研究区曲流河储集层微相砂体的识别与解剖分析结果（见图7、图8）。结果显示, 研究区内有5个点坝呈串珠状排列, 废弃河道特征明显, 泛滥平原作为背景相分布于周围, 以洪泛泥岩为主要沉积, 与点坝形成明显区分。

图7 连井剖面分析结果（剖面位置见图2）

图8 沉积微相及侧积泥岩平面分布图

4 点坝内部三维构型分析

点坝作为曲流河最重要的地貌单元, 形成于侧向加积作用, 由多个侧积层与侧积体组成[18, 19, 20]。前人研究表明, 点坝内部构型主要由侧积体和侧积层这2种要素构成。曲流河点坝构型精细解剖的关键在于对侧

积层与侧积体的相关构型参数进行定量化表征[18]。

4.1 侧积层倾角定量计算方法

针对点坝内部侧积层产状的测量, 目前研究已经相对成熟[5, 6, 7, 8, 9, 21, 22]。本文在调研前人成熟研究方法的基础上, 采用业内较为经典的经验公式方法, 对研究区内点坝侧积层倾角进行定量计算。

国内外对曲流河点坝内部构型模式进行了大量研究, 总结出一系列经验公式[8, 9, 10, 22, 23, 24]。其中, Leeder[23]收集了107个高弯度曲流河实例, 建立了高弯度条件下点坝内部侧积层倾角公式。

\[\lg W=1.54\lg h+0.83\ \ （4）\]

\[{{W}_{\text{c}}}=\frac{2}{3}W\ \ （5）\]

\[W=\frac{1.5h}{\tan \gamma } （6）\]

鉴于Leeder公式目前已经得到业内的广泛认可, 本文利用该公式对研究区侧积层倾角进行计算, 根据废弃河道统计结果, 古河道满岸厚度主要为5.0~6.5 m, 推算废弃河道满岸宽度为80~120 m, 侧积层倾角约为5° 左右。

4.2 侧积体规模定量计算方法

4.2.1 经验公式求取

依据前人研究成果[6, 7, 8, 9, 10, 20], 本文同样采用Leeder公式对研究区侧积体的规模进行定量计算。依据（6）式可知, 侧积体的规模为满岸河道宽度的2/3, 根据前面推算的废弃河道满岸宽度计算得到研究区侧积体规模为55~80 m。

4.2.2 水平井测井资料求取

通过识别水平井中侧积夹层, 可得到两相邻侧积层的砂岩长度, 即为该侧积体的视宽度, 利用水平井和侧积层倾向之间夹角对其进行修正, 就可计算出该侧积体的真实宽度值。H2水平井钻遇3个侧积层、2期侧积体, 2期侧积体规模分别为73 m和75 m, 其对应夹角为20° , 由此计算出H2井钻遇的侧积体规模分别为68.6 m和70.5 m（见图9）。

图9 利用测井资料求取H2水平井钻遇侧积体规模

综上所述, 以经验公式方法为基础, 辅以水平井测井资料分析结果加以验证, 二者计算结果相近, 且水平井测井资料分析结果处于经验公式法计算结果范围之内, 故最终确定研究区侧积体宽度为55~80 m, 以70 m附近相对集中。

4.3 点坝三维构型解剖成果

以上述分析结果为基础, 在已识别出的5个点坝内部进行精细构型解剖, 主要以点坝内部具有侧积层特征的井点为基础, 以水平井资料做验证, 结合侧积体的规模、产状, 分析侧积层的空间展布特征, 参照国内较为经典的曲流河点坝构型模式[5], 在点坝内部完成对侧积层顶部平面投影的绘制（见图8）。

5 多点坝构型建模与剩余油分布

相比传统建模技术, 构型级别的建模可以实现对三、四级甚至更小级别界面的模拟, 大大提高储集层非均质性的表征精度, 前人针对曲流河点坝构型三维表征展开大量工作, 建立许多建模方法[25, 26, 27, 28, 29]以及可以表征3级构型界面的三维模型。目前多利用网格来表征侧积体, 模型网格数量异常庞大, 计算工作量大且时间长, 若对模型进行粗化, 则无法保存侧积层的完整形态, 是制约侧积层模型在油田广泛应用的瓶颈所在[30, 31]。

5.1 曲流河多点坝模型建立

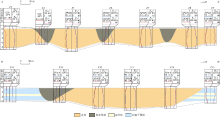
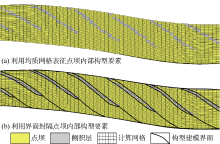
本文在构型分析的基础上采用界面约束原理建立区域三维构型模型（见图10）。首先根据构型精细解剖成果, 数字化表征点坝内部侧积层、侧积体等不同构型要素的构型界面; 然后依据点坝的侧向加积过程, 利用构型界面将点坝内部不同构型要素的顶底界面进行逐级封隔, 并按照其空间叠置顺序在点坝内部进行组合封装; 最后在侧积层、侧积体内部分别进行网格细分, 因为不同侧积层、侧积体之间由相关界面分隔, 可以在粗化处理时针对不同封隔体建立不同的网格精度, 有效解决模型网格数与侧积层精度之间的矛盾（见图11）。

图10 点坝构型建模原理

图11 单一点坝构型建模流程

利用上述方法, 将不同点坝在复合河道内部进行重组叠合, 建立研究区目的层位能表征三级构型界面的岩相模型和相关物性模型（见图12）。岩相模型作为属性建模的相控约束条件, 主要采用确定性模拟和随机模拟相结合的方式进行构建, 在废弃河道与侧积层内部, 主要采取确定性建模方法定义其中的优势岩相。在点坝内部侧积体与泛滥平原, 则采用了适用于小井距、能较好模拟复杂各向异性的序贯指示模拟方法, 对其

内部砂岩分布规律进行有效表征。最后, 以岩相模型作为相控条件, 采用序贯高斯模拟的方法, 建立相关三维物性模型。在模拟过程中, 侧积层、侧积体对应的岩性、物性数据严格按照已知钻井数据, 通过合理设置相关变差函数, 保证最终模型各构型单元模拟结果符合地下真实情况。

图12 研究区目标砂体三维构型模型

曲流河内部各种结构单元均在模型中得到很好再现（见图12）。曲流河河道具明显弯曲性。点坝与废弃河道侧向接触。在点坝砂体内部发育侧积层, 侧积层平面弧形特征和剖面倾斜形态得到很好的再现。考虑数值模拟过程中需要对网格总量进行控制（通常不超过106个）, 采用非均匀粗化对构型模型进行粗化处理, 即通过界面约束, 分别对侧积层、侧积体施加不同的网格密度, 确保在粗化砂体模型的同时保留了侧积层的形态完整（见图11d）。粗化后的模型在保证相关点坝、废弃河道、侧积层精准展示的同时, 大幅缩减了网格数量, 总有效网格数为78× 104个。实现了以较小网格数还原地下构型分布样式, 为油藏数值模拟、剩余油分布预测提供了模型基础。

5.2 利用数值模拟预测点坝剩余油分布

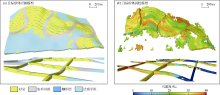
储集层构型模型研究最终目的是预测剩余油分布。本文利用数值模拟方法对目标砂体开展剩余油预测。数值模拟结果表明, 由于网格数量和类型设置合理, 模型具有较快的运算速度和较好的收敛性, 适用于油田工业化生产中反复多次的历史拟合计算。图13为模型运算至2017年6月的剩余油分布图, 为清晰区分各类构型单元, 隐去了废弃河道与侧积层等相关部分的网格。

研究结果表明, 在复合河道的层次, 不同点坝之间主要受废弃河道的遮挡作用, 井网不完善的地方存在剩余油。如点坝4内部因缺乏注水井, 相比其他4个点坝拥有更高的剩余油饱和度（见图13a）。在单一点坝内部, 剩余油分布更多地受3级构型界面（侧积层）的影响, 河道底部主要为高渗透带, 注入水快速突进, 剩余油饱和度相对较低; 河道中部和上部因受到侧积层遮挡作用, 成为主要的剩余油分布区域, 河道上部比河道中部拥有更高的剩余油饱和度（见图13b）。不同侧积体内部的剩余油含量不同, 因注入水会优先沿着侧积层的水平走向进行驱替, 然后再逐一扩展到相邻的侧积体中, 因此, 离注水井垂直侧积层走向距离最远, 而没有采油井钻遇的侧积体中上部存在最多的剩余油。

图13 构型界面约束下的储集层剩余油分布预测结果

6 结论

本文利用水平井电阻率曲线对废弃河道两侧砂泥岩界面倾角进行定性— 定量计算, 确定废弃河道的弯曲方式, 是对现有曲流河砂体构型解剖技术的一种补充与完善。

研究区水平井H1在水平段尾部泥岩处钻遇废弃河道沉积, 由于左侧界面产状远大于侧积层产状, 根据废弃河道的地质形态, 综合判定左侧为废弃河道凹岸, 右侧为废弃河道凸岸, 进而确定研究区废弃河道的真实走向。

点坝侧积体规模主要为55~80 m, 侧积层泥岩倾角以5° ~6° 附近相对集中, 倾向指向废弃河道发育一侧, 自点坝上部向点坝下部延伸, 发育深度占整个点坝砂体厚度的2/3左右。

利用界面搭建相关构型要素, 采用非均匀粗化对侧积层、侧积体分别施加不同的网格密度, 对研究区多点坝复合曲流河砂体进行精细三维构建。该方法有效解决模型网格数与侧积层精度之间的矛盾, 实现了构型模型在数值模拟的工业化应用, 进而服务于油田优化注水与剩余油预测挖潜。

符号注释：

GR— — 自然伽马, API; h— — 河道满岸深度, m; H— — 2个侧积层之间的垂向距离, m; L— — A点与C点之间的距离, m; r— — 电极系在泥岩中的探测半径, m; R— — 电极系在砂岩中的探测半径, m; Rlld— — 深侧向电阻率, Ω · m; Rlls— — 浅侧向电阻率, Ω · m; RP40H— — P40H测井电阻率, Ω · m; SP— — 自然电位, mV; W— — 河道满岸宽度, m; Wc— — 侧积体水平宽度, m; α — — 砂泥岩界面与井轨迹夹角, （° ）; β — — 井轨迹倾角, （° ）; θ — — 砂泥岩界面倾角, （° ）; γ — — 侧积层倾角, （° ）。

（编辑 王晖）

The authors have declared that no competing interests exist.

参考文献
[1] 马世忠, 吕桂友, 闫百泉, 等. 河道单砂体“建筑结构控三维非均质模式”研究[J]. 地学前缘, 2008, 15(1): 57-64.
MA Shizhong, LYU Guiyou, YAN Baiquan, et al. Research on three-dimensional heterogeneous model of channel sand body controlled by architecture[J]. Earth Science Frontiers, 2008, 15(1): 57-64. [本文引用:1]
[2] 张莉, 鲍志东, 林艳波, 等. 浅水三角洲砂体类型及沉积模式: 以松辽盆地南部乾安地区白垩系姚家组一段为例[J]. 石油勘探与开发, 2017, 44(5): 727-736.
ZHANG Li, BAO Zhidong, LIN Yanbo, et al. Genetic types and sedimentary model of sand bodies in a shallow-water delta: A case study of the first Member of Cretaceous Yaojia Formation in Qian’an area, south of Songliao Basin, East China[J]. Petroleum Exploration and Development, 2017, 44(5): 727-736. [本文引用:1]
[3] 裘亦楠. 中国陆相碎屑岩储层沉积学的进展[J]. 沉积学报, 1992, 10(3): 16-24.
QIU Yinan. Developments in reservoir sedimentology of continental clastic rocks in China[J]. Acta Sedimentologica Sinica, 1992, 10(3): 16-24. [本文引用:1]
[4] MA S Z, ZHANG J, JIN N D, et al. The 3-D architecture of point bar and the forming and distribution of remaining oil[R]. SPE 57308, 1999. [本文引用:1]
[5] 吴胜和, 岳大力, 刘建民, 等. 地下古河道储层构型的层次建模研究[J]. 中国科学: 地球科学, 2008, 38(S1): 111-121.
WU Shenghe, YUE Dali, LIU Jianmin, et al. Research on hierarchical modeling of underground ancient river reservoir structure[J]. SCIENCE CHINA Earth Sciences, 2008, 51(S2): 126-137. [本文引用:5]
[6] 岳大力, 吴胜和, 谭河清, 等. 曲流河古河道储层构型精细解剖: 以孤东油田七区西馆陶组为例[J]. 地学前缘, 2008, 15(1): 101-109.
YUE Dali, WU Shenghe, TAN Heqing, et al. An anatomy of paleochannel reservoir architecture of meand ering river reservoir: A case study of Guantao formation, the west 7th block of Gudong oilfield[J]. Earth Science Frontiers, 2008, 15(1): 101-109. [本文引用:4]
[7] 单敬福, 张吉, 赵忠军, 等. 地下曲流河点坝砂体沉积演化过程分析: 以吉林油田杨大城子油层第23小层为例[J]. 石油学报, 2015, 36(7): 809-819.
SHAN Jingfu, ZHANG Ji, ZHAO Zhongjun, et al. Analysis of sedimentary and evolution process for underground meand ering river point bar: A case study from No. 23 thin layer of Yangdachengzi oil reservoir in Jilin oilfield[J]. Acta Petrolei Sinica, 2015, 36(7): 809-819. [本文引用:5]
[8] 周银邦, 吴胜和, 计秉玉, 等. 曲流河储层构型表征研究进展[J]. 地球科学进展, 2011, 26(7): 695-702.
ZHOU Yinbang, WU Shenghe, JI Bingyu, et al. Research progress on the characterization of fluvial reservoir architecture[J]. Advances in Earth Science, 2011, 26(7): 695-702. [本文引用:4]
[9] 唐金荣, 何宇航. 河流相储层单砂体识别与应用[J]. 大庆石油地质与开发, 2012, 31(3): 68-72.
TANG Jinrong, HE Yuhang. Recognition of the individual sand body in fluvial facies reservoirs and its application[J]. Petroleum Geology & Oilfield Development in Daqing, 2012, 31(3): 68-72. [本文引用:5]
[10] 周新茂, 胡永乐, 高兴军, 等. 曲流河单砂体精细刻画在老油田二次开发中的应用[J]. 新疆石油地质, 2010, 31(3): 284-287.
ZHOU Xinmao, HU Yongle, GAO Xingjun, et al. Application of fine description of single sand body in meand ering river to old oilfield redevelopment[J]. Xinjiang Petroleum Geology, 2010, 31(3): 284-287. [本文引用:3]
[11] 李胜利, 于兴河, 姜涛, 等. 河流辫-曲转换特点与废弃河道模式[J]. 沉积学报, 2017, 35(1): 1-9.
LI Shengli, YU Xinghe, JIANG Tao, et al. Meand er-braided transition features and aband oned channel patterns in fluvial environment[J]. Acta Sedimentologica Sinica, 2017, 35(1): 1-9. [本文引用:1]
[12] 张本华. 曲流河储层构型中废弃河道的识别及其分布模式: 以孤岛油田馆上段为例[J]. 油气地质与采收率, 2013, 20(3): 18-21.
ZHANG Benhua. Discussion on aband oned channels recognition and distribution models on meand ering river reservoir architecture research: Case study of upper member of Guantao formation in Gudao oilfield[J]. Petroleum Geology and Recovery Efficiency, 2013, 20(3): 18-21. [本文引用:1]
[13] 耿长喜, 孙宝刚, 赵杰, 等. 大庆油田水平井录井地质导向技术[J]. 大庆石油地质与开发, 2014, 33(5): 231-234.
GENG Changxi, SUN Baogang, ZHAO Jie, et al. Geo-steering technique for horizontal well mud logging in Daqing[J]. Petroleum Geology & Oilfield Development in Daqing, 2014, 33(5): 231-234. [本文引用:1]
[14] 高永德, 陈鸣, 蔡建荣, 等. 基于地层边界探测的主动型地质导向技术在南海西部复杂油层中的应用[J]. 中国海上油气, 2014, 26(5): 63-69.
GAO Yongde, CHEN Ming, CAI Jianrong, et al. An application of the active geosteering technique based on stratigraphic-boundary detection in complex reservoir in the western South in China[J]. China Offshore Oil and Gas, 2014, 26(5): 63-69. [本文引用:1]
[15] 吴意明, 郝以岭, 熊书权. 边界探测技术在水平井随钻地质导向中的应用[J]. 海洋石油, 2013, 33(2): 89-93.
WU Yiming, HAO Yiling, XIONG Shuquan. Application and boundary detection technology to geo-steering services in horizontal well[J]. Offshore Oil, 2013, 33(2): 89-93. [本文引用:1]
[16] 杨震, 刘庆成, 岳步江, 等. 随钻电磁波测井中极化角的形成机理及其影响因素模拟分析[J]. 测井技术, 2010, 34(3): 210-214.
YANG Zhen, LIU Qingcheng, YUE Bujiang, et al. On mechanism of polarization angle of electromagnetic logging while drilling and its influence factors simulation[J]. Well Logging Technology, 2010, 34(3): 210-214. [本文引用:1]
[17] 王伟, 殷凯. 大斜度井和水平井随钻测井曲线形态异常分析及在地层划分中的应用[J]. 中国海上油气, 2009, 21(1): 27-30.
WANG Wei, YIN Kai. An analysis of abnormal LWD curve shapes in highly-deviated wells and horizontal wells and its application in stratigraphic division[J]. China Offshore oil and gas, 2009, 21(1): 27-30. [本文引用:1]
[18] 周新茂, 高兴军, 田昌炳, 等. 曲流河点坝内部构型要素的定量描述及应用[J]. 天然气地球科学, 2010, 21(3): 421-426.
ZHOU Xinmao, GAO Xingjun, TIAN Changbing, et al. Quantitative description of internal architecture in point bar of meand ering river[J]. Natural Gas Geoscience, 2010, 21(3): 421-426. [本文引用:2]
[19] 闫百泉, 张鑫磊, 于利民, 等. 基于岩心及密井网的点坝构型与剩余油分析[J]. 石油勘探与开发, 2014, 41(5): 597-604.
YAN Baiquan, ZHANG Xinlei, YU Limin, et al. Point bar configuration and residual oil analysis based on core and dense well pattern[J]. Petroleum Exploration and Development, 2014, 41(5): 597-604. [本文引用:1]
[20] ZHANG L, BAO Z D, DOU L X, et al. Sedimentary characteristics and pattern of distributary channels in shallow water deltaic red bed succession: A case from the Late Cretaceous Yaojia formation, southern Songliao Basin, NE China[J]. Journal of Petroleum Science and Engineering, 2018, 171: 1171-1190. [本文引用:2]
[21] MIALL A D. Architectural-elements analysis: A new method of facies analysis applied to fluvial deposits[J]. Earth Science Reviews, 1985, 22(4): 261-308. [本文引用:1]
[22] 薛培华. 河流点坝相储层模式概论[M]. 北京: 石油工业出版社, 1991.
XUE Peihua. Introduction to reservoir models of point bar facies[M]. Beijing: Petroleum Industry Press, 1991. [本文引用:2]
[23] LEEDER M R. Fluviatile fining-upwards cycles and the magnitude of palaeochannels[J]. Geological Magazine, 1973, 110(3): 265-276. [本文引用:2]
[24] SCHUMM S A. Sinuosity of alluvial rivers on the great plains[J]. Geological Society of America Bulletin, 1963, 74(9): 1089-1100. [本文引用:1]
[25] 范峥, 吴胜和, 岳大力, 等. 曲流河点坝内部构型的嵌入式建模方法研究[J]. 中国石油大学学报(自然科学版), 2012, 36(3): 1-6.
FAN Zheng, WU Shenghe, YUE Dali, et al. Embedding modeling method for internal architecture of point bar sand body in meand ering river reservoir[J]. Journal of China University of Petroleum (Edition of Natural Science), 2012, 36(3): 1-6. [本文引用:1]
[26] 舒晓, 赵永军, 王兵杰. 一种新的曲流河点坝砂体内部构型模拟方法[J]. 石油地球物理勘探, 2013, 48(S1): 151-156.
SHU Xiao, ZHAO Yongjun, WANG Bingjie. An enhanced method for modeling internal architecture of point bar sand body in meand ering alluvial rivers[J]. Oil Geophysical Prospecting, 2013, 48(S1): 151-156. [本文引用:1]
[27] 尹艳树. 层次建模方法及其在河流相储层建筑结构建模中的应用[J]. 石油地质与工程, 2011, 25(6): 1-4.
YIN Yanshu. Hierarchical modeling method and its application in the construction of fluvial architectural elements model[J]. Petroleum Geology and Engineering, 2011, 25(6): 1-4. [本文引用:1]
[28] 刘可可, 侯加根, 刘钰铭, 等. 多点地质统计学在点坝内部构型三维建模中的应用[J]. 石油与天然气地质, 2016, 37(4): 577-583.
LIU Keke, HOU Jiagen, LIU Yuming, et al. Application of multiple-point geostatistics in 3D internal architecture modeling of point bar[J]. Oil & Gas Geology, 2016, 37(4): 577-583. [本文引用:1]
[29] 李宇鹏, 吴胜和, 耿丽慧, 等. 基于空间矢量的点坝砂体储层构型建模[J]. 石油学报, 2013, 34(1): 133-139.
LI Yupeng, WU Shenghe, GENG Lihui, et a1. Spatial-vector-based dicators of water flooding effects in offshore oilfield[J]. Acta Petrolei Sinica, 2013, 34(1): 133-139. [本文引用:1]
[30] 高兴军, 宋新民, 孟立新, 等. 特高含水期构型控制隐蔽剩余油定量表征技术[J]. 石油学报, 2016, 37(S2): 99-111.
GAO Xingjun, SONG Xinmin, MENG Lixin, et al. Quantitative characterization of the hidden remaining oil controlled by reservoir architecture at extra high water cut stage[J]. Acta Petrolei Sinica, 2016, 37(S2): 99-111. [本文引用:1]
[31] 王鸣川, 朱维耀, 董卫宏, 等. 曲流河点坝型厚油层内部构型及其对剩余油分布的影响[J]. 油气地质与采收率, 2013, 20(3): 14-17.
WANG Mingchuan, ZHU Weiyao, DONG Weihong, et a1. Study on distribution and influence factors of remaining oil in point bar of meand ering river[J]. Petroleum Geology and Recovery Efficiency, 2013, 20(3): 14-17. [本文引用:1]