第一作者简介:窦宏恩(1962-),男,甘肃宁县人,博士,中国石油勘探开发研究院高级工程师,主要从事油气开发基础理论、油气开发战略及科技发展战略等研究工作。地址:北京市海淀区学院路20号,中国石油勘探开发研究院油气开发战略规划研究所,邮政编码:100083。E-mail: douhongen@petrochina.com.cn
通过回顾水驱特征曲线的产生过程,讨论了国家行业标准《石油可采储量计算方法(SY/T 5367—1998)》中推荐的张金庆、俞启泰水驱特征曲线的本质及特性,并对水驱特征曲线的一些技术问题进行了深入探讨。指出:①现有水驱特征曲线均以油田实践经验和统计方法获得的经验公式为基础推导而得,都能很好表征水驱油特征;②将水驱特征参数进行多参数组合,同时采用不同的数学运算,只要这些参数组合及数学运算满足线性关系,就能推导出新的水驱特征曲线,通过改变组合方式提出新型水驱特征曲线已无实际意义;③高含水期水驱特征曲线上翘主要是由于含水上升到一定程度后,流度比随着含水率的快速上升而出现拐点,后期流度比快速上升改变了原有的两相流流动动态所致;④开发进入含水期,具有线性关系的水驱特征曲线都可以使用,即使出现拐点,只要在拐点以上部分出现直线段,均可采用线性关系的水驱特征曲线进行预测;⑤水驱油田实际数据证实甲型、张金庆及俞启泰水驱特征曲线在高含水期都可较好预测水驱油田原油可采储量,可以继续大力推广使用。
Through reviewing the generation process and essential characteristics of waterflooding curves, the essence and characteristics of Zhang Jinqing waterflooding curve and Yu Qitai waterfooding curve recommended in Chinese Petroleum Industry Standard “Calculation methods for Recoverable Oil Reserves (SY/T5367—1998)” were discussed, and some technical issues related to the curves were examined in-depth. We found that: (1) All the waterflooding curves are based on empirical formulas derived from oilfield production experience and statistics methods, and can characterize oil displacement features by water quite well. (2) A new waterflooding curve can be derived by combining waterflooding parameters and using different mathematical calculations as long as the parameter combinations and mathematical operation meet a linear relationship, so proposing new waterflooding curves by changing the combination mode has no practical significance anymore. (3) The upwarp of waterflooding curve in the extremely high water cut stage is because the mobility ratio curve has a inflection point with the rapid rise of water cut after reaching a certain value, and the later rapid rise of mobility ratio changes the original two-phase flow dynamics. (4) After entering into water cut stage, all the waterflooding curves with linear relationship can be used to make prediction, even curves with inflection points, as long as they have a straight line section above the inflection point. (5) Actual data of waterflooding oilfields has proved that Type A, Zhang Jinqing and Yu Qitai waterflooding curves all can predict accurately oil recoverable reserves in extremely high water cut stage and can be promoted.
20世纪50— 80年代, 前苏联学者根据水驱油田开发规律统计发现了甲、乙、丙、丁型水驱特征曲线[1, 2, 3, 4, 5, 6, 7], 这几种水驱特征曲线在中国得到广泛应用。到目前为止, 经中国学者的进一步研究与发展, 已研发出多种新的水驱特征曲线[8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18], 最具代表性的是1998年《石油勘探与开发》第3期发表的《一种简单实用的水驱特征曲线》[8]和第5期发表的《一种广义水驱特征曲线》[9]。这2篇文章提出的方法简单实用, 原油可采储量预测值与水驱油田实际数据相比吻合程度较高, 被大家广泛采用, 并于1998年被国家石油行业标准《石油可采储量计算方法(SY/T 5367— 1998)》[10]采纳, 文献[8]和[9]的水驱特征曲线在国家石油行业标准中分别被命名为张金庆水驱特征曲线和俞启泰水驱特征曲线。2010年国家石油行业标准《石油可采储量计算方法(SY/T 5367— 2010)》[11]删除了这2种水驱特征曲线。
本文经过深入研究水驱特征曲线的本质及特性, 对国家石油行业标准中水驱特征曲线的一些技术问题进行讨论, 以期对同业者正确理解和使用水驱特征曲线有所帮助。
水驱特征曲线是油田开发过程中流体流量之间的相互关系曲线, 表征了水驱开发过程中的宏观特征。
水驱特征曲线是由统计数学方法建立起来的一种经验模型, 具有一定的局限性, 应根据油藏实际情况筛选使用。周维四等[1]认为:从统计学看, 来自某个母体的统计规律只适用于该母体, 不属于该母体的子样本则不能使用。本文认为:只要统计数据的样本(子样本)统计规律具有该母体样本的属性或者属于该母体, 该统计规律所形成的模型就可使用。
国家石油行业标准《石油可采储量计算方法(SY/T 5367— 1998)》[10]和《石油可采储量计算方法(SY/T 5367— 2010)》[11]除均推荐采用甲型、乙型、丙型和丁型水驱特征曲线外, SY/T 5367— 1998标准还推荐采用张金庆和俞启泰水驱特征曲线。张金庆水驱特征曲线建立的基础是丙型和丁型曲线, 俞启泰水驱特征曲线与甲型曲线具有相似的数学性质, 为更好地理解与使用水驱特征曲线, 本文在回顾甲型、丙型和丁型水驱特征曲线产生背景的基础上, 对张金庆和俞启泰水驱特征曲线的相关技术问题进行讨论。
1959年, 前苏联科学家马克西莫夫根据前苏联格罗兹内油区的实际数据, 经过统计分析, 将累计产油量和累计产水量之间的统计关系表示为[1]:
${{W}_{\text{p}}}={{a}_{1}}{{e}^{{{b}_{1}}{{N}_{\text{p}}}}}$ (1)
对(1)式两边取常用对数, 可改写为:
$\lg {{W}_{\text{p}}}={{A}_{1}}+{{B}_{1}}{{N}_{\text{p}}}$ (2)
1978年中国已故中国科学院院士童宪章将(2)式命名为甲型水驱特征曲线, 在中国水驱油田得到了广泛应用。该曲线在1998年被写入国家石油行业标准中[10]。
由(1)式可得到累计产油量与含水率之间的关系式:
${{N}_{\text{p}}}=\frac{\lg \frac{{{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right)}{1-{{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right)}-{{A}_{1}}-\lg \left( 2.303{{B}_{1}} \right)}{{{B}_{1}}}$ (3)
若含水率为极限含水率fwl, 油藏的地质储量为N, 则原油采收率为:
${{E}_{\text{R}}}=\frac{\lg \frac{{{f}_{\text{wl}}}}{1-{{f}_{wl}}}-{{A}_{1}}-\lg \left( 2.303{{B}_{1}} \right)}{N{{B}_{1}}}$ (4)
1981年前苏联学者谢巴切夫提出了丙型水驱特征曲线, 其关系式为:
$\frac{{{L}_{\text{p}}}}{{{N}_{\text{p}}}}={{A}_{3}}+{{B}_{3}}{{L}_{\text{p}}}$ (5)
1972年前苏联学者纳扎洛夫提出了丁型水驱特征曲线, 其表达式为:
$\frac{{{L}_{\text{p}}}}{{{N}_{\text{p}}}}={{A}_{4}}+{{B}_{4}}{{W}_{\text{p}}}$ (6)
由(5)和(6)式可得到累计产油量与含水率之间的关系式:
${{N}_{\text{p}}}=\frac{1-\sqrt{{{A}_{3}}\left[ 1-{{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right) \right]}}{{{B}_{3}}}$ (7)
${{N}_{\text{p}}}=\frac{1-\sqrt{\left( {{A}_{4}}-1 \right)\frac{1-{{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right)}{{{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right)}}}{{{B}_{4}}}$ (8)
若含水率为极限含水率fwl, 油藏的地质储量为N, 则得到丙型和丁型水驱特征曲线在极限条件下的原油采收率分别为:
${{E}_{\text{R}}}=\frac{1-\sqrt{{{A}_{3}}\left( 1-{{f}_{\text{w}l}} \right)}}{N{{B}_{3}}}$ (9)
${{E}_{\text{R}}}=\frac{1-\sqrt{\left( {{A}_{4}}-1 \right)\frac{1-{{f}_{wl}}}{{{f}_{wl}}}}}{N{{B}_{4}}}$ (10)
1998年张金庆综合各种类型含水率与采出程度的关系, 提出了一种简单的新型水驱特征曲线[8]。1998年被国家石油行业标准采用[10]。其表达式为:
$\frac{{{W}_{\text{p}}}}{{{N}_{\text{p}}}}=-{{A}_{5}}+{{B}_{5}}\frac{{{W}_{\text{p}}}}{N{{_{\text{P}}^{{}}}^{\text{2}}}}$ (11)
由(11)式可得到累计产油量与含水率之间的关系:
${{N}_{\text{p}}}={{B}_{5}}-{{B}_{5}}\sqrt{\frac{{{A}_{5}}\left[ 1-{{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right) \right]}{{{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right)+{{A}_{5}}\left[ 1-{{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right) \right]}}$ (12)
若含水率为极限含水率fwl, 油藏的地质储量为N, 则极限条件下的原油采收率为:
${{E}_{\text{R}}}=\frac{{{B}_{5}}-{{B}_{5}}\sqrt{\frac{{{A}_{5}}\left( 1-{{f}_{wl}} \right)}{{{f}_{wl}}+{{A}_{5}}\left( 1-{{f}_{wl}} \right)}}}{N}$ (13)
张金庆在文献[8]中将(5)和(6)式分别改写为:
${{N}_{p}}={b}'+{c}'\frac{{{N}_{\text{p}}}}{{{L}_{p}}}$ (14)
${{N}_{p}}={b}'+{c}'\frac{{{N}_{\text{p}}}}{{{L}_{p}}-{{N}_{\text{p}}}}$ (15)
张金庆在文献中没有区分(5)和(6)式中的模型常数A3、B3、A4、B4, 对丙型和丁型曲线两个不同的水驱特征曲线使用了相同的系数, 均采用a、b进行替代, 目的是将丙型和丁型水驱特征曲线表示为统一的表达式。从文献中还可以看到张金庆并没有在两式之间进行任何运算, 也没有混淆使用这几个模型常数。
但根据(5)和(6)式, 采用文献[19]的思路, 可推导出(14)和(15)式。
由(5)式可得:
${{N}_{p}}=\frac{{{L}_{p}}-{{A}_{3}}{{N}_{p}}}{{{B}_{3}}{{L}_{p}}}$ (16)
式中
${{L}_{p}}={{W}_{p}}+{{N}_{p}}$ (17)
(17)式代入(16)式变形得:
${{N}_{p}}=\frac{1}{{{B}_{3}}}-\frac{{{A}_{3}}}{{{B}_{3}}}\frac{{{N}_{p}}}{{{L}_{p}}}$ (18)
令:
$\left\{ \begin{align} & a_{0}^{1}=\frac{1}{{{B}_{3}}} \\ & b_{0}^{1}=-\frac{{{A}_{3}}}{{{B}_{3}}} \\ \end{align} \right.$ (19)
将(19)式代入(18)式可得(14)式所表示的形式。
同理, 对(6)式变形得:
${{N}_{p}}=\frac{1}{{{B}_{4}}}-\frac{{{A}_{4}}-1}{{{B}_{4}}}\frac{{{N}_{p}}}{{{W}_{p}}}$ (20)
令:
$\left\{ \begin{align} & {{a}_{0}}=\frac{1}{{{B}_{4}}} \\ & {{b}_{0}}=-\frac{{{A}_{4}}-1}{{{B}_{4}}} \\ \end{align} \right.$ (21)
将(21)式代入(20)式可得(15)式所表示的形式。
(14)和(15)式的通式可表示为:
${{N}_{p}}={{{a}'}_{0}}+{{{b}'}_{0}}\frac{{{N}_{p}}}{{{W}_{p}}+n{{N}_{p}}}$ (22)
当n=1时, (22)式为丙型水驱特征曲线, 即(14)式; 当n=0时, (22)式为丁型水驱特征曲线, 即(15)式。由此可见, (14)和(15)两式是由(5)和(6)式的数学变换得到的, 且都是正确的。
从另一个侧面考虑, 如果不能从(5)和(6)式中推导出(14)和(15)式, 也可根据(5)和(6)式构造一个新函数, 这个新构造的函数只要通过2参数或者3参数组合, 在数学上满足线性关系, 就是一条新的水驱特征曲线。所以, 新构造的函数(如(14)和(15)式)都是正确的。
张金庆水驱特征曲线是由中国学者首次建立的一种新的、简单实用的水驱特征曲线, 该水驱特征曲线得到了较广泛的应用[13, 17, 19, 20]。
俞启泰根据水驱油田的水驱规律, 提出了累计产液量、累计产水量比值与累计产油量的统计关系式[9]:
${{N}_{\text{p}}}=a{{\left( \frac{{{L}_{p}}}{{{W}_{p}}} \right)}^{b}}$ (23)
根据(23)式可得到水驱特征曲线:
$\lg {{N}_{\text{p}}}={{a}_{2}}+b\lg \frac{{{L}_{p}}}{{{W}_{\text{p}}}}$ (24)
(24)式称为俞启泰广义水驱特征曲线, 在1998年被国家石油行业标准[10]采用。后来一些学者[21, 22, 23, 24]使用俞启泰水驱特征曲线开展了许多研究工作, 但2010年国家石油行业标准[11]中删除了俞启泰水驱特征曲线。
对比马克西莫夫提出的统计关系(1)式和俞启泰提出的函数关系(23)式, 其函数通式为:
$y=a{{b}^{x}}$ (25)
在(1)式中, $b={{e}^{{{b}_{1}}}}$, x=Np; 在(23)式中, $x=\text{ln}\frac{{{L}_{\text{p}}}}{{{W}_{\text{p}}}}$。
由上述分析看出俞启泰提出的(23)式与马克西莫夫(1)式具有相同形式。另外, 经许多水驱油田应用证实采用俞启泰水驱特征曲线分析水驱动态及估算可采储量[22, 23]简单实用, 精度较高。为了使俞启泰水驱特征曲线得到更广泛应用, 本文推导出其水驱采收率计算公式:
${{E}_{\text{R}}}=\frac{{{10}^{{{a}_{2}}}}}{N}\left\{ \frac{b\left( 1+{{f}_{wl}} \right)-\left( 1-{{f}_{wl}} \right)}{2b{{f}_{wl}}}-\begin{matrix}^{^{^{^{{}}}}} \\ ^{^{^{^{{}}}}} \\ \end{matrix} \right.$ ${{\left. \frac{\sqrt{{{\left[ \left( 1-{{f}_{wl}} \right)\left( b-1 \right) \right]}^{2}}-4b{{f}_{wl}}\left( 1-{{f}_{wl}} \right)}}{2b{{f}_{wl}}} \right\}}^{b}}$ (26)
水驱特征曲线是最早由前苏联科学家采用油田和实验室数据, 通过统计规律得到的一种能描述水驱油规律的经验关系式, 随后学者将其推广并发展出多种类型的表达形式, 并以研究者姓名进行命名。1978年童宪章院士将马克西莫夫水驱特征曲线命名为甲型水驱特征曲线, 随后中国学者继续以乙、丙、丁次序来命名水驱特征曲线。
前苏联学者给出的水驱特征曲线, 基本都是根据经验数据统计回归得到, 均未从理论上进行推导, 但都能表示为含水率与原油采出程度的关系, 方便进行可采储量预测。分析水驱特征曲线形态可以发现, 因地下油水黏度比等的差异, 曲线会表现出不同的凹凸特征。近年来, 发展出超过100种新型水驱特征曲线, 采用排序方法进行命名的确已显得有些不足。
水驱特征曲线是在油藏采用水驱开发且有采出水的前提下建立的一种分析油藏水驱开发动态的经验方法。任何一种水驱特征曲线描述的都是无水采油期后的产油量、产水量及产液量变化规律, 反映的是油藏水驱开发的生产特征。因此任何一种水驱特征曲线都不能用来计算无水期的累计产油量和采出程度等参数。
俞启泰水驱特征曲线比马克西莫夫的2参数模型多1个参数, 所以被称为广义水驱特征曲线, 表达了水驱油过程中累计产油量、累计产液量与累计产水量3个参数之间的显式关系。
根据油田水驱(或其他驱替方式)开发中的各种采出参数进行统计分析, 只要构造一个函数, 将驱替特征参数(如累计产油量、累计产水量、累计产液量、水油比、液油比、含水率)进行2参数或3参数组合, 在数学上呈现线性关系, 就能形成新型水驱特征曲线。将这些特征参数进行2参数或3参数的随机组合, 可产生35种组合方式, 能满足直线关系的数学运算也有很多种(如乘除法、平方和开方、指数和幂、对数和双对数、或者某种混合运算等), 如果采用20种不同的数学运算与35种参数组合进行推导, 可得到700种水驱特征曲线。
因此, 这里需要强调一点, 水驱特征曲线只能用来计算见水后的累计产油量和采出程度等参数, 且不能将各种不同水驱特征曲线估算的原油可采储量等参数进行相互间的对比以验证结果的可靠性。但可以与Arps递减分析及数值模拟等方法得到的估算值进行比较。
近年来, 针对水驱特征曲线在高含水期上翘的问题, 学者们已做过许多研究, 建立了多种描述高含水期水驱动态的特征曲线[25, 26, 27, 28, 29, 30, 31, 32], 普遍认为在高含水期, 水驱特征曲线上翘的原因是油、水相对渗透率比值与含水饱和度的变化不再遵循指数关系:
$\frac{{{K}_{ro}}\left( {{S}_{w}} \right)}{{{K}_{rw}}\left( {{S}_{w}} \right)}=m{{e}^{-n{{S}_{w}}}}$ (27)
文献[25, 29]将高含水期$\frac{{{K}_{ro}}}{{{K}_{rw}}}$与Sw的关系描述为:
$\frac{{{K}_{ro}}\left( {{S}_{w}} \right)}{{{K}_{rw}}\left( {{S}_{w}} \right)}=m{{e}^{-\left( nS_{w}^{2}+c{{S}_{w}} \right)}}$ (28)
本文假设原油在地层中的流动为平面径向流, 分析水驱特征曲线在高含水期上翘的真正原因。
地下含水率可表示为:
${{f}_{\text{w}}}\left( {{S}_{w}} \right)=\frac{{{Q}_{w}}}{{{Q}_{w}}+{{Q}_{o}}}$ (29)
其中
${{Q}_{w}}={{B}_{w}}{{Q}_{w\operatorname{s}}}=\frac{2\pi K{{K}_{rw}}\left( {{S}_{w}} \right)h}{{{\mu }_{w}}}\frac{\Delta p}{\ln \frac{{{r}_{e}}}{{{r}_{w}}}}$ (30)
${{Q}_{o}}={{B}_{o}}{{Q}_{o\operatorname{s}}}=\frac{2\pi K{{K}_{ro}}\left( {{S}_{w}} \right)h}{{{\mu }_{o}}}\frac{\Delta p}{\ln \frac{{{r}_{e}}}{{{r}_{w}}}}$ (31)
地面含水率可表示为:
${{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right)=\frac{{{Q}_{ws}}}{{{Q}_{ws}}+{{Q}_{\operatorname{o}\operatorname{s}}}}$ (32)
根据(30)和(31)式, 地下水油比可表示为:
$WOR={{\left( WOR \right)}_{s}}\frac{{{B}_{w}}}{{{B}_{o}}}$ (33)
由(32)式整理得:
${{\left( WOR \right)}_{s}}=\frac{1}{\frac{1}{{{f}_{\text{ws}}}({{S}_{\operatorname{w}}})}-1}$ (34)
将(34)式代入(33)式, 地下水油比可进一步表示为:
$WOR=\frac{1}{\frac{1}{{{f}_{\text{ws}}}({{S}_{\operatorname{w}}})}-1}\frac{{{B}_{w}}}{{{B}_{o}}}$ (35)
流度比可表示为:
$M=\frac{{{\mu }_{o}}}{{{\mu }_{w}}}\frac{{{K}_{rw}}\left( {{S}_{w}} \right)}{{{K}_{ro}}\left( {{S}_{w}} \right)}$ (36)
将(30)、(31)和(36)式代入(32)式整理得:
$M=\frac{1}{\frac{1}{{{f}_{\text{ws}}}\left( {{S}_{\operatorname{w}}} \right)}-1}\frac{{{B}_{w}}}{{{B}_{o}}}$ (37)
忽略毛细管压力和重力影响, 地下水驱油过程中地下含水率与流度比及水油比的关系可分别表示为:
${{f}_{\text{w}}}\left( {{S}_{w}} \right)=\frac{1}{1+\frac{{{\mu }_{w}}}{{{\mu }_{o}}}\frac{{{K}_{ro}}\left( {{S}_{w}} \right)}{{{K}_{rw}}\left( {{S}_{w}} \right)}}=\frac{1}{1+\frac{1}{M}}$ (38)
${{f}_{\text{w}}}\left( {{S}_{w}} \right)=\frac{{{B}_{w}}{{Q}_{w\operatorname{s}}}}{{{B}_{w}}{{Q}_{w\operatorname{s}}}+{{B}_{o}}{{Q}_{o\operatorname{s}}}}=\frac{1}{1+\frac{1}{WOR}}$ (39)
将(33)、(34)式代入(39)式得到地下含水率与地面含水率的关系为:
${{f}_{\text{w}}}\left( {{S}_{w}} \right)=\frac{1}{1+\frac{{{B}_{o}}}{{{B}_{w}}}\left[ \frac{1}{{{f}_{\text{ws}}}({{S}_{\operatorname{w}}})}-1 \right]}$ (40)
比较(35)和(37)式、(38)和(39)式可以看出:当忽略毛细管压力和重力影响时, 油水比和地面含水率的关系式与流度比和地面含水率的关系式是相同的; 流度比和地下含水率的关系式与水油比和地下含水率的关系式也是相同的。当地下原油体积系数和地下水体积系数都等于1时, 地下含水率与地面含水率相等。通常, 地下原油体积系数为1.0~1.3, 地下水体积系数为1.00~1.05。
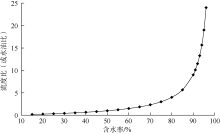
含水率变化区间为[0, 100%], 这里设定原油体积系数和地下水体积系数都等于1, 流度比随含水率变化与现场实际值的符合程度高, 根据(37)式(或(35)式)绘制含水率取值为15%~99%时的流度比(或水油比)变化曲线(简称为理论曲线)。其中含水率取值15%~90%时, 计算步长取为15%; 含水率超过90%时, 计算步长按1%取值(见图1)。
(37)式(或(35)式)为单调增函数, 当含水率低于80%时, 流度比(或水油比)小于4.0, 流度比(或水油比)上升速度较慢; 当含水率超过80%时, 流度比(或水油比)快速上升(曲线在含水率约为85%时出现拐点), 含水率等于90%时, 含水率变化了10%, 流度比(或水油比)上升到9.0, 上升125%; 当含水率从90%上升到95%, 仅增加5%, 流度比(或水油比)从9上升到19, 上升111%; 当含水率从95%上升到99%, 仅增加4%, 流度比(或水油比)从19上升到99, 上升521%。可以看出, 特高含水期含水率的微小变化就会引起流度比(或水油比)的快速上升, 特别是当含水率超过90%以后, 流度比(或水油比)更是加速上升。
从驱油角度而言, 流度比越大, 水驱过程中水窜、水淹、指进或舌进现象越严重, 水驱油波及效率越低, 驱油效果越差。高含水期水驱特征曲线上翘主要是因为含水上升到80%以后流度比(或水油比)随着含水率的快速上升而出现拐点, 后期流度比(或水油比)快速上升改变了原有的两相流流动动态所致; (27)式中$\ln \frac{{{K}_{ro}}}{{{K}_{rw}}}$-Sw关系偏离半对数直线关系是两相流流动动态改变的体现。
图2是根据文献[25]提供的濮城油田沙一下油藏数据绘制的流度比与含水率的关系曲线与理论曲线的对比, 两者几乎重合, 说明对理论曲线分析所得的观点可以得到油田现场实际开发数据的支撑。
高含水期水驱特征曲线出现拐点并上翘是高含水期采油的一种必然现象, 高含水期采用纯水驱采油效果差、经济效益低, 必须采取其他开采方式或者转换开发方式, 降低流度比快速上升带来的不利影响, 才能提高驱油效率和开发效益。
1959年Craft和Hawkins通过实验数据拟合发现$\frac{{{K}_{ro}}}{{{K}_{rw}}}$-Sw符合(27)式的指数递减关系, 该关系曲线的中间部分近似于直线, 基于此, (27)式被用于推导水驱特征曲线, 甲型、乙型以及Ershghi I等[33]提出的X-Plot水驱特征曲线都采用了(27)式。多年来许多研究者均认为:高含水期水驱特征曲线上翘是由于(27)式中e的指数项采用Sw的线性函数表征不足以反应高含水期的动态特征, 而应采用Sw的二次函数关系进行表征, 进而改写成(28)式。事实上, 不论e的指数项改写成Sw的何种函数形式, 本质依然是指数函数。采用二次多项式、复杂的幂函数等多种形式的水驱特征曲线进行高含水期动态分析和储量预测, 因曲线多表现为非线性, 曲线的切线不具有唯一性, 因而曲线的后期变化趋势线难以准确确定, 即使非线性曲线的前期拟合效果非常好, 通常也不能用于可采储量等参数的预测。
采用文献[25]提供的濮城油田沙一下油藏的数据对甲型、俞启泰与张金庆水驱特征曲线进行进一步讨论。图3所示为甲型水驱特征曲线, 相关系数平方为0.999, 采用甲型水驱特征曲线预测水驱可采储量是可行的。采用该曲线拟合1992年的累计产油量为631.91× 104 m3, 与实际值相比高0.89%, 精度满足要求, 预测的水驱最终可采储量为705.38× 104 m3。
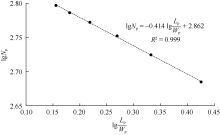
图4所示为采用俞启泰水驱特征曲线对该油田水驱生产数据的拟合, 相关系数平方为0.999, 采用该曲线进行可采储量预测是可行的。采用该曲线拟合1992年的水驱累计产油量为619.40× 104 m3, 比实际值低1.10%, 精度满足要求, 预测最终水驱可采储量为661.46× 104 m3。
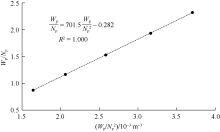
图5所示为采用张金庆水驱特征曲线对该油田水驱生产数据的拟合, 回归相关系数平方为1.000, 同样采用该曲线进行可采储量预测是可行的。采用该曲线拟合1992年的水驱累计产油量为614.00× 104 m3, 比实际值低2.00%, 也能满足精度要求, 预测的最终水驱可采储量为648.44× 104 m3。
资料显示[34], 濮城油田沙一下为高渗整装油藏, 1980年投入开发, 地质储量1 384.15× 104 m3, 标定采收率51.30%; 1992年含水率为94.69%, 2013年上升到97.74%, 该年度地质储量采出程度已达到50.89%, 油田还在继续开发中。甲型水驱特征曲线预测水驱采收率50.96%, 俞启泰水驱特征曲线预测水驱采收率47.79%, 张金庆水驱特征曲线预测水驱采收率46.84%。对比3种水驱特征曲线的预测值与目前实际水驱开发的状况, 甲型水驱特征曲线预测结果与目前实际情况较为吻合, 俞启泰和张金庆水驱特征曲线预测结果略偏低。
文献[25]与[29]提出的新方法也预测了濮城油田沙一下油藏的原油采收率, 分别为48.25%和48.50%, 经笔者与该油藏2013年度油田的实际石油地质储量采出程度对比, 其预测原油采收率值也偏低。可以看出, 不同的水驱特征曲线虽然曲线拟合十分良好(相关系数平方0.995~1.000), 累计产油量的拟合程度也都很高, 但外推预测最终水驱采收率时, 却出现了一定差异。分析原因, 主要是因为水驱特征曲线与统计样本有关, 影响样本的主要因素有油藏流体物性及储集层物性。这足以说明每种水驱特征曲线都有其自身的适应范围, 不是每种水驱特征曲线都能适合所有水驱油田, 使用时应该谨慎筛选, 必须有针对性。
综上所述, 开发进入含水期, 具有线性关系的水驱特征曲线都可以使用, 即使出现拐点, 只要在拐点以上部分出现直线段, 采用线性关系的水驱特征曲线进行预测, 均可得到可靠的结果。
现有水驱特征曲线的推导均以油田实践经验和统计方法获得的经验公式为基础, 而非通过纯粹油水流动方程得到, 其重要性在于曲线能真正表征水驱油藏的动态特征, 反映水驱油藏累计产油量、产水量、产液量和含水率等之间的变化规律。
将水驱特征参数进行多参数组合, 同时采用不同的数学运算, 只要这些参数组合及数学运算满足线性关系, 就能推导出新的水驱特征曲线, 满足这种直线关系的组合多达700种, 通过改变组合方式提出新型水驱特征曲线已无实际意义。
水驱特征曲线不能用来计算无水期的累计产油量和采出程度等参数。高含水期水驱特征曲线上翘的主要原因是含水上升到一定程度后流度比随着含水率的快速上升而出现拐点, 后期流度比快速上升改变了原有的两相流流动动态所致。开发进入含水期, 具有线性关系的水驱特征曲线都可以使用, 即使出现拐点, 只要在拐点以上部分出现直线段, 采用具有线性关系的水驱特征曲线进行预测, 均可得到可靠的结果。
水驱油田实际数据证实甲型、张金庆及俞启泰水驱特征曲线在高含水期都可较好预测水驱油田原油可采储量, 可以继续大力推广使用。建议将张金庆及俞启泰水驱特征曲线重新纳入国家石油行业标准。
致谢:本文在撰写过程中, 曲德斌博士提出了很好的建议, 在此表示感谢。
符号注释:
a, a0, a1, a2, ${{{a}'}_{0}}$, $a_{0}^{1}$, A1, A3, A4, A5, b, b1, b0, ${b}'$, ${{{b}'}_{0}}$, $b_{0}^{1}$, B1, B3, B4, B5, c, ${c}'$, m, n— — 模型回归常数; Bo, Bw— — 地层原油、地层水体积系数, m3/m3; ER— — 水驱阶段的原油最终采收率, %; fw(Sw)— — 地下含水率, %; fwl— — 水驱阶段极限含水率, %; fws(Sw)— — 地面含水率, %; h— — 油层有效厚度, m; K— — 油藏绝对渗透率, m2; Kro(Sw), Krw(Sw)— — 油、水相的相对渗透率, 无因次; Lp— — 地面条件累计产液量, 104 m3; M— — 流度比, 无因次; N— — 原始石油地质储量, 104 m3; Np— — 水驱油阶段地面条件累计产油量, 104 m3; Qo— — 地层条件产油量, m3/s; Qos— — 地面条件产油量, m3/s; Qw— — 地层条件产水量, m3/s; Qws— — 地面条件产水量, m3/s; re— — 泄油半径, m; rw— — 井筒半径, m; R— — 相关系数, 无因次; Sw— — 含水饱和度, %; Wp— — 地面条件累计产水量, 104 m3; WOR— — 地层条件水油体积比, 无因次; (WOR)s— — 地面条件水油体积比, 无因次; Δ p— — 生产压差, Pa; μ o, μ w— — 地层原油、地层水黏度, Pa· s。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|