引用本文
范宜仁, 胡旭飞, 邓少贵, 袁习勇, 李海涛. 倾斜层理地层随钻电磁波测井响应特征[J]. 石油勘探与开发, 2019,46(4): 675-683.
FAN Yiren, HU Xufei, DENG Shaogui, YUAN Xiyong, LI Haitao. Logging while drilling electromagnetic wave responses in inclined bedding formation[J]. Petroleum Exploration & Development, 2019,46(4): 675-683.  
Doi: 10.11698/PED.2019.04.05
Permissions
Copyright©2019, 石油勘探与开发》编辑部
石油勘探与开发》编辑部 所有
倾斜层理地层随钻电磁波测井响应特征
范宜仁1,2,3,4, 胡旭飞5, 邓少贵1,2,3,4, 袁习勇1,2,3,4, 李海涛1,2,3,4
1. 中国石油大学（华东）地球科学与技术学院,山东青岛 266580
2. 深层油气地质与勘探教育部重点实验室,山东青岛266580
3. 海洋国家实验室海洋矿产资源评价与探测功能实验室,山东青岛 266071
4. 中国石油大学CNPC测井重点实验室,山东青岛 266580
5. 中国石油大学（北京）克拉玛依校区石油学院,新疆克拉玛依 834000
联系作者简介：胡旭飞（1986-）,男,山西晋中人,现为中国石油大学（北京）克拉玛依石油学院讲师,主要从事电法测井正反演和机器类学习算法研究。地址：新疆克拉玛依市安定路355号,中国石油大学（北京）克拉玛依石油学院,邮政编码：834000。 E-mail：B14010015@s.upc.edu.cn

第一作者简介：范宜仁（1962-）,男,福建大田人,博士,中国石油大学（华东）教授,主要从事岩石物理实验,电测井理论、方法与应用及复杂油气层测井评价方法等研究。地址：山东省青岛市黄岛区长江西路66号,中国石油大学（华东）工科楼C501室,邮政编码：266580。 E-mail：fanyiren@upc.edu.cn

收稿日期: 2018-10-15
基金项目: 国家自然科学基金项目（41474100,41574118）
摘要

为实时反演、快速重构地层真电阻率,消除常规随钻电磁波测井正演基于含垂直对称轴的横向各向同性（VTI）地层模型仅考虑水平和垂直方向电阻率的局限性,基于并矢格林函数给出一套含倾斜对称轴的横向各向同性（TTI）地层的随钻电磁波测井正演计算方法。采用各向异性角和各向异性方位来表征TTI地层的各向异性特性,通过数值算例验证了算法的正确性,分析了不同介质情况下的半空间电磁波反射和透射特征,指出使用新算法的必要性。数值模拟结果还表明,TTI地层中,存在临界井斜角和临界各向异性角,在这两个临界角的两侧,随钻电磁波测井响应随井斜角与各向异性角的变化规律相反;此外,在界面处的“犄角”不仅与井斜、电阻率对比度等因素有关,还与各向异性角和各向异性方位有关。图13表3参15

关键词: 随钻电磁波测井; VTI介质; TTI介质; 各向异性角; 各向异性方位; 并矢格林函数
中图分类号:P631.4 文献标志码:A 文章编号:1000-0747(2019)04-0675-09
Logging while drilling electromagnetic wave responses in inclined bedding formation
FAN Yiren1,2,3,4, HU Xufei5, DENG Shaogui1,2,3,4, YUAN Xiyong1,2,3,4, LI Haitao1,2,3,4
1. School of Geosciences, China University of Petroleum, Qingdao 266580, China
2. Key Laboratory of Deep Oil & Gas Geology and Exploration, Ministry of Education, China University of Petroleum, Qingdao 266580, China;
3. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
4. CNPC Key Laboratory for Well Logging, China University of Petroleum, Qingdao 266580, China
5. China University of Petroleum-Beijing at Karamay, Karamay 834000, China
Abstract

For real-time inversion and fast reconstruction of formation true resistivity, the forward modeling of electromagnetic wave logging while drilling is usually based on the transversely isotropic formation model with vertical symmetry axis (VTI medium), but it only considers the horizontal and vertical resistivity. It has certain limitation during practical application. This paper presents a forward calculation method of electromagnetic wave logging while drilling in transversely isotropic (TTI) strata with inclined symmetry axis based on the Dyadic Green's function. Anisotropic angle and azimuth are used to characterize TTI formation. The proposed algorithm is verified by numerical examples, the half-space electromagnetic wave reflection and transmission characteristics with different media are analyzed, and the necessity to use the new algorithm is pointed out. Numerical simulation also shows that there exist a critical borehole dip and critical anisotropic angle in TTI formation. Electromagnetic wave logging while drilling responses follows opposite rule before and after these two critical angles. Besides, the “horns” at the interface are not only related to well deviation, resistivity contrast, but also related to anisotropic angle and anisotropic azimuth.

Keyword: electromagnetic wave logging while drilling; VTI medium; TTI medium; anisotropic dip; anisotropic azimuth; Dyadic Green's function
1 问题提出

随钻电磁波电阻率测井数据能够用于流体识别和流体饱和度计算等储集层评价研究。为了实现快速反演, 实时获取地层的真实地层参数, 通常需要将复杂井眼和地层环境（三维问题）简化为一系列一维（1D）地层模型[1, 2, 3, 4, 5], 这种方法在随钻测井中是可行的, 原因主要有两点：①随钻测井过程中, 井眼及钻井液侵入影响较小, 可以忽略; ②测井尺度下, 复杂的井眼轨迹可通过逐步开窗的方式进行约束, 简化为一系列形状单一的井眼轨迹（即一系列1D地层模型）。传统的1D快速随钻电磁波数值模拟主要基于含垂直对称轴的横向各向同性（VTI）地层模型。低能沉积环境条件下, 如深海和深湖中沉积形成的地层, 可呈现出标准的VTI介质特征（见图1a）, VTI介质属于单轴各向异性介质的特例, 表现为任意水平方向上, 介质具有相同电阻率Rh; 垂直方向上, 介质具有不同的电阻率Rv, 一般情况下Rh≤ Rv。该类介质的电磁场计算研究较为深入, 可通过引入赫兹位函数, 将电磁场波动方程简化为两个互相不耦合的标量波动方程, 最终得到的电磁场表达式为含0阶和1阶Bessel函数的一重积分[5, 6, 7]。

图1 不同沉积环境下的地层特征

随着石油勘探开发的不断深入, 各种复杂地层情况下的油气藏成为研究重点, 这使得VTI地层模型应用受到一定限制, 并非所有的地层都能简化为VTI模型。高能沉积环境（河流和沙漠环境）条件下形成的地层, 常见倾斜层理（见图1b）, 此时的地层为含倾斜对称轴的横向各向同性（TTI）地层, 具体表现为：沿层理方向电阻率相同, 垂直层理方向的电阻率不同, 如果仍然将其简化为VTI地层模型, 则反演得到的电阻率等参数就不再可靠, 若将其用于定性评价和定量计算, 则解释的符合率会下降。明确TTI介质条件下的电磁波类测井响应特征, 能够更加全面有效地进行测井定性及定量评价。

基于TTI介质的电磁场理论和计算均较复杂, 目前国内在这方面未见相关文献, 斯伦贝谢Anderson等人[8, 9]简单讨论了由倾斜层理引起的地层各向异性的感应测井响应特征; Wang等人[10, 11, 12]给出了倾斜层理引起的地层各向异性的多分量感应测井正反演数值模拟算法, 并讨论分析了不同的倾斜层理情况下多分量感应测井的响应特征。Anderson和Wang等人均指出[8, 9, 10, 11, 12], 倾斜层理对测井响应特征的影响不容忽视, 尤其在实际资料运用中, 要考虑实际地层条件, 建立合适的地层模型。笔者首先从矢量格林函数出发, 采用各向异性角和各向异性方位表征含倾斜层理TTI介质的各向异性特性, 推导出TTI介质的电磁场求解方法; 然后采用数值模拟方法, 以半空间介质为例, 分析VTI介质和TTI介质的电磁波反射和透射特征, 指出了传统的赫兹位函数方法以及广义反射系数等方法的局限性, 并验证了算法的可靠性, 得到不同井斜、各向异性角和各向异性方位情况下的随钻电磁波响应特征。

2 TTI地层正演数值模拟
2.1 基于并矢格林函数的各向异性介质电磁场

无限厚各向异性介质中, 电场的波动方程可以表示为：

$\nabla \times \nabla \times E\left( r-{r}' \right)-\operatorname{i}\omega \mu {{\mathrm{\vec{ }\!\!\sigma\!\!\text{ }}}_{c}}E\left( r-{r}' \right)=-\nabla \times M$ （1）

VTI介质中, 各向异性地层的电导率张量可表示为：

${{\mathrm{\vec{ }\!\!\sigma\!\!\text{ }}}_{\mathsf{c}}}=\left( \begin{matrix}{{\sigma }_{h}} & 0 & 0 \\ 0 & {{\sigma }_{h}} & 0 \\ 0 & 0 & {{\sigma }_{v}} \\ \end{matrix} \right)$ （2）

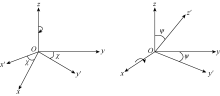
TTI介质中, 可定义各向异性角Ψ 和各向异性方位χ 表征其各向异性特性（见图2）, 则TTI介质中电导率张量${{\mathrm{\vec{ }\!\!\sigma\!\!\text{ }}}_{\mathsf{b}}}$可表述为：

${{\mathsf{\vec{\sigma }}}_{\mathrm{b}}}=\mathrm{\vec{R}}_{\mathrm{ }\!\!\chi\!\!\text{ }}^{T}\mathrm{\vec{R}}_{\mathrm{ }\!\!\psi\!\!\text{ }}^{T}{{\mathrm{\vec{ }\!\!\sigma\!\!\text{ }}}_{\mathrm{c}}}{{\mathrm{\vec{R}}}_{\mathrm{ }\!\!\psi\!\!\text{ }}}{{\mathrm{\vec{R}}}_{\mathrm{ }\!\!\chi\!\!\text{ }}}$ （3）

${{\mathrm{\vec{R}}}_{\mathrm{ }\!\!\psi\!\!\text{ }}}=\left( \begin{matrix} \cos \psi & 0 & \sin \psi \\ 0 & 1 & 0 \\ -\sin \psi & 0 & \cos \psi \\ \end{matrix} \right)$, ${{\mathrm{\vec{R}}}_{\mathrm{ }\!\!\chi\!\!\text{ }}}=\left( \begin{matrix} \cos \chi & \sin \chi & 0 \\ -\sin \chi & \cos \chi & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right)$

图2 单轴各向异性地层电导率张量旋转示意图

利用傅里叶变换, 空间域电场表达式为：

$\mathrm{E}\left( \mathrm{r}-\mathrm{{r}'} \right)=\frac{1}{{{\left( 2\text{ }\!\!\pi\!\!\text{ } \right)}^{3}}}\iiint{\mathrm{\tilde{E}}\left( {{k}_{x}}, {{k}_{y}}, {{k}_{z}} \right){{\text{e}}^{i\mathrm{k}\cdot \left( \mathrm{r}-\mathrm{{r}'} \right)}}\text{d}{{k}_{x}}\text{d}{{k}_{y}}\text{d}{{k}_{z}}}$（4）

（4）式可进一步改写为：

$\mathrm{E}\left( \mathrm{r}-\mathrm{{r}'} \right)=\frac{1}{{{\left( 2\text{ }\!\!\pi\!\!\text{ } \right)}^{3}}}\iiint{{{\mathrm{W}}^{-1}}\cdot \nabla \times \mathrm{M}{{\text{e}}^{i\mathrm{k}\cdot \left( \mathrm{r}-\mathrm{{r}'} \right)}}\text{d}{{k}_{x}}\text{d}{{k}_{y}}\text{d}{{k}_{z}}}$（5）

其中 $\mathrm{W}=\mathrm{k}\cdot \mathrm{k}+i\omega \mu {{\mathsf{\vec{\sigma }}}_{\mathrm{c}}}$

$\mathrm{k}=\left( \begin{matrix} 0 & -{{k}_{z}} & {{k}_{y}} \\ {{k}_{z}} & 0 & -{{k}_{x}} \\ -{{k}_{y}} & {{k}_{x}} & 0 \\ \end{matrix} \right)$

${{\mathrm{W}}^{-1}}=\frac{adj\left( \mathrm{W} \right)}{\left| \mathrm{W} \right|}$

行列式|W|是如下关于kz的一个4阶多项式：

$\left| \mathrm{W} \right|=ak_{z}^{4}+bk_{z}^{3}+ck_{z}^{2}+d{{k}_{z}}+e$ （6）

式中a, b, c, d, e为关于kx, ky的表达式, 进一步可表示为：

$\left| \mathrm{W} \right|=a\left( {{k}_{z}}-k_{z, \text{I}}^{+} \right)\left( {{k}_{z}}-k_{z, \text{I}}^{-} \right)\left( {{k}_{z}}-k_{z, \text{II}}^{+} \right)\left( {{k}_{z}}-k_{z, \text{II}}^{-} \right)$ （7）

当|W|=0时, kz存在4个解, 表示两种类型的波, $k_{z, \text{I}}^{+}$和$k_{z, \text{II}}^{+}$为Ⅰ 型波和Ⅱ 型波向上的z方向的波数, $k_{z, \text{I}}^{-}$和$k_{z, \text{II}}^{-}$为Ⅰ 型波和Ⅱ 型波向下的z方向的波数[13, 14]。

将（7）式代入（5）式得：

$\begin{align} & \mathrm{E}\left( R \right)=\frac{1}{{{\left( 2\text{ }\!\!\pi\!\!\text{ } \right)}^{3}}}\iiint{\frac{1}{a\left( {{k}_{z}}-k_{z, \text{I}}^{+} \right)\left( {{k}_{z}}-k_{z, \text{I}}^{-} \right)}}\times \\ & \ \ \ \ \ \ \ \ \ \ \ \frac{adj\left( W \right)}{\left( {{k}_{z}}-k_{z, \text{II}}^{+} \right)\left( {{k}_{z}}-k_{z, \text{II}}^{-} \right)}\cdot \nabla \times \mathrm{M}{{\text{e}}^{ik\cdot \left( r-{r}' \right)}}\text{d}k \\ \end{align}$ （8）

式中 R=r-r° , dk=dkxdkydkz。

利用留数定理, 当接收线圈位置z在源位置z° 的上方时, 则电场E(R)为：

$\mathrm{E}\left( R \right)=\frac{i}{{{\left( 2\text{ }\!\!\pi\!\!\text{ } \right)}^{2}}}\iint{\left[ \mathrm{W}\left( k_{z, \text{I}}^{+} \right){{\text{e}}^{ik_{z, \text{I}}^{+}\left( z-{z}' \right)}}+\mathrm{W}\left( k_{z, II}^{+} \right){{\text{e}}^{ik_{z, \text{II}}^{+}\left( z-{z}' \right)}} \right]}\cdot \nabla \times \mathrm{M}{{\text{e}}^{i{{\mathrm{k}}_{\mathrm{s}}}\cdot {{\mathrm{r}}_{s}}}}\text{d}{{\mathrm{k}}_{\mathrm{s}}}$ （9）

其中：

${{\mathrm{r}}_{\mathrm{s}}}=\left( x-{x}' \right)\hat{x}+\left( y-{y}' \right)\hat{y}$

${{\mathrm{k}}_{\mathrm{s}}}={{k}_{x}}\hat{x}+{{k}_{y}}\hat{y}$

$\text{d}{{\mathrm{k}}_{\mathrm{s}}}=\text{d}{{k}_{x}}\text{d}{{k}_{y}}$

$\mathrm{W}\left( k_{z, \text{I}}^{+} \right)={{\left. \frac{adj\left[ \mathrm{W}\left( k_{z, \text{I}}^{+} \right) \right]}{a\left( {{k}_{z}}-k_{z, \text{I}}^{-} \right)\left( {{k}_{z}}-k_{z, \text{II}}^{+} \right)\left( {{k}_{z}}-k_{z, \text{II}}^{-} \right)} \right|}_{{{k}_{z}}=k_{z, \text{I}}^{+}}}$

$\mathrm{W}\left( k_{z, \text{II}}^{+} \right)={{\left. \frac{adj\left[ \mathrm{W}\left( k_{z, \text{II}}^{+} \right) \right]}{a\left( {{k}_{z}}-k_{z, \text{I}}^{-} \right)\left( {{k}_{z}}-k_{z, \text{I}}^{+} \right)\left( {{k}_{z}}-k_{z, \text{II}}^{-} \right)} \right|}_{{{k}_{z}}=k_{z, \text{II}}^{+}}}$

当接收线圈位置z在源位置z'的下方时, 电场E(R)为：

$\mathrm{E}\left( R \right)=\frac{i}{{{\left( 2\text{ }\!\!\pi\!\!\text{ } \right)}^{2}}}\iint{\left[ \mathrm{W}\left( k_{z, \text{I}}^{-} \right){{\text{e}}^{ik_{z, \text{I}}^{-}\left( z-{z}' \right)}}+\mathrm{W}\left( k_{z, \text{II}}^{-} \right){{\text{e}}^{ik_{z, \text{II}}^{-}\left( z-{z}' \right)}} \right]}\cdot \nabla \times \mathrm{M}{{\text{e}}^{i{{\mathrm{k}}_{\mathrm{s}}}\cdot {{\mathrm{r}}_{s}}}}\text{d}{{\mathrm{k}}_{\mathrm{s}}}$ （10）

其中：

$\mathrm{W}\left( k_{z, \text{I}}^{-} \right)={{\left. \frac{adj\left[ \mathrm{W}\left( k_{z, \text{I}}^{-} \right) \right]}{a\left( {{k}_{z}}-k_{z, \text{I}}^{+} \right)\left( {{k}_{z}}-k_{z, \text{II}}^{+} \right)\left( {{k}_{z}}-k_{z, \text{II}}^{-} \right)} \right|}_{{{k}_{z}}=k_{z, \text{I}}^{-}}}$

$\mathrm{W}\left( k_{z, \text{II}}^{-} \right)={{\left. \frac{adj\left[ \mathrm{W}\left( k_{z, II}^{-} \right) \right]}{a\left( {{k}_{z}}-k_{z, \text{I}}^{-} \right)\left( {{k}_{z}}-k_{z, \text{I}}^{+} \right)\left( {{k}_{z}}-k_{z, \text{II}}^{+} \right)} \right|}_{{{k}_{z}}=k_{z, \text{II}}^{-}}}$

N层介质中, 设信号源在第S层, 接收线圈在第L层, 接收线圈位置电场为：

$~\mathrm{E}\left( R \right)={{\delta }_{LS}}{{\mathrm{E}}_{\mathrm{d}}}\left( R \right)+{{\mathrm{E}}_{\mathrm{s}}}\left( R \right)$ （11）

δ LS为Kronecker delta函数, 当L=S时, δ LS=1; 当L≠ S时, δ LS=0; Ed（R）为直达场, Es（R）为散射场（包括反射和透射场）。因此, 只要推导出直达场和散射场, 就可以得到各层介质中的电场。相应的磁场分量可以通过如下表达式, 由电场分量获取：

$\mathrm{H}=\frac{1}{-i\omega \mu }\nabla \times \mathrm{E}$ （12）

多层TTI介质中的电磁场推导可参考Wang等人文献[10, 11, 12], 限于篇幅, 本文不再详述。

2.2 传统随钻电磁波电阻率测井原理

基于上节推导可得到TTI介质中接收线圈处的电磁场, 进而计算得到接收线圈的电动势。以传统随钻电磁波测井的单发双收线圈结构为例, 设两个接收线圈处的电动势分别为V1和V2, 则幅度比EATT和相位差∆ ϕ 定义如下：

$EATT=20\lg \frac{|{{V}_{2}}|}{|{{V}_{1}}|}$ （13）

$\Delta \phi \text{=}{{\phi }_{1}}-{{\phi }_{2}}$ （14）

利用相位差和幅度比的刻度图版即可将相位差和幅度比转换为幅度比电阻率Rad和相位差电阻率Rps。

3 算法验证及半空间反射和透射分析

首先利用相位差和幅度比电阻率的刻度图版来验证算法的正确性, 图3为传统随钻电磁波频率为2 MHz、发射线圈到仪器记录点距离为40.64 cm（16英寸）的相位差电阻率和幅度比电阻率刻度图版, 可见基于并矢格林函数的解析方法得到的计算结果与传统的利用Hertz位函数的解析方法得到的计算结果完全吻合。其次, 采用两个5层地层模型进行验证（井斜分别为0和30° , 层厚均为2.0 m, 电阻率参数见表1）, 如图4a和4b所示, 可以看到, 本文提出的算法在多层介质中同样适用。

图3 幅度比和相位差刻度图版验证

表1 两个5层地层模型的电阻率参数

图4 5层地层模型算法验证（模型1和模型2）

为研究不同介质界面处的电磁波反射和透射特征, 笔者给出半空间的反射和透射系数。图5为不同情况下的半空间介质模型, 表2为对应不同半空间介质模型下的参数。σ 1u和σ 2u表示上层电导率, σ 1d和σ 2d表示下层电导率。上层地层如为各向同性地层, 则σ 1u=σ 2u; 如为各向异性地层, 则σ 1u≠ σ 2u, 下层地层类似。

图5 不同半空间介质模型

表2 不同半空间介质模型地层参数

各向同性地层和VTI地层中, Ψ =0, χ =0; TTI地层中, Ψ ≠ 0, 限于篇幅, 设定χ 等于0（当χ ≠ 0时, 反射和透射情况相同, 此处不再详述）。图6为对应不同模型界面处的Fresnel反射和透射系数随入射角的变化情况。Ri, j和Ti, j分别表示Fresnel反射和透射系数, i和j为电磁波类型（Ⅰ 型或Ⅱ 型波）。从图6a到图6c可以看到, 当界面两侧的介质为各向同性或VTI介质时, 即Ψ =0, χ =0的情况下, RⅠ , Ⅱ =RⅡ , Ⅰ =TⅠ , Ⅱ =TⅡ , Ⅰ =0, 仅存在RⅠ , Ⅰ , RⅡ , Ⅱ , TⅠ , Ⅰ 和TⅡ , Ⅱ , 说明不存在交叉反射波和透射波, 即当入射波为Ⅰ 型时, 会产生反射Ⅰ 型和透射Ⅰ 型波; 当入射波为Ⅱ 型时, 情况类似。因此, 界面两侧为各向同性或VTI介质时, Ⅰ 型波和Ⅱ 型波在界面处的反射和透射不耦合, 可以分别考虑及单独计算Ⅰ 型波和Ⅱ 型波（也称为TE波即横电波和TM波即横磁波）的电磁场, 这就是传统基于VTI介质计算TE波和TM波电磁场的理论基础。从图6d到6f可以看出, 当界面一侧存在TTI地层时, 各个交叉分量（RⅠ , Ⅱ , RⅡ , Ⅰ , TⅠ , Ⅱ , TⅡ , Ⅰ ）均不再为0, 说明经过反射和透射后, Ⅰ 型波和Ⅱ 型波耦合, 其电磁场为两种类型波的耦合场, 此时传统基于VTI介质的电磁场计算方法已不再适用, 可以用本文提出的基于并矢格林函数的方法进行计算。

图6 不同半空间介质界面处的Fresnel系数

4 数值算例

设各向异性地层为无限厚, 一个方向的电阻率R1=2.0 Ω · m, 另一个方向的电阻率R2=20.0 Ω · m, 以传统随钻电磁波频率为2 MHz、发射线圈到仪器记录点距离为40.64 cm（16英寸）的相位差为例, 分析其受各向异性角和各向异性方位影响。图7为传统随钻电磁波相位差随井斜角θ 的变化情况, 当ψ =0时, 相位差随井斜角θ 增大呈单调递减趋势, 各向异性方位χ 对相位差随井斜角θ 的变化没有影响; 当ψ ≠ 0时, 如果χ =0, 则存在一个临界井斜角θ c=90-ψ , 即当ψ 分别为30° 、45° 和60° 时, θ c分别为60° 、45° 和30° （见图7a）。当井斜角θ ≤ θ c时, 随着井斜角的增大, 相位差递减; 当θ > θ c时, 随着井斜角的增大, 相位差增大。如果χ ≠ 0, 仍存在临界井斜角θ c, 规律与图7a所示相同（见图7b）, 但θ c≠ 90-ψ 。

图7 相位差随井斜角θ 的变化

图8为传统随钻电磁波相位差随各向异性角ψ 的变化。首先可以看到, 当θ =0时, 相位差随ψ 增大呈单调递减趋势, χ 对相位差随ψ 的变化没有影响; 当θ ≠ 0, 若χ =0, 则存在一个临界各向异性角ψ c=90-θ , 即当θ 分别为30° 、45° 和60° 时, ψ c分别为60° 、45° 和30° （见图8a）, 当ψ ≤ ψ c时, 随着各向异性角的增大, 相位差递减; 当ψ > ψ c时, 随着各向异性角的增大, 相位差增大。如果χ ≠ 0, 仍存在临界各向异性角ψ c（见图8b）, 变化规律与图8a所示相同, 但ψ c≠ 90-θ 。

图8 相位差随各向异性角ψ 的变化

值得注意的是, 通常认为, 随钻电磁波在界面处产生的“ 犄角” 主要由井斜和电阻率对比度等因素造成（本质为界面两侧的电场不连续[15]）, 但实际上各向异性角和各向异性方位也是影响“ 犄角” 产生的重要因素。图9a为两层地层模型及其参数, 上部地层设为各向同性地层（χ 0=0, ψ 0=0）, 下部为单轴各向异性地层。

图9 两层介质、不同井斜角传统随钻电磁波测井响应（ψ 1=0, χ 1=0）

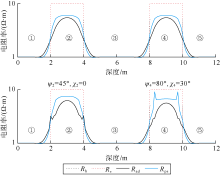
首先设下部地层的各向异性方位角χ 1=0, 考察下部地层不同ψ 1和θ 情况下, 传统随钻电磁波测井在界面处的响应。当下部地层为VTI地层, 即ψ 1=0和χ 1=0（见图9b和图9c）, 可见随着井斜角的增大, 下部地层幅度比电阻率Rad和相位差电阻率Rps均增大, 且当井斜角θ 小于60° 时, 界面处不会产生犄角; 当下部为TTI地层, 设各向异性角ψ 1=30° 时（见图10a和10b）, 当θ 分别为30° 、45° 和60° 时, 与图9b和9c相比, 下层的Rad和Rps电阻率幅度发生明显变化, 此外, Rad在界面处产生明显“ 犄角” ; 当θ =60° 时, Rps在界面处产生明显犄角。因此, 与VTI地层相比, 相同井斜角情况下, 各向异性角的存在可能会使随钻电磁波测井在界面处产生“ 犄角” 。

图10 两层介质、不同井斜角传统随钻电磁波测井响应（ψ 1=30° , χ 1=0）

基于图9a的两层地层模型及参数, 考查下部地层不同各向异性方位角χ 1≠ 0时传统随钻电磁波测井响应在界面处的响应。由图11中可以看到, Rad和Rps在界面处的“ 犄角” 幅度会受各向异性方位的变化而变化, 因此各向异性方位也是影响“ 犄角” 产生的原因之一。

图11 不同各向异性方位χ 情况下传统随钻电磁波测井响应（θ =30° , ψ 1=30° ）

图12为两个模拟实例, 均为5层地层, 井斜为45° , 具体地层参数见表3。其中图12a中各层不存在倾斜层理, 图12b中第2和第4层均存在倾斜层理, 但其各向异性角和各向异性方位不同。图13为发射频率2.0 MHz、发射线圈到仪器记录点距离为40.64 cm（16 in）的传统随钻电磁波测井响应。由图13可见, 尽管两个地层模型的电阻率参数相同, 但其各向异性的特性不同, 随钻电磁波测井幅值及其在界面处的响应特征均会发生变化, 因此, 如果将地层始终简化为VTI地层而不考虑其内部层理变化, 则无论其测井响应还是反演得到的地层真电阻率均不能表征真正的地层电性特征。

图12 5层地层模型实例

表3 两个5层地层模型的地层参数

图13 5层地层模型传统随钻电磁波测井响应特征（分别含VTI地层和含TTI地层）

5 结论

为满足快速电阻率反演需求, 传统随钻电磁波测井正演主要基于VTI地层模型, 但实际地层更加复杂, VTI地层仅仅是各向异性地层的一个特例, 笔者从并矢格林函数出发, 详细推导了一套多层TTI地层的随钻电磁波测井正演计算方法。基于数值算例对算法进行了验证, 结果表明笔者提出的算法不仅适用于VTI地层, 也适用于TTI地层, 具有较强的普适性。

通过半空间电磁波反射和透射特征数值模拟, 可以得到当界面两侧为各向同性或者VTI地层时, 两种类型的电磁波（Ⅰ 型波和Ⅱ 型波）产生的电磁场不耦合, 随钻电磁波的正演数值模拟可采用传统的赫兹位函数方法; 当界面的某侧为TTI地层时, 两种类型的电磁波（Ⅰ 型波和Ⅱ 型波）产生的电磁场会耦合, 随钻电磁波的正演数值模拟可采用本文算法。

各向异性角ψ 和各向异性方位χ 对传统随钻电磁波测井的响应不容忽视。TTI地层中, 存在临界井斜角θ c和临界各向异性角ψ c, 当θ ≤ θ c时, 随着井斜角的增大, 相位差递减; 当θ > θ c时, 随着井斜角的增大, 相位差增大; 当ψ ≤ ψ c时, 随着各向异性角的增大, 相位差递减; 当ψ > ψ c时, 随着各向异性角的增大, 相位差增大。此外, 当χ =0时, θ c=90-ψ , ψ c=90-θ 。

随钻电磁波在界面处产生的“ 犄角” , 不仅与井斜、电阻率对比度等因素有关, 而且也受各向异性角和各向异性方位的影响, 如含倾斜层理地层中, 在低井斜角情况下, 也有可能产生“ 犄角” 。

符号注释：

E— — 电场, V/m; Ed（R）— — 直达场, V; Es（R）— — 散射场, V; $\mathrm{\tilde{E}}\left( {{k}_{x}}, {{k}_{y}}, {{k}_{z}} \right)$— — 电磁场波数域表达式; EATT— — 幅度比, dB; f— — 频率, Hz; H— — 磁场, A/m; i, j— — 电磁波类型（Ⅰ 型波和Ⅱ 型波）; k— — 波数, 无因次; kx— — x方向波数, rad/m; ky— — y方向波数, rad/m; kz— — z方向波数, rad/m; $k_{z, \text{I}}^{+}$和$k_{z, \text{II}}^{+}$— — Ⅰ 型波和Ⅱ 型波向上的z方向的波数, rad/m; $k_{z, \text{I}}^{-}$和$k_{z, \text{II}}^{-}$— — Ⅰ 型波和Ⅱ 型波向下的z方向的波数, rad/m; M— — 磁流源, A· m2; M0— — 磁流源强度, A· m2; r— — 接收位置（x, y, z）, m; r° — — 源位置（x° , y° , z° ）, m; Rad— — 幅度比电阻率, Ω · m; Rh— — 水平电阻率, Ω · m; Ri, j— — Fresnel反射系数; Rps— — 相位差电阻率, Ω · m; Rv— — 垂直电阻率, Ω · m; ${{\mathrm{\vec{R}}}_{\mathrm{ }\!\!\psi\!\!\text{ }}}$— — 各向异性角旋转矩阵, （° ）; ${{\mathrm{\vec{R}}}_{\mathrm{ }\!\!\chi\!\!\text{ }}}$— — 各向异性方位旋转矩阵, （° ）; Ti, j— — Fresnel透射系数; V1和V2— — 两个接收线圈的感应电动势, V; |V1|和|V2|— — 感应电动势V1和V2的幅度值, V; μ — — 自由空间的磁导率, H/m; ω — — 角频率, rad/s; σ h— — 水平电导率, S/m; σ ν — — 垂直电导率, S/m; Ψ — — 各向异性角, （° ）; χ — — 各向异性方位, （° ）; ${{\mathrm{\vec{ }\!\!\sigma\!\!\text{ }}}_{\mathsf{c}}}$— — VTI介质中的电导率张量, S/m; ${{\mathrm{\vec{ }\!\!\sigma\!\!\text{ }}}_{\mathsf{b}}}$— — TTI介质中的电导率张量, S/m; δ LS— — Kronecker delta函数, 当L=S时, δ LS=1, 当L≠ S时, δ LS=0; ∆ ϕ — — 相位差, （° ）; ϕ 1, ϕ 2— — 感应电动势V1和V2的相位角, （° ）; θ — — 井斜角, （° ）; θ c— — 临界井斜角, （° ）; ψ c— — 临界各向异性角, （° ）; σ 1u, σ 2u— — 两层地层模型中的上部地层两个方向的电导率, S/m; σ 1d, σ 2d— — 两层地层模型中的下部地层两个方向的电导率, S/m; — — 哈密顿算子。

参考文献
[1] 王磊, 范宜仁, 袁超, 等. 随钻方位电磁波测井反演模型选取及适用性[J]. 石油勘探与开发, 2018, 45(5): 914-922.
WANG Lei, FAN Yiren, YUAN Chao, et al. Selection criteria and feasibility of the inversion model for azimuthal electromagnetic logging while drilling (LWD)[J]. Petroleum Exploration and Development, 2018, 45(5): 914-922. [本文引用:1]
[2] 胡旭飞, 范宜仁, 吴非, 等. 随钻方位电磁波测井多参数快速反演[J]. 地球物理学报, 2018, 61(11): 4690-4701.
HU Xufei, FAN Yiren, WU Fei, et al. Fast multiple parameter inversion of azimuthal LWD electromagnetic measurement[J]. Chinese Journal of Geophysics, 2018, 61(11): 4690-4701. [本文引用:1]
[3] HU Xufei, FAN Yiren. Huber inversion for logging-while-drilling resistivity measurements in high angle and horizontal wells[J]. Geophysics, 2018, 83(4): D113-D125. [本文引用:1]
[4] PARDO D, TORRES-VERDÍN C. Fast 1D inversion of logging- while-drilling resistivity measurements for improved estimation of formation resistivity in high-angle and horizontal wells[J]. Geophysics, 2015, 80(2): E111-E124. [本文引用:1]
[5] PARDO D, TORRES-VERDÍN C, ALI B S. Fast and automatic inversion of LWD resistivity measurements for petrophysical interpretation[R]. Long Beach, California, USA: SPWLA 56th Annual Logging Symposium, 2015. [本文引用:2]
[6] ZHONG Lili, LI Jing, BHARDWAJ A, et al. Computation of triaxial induction logging tools in layered anisotropic dipping formations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(4): 1148-1163. [本文引用:1]
[7] 肖加奇, 张庚骥. 水平井和大斜度井中的感应测井响应计算[J]. 地球物理学报, 1995, 38(3): 396-404.
XIAO Jiaqi, ZHANG Gengji. Computation of induction logging responses in horizontal and highly deviated wells[J]. Chinese Journal of Geophysics, 1995, 38(3): 396-404. [本文引用:1]
[8] ANDERSON B, BARBER T, GIANZERO S. The effects of crossbeding ansisotropy on induction tool response[J]. Perophysics, 1998, 42(2): 137-149. [本文引用:2]
[9] ANDERSON B, BARBER T, GIANZERO S. The effect of crossbedding anisotropy on induction tool response[R]. Keystone, Colorado, USA: SPWLA Thirty-ninth Annual Logging Symposium, 1998. [本文引用:2]
[10] WANG Gongli, BARBER T, WU P, et al. A new model for understand ing triaxial induction response in dipping crossbedded formations[R]. Long Beach, California, USA: SPWLA 56th Annual Logging Symposium, 2015. [本文引用:3]
[11] WANG Gongli, BARBER T, WU P, et al. Triaxial induction tool response in dipping and crossbedded formations[R]. Denver: SEG Annual Meeting, 2014. [本文引用:3]
[12] WANG Gongli, BARBER T, WU P, et al. Fast inversion of triaxial induction data in dipping crossbedded formations[J]. Geophysics, 2017, 82(2): D31-D45. [本文引用:3]
[13] EROGLU A, LEE Y, LEE J. Dyadic Green’s functions for multi-layered uniaxially anisotropic media with arbitrarily oriented optic axes[J]. IET Microwaves, Antennas Progpag, 2011, 5(15): 1779-1788. [本文引用:1]
[14] EROGLU A. Wave propagation and radiation in gyrotropic and anisotropic media[M]. Berlin: Springer, 2010. [本文引用:1]
[15] 杨震, 刘庆成, 岳步江, 等. 随钻电磁波测井中极化角的形成机理及其影响因素模拟分析[J]. 测井技术, 2010, 34(3): 210-214.
YANG Zhen, LIU Qingcheng, YUE Bujiang, et al. On mechanism of polarization angle of electromagnetic logging while drilling and its influence factors simulation[J]. Well Logging Technology, 2010, 34(3): 210-214. [本文引用:1]