第一作者简介:胡永建(1970-),男,河南商水人,硕士,中国石油集团工程技术研究院高级工程师,主要从事石油钻井井下仪器及通讯设备研制。地址:北京市昌平区能源南街9号院,邮政编码:102206。Email: huyongjian32788@163.com
钻井液脉冲信号是非稳定信号,用小波强制去噪算法完成信号去噪,包括基线漂移修正、帧同步与指令信号的2级去噪处理。通过区分不同特征的信号脉冲,2级去噪处理能够减少基线漂移的影响,同时便于确定信号识别的自动峰值检测阈值量程。在信号识别算法中定义了上、下沿相对突出度阈值用于峰值检测,该算法参数能充分利用信号峰的变化程度,同时满足灵活的上、下沿阈值组合处理。使用帧同步脉冲确定第1个指令脉冲的位置,依次将指令脉冲作为位同步脉冲对后续指令脉冲解码,该同步解码方法可以减少帧同步脉冲位置不确定性带来的影响,并消除时基漂移的误差累积。编制了专用工具软件完成算法的参数整定,对于通用编码信号解码成功率约为95%;对于增加了校验字节的编码信号,使用自动阈值调节算法后的解码成功率高达99%。
Wavelet forced de-noising algorithm is suitable for denoising of unsteady drilling fluid pulse signal, including baseline drift rectification and two-stage de-noising processing of frame synchronization signal and instruction signal. Two-stage de-noising processing can reduce the impact of baseline drift and determine automatic peak detection threshold range for signal recognition by distinguishing different features of frame synchronization pulse and instruction pulse. Rising and falling edge relative protruding threshold is defined for peak detection in signal recognition, which can make full use of the degree of the signal peak change and detect peaks flexibly with rising and falling edge relative protruding threshold combination. A synchronous decoding method was designed to reduce position uncertainty of the frame synchronization pulse and eliminate the accumulative error of time base drift, which determines the first instruction pulse position according to position of the frame synchronization pulse and decodes subsequent instruction pulse by taking current instruction pulse as new bit synchronization pulse. Special tool software was developed to tune algorithm parameters, which has a decoding success rate of about 95% for the universal coded signals. For the special coded signals with check byte, decoding success rate using the automatic threshold adjustment algorithm is as high as 99%.
钻井液脉冲信号遥测系统在井下控制工程中用于上传信息[1]。与微波、振动[2, 3]等新技术相比, 钻井液脉冲是占据优势的井下数据传输技术。NOV公司随钻测量系统BlackStar Ⅱ 同时配备了电磁波和钻井液脉冲, 互为补充和备份[4]。中国石油集团工程技术研究院研制的高频磁耦合有缆钻杆(信息钻杆)也使用钻井液脉冲作为备份信道。
钻井液脉冲在传输时受到泥浆泵、空气包、地面管汇、立管压力传感器位置、钻柱串尺寸、井深、钻井液特性等因素的影响[5]。噪声源包括钻进时产生的噪声、钻具在井眼内的运动噪声以及泥浆泵噪声[6]。信号检测和解码技术是钻井液脉冲技术成功应用的关键[7]。
早期的匹配滤波器算法[8]能够消除钻井液噪声的影响。由于钻井液脉冲信号与泥浆泵噪声在频域重叠, 标准滤波器算法难以胜任, 自适应滤波器算法应运而生:如使用2级滤波算法、低通滤波器获取信号的直流成分、带通滤波器滤除带外噪声[9]; 使用平均滤波算法消除直流分量实现2级滤波算法[10]; 使用最小均方判据构建自适应有限冲击响应滤波器等[8]。由于泵噪声是主要噪声来源, 利用两组立管压力传感器也可以消除泵噪声[11]。滤波器参数、门限阈值的设定影响去噪效果; 门限信号识别算法的门限大小影响解码成功率。正常情况下地面系统能够自动检测及解码, 但在钻井液相对密度大、发生气侵等特殊情况下需要人工调节参数或阈值[12], 这导致作业时间延长和施工难度增加。
傅立叶滤波算法难以揭示非稳定信号的特征, 小波变换能够展现不同尺度的信号特征, 从噪声信号中提取有用信息[13]。离散小波变换可以提高信噪比, 降低误码率[14]。连续小波变换也可用于非平稳连续脉冲信号的检测[15]。
为了实现钻井液脉冲信号的自动去噪与识别, 通过分析钻井液脉冲信号特征, 将解码过程划分为去噪与识别两个密切相关的处理阶段。设计了基于小波分析的去噪算法, 通过分析去噪后的信号特征及通用调制编码方式设计了识别算法, 利用大容量样本完成两个阶段算法的参数整定。最后使用自动阈值调节的信道编码方式进一步提高解码成功率。
钻井液脉冲遥测系统利用调制编码后的钻井液压力脉冲信号传递信息。本文研究的对象是常用的脉冲位置调制编码信号, 每条信号的开始处编码了一个较宽的帧同步脉冲用于区分每条指令, 其宽度是指令脉冲宽度的3倍, 为6个时隙, 脉冲之间有1个以上的保护时隙, 该保护时隙一方面用于为脉冲器储能电容充电, 另一方面提供脉冲恢复时间, 可以消除码间干扰。该调制编码方式具有一定典型性。
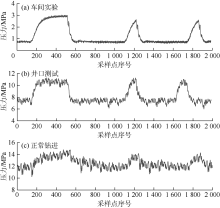
图1a是车间实验时正脉冲发生器产生的压力信号波形, 显示了一个较宽帧同步脉冲和随后两个指令脉冲, 其驱动电信号为方波, 立管压力信号的采样率为256 S/s。由于脉冲发生器主阀头运动的加减速时间和钻井液信道衰减两个方面的原因, 信号上升时间有所增加, 但依然保留了较丰富的高频成分。泥浆泵产生的1~20 Hz的噪声[11]是噪声主要来源, 图1b是某施工现场的井口测试信号, 图1c是正常施工时的信号, 可见现场信号信噪比下降、高频有效成分减少。
钻井液脉冲信号是典型的非稳定信号, 小波分析直接用双通道滤波器组处理信号, 有较好的去噪效果。一维离散小波变换的Mallat算法包含分解与重构两部分[16], 其分解算法公式如下:
$C_{j+1, k}^{{}}=\sum\limits_{m\in Z}{h(m-2k)C_{j, m}^{{}}}$ (1)
$D_{j+1, k}^{{}}=\sum\limits_{m\in Z}{g(m-2k)D_{j, m}^{{}}}$ (2)
重构算法公式如下:
$C_{j, m}^{{}}=\sum\limits_{k\in Z}{h(m-2k)C_{j+1, k}^{{}}+}\sum\limits_{k\in Z}{g(m-2k)D_{j+1, k}^{{}}}$ (3)
小波去噪效果的优劣与基函数的选择、分解层数、阈值处理方法有关。这里使用强制去噪处理, 即将小波分解结构中的高频系数全部置零后完成小波重构。
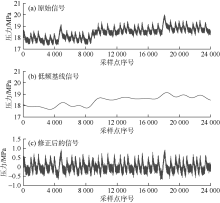
使用小波分析可以实现基线漂移修正[17]。图2a是存在基线漂移的一段钻井液脉冲信号。为了得到反映基线漂移的低频基线信号, 使用小波强制去噪算法处理原始信号, 处理过程为:①直接选用整定后的参数(小波基:离散Meyer; 分解层数:10层)去除高频部分后重构得到低频基线信号的波形(见图2b); ②将原始信号减去基线信号得到修正后的信号波形(见图2c)。可以看到在消除基线漂移的同时, 较宽的帧同步脉冲的低频有效成分也有所损失。信号的采样长度越长, 基线漂移对解码效果的影响越大。
由于帧同步脉冲宽度是指令脉冲宽度的3倍, 两种不同的脉冲在时域上有不同的尺度特征, 可以利用该特征分割指令帧信号。为此设计了2级处理的小波去噪算法:①根据帧同步脉冲宽度特征完成第1级信号去噪, 根据识别后的识别帧同步脉冲将全部脉冲信号序列分割为单个长度较短的指令脉冲序列; ②根据指令脉冲宽度特征完成第2级信号去噪并完成识别。这种2级处理去噪算法可以缩短指令脉冲序列的处理长度, 减小基线漂移的影响, 同时便于确定信号识别阶段的自动峰值检测阈值量程, 提高解码成功率。
在连续信号采集过程中, 为避免漏掉信号, 并减少耗时的解码计算次数, 每当采集到2倍信号时长的原始信号后开始解码计算。
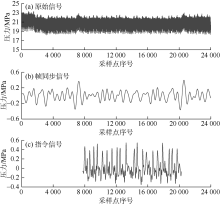
①对采样得到的2倍信号长度的信号进行小波去噪, 尝试得到帧同步信息。对图3a所示的原始信号进行基线漂移修正, 该信号包含2个帧同步脉冲, 即至少包含一条完整信号。可直接选用整定后的参数(小波基:离散Meyer; 分解层数:8层)对经过基线漂移修正的信号强制去噪获得去噪后的帧同步信号(见图3b), 可以看到, 通过合适的参数选择, 较宽的帧同步脉冲的特征得到加强。
②从原始信号中重新选择两个帧同步脉冲之间的信号进行基线漂移修正。较短的信号有更小的基线漂移, 也有一致的指令信号变化幅度。可直接选用整定后的参数(小波基:离散Meyer; 分解层数:6层)对信号强制去噪获得去噪后的信号(见图3c), 此时指令信号特征更加明显。
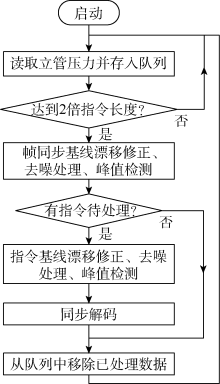
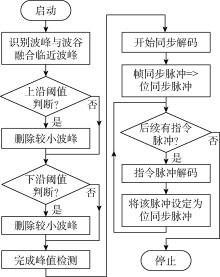
图4为信号去噪基本流程, 使用一个数据队列保存定时从立管压力传感器采集到的压力值, 当采集数据达到2倍信号长度时进行帧同步与指令信号2级去噪处理。信号去噪算法的参数清单如表1所示。
| 表1 信号去噪算法参数 |
从图2c可以看到, 即便经过了基线漂移修正, 各个脉冲的底部也不在同一高度, 这意味着以信号绝对值为门限阈值的峰值检测算法会浪费宝贵的脉冲变化幅度。另外, 帧同步脉冲与指令脉冲的上升沿和下降沿有不同的信号变化量。可以通过检测脉冲峰的上沿、下沿变化量来检测去噪后信号的峰值。
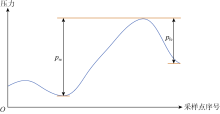
分别定义上沿突出度(pre)及下沿突出度(pfe)(见图5), pre定义为波峰顶部距左侧最近波谷的高度差, 如左侧是信号边缘且单调下降, 则为距左边缘的高度差; pfe定义为波峰顶部距右侧最近波谷的高度差, 如果右侧是信号边缘且单调下降, 则为距右边缘的高度差。
为了实现信号自动识别, 定义上沿相对突出度(pRre)及下沿相对突出度(pRfe):
${{p}_{\text{Rre}}}=\frac{{{p}_{\text{re}}}}{{{p}_{\text{range}}}}\times 100%$ (4)
${{p}_{\text{Rfe}}}=\frac{{{p}_{\text{fe}}}}{{{p}_{\text{range}}}}\times 100%$ (5)
式中突出度范围(prange)可以简单定义为去噪信号的最大值。检测过程中只保留符合条件的脉冲峰。
在给定了上沿、下沿相对突出度阈值之后, 即可以通过脉冲上沿或下沿检测峰值, 也可以同时根据上下沿检测峰值。
帧同步脉冲与后续指令脉冲之间有严格的时序关系, 理论上帧同步脉冲可以同时用于位同步解码。对图2c所示信号进行不同小波基的去噪计算, 发现对于不同基函数, 去噪后信号波峰的位置也不同。帧同步脉冲波峰位置的偏差会导致位同步不准确。此外, 生成驱动电信号的时钟与立管压力采样时钟的偏差和漂移也会导致位同步不准确。
本文使用指令脉冲作为位同步脉冲来提高解码成功率。由于指令脉冲有相似的宽度及信号特征, 其去噪后信号的波峰位置也保持同步, 可以准确地确定每一个指令脉冲的波峰位置。在后续指令脉冲的解码过程中, 只需依次使用前一个指令脉冲作为位同步脉冲, 这样当指令较长时不会因为时隙的误差积累而降低解码成功率。
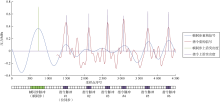
图6显示了经帧同步与指令信号2级去噪处理后的波形局部, 包含帧同步、指令信号经小波去噪的重构信号及满足上沿相对突出度阈值的峰值检测结果(帧同步:仅使用70%的上沿相对突出度阈值, 指令:仅使用50%的上沿相对突出度阈值), 显示的峰值检测结果是上沿突出度绝对值, 量程按完整指令脉冲序列的最大值确定。通过帧同步脉冲能够确定第一个指令脉冲的时隙位置, 底部的时隙位置示意图指示了脉冲位置。
信号识别的基本流程如图7所示, 信号识别算法参数清单如表2所示。对于自动峰值检测, 特别是帧同步去噪信号的自动峰值检测, 在没有钻井液脉冲信号时, prange较小, 可能导致识别出错误的帧同步脉冲, 此时需要通过关联帧同步数量、间隔等条件判断是否为噪声。
| 表2 信号识别算法参数 |
大容量样本不仅用于参数整定, 也决定了整定后算法参数的适用性。即使对于同一口井, 由于井深、钻井液密度等施工条件的不同, 对解码成功率的影响也有所不同, 如何选择合适的样本对于参数整定而言至关重要。
一口定向井的信号数据可能有成千上万条, 全部选取会导致参数整定的计算量过大而无法实现。以人工方式逐井、逐段选择样本数据, 按顺序以相同时间间隔依次抽样, 样本长度约为2倍信号长度。对于已明确的异常工况, 如开关泵、上下活动钻具等阶段的数据不予选取。最终从20余口井中选取了2 000余个样本数据。另外制备了一些无有效信号的“ 噪声” 样本用来检测信号识别算法。
现场施工仪器使用常规滤波去噪算法, 样本数据包含了现场施工仪器无法正确解码的情况, 对于全部样本数据, 现场施工仪器解码成功率约为90%。
本算法包含的10项参数均与大容量样本的解码成功率相关。参数之间亦相互影响, 是典型的多参数融合问题。编制了专用工具软件, 用步长扫描的方法划分网格来完成参数整定。
为了缩短整定时间, 通过去掉明显不适合的小波基, 使用二分法等手段来加快搜索。使用高性能工作站耗时数千小时分批完成了自动扫描工作, 选择解码成功率最高的参数值组合作为整定值(见表3)。此整定参数组合的大容量样本自动解码成功率为94.9%, 该结果适用于前文定义的钻井液脉冲信号的通用编码条件。对于无信号的“ 噪声” 样本, 算法依据有效同步头、指令最小及最大长度、有效脉冲宽度等条件来区分, 可有效识别99.5%以上的全噪声信号。
| 表3 参数整定 |
为了验证样本能否表征全部数据的特征, 使用整定参数对现场1口定向井约3 d定向阶段的全部数据完成解码, 解码成功率为96.1%。该定向段约有900个样本, 解码错误的发生并无规律。依次按每5个样本抽取1个统计, 得到的5组样本集合(每组约180个样本)的解码成功率的标准偏差约为1%, 说明抽样样本较好地反映了全部样本的特征。
如表3所示, 该算法包含10项参数, 其中小波基、分解层数等6项参数的选值是离散的; 而4项相对突出度阈值是连续变化的, 范围为0%~100%。
为研究各个参数对解码成功率的影响, 可以针对该参数的不同取值, 通过工具软件扫描得到此时的最大解码成功率, 该方法由于耗时巨大而难以实现。这里使用整定后的参数, 仅改变其中1项参数的值来计算解码成功率, 可一定程度地反映该参数的影响。
图8给出了改变帧同步小波基函数(54种)对解码成功率的影响。可见, 对于帧同步小波基函数, 最高的离散Meyer(dmey)解码成功率比位列第2的sym7要高8.1%; 对于指令小波基函数的类似计算表明, 最高依然是dmey, 比位列第2的db9要高11.3%。选择dmey小波基有明显优势。
对于基线漂移修正, 改变指令基线分解层数的计算表明:8层以下的解码成功率为0%, 随着层数增加, 在10层达到峰值94.9%, 之后逐渐回落到无基线漂移时的92.2%, 可见基线漂移修正使解码成功率提高了2.7%。帧同步基线分解层数的情况类似。
对于指令信号分解层数, 分解层数为6时解码成功率最高达94.9%, 远高于5层的49.8%和7层的37.5%, 帧同步信号分解层数的情况类似。
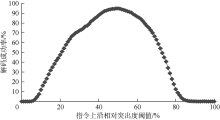
对于相对突出度阈值, 图9给出了指令上沿相对突出度阈值的影响, 曲线变化在解码成功率极值94.9%附近较为平坦。
如果仅使用指令下沿相对突出度阈值则解码成功率为61.9%, 同时使用指令上沿及下沿相对突出度阈值的解码成功率为80.2%。即单独使用上沿相对突出度阈值有更高的解码成功率, 最多可提高解码成功率33%, 定量证实了他人的试验判断结果[18]。
通过参数影响的分析可以看到:在10项算法参数中, 无论是帧同步还是指令信号处理, 小波基函数的选择以及小波分解层数都具有一定的确定性; 仅有3项相对突出度阈值的大小对解码成功率的影响较大, 但可以通过后述的自动阈值调节来解决, 从而保证了本算法整定参数的鲁棒性。
大容量样本均来自于现场施工数据, 使用常规滤波去噪算法的现场施工仪器解码成功率约为90%, 低于本算法的94.9%。由于各种算法的复杂性, 事实上难以直接做横向比较。
为了验证本算法的适应性, 对新施工5口井各提取了100个样本进行识别, 解码成功率为95.2%, 单独统计每口井的解码成功率, 得到的标准偏差约为2%, 说明适应性较好。
用专用螺杆钻具实验台做打压实验来检验算法, 与施工现场相比, 此时信号的泵噪声较小但基线漂移更剧烈。耗时8 d进行了2 300余次信号收发测试, 算法自动解码成功率为100%。
使用工具软件对大容量样本中无法解码的样本逐个调节相对突出阈值参数, 调节后能够解码的样本数量增加了, 解码成功率达到了99.3%, 这表示使用自动阈值调节算法也能达到同样的解码成功率。
通讯领域通过信道编码来减少误码。在指令编码中加入1个字节的校验和, 在解码过程中根据校验字节确定解码是否成功。如不成功则步进调节相对突出度阈值直至解码成功或达到阈值极限。自动阈值调节摆脱了对3项相对突出度阈值参数的依赖性。
信号去噪与解码过程是相互关联的整体信号处理过程, 解码成功率是具有更普遍意义的评估指标。
小波强制去噪适合钻井液脉冲去噪处理, 设计了根据脉冲宽度区分帧同步与指令脉冲的小波分析2级去噪处理算法。该算法通过识别较宽的帧同步脉冲将脉冲序列分割为较短的指令脉冲序列, 有助于减少基线漂移的影响, 同时便于确定信号识别的自动峰值检测阈值量程, 提高解码成功率。
定义了相对突出度指标用于峰值检测, 与绝对值门限判断相比, 能够充分利用波峰的变化量, 同时可以区分上、下沿, 具有去噪功能。对于指令解码, 脉冲上沿更具重要性。
不同的小波基函数会导致脉冲的波峰位置不同, 将每一个指令脉冲逐一作为位同步脉冲, 为后续指令脉冲解码, 可以减少因时钟漂移等带来的时基误差累积, 提高解码成功率。
制备了大容量样本完成参数整定, 整定参数有一定的鲁棒性。通用编码方式的自动解码成功率达到95%, 优于现场施工仪器的常规滤波算法。自动阈值调整算法的解码成功率可以达到99%。
符号注释:
Cj, k, Dj, k— — 第j层低频、高频小波系数的第k个元素; g, h— — 一维离散小波变换Mallat算法的高频、低频分解滤波器, 无因次; j— — 小波变换的分解层数; k, m— — 小波系数的元素序号; pre, pfe— — 上沿、下沿突出度, MPa; prange— — 突出度范围, MPa; pRre, pRfe— — 上沿、下沿相对突出度, %; Z— — 整数集合。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|