引用本文
曹耐, 雷刚. 致密储集层加压-卸压过程应力敏感性[J]. 石油勘探与开发, 2019,46(1): 132-138.
CAO Nai, LEI Gang. Stress sensitivity of tight reservoirs during pressure loading and unloading process[J]. Petroleum Exploration & Development, 2019,46(1): 132-138.  
Doi: 10.11698/PED.2019.01.13
Permissions
Copyright©2019, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
致密储集层加压-卸压过程应力敏感性
曹耐1, 雷刚2
1. 中国石油大学（北京）,北京102249
2. King Fahd University of Petroleum and Minerals, Dhahran 31261, Kingdom of Saudi Arabia
联系作者简介:雷刚（1987-）,男,湖北荆州人,博士,现为沙特法赫德国王石油与矿业大学博士后,主要从事非常规油气田开发方面研究。地址：King Fahd University of Petroleum and Minerals, Dhahran 31261, Kingdom of Saudi Arabia。E-mail：lg1987cup@126.com

第一作者简介：曹耐（1988-）,女,山东济南人,中国石油大学（北京）在读博士生研究生,主要从事非常规油气田开发方面研究。地址：北京市昌平区府学路18号中国石油大学（北京）石油工程学院,邮政编码：102249。E-mail：caonai99@163.com

收稿日期: 2018-09-07
基金项目: 国家科技重大专项（2016ZX05037-003,2017ZX05049-003）
摘要

通过开展人造致密岩心应力敏感滞后性室内实验,分析了致密储集层加压-卸压过程应力敏感性。基于实验结果,考虑岩心颗粒不同排列方式和变形方式,以颗粒堆积模型为基础,根据Hertz接触变形原理建立了致密储集层应力敏感滞后性定量表征模型,对致密储集层应力敏感滞后性造成的渗透率损失进行了量化分析,并通过对比模型计算结果与室内实验结果对新建模型进行了验证。研究表明,加压阶段前期,在岩石结构变形和本体变形共同作用下,岩心渗透率随着有效应力的增加快速下降,当有效应力超过一定值后,岩石结构变形趋于稳定,仅发生本体变形,岩心渗透率变化趋于平缓;卸压阶段,岩石本体变形随有效应力的降低得以逐渐复原,而结构变形不能复原,岩心渗透率无法完全恢复,应力敏感滞后现象明显。图7表1参25

关键词: 致密储集层; 应力敏感滞后; 渗透率应力敏感; 室内实验; 理论模型
中图分类号:TE112.23 文献标志码:A 文章编号:1000-0747(2019)01-0132-07
Stress sensitivity of tight reservoirs during pressure loading and unloading process
CAO Nai1, LEI Gang2
1. China University of Petroleum(Beijing), Beijing 102249, China
2.King Fahd University of Petroleum and Minerals, Dhahran 31261, Kingdom of Saudi Arabia
Abstract

Laboratory experiments were conducted on laboratory-made tight cores to investigate the stress-dependent permeability hysteresis of tight reservoirs during pressure loading and unloading process. Based on experiment results, and Hertz contact deformation principle, considering arrangement and deformation of rock particles, a quantitative stress dependent permeability hysteresis theoretical model for tight reservoirswas established to provide quantitative analysis for permeability loss. The model was validated by comparing model calculated results and experimental results. The research results show that during the early pressure-loading period, structural deformation and primary deformation worked together, rock permeability reduced dramatically with increasing effective stress. When the effective stress reached a certain value, the structural deformation became stable while the primary deformation continued; thepermeability variation tended to be smooth and steady. In the pressure unloading process, the primary deformation recovered with the decreasing effective stress, while the structural deformation could not. The permeability thus could not fully recover, and the stress-dependent hysteresis was obvious.

Keyword: tight reservoir; stress sensitivity hysteresis; permeability stress sensitivity; laboratory experiment; theoretical model
0 引言

开采过程中, 随着地层压力下降, 储集层多孔介质所承受的有效应力增加, 岩石发生弹塑性变形, 多孔介质孔隙体积缩小, 岩石渗透率降低, 从而导致储集层产能降低, 开发效果变差[1, 2]。为了补充和保持地层压力, 致密储集层常采用注水或注气开发[3, 4]。伴随着流体（水或气）注入, 储集层能量不断恢复, 而储集层物性参数（渗透率、孔隙度）不能恢复至原始状态, 岩石这种性质被称作应力敏感滞后效应[5]。相对于常规储集层, 应力敏感滞后效应在致密储集层中尤为明显[6]。这是致密储集层出现永久性应力敏感损害的主要原因, 对于油井产量或储集层采收率具有重大影响[7, 8]。

目前, 中外学者主要通过实验手段对储集层应力敏感进行了大量的研究, 对实验结果的解释多根据经验, 以定性规律研究为主。而且研究主要集中在对加压阶段的分析, 该阶段有效应力不断增大, 主要研究方法可分为：①通过开展大量室内实验得到渗透率、孔隙度随有效应力变化的经验公式; ②建立岩石粒度组成模型, 通过力学分析得到不同有效应力下岩石渗透率、孔隙度计算公式。由于实验研究方法及岩石物性差异, 研究成果存在许多不一致。而应力敏感滞后现象发生于储集层卸压阶段, 因此, 针对应力敏感滞后现象的研究重点应在于卸压阶段的储集层应力敏感。

1985年, Wissler和Simmons[9]对砂岩应变的可恢复和不可恢复性进行了报道和分析。Bernabe[10]通过实验发现了岩石渗透率应力敏感滞后效应, 并认为对岩样进行时效处理（老化处理）后, 岩石应力敏感滞后效应会消除或降低到最小程度。且经过多次老化后, 岩石不再依赖于应力路径, 不存在应力敏感滞后效应。Warpinski和Teufel[11, 12]通过研究认为经过时效处理后的岩样, 多次循环加载后, 岩石应力敏感滞后效应消失。Tadesse和Li[13]对不同尺度、不同岩性的岩样进行了应力敏感实验, 发现纳米级岩样应力敏感滞后性较微米、毫米级岩样更为明显, 岩石应力敏感滞后性受到岩石孔隙尺寸、分布及岩石矿物成分等因素影响, 不同的岩石应力敏感滞后性不同。石玉江等[14]通过对致密岩石施加从小到大的净覆压, 在覆压增至最大压力45MPa后再施加2种回返压力, 以测试岩石的应力敏感滞后效应。实验结果表明, 岩屑砂岩和含泥砂岩的应力敏感滞后效应要比石英砂岩强, 低孔、低渗砂岩的应力敏感滞后效应比高孔、高渗砂岩明显。阮敏等[15]认为低渗致密砂岩受压时, 颗粒间泥质产生塑性形变, 泥质被挤向四周, 从而堵塞孔道, 在该阶段, 岩石渗透率快速下降, 继续加压时, 越来越多颗粒开始直接接触, 岩石发生一些弹性形变; 而当卸压时, 弹性形变可以恢复, 但发生了塑性变形的泥质及微细喉道均不可能重新恢复到原态, 岩石渗透率的可恢复量较小。王秀娟[16]通过研究发现随注水时间延长, 储集层渗透率有不同程度的恢复, 且恢复程度与储集层初始渗透率大小有关。储集层初始渗透率越低, 其应力敏感滞后效应越明显。

上述针对卸压阶段的储集层应力敏感研究主要通过室内实验进行, 多为定性研究, 理论研究成果较少。因此有必要从理论角度对储集层应力敏感滞后现象进行量化分析, 对实验结果及规律进行解释。笔者在致密储集层加压-卸压阶段应力敏感滞后性室内实验结果的基础上, 结合Hertz变形理论, 建立致密储集层加压-卸压阶段应力敏感滞后性理论模型, 并通过实验结果与模型计算结果对比验证模型的正确性; 根据模型计算结果量化分析致密储集层应力敏感滞后现象, 以四颗粒密堆积单元为基础, 从理论角度分析解释致密储集层加压-卸压阶段岩石变形过程, 为实验结果提供合理解释并为致密储集层应力敏感滞后现象提供理论依据。

1 致密储集层应力敏感滞后性实验
1.1 实验岩心

本实验选用环氧树脂压制胶结法制备人造均质致密岩心[17]。岩心制备过程中, 选用粒径区间为0.10~0.15mm及0.15~0.20 mm的石英砂, 固化温度为21℃, 固化时间为6.5 h。所制岩心经与天然岩心驱油及应力敏感对比实验验证, 其孔隙度、渗透率、驱替效果及力学性质与天然岩心相似。选取6块人造均质致密岩心进行实验分析, 基本物性参数见表1。

表1 岩心基本参数
1.2 实验装置

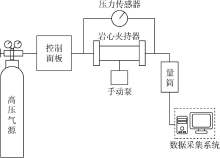
本实验采用干燥N2作为驱替介质。实验装置如图1所示, 气源的驱动压力由高压注射泵提供, 泵参数包括：排量0.01μ L/min~50.00 mL/min, 泵速精度0.01μ L/min, 工作压力7 kPa, 泵压0.068~68.000MPa。岩心夹持器用以固定实验岩心, 实验围压通过手动泵施加, 岩心入口端和出口端压降由压力传感器记录。

图1 实验装置示意图

1.3 实验流程

实验前对岩样进行清洗烘干处理, 烘干时间为48h, 实验温度为室温。本次实验依照中国石油天然气行业标准SY/T6385— 2016《覆压下岩石孔隙度和渗透率测定方法》, 采用围压升降法对致密岩心加压-卸压过程进行应力敏感评价。实验结果在保持岩心进口压力值不变的情况下得到。具体实验步骤为：①加压阶段：保持岩样进口压力不变, 缓慢增加围压, 使其从5MPa逐级增大至15MPa, 待岩心出口端流量稳定后, 进行岩心气测渗透率测定; ②卸压阶段：逐渐减小围压, 使其从15MPa降低至5MPa, 待岩心出口端流量稳定后, 进行岩心气测渗透率测定。本实验采用的有效应力计算公式[18, 19]为：

$\sigma ={{\sigma }_{\text{c}}}-\eta p$ （1）

（1）式中, η 为有效应力系数, 一般取为岩石孔隙度[20, 21]。

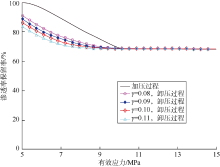
实验结果如图2所示, 6块岩心渗透率保留率（岩石变形后的渗透率与初始渗透率的比值）变化曲线形态基本一致。在有效应力增加早期, 即从5 MPa增加到10MPa时, 岩心渗透率随有效应力增加发生剧烈变化, 下降幅度较大; 有效应力超过10MPa后, 岩心渗透率变化趋于平缓。6块实验岩心均存在应力敏感滞后现象, 即卸压后岩心渗透率不能完全恢复, 存在一定程度渗透率损失。有效应力在5~10MPa变化时, 加压阶段岩心渗透率下降以及卸压阶段岩心渗透率恢复均较为明显, 但相同应力下, 卸压阶段与加压阶段渗透率差异明显。当有效应力超过一定数值后, 加压阶段与卸压阶段渗透率保留率变化曲线重合。说明有效应力增加早期, 岩心发生结构变形和本体变形, 渗透率变化明显; 而当有效应力超过一定值后, 岩心孔隙结构变化趋于稳定, 岩心变形为本体变形, 渗透率变化也随之趋于稳定。

图2 实验岩心加压-卸压过程渗透率保留率变化曲线

2 致密储集层应力敏感滞后性理论模型
2.1 Hertz接触变形原理

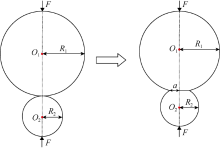
如图3所示, 相互接触的两圆球体颗粒（颗粒半径分别为R1和R2）的初始接触状态为点接触, 当其受到外部应力时, 两圆球体颗粒发生变形, 此时两圆球体的接触区域为一圆形平面, 其半径为a。

图3 两圆球体接触Hertz变形示意图

Hertz变形法则假设压力呈半椭圆球面分布, 与接触面上点位置相关[22], 由于相对于圆球体颗粒体积, 两颗粒接触区域面积很小, 可将其视为作用在半无限大体上的力在很小区域上分布。圆球体颗粒接触面半径满足[17, 18, 19, 20]：

$a=\sqrt[3]{\frac{3F}{4}\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}\left( \frac{1-{{\nu }_{1}}^{2}}{{{E}_{1}}}+\frac{1-{{\nu }_{2}}^{2}}{{{E}_{2}}} \right)}$ （2）

2.2 加压-卸压阶段应力敏感滞后性理论模型

本文建立的加压-卸压阶段应力敏感滞后性理论模型的假设如下。

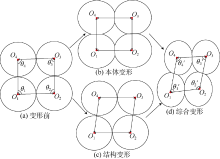
①岩石孔隙由等粒径岩石颗粒堆积而成, 且基本堆积单元为四颗粒密堆积[23, 24, 25]。岩石孔隙初始状态如图4a所示, 颗粒半径为R, 变形前四边形O1O2O3O4的内角分别为θ 1, θ 2, θ 3和θ 4, 其中θ 1=θ 3, θ 2=θ 4。

图4 岩石孔隙变形示意图

②加压过程中, 岩石孔隙发生本体变形和结构变形[21]：其中本体变形遵循Hertz变形法则, 变形后颗粒的接触方式由最初的点接触变为面接触（见图4b）, 接触区域为半径为a的圆形接触面; 孔隙的结构变形由颗粒排列方式的改变造成（见图4c）; 综合考虑本体变形和结构变形, 岩石孔隙综合变形如图4d所示。变形后四边形O1O2O3O4的内角分别为${{\theta }_{1}}^{\prime }$, ${{\theta }_{2}}^{\prime }$, ${{\theta }_{3}}^{\prime }$, ${{\theta }_{4}}^{\prime }$, 其中${{\theta }_{1}}^{\prime }$=${{\theta }_{3}}^{\prime }$, ${{\theta }_{2}}^{\prime }$=${{\theta }_{4}}^{\prime }$。

③卸压过程中, 岩石孔隙的本体变形逐渐得以恢复, 而岩石孔隙的结构变形, 即四颗粒排列方式不能恢复。

加压过程中, 根据Hertz理论及模型假设, 将R1=R2=R, E1=E2=E及ν 1=ν 2=ν 代入（2）式, 颗粒接触面半径和变形后颗粒球心距接触面距离分别为[24]：

$a=\sqrt[3]{\frac{3F}{4}\frac{R\left( 1-{{\nu }^{2}} \right)}{E}}$ （3）

$b=\sqrt{{{R}^{2}}-{{a}^{2}}}$ （4）

加压阶段模型有效应力为：

${{\sigma }_{\text{jp}}}=\frac{2F}{\text{ }\!\!\pi\!\!\text{ }{{b}^{2}}}+{{\sigma }_{0}}$ （5）

加压阶段, 颗粒变形前、后岩石孔隙渗流面积分别为[23]：

$A=4{{R}^{2}}-\text{ }\!\!\pi\!\!\text{ }{{R}^{2}}$ （6）

${A}'=4{{b}^{2}}\sin \theta -4ab-\left( \text{ }\!\!\pi\!\!\text{ }-4\arctan \frac{a}{b} \right){{R}^{2}}$ （7）

（7）式中, θ 为有效应力函数, 随有效应力增加而逐渐减小, 其变化范围为π /3≤ θ ≤ π /2。考虑到实验过程中, 当有效应力增加至初始有效应力的2倍后, 岩心渗透率变化趋于稳定, 此时岩心主要发生本体变形, 加压阶段有效应力函数可分段表达为：

$\theta =\left\{ \begin{matrix} \frac{\text{ }\!\!\pi\!\!\text{ }}{3}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6}{{\left( \frac{{{\sigma }_{\text{0}}}}{{{\sigma }_{\text{jp}}}} \right)}^{\beta }}\quad \frac{{{\sigma }_{\text{0}}}}{{{\sigma }_{\text{jp}}}}\le 2 \\ \frac{\text{ }\!\!\pi\!\!\text{ }}{3}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6}\frac{1}{{{2}^{\beta }}}\quad \quad \frac{{{\sigma }_{\text{0}}}}{{{\sigma }_{\text{jp}}}}2 \\\end{matrix} \right.$ （8）

由（7）式及（8）式可知, 岩石发生形变后, 岩石孔隙渗流面积为颗粒半径及有效应力的函数, 加压阶段孔隙度保留率可表达为：

$\frac{\phi }{{{\phi }_{0}}}={{\left[ 1-\frac{\sqrt{A\left( R, {{\sigma }_{\text{0}}} \right)}-\sqrt{{A}'\left( R, {{\sigma }_{\text{jp}}} \right)}}{\sqrt{A\left( R, {{\sigma }_{\text{0}}} \right)}} \right]}^{3}}={{\left[ \frac{{A}'\left( R, {{\sigma }_{\text{jp}}} \right)}{A\left( R, {{\sigma }_{\text{0}}} \right)} \right]}^{\frac{3}{2}}}$

（9）

基于（9）式可以得到加压阶段岩石发生变形后其渗透率保留率表达式：

$\frac{K}{{{K}_{0}}}=\frac{\phi {A}'\left( R, {{\sigma }_{\text{jp}}} \right)}{{{\phi }_{0}}A\left( R, {{\sigma }_{\text{0}}} \right)}={{\left[ \frac{{A}'\left( R, {{\sigma }_{\text{jp}}} \right)}{A\left( R, {{\sigma }_{\text{0}}} \right)} \right]}^{\frac{5}{2}}}$ （10）

卸压过程中, 颗粒本体变形能够恢复, 即颗粒接触面半径随着有效应力减小而逐渐减小, 而颗粒结构变形不能恢复, 即颗粒排列方式不能恢复。假设岩石受到有效应力为σ xpmax后开始卸压, 此时有效应力函数为θ xp。卸压开始后, θ xp值逐渐变大, 但不能完全恢复到θ 值。此时变形后颗粒球心距接触面距离和颗粒接触面半径分别为：

$b=\sqrt{{2{{F}_{\text{xp}}}}/{\text{ }\!\!\pi\!\!\text{ }{{\sigma }_{\text{xp}}}}\; }\quad {{\sigma }_{0}}\le {{\sigma }_{\text{xp}}}\le {{\sigma }_{\text{xpmax}}}$ （11）

$a=\sqrt{{{R}^{2}}-{{b}^{2}}}$ （12）

卸压阶段开始后, 岩石孔隙渗流面积为：

${{A}_{\text{xp}}}=4{{b}^{2}}\sin {{\theta }_{\text{xp}}}-4ab-\left( \text{ }\!\!\pi\!\!\text{ }-4\arctan \frac{a}{b} \right){{R}^{2}}$（13）

卸压阶段有效应力函数表达式为：

${{\theta }_{\text{xp}}}=\theta \left[ 1-\frac{\gamma \left( {{\sigma }_{\text{xpmax}}}-{{\sigma }_{\text{xp}}} \right)}{{{\sigma }_{\text{xpmax}}}-{{\sigma }_{\text{0}}}} \right]$ （14）

压力卸载后, 岩石孔隙度保留率可表达为：

$\frac{{{\phi }_{\text{xp}}}}{{{\phi }_{0}}}={{\left[ \frac{{{A}_{\text{xp}}}\left( R, {{\sigma }_{\text{xp}}} \right)}{A\left( R, {{\sigma }_{\text{0}}} \right)} \right]}^{\frac{3}{2}}}$ （15）

同时, 压力卸载后岩石渗透率保留率可表达为：

$\frac{{{K}_{\text{xp}}}}{{{K}_{0}}}={{\left[ \frac{{{A}_{\text{xp}}}\left( R, {{\sigma }_{\text{xp}}} \right)}{A\left( R, {{\sigma }_{\text{0}}} \right)} \right]}^{\frac{5}{2}}}$ （16）

3 模型验证与分析
3.1 模型验证

根据本文新建应力敏感滞后性理论模型, 采用上述实验中所用6块人造均质致密岩心的粒径及岩性参数, 通过Matlab编程进行计算, 基于计算结果得到加压-卸压过程中岩心渗透率保留率变化曲线, 并将模型计算结果与实验结果进行对比（见图5）。

图5 岩心渗透率保留率计算结果与实验数据对比

对比结果表明, 岩心渗透率保留率计算结果与实验结果具有较好的一致性, 二者在加压阶段前期都经历了显著下降, 而在加压阶段后期逐渐稳定; 二者在有效应力降至初值后都有一定的不可恢复性损失, 且损失程度相当, 复原趋势相似。

3.2 模型计算结果影响因素

为了提高模型精度, 明确不同参数对模型计算结果的影响, 针对影响岩石结构变形的模型变形参数进行了讨论。

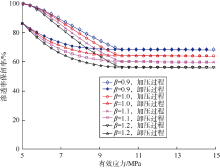
针对不同的岩石变形速度参数β , 根据新建模型对加压-卸压阶段岩石渗透率保留率进行计算, 分析β 对岩石渗透率保留率的影响。如图6所示, 岩石渗透率保留率随β 增大而减小, 这是因为β 与θ 随有效应力变化的速率正相关, β 越大, θ 变化越快, 岩心结构变形越剧烈, 岩石渗透率保留率变化越明显, 即应力敏感滞后现象越明显。β 受岩石泊松比、弹性模量、有效应力系数及颗粒半径综合影响, 对应不同岩性储集层其取值也有所不同, 可通过确定β 取值, 提高针对不同类型致密储集层（砂岩、泥岩、碳酸盐岩等）应力敏感滞后现象造成的渗透率损失的预测精度。

图6 不同β 下加压-卸压过程岩石渗透率保留率曲线

岩石变形程度参数γ 受有效应力系数及岩石颗粒半径综合影响, 针对不同的γ , 根据新建模型对卸压阶段岩石渗透率保留率进行计算, 分析γ 对卸压阶段岩石渗透率保留率的影响, 并将计算结果与加压过程渗透率保留率进行对比。如图7所示, 卸压阶段随着γ 增大, θ 损失程度增大, 岩石结构变形不可恢复程度增大, 岩石渗透率应力敏感滞后性增强。

图7 不同γ 下卸压阶段岩石渗透率保留率曲线

由于致密储集层种类复杂, 不同的岩石应力敏感滞后性不同[13]。针对不同岩性致密储集层, 可通过确定相应的岩石变形参数, 预测该类储集层应力敏感滞后性造成的渗透率损失; 在开发过程中, 制定合理生产压差的同时也要考虑储集层的岩性因素。

4 结论

在致密储集层加压-卸压阶段应力敏感滞后性室内实验结果的基础上, 建立了致密储集层加压-卸压应力敏感滞后性理论模型。新建模型经与实验结果对比验证, 可作为致密储集层应力敏感滞后性量化分析的工具, 为开发过程中该类储集层的应力敏感滞后现象提供理论分析依据。

加压过程中, 有效应力增加早期, 岩石发生结构变形和本体变形, 岩心渗透率随有效应力变化发生剧烈变化, 岩心渗透率下降幅度相对较大; 有效应力超过一定值后, 岩石孔隙结构变形趋于稳定, 岩石仅发生本体变形, 岩心渗透率变化趋于平缓。

卸压后, 岩石本体变形能够恢复, 而结构变形不能恢复, 从而造成岩石孔隙不可恢复性损失, 使岩石渗透率无法完全恢复至初始状态。

应力敏感滞后性随着岩石变形参数增大而增强。在致密储集层开发过程中, 针对不同岩性的储集层, 通过确定相应的岩石变形参数可对其应力敏感滞后现象进行预测。需要说明的是, 不同岩性储集层的变形参数仍需进一步研究和界定。这有助于提高对应力敏感滞后现象造成的渗透率损失的预测精度, 从而进行更准确的产量预测。在制定开发方案时, 除确定合理生产压差外, 还需将储集层的岩性、物性等纳入为考虑因素。

符号注释：

a— — 两圆球体颗粒接触面半径, m; A, A° — — 加压阶段变形前、后岩石孔隙渗流面积, m2; Axp— — 卸压阶段岩石孔隙渗流面积, m2; b— — 变形后颗粒球心距接触面距离, m; E— — 圆球体颗粒弹性模量, Pa; E1, E2— — 颗粒1、颗粒2的弹性模量, Pa; F, Fxp— — 加压、卸压阶段颗粒负载应力, N; K— — 加压阶段岩石变形后的渗透率, 10-3μ m2; K0— — 岩石初始渗透率, 10-3μ m2; Kxp— — 卸压后岩石渗透率, 10-3μ m2; p— — 流体压力, Pa; R— — 圆球体颗粒半径, m; R1, R2— — 颗粒1、颗粒2的半径, m; β — — 表征θ 随有效应力变化速度的参数; γ — — 表征卸压阶段θ 损失程度的参数; η — — 有效应力系数; θ , θ xp— — 加压、卸压阶段有效应力函数; θ 1, θ 2, θ 3, θ 4— — 变形前四边形O1O2O3O4的内角, （° ）; ${{\theta }_{1}}^{\prime }$, ${{\theta }_{2}}^{\prime }$, ${{\theta }_{3}}^{\prime }$, ${{\theta }_{4}}^{\prime }$— — 变形后四边形O1O2O3O4的内角, （° ）; ν — — 圆球体颗粒泊松比; ν 1, ν 2— — 颗粒1、颗粒2的泊松比; σ — — 有效应力, Pa; σ 0— — 初始有效应力, Pa; σ c— — 上覆岩石压力, 本文实验中取围压, Pa; σ jp— — 加压过程中的有效应力, Pa; σ xp— — 卸压过程中有效应力, Pa; σ xpmax— — 卸压起始有效应力, Pa; ϕ — — 加压阶段岩石变形后的孔隙度, %; ϕ 0— — 岩石初始孔隙度, %; ϕ xp— — 卸压后岩石孔隙度, %。

The authors have declared that no competing interests exist.

参考文献
[1] 宋岩, 李卓, 姜振学, 等. 非常规油气地质研究进展与发展趋势[J]. 石油勘探与开发, 2017, 44(4): 638-648.
SONG Yan, LI Zhuo, JIANG Zhenxue, et al. Progress and development trend of unconventional oil and gas geological research[J]. Petroleum Exploration and Development, 2017, 44(4): 638-648. [本文引用:1]
[2] 邱中建, 赵文智, 邓松涛. 我国致密砂岩气和页岩气的发展前景和战略意义[J]. 中国工程科学, 2012, 14(6): 4-8.
QIU Zhongjian, ZHAO Wenzhi, DENG Songtao. Development prospect and strategic significanceof tight gas and shale gas in China[J]. Engineering Sciences, 2012, 14(6): 4-8. [本文引用:1]
[3] 胡素云, 朱如凯, 吴松涛, 等. 中国陆相致密油效益勘探开发[J]. 石油勘探与开发, 2018, 45(4): 737-748.
HU Suyun, ZHU Rukai, WU Songtao, et al. Profitable exploration and development of continental tight oil in China[J]. Petroleum Exploration and Development, 2018, 45(4): 737-748. [本文引用:1]
[4] HUGHES D J. Drilling deeper: A reality check on US government forecasts for a lasting tight oil and shale gas boom[R]. Corvallis, Oregon, United States: Post Carbon Institute, 2014. [本文引用:1]
[5] 李传亮. 储层岩石应力敏感性认识上的误区: 回应刘晓旭博士[J]. 特种油气藏, 2008, 15(3): 26-28.
LI Chuanliang. A misunderstand ing in reservoir rock stress sensitivity: In reply to Dr Liu Xiaoxu[J]. SpecialOiland GasReservoirs, 2008, 15(3): 26-28. [本文引用:1]
[6] 刘仁静, 刘慧卿, 张红玲, 等. 低渗透储层应力敏感性及其对石油开发的影响[J]. 岩石力学与工程学报, 2011, 30(增刊1): 2697-2702.
LIU Renjing, LIU Huiqing, ZHANG Hongling, et al. Study of stress sensitivity and its influence on oil development in low permeability reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Supp. 1): 2697-2702. [本文引用:1]
[7] 陈金辉, 康毅力, 游利军, 等. 低渗透储层应力敏感性研究进展及展望[J]. 天然气地球科学, 2011, 22(1): 182-189.
CHEN Jinhui, KANG Yili, YOU Lijun, et al. Review and prospect about study on stress-sensitivity of low-permeability reservoir[J]. Natural Gas Geoscience, 2011, 22(1): 182-189. [本文引用:1]
[8] 陈祖安, 伍向阳, 方华, 等. 岩石气体介质渗透率的瞬态测量方法[J]. 地球物理学报, 1999, 42(增刊1): 167-171.
CHEN Zu’an, WU Xiangyang, FANG Hua, et al. Gas transit measurement method of permeability on rock[J]. Chinese Journal of Geophysics, 1999, 42(Supp. 1): 167-171. [本文引用:1]
[9] WISSLER T M, SIMMONS G. The physical properties of a set of sand stones: Part II. Permanent and elastic strains during hydrostaticcompression to 200 MPa[J]. International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts, 1985, 22(6): 393-406. [本文引用:1]
[10] BERNABE Y. The effective pressure law for permeability during pore pressure and confining pressure cycling of several crystalline rocks[J]. Journal of Geophysical Research: Solid Earth, 1987, 92(B1): 649-657. [本文引用:1]
[11] WARPINSKI N R, TEUFEL LW. Determination of the effective stress law for permeability and deformation in low-permeability rocks[J]. SPE Formation Evaluation, 1992, 7(2): 123-131. [本文引用:1]
[12] TEUFEL L W, RHETT D W, FARRELL H E. Effect of reservoir depletion and pore pressure drawdown on in situ stress and deformation in the Ekofiskfield, North Sea[R]. Norman, OK, USA: 32. US Symposium on Rock Mechanics, 1991. [本文引用:1]
[13] TADESSE W T, LI X P. Experimental Investigation on permeability and porosity hysteresis of tight formations[R]. SPE 1820226, 2017. [本文引用:2]
[14] 石玉江, 孙小平. 长庆致密碎屑岩储集层应力敏感性分析[J]. 石油勘探与开发, 2001, 28(5): 85-87.
SHI Yujiang, SUN Xiaoping. Stress sensitivity analysis of Changqing tight clastic reservoir[J]. Petroleum Exploration and Development, 2001, 28(5): 85-87. [本文引用:1]
[15] 阮敏, 王连刚. 低透油田开发与压敏效应[J]. 石油学报, 2002, 23(3): 73-76.
RUAN Min, WANG Liangang. Low-permeability of oilfield development and pressure-sensitive effect[J]. Acta Petrolei Sinica, 2002, 23(3): 73-76. [本文引用:1]
[16] 王秀娟, 赵永胜, 文武, 等. 低渗透储层应力敏感性与产能物性下限[J]. 石油与天然气地质, 2003, 24(2): 162-166.
WANG Xiujuan, ZHAO Yongsheng, WEN Wu, et al. Stress sensitivity and poroperm lower limit of deliverability in the low-permeability reservoir[J]. Oil & Gas Geology, 2003, 24(2): 162-166. [本文引用:1]
[17] 周春玲, 朱趁安, 王妍琼, 等. 人造岩心的研制及渗透率影响因素研究[J]. 石油化工应用, 2017, 36(9): 84-89.
ZHOU Chunling, ZHU Chen’an, WANG Yanqiong, et al. Study on the development of man-made core and the influencing factors of permeability[J]. Petrochemical Industry Application, 2017, 36(9): 84-89. [本文引用:2]
[18] GANGI AF. Variation of whole and fractured porous rock permeability with confining pressure[J]. International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts, 1978, 15(5): 249-257. [本文引用:2]
[19] MCKEE C R, BUMB A C, KOENIG RA. Stress-dependent permeability and porosity of coal and other geologic formations[R]. SPE Formation Evaluation, 1988, 3: 81-91. [本文引用:2]
[20] 乔丽苹, 王者超, 李术才. 基于致密砂岩储层渗透率的有效应力特性研究[J]. 岩石力学与工程学报, 2011, 30(7): 1422-1427.
QIAO Liping, WANG Zhechao, LI Shucai. Effective stress law for permeability of tight gas reservoir sand stone[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7): 1422-1427. [本文引用:2]
[21] 李传亮, 孔祥言, 徐献芝, 等. 多孔介质的双重有效应力[J]. 自然杂志, 1999, 21(5): 288-292.
LI Chuanliang, KONG Xiangyan, XU Xianzhi, et al. Double effective stress of porous media[J]. Nature Magazine, 1999, 21(5): 288-292. [本文引用:2]
[22] 杨咸启, 钱胜, 褚园, 等. HERTZ型与非HERTZ型接触理论计算方法[J]. 黄山学院学报, 2017, 19(5): 13-18.
YANG Xianqi, QIAN Sheng, CHU Yuan, et al. The calculation method of Hertzian and non-Hertzian contact theory[J]. Journal of Huangshan University, 2017, 19(5): 13-18. [本文引用:1]
[23] 董平川, 雷刚, 计秉玉, 等. 考虑变形影响的致密砂岩油藏非线性渗流特征[J]. 岩石力学与工程学报, 2013, 32(S2): 3187-3196.
DONG Pingchuan, LEI Gang, JI Bingyu, et al. Nonlinear seepage regularity of tight sand stone reservoirs with consideration of medium deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3187-3196. [本文引用:2]
[24] 雷刚, 董平川, 杨书, 等. 基于岩石颗粒排列方式的低渗透储层应力敏感性分析[J]. 岩土力学, 2014, 35(增刊1): 209-214.
LEI Gang, DONG Pingchuan, YANG Shu, et al. Study of stress-sensitivity of low-permeability reservoir based onarrangement of particles[J]. Rock and Soil Mechanics, 2014, 35(Supp. 1): 209-214. [本文引用:2]
[25] 曹耐, 董平川, 雷刚, 等. 不同填充模式裂缝型致密储层应力敏感性定量研究[J]. 断块油气田, 2018, 25(6): 747-751.
CAO Nai, DONG Pingchuan, LEI Gang, et al. Quantitative study of stress sensitivity for fractured tight reservoir with different filled patterns[J]. Fault-Block Oil & Gas Field, 2018, 25(6): 747-751. [本文引用:1]