引用本文
刘乃震, 张兆鹏, 邹雨时, 马新仿, 张一诺. 致密砂岩水平井多段压裂裂缝扩展规律[J]. 石油勘探与开发, 2018,45(6): 1059-1068.
LIU Naizhen, ZHANG Zhaopeng, ZOU Yushi, MA Xinfang, ZHANG Yinuo. Propagation law of hydraulic fractures during multi-staged horizontal well fracturing in a tight reservoir[J]. Petroleum Exploration & Development, 2018,45(6): 1059-1068.  
Doi: 10.11698/PED.2018.06.14
Permissions
Copyright©2018, 《石油勘探与开发》编辑部
致密砂岩水平井多段压裂裂缝扩展规律
刘乃震1, 张兆鹏2, 邹雨时2, 马新仿2, 张一诺2
1. 中国石油集团长城钻探工程有限公司,北京 100101
2. 中国石油大学（北京）,北京 102249

第一作者简介：刘乃震（1960-）,男,辽宁昌图人,博士,中国石油集团长城钻探工程有限公司教授级高级工程师,主要从事钻井、完井、储集层改造方面的研究与管理工作。地址：北京市朝阳区安立路101号名人大厦,邮政编码：100101。E-mail: lmlm1985@163.com

收稿日期: 2018-04-19
摘要

基于真三轴水力压裂模拟系统,开展已压裂缝内流体压力、段间距、射孔参数、水平应力差和水平井段固井质量对致密砂岩储集层多裂缝扩展形态影响的实验。通过岩样剖分和压力曲线特征的类比分析得到以下认识：已压缝处于临界闭合状态时,高水平应力差和小段间距将导致多裂缝合并,而已压缝内高净压力和缝宽不对称分布可能抑制后续裂缝扩展;较大段间距使得后续裂缝处于诱导应力递减区域,降低应力干扰程度;采用大密度深穿透射孔,有利于降低裂缝起裂压力;缝内净压力一定时,低水平应力差将增大水平应力反转程度,增大后续裂缝偏转角度;水平段固井质量较差时,裂缝在井筒与地层结合处起裂,形成纵向缝;各段裂缝起裂压力呈上升趋势,压力增长幅度可达30%;形成横切缝时,起裂后压力迅速下降,延伸压力低;裂缝发生偏转时,起裂后压力波动下降,延伸压力较高,为迂曲窄缝;形成纵向缝时,压力剧烈波动上升,呈现多峰值特征,起裂阶段和延伸阶段区别不明显。图16表1参26

关键词: 致密砂岩; 水平井; 多段压裂; 射孔; 缝内净压力; 缝间应力干扰; 裂缝扩展
中图分类号:TE357.1 文献标志码:A 文章编号:1000-0747(2018)06-1059-10
Propagation law of hydraulic fractures during multi-staged horizontal well fracturing in a tight reservoir
LIU Naizhen1, ZHANG Zhaopeng2, ZOU Yushi2, MA Xinfang2, ZHANG Yinuo2
1. CNPC Great Wall Drilling Company, Beijing 100101, China
2. China University of Petroleum (Beijing), Beijing 102249, China
Abstract

A novel laboratory simulation method for modeling multi-staged fracturing in a horizontal well was established based on a true tri-axial hydraulic fracturing simulation system. Using this method, the influences of net pressure in hydraulic fracture, stage spacing, perforation parameter, horizontal stress bias and well cementation quality on the propagation geometry of multiple fractures in a tight sandstone formation were studied in detail. The specimen splitting and analogy analysis of fracturing curve patterns reveals: Multiple fractures tend to merge under the condition of high horizontal stress bias and short stage spacing with pre-existing hydraulic fractures under critical closure situation, and the propagation of subsequent fractures is possibly suppressed because of high net pressure in pre-created fractures and asymmetric distribution of fracture width. And the subsequently created fractures are situated in the induced stress decreasing zone due to lone stage spacing, leading to weak stress interference, and perforation with intense density and deep penetration facilitates the decrease of initiation fracture pressure. The deflection angle of subsequent fracture and horizontal stress variation tend to be amplified under low horizontal bias with constant net pressure in fractures. The longitudinal fracture is likely to be initiated at the interface of wellbore and concrete sample with poor cementation quality. The initiation fracture pressure of the different stages increases in turn, with the largest increase of 30%. Pressure quickly declines after initiation with low propagation pressure when the transverse hydraulic fracture is formed. The pressure reduces with fluctuation after the initiation of fracture when the fracture deflects, the extension pressure is high, and the fracture formed is tortuous and narrow. There is a violently fluctuant rise of pressure with multiple peak values when longitudinal fracture created, and it is hard to distinguish the features between the initiation stage and propagation stage.

Keyword: tight sandstone; horizontal well; multi-staged fracturing; perforation; net pressure in fracture; stress interference between fractures; fracture propagation
0 引言

为了实现致密储集层高效开发, 需采用水平井多段多簇压裂技术产生密集且垂直于井筒的多条横切缝来扩大储集层泄流面积[1, 2, 3, 4]。但生产测井数据表明, 30%甚至更多的射孔簇对产量没有贡献[4]。水平井段储集层非均质性和完井质量差异均会导致射孔簇不均匀的产量贡献。储集层非均质性主要考虑岩性非均质、天然裂缝密度和应力状态非均质等; 完井质量主要包括段间距、射孔簇数量和簇间距、排量、压裂液类型、单段支撑剂量和裂缝产生顺序等。已有研究表明, 近间距起裂的多裂缝之间存在强应力干扰, 即“ 应力阴影” 效应, 其对裂缝的扩展路径和缝宽会有显著影响[2, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]。先形成的裂缝可导致后续压裂段的裂缝发生偏转, 不再垂直于井筒, 甚至是沿着水平井筒形成纵向缝; 而同一压裂段内, 中间簇起裂的裂缝会受到更大的压应力而导致缝宽减小或导流能力降低, 甚至会导致裂缝停止延伸或合并, 从而造成水平段储集层的非均匀改造, 降低压裂后的产量。虽然针对水平井多段压裂裂缝起裂及扩展问题已经开展了大量理论研究, 但缺少最直接的物理实验对其进行验证, 而且已有研究并未涉及后续段压裂时已压段缝内流体压力以及水平井段固井质量对水平井多段压裂多裂缝展布的影响规律。

针对上述问题, 本文基于真三轴水力压裂模拟系统, 设计一种可开展水平井多段压裂裂缝起裂及扩展的物理模拟实验方法。实验考虑不同净压力引起的附加应力, 分析水平应力差、射孔深度、已压裂缝内流体压力和水平井段固井质量对水平井多段压裂裂缝扩展形态的影响, 总结压裂曲线特征, 并结合实验结果开展现场实例研究。

1 裂缝诱导应力场理论模型

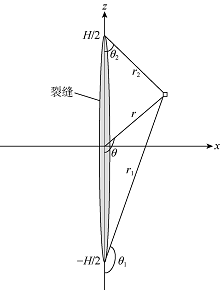
水平井分段压裂在储集层产生多条水力裂缝, 存在多裂缝应力干扰问题。应力干扰实质为水力裂缝张开产生的诱导应力场。诱导应力叠加到原地应力场上将会导致原地应力发生改变。研究表明, 应力干扰与裂缝形态相关, 当缝长大于缝高时, 垂直于缝长的截面近似为平面应变, 缝高是控制岩体变形的特征量, 应力场受缝高影响[2]。一般水力裂缝长度远大于缝高, 因此基于缝高进行裂缝诱导应力场计算。对于二维固定缝高裂缝（见图1）, 根据Sneddon公式[15, 16]可知裂缝诱导应力场为：

\[\left\{ \begin{align} & \sigma _{\text{c}xx}
{{}}={{p}_{\text{net}}}\left[ \frac{r}{\sqrt{{{r}_{1}}{{r}_{2}}}}\cos \left( \theta -\frac{{{\theta }_{1}}+{{\theta }_{2}}}{2} \right)-1 \right]- \\ & \quad \quad \ \frac{{{\left( \frac{H}{2} \right)}
{2}}{{p}_{\text{net}}}r}{{{\left( {{r}_{1}}{{r}_{2}} \right)}
{1.5}}}\sin \theta \sin \frac{3}{2}\left( {{\theta }_{1}}+{{\theta }_{2}} \right) \\ & \sigma _{\text{c}zz}
{{}}={{p}_{\text{net}}}\left[ \frac{r}{\sqrt{{{r}_{1}}{{r}_{2}}}}\cos \left( \theta -\frac{{{\theta }_{1}}+{{\theta }_{2}}}{2} \right)-1 \right]+ \\ & \quad \quad \ \frac{{{\left( \frac{H}{2} \right)}
{2}}{{p}_{\text{net}}}r}{{{\left( {{r}_{1}}{{r}_{2}} \right)}
{1.5}}}\sin \theta \sin \frac{3}{2}\left( {{\theta }_{1}}+{{\theta }_{2}} \right) \\ & \sigma _{\text{c}yy}
{{}}=\nu \left( \sigma _{\text{c}xx}
{{}}+\sigma _{\text{c}zz}
{{}} \right) \\ \end{align} \right.\ \ (1)\]

其中 \(r=\sqrt{{{x}
{2}}+{{z}
{2}}}\)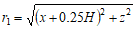

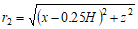
\({{\theta }_{1}}=\arctan \left( \frac{z}{x+0.5H} \right) {{\theta }_{2}}=\arctan \left( \frac{z}{x-0.5H} \right)\)

图1 固定高度垂直裂缝诱导应力场模型

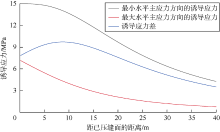
利用（1）式计算得到净压力为15 MPa、缝高为40 m时垂直裂缝面方向的诱导应力分布（见图2）。最小水平主应力方向的诱导应力\({{\sigma }_{\text{c}xx}}\)随着与已压裂缝面距离的增大而呈现出先缓慢减小后迅速降低的趋势。最大水平主应力方向的诱导应力\({{\sigma }_{\text{c}yy}}\)随着与已压裂缝面距离的增大而呈现出平缓下降的趋势。诱导应力差\({{\sigma }_{\text{c}xx}}-{{\sigma }_{\text{c}yy}}\)（\(\Delta \sigma \)）随着与已压裂缝面距离的增大而呈现出先增大后减小的趋势且存在一个最大值。

图2 诱导应力与距已压裂缝面距离关系曲线

当诱导应力场附加在原地应力场后, 已压缝附近某处的水平应力差可能反转, 即诱导应力差与原水平主应力差的比值大于1, 造成水力裂缝在该处向原最小水平主应力方向偏转, 甚至发生90° 的转向而形成纵向缝。因此, 可以通过诱导应力差衡量诱导应力对原水平主应力差的改变程度[17, 18, 19, 20, 21, 22]。

2 水平井多段压裂物理模拟实验
2.1 实验仪器与流程

研究层位选定苏里格气田53区块盒8段, 平均渗透率为0.87× 10-3 μ m2, 平均孔隙度为9.0%, 单轴弹性模量为24.7 GPa, 泊松比为0.24, 抗拉强度为2.2 MPa, 水平最大主应力为61.3 MPa, 水平最小主应力为49.2 MPa。

实验采用一套真三轴水力压裂模拟系统[14]（见图3）。实验依据地应力差异系数模拟真实地层应力环境, 通过油压泵组和液压缸推动加压板, 为岩心室内的岩样施加三轴应力, 其中x轴的最大加载应力为15 MPa, y、z轴的最大加载应力为30 MPa。应力加载完成后, 使用空气泵推动中间容器内的活塞将压裂液挤入管线, 通过六通阀经注液管线进入井筒压裂岩样。与管线相连的温度传感器和压力传感器分别实时记录井口温度和压力变化数据。

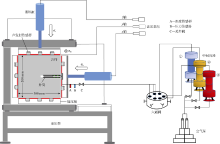图3 真三轴水力压裂模拟系统示意图（据文献[14]修改）

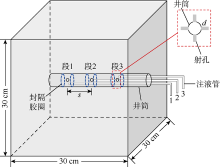
实验制备尺寸为30 cm× 30 cm× 30 cm的混凝土立方体试样（见图4）。试样由比例为3∶ 1∶ 1的水泥、砂和水混合而成, 物性与天然岩样相似。制备水泥试样时, 预置实验井筒, 实现固井过程。

图4 水泥试样和水平井多段压裂模拟井筒

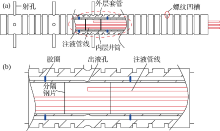
为实现水平井分段压裂（实验中考虑了3段）, 实验设计制作了可重复使用的水平井分段压裂实验井筒（见图4、图5）, 分为外层套管、内层井筒和注液管线3个部分, 内层井筒插入外层套管组装形成实验井筒。

图5 水平井分段压裂实验井筒示意图

外层套管为外径2.0 cm、内径1.6 cm、长度20.0 cm的钢管（见图5a）。在每一个压裂段的中心位置以90° 的相位角设置4个直径为3 mm的通孔, 将射孔段（外径3 mm、表面割缝的薄壁钢管）与通孔垂直焊接在一起, 模拟实际射孔形成的通道。在外层套管的外表面每间隔3 mm加工深度1 mm、宽度2 mm的螺纹凹槽, 同时对钢管外壁进行喷砂处理, 提高水泥与钢管外壁的黏结程度, 模拟较好的固井质量。针对较差的固井质量, 对钢管外壁作光滑处理。

内层井筒为外径1.5 cm、内径0.8 cm、长度20.0 cm的钢管（见图5b）。在内层井筒对应外层套管射孔段处设置直径3 mm的出液孔, 并在每个射孔段的环空部分用密封胶圈封隔, 以模拟封隔器的作用。

注液管线的外径为3 mm、内径为2 mm。为实现分段注液, 将3根注液管线一端分别延伸至3个压裂段的中心位置, 并在内层井筒的每个压裂段焊接分隔钢片, 防止压裂液进入其他压裂段。将注液管线另一端和3个中间容器分别与六通阀相连并一一对应。因此, 某一段注液时, 将六通阀上该段注液管线与对应的中间容器所连接的阀门开启, 六通阀上其他阀门处于关闭状态, 可以实现对单个压裂段泵注压裂液。

具体实验步骤如下。

①连接管线, 并将岩样按照井筒轴线沿x轴方向放入实验系统的岩心室内。

②沿x轴方向将液压活塞推送至腔体内部, 沿z轴方向施加垂向应力, 分别沿y、x轴方向施加最大水平主应力和最小水平主应力至设定值并维持稳定。

③将模拟井筒内部的3根注入液管连接到六通阀上, 同时将3个装有不同颜色压裂液的中间容器也连接到六通阀上, 其中①号中间容器混有蓝色染色剂、②号中间容器混有绿色染色剂、③号中间容器混有红色染色剂。

④开启当前压裂段注液管线和相应中间容器连接六通阀上的阀门, 如①号中间容器对应第1个压裂段的注液管线, 以此类推, 同时保持其余阀门关闭。开启注液系统, 以恒定排量向井筒中泵注压裂液进行压裂实验, 同时应用压力传感器记录整个过程中的井口压力变化, 直到完成既定的注液体积, 在压力波动较小时停泵, 并关闭相应注液管线阀门。

⑤室内压裂模拟实验时, 裂缝通常能够延伸至岩样表面, 压裂液易流出, 缝内流体压力较低。为避免这一现象, 将已压裂段注液管线通过六通阀与装有高黏度流体的中间容器相连。开启注液系统, 以恒定压力向已压裂段内注入极高黏度流体, 从而维持已压段裂缝内流体压力, 阻止裂缝闭合, 模拟现场压裂停泵后支撑剂和流体支撑裂缝面的效果。

⑥第2段压裂时, 调整相应管线阀门, 对第1段开展步骤⑤, 并重复步骤④。第3段压裂时, 调整相应管线阀门, 同时对第1段和第2段开展步骤⑤, 并重复步骤④。

⑦实验结束后取出岩样, 根据裂缝面的染色情况区分不同段起裂的水力裂缝, 并使用线切割仪进行岩样剖分, 分析近水平井筒多裂缝扩展路径。

2.2 实验参数

基于相似理论确定注入参数和井筒参数。注入参数的设计参考柳贡慧等[23]的理论研究。基于苏53区块盒8段致密气藏压裂施工所用排量和压裂液黏度等条件, 结合水泥试样尺寸和实验模拟系统的工作参数, 通过相似准则[23, 24]设计并计算注入参数。现场排量为3.5~5.0 m3/min, 净压力为15~25 MPa, 设计实验泵注排量为50 mL/min, 累计泵注液量为120~160 mL, 实验压裂液黏度为63 mPa· s。

井筒参数根据几何相似原则确定。实验模型段间距与现场实际段间距应满足如下几何相似关系：

\[\frac{{{s}_{\text{M}}}}{{{s}_{\text{F}}}} \text{=}\frac{{{L}_{\text{M}}}}{{{L}_{\text{F}}}}\ \ (2)\]

现场水平井分段压裂实际段间距为40~70 m、裂缝半长为250~350 m, 实验裂缝半长为15~20 cm, 利用（2）式计算得到实验段间距为1.75~5.60 cm。为方便实验对比, 实验设置小段间距为2 cm、大段间距为5 cm。本文研究射孔对水力裂缝起裂压力的影响, 为减小井筒附加应力场对裂缝起裂的影响, 本实验设置射孔深度为井筒直径的1~5倍, 即1~5 cm。

实验基于正断层应力机制（\({{\sigma }_{\text{v}}}\ge {{\sigma }_{\text{H}}}{{\sigma }_{\text{h}}}\)）设置地应力加载值。采用Beugelsdijk等[22]开展多裂缝介质水力裂缝扩展实验时定义的水平应力差异系数和无因次净压力的概念, 由于水平应力差异系数决定流体向天然裂缝的滤失能力, 而无因次净压力决定裂缝偏转程度, 因此实验依据实际地层水平应力差异系数和无因次净压力设置实验条件。

\[{{K}_{h}}=\frac{{{\sigma }_{H}}-{{\sigma }_{h}}}{{{\sigma }_{h}}}\ \ (3)\]

\[{{p}_{netD}}=\frac{{{p}_{\text{f}}}-{{\sigma }_{h}}}{{{\sigma }_{H}}-{{\sigma }_{h}}}\ \ (4)\]

研究区水平最大主应力为61.3 MPa、水平最小主应力为49.2 MPa、储集层应力差异系数为0.25, 据此设计实验应力加载条件（见表1）。需要注意的是, 后续压裂段施工过程中, 已压裂段的裂缝处于闭合或开启两种状态：当已压裂段停泵后缝内流体无因次净压力较低时（如等于0）, 后续段压裂过程中已压裂缝处于闭合临界状态; 而当已压裂缝内流体无因次净压力较高时（如等于2）, 后续段压裂过程中已压裂缝处于完全开启状态。

本文共进行了6块岩样的压裂实验（见表1）, 其中1— 5号岩样固井质量较好, 6号岩样固井质量较差。

表1 实验参数与固井质量
3 多裂缝扩展形态及压力曲线特征
3.1 已压缝内净压力对多裂缝形态的影响

设置水平应力差异系数为1.00, 实验段间距为2.0 cm, 射孔深度为1.0 cm。净压力为零的1号岩样和净压力为水平应力差2倍的4号岩样的裂缝扩展形态见图6。两个岩样的缝1均沿水平最大主应力方向延伸形成横切缝。1号岩样缝1两侧扩展均匀, 缝宽对称分布（见图6a）。而4号岩样的缝1主要在井筒上侧射孔处发生起裂, 此处裂缝扩展更为充分, 裂缝宽度较大; 而井筒下侧裂缝宽度较小, 这将导致后续注入流体压力的不对称加载（见图6b）。

图6 已压缝内净压力对多裂缝形态的影响

3.1.1 应力干扰极限距离

应力干扰极限距离用于度量诱导应力最大作用范围。1号岩样进行第2段压裂时, 缝1处于临界闭合状态, 缝2在近井筒远离缝1偏转一定角度后, 下侧在井筒远端重新偏向原最大水平主应力方向, 应力干扰作用减弱, 缝1垂直缝面的应力干扰极限距离为7 cm, 对应现场应力干扰极限距离为93 m（见图6a）。4号岩样缝1净压力为水平应力差的2倍, 缝2与缝3下侧以近似45° 角远离缝1偏转至边界, 缝1的垂直缝面应力干扰极限距离至少为15 cm, 相应实际极限距离应大于200 m（见图6b）。因此已压缝内净压力越大, 应力干扰极限距离越大。

3.1.2 多裂缝合并

1号岩样中缝2上侧在远端重新偏向缝1并最终合并, 缝3在偏转小角度后也与缝2合并（见图6a）, 说明高水平应力差的常规砂岩储集层进行小段间距水平井分段压裂时, 可能会出现多裂缝合并现象。因为流体摩阻和滤失的影响, 缝1上侧远端流体压力减小, 缝端可能已经闭合, 应力干扰减弱。虽然后续裂缝处于先压裂缝应力干扰极限距离内, 但是诱导应力场变化已经导致裂缝面附近水平最大主应力方向朝向缝1偏转。由于段间距较小, 缝2偏转后的扩展路径与缝3重合, 缝3在起裂后即与缝2合并。

3.1.3 裂缝非对称扩展

与1号岩样不同, 4号岩样中缝2、缝3上侧扩展均受到抑制（见图6b）。缝1中流体压力的不对称加载导致上侧形成的干扰应力更大, 垂直裂缝面的最小主应力方向上产生较大的附加诱导应力, 裂缝起裂后延伸很短距离即停止扩展。致密储集层压裂时, 如果支撑剂在缝内铺置不均匀, 当裂缝闭合时, 支撑剂铺置较多的一侧裂缝宽度较大, 维持了对裂缝附近地层的挤压状态, 后续裂缝的应力干扰现象明显; 而另一侧由于铺砂浓度低, 裂缝内未能形成有效支撑, 裂缝附近地层的挤压状态得到释放, 诱导应力较小。因此, 可以推断已压缝内支撑剂铺置的均匀程度也将会影响后续裂缝的扩展。

3.1.4 压力曲线特征

由于诱导应力场的叠加, 后续裂缝的起裂压力呈依次上升趋势。当无因次净压力为0时, 1号岩样中缝2和缝3的起裂压力相对于缝1分别增加8.1%和9.0%（见图7a）; 当无因次净压力为2时, 4号岩样中缝2和缝3的起裂压力分别增加21.6%和29.3%（见图7b）。因此, 起裂压力的增长幅度与已压缝内净压力大小呈正相关的关系。

图7 不同已压缝内净压力下的泵注压力曲线

图7显示, 两块岩样缝1的延伸压力均较平缓, 而后续裂缝的延伸压力均出现明显的波动, 且无因次净压力越大, 波动程度越剧烈。这是因为缝1为平直的横切缝, 所以压裂液流动所受阻力较小, 延伸压力平稳。而后续裂缝由于发生偏转, 裂缝迂曲, 裂缝宽度较小, 流体流动阻力较大, 压力产生剧烈波动。因此, 根据泵注压力曲线可以判断裂缝形态和应力干扰情况, 从而优化施工参数。

3.2 段间距和射孔参数对多裂缝形态的影响

设置水平应力差异系数为0.25, 已压缝内无因次净压力为0。实验结果表明, 段间距的大小对多裂缝的扩展形态具有明显影响。当实验段间距为2 cm、对应现场实际段间距为30 m时, 2号岩样后续裂缝远离井筒后逐渐向远离上一压裂段裂缝方向偏转（见图8a）。当实验段间距增加至5 cm、对应现场实际段间距为80 m时, 3号岩样缝1和缝2近似垂直水平井筒延伸, 而缝3向远离缝2方向偏转（见图8b）。结合图2可以发现, 虽然处于临界闭合状态的裂缝能够增加已压裂缝两侧水平最小主应力, 导致后续裂缝扩展发生偏转, 但是较大段间距使得后续压裂段处于诱导应力差递减区域, 因此3号岩样中缝2几乎不受到应力干扰, 而缝3由于应力干扰叠加作用发生偏转。

图8 段间距对多裂缝形态的影响

射孔参数对裂缝起裂压力影响显著。设置2号岩样射孔深度为5 cm、3号岩样射孔深度为1 cm。泵注压力曲线显示2号岩样各段起裂压力较3号岩样分别下降了18.8%、18.9%和9.5%（见图9）。这是因为随着射孔深度的增加, 孔眼长度增加, 液体压力在孔壁上有效作用面积增大, 用于破裂地层的液体能量增大, 使得孔眼的周向应力增加, 地层破裂压力降低[25]。另外, 将小段间距等效为射孔密度较大的情形, 发现随着射孔密度的增加, 孔眼距离不断减小, 多孔应力集中效应增强, 使得孔眼附近的应力增大。因此破裂压力的减小可以归结为无限大物体开多孔应力集中相互影响的结果[26]。现场可通过大密度深穿透射孔来降低岩石起裂压力。

与3号岩样（见图9b）相比, 2号岩样中各段裂缝起裂后压力下降幅度较小, 延伸压力波动剧烈且比3号岩样高1~2 MPa（见图9a）, 裂缝迂曲且缝宽较小, 这主要是因为小段间距造成应力干扰较强。

图9 不同段间距和射孔参数下的压力曲线

3.3 水平应力差对多裂缝形态的影响

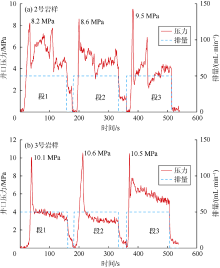
设置水平应力差异系数为0.25, 段间距为2.0 cm, 射孔深度为5 cm, 已压缝内无因次净压力为2。5号岩样的多裂缝扩展形态与4号岩样相似, 缝1也为垂直井筒的横切缝, 缝2和缝3以一定角度偏转（见图10a）。不同的是, 5号岩样的缝2首先以纵向缝扩展至缝3的射孔处, 导致缝3起裂后与缝2的扩展轨迹重合, 二者均以近60° 的偏转角远离缝1延伸（见图10b）。

图10 水平应力差对裂缝扩展形态的影响

定义水平应力反转程度为：

\[f\left( \frac{r}{H} \right)=\frac{\sigma _{\text{c}xx}
{{}}-\sigma _{\text{c}yy}
{{}}}{{{\sigma }_{\text{H}}}-{{\sigma }_{\text{h}}}}\ \ (5)\]

式中, \(\frac{r}{H}\)为无因次距离。分别将（1）式中\(\sigma _{\text{c}xx}
{{}}\)、\(\sigma _{\text{c}yy}
{{}}\)的表达式代入（5）式, 得到：

\[f\left( \frac{r}{H} \right)=\frac{{{p}_{\text{net}}}}{{{\sigma }_{\text{H}}}-{{\sigma }_{\text{h}}}}\times \left\{ \frac{\frac{r}{H}}{\sqrt{{{\left( \frac{r}{H} \right)} {2}}+0.25}}\left[ \frac{0.25}{{{\left( \frac{r}{H} \right)} {2}}+0.25}-2\nu +1 \right]-1+2\nu \right\}\ \ (6)\]

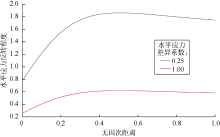
由（6）式可知, 当缝内流体净压力一定时, 水平应力反转程度不仅与缝高、距缝面距离和岩石泊松比有关, 还与水平应力差有关。当水平应力反转程度大于1时即会发生应力反转。令实验缝高为30 cm、泊松比为0.24, 取4号和5号岩样的地应力参数, 绘制不同水平应力差下水平应力反转程度与无因次距离的关系曲线（见图11）。

图11 水平应力反转程度与无因次距离关系曲线

由图11可知, 当缝内流体净压力一定时, 低水平应力差下更容易产生应力反转, 且应力反转区域更大。由于5号岩样水平应力差异系数为0.25, 距缝1的距离大于1.5 cm后水平应力反转程度大于1, 后续段裂缝受到已压裂缝的影响程度将显著增大, 甚至可能出现应力反转形成纵向缝。因此, 5号岩样中缝2与缝3扩展路径偏转角度较4号岩样大, 其中缝2沿着水平井筒扩展了一段距离。

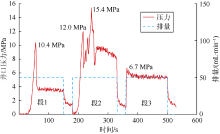
5号岩样各压裂段的压力曲线形态差异较大（见图12）。缝2在井筒与岩石结合处开裂形成纵向缝, 在压力曲线上反映为12.0 MPa和15.4 MPa两个峰值点, 之后迅速降低至7.14~9.15 MPa延伸压力。由于缝3与缝2沟通, 未见明显破裂压力, 但由于缝2迂曲, 后续注入压力较缝1高。5号岩样由于缝2形成纵向缝, 各段起裂压力不再呈现依次上升的趋势。

图12 5号岩样压力曲线

3.4 水平段固井质量对多裂缝形态的影响

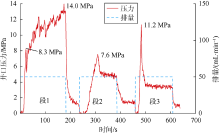
光滑的井筒外壁与岩样接触代表固井质量较差的情况。6号岩样实验结果显示（见图13、图14）, 缝1在井筒与岩样结合处开裂（射孔跟部）, 形成近似平行井筒的纵向缝, 其压力在达到8.3 MPa后略微降低, 再缓慢剧烈波动上升至高峰值14.0 MPa。与5号岩样的缝2压力变化类似, 该段纵向缝压力曲线呈现多峰值特征, 裂缝起裂过程与延伸过程区别不明显, 且压力较高。缝2整体压力处于低值, 与5号岩样第3段裂缝相似, 可以判断缝2起裂后即与缝1沟通, 难以再次形成新缝。因此, 在固井质量差的水平井段, 由于井筒与岩样结合处开裂造成近井筒区域应力改变, 水力裂缝有较大几率形成纵向缝, 同时影响后续裂缝的扩展路径, 最终减小储集层改造体积。

图13 固井质量较差对裂缝形态的影响

图14 固井质量较差时的压力曲线

4 实例验证

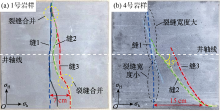
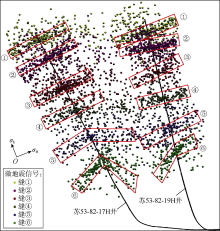
苏53-82-17H和苏53-82-19H是苏53区块2口压裂水平井, 均为6段压裂, 其中苏53-82-17H设计段间距为130~150 m, 平均无因次净压力为1.1; 苏53-82-19H设计段间距为110~125 m, 平均无因次净压力为1.8。压裂过程中进行微地震裂缝监测, 实时获得裂缝扩展情况（见图15）。

图15 地面微地震裂缝监测图（①— ⑥为裂缝编号）

裂缝扩展情况呈现出3个特点：①苏53-82-17H井①— ④号裂缝由于段间距较大, 后续裂缝处于诱导应力递减区域, 且缝内流体净压力较小, 导致应力干扰极限距离较短, 后续裂缝扩展并未受到较强的应力干扰, 裂缝依旧沿最大水平主应力方向延伸; ②苏53-82-19H井缝①和缝②下侧在10 MPa较高水平地应力差和小段间距情况下发生多裂缝合并现象; ③水平井段中部裂缝总体受干扰程度较低, 诱导应力叠加作用导致越靠近跟端裂缝偏转越明显。

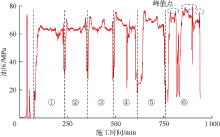
值得注意的是, 苏53-82-17H井缝⑥上侧出现大角度偏转。这是因为水平应力差相对于缝内净压力小, 水平应力改变程度均大于1, 有较大几率发生应力反转形成纵向缝。同时压力在高值波动, 呈现多个峰值点（见图16）, 说明该段可能固井质量较差, 裂缝从井筒与地层结合处开裂, 沿井筒形成了一段迂曲窄缝。苏53-82-19H井缝⑥呈不对称扩展, 根据4号岩样的实验结果分析认为可能是缝⑤的支撑剂铺置不均匀, 导致上侧支撑裂缝宽度较大, 维持了地层挤压状态, 对缝⑥上侧的扩展产生抑制。

图16 苏53-82-17H井分段压裂压力曲线
（①— ⑥为裂缝编号）

结果表明, 实验获得的裂缝扩展规律和压力曲线特征可用于现场实际裂缝形态的解释分析, 为施工参数的优化提供一定指导。

5 结论

通过实验得到已压缝处于临界闭合状态时（无因次净压力为0）, 应力干扰极限距离在93 m左右, 且在较高水平应力差和小段间距压裂时存在多裂缝合并; 当已压缝内无因次净压力为2时, 应力干扰极限距离将大于200 m。已压缝缝宽不对称分布导致不均匀诱导应力, 缝内流体净压力较大时, 可能抑制后续裂缝扩展。较大的段间距会使后续裂缝处于诱导应力递减区域, 应力干扰程度降低, 裂缝偏转不明显。采用大密度深穿透射孔工艺有利于提高作用于孔壁的液体能量, 增强多孔应力集中效应, 有效降低裂缝起裂压力。当缝内流体净压力一定时, 低水平应力差将增大水平应力改变程度。当水平应力改变程度大于1时, 后续裂缝偏转角度越大, 压裂形成纵向缝的几率越大。水平段固井质量较差时, 裂缝在井筒与地层结合处起裂, 裂缝主要沿着水平井筒延伸形成纵向缝。水平井多段压裂时, 各段裂缝起裂压力呈上升趋势, 当已压缝内无因次净压力为2时, 压力增长幅度可达30%。形成平直横切缝时, 起裂后压力迅速下降, 延伸压力低。当裂缝发生偏转时, 起裂后压力下降幅度减小, 延伸阶段压力波动下降, 延伸压力较高, 形成迂曲窄缝。当形成纵向缝时, 压力剧烈波动上升, 呈现多峰值特征, 起裂阶段和延伸阶段区别不明显。

符号注释：

d— — 射孔深度, cm; f— — 水平应力反转程度, 无因次; H— — 缝高, m; Kh— — 水平应力差异系数, 无因次; L— — 裂缝半长, m; pf— — 已压缝内流体压力, MPa; pnet— — 已压缝内流体净压力, MPa; pnetD— — 无因次净压力; s— — 段间距, cm; x, y, z— — 直角坐标系, m; σ h— — 最小水平主应力, MPa; σ H— — 最大水平主应力, MPa; σ v— — 垂向应力, MPa; Δ σ — — 诱导应力差, MPa; σ cxx, σ cyy, σ czz— — 压裂裂缝产生的诱导正应力分量, MPa; ν — — 泊松比, 无因次。下标：M— — 物理实验数据; F— — 现场数据。

The authors have declared that no competing interests exist.

参考文献
[1] 吴奇, 胥云, 王晓泉, 等. 非常规油气藏体积改造技术: 内涵、优化设计与实现[J]. 石油勘探与开发, 2012, 39(3): 252-258.
WU Qi, XU Yun, WANG Xiaoquan, et al. Volume fracturing technology of unconventional reservoirs: Connotation, optimization design and implementation[J]. Petroleum Exploration and Development, 2012, 39(3): 252-258. [本文引用:1]
[2] 胥云, 陈铭, 吴奇, 等. 水平井体积改造应力干扰计算模型及其应用[J]. 石油勘探与开发, 2016, 43(5): 780-786.
XU Yun, CHEN Ming, WU Qi, et al. Stress interference calculation model and its application in volume stimulation of horizontal wells[J]. Petroleum Exploration and Development, 2016, 43(5): 780-786. [本文引用:3]
[3] CIPOLLA C L, WARPINSKI N R, MAYERHOFER M J, et al. The relationship between fracture complexity, reservoir properties, and fracture treatment design[R]. SPE 115769, 2008. [本文引用:1]
[4] MILLER C K, WATERS G A, RYLANDER E I. Evaluation of production log data from horizontal wells drilled in organic shales[R]. SPE 144326, 2011. [本文引用:2]
[5] WARPINSKI N R, BRANAGAN P T. Altered-stress fracturing[J]. Journal of Petroleum Technology, 1989, 41(9): 990-997. [本文引用:1]
[6] SOLIMAN M Y, HUNT J L, RABAA A M. Fracturing aspects of horizontal wells[J]. Journal of Petroleum Technology, 1990, 42(8): 966-973. [本文引用:1]
[7] OLSON J E, TALEGHANI A D. Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures[R]. SPE 119739, 2009. [本文引用:1]
[8] WATERS G A, DEAN B K, DOWNIE R C, et al. Simultaneous hydraulic fracturing of adjacent horizontal wells in the Woodford Shale[R]. SPE 119635, 2009. [本文引用:1]
[9] BUNGER A P, JEFFREY R G, KEAR J, et al. Experimental investigation of the interaction among closely spaced hydraulic fractures[J]. Strength of Materials, 2011, 19(8): 1160-1165. [本文引用:1]
[10] WU K, OLSON J E. Simultaneous multi-fracture treatments: Fully coupled fluid flow and fracture mechanics for horizontal wells[R]. SPE 167626, 2014. [本文引用:1]
[11] 潘林华, 张士诚, 程礼军, 等. 水平井“多段分簇”压裂簇间干扰的数值模拟[J]. 天然气工业, 2014, 34(1): 74-79.
PAN Linhua, ZHANG Shicheng, CHENG Lijun, et al. A numerical simulation of the inter-cluster interference in multi-cluster staged fracking for horizontal wells[J]. Natural Gas Industry, 2014, 34(1): 74-79. [本文引用:1]
[12] 郭建春, 周鑫浩, 邓燕. 页岩气水平井组拉链压裂过程中地应力的分布规律[J]. 天然气工业, 2015, 35(7): 44-48.
GUO Jianchun, ZHOU Xinhao, DENG Yan. Distribution rules of earth stress during zipper fracturing of shale gas horizontal cluster wells[J]. Natural Gas Industry, 2015, 35(7): 44-48. [本文引用:1]
[13] 赵金洲, 陈曦宇, 刘长宇, 等. 水平井分段多簇压裂缝间干扰影响分析[J]. 天然气地球科学, 2015, 26(3): 533-538.
ZHAO Jinzhou, CHEN Xiyu, LIU Changyu, et al. The analysis of crack interaction in multi-stage horizontal fracturing[J]. Natural Gas Geoscience, 2015, 26(3): 533-538. [本文引用:1]
[14] ZOU Y, ZHANG S C, MA X F, et al. Numerical investigation of hydraulic fracture network propagation in naturally fractured shale formations[J]. Journal of Structural Geology, 2016, 84: 1-13. [本文引用:2]
[15] GREEN A E, SNEDDON I N. The distribution of stress in the neighborhood of a crack in an elastic solid[J]. Proceedings of the Royal Society of London, 1946, 187(1009): 229-260. [本文引用:1]
[16] SNEDDON I N, ELLIOT H A. The opening of a griffith crack under internal pressure[J]. Quarterly of Applied Mathematics, 1946, 4(3): 262-267. [本文引用:1]
[17] 曾凡辉, 郭建春, 刘恒, 等. 致密砂岩气藏水平井分段压裂优化设计与应用[J]. 石油学报, 2013, 34(5): 959-968.
ZENG Fanhui, GUO Jianchun, LIU Heng, et al. Optimization design and application of horizontal well staged fracturing in tight gas reservoirs[J]. Acta Petrolei Sinica, 2013, 34(5): 959-968. [本文引用:1]
[18] 包劲青, 刘合, 张广明, 等. 分段压裂裂缝扩展规律及其对导流能力的影响[J]. 石油勘探与开发, 2017, 44(2): 281-288.
BAO Jinqing, LIU He, ZHANG Guangming, et al. Fracture propagation laws in staged hydraulic fracturing and their effects on fracture conductivities[J]. Petroleum Exploration and Development, 2017, 44(2): 281-288. [本文引用:1]
[19] 赵金洲, 陈曦宇, 李勇明, 等. 水平井分段多簇压裂模拟分析及射孔优化[J]. 石油勘探与开发, 2017, 44(1): 117-124.
ZHAO Jinzhou, CHEN Xiyu, LI Yongming, et al. Numerical simulation of multi-stage fracturing and optimization of perforation in a horizontal well[J]. Petroleum Exploration and Development, 2017, 44(1): 117-124. [本文引用:1]
[20] 陈铭, 胥云, 吴奇, 等. 水平井体积改造多裂缝扩展形态算法: 不同布缝模式的研究[J]. 天然气工业, 2016, 36(8): 79-87.
CHEN Ming, XU Yun, WU Qi, et al. Algorithm for multi-fracture propagation morphology in horizontal well volume fracturing: Investigation on different fracture distribution patterns[J]. Natural Gas Industry, 2016, 36(8): 79-87. [本文引用:1]
[21] MA X F, ZOU Y S, LI N, et al. Experimental study on the mechanism of hydraulic fracture growth in a glutenite reservoir[J]. Journal of Structure Geology, 2017, 97: 37-47. [本文引用:1]
[22] BEUGELSDIJK L J, PATER C J, SATO K. Experimental hydraulic fracture propagation in a multi-fractured medium[R]. SPE 59419-MS, 2000. [本文引用:2]
[23] 柳贡慧, 庞飞, 陈治喜. 水力压裂模拟实验中的相似准则[J]. 中国石油大学学报(自然科学版), 2000, 24(5): 45-48.
LIU Gonghui, PANG Fei, CHEN Zhixi. Similarity criterion in simulation experiment of hydraulic fracturing[J]. Journal of China University of Petroleum (Edition of Natural Science), 2000, 24(5): 45-48. [本文引用:2]
[24] 马新仿, 李宁, 尹丛彬, 等. 页岩水力裂缝扩展形态与声发射解释: 以四川盆地志留系龙马溪组页岩为例[J]. 石油勘探与开发, 2017, 44(6): 974-981.
MA Xinfang, LI Ning, YIN Congbin, et al. Hydraulic fracture propagation geometry and acoustic emission interpretation: A case study of Silurian Longmaxi Formation shale in Sichuan Basin, SW China[J]. Petroleum Exploration and Development, 2017, 44(6): 974-981. [本文引用:1]
[25] 李根生, 刘丽, 黄中伟, 等. 水力射孔对地层破裂压力的影响研究[J]. 中国石油大学学报(自然科学版), 2006, 30(5): 42-45.
LI Gensheng, LIU Li, HUANG Zhongwei, et al. Study of effect of hydraulic perforating on formation fracturing pressure[J]. Journal of China University of Petroleum (Edition of Natural Science), 2006, 30(5): 42-45. [本文引用:1]
[26] 雷鑫, 张士诚, 许国庆, 等. 射孔对致密砂岩气藏水力压裂裂缝起裂与扩展的影响[J]. 东北石油大学学报, 2015, 39(2): 94-101.
LEI Xin, ZHANG Shicheng, XU Guoqing, et al. Effect of perforation on initiation and propagation of hydraulic fracturing in tight sand stone gas reservoirs[J]. Journal of Northeast Petroleum University, 2015, 39(2): 94-101. [本文引用:1]