引用本文
张景楠, 狄勤丰, 华帅, 叶峰, 李原, 王文昌. 泡沫驱油核磁共振实验及泡沫动态稳定性评价[J]. 石油勘探与开发, 2018,45(5): 853-860.
ZHANG Jingnan, DI Qinfeng, HUA Shuai, YE Feng, LI Yuan, WANG Wenchang. Nuclear magnetic resonance experiments on foam flooding and evaluation of foam dynamic stability[J]. Petroleum Exploration & Development, 2018,45(5): 853-860.  
Doi: 10.11698/PED.2018.05.11
Permissions
Copyright©2018, 石油勘探与开发》编辑部
石油勘探与开发》编辑部 所有
泡沫驱油核磁共振实验及泡沫动态稳定性评价
张景楠1,2, 狄勤丰1,2, 华帅1,2, 叶峰1,2, 李原1,2, 王文昌1,2
1. 上海大学上海市应用数学和力学研究所,上海 200072
2. 上海市力学在能源工程中的应用重点实验室,上海 200072

联系作者简介：狄勤丰（1963-）,男,江苏溧阳人,博士,上海大学上海市应用数学和力学研究所教授,主要从事石油工程中力学问题的研究。地址：上海市静安区延长路149号,上海大学上海市应用数学和力学研究所,邮政编码：200072。E-mail：qinfengd@sina.com

第一作者简介：张景楠（1988-）,男,甘肃庆阳人,上海大学上海市应用数学和力学研究所在读博士研究生,主要从事提高采收率技术及岩心驱替核磁共振可视化等方面的研究。地址：上海市静安区延长路149号,上海大学上海市应用数学和力学研究所,邮政编码：200072。E-mail：zjn305@163.com

收稿日期: 2018-02-06
基金项目: 国家自然科学基金（50874071,51704191）; 上海市重点学科建设项目（S30106）; 中国石油科技创新基金（2017D-5007-0209）
摘要

将核磁共振技术与传统岩心驱替实验相结合形成一种泡沫驱油核磁共振实验方法,在此基础上建立了评价泡沫在岩心中驱油时动态稳定性的新方法,研究了泡沫体系S-2（主要成分为十二烷基硫酸钠）和S-NP-2（主要成分为十二烷基硫酸钠和二氧化硅纳米颗粒）在直接泡沫驱和水驱后泡沫驱下的驱油特征以及泡沫的动态稳定性。研究表明,通过核磁共振图像和 T2（横向弛豫时间）谱可以直观反映泡沫的驱油特征;水驱后进一步使用泡沫体系S-2和S-NP-2驱替后的驱油效率提高幅度分别为18.05%和25.68%,最终驱油效率分别达到63.72%和67.50%,高于直接使用泡沫驱替时的驱油效率;同一泡沫体系在水驱后泡沫驱的方式中比在直接泡沫驱的方式中稳定性更好,相同驱替方式下泡沫体系S-NP-2比泡沫体系S-2更稳定。图12表6参26

关键词: 泡沫驱; 驱替实验; 驱油效率; 核磁共振; 泡沫稳定性; 评价方法
中图分类号:TE357.46 文献标志码:A 文章编号:1000-0747(2018)05-0853-08
Nuclear magnetic resonance experiments on foam flooding and evaluation of foam dynamic stability
ZHANG Jingnan1,2, DI Qinfeng1,2, HUA Shuai1,2, YE Feng1,2, LI Yuan1,2, WANG Wenchang1,2
1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai 200072, China
2. Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai 200072, China
Abstract

A visualization experimental method of foam flooding was developed by combining nuclear magnetic resonance (NMR) and traditional core flooding method. On this basis, a new method to evaluate the dynamic stability of foam in the core during displacement process was established. Using this method, the displacement characteristics and dynamic stability of foam of S-2 (the main component is sodium lauryl sulfate) and S-NP-2 (the main components are sodium lauryl sulfate and silica nanoparticles) in two different displacement modes, i.e. direct foam flooding and foam flooding after water flooding, were studied. The results show that the NMR images and the T2(transverse relaxation time) spectrum reflected the displacement characteristics. The flooding efficiency of S-2 and S-NP-2 after water flooding was increased by 18.05% and 25.68% and reached 63.72% and 67.50% respectively at last, higher than direct foam flooding. The same foam system had better stability in foam flooding after water flooding than in direct foam flooding, and foam S-NP-2 is more stable than foam S-2 under the same displacement mode.

Keyword: foam flooding; flooding experiment; flooding efficiency; nuclear magnetic resonance (NMR); foam stability; evaluation method
0 引言

泡沫驱可以显著提高原油采收率已得到广泛认同[1, 2, 3], 利用常规的岩心驱替装置无法观察到岩心内部流体的流动特征, 导致泡沫在微孔道中的作用机理研究存在困难。目前主要使用基于微观显微技术观察薄片模型的方法来研究泡沫微观驱油特征[4, 5], 由于该方法要求薄片模型厚度必须小于3 mm以保证其透光性, 限制了流体沿模型厚度方向的流动, 因此该方法只能模拟二维流动, 不能真实地反映储集层流体流动特征[6]。此外, 泡沫的稳定性是影响泡沫驱油效率的关键因素[7]。目前泡沫稳定性评价方法主要有体积法、电导率法和压力法等[8], 其中体积法又分为Ross-Miles法、振荡法及Waring-Blender法[9, 10, 11]。体积法因操作简单, 适用范围广泛, 是目前评价泡沫稳定性常用的方法, 但因为实际操作过程中人为误差较大, 难以定量描述泡沫的性能。电导率法和压力法灵敏度高, 但是装置复杂, 费用较高, 不易操作[12]。而且以上方法均是在静置的容器中评价泡沫的稳定性, 属于静态稳定性范畴。实际的泡沫驱油过程发生在多孔介质中, 泡沫在其中的运移是一种不断消泡并不断再生成的动态过程, 使用脱离多孔介质的静态评价方法不能真实反映泡沫在储集层中的稳定性[6, 13], 而对于泡沫在驱替过程中的动态稳定性研究较少。阻力因子可以反映泡沫在驱替过程中的封堵能力, 在一定程度上能够体现泡沫的动态稳定性。然而该方法主要基于泡沫驱过程中贾敏效应引起的压力变化[14], 在实际实验过程中, 压力变化受多种因素的影响[15], 而且泡沫驱过程中压力很难达到稳定, 需要注入大量的泡沫才能使压力趋于平稳。因此, 有必要建立一种新的泡沫动态稳定性评价方法。

本文将核磁共振技术与传统泡沫驱替实验相结合, 开展泡沫驱油核磁共振实验。利用核磁共振T2（横向弛豫时间）谱反映岩心中流体所处的孔隙平均尺寸变化及岩心中流体质量变化[16, 17], 通过获取核磁共振图像直观地观察泡沫在岩心中的驱油特征。同时基于核磁共振T2谱和质量守恒定律, 建立一种评价泡沫在岩心中驱油时动态稳定性的新方法。在此基础上, 研究两种泡沫体系在不同驱替方式（直接泡沫驱和水驱后泡沫驱）下的驱油特征及泡沫的动态稳定性。

1 泡沫驱油核磁共振实验
1.1 实验原理

岩心内液体分子的运动使得分子多次与岩石微通道壁面发生碰撞, 在每次碰撞中会发生两种弛豫过程, 即纵向弛豫和横向弛豫。通常纵向弛豫的测量时间较长且测点数较少, 因此在岩心的核磁共振测试中一般测试横向弛豫。横向弛豫包含3种不同的弛豫机制：自由弛豫、表面弛豫及扩散弛豫[18]。3种弛豫机制对横向弛豫时间的影响主要取决于流体类型、孔隙尺寸、表面弛豫强度等, 利用核磁共振T2谱可以对样品进行一系列的物性分析[19]。横向弛豫时间与岩心内液体所处的孔隙尺寸成正比, 信号幅度与横向弛豫时间围成的峰面积与岩心内液体质量成正比[20]。核磁共振成像原理是：通过在目标物体上施加3个相互垂直可控的线性梯度磁场实现核磁信号的空间定位, 接收设备获取核磁共振信号的幅度及与之对应的空间位置信息, 经过一定的处理可以得到样品的核磁共振图像[17]。

1.2 水、泡沫与油的核磁信号区分方法

泡沫驱油核磁共振实验中, 为了直观研究泡沫的驱油特征, 需要在获取的核磁共振T2谱和图像中明确区分水、油及泡沫。水驱油时, 由于油和水的核磁共振弛豫时间有重叠部分, 导致两者的核磁信号不能明确区分, 因而无法在实验获得的T2谱中区分油峰和水峰, 也无法在图像中区分油和水的分布。使用MnCl2水溶液代替清水进行驱替时, Mn2+与水中H质子直接接触会产生自旋交换作用, 使得水中H质子的弛豫衰减加快[21], 油和水的弛豫时间不再有重叠部分, 从而达到区分两者核磁信号的目的。多次实验结果表明, 使用质量分数为0.5%的MnCl2水溶液代替水进行驱替时可以达到区分油、水核磁信号的最佳效果[22]。泡沫驱油时, 泡沫中的气相不产生核磁信号, 而油和泡沫中水相的核磁共振弛豫时间同样有重叠部分。实验表明, 向泡沫液中加入质量分数为0.5%的MnCl2, 同样可实现泡沫与油的核磁信号区分。但是使用该方法的前提是要保证添加MnCl2后不会影响泡沫体系的性能。因此, 使用Waring-Blender法对添加MnCl2前后两种泡沫体系（S-2和S-NP-2）的性能进行了评价, 每组实验重复3次后取平均值, 实验结果如表1所示。

表1 25 ℃时不同MnCl2浓度下泡沫的起泡体积和半衰期

由表1可知, 添加MnCl2前后泡沫体系的起泡性和稳定性基本相同, 表明向泡沫体系中加入质量分数为0.5%的MnCl2不会显著影响泡沫的性能。因此, 本文在泡沫体系配制和水驱时均使用质量分数为0.5%的MnCl2水溶液代替清水。

1.3 实验材料

泡沫驱油核磁共振实验所用材料包括：蒸馏水、MnCl2、模拟油（由过滤后的柴油和原油按照10:1的质量比进行配制, 25 ℃时黏度为2.5 mPa· s）、氮气、岩心（人造岩心, 物性参数如表2所示）、泡沫体系S-2（主要成分为十二烷基硫酸钠, 质量分数为3%）、泡沫体系S-NP-2（主要成分为十二烷基硫酸钠和二氧化硅纳米颗粒, 质量分数分别为3.0%和0.5%）等。其中, 泡沫体系S-NP-2是在泡沫体系S-2的基础上, 与不同粒径、不同润湿性的纳米颗粒及不同修饰剂进行复配, 通过大量实验获得的一种纳米颗粒稳定型起泡体系。由表1可知, 泡沫体系S-NP-2的起泡性和稳定性均优于泡沫体系S-2。

表2 岩心样品物性参数
1.4 实验装置及步骤

基于核磁共振成像技术的可视化驱替实验装置如图1所示, 主要包括恒速恒压泵、中间容器、泡沫发生器、特种岩心夹持器、核磁共振单元、控制单元、计量单元等。

图1 核磁共振泡沫驱替实验装置

实验步骤为：①检测岩心磁性, 确保实验用岩心不含铁等干扰磁场的物质; ②测试岩心物性参数; ③抽真空加压, 饱和水; ④核磁共振T2谱和成像参数调试; ⑤饱和油, 建立束缚水, 待岩心出口含水率为零后静置老化48 h; ⑥水驱：以0.5 mL/min的速度恒速注入水, 水驱至出口含水率大于98%后停止, 回压0 MPa; ⑦泡沫驱：控制泡沫的气液比为1:1, 注入速度为0.5 mL/min, 驱替至出口含水率大于98%后停止, 回压0 MPa; ⑧注入过程中记录注入压力和出液量, 并获取核磁共振T2谱和图像。

2 实验结果及讨论

为了研究泡沫体系S-2和S-NP-2直接驱油（驱替方式1）及水驱后驱油（驱替方式2）的特征及效果, 使用1#— 4#岩心分别进行了4组实验。其中1#和2#岩心采用驱替方式1, 3#和4#岩心采用驱替方式2。1#和3#岩心使用泡沫体系S-2, 2#和4#岩心使用泡沫体系S-NP-2。

2.1 驱油效率

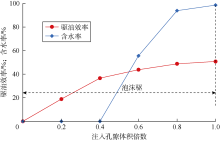
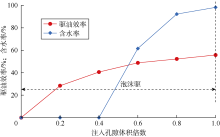
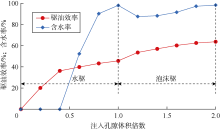
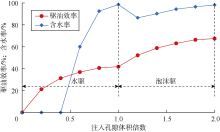
通过出口计量方式得到的4组实验的驱油效率和出口含水率随注入孔隙体积倍数（PV）的变化曲线如图2— 图5所示。

图2 1#岩心实验的驱油效率和含水率

由图2、图3可知, 对于1#岩心和2#岩心, 直接使用泡沫驱替, 驱至0.4 PV时岩心出口端开始见水, 此后出口含水率急剧上升, 驱油效率趋于平缓; 驱至1.0 PV时出口含水率大于98%, 此时1#岩心和2#岩心的驱油效率分别为50.80%和55.80%。由图4、图5可知, 对于3#岩心和4#岩心, 水驱至1.0 PV时出口含水率均大于98%, 此时驱油效率分别为45.67%和41.82%; 进一步使用泡沫进行驱替, 出口含水率明显下降后又缓慢上升, 直至出口含水率大于98%时停止驱替, 此时3#岩心和4#岩心的驱油效率分别为63.72%和67.50%。

图3 2#岩心实验的驱油效率和含水率

图4 3#岩心实验的驱油效率和含水率

图5 4#岩心实验的驱油效率和含水率

从表3中可以看出, 1#岩心和2#岩心泡沫驱后的驱油效率分别低于3#岩心和4#岩心泡沫驱后的驱油效率, 表明驱替方式2相比于驱替方式1能够获得更高的驱油效率。2#岩心和4#岩心泡沫驱后的驱油效率分别高于1#岩心和3#岩心泡沫驱后的驱油效率, 表明相同驱替方式下使用泡沫体系S-NP-2取得的驱油效果更好。水驱后使用泡沫驱, 3#岩心驱油效率提高幅度为18.05%, 4#岩心驱油效率提高幅度为25.68%, 可见水

驱后转泡沫驱可以明显提高驱油效率, 且泡沫体系S-NP-2提高采收率效果更好。

表3 4组泡沫驱替实验的驱油效率
2.2 阻力因子

阻力因子是注泡沫时压力达到平稳后岩心两端的压差与相同条件下单纯注水时岩心两端的压差之比, 是评价泡沫封堵能力的重要指标[23]。由于实验过程中图像采集和T2谱测试阶段需要停止泡沫的注入, 相比传统的泡沫驱替实验, 很难得到整个驱替过程完整连续的压力监测曲线。因此, 在最后一次图像采集和T2谱测试结束后, 持续注入泡沫至压力平稳, 记录此时的压差为注泡沫压差。

从表4中可以看出, 4组实验中泡沫均起到了很好的封堵作用。其中, 1#岩心和2#岩心的阻力因子分别小于3#岩心和4#岩心的阻力因子, 表明水驱后使用泡沫驱相比于直接使用泡沫驱能够取得更好的封堵效果。2#岩心和4#岩心的阻力因子分别大于1#岩心和3#岩心的阻力因子, 表明相同驱替方式下泡沫体系S-NP-2的封堵能力更好。

表4 4组泡沫驱替实验的阻力因子
2.3 核磁共振图像

4组泡沫驱油实验的核磁共振图像如图6和图7所示, 图中黑色无信号区域为水或泡沫, 其余彩色部分为油。

图6 直接泡沫驱岩心核磁共振图像

图7 水驱后泡沫驱岩心核磁共振图像

从图6中可以看出, 直接使用泡沫驱油至0.5 PV时, 产生明显的驱替前缘, 剩余油集中分布在驱替前缘的前方（岩心中右部区域）; 驱替前缘的后方仅有少量残余油分布; 驱至1.0 PV时, 没有明显的剩余油富集区, 少量残余油遍布在整个岩心, 表明泡沫的波及效率较高, 洗油效果显著。从图7中可以看出, 水驱1.0 PV后岩心中的含油饱和度明显降低, 但由于水的洗油效果相对较差, 水驱后大量残余油遍布在整个岩心; 进一步使用泡沫驱替时的驱油特征与直接使用泡沫驱油的特征较为相似, S-2和S-NP-2的驱油特征也没有明显的区别; 两种泡沫体系驱替1.0 PV后, 仅有少量残余油分布在岩心内, 可见相比于水, 泡沫的洗油效果更好。

通过核磁共振图像可以直观观察泡沫的驱油特征, 但是对于两种性能不同的泡沫体系, 很难反映两者在岩心中驱油特征的异同。

2.4 核磁共振T2谱

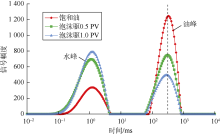
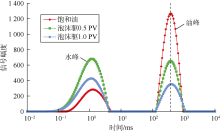
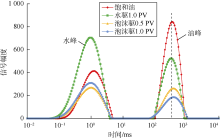
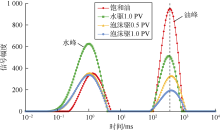
两种泡沫体系在驱替方式1下的核磁共振T2谱如图8、图9所示, 在驱替方式2下的核磁共振T2谱如图10、图11所示。图中左侧弛豫时间较短的峰为水峰, 右侧弛豫时间较长的峰为油峰。

图8 1#岩心实验的T2谱

图9 2#岩心实验的T2谱

图10 3#岩心实验的T2谱

图11 4#岩心实验的T2谱

从图8— 图11中可以看出, 随着驱替剂的注入, 油峰均逐渐下降, 表明泡沫驱油效果明显。1#岩心和2#岩心直接进行泡沫驱, 油峰下降过程中顶点没有明显的偏移, 表明在未水驱情况下直接使用泡沫驱油时, 岩心内不同大小孔隙出油比较均匀。3#岩心和4#岩心先水驱再泡沫驱, 水驱时油峰下降过程中顶点出现偏移, 其中3#岩心向左偏移46.29 ms, 4#岩心向左偏移23.94 ms。这是因为水驱油时大孔隙出油较多, 则弛豫时间缩短, 油峰向左偏移。水驱结束后继续使用泡沫驱, 两块岩心的油峰顶点均向右偏移, 3#岩心向右偏移71.96 ms, 4#岩心向右偏移77.14 ms。表明泡沫起到了一定的调剖作用, 该阶段小孔隙出油较多, 则弛豫时间延长, 油峰向右偏移。

3 驱油过程中泡沫动态稳定性评价方法

本文尝试基于核磁共振T2谱和质量守恒定律建立一种评价泡沫在驱油过程中动态稳定性的新方法。

3.1 方法的建立

3.1.1 质量守恒方程

泡沫驱油时, 在岩心入口端注入水相和气相, 出口端流出气相、水相和油相, 如图12所示。根据质量守恒定律[24], 在一定时间内, 岩心质量变化量等于流入岩心与流出岩心的流体质量差, 据此建立泡沫驱油的质量守恒方程：

$\Delta m={{m}_{\text{w, in}}}+{{m}_{\text{g, in}}}-\left( {{m}_{\text{w, out}}}+{{m}_{\text{g, out}}}+{{m}_{\text{o, out}}} \right)$ （1）

图12 岩心泡沫驱示意图

3.1.2 气液体积比与气液质量比的转换

室内实验控制的气液比一般为气液体积比, 为了代入质量守恒方程, 需要将气液体积比转化为质量比。岩心入口端气液质量比和体积比计算公式分别为：

${{n}_{\text{m, in}}}=\frac{{{m}_{\text{g, in}}}}{{{m}_{\text{w, in}}}}$ （2）

${{n}_{\text{v, in}}}=\frac{{{V}_{\text{g, in}}}}{{{V}_{\text{w, in}}}}$ （3）

由理想气体状态方程可得：

${{\rho }_{\text{g, in}}}=\frac{{{p}_{\text{in}}}M}{R{{T}_{\text{in}}}}$ （4）

由（2）— （4）式可知：

${{n}_{\text{m, in}}}=\frac{{{m}_{\text{g, in}}}}{{{m}_{\text{w, in}}}}=\frac{{{V}_{\text{g, in}}}{{\rho }_{\text{g, in}}}}{{{V}_{\text{w, in}}}{{\rho }_{\text{w, in}}}}={{n}_{\text{v, in}}}\frac{{{p}_{\text{in}}}M}{{{\rho }_{\text{w, in}}}R{{T}_{\text{in}}}}$ （5）

因为水相中添加了表面活性剂等, 具体计算时需要参照GB/T 2013— 2010《液体石油化工产品密度测定法》中所述的方法对水相密度进行严格测试。

3.1.3 泡沫驱过程中油水的质量变化量

通过积分可以获得核磁共振T2谱水峰曲线和油峰曲线与横坐标围成的峰面积。峰面积与岩心内与之对应的流体的质量成正比, 据此可以获得泡沫驱过程中油和水的质量变化量, 即：

$\Delta {{m}_{\text{o}}}=-{{m}_{\text{o, out}}}=\frac{{{m}_{\text{oi}}}}{{{A}_{\text{oi}}}}\Delta {{A}_{\text{o}}}$ （6）

$\Delta {{m}_{\text{w}}}={{m}_{\text{w, in}}}-{{m}_{\text{w, out}}}=\frac{{{m}_{\text{wi}}}}{{{A}_{\text{wi}}}}\Delta {{A}_{\text{w}}}$ （7）

3.1.4 泡沫动态不稳定因子

将（5）— （7）式代入（1）式可得：

${{n}_{\text{m, in}}}=\frac{{{m}_{\text{g, out}}}-\left[ \Delta {{m}_{\text{o}}}+\left( {{n}_{\text{m, in}}}+1 \right)\Delta {{m}_{\text{w}}}-\Delta m \right]}{{{m}_{\text{w, out}}}}$ （8）

驱替至出口含水率大于98%且出口出现连续泡沫时岩心内部泡沫气液比为：

${{n}_{\text{m}}}=\frac{{{m}_{\text{g, in}}}-{{m}_{\text{g, out}}}}{{{m}_{\text{w, in}}}-{{m}_{\text{w, out}}}+{{m}_{\text{w}}}}=$

${{n}_{\text{m, in}}}-\frac{{{n}_{\text{m, in}}}{{m}_{\text{w}}}+\Delta {{m}_{\text{o}}}+\left( {{n}_{\text{m, in}}}+1 \right)\Delta {{m}_{\text{w}}}-\Delta m}{\Delta {{m}_{\text{w}}}+{{m}_{\text{w}}}}$ （9）

令：

$s=-\frac{{{n}_{\text{m, in}}}{{m}_{\text{w}}}+\Delta {{m}_{\text{o}}}+\left( {{n}_{\text{m, in}}}+1 \right)\Delta {{m}_{\text{w}}}-\Delta m}{\Delta {{m}_{\text{w}}}+{{m}_{\text{w}}}}$ （10）

则：

${{n}_{\text{m}}}={{n}_{\text{m, in}}}+s$ （11）

王力等[25]通过观察大量的氮气泡沫驱实验发现, 气液比在一定程度上体现了泡沫的稳定性, 气液比较低时, 泡沫生成缓慢且生成量较少, 在岩心驱替过程中压力较低, 阻力因子较小; 气液比较高时, 产生的泡沫体积大且稀疏、易灭, 阻力因子也较小。

（11）式中的s体现了泡沫进入岩心后气液比的变化程度。当s=0时, nm=nm, in, 表明泡沫进入岩心后气液比未发生变化, 泡沫的破灭速度和生成速度达到动态平衡, 为理想的稳定状态; 当s> 0时, nm> nm, in, 表明泡沫进入岩心后气液比增大, 岩心内液体比例减小, 泡沫排液; 当s< 0时, nm< nm, in, 表明泡沫进入岩心后气液比减小, 岩心内气体比例减小, 泡沫消泡; $\left| s \right|$越小, 泡沫进入岩心后气液比的变化程度越小, 泡沫越接近理想的稳定状态, 稳定性越好。因此, 定义泡沫的动态不稳定因子为：

$f=\left| s \right|$ （12）

可见, f越大, 泡沫的动态稳定性越差; f越小, 泡沫的动态稳定性越好。

3.2 泡沫稳定性评价

根据以上方法, 对4组实验泡沫驱油过程中泡沫在岩心中的稳定性进行了评价。本文泡沫驱实验使用的气体为氮气, 摩尔质量为0.028 kg/mol; 等温渗流, 温度为298.15 K, 入口气液体积比为1.00。4组实验中泡沫动态不稳定因子计算结果如表5所示。

表5 4组实验泡沫动态不稳定因子计算结果

从表5中可以看出, 同一泡沫体系在驱替方式2中的稳定性较好。这是因为在驱替方式1中直接使用泡沫驱时, 含油饱和度较高, 泡沫液膜遇油后形成一种“ 假乳液膜” , 降低了泡沫的稳定性[26]。同时有效的表面活性剂浓度减小, 在后续驱油过程中重新生成泡沫的能力也减弱。而驱替方式2中水驱阶段使含油饱和度显著降低, 后续泡沫驱时避免了高含油饱和度的影响。也正是由于以上原因, 驱替方式2相比于驱替方式1可以获得更高的驱油效率。

3.3 可靠性验证

阻力因子可以直接体现泡沫在多孔介质中的封堵性能, 由于稳定性的优劣决定了泡沫的封堵效果, 因此阻力因子能在一定程度上反映泡沫在岩心驱替过程中的稳定性。将4组实验的泡沫动态不稳定因子及阻力因子进行对比（见表6）, 可以看出, 相同驱替方式下, 泡沫体系S-NP-2的动态不稳定因子小于泡沫体系S-2, 泡沫体系S-NP-2对应的阻力因子也高于泡沫体系S-2。因此, 两种方法均表明, 相同驱替方式下泡沫体系S-NP-2在岩心驱替过程中的稳定性优于泡沫体系S-2。这说明采用本文建立的泡沫动态稳定性评价方法得到的结果与采用阻力因子法得到的结果相吻合, 这也验证了本文建立方法的可靠性。

表6 4组实验的动态不稳定因子及阻力因子对比
4 结论

形成了一种泡沫驱油核磁共振实验方法, 可以通过核磁共振图像和T2谱直观反映泡沫的驱油特征。不同驱替方式下, 泡沫的洗油效果显著, 波及效率较高。通过横向弛豫时间的变化可以看出水驱后使用泡沫驱时泡沫起到了一定的调剖作用。

在回压为0 MPa的条件下, 水驱后使用泡沫体系S-2和S-NP-2驱替后的驱油效率提高幅度分别为18.05%和25.68%, 最终驱油效率分别达到63.72%和67.50%, 高于直接使用泡沫驱时的驱油效率。

基于核磁共振T2谱和质量守恒定律建立了一种研究泡沫在岩心中驱油时动态稳定性的新方法。使用该方法研究表明, 相同驱替方式下, 泡沫体系S-NP-2在岩心驱替过程中的稳定性优于泡沫体系S-2。

符号注释：

Aoi, Awi— — 饱和油和饱和水状态下油峰和水峰曲线与T2谱横坐标围成的峰面积, 无因次; Δ Ao, Δ Aw— — 油峰和水峰曲线与T2谱横坐标围成的峰面积的变化量, 无因次; f— — 泡沫的动态不稳定因子; moi, mwi— — 饱和油和饱和水状态下岩心中油和水的质量, kg; Δ m— — 岩心质量变化量, kg; Δ mo, Δ mw— — 岩心中油和水的质量变化量, kg; mw— — 泡沫驱前岩心中水相的质量, kg; mg, in, mw, in— — 岩心入口端气相和水相的质量, kg; mg, out, mo, out, mw, out— — 岩心出口端气相、油相和水相的质量, kg; M— — 摩尔质量, kg/mol; nm— — 岩心内部气液比, 无因次; nm, in, nv, in— — 岩心入口端气液质量比和体积比, 无因次; pin— — 岩心入口端压力, Pa; R— — 理想气体常数, 8.314 J/（mol· K）; Tin— — 岩心入口端温度, K; Vg, in, Vw, in— — 岩心入口端气相和水相的体积, m3; ρ g, in— — 岩心入口端气相密度, kg/m3; ρ w, in— — 岩心入口端水相密度, kg/m3。

The authors have declared that no competing interests exist.

参考文献
[1] 周国华, 宋新旺, 王其伟. 泡沫复合驱在胜利油田的应用[J]. 石油勘探与开发, 2006, 33(3): 369-373.
ZHOU Guohua, SONG Xinwang, WANG Qiwei. Application of foam combination flooding in Shengli Oilfield[J]. Petroleum Exploration and Development, 2006, 33(3): 369-373. [本文引用:1]
[2] 庞占喜, 刘慧卿, 盖平原, 等. 热力泡沫复合驱物理模拟和精细数字化模拟[J]. 石油勘探与开发, 2012, 39(6): 791-797.
PANG Zhanxi, LIU Huiqin, GAI Pingyuan, et al. Physical simulation and fine digital study of thermal foam compound flooding[J]. Petroleum Exploration and Development, 2012, 39(6): 791-797. [本文引用:1]
[3] 王其伟. 泡沫驱油发展现状及前景展望[J]. 石油钻采工艺, 2013, 35(2): 94-97.
WANG Qiwei. Present situation and development prospect of foam flooding[J]. Oil Drilling & Production Technology, 2013, 35(2): 94-97. [本文引用:1]
[4] 李雪松, 王军志, 王曦. 多孔介质中泡沫驱油微观机理研究[J]. 石油钻探技术, 2009, 37(5): 109-113.
LI Xuesong, WANG Junzhi, WANG Xi. Studies of microcosmic foam driving mechanism in porous medium[J]. Petroleum Drilling Techniques, 2009, 37(5): 109-113. [本文引用:1]
[5] GUO F, ARYANA S. An experimental investigation of nanoparticle- stabilized CO2 foam used in enhanced oil recovery[J]. Fuel, 2016, 186: 430-442. [本文引用:1]
[6] LIFTON V A. Microfluidics: An enabling screening technology for enhanced oil recovery (EOR)[J]. Lab on a Chip, 2016, 16(10): 1777-1796. [本文引用:2]
[7] WEI B, LI H, LI Q, et al. Investigation of synergism between surface-grafted nano-cellulose and surfactants in stabilized foam injection process[J]. Fuel, 2017, 211: 223-232. [本文引用:1]
[8] 王莉娟, 张高勇, 董金凤, 等. 泡沫性能的测试和评价方法进展[J]. 日用化学工业, 2005, 35(3): 171-173.
WANG Lijuan, ZHANG Gaoyong, DONG Jinfeng, et al. Progress in test and evaluation methods for foaming performance[J]. China Surfactant Detergent & Cosmetics, 2005, 35(3): 171-173. [本文引用:1]
[9] FARHADI H, RIAHI S, AYATOLLAHI S, et al. Experimental study of nanoparticle-surfactant-stabilized CO2 foam: Stability and mobility control[J]. Chemical Engineering Research & Design, 2016, 111: 449-460. [本文引用:1]
[10] SINGH R, MOHANTY K K. Synergy between nanoparticles and surfactants in stabilizing foams for oil recovery[J]. Energy & Fuels, 2015, 29(2): 467-479. [本文引用:1]
[11] BINKS B P, HOROZOV T S. Aqueous foams stabilized solely by silica nanoparticles[J]. Angewand te Chemie (International ed. in English), 2005, 44(24): 3722-3725. [本文引用:1]
[12] RAYMUNDO A, EMPIS J, SOUSA I. Method to evaluate foaming performance[J]. Journal of Food Engineering, 1998, 36(4): 445-452. [本文引用:1]
[13] 杜东兴, 王德玺, 贾宁洪, 等. 多孔介质内CO2泡沫液渗流特性实验研究[J]. 石油勘探与开发, 2016, 43(3): 456-461.
DU Dongxing, WANG Dexi, JIA Ninghong, et al. Experiments on CO2 foam seepage characteristics in porous media[J]. Petroleum Exploration and Development, 2016, 43(3): 456-461. [本文引用:1]
[14] 李兆敏, 李冉, 刘伟, 等. 泡沫在油气田开发中的应用及展望(Ⅱ): 泡沫流体在近井及地层中的应用[J]. 油田化学, 2013, 30(1): 155-160.
LI Zhaomin, LI Ran, LIU Wei, et al. Application and outlook of foam in oil and gas field development(Ⅱ): Application of foam fluid in immediate vicinity of wellbore and formation[J]. Oilfield Chemistry, 2013, 30(1): 155-160. [本文引用:1]
[15] 张广卿, 刘伟, 李敬, 等. 泡沫封堵能力影响因素实验研究[J]. 油气地质与采收率, 2012, 19(2): 44-46.
ZHANG Guangqing, LIU Wei, LI Jing, et al. Experimental study on the factors influencing the blocking ability of foam[J]. Petroleum Geology and Recovery Efficiency, 2012, 19(2): 44-46. [本文引用:1]
[16] 周波, 侯平, 王为民, 等. 核磁共振成像技术分析油运移过程中含油饱和度[J]. 石油勘探与开发, 2005, 32(6): 78-81.
ZHOU Bo, HOU Ping, WANG Weimin, et al. Oil saturation analysis in migration pathways with NMR imaging technique[J]. Petroleum Exploration and Development, 2005, 32(6): 78-81. [本文引用:1]
[17] 狄勤丰, 张景楠, 华帅, 等. 聚合物-弱凝胶调驱核磁共振可视化实验[J]. 石油勘探与开发, 2017, 44(2): 270-274.
DI Qinfeng, ZHANG Jingnan, HUA Shuai, et al. Visualization experiments on polymer-weak gel profile control and displacement by NMR technique[J]. Petroleum Exploration and Development, 2017, 44(2): 270-274. [本文引用:2]
[18] 俎栋林. 核磁共振成像学[M]. 北京: 高等教育出版社, 2004.
ZU Donglin. Magnetic resonance imaging[M]. Beijing: Higher Education Press, 2004. [本文引用:1]
[19] 李彰明, 曾文秀, 高美连, 等. 典型荷载条件下淤泥孔径分布特征核磁共振试验研究[J]. 物理学报, 2014, 63(5): 057401.
LI Zhangming, ZENG Wenxiu, GAO Meilian, et al. Nuclear magnetic resonance experimental study on the characteristics of pore-size distribution in muck under several typical loading cases[J]. Acta Physica Sinica, 2014, 63(5): 057401. [本文引用:1]
[20] 谷潇雨, 蒲春生, 黄海, 等. 渗透率对致密砂岩储集层渗吸采油的微观影响机制[J]. 石油勘探与开发, 2017, 44(6): 948-954.
GU Xiaoyu, PU Chunsheng, HUANG Hai, et al. Micro-influencing mechanism of permeability on spontaneous imbibition recovery for tight sand stone reservoirs[J]. Petroleum Exploration and Development, 2017, 44(6): 948-954. [本文引用:1]
[21] 狄勤丰, 张景楠, 叶峰. 驱替过程中重力舌进特征的核磁共振可视化实验[J]. 石油学报, 2017, 38(10): 1183-1188.
DI Qinfeng, ZHANG Jingnan, YE Feng. Nuclear magnetic resonance visualization experiment of gravity tongue characteristics in the displacement process[J]. Acta Petrolei Sinica, 2017, 38(10): 1183-1188. [本文引用:1]
[22] CHENG Y C, DI Q F, GU C Y, et al. Visualization study on fluid distribution and end effects in core flow experiments with low-field mri method[J]. Journal of Hydrodynamics, Ser. B, 2015, 27(2): 187-194. [本文引用:1]
[23] 王增林. 强化泡沫驱提高原油采收率技术[M]. 北京: 中国科学技术出版社, 2007.
WANG Zenglin. Enhanced foam flooding for EOR[M]. Beijing: China Science and Technology Press, 2007. [本文引用:1]
[24] 孔祥言. 高等渗流力学[M]. 合肥: 中国科学技术大学出版社, 2010.
KONG Xiangyan. Advanced fluid flow in porous media[M]. Hefei: University of Science and Technology of China Press, 2010. [本文引用:1]
[25] 王力. 氮气泡沫稳定性评价[J]. 石油地质与工程, 2009, 23(4): 119-122.
WANG li. Stability evaluation of nitrogen foam[J]. Petroleum Geology and Engineering, 2009, 23(4): 119-122. [本文引用:1]
[26] 廖广志, 李立众, 孔繁华. 常规泡沫驱技术[M]. 北京: 石油工业出版社, 1999.
LIAO Guangzhi, LI Lizhong, KONG Fanhua. Conventional foam flooding techology[J]. Beijing: Petroleum Industry Press, 1999. [本文引用:1]