引用本文
柳潇雄, 蒋有伟, 吴永彬, 王家禄. 双水平井蒸汽辅助重力泄油恒温电预热数学模型与指标预测[J]. 石油勘探与开发, 2018,45(5): 839-846.
LIU Xiaoxiong, JIANG Youwei, WU Yongbin, WANG Jialu. A mathematical model and relevant index prediction for constant-temperature electric heating of dual-horizontal-well SAGD start-up[J]. Petroleum Exploration & Development, 2018,45(5): 839-846.  
Doi: 10.11698/PED.2018.05.09
Permissions
Copyright©2018, 石油勘探与开发》编辑部
石油勘探与开发》编辑部 所有
双水平井蒸汽辅助重力泄油恒温电预热数学模型与指标预测
柳潇雄1,2, 蒋有伟1,2, 吴永彬1,2, 王家禄2
1. 提高石油采收率国家重点实验室,北京 100083
2. 中国石油勘探开发研究院,北京 100083

第一作者简介：柳潇雄（1991-）,男,重庆人,中国石油勘探开发研究院在读硕士研究生,主要从事热力采油、油藏工程、油藏数值模拟和油藏开发软件研发方面的工作。地址：北京市海淀区学院路20号,中国石油勘探开发研究院热力采油研究所,邮政编码：100083。E-mail: Albert_Liu9513@foxmail.com

收稿日期: 2018-02-09
基金项目: 中国石油勘探开发研究院超前研究项目“稠油高能电磁/电阻加热开采技术研究”（2015YJ-07）
摘要

建立了恒温控制模式下双水平井蒸汽辅助重力泄油（SAGD）油层电预热数学模型,并采用拉普拉斯变换和Stehfest数值反演对模型进行求解,同时选取双水平井SAGD开发区块典型井组,运用数值模拟方法验证了模型的准确性与可靠性。基于叠加原理,求解了地层中多井工作时的地温分布与能耗参数,建立了电加热相对于蒸汽加热的累计节能、节水和节省燃料当量的计算方法。通过对影响预热效果的主要参数进行敏感性分析,证实预热效果对加热温度最为敏感,呈非线性负相关特征;预热效果与孔隙度正线性相关,与井筒半径、含油饱和度负线性相关。采用新模型可实现地温分布、能耗参数、节能节水、节省燃料等关键指标的预测,同时结合油层预热达标温度,可以预测恒温模式预热所需的时间和能耗。图9表2参15

关键词: 双水平井; 蒸汽辅助重力泄油; 恒温电加热; 地温分布; 能耗; 节能; 节水; 节省燃料
中图分类号:TE341 文献标志码:A 文章编号:1000-0747(2018)05-0839-08
A mathematical model and relevant index prediction for constant-temperature electric heating of dual-horizontal-well SAGD start-up
LIU Xiaoxiong1,2, JIANG Youwei1,2, WU Yongbin1,2, WANG Jialu2
1. State Key Laboratory of Enhanced Oil Recovery, Beijing 100083, China
2. Research Institute of Petroleum Exploration & Development, PetroChina, Beijing 100083, China;
Abstract

Through Laplace transform and Stehfest numerical inversion, this research established a mathematical model for constant temperature electric heating of dual-horizontal-well steam-assisted gravity drainage (SAGD) start-up. To verify the model, a finite element simulation based on a typical SAGD block was completed, which proved the excellent agreement between the model solution and simulation results. Moreover, by means of superposition principle, underground temperature distribution and energy-related parameters during the multiwell operation were obtained, as well as a computational method targeted at quantifying the conserved energy, water and fuel of electric heating against steam heating. A parametric sensitivity analysis of electric heating was undertaken, which proved that the start-up effect is most sensitive to heating temperature, featuring a nonlinear negative correlation. Additionally, start-up effect is positively linear-correlative to porosity, and negatively linear-correlative to wellbore radius and oil saturation. The proposed model can be employed to predict key indexes such as underground temperature distribution, energy-consumption parameters, and accumulated conserved amounts of energy, water and fuel versus steam heating. Under a specified terminal temperature, temporal and energy quantities required by the start-up can also be determined.

Keyword: dual horizontal well; SAGD; constant-temperature electric heating; underground temperature distribution; energy consumption; energy conservation; water conservation; fuel conservation
0 引言

常见的蒸汽辅助重力泄油（SAGD）预热方式为蒸汽循环预热, 存在沿途热损失大、蒸汽用量大等缺点, 同时储集层非均质性对预热效果会造成严重影响[1]。油层电预热可以弥补蒸汽预热的不足：①不需要向油层注入蒸汽, 预热效果较为均匀; ②避免了蒸汽制备所带来的地面用水消耗和蒸汽集输沿程大量的热损失, 为油田现场节省了大量的能耗和水耗[2]。同时油层电加热技术设备复杂程度低, 便于调节控制和安装调试, 节省了地面作业空间, 是一项具有广阔应用前景的热采技术[3]。

在SAGD电预热方面, 近年来已有数位学者开展了量化研究。2013年, Moini等[4]建立了SAGD电预热能耗计算模型, 该模型的局限性在于：①无法确定预热过程中的温度分布, 只能计算能耗; ②模型为单井模型, 未考虑多井干扰效应; ③没有对电加热技术相对于蒸汽加热的节能、节水及降耗进行量化。2016年魏绍蕾等[5]建立了SAGD电预热的数学模型, 2017年Medizade等[6]提出了计算恒功率模式下的热量消耗与温度分布的有限元数值模型, 但上述模型都是基于恒功率模式的模型, 不涉及恒温模式的求解。随着电加热技术的发展, 特别是新型控制元器件的发展, 电加热控制模式可发展为恒温模式, 与传统的恒功率加热相比, 恒温加热具有控温直观、能有效防止近井原油过热焦化[7, 8]等优势, 且在一定条件下有望能耗更低。如何量化恒温模式下油层电加热的关键技术指标, 是目前SAGD技术亟待解决的问题。

本文提出了恒温模式下双水平井SAGD电预热数学模型, 可以求解恒温电预热期间的地温分布和能耗参数, 并建立了电加热相对于蒸汽加热的节能、节水和节省燃料当量的计算方法, 结合油层预热达标温度还可预测电预热所需的时间和能耗。

1 恒温模式的控制原理

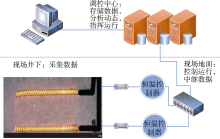
恒温模式控制主要依靠反馈调节机制实现（见图1）, 现场作业时, 在井筒中安装用于监测加热电缆温度的热电偶, 将采集的温度信号传输到位于地面的恒温控制器（PID）进行反馈调节。实测温度和设定温度由控制器的中控芯片实时智能调控：当实测温度低于设定温度时, 中控芯片发出运行指令, 系统继续加热; 当实测温度高于设定温度时, 中控芯片则发出暂停指令, 系统中断加热。经由通断调节, 加热系统达到动态平衡, 加热器的实际温度在一个微小的幅度内上下波动（波动幅度称为PID的控制精度）。同时实时监测数据经PID和中继器发送到远程调控中心进行存储和分析, 实现数据的动态监测[9]。

图1 双水平井SAGD恒温电预热智能调控示意图

2 恒温模式下SAGD电预热数学模型
2.1 模型基础假设条件

SAGD电预热模型假设条件为：①两口水平井的井身相互平行; ②地层均质等厚; ③油层的热物性参数（如导热系数、热扩散系数等）不随温度变化; ④电预热期间流体不发生运移, 忽略重力作用; ⑤地层中不存在对流传热; ⑥加热器和井壁间存在的能量损耗采用电热转换、传递效率等相关参数进行量化。

2.2 无限大地层中恒温加热的面源解

均质无限大圆柱状地层中心有一口水平井, 通过井筒恒温加热周围地层, 径向坐标系中热传导方程表示为[5]：

$\frac{1}{a}\frac{\partial T}{\partial t}=\frac{{{\partial }^{2}}T}{\partial {{r}^{2}}}+\frac{1}{r}\frac{\partial T}{\partial r}$ （1）

为了规范求解, 对（1）式进行无因次化, 无因次温度增量为：

${{T}_{\text{D}}}=\frac{T-{{T}_{0}}}{{{T}_{\text{h}}}-{{T}_{0}}}=\frac{\Delta T}{{{T}_{\text{h}}}-{{T}_{0}}}$ （2）

无因次时间为：

${{t}_{\text{D}}}=\frac{at}{r_{\text{w}}^{2}}$ （3）

无因次距离为：

${{r}_{\text{D}}}=\frac{r}{{{r}_{\text{w}}}}$ （4）

无因次化后热传导方程可表示为：

$\frac{{{\partial }^{2}}{{T}_{\text{D}}}}{\partial r_{\text{D}}^{2}}+\frac{1}{{{r}_{\text{D}}}}\frac{\partial {{T}_{\text{D}}}}{\partial {{r}_{\text{D}}}}=\frac{\partial {{T}_{\text{D}}}}{\partial {{t}_{\text{D}}}}$ （5）

其中, 初始条件为：

$T\left( r, t \right){{|}_{t=0}}={{T}_{0}}\Leftrightarrow {{T}_{\text{D}}}\left( {{r}_{\text{D}}}, {{t}_{\text{D}}} \right){{|}_{{{t}_{\text{D}}}=0}}=0$ （6）

内边界条件为：

$T\left( r, t \right){{|}_{r\to {{r}_{\text{w}}}}}={{T}_{\text{h}}}\Leftrightarrow {{T}_{\text{D}}}\left( {{r}_{\text{D}}}, {{t}_{\text{D}}} \right){{|}_{{{r}_{\text{D}}}\to 1}}=1$ （7）

外边界条件为：

$T\left( r, t \right){{|}_{r\to \infty }}={{T}_{0}}\Leftrightarrow {{T}_{\text{D}}}\left( {{r}_{\text{D}}}, {{t}_{\text{D}}} \right){{|}_{{{r}_{\text{D}}}\to \infty }}=0$ （8）

对无因次时间${{t}_{D}}$定义如下拉普拉斯变换：

$L\left[ {{T}_{D}}\left( {{r}_{D}}, {{t}_{D}} \right) \right]=\int_{0}^{\infty }{{{\text{e}}^{-s{{t}_{D}}}}}{{T}_{D}}\left( {{r}_{D}}, {{t}_{D}} \right)d{{t}_{D}}={{\tilde{T}}_{D}}\left( {{r}_{D}}, s \right)$ （9）

对（5）式进行拉普拉斯变换, 解得拉氏域中的无因次温度增量为：

${{\tilde{T}}_{D}}\left( {{r}_{D}}, s \right)=\frac{{{K}_{0}}\left( {{r}_{D}}\sqrt{s} \right)}{s{{K}_{0}}\left( \sqrt{s} \right)}$ （10）

考虑到（10）式的形式难以寻求解析反演解, 在此采用Stehfest数值反演算法[10, 11], 对（10）式进行数值反演, 则无因次温度增量在实空间的解为：

${{T}_{D}}\left( {{r}_{D}}, {{t}_{D}} \right)={{L}^{1}}\left[ {{{\tilde{T}}}_{D}}\left( {{r}_{D}}, s \right) \right]$ （11）

进而得到无限大地层中恒温加热模型的面源解为：

$T\left( r, t \right)=\left( {{T}_{h}}-{{T}_{0}} \right){{L}^{-1}}\left[ {{{\tilde{T}}}_{D}}\left( {{r}_{D}}, s \right) \right]+{{T}_{0}}$ （12）

2.3 恒温加热的油层能耗计算

在恒功率控制条件下, 通过简单乘积运算就可得到累计能耗, 而恒温控制条件下, 实时功率随时间不断变化, 最后的累计能耗无法经过简单运算得到, 能耗计算相对困难, 下面对其进行讨论。

由傅里叶定律解得地层中的热流密度为：

${{q}_{h}}={{L}^{-1}}\left( {{{\tilde{q}}}_{h}} \right)=\lambda \frac{{{T}_{h}}-{{T}_{0}}}{{{r}_{w}}}{{L}^{-1}}\left[ \frac{{{K}_{1}}\left( {{r}_{D}}\sqrt{s} \right)}{\sqrt{s}{{K}_{0}}\left( \sqrt{s} \right)} \right]$ （13）

井筒热流密度为：

${{q}_{w}}={{\left. {{q}_{h}} \right|}_{{{r}_{D}}=1}}=\lambda \frac{{{T}_{h}}-{{T}_{0}}}{{{r}_{w}}}{{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{s} \right)}{\sqrt{s}{{K}_{0}}\left( \sqrt{s} \right)} \right]$ （14）

对（14）式积分, 得到油层消耗的热功率为：

${{q}_{f}}=2\pi l\lambda \left( {{T}_{h}}-{{T}_{0}} \right){{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{s} \right)}{\sqrt{s}{{K}_{0}}\left( \sqrt{s} \right)} \right]$ （15）

地面消耗的电功率为：

${{q}_{s}}=\frac{2\pi l\lambda }{{{\eta }_{\text{e}}}{{\eta }_{\text{ct}}}}\left( {{T}_{\text{h}}}-{{T}_{0}} \right){{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{s} \right)}{\sqrt{s}{{K}_{0}}\left( \sqrt{s} \right)} \right]$ （16）

油层累计消耗的热能为：

${{Q}_{\text{f}}}=\frac{2\text{ }\!\!\pi\!\!\text{ }r_{\text{w}}^{2}l\lambda \left( {{T}_{\text{h}}}-{{T}_{0}} \right)}{a}\int_{0}^{{{\tau }_{\text{D}}}}{{{L}^{-1}}}\left[ \frac{{{K}_{1}}\left( \sqrt{s} \right)}{\sqrt{s}{{K}_{0}}\left( \sqrt{s} \right)} \right]d{{t}_{D}}$ （17）

对（17）式进行拉普拉斯变换有：

$L\left( {{Q}_{\text{f}}} \right)=\frac{2\text{ }\!\!\pi\!\!\text{ }r_{\text{w}}^{2}l\lambda \left( {{T}_{\text{h}}}-{{T}_{0}} \right)}{a}\left[ \frac{{{K}_{1}}\left( \sqrt{s} \right)}{{{s}^{\frac{3}{2}}}{{K}_{0}}\left( \sqrt{s} \right)} \right]$ （18）

对（18）式进行拉普拉斯逆变换有：

${{Q}_{\text{f}}}=\frac{2\text{ }\!\!\pi\!\!\text{ }r_{\text{w}}^{2}l\lambda \left( {{T}_{\text{h}}}-{{T}_{0}} \right)}{a}{{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{s} \right)}{{{s}^{\frac{3}{2}}}{{K}_{0}}\left( \sqrt{s} \right)} \right]$ （19）

则地面累计消耗的电能为：

${{Q}_{\text{s}}}=\frac{2\text{ }\!\!\pi\!\!\text{ }r_{\text{w}}^{2}l\lambda \left( {{T}_{\text{h}}}-{{T}_{0}} \right)}{a{{\eta }_{\text{e}}}{{\eta }_{\text{ct}}}}{{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{s} \right)}{{{s}^{\frac{3}{2}}}{{K}_{0}}\left( \sqrt{s} \right)} \right]$ （20）

2.4 运用叠加原理处理多井干扰

因为双水平井SAGD设计有一上一下2口水平井进行加热, 存在多井干扰。根据热传导方程的特点, 运用叠加原理可以量化多井同时加热的温度分布问题, 多口井同时向油层注入能量时, 地层中任一点的温度增量等于每口井单独工作时在该点引发的温度增量的代数和, 由（12）式可得：

$\Delta {{T}_{m}}=\sum\limits_{i=1}^{m}{\left( {{T}_{\text{h, }i}}-{{T}_{0}} \right)}{{L}^{-1}}\left[ \frac{{{K}_{0}}\left( {{r}_{\text{D}, i}}\sqrt{{{s}_{i}}} \right)}{{{s}_{i}}{{K}_{0}}\left( \sqrt{{{s}_{i}}} \right)} \right]$ （21）

如果每口井的加热温度和加热时间都相同, 则（21）式可整理为：

$\Delta {{T}_{m}}=\left( {{T}_{\text{h}}}-{{T}_{0}} \right){{L}^{-1}}\left[ \sum\limits_{i=1}^{m}{\frac{{{K}_{0}}\left( {{r}_{\text{D, }i}}\sqrt{s} \right)}{s{{K}_{0}}\left( \sqrt{s} \right)}} \right]$ （22）

同理, 多井工作时地层消耗的热功率为：

${{q}_{\text{f, }m}}=2\text{ }\!\!\pi\!\!\text{ }\lambda \sum\limits_{i=1}^{m}{{{l}_{i}}}\left( {{T}_{\text{h, }i}}-{{T}_{0}} \right){{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{{{s}_{i}}} \right)}{\sqrt{{{s}_{i}}}{{K}_{0}}\left( \sqrt{{{s}_{i}}} \right)} \right]$ （23）

多井工作时地面消耗的电功率为：

${{q}_{\text{s, }m}}=2\text{ }\!\!\pi\!\!\text{ }\lambda \sum\limits_{i=1}^{m}{\frac{{{l}_{i}}\left( {{T}_{\text{h, }i}}-{{T}_{0}} \right)}{{{\eta }_{\text{e, }i}}{{\eta }_{\text{ct, }i}}}}{{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{{{s}_{i}}} \right)}{\sqrt{{{s}_{i}}}{{K}_{0}}\left( \sqrt{{{s}_{i}}} \right)} \right]$ （24）

由（19）式, 多井工作时油层累计消耗的热能为：

${{Q}_{\text{f, }m}}=\frac{2\text{ }\!\!\pi\!\!\text{ }\lambda }{a}\sum\limits_{i=1}^{m}{r_{\text{w, }i}^{2}}{{l}_{i}}\left( {{T}_{\text{h, }i}}-{{T}_{0}} \right){{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{{{s}_{i}}} \right)}{s_{i}^{\frac{3}{2}}{{K}_{0}}\left( \sqrt{{{s}_{i}}} \right)} \right]$ （25）

由（20）式, 多井工作时地面累计消耗的电能为：

${{Q}_{\text{s, }m}}=\frac{2\text{ }\!\!\pi\!\!\text{ }\lambda }{a}\sum\limits_{i=1}^{m}{\frac{r_{\text{w, }i}^{2}{{l}_{i}}}{{{\eta }_{\text{e, }i}}{{\eta }_{\text{ct, }i}}}}({{T}_{\text{h, }i}}-{{T}_{0}}){{L}^{-1}}\left[ \frac{{{K}_{1}}(\sqrt{{{s}_{i}}})}{s_{i}^{\frac{3}{2}}{{K}_{0}}(\sqrt{{{s}_{i}}})} \right]$ （26）

如果每口井的加热段长度、加热温度、加热时间、地面电能的传输效率、电热转化-传递效率都相同, 则（24）式可化为：

${{q}_{\text{s, }m}}=\frac{2\text{ }\!\!\pi\!\!\text{ }\lambda lm}{{{\eta }_{\text{e}}}{{\eta }_{\text{ct}}}}\left( {{T}_{\text{h}}}-{{T}_{0}} \right){{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{{{s}_{i}}} \right)}{\sqrt{{{s}_{i}}}{{K}_{0}}\left( \sqrt{{{s}_{i}}} \right)} \right]$ （27）

如果每口井的井筒半径也相同, 则（26）式可化为：

${{Q}_{\text{s, }m}}=\frac{2\text{ }\!\!\pi\!\!\text{ }\lambda r_{\text{w}}^{2}lm}{a{{\eta }_{\text{e}}}{{\eta }_{\text{ct}}}}\left( {{T}_{\text{h}}}-{{T}_{0}} \right){{L}^{-1}}\left[ \frac{{{K}_{1}}\left( \sqrt{s} \right)}{{{s}^{\frac{3}{2}}}{{K}_{0}}\left( \sqrt{s} \right)} \right]$ （28）

对于双水平井SAGD, m=2。

2.5 节能、节水与节省燃料计算

电加热区块的电能传输效率与传输过程中电能损耗率之间的关系为：

${{\eta }_{\text{e}}}=1-{{\delta }_{\text{e}}}$ （29）

下入油层电加热器的电热转换-传热效率与相应过程中电能损耗率之间的关系为：

${{\eta }_{\text{ct}}}=1-{{\delta }_{\text{ct}}}$ （30）

如果在油层中累计消耗的热能为Qf, 那么采用电加热地面所需消耗的累计电能可表示为：

${{Q}_{\text{s}}}=\frac{{{Q}_{\text{f}}}}{\left( 1-{{\delta }_{\text{e}}} \right)\left( 1-{{\delta }_{\text{ct}}} \right)}$ （31）

同一区块蒸汽加热时, 蒸汽热能的传输效率与传输过程中热能损耗率之间的关系为：

${{\eta }_{\text{v}}}=1-{{\delta }_{\text{v}}}$ （32）

蒸汽携载的能量即为热能, 在油层中不存在转化效率的问题。如果在油层中累计消耗的热能为Qf, 那么采用蒸汽加热地面所需的累计能耗可表示为：

${{Q}_{\text{g}}}=\frac{{{Q}_{\text{f}}}}{{{\eta }_{\text{v}}}}=\frac{{{Q}_{\text{f}}}}{1-{{\delta }_{\text{v}}}}$ （33）

由（31）式和（33）式得到相同油层累计能耗下, 采用电加热比采用蒸汽加热可节省地面能耗：

$\Delta Q=\frac{\left( 1-{{\delta }_{\text{e}}} \right)\left( 1-{{\delta }_{\text{ct}}} \right)-\left( 1-{{\delta }_{\text{v}}} \right)}{\left( 1-{{\delta }_{\text{v}}} \right)\left( 1-{{\delta }_{\text{e}}} \right)\left( 1-{{\delta }_{\text{ct}}} \right)}{{Q}_{\text{f}}}=\frac{{{\eta }_{\text{e}}}{{\eta }_{\text{ct}}}-{{\eta }_{\text{v}}}}{{{\eta }_{\text{v}}}{{\eta }_{\text{e}}}{{\eta }_{\text{ct}}}}{{Q}_{\text{f}}}$ （34）

电加热与蒸汽加热相比, 节省地面能耗百分比为：

${{P}_{\text{ }\!\!\Delta\!\!\text{ }Q}}=\left[ 1-\frac{1-{{\delta }_{\text{v}}}}{\left( 1-{{\delta }_{\text{e}}} \right)\left( 1-{{\delta }_{\text{ct}}} \right)} \right]\times 100%=\left( 1-\frac{{{\eta }_{\text{v}}}}{{{\eta }_{\text{e}}}{{\eta }_{\text{ct}}}} \right)\times 100%$

（35）

蒸汽加热时, 注入地下的热能由蒸汽的汽化潜热提供。如果地面累计消耗的能量为Qg, 则需向油层注入的累计热能为Qf, 那么在地面消耗的累计用水当量可表示为：

${{m}_{\text{w}}}=\frac{{{Q}_{\text{g}}}}{x{{H}_{\text{v}}}}=\frac{{{Q}_{\text{f}}}}{\left( 1-{{\delta }_{\text{v}}} \right)x{{H}_{\text{v}}}}=\frac{{{Q}_{\text{f}}}}{{{\eta }_{\text{v}}}x{{H}_{\text{v}}}}$ （36）

由于电加热的用水量为零, 所以mw即为同一区块电加热所节省的地面用水当量。

蒸汽加热通常用燃油或者天然气作为锅炉燃料, 如果蒸汽加热地面累计消耗的能量为Qg（相当于向油层注入的热能为Qf）, 那么在地面需要消耗的燃油质量累计为：

${{m}_{\text{o}}}=\frac{{{Q}_{\text{g}}}}{{{\eta }_{\text{bo}}}{{H}_{\text{o}}}}=\frac{{{Q}_{\text{f}}}}{{{\eta }_{\text{v}}}{{\eta }_{\text{bo}}}{{H}_{\text{o}}}}$ （37）

或者在地面需要消耗的天然气体积（标准状况下）累计为：

${{V}_{\text{g}}}=\frac{{{Q}_{\text{g}}}}{{{\eta }_{\text{bg}}}{{H}_{\text{g}}}}=\frac{{{Q}_{\text{f}}}}{{{\eta }_{\text{v}}}{{\eta }_{\text{bg}}}{{H}_{\text{g}}}}$ （38）

由于电加热无需消耗燃料, 因此mo或Vg即为电加热相对蒸汽加热所能节省的燃油或燃气当量。

3 模型验证

选取新疆风城油田双水平井SAGD开发区块A井组, 采用本文模型（模型解）与COMSOL Multiphysics模拟器（数值解）模拟计算地层中部温度和地面累计能耗, 对比计算结果, 验证新建模型的准确性与可靠性。

A井组基本参数见表1, 地层的热物性参数取岩石、原油和地层水体积分数的加权平均值, 设定加热条件为双水平井恒温240 ℃, 加热120 d。

表1 新疆风城双水平井SAGD开发区块A井组基本参数

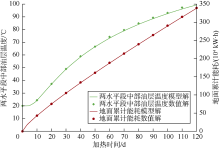
对A井组建立有限元数值模型, 利用三角形非结构化网格对模拟区域进行有限元剖分, 同时对井筒附近的网格进行加密和优化, 以提高模拟精度, 计算结果对比见图2。

图2 A井组模型解和数值解对比

对比图2中模型解与数值解曲线：两井中部温度最大相对误差为1.40%, 平均相对误差为0.80%; 地面累计能耗最大相对误差为0.85%, 平均相对误差为0.28%。结果表明模型解与数值解吻合良好, 新建模型准确、可靠。

4 电预热参数敏感性分析

由A井组流体物性资料可知, 当温度超过130 ℃时, 该区块原油黏度即可下降到100 mPa· s以下, 该温度即可满足生产阶段对流体流动性需求。因此, 双水平井SAGD可采用两大指标来评价预热效果：①时间指标, 即两水平段中部油层温度达到130 ℃时所需要的预热时间; ②能耗指标, 即两水平段中部油层温度达到130 ℃时地面累计消耗的电能。

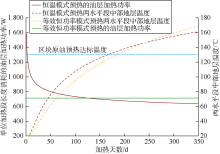
双水平井SAGD电预热过程中, 影响预热效果的因素主要有4个：①加热温度; ②井筒半径; ③孔隙度; ④含油饱和度。为评价电预热参数的敏感性, 这里选用A井组基础参数, 以双水平井SAGD恒温240 ℃电预热为基准方案, 设定影响因素的变动范围为± 15%, 在某一因素变化、其余参数保持不变的条件下, 考察时间、能耗两大评价指标的敏感性特征, 计算结果见图3。

图3 油层电预热参数敏感性关系曲线

由图3可知, 影响时间、能耗两大评价指标的4个主要因素, 其敏感性由大到小排序为：加热温度、孔隙度、井筒半径、含油饱和度。预热效果对加热温度的变动最为敏感, 呈非线性负相关特征, 随着加热温度的升高, 时间、能耗两大评价指标下降的速度逐渐趋缓; 孔隙度与时间、能耗指标正线性相关; 井筒半径、含油饱和度与时间、能耗指标负线性相关。总体来看, 时间、能耗评价指标变化幅度大于加热温度变化幅度, 对加热温度敏感程度较高; 时间、能耗评价指标变化幅度小于孔隙度、井筒半径、含油饱和度的变化幅度, 对这3项参数的敏感程度较低。

5 应用实例

仍选用A井组的基础参数, 应用新模型计算水平井段附近地温分布、井筒功率与两水平段中部油层的升温曲线、地面能耗、地面减耗等关键指标; 同时将恒温模式与恒功率模式下的相关指标进行对比, 分析其变化规律。

恒温模式与恒功率模式相关指标的对比基础为两种模式最终累计能耗相等。恒温模式下相关指标采用新建模型预测, 等效恒功率模式下相关指标采用参考文献[5]中的模型进行计算。

5.1 水平井段附近地温分布

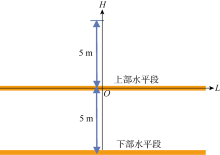
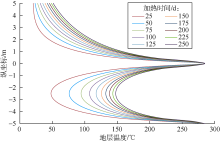
在两水平井水平段的连井剖面上, 以上部水平段轴心线为横轴（L轴）, 垂直方向为纵轴（H轴）, 上部水平井段中点为原点（O点）建立坐标系（见图4）。随后应用新模型求解A井组在285 ℃恒温电预热条件下, 沿纵轴方向不同位置（-5~5 m）、不同预热时间的地层温度分布（见图5）。

图4 两水平井水平井段的剖面坐标系

图5 不同加热时间双水平段附近地层温度分布

由图5分析知, 在两水平段之间, 同一时刻中部的地层温度最低, 越远离两井中部, 地层温度越高; 在两井之外, 距离井筒越远, 温度越低。随着加热的持续, 不同位置的地温升高步调不一致：靠近井筒地层初期升温速率大, 后期升温速率迅速衰减; 远离井筒地层初期升温速率小, 后期升温速率衰减缓慢。

5.2 实时功率与升温曲线

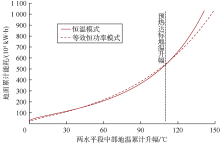
A井组在恒温285 ℃、电预热350 d条件下, 实时井筒功率与两水平段中部升温曲线见图6。分析井筒功率曲线可知, 恒温模式预热所消耗的热功率初始时刻最高, 而后持续下降, 而等效恒功率模式预热的功率保持恒定（单位井身长度消耗的井筒功率为726.30 W）。从升温曲线看：①无论是恒温模式还是等效恒功率模式电预热初期都出现了一定时长的停滞期, 这是因为初期的热流尚未波及到两水平段中部, 因此中部地温停滞在初始地温水平上; ②两种电预热模式两水平段中部的升温曲线都呈上凸形态, 即升温速率越来越慢。总体表现为前期恒温模式下两水平段中部地温上升更快, 随加热时间的延长, 恒温模式与等效恒功率模式的升温曲线约在第238 d相交, 交叉处两水平段中部地温约为145 ℃, 随后恒功率模式地温上升速度高于恒温模式; ③恒温模式加热在第166 d预热达标（区块原油预热达标温度为130 ℃）, 而等效恒功率模式预热在186 d预热达标, 恒温模式时间缩短20 d。这里必须指出, 恒温模式加热时间缩短建立在交叉点地温高于预热达标地温的基础上, 现场实践中, 也需要满足此条件才能让恒温模式所需的预热时间比等效的恒功率模式短。

图6 不同预热模式下实时油层加热功率与升温曲线

5.3 地面累计能耗与地层升温幅度的关系

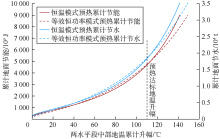
A井组在285 ℃、电预热350 d条件下, 恒温模式与等效恒功率模式预热的地面累计能耗与地温升幅的关系对比曲线见图7, 可以看到：①两种模式下随着地层温度升高, 单位升温幅度所耗费的能量均有所增加, 曲线呈明显的下凹形态; ②A井组在地温升幅为110 ℃时预热达标, 达标时恒温模式预热耗电能539× 104 kW· h, 而等效恒功率模式预热耗电能546× 104 kW· h, 恒温模式预热可节省电能7× 104 kW· h。同样必须指出, 恒温模式预热能耗更低建立在预热达标升温幅度处于两次交叉点之间的基础上, 现场实践中, 仍需满足此条件才能让恒温模式的预热能耗低于其等效的恒功率模式。

图7 不同预热模式下地面累计能耗与地温升幅的关系

5.4 地面累计节能、节水、节省燃料与地温升幅的关系

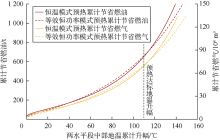
根据A井组的实际开发经验, 结合相关文献[12, 13, 14, 15]中提供的参数, 确定出电预热、蒸汽加热各项指标计算所需的相关参数（见表2）。利用新建模型, 计算A井组285 ℃、电预热350 d条件下, 恒温模式电预热与蒸汽预热相比的地面累计节能、节水、节省燃料与地温升幅的关系, 并和等效恒功率模式预热的相关参数进行对比（见图8、图9）。

表2 电预热相对蒸汽加热各项降耗指标计算相关参数

图8 不同预热模式地面累计节能节水与地温升幅的关系

图9 不同预热模式地面累计节省燃料与地温升幅的关系地温升幅的关系

采用表2基础数据, 由（35）式计算得, A井组电预热与蒸汽预热相比, 在同等油层能耗条件下, 可以节省19.5%的地面能耗。由图8可知, 285 ℃恒温模式预热达标时, 可累计节省地面能耗约4.70× 1012 J, 累计节省地面用水当量约1.84× 104 t。等效恒功率模式预热达标时, 累计节省地面能耗约4.76× 1012 J, 累计节省地面用水当量约1.86× 104 t。由图9可知, 285 ℃恒温模式预热达标时, 累计节省的能量相当于燃油654 t, 或者天然气69.7× 104 m3（标况体积）。等效恒功率模式预热达标时, 累计节省的能量相当于燃油666 t, 或者天然气70.9× 104 m3（标况体积）。

6 结论

建立了恒温模式下双水平井SAGD电预热数学模型以及电加热相对于蒸汽加热的累计节能、节水和节省燃料当量的计算方法, 经验证准确、可靠。

预热效果对加热温度最为敏感, 呈非线性负相关特征; 预热效果与孔隙度正线性相关, 与井筒半径、含油饱和度负线性相关。

新模型可实现恒温模式下地温分布、能耗参数、节能节水、节省燃料等关键指标的预测, 同时结合油层达标温度, 可以预测电预热所需的时间和能耗。

符号注释：

a— — 热扩散系数, m2/s; Hg— — 燃气的标准体积热值, J/m3; Ho— — 燃油的质量热值, J/kg; Hv— — 蒸汽的汽化潜热, J/kg; i— — 多井（或多加热器）工作时, 井（或加热器）的编号; ${{K}_{0}}\left( {{x}_{1}} \right)$— — 第二类0阶修正贝塞尔函数; ${{K}_{1}}\left( {{x}_{1}} \right)$— — 第二类1阶修正贝塞尔函数; l— — 单井加热段长度, m; $L\left( {{x}_{1}} \right)$— — 拉普拉斯变换算子; ${{L}^{1}}\left( {{x}_{1}} \right)$— — 拉普拉斯逆变换算子; m— — 井（或加热器）工作的数量; mo— — 蒸汽加热时燃油锅炉累计消耗的燃油质量（也是同等条件下与蒸汽加热相比, 电加热节省的燃油当量）, kg; mw— — 蒸汽加热时地面累计消耗的用水量（也是同等条件下与蒸汽加热相比, 电加热节省的用水当量）, kg; ${{P}_{\text{ }\!\!\Delta\!\!\text{ }Q}}$— — 与蒸汽加热相比电加热节省的地面能耗百分比, %; qf— — 井筒处消耗的热功率, W; qf, m— — 多井工作时, 井筒处消耗的热功率之和, W; qh— — 实空间中的热流密度, J/(m2· s); ${{\tilde{q}}_{\text{h}}}$— — 拉氏域中的热流密度, J/m2; qs— — 地面消耗的热功率, W; qs, m— — 多井工作时, 地面消耗的电功率之和, W; qw— — 井筒上的热流密度, J/(m2· s); Qf— — 油层累计消耗的热能, J; Qf, m— — 多井工作时, 油层累计消耗的热能, J; Qg— — 蒸汽加热的累计地面能耗, J; Qs— — 地面累计消耗的电能, J; Qs, m— — 多井工作时, 地面累计消耗的电能, J; Δ Q— — 与蒸汽加热相比电加热节省的地面能耗, J; r— — 距离井筒中心的距离, m; rD— — 距离井筒的无因次距离; rw— — 井筒半径, m; s— — 拉氏变量, 无因次; t— — 加热时间, s; tD— — 无因次加热时间; T— — 地层温度, K; T0— — 地层的初始温度, K; TD— — 地层的无因次温度增量; Th— — 加热温度, K; ${{\tilde{T}}_{\text{D}}}$— — 拉氏域中的无因次温度增量; Δ T— — 地层温度增量, K; Δ Tm— — 多井工作时在地层中引发的温度增量, K; Vg— — 蒸汽加热时燃气锅炉累计消耗的标准状况下天然气体积（也是同等条件下与蒸汽加热相比, 电加热节省的燃气当量）, m3; x— — 锅炉出口的蒸汽干度, 无因次; x1— — 函数自变量; ${{\delta }_{\text{ct}}}$— — 电热转换与传递损耗率, %; ${{\delta }_{\text{e}}}$— — 电能的传输损耗率, %; ${{\delta }_{\text{v}}}$— — 蒸汽的传输损耗率, %; ${{\eta }_{\text{bg}}}$— — 燃气锅炉的热效率, %; ${{\eta }_{\text{bo}}}$— — 燃油锅炉的热效率, %; ${{\eta }_{\text{ct}}}$— — 电热转化-传递效率, %; ${{\eta }_{\text{e}}}$— — 电能的传输效率, %; ${{\eta }_{\text{v}}}$— — 蒸汽的传输效率, %; λ — — 地层的综合导热系数, W/(m· K); ${{\tau }_{\text{D}}}$— — 某一加热温度下加热终止的无因次时刻。

The authors have declared that no competing interests exist.

参考文献
[1] 梁光跃, 刘尚奇, 沈平平, 等. 油砂蒸汽辅助重力泄油汽液界面智能调控模型优选[J]. 石油勘探与开发, 2016, 43(2): 275-280.
LIANG Guangyue, LIU Shangqi, SHEN Pingping, et al. A new optimization method for steam-liquid level intelligent control model in oil sand s steam-assisted gravity drainage (SAGD) process[J]. Petroleum Exploration and Development, 2016, 43(2): 275-280. [本文引用:1]
[2] CARRIZALES M A, JOHNS R T. Production improvement of heavy-oil recovery by using electromagnetic heating[R]. Denver: SPE Annual Technical Conference and Exhibition, 2008. [本文引用:1]
[3] JHA A K, JOSHI N, SINGH A. Applicability and assessment of micro-wave assisted gravity drainage (MWAGD) applications in Mehsana heavy oil field, India[R]. Cairo: North Africa Technical Conference and Exhibition, 2012. [本文引用:1]
[4] MOINI B, EDMUNDS N. Quantifying heat requirements for SAGD startup phase: Steam injection, electrical heating[J]. Journal of Canadian Petroleum Technology, 2013, 52(2): 89-94. [本文引用:1]
[5] 魏绍蕾, 程林松, 张登辉, 等. 稠油油藏双水平井SAGD生产电预热模型[J]. 西南石油大学学报(自然科学版), 2016, 38(1): 92-98.
WEI Shaolei, CHENG Linsong, ZHANG Denghui, et al. Analytical solution for double-horizontal-well SAGD electirc preheating model of heavy oil resevoirs[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2016, 38(1): 92-98. [本文引用:3]
[6] MEDIZADE M M, SUMMERS J T. Finite element modeling of reservoir heating by an electrical cable[R]. Bakersfield: SPE Western Regional Meeting, 2017. [本文引用:1]
[7] 关文龙, 席长丰, 陈龙, 等. 火烧辅助重力泄油矿场调控技术[J]. 石油勘探与开发, 2017, 44(5): 753-760.
GUAN Wenlong, XI Changfeng, CHEN Long, et al. Field control technology of combustion assisted gravity drainage (CAGD)[J]. Petroleum Exploration and Development, 2017, 44(5): 753-760. [本文引用:1]
[8] 李秋, 易雷浩, 唐君实, 等. 火驱油墙形成机理及影响因素[J]. 石油勘探与开发, 2018, 45(3): 474-481.
LI Qiu, YI Leihao, TANG Junshi, et al. Mechanisms and influencing factors of the oil bank in fire flooding[J]. Petroleum Exploration and Development, 2018, 45(3): 474-481. [本文引用:1]
[9] 何芝强. PID控制器参数整定方法及其应用研究[D]. 杭州: 浙江大学, 2005.
HE Zhiqiang. Parameters tuning of PID controller and its application[D]. Hangzhou: Zhejiang University, 2005. [本文引用:1]
[10] STEHFEST H. Algorithm 368: Numerical inversion of Laplace transforms[J]. Communications of the ACM, 1970, 13(1): 47-49. [本文引用:1]
[11] STEHFEST H. Remark on algorithm 368: Numerical inversion of Laplace transforms[J]. Communications of the ACM, 1970, 13(10): 624-625. [本文引用:1]
[12] 王勋. 输电电网实时计算与分析[D]. 保定: 华北电力大学, 2009.
WANG Xun. Real-time energy losses calculating and analyzing in the transmission network[D]. Baoding: North China Electric Power University, 2009. [本文引用:1]
[13] 张啸枫. 蒸汽辅助重力驱注蒸汽热损失及产量预测[D]. 成都: 西南石油大学, 2005.
ZHANG Xiaofeng. Injected steamheat loss and production rate of SAGD[D]. Chengdu: Southwest Petroleum University, 2005. [本文引用:1]
[14] 李柳强. 燃油锅炉热效率及影响因素分析[J]. 节能技术, 2013, 9(29): 134-136.
LI Liuqiang. Analysis of influencing factors and heat efficiency of oil-fired boiler[J]. Energy Conservation Technology, 2013, 9(29): 134-136. [本文引用:1]
[15] 王建国. 燃气锅炉热效率分析[J]. 区域供热, 2005(5): 25-27.
WANG Jianguo. Analysis of heat efficiency of gas-fired boiler[J]. District Heating, 2005(5): 25-27. [本文引用:1]