引用本文
张东晓, 陈云天, 孟晋. 基于循环神经网络的测井曲线生成方法[J]. 石油勘探与开发, 2018,45(4): 598-607.
ZHANG Dongxiao, CHEN Yuntian, MENG Jin. Synthetic well logs generation via Recurrent Neural Networks[J]. Petroleum Exploration & Development, 2018,45(4): 598-607.  
Doi: 10.11698/PED.2018.04.06
Permissions
Copyright©2018, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
基于循环神经网络的测井曲线生成方法
张东晓, 陈云天, 孟晋
北京大学工学院,北京 100871
联系作者简介：陈云天（1993-）,男,北京市人,北京大学工学院在读博士研究生,主要从事统计建模、油气领域大数据与人工智能研究。地址：北京市海淀区北京大学王克桢楼1009,邮政编码：100871。E-mail：chenyt@pku.edu.cn

第一作者简介：张东晓（1967-）,男,江西武宁人,博士,美国国家工程院院士,北京大学工学院教授,主要从事渗流机理、随机不确定性和历史拟合方法、非常规油气开采等方面的研究工作。地址：北京市海淀区北京大学王克桢楼1008,邮政编码：100871。E-mail：dxz@pku.edu.cn

收稿日期: 2018-06-06
基金项目: 国家自然科学基金（U1663208,51520105005）; 国家科技重大专项（2017ZX05009-005,2016ZX05037-003）
摘要

为了在不增加经济成本的基础上补充缺失的测井信息,提出利用机器学习方法根据已有的部分测井曲线生成人工测井曲线,并进行了实验验证和应用效果分析。考虑到传统全连接神经网络（FCNN）无法描述数据的空间相关性,基于一种循环神经网络（RNN）即长短期记忆神经网络（LSTM）来构建测井曲线生成方法。该方法生成的曲线不仅考虑了不同测井曲线的内在联系,同时兼顾了测井信息随深度的变化趋势和前后关联。将标准LSTM与串级系统相结合,提出了一种串级长短期记忆神经网络（CLSTM）。采用真实测井数据进行实验,LSTM明显优于传统FCNN,生成的测井数据精度更高;CLSTM更适用于测井曲线生成这种多序列数据问题;提出的基于机器学习的人工测井曲线生成方法更准确经济。图8表2参32

关键词: 测井曲线; 生成方法; 机器学习; 全连接神经网络; 循环神经网络; 长短期记忆神经网络; 人工智能
中图分类号:TE151 文献标志码:A 文章编号:1000-0747(2018)04-0598-10
Synthetic well logs generation via Recurrent Neural Networks
ZHANG Dongxiao, CHEN Yuntian, MENG Jin
College of Engineering, Peking University, Beijing 100871, China
Abstract

To supplement missing logging information without increasing economic cost, a machine learning method to generate synthetic well logs from the existing log data was presented, and the experimental verification and application effect analysis were carried out. Since the traditional Fully Connected Neural Network (FCNN) is incapable of preserving spatial dependency, the Long Short-Term Memory (LSTM) network, which is a kind of Recurrent Neural Network (RNN), was utilized to establish a method for log reconstruction. By this method, synthetic logs can be generated from series of input log data with consideration of variation trend and context information with depth. Besides, a cascaded LSTM was proposed by combining the standard LSTM with a cascade system. Testing through real well log data shows that: the results from the LSTM are of higher accuracy than the traditional FCNN; the cascaded LSTM is more suitable for the problem with multiple series data; the machine learning method proposed provides an accurate and cost effective way for synthetic well log generation.

Keyword: well log; generating method; machine learning; Fully Connected Neural Network; Recurrent Neural Network; Long Short-Term Memory; artificial intelligence
0 引言

测井数据在储集层描述和油气资源评估中具有十分重要的作用。地质学家和工程师通过对测井曲线进行分析可以极大地加深对地下储集层情况的认知, 并在测井数据的支持下建立较为精确的地质模型。然而由于井径扩大、仪器故障等原因, 实际应用中经常出现部分井段测井数据失真或缺失的情况, 甚至出于成本考虑而放弃获取整套测井数据。重新测井往往需要很高的成本, 对于已经实现完井操作的井眼, 重新测井难以实现。为了节约成本, 研究者们提出可以采用多种方法直接利用已有测井数据人工生成测井曲线, 从而补全缺失井段信息。例如, 可以根据地质信息使用某些物理模型直接反演测井曲线[1, 2]。然而这些物理模型通常有很多假设, 极大简化了真实地层情况, 挑选模型时也掺杂着研究者的主观经验, 因此生成的测井曲线的质量难以保证。另外, 还可以根据各种测井数据间的内在联系生成测井曲线, 一些传统的分析手段和方法（交会图、多元回归等）可以用来完成这一任务[3, 4]。但是由于地下情况复杂和非均质性较强, 测井数据之间经常呈现极强的非线性关系, 数据间的映射关系也极为复杂, 应用传统方法的效果较差。

近年来随着机器学习方法在科学和工程领域的广泛应用, 很多研究者也建议使用数据驱动方法来解决地质问题, 例如利用支持向量机（SVM）、模糊逻辑模型（FLM）和人工神经网络（ANN）等方法来估计地质参数[5, 6]、判别岩性[7, 8]、确定地层界线[9, 10]等。其中人工神经网络是近年来的研究热点之一, 很多研究者尝试使用人工神经网络生成测井曲线[11, 12, 13, 14, 15]。这些人工神经网络都是传统的全连接神经网络（FCNN）, 构造的是一种点对点的映射, 即通过该方法生成的某一深度的测井数据只和其他测井曲线同处于该深度的信息有关, 而忽略了测井曲线随深度的变化趋势和数据的前后关联。这与实际地质分析经验和地质学思想相违背, 因此生成的测井曲线是否准确还有待商榷。由于FCNN无法保存、利用先前信息, 无法预测序列数据, 许多研究者通过耦合其他方法（小波变换[16]、奇异谱分析[17]等）来对FCNN进行改进, 然而这些改进实现起来往往十分复杂和繁琐。为了生成序列测井数据, 更加合理的选择是利用循环神经网络（RNN）[18]。在循环神经网络结构中, 每个神经单元内存在一个能够重复使用该单元的自循环结构, 这一循环结构使得先前的信息可以保留并在之后被使用。由于信息可以在循环神经网络中自由流动, 基于该方法生成的测井曲线综合考虑了不同测井曲线间的内在联系和随深度的变化趋势, 更加符合地质学思想。

本文使用一种广泛应用于深度学习的先进循环神经网络即长短期记忆神经网络（LSTM）[19]来生成测井曲线。该网络架构在每个自循环结构内引入门结构, 进一步模仿生物神经元信息传导模式, 不需任何额外的调整即可储存更加长期的序列信息。这一优点使其在人工智能和深度学习领域获得了极大关注, 在自然语言处理[20]、机器翻译[21]、语音识别[22]等领域都得到了广泛应用。另外, RNN和LSTM也被应用于水文学领域来处理包含时间序列数据的问题[23, 24]。然而目前还未见利用LSTM生成测井曲线的相关研究报道。

本研究的目的是根据已有测井数据, 通过使用LSTM生成人工测井曲线来补全缺失测井数据。首先, 阐述FCNN、RNN和LSTM的理论基础以及相应的网络结构设计和特殊设置。其次, 分析LSTM在真实水平井和直井测井数据上的应用效果, 并在多个测井深度与传统FCNN进行对比。

1 原理与方法
1.1 全连接神经网络

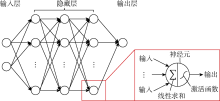
人工神经网络是一种具有分层结构的模型, 能够近似模拟输入和输出变量之间的非线性函数关系。从数学的角度来看, 只要拥有足够多的基函数（basis function）, 神经网络可以对任何函数在任意给定精度下进行建模[25, 26]。FCNN是最常用的人工神经网络, 具有典型的分层结构。FCNN中具有运算能力的基本单元是层状分布的神经元, 每个神经元与其相邻层中的所有神经元相互连接, 同一层中的神经元之间互不连接。不同神经元之间的连接强度由权重表示, 权重随着网络的训练进行调整。图1展示了一种典型的4层FCNN结构（输入层不计入层数）。如图1所示, 每个神经元的输出都通过非线性函数计算得到, 而非线性函数的输入是神经元输入的代数和。这一非线性函数也称为激活函数, 最常用的激活函数是sigmoid函数、tansig函数和ReLU函数[27]。

图1 典型4层FCNN结构示意图

1.2 循环神经网络与长短期记忆神经网络

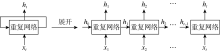
FCNN在许多情况下表现良好, 但该网络必须接受固定大小的输入, 并使用固定数量的计算步骤产生固定大小的输出, 因此其应用受到很大限制, 尤其是无法有效处理序列数据问题[28]。换言之, FCNN无法根据序列数据中先前步骤的预测结果影响目前步骤中的计算, 无法分析序列数据中前后数据间的相互影响[29]。RNN的架构可以让先前步骤中的信息持续存在并影响后续步骤, 因此RNN能够有效处理序列数据问题。典型的RNN结构及其展开版本如图2所示。循环结构是RNN与传统FCNN的主要区别。该循环结构允许信息逐步传递。RNN可以看作同一网络的多个副本, 前一步的输出传递到当前步的副本中影响计算结果。因此, RNN的输出不仅受到当前步骤输入的影响, 还受到过去所有步骤输入的影响。RNN的这种链式结构使它在序列数据分析中具有很大优势, 它也是解决序列数据（如测井数据）问题的最自然的网络结构。

图2 标准循环神经网络及其展开版本的示意图

在RNN的每层网络中, 序列数据中的每个元素都会按照下式进行计算：

${{h}_{t}}=\text{tanh}\left( {{w}_{\text{ih}}}{{x}_{t}}+{{b}_{\text{ih}}}+{{w}_{\text{hh}}}{{h}_{t-1}}+{{b}_{\text{hh}}} \right)$ （1）

如（1）式所示, 第t步的隐状态不仅由第t步的输入决定, 还由第t-1步的隐状态决定。第t步的最终输出结果是基于第t步的隐状态计算的。因为隐状态总是具有比原始输入更多的维度和更广的取值范围, 所以使用隐状态可以增强模型的表达能力, 有助于神经网络基于有限的观测值表达复杂的分布。除了网络中的循环结构, RNN还具有参数共享的特性, 即网络中的可训练参数wih, whh, bih和bhh在不同的时间步中共享。这与卷积神经网络（CNN）极为相似, CNN在空间位置之间共享卷积核参数, 而RNN在序列数据的时间步之间共享参数。共享参数使模型更加简单, 并且使RNN能够适应任意长度的序列数据, 从而提升模型的适用性。

RNN的优点之一是能够利用先前步骤中的信息来估计当前步骤的结果。然而, 如果相关信息所在位置与当前步骤之间距离非常大, RNN就会表现不佳[30]。长短期记忆神经网络（LSTM）是一种特殊的循环神经网络, 专门用来学习序列数据内的长期依赖性。在LSTM中, 记录长距离信息是网络的默认行为[29]。

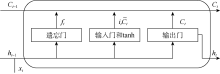
LSTM具有与标准RNN类似的链状重复网络结构。标准RNN中的重复网络非常简单, 而LSTM中的重复网络具有4个交互层, 包括3个门层和1个tanh层（见图3）。处理器状态是LSTM中的关键变量, 它携带着先前步骤的信息, 并逐步穿过整个LSTM。交互层中的门可以根据上一步的隐状态和当前步骤的输入来部分删除上一步的处理器状态和添加新信息到当前步骤的处理器状态中。每个重复网络的输入包括上一步的隐状态和处理器状态以及当前步骤的输入。处理器状态根据4个交互层的计算结果进行更新。更新后的处理器状态和隐状态构成输出并传递到下一步。

图3 LSTM的重复网络结构图

第1个交互层被称为遗忘门层, 它决定当前步骤忘记什么信息。遗忘门由（2）式描述。这一层的输出ft是1个在0~1的数字, 决定了上一步的处理器状态中哪些部分应该被传递下去。

${{f}_{t}}=\sigma \left[ {{W}_{\text{f}}}\left( {{h}_{t-1}}, {{x}_{t}} \right)+{{b}_{\text{f}}} \right]$ （2）

第2个交互层被称为输入门层, 它决定了哪些新的信息应该添加到处理器状态中。输入门由（3）式描述。这一层的输出决定第3个交互层中哪些信息将被保留并更新。

${{i}_{t}}=\sigma \left[ {{W}_{\text{i}}}\left( {{h}_{t-1}}, {{x}_{t}} \right)+{{b}_{\text{i}}} \right]$ （3）

第3个交互层是tanh层, 它创建了一个可以添加到处理器状态中的新候选值, 由（4）式描述。

${{\tilde{C}}_{t}}=\text{tanh}\left[ {{W}_{\text{c}}}\left( {{h}_{t-1}}, {{x}_{t}} \right)+{{b}_{\text{c}}} \right]$ （4）

在上述3层计算之后, 携带记忆信息的旧处理器状态Ct-1与包含新信息的候选值${{\tilde{C}}_{t}}$结合, 如（5）式所示。来自遗忘门的计算结果ft决定在Ct-1中忘记哪些信息, 而来自输入门的计算结果it决定在${{\tilde{C}}_{t}}$中的哪些信息被保留和添加。

${{C}_{t}}={{f}_{t}}{{C}_{t-1}}\text{+}{{i}_{t}}{{\tilde{C}}_{t}}$ （5）

最后1层是输出门层, 它基于更新后的处理器状态生成LSTM的输出值, 如（6）式所示。

${{h}_{t}}=\sigma \left[ {{W}_{\text{o}}}\left( {{h}_{t-1}}, {{x}_{t}} \right)+{{b}_{\text{o}}} \right]\text{tanh}{{C}_{t}}$ （6）

LSTM是一种在重复网络中具有4个相互作用层的循环神经网络。它不仅能够像标准循环神经网络那样从序列数据中提取信息, 还能够保留来自于先前较远步骤的具有长期相关性的信息。测井数据是序列数据, 其变化趋势富有含义。此外, 由于测井曲线的采样间隔相对较小, 测井曲线中存在长期（空间）相关性, 而LSTM有足够的长期记忆来处理这种问题。因此, LSTM是生成人工测井数据的理想工具。

2 实验

为了测试LSTM的性能, 进行了两个实验, 即测井曲线自动补全实验和人工测井曲线生成实验。实验的主要目的是：①评价LSTM根据不完整测井曲线自身的信息自动补全缺失段数据的能力; ②评价LSTM基于邻井信息生成人工测井曲线的准确度; ③比较LSTM与传统FCNN的性能。

2.1 测井曲线自动补全实验

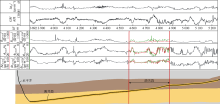
本实验中水平井测井曲线部分缺失。利用LSTM可以基于同一口井中数据完整的测井段来估计缺失的测井数据, 进而补全测井曲线。该水平井位于美国Eagle Ford储集层[31], 测井曲线共5条, 包含自然伽马、阵列感应电阻率、中子孔隙度、横波时差和纵波时差（见图4）。测井段总长1 524 m, 测深为3 719~5 243 m, 穿过两个地层, 地层分界点在测深4 633 m处。本实验中, 测深4 572~4 877 m的阵列感应电阻率、中子孔隙度和横波时差曲线被人为删除, 以模拟缺失的测井曲线, 缺失段长度为总测量长度的20%。

图4 自动补全的测井曲线和水平井走向示意图

训练数据集由3 719~4 572 m及4 877~5 243 m两个完整测井段组成, 测井曲线采样间隔为0.061 m（0.2 ft）, LSTM训练的序列长度设为500, 即30.5 m（100 ft）。这一训练长度意味着在此LSTM模型中, 每一个采样点前方30.5 m范围内的数据对该采样点的取值有影响。通过调节这一长度可以改变LSTM在训练过程中的记忆范围。两个完整测井段的训练序列是分开提取的, 提取后再随机混合生成训练数据集。最终, 一共有19 002组训练数据, 每组数据的序列长度为500, 以自然伽马和纵波时差作为输入, 阵列感应电阻率、中子孔隙度和横波时差作为输出。训练过程中批尺寸（batch size）为100, 即每次训练随机抽取100组训练数据。此实验中采用的LSTM模型包含2个长短期记忆层和1个全连接层, 长短期记忆层的隐状态为30维。为了避免过拟合, 模型采用了丢弃操作（dropout）, 丢弃概率为30%。

在应用LSTM进行曲线补全的过程中, 首先选取缺失段之前的部分序列数据作为预热数据, 通过这些数据对LSTM的隐状态及处理器状态进行更新。然后基于更新后的隐状态与处理器状态顺序计算缺失段数据的预测值, 具体流程如图5所示。图5中h0和C0是预热段的初始隐状态和处理器状态, hd-1和Cd-1是预热段的输出, 它们被传递到缺失段的第1步中作为缺失段的输入。假设缺失段起始测深处采样点序号为d, 则在d-1处可由LSTM模型基于预热数据计算获得隐状态hd-1和处理器状态Cd-1。然后根据d处的自然伽马和纵波时差数据, 预测d处的隐状态hd和处理器状态Cd, 进而获得d处的阵列感应电阻率、中子孔隙度和横波时差。然后依据d处的隐状态和处理器状态, 结合d+1处的输入测井曲线, 计算获得d+1处的隐状态、处理器状态及输出测井曲线。每次预测都基于序列中上一步的预测结果, 最终对整个缺失段进行数据补全。

图5 预热过程的流程图

从图4中可以看出, LSTM可以很好地提取出序列数据中的模式, 并根据这些模式进行数据预测与曲线补全。对于横波时差和中子孔隙度, 基于LSTM的人工曲线与实际测井曲线不但具有相似的变化趋势, 还具有相近的数值, 说明LSTM生成的曲线具有较高的可信度。对于阵列感应电阻率, 虽然人工曲线的绝对数值与实际测井曲线不同, 但是在曲线的变化趋势上具有一定的相似度, 在一定程度上可以作为缺失曲线取值的参考。阵列感应电阻率人工曲线与实际测井曲线在地层交界处差别较大, 这可能是因为电阻率会受到含油性和矿化度的影响, 而这些影响在输入变量中没有较好地体现。此外, 地层交界处的电阻率变化模式本身可能与上下地层内的变化模式不同。由于这一变化模式在训练数据集中并没有出现, LSTM模型很难做出准确的预测。综合而言, 在一口井的部分测井曲线缺失时, 可以利用LSTM依据同一口井中完整段测井曲线对缺失段测井曲线进行数据补全。当然, 如果待补全井的邻井拥有完整的测井曲线, 且这些曲线可用于模型训练, 那么测井曲线自动补全的精度会得到显著提升。

2.2 人工测井曲线生成实验

本实验中, 分别使用LSTM和传统FCNN生成人工测井数据, 并对比两种方法所生成的数据的准确度。本实验的数据来自于大庆油田的6口直井。A1、A2、A3、A4、A5、A6井的测深分别为780~1 136, 795~1 117, 747~1 059, 920~1 236, 842~1 189和716~1 007 m。因为直井比水平井穿过的地层更多, 所以输入与输出测井曲线之间的映射关系更复杂。每口直井都含有7条测井曲线, 包括微电极测井曲线的幅度差、井径、自然电位、自然伽马、高分辨率声波时差、补偿声波和密度。前4条曲线作为输入, 后3条曲线作为输出。在构建训练数据集的过程中, 每口井的训练序列独立提取, 然后随机混合生成训练数据集。测井曲线采样间隔为0.05 m, 训练序列长度为500, 则A1— A6井在作为训练数据时提供的序列数分别为6 595, 5 919, 5 713, 5 791, 5 797和5 295组。实验采用留一法, 即总共进行6组实验, 每组实验取6口井中的1口作为检测数据集, 另外5口作为训练数据集。作为检测数据集的井不进行序列提取, 而将整口井的4条输入测井曲线作为4条完整序列输入LSTM, 以便对3条输出测井曲线进行预测。在神经网络结构方面, LSTM采用了两个隐状态为30维的长短期记忆层与两个全连接层, 丢弃操作的丢弃概率为30%。此外, 本文还构建了3个分别为4, 8及12层的FCNN作为对比模型, 这3个FCNN具有与LSTM相近的参数量。

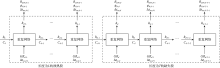
在传统LSTM的基础上, 本文还提出了一种具有串级系统的长短期记忆神经网络（CLSTM）。在该串级LSTM中, 首先根据已知测井曲线估计未知测井曲线中的1条, 然后将获得的估计值与已知测井曲线合并作为新的输入, 再根据此输入估计剩余未知测井曲线中的1条。重复这样的步骤, 最终完成对所有未知测井曲线的估计。如图6所示, 以A1— A6井为例, 首先根据已知的4条测井曲线估计高分辨率声波时差曲线, 然后把获得的高分辨率声波时差曲线添加到输入中, 由5条测井曲线预测补偿声波曲线, 最后利用高分辨率声波时差、补偿声波及另外4条已知测井曲线预测密度曲线。串级LSTM主要具有两个优点：其一, 由于每次只预测1条测井曲线, 待测曲线之间的相互干扰减小, 有利于提升模型精度; 其二, 由于采用了串级思想, 模型具有更强的输入兼容性, 如针对某1口具有5条已知测井曲线的井, 可以直接从串级LSTM的中间步骤开始训练, 而不需要对模型重新训练。串级LSTM的缺点在于它的网络复杂度比标准LSTM更高。不过由于人工测井曲线中输入变量维度一般小于10, 即便使用串级LSTM, 其网络参数量也能控制在5× 104以内, 远小于现在常用的深度神经网络。考虑到目前的计算能力, 串级LSTM的复杂度完全可以接受。

图6 串级LSTM的架构

为了具体评价各种模型预测人工测井数据的精度, 针对大庆油田的6口直井分别使用串级LSTM、标准LSTM、4层FCNN、8层FCNN及12层FCNN进行预测, 并对比预测结果（见表1）。模型的准确度采用测井数据估计值的均方误差的平均值和标准差表示, 表1中数据为基于每种模型针对不同井进行多次实验后, 高分辨率声波时差、补偿声波和密度这3条测井曲线估计值均方误差的平均值及标准差。由表1可知, 串级LSTM和标准LSTM的预测结果比4层FCNN、8层FCNN及12层FCNN的预测结果更准确。除了A2井以外, 5种模型都具有较好的预测结果。这说明A2井的测井曲线之间可能具有和另外5口井不同的隐藏模式, 而且这些隐藏模式并没有出现在训练数据集中。但是, 串级LSTM和标准LSTM对A2井的预测结果相对于其他模型有明显优势, 这表明LSTM对未曾出现过的模式具有较好的鲁棒性。此外, 与标准LSTM相比, 串级LSTM不但具有更高的预测准确率, 还具有更小的不确定性。

表1 不同模型生成人工测井曲线的均方误差及标准差

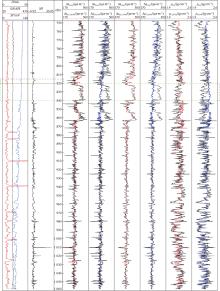
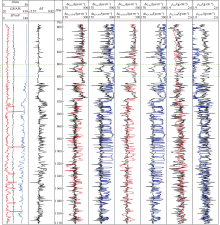
为了分析串级LSTM和FCNN生成人工测井曲线的效果, 将6口井中串级LSTM预测结果最好的A3井与预测结果最差的A2井的人工曲线分别绘制并进行对比, 如图7、图8所示。图中深度标尺左侧为输入的4条已知测井曲线, 右侧为基于串级LSTM和8层FCNN生成的人工测井曲线以及作为参照的实际测井曲线。通过观察A3井测深820~840 m（见图7中绿色虚线框）的测井曲线可以发现, 高分辨率声波时差与补偿声波的数值在此区间内存在1个阶跃式增加, 但是由于作为输入的4条测井曲线在此区间内并没有明显的变化, 使得FCNN未能成功估计出目标测井曲线中的这一阶跃变化, 生成了具有较大偏差的人工测井曲线。而串级LSTM基于序列数据进行预测, 因此可以通过输入曲线在测深815~820 m（见图7中红色虚线框）的变化趋势, 进而准确地判断出高分辨率声波时差与补偿声波在测深820 m处存在阶跃式增加。这一现象在A2井测深860~880 m（见图8中绿色虚线框）再次出现。这说明串级LSTM能够综合分析预测点前的数据和预测点处输入的影响, 准确预测目标曲线的趋势性变化, 因此串级LSTM对于测井曲线这种序列数据具有较好的预测能力。图8展示了A2井的人工测井曲线, 可以看出串级LSTM与FCNN的预测结果都存在偏差, 但是串级LSTM更好地预测了目标测井曲线的整体变化趋势。此外, 串级LSTM的波动性也更弱, 这说明在遇到含有未知模式的数据时, 串级LSTM具有比FCNN更强的鲁棒性。

图7 基于串级LSTM和FCNN生成的A3井的人工测井曲线

图8 基于串级LSTM和FCNN生成的A2井的人工测井曲线

串级LSTM的高精度与稳定性得益于预测过程中的每一级都把预测结果作为新的输入信息, 不但能在训练过程中更为有效地提取训练数据中所隐含的模式, 还能在预测过程中更高效地利用所有可获得的输入信息。在应用串级LSTM时需要注意层级的预测顺序。因为每一级的预测结果都会成为下一级的输入, 所以预测误差也会在一定程度上传递到下一级中, 导致误差累积的问题。针对这一问题, 建议在应用串级LSTM时先在浅层级中预测相对简单的测井曲线, 随着层级加深再逐步预测复杂的测井曲线。此外, 浅层级中增加的输入变量所蕴含的新信息会被深层级模型利用, 在一定程度上抵消浅层级到深层级过程中累积的预测误差, 甚至在深层级中达到更好的预测效果。本文应用串级LSTM时, 首先在第1级预测高分辨率声波时差曲线, 而后在第2级预测补偿声波曲线, 最后预测密度曲线。由表2可知, 虽然串级LSTM在预测密度曲线时存在误差累积, 但是因为在输入变量中比标准LSTM多两条测井曲线, 所以最终预测精度更高。

表2 串级LSTM与标准LSTM生成人工测井曲线的均方误差及标准差对比
3 讨论

本文将机器学习中的LSTM用于测井曲线的补全与人工测井曲线的生成。LSTM能够有效提取在空间上具有长期相关性的测井曲线的模式, 并基于这些模式对测井曲线进行估计与重构。此外, 本文还在标准LSTM的基础上结合串级系统设计了串级LSTM, 在需要人工生成多条测井曲线时, 串级LSTM具有比标准LSTM更高的预测准确度。

在测井曲线自动补全实验中, 利用LSTM对1口Eagle Ford页岩水平井的残缺测井曲线进行了自动补全。测井曲线中有20%的数据缺失且缺失段处于水平井穿过的两个地层的交界处。由于测井曲线在不同地层中具有不同的隐藏模式, 缺失段所处的位置增加了自动补全曲线的难度。然而利用LSTM仍然获得了令人满意的结果。该实验中的训练数据不包含其他井的测井曲线, 仅依赖同一口井已知的部分测井曲线就可以进行测井曲线补全。

在人工测井曲线生成实验中, 以大庆油田的6口直井为例进行了分析, 并对标准LSTM、串级LSTM和FCNN进行了对比。在串级LSTM中, 首先在浅层级对相对容易预测的曲线进行重构, 然后把生成的人工测井曲线作为下一级的输入。深层级的预测结果不但基于训练数据中的输入值, 还受浅层级预测结果的影响。这种方法能够更有效地提取输入数据中蕴含的信息, 提升模型的预测准确度, 尤其适用于需要人工生成多条测井数据的情况。实验结果表明, 串级LSTM在人工测井曲线生成的问题上具有明显优势。该实验基于直井数据进行, 由于水平井测井段穿过地层数量少于直井, 因此测井曲线的隐藏模式更简单, 基于串级LSTM生成的人工测井曲线应具有更高精度。

在页岩油气开发中, 总成本中很大一部分来自于完井过程, 然而大约30%~50%的射孔段对产量并没有贡献[32]。为了降低开发成本, 需要通过分析测井曲线增加对地层的认知, 然而目前的测井成本较高, 对于水平井而言更是如此, 其测井成本大约是直井的10倍[32]。本文提出的基于LSTM生成人工测井曲线的方法可以在一定程度上解决这一问题。可以利用1个区块内已有的测井曲线训练生成模型。然后对于新钻探的水平井或直井, 基于部分易于获得的测井曲线, 自动生成全套测井曲线。这种人工测井曲线成本较低, 容易得到大规模应用并获得大量详实的人工测井数据, 有利于进行区块乃至盆地级别的评估与分析。此外, 本文基于LSTM的人工测井曲线生成方法还可以应用于随钻估计和预测。根据钻井过程中采集到的数据实时生成测井曲线, 作为调整钻遇过程和设计完井策略的参考信息。针对缺少基础测井曲线的区块, 也可以考虑结合迁移学习的方法, 利用其他区块训练获得的模型进行预测分析。

4 结语

作为一种特殊的循环神经网络, LSTM比标准循环神经网络和传统全连接神经网络更适用于生成测井数据。此外, LSTM能够更有效地从训练数据中提取信息, 所以在训练数据较少时, LSTM仍然可以完成有效训练。本文提出的基于LSTM生成人工测井曲线的方法精度较高且成本较低。这种方法有助于更好地认识地层并改进钻完井策略, 从而达到油气开发降本增效的目的。

符号注释：

C— — 处理器状态; Ct— — 第t步的处理器状态; ${{\tilde{C}}_{t}}$— — 第t步tanh层的输出; d— — 缺失段起始测深处的采样点序号; D— — 井径, cm; ft— — 第t步遗忘门层的输出; GR— — 自然伽马, API; h— — 隐状态; ht— — 第t步的隐状态; H— — 深度, m; it— — 第t步输入门层的输出; L— — 预热段序列长度; Rat30— — 阵列感应电阻率, Ω · m; Δ R— — 微电极测井曲线的幅度差; SP— — 自然电位, mV; T— — 缺失段序列长度; whh, bhh— — 隐状态与隐状态间的权重和偏置项, 可训练; wih,

bih— — 输入与隐状态间的权重和偏置项, 可训练; Wc, bc— — tanh层的权重与偏置项; Wf, bf— — 遗忘门层的权重与偏置项; Wi, bi— — 输入门层的权重与偏置项; Wo, bo— — 输出门层的权重与偏置项; xt— — 第t步的输入; Δ tb— — 补偿声波, μ s/m; Δ tco— — 纵波时差, μ s/m; Δ th— — 高分辨率声波时差, μ s/m; Δ tsm— — 横波时差, μ s/m; ρ — — 密度, g/cm3; σ — — sigmoid函数; ϕ N— — 中子孔隙度, %。下标：CLSTM— — 基于串级LSTM生成的数据; FCNN— — 基于FCNN生成的数据; LSTM— — 基于LSTM生成的数据; test— — 实际测量数据; train— — 构成训练数据集的完整段数据。

The authors have declared that no competing interests exist.

参考文献
[1] ASQUITH G B, KRYGOWSKI D, GIBSON C R. Basic well log analysis[M]. Tulsa: American Association of Petroleum Geologists, 2004. [本文引用:1]
[2] BATEMAN R M. Openhole log analysis and formation evaluation[M]. 2nd ed. Richardson, Texas: Society of Petroleum Engineers, 2012 [本文引用:1]
[3] ESKANDARI H, REZAEE M, MOHAMMADNIA M. Application of multiple regression and artificial neural network techniques to predict shear wave velocity from wireline log data for a carbonate reservoir South-West Iran[J]. CSEG Recorder, 2004, 29(7): 40-48. [本文引用:1]
[4] WENDT W, SAKURAI S T, NELSON P. Permeability prediction from well logs using multiple regression[M]. Amsterdam: Elsevier, 1986: 181-221. [本文引用:1]
[5] ZERROUKI A A, AIFA T, BADDARI K. Prediction of natural fracture porosity from well log data by means of fuzzy ranking and an artificial neural network in Hassi Messaoud oil field, Algeria[J]. Journal of Petroleum Science and Engineering, 2014, 115: 78-89. [本文引用:1]
[6] ITURRAR N-VIVEROS U, PARRA J O. Artificial Neural Networks applied to estimate permeability, porosity and intrinsic attenuation using seismic attributes and well-log data[J]. Journal of Applied Geophysics, 2014, 107: 45-54. [本文引用:1]
[7] WANG G, CARR T R, JU Y, et al. Identifying organic-rich Marcellus Shale lithofacies by support vector machine classifier in the Appalachian basin[J]. Computers & Geosciences, 2014, 64: 52-60. [本文引用:1]
[8] SILVA A A, NETO I A L, MISS GIA R M, et al. Artificial neural networks to support petrographic classification of carbonate-siliciclastic rocks using well logs and textural information[J]. Journal of Applied Geophysics, 2015, 117: 118-125. [本文引用:1]
[9] SINGH U K. Fuzzy inference system for identification of geological stratigraphy off Prydz Bay, East Antarctica[J]. Journal of Applied Geophysics, 2011, 75(4): 687-698. [本文引用:1]
[10] SILVERSIDES K, MELKUMYAN A, WYMAN D, et al. Automated recognition of stratigraphic marker shales from geophysical logs in iron ore deposits[J]. Computers & Geosciences, 2015, 77: 118-125. [本文引用:1]
[11] ROLON L, MOHAGHEGH S D, AMERI S, et al. Using artificial neural networks to generate synthetic well logs[J]. Journal of Natural Gas Science and Engineering, 2009, 1(4/5): 118-133. [本文引用:1]
[12] ALIZADEH B, NAJJARI S, KADKHODAIE-ILKHCHI A. Artificial neural network modeling and cluster analysis for organic facies and burial history estimation using well log data: A case study of the South Pars Gas Field, Persian Gulf, Iran[J]. Computers & Geosciences, 2012, 45: 261-269. [本文引用:1]
[13] MO X, ZHANG Q, LI X. Well logging curve reconstruction based on Genetic Neural Networks[C]//Proceedings of the 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD). Zhangjiajie, China: IEEE, 2015. [本文引用:1]
[14] LONG W, CHAI D, AMINZADEH F. Pseudo density log generation using artificial neural network[R]. SPE 180439-MS, 2016. [本文引用:1]
[15] SALEHI M M, RAHMATI M, KARIMNEZHAD M, et al. Estimation of the non records logs from existing logs using artificial neural networks[J]. Egyptian Journal of Petroleum, 2016, 26(4): 957-968. [本文引用:1]
[16] ADAMOWSKI J, CHAN H F. A wavelet neural network conjunction model for groundwater level forecasting[J]. Journal of Hydrology, 2011, 407(1/2/3/4): 28-40. [本文引用:1]
[17] SAHOO S, RUSSO T, ELLIOTT J, et al. Machine learning algorithms for modeling groundwater level changes in agricultural regions of the US[J]. Water Resources Research, 2017, 53(5): 3878-3895. [本文引用:1]
[18] SCHUSTER M, PALIWAL K K. Bidirectional recurrent neural networks[J]. IEEE Transactions on Signal Processing, 1997, 45(11): 2673-2681. [本文引用:1]
[19] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. [本文引用:1]
[20] MIKOLOV T, KARAFI T M, BURGET L, et al. Recurrent neural network based language model[R]. Makuhari, Chiba, Japan: 11th Annual Conference of the International Speech Communication Association, 2010. [本文引用:1]
[21] SUTSKEVER I, VINYALS O, LE Q V. Sequence to sequence learning with neural networks[R]. Montreal, Canada: Advances in Neural Information Processing Systems 27 (NIPS 2014), 2014. [本文引用:1]
[22] GRAVES A, JAITLY N. Towards end-to-end speech recognition with recurrent neural networks[C]//Proceedings of the 23rd International Conference on Machine Learning. Washington D. C. : IEEE Computer Society Press, 2014. [本文引用:1]
[23] SILVA I N D, CAGNON J Â, SAGGIORO N J. Recurrent neural network based approach for solving groundwater hydrology problems[EB/OL]. (2013-01-16)[2018-05-20]. https://www.intechopen.com/books/artificial-neural-networks-architectures-and-applications/recurrent-neural-network-based-approach-for-solving-groundwater-hydrology-problems. [本文引用:1]
[24] ZHANG J, ZHU Y, ZHANG X, et al. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas[J]. Journal of Hydrology, 2018, 561: 918-929. [本文引用:1]
[25] CYBENKO G. Approximation by superpositions of a sigmoidal function[J]. Mathematics of Control, Signals and Systems, 1989, 2(4): 303-314. [本文引用:1]
[26] HORNIK K. Approximation capabilities of multilayer feedforward networks[J]. Neural Networks, 1991, 4(2): 251-257. [本文引用:1]
[27] LI F F, KARPATHY A, JOHNSON J. Convolutional neural networks for visual recognition[R]. Palo Alto: Stanford University, 2015. [本文引用:1]
[28] KARPATHY A. The unreasonable effectiveness of recurrent neural networks[EB/OL]. (2015-05-21)[2018-05-26]. http://karpathy.github.io/2015/05/21/rnn-effectiveness/. [本文引用:1]
[29] OLAH C. Understand ing LSTM networks[EB/OL]. (2015-08-27) [2018-05-26]. http://colah.github.io/posts/2015-08-Understanding-LSTMs/. [本文引用:2]
[30] BENGIO Y, SIMARD P, FRASCONI P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166. [本文引用:1]
[31] BREYER J A. The Eagle Ford Shale: A renaissance in U. S. oil production[M]. Tulsa: American Association of Petroleum Geologists, 2016. [本文引用:1]
[32] PARSHALL J. Drilling data provide solution to horizontal well log costs[J]. Journal of Petroleum Technology, 2015, 67(8): 35-38. [本文引用:2]