第一作者简介:孙贺东(1973-),男,河北唐山人,博士,中国石油勘探开发研究院高级工程师,主要从事气井试井及产能评价方面的科研工作。地址:河北省廊坊市44号信箱,中国石油勘探开发研究院气田开发研究所,邮政编码:065007。E-mail: sunhed@petrochina.com.cn
联系作者简介:欧阳伟平(1986-),男,江西萍乡人,博士,中国石油川庆钻探长庆井下技术作业公司工程师,主要从事试井分析及储集层动态评价方面的研究工作。地址:陕西省西安市未央区凤城四路长庆大厦,邮政编码:710018。E-mail: ouywp56@163.com
针对水力压裂形成的裂缝导流能力会随空间以及时间发生变化这一特点,建立考虑裂缝空间、时间双重变导流和应力敏感效应的致密气压裂直井渗流的新型数学模型,采用混合有限元方法对模型进行求解,获得新模型的Blasingame现代产量递减分析典型曲线。以此为基础,讨论了裂缝空间、时间双重变导流及应力敏感效应对Blasingame曲线形态的影响。研究表明:空间变导流效应主要表现为降低早期典型曲线值;时间变导流效应会导致产量及产量积分曲线下掉,形成S型典型曲线;双重变导流则是两者效应的叠加;时间、空间变导流效应均不会延缓地层进入拟稳态阶段的时间。应力敏感会降低曲线值,但不会使曲线陡降;应力敏感会延缓地层进入拟稳态阶段的时间。忽略变导流效应和应力敏感效应,不会对井控动态储量的计算结果产生较大影响,但会给裂缝、储集层参数解释带来较大误差。经苏里格气田致密气压裂井的常规现代产量递减分析与模型对比,证实新方法可靠实用,且比常规方法精度更高,可用于存在裂缝变导流致密气压裂井的现代产量递减分析。
Considering the characteristics that the fracture conductivity formed by hydraulic fracturing varies across space and time, a new mathematical model was established for seepage flow in tight gas fractured vertical wells which takes into account the effects of dual variable conductivity and stress sensitivity. The Blasingame advanced production decline curves of the model were obtained using the mixed finite element method. On this basis, the effects of fracture space and time dual variable conductivity and stress sensitivity on Blasingame curve were analyzed. The study shows that the space variable conductivity mainly reduces decline curve value at the early stage; the time variable conductivity can result in drops of the production and the production integral curves, leading to a S-shaped curve; dual variable conductivity is the superposition of the effects given by the two variable conductivities; both time and space variable conductivities cannot delay the time with which the formation fluid flow reaches the quasi-steady state. The stress sensitivity reduces the curve value gradually rather than sharply, delaying the time the flow reaching the quasi-steady state. Ignoring the effects of variable conductivity and stress sensitivity will not affect the estimation on well controlled dynamic reserves. However, it can result in large errors in the interpretation of fractures and reservoir parameters. Conventional advanced production decline analyses of a tight gas fractured well in the Sulige gas field showed that the new model is more effective and reliable than the conventional model, and thus it can be widely applied in advanced production decline analysis of wells with the same characteristics in other gas fields.
现代产量递减分析方法[1]是近年来油气藏工程学科中进行单井、井组生产动态分析的新兴技术, 它以不稳定渗流理论为基础, 根据油气井的日常生产数据, 采用Blasingame[2, 3]递减典型曲线拟合分析压力和产量之间的关系, 最终通过典型曲线拟合获取储集层参数与井控储量。现代产量递减分析方法自Blasingame提出双对数图版拟合后得到广泛应用, 随后许多学者将其扩展到不同类型井型[4, 5, 6]和储集层[7, 8, 9]。水力压裂是目前提高致密气单井产量的最常用的方法, 而压裂井现代产量递减分析除获取储集层参数和井控储量以外, 还可作为评价压裂效果、获取裂缝参数的技术手段。目前用于压裂井现代产量递减分析的渗流模型几乎均把裂缝假设成导流能力恒定[6, 7, 8, 9], 这将会给普遍存在变导流情况的压裂井生产数据分析带来较大误差。
裂缝变导流能力可分为空间变导流和时间变导流两类, 空间变导流是由于压裂施工中支撑剂充填不均, 裂缝为楔形缝, 导流能力随裂缝延伸而变化; 时间变导流是由于支撑剂破碎、嵌入地层、岩屑堵塞等因素导致裂缝导流能力随时间发生变化。裂缝导流能力变化主要与支撑剂铺置浓度、支撑剂物理性质、裂缝闭合应力以及岩石硬度有关, 也与储集层温度、流体性质以及盐水环境等因素有关。由于裂缝导流能力的影响因素多, 理论上很难采用通用的数学公式加以表征, 因此目前主要根据室内支撑剂导流能力测试来衡量裂缝变导流效应, 再利用不同函数关系对测试数据进行回归分析。国内外学者做了大量支撑剂导流实验来研究裂缝变导流效应[10, 11, 12], 其中空间变导流有线性、指数和对数3种变化形式, 而时间变导流主要有对数关系和指数关系2种变化形式。不少学者根据裂缝变导流公式建立油气井不稳定渗流模型, 然后应用于试井解释及生产动态分析[13, 14, 15, 16]。然而, 考虑裂缝空间与时间双重变导流的现代产量递减分析目前未查到相关的文献报道。
针对这一技术问题, 本文根据目前常用的裂缝变导流关系式, 建立一种同时考虑裂缝空间和时间变导流的致密气非稳态渗流数学模型。利用混合有限元方法对模型进行求解, 获得Blasingame现代产量递减分析典型曲线, 进而分析变导流因素对典型曲线的影响, 最后通过现场实例应用论证模型的可靠性及实用性。
对均质有界储集层中1口有限导流垂直压裂气井, 物理模型假设条件为:①储集层具有应力敏感效应, 考虑渗透率应力敏感, 忽略孔隙度应力敏感; ②致密气为干气或者低含水饱和度致密气, 水处于束缚状态, 不存在启动压力梯度效应, 气体在储集层中的流动为单相渗流, 且满足达西定律; ③水力压裂后形成1条有限导流裂缝, 裂缝具有空间变导流和时间变导流特性, 气体在裂缝中的流动为一维流动, 考虑压裂液对储集层的伤害, 用裂缝表皮系数来衡量其对储集层伤害的大小; ④裂缝体积与井控体积相比非常小, 裂缝渗透率远大于储集层渗透率, 裂缝压力降低造成裂缝内气体体积膨胀对整个流动的影响非常小, 可忽略裂缝控制方程中拟压力对时间的导数项; ⑤考虑气体压缩系数及黏度随压力变化而变化, 气体压缩系数及偏差因子采用Dranchuk-Purvis-Robinson方法[17]计算, 气体黏度采用Lee方法[18]计算。⑥不考虑井筒储集效应、温度变化等其他因素对流动的影响。
据文献[19], 储集层控制方程为:
$\frac{\partial }{\partial x}\left[ {{K}_{\text{r}}}\left( p \right)\frac{\partial \psi }{\partial x} \right]+\frac{\partial }{\partial y}\left[ {{K}_{\text{r}}}\left( p \right)\frac{\partial \psi }{\partial y} \right]-$${{\alpha }_{3}}T{{q}_{f}}={{\alpha }_{1}}\phi {{C}_{t}}\left( p \right)\mu \left( p \right)\frac{\partial \psi }{\partial t}$ (1)
其中 $\psi \left( p \right)=2\int_{0}^{p}{\frac{p}{\mu Z}}\text{d}p$
裂缝控制方程为:
$\frac{\partial }{\partial l}\left[ {{K}_{\text{f}}}\left( l, t \right)\frac{\partial \psi }{\partial l} \right]+{{\alpha }_{3}}T{{q}_{f}}=0$ (2)
初始条件为:
$\psi \left( x, y, 0 \right)={{\psi }_{\text{i}}}$ (3)
内边界条件为:
已知井口产量时,
${{\left. \frac{\partial \psi }{\partial l} \right|}_{{{\Gamma }_{\text{in}}}}}=\frac{{{\alpha }_{2}}{{q}_{\text{sc}}}\left( t \right)T}{{{w}_{f}}{{K}_{f}}\left( 0, t \right)h}$ (4)
已知井底压力时,
${{\left. \psi \right|}_{{{\Gamma }_{\text{in}}}}}={{\psi }_{\text{w}}}\left( t \right)$ (5)
封闭外边界为:
${{\left. \frac{\partial \psi }{\partial N} \right|}_{{{\Gamma }_{\text{out}}}}}=0$ (6)
物质平衡方程为:
$\frac{{\bar{p}}}{Z}=\frac{{{p}_{\text{i}}}}{{{Z}_{\text{i}}}}\left( 1-\frac{{{G}_{\text{p}}}}{G} \right)$ (7)
1.3.1 空间变导流
裂缝导流能力随裂缝长度呈线性、指数或对数关系变化, 计算公式分别为[14]:
${{F}_{\text{cl}}}={{F}_{\text{c0}}}\left( 1-{{a}_{s}}{{l}_{\text{D}}} \right)$ (8)
${{F}_{\text{cl}}}={{F}_{\text{c0}}}{{\text{e}}^{-{{b}_{s}}{{l}_{\text{D}}}}}$ (9)
${{F}_{\text{cl}}}={{F}_{\text{c0}}}\left[ 1-{{c}_{\operatorname{s}}}\ln \left( 1+{{l}_{\text{D}}} \right) \right]$ (10)
1.3.2 时间变导流
裂缝导流能力随生产时间呈对数或指数关系变化, 计算公式分别为[10, 11]:
${{F}_{\text{ct}}}={{F}_{\text{ci}}}\left[ 1-\chi \ln \left( 1+t \right) \right]$ (11)
${{F}_{\text{ct}}}={{F}_{\text{ci}}}{{\text{e}}^{-\gamma t}}+{{F}_{\text{cr}}}$ (12)
对目前常用的指数变化关系(12)式进行修改:
${{F}_{\text{ct}}}={{F}_{\text{ci}}}\left( \eta {{\text{e}}^{-\frac{t}{8\ 760C}}}+1-\eta \right)$ (13)
系数η 控制导流能力衰减幅度, 系数C控制导流能力的衰减速度, 修改后系数的物理意义更明确, 有助于生产数据解释及分析。
1.3.3 双重变导流
同时考虑空间变导流和时间变导流, 即裂缝导流能力不仅随裂缝位置而变, 同时还随着时间而变。以空间变导流和时间变导流均采用指数关系变化为例, 推导出双重变导流计算公式:
${{F}_{\text{c}}}\left( l, t \right)={{F}_{\text{ci0}}}{{\text{e}}^{-{{b}_{s}}{{l}_{\text{D}}}}}\left( \eta {{\text{e}}^{-\frac{t}{8\ 760C}}}+1-\eta \right)$ (14)
以此类推可以获得不同函数组合情况下的双重变导流公式。
致密气储集层可能会存在应力敏感、启动压力梯度及滑脱效应等非线性渗流特征。应力敏感效应主要表现为储集层渗透率不再为常数, 而是随有效应力的增大而减小。大量实验[20, 21, 22]表明致密气储集层具有较强的应力敏感效应, 对于分析长时间生产数据的产量递减分析来说必须予以考虑。气藏中存在启动压力梯度主要是由于气水作用造成[23, 24], 这与油藏中的启动压力梯度有本质区别, 因此气藏中存在一定程度的水是产生启动压力梯度的必要条件。此外, 致密气储集层可能还存在滑脱效应, 滑脱效应会增加视渗透率, 储集层越致密, 储集层压力越低, 滑脱效应越强, 目前考虑滑脱效应的渗流模型主要应用于埋深较浅的煤层气中[25, 26], 而对于储集层压力普遍较高的致密砂岩气藏, 滑脱效应的影响还有待考察。
1.4.1 滑脱效应
滑脱效应的大小主要由滑脱因子与储集层平均压力决定, 可由Klinkenberg公式表征[27]:
${{K}_{\text{g}}}={{K}_{\infty }}\left( 1+\frac{b}{{{p}_{\text{m}}}} \right)$ (15)
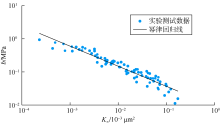
为了考察致密砂岩气藏中滑脱效应对渗流影响的大小, 采用苏里格气田岩心做了96次滑脱效应实验, 结果见图1, 经双对数线性回归得滑脱因子与绝对渗透率之间的关系式为:
$b=0.009\ 11K_{\infty }^{^{-0.606\ \ 1}}$ (16)
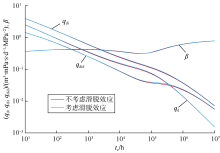
假设致密气储集层绝对渗透率为0.1× 10-3 μ m2, 原始储集层压力30 MPa, 生产后期的储集层平均压力为10 MPa, 根据(15)式与(16)式可计算得到滑脱效应对早期、后期储集层视渗透率的影响分别为0.12%和0.37%。即使储集层绝对渗透率为0.01× 10-3 μ m2, 对早期、后期储集层视渗透率的影响也仅有0.49%和1.48%。计算该储集层条件下滑脱效应对Blasingame曲线的影响(见图2), 对比可知, 考虑和不考虑滑脱效应情况下, 两者曲线基本重合, 说明其对产量递减曲线的影响非常小, 可以在致密气井产量递减分析过程中将其忽略。
1.4.2 应力敏感效应
储集层应力敏感的评价方法有很多种[28], 目前多采用指数和幂律关系式。鉴于实验测试数据幂律关系式回归的相关度更高, 本文采用渗透率随有效应力呈幂律关系变化的公式[29]:
${{K}_{\text{r}}}\left( p \right)={{K}_{\text{ri}}}{{\left( \frac{{{\sigma }_{\text{e}}}}{{{\sigma }_{\text{ei}}}} \right)}^{-{{S}_{\text{p}}}}}={{K}_{\text{ri}}}{{\left( \frac{\sigma -p}{\sigma -{{p}_{\text{i}}}} \right)}^{-{{S}_{\text{p}}}}}$ (17)
$\iint_{\Omega }{{{F}_{\text{eq}}}}\text{d}\Omega =\iint_{{{\Omega }_{\text{m}}}}{{{F}_{\text{eq}}}}\text{d}{{\Omega }_{\text{m}}}+{{w}_{\text{f}}}\int_{{{\overline{\Omega }}_{\text{f}}}}{{{F}_{\text{eq}}}}\text{d}{{\overline{\Omega }}_{\text{f}}}$ (18)
将整个计算区域划分为两个部分, 一个是二维流动的储集层区域, 一个是一维流动的裂缝区域。
利用Galerkin加权余量法[32]分别离散储集层和裂缝的控制方程, 得到储集层区域二维有限元方程为:
$\begin{align} & A{{K}_{\text{r}}}\left( p \right)\left[ {{b}_{i}}{{b}_{i}}+{{c}_{i}}{{c}_{i}}+\frac{{{\alpha }_{1}}\phi \mu \left( p \right){{C}_{\text{t}}}\left( p \right)}{6\Delta t{{K}_{\text{r}}}\left( p \right)} \right]\psi _{i}^{n+1}+ \\ & A{{K}_{\text{r}}}\left( p \right)\left[ {{b}_{i}}{{b}_{j}}+{{c}_{i}}{{c}_{j}}+\frac{{{\alpha }_{1}}\phi \mu \left( p \right){{C}_{\text{t}}}\left( p \right)}{12\Delta t{{K}_{\text{r}}}\left( p \right)} \right]\psi _{j}^{n+1}+ \\ & A{{K}_{\text{r}}}\left( p \right)\left[ {{b}_{i}}{{b}_{k}}+{{c}_{i}}{{c}_{k}}+\frac{{{\alpha }_{1}}\phi \mu \left( p \right){{C}_{\text{t}}}\left( p \right)}{12\Delta t{{K}_{\text{r}}}\left( p \right)} \right]\psi _{k}^{n+1}- \\ & \frac{{{K}_{\text{r}}}\left( p \right)L}{3}\frac{\partial \psi _{i}^{n+1}}{\partial N}-\frac{{{K}_{\text{r}}}\left( p \right)L}{6}\frac{\partial \psi _{j(k)}^{n+1}}{\partial N}= \\ & \frac{{{\alpha }_{1}}A\phi \mu \left( p \right){{C}_{\text{t}}}\left( p \right)}{6\Delta t}\psi _{i}^{n}+\frac{{{\alpha }_{1}}A\phi \mu \left( p \right){{C}_{\text{t}}}\left( p \right)}{12\Delta t}\psi _{j}^{n}+ \\ \end{align}$ $\frac{{{\alpha }_{1}}A\phi \mu \left( p \right){{C}_{\text{t}}}\left( p \right)}{12\Delta t}\psi _{k}^{n}$ (19)
裂缝区域一维有限元方程为:
$\frac{{{F}_{\text{c}}}\left( l, t \right)}{L}\psi _{i}^{n+1}-\frac{{{F}_{\text{c}}}\left( l, t \right)}{L}\psi _{j}^{n+1}+{{F}_{\text{c}}}\left( l, t \right)\frac{\partial {{\psi }_{i}}}{\partial l}=0$ (20)
由(19)式和(20)式建立储集层区域的有限元刚度矩阵和裂缝区域的刚度矩阵, 再将两者组合成系统刚度矩阵。根据窜流关系式, 通过储集层和裂缝单元叠加消除裂缝与储集层交界处的边界项, 即(19)式等号左端最后两项以及(20)式等号左端最后一项, 具体组合方法可参照文献[30, 31]。
裂缝导流能力、储集层渗透率、气体黏度以及压缩系数均会随着时间而变, 实际计算中每个时间步根据各参数的具体计算方法来计算。此外, 模型采用两种方法计算储集层平均压力:①根据生产数据迭代获取井控储量时采用(7)式计算储集层平均压力; ②全历史曲线拟合时采用网格单元压力加权平均的方法计算储集层平均压力。最后利用线性方程组求解器求解组合成的线性方程组, 从而获得模型的解。
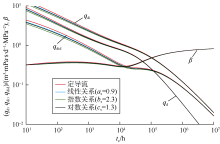
假定储集层渗透率为0.1× 10-3 μ m2, 原始储集层压力为30 MPa, 储集层温度为100 ℃, 有效厚度为8 m, 孔隙度为10%, 圆形封闭半径为500 m, 天然气相对密度为0.7, 裂缝半长为100 m, 单独考虑裂缝空间变导流, 缝口导流能力为200× 10-3 μ m2· m。为了便于对比分析, 可设置变导流系数as, bs, cs的值使得缝端导流能力均为20× 10-3 μ m2· m。
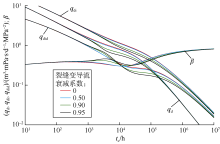
通过计算得不同裂缝空间变导流条件下的Blasingame典型曲线(见图3)。对比计算结果可知, 裂缝空间变导流能力对产量递减典型曲线影响主要在早期, 变导流会降低早期典型曲线值, 类似于裂缝表皮系数的影响, 常规不考虑变导流的模型会造成表皮系数解释结果偏大。不同变导流条件下晚期典型曲线几乎重合, 尤其β 曲线完全重合可以说明空间变导流不影响压力的扩散速度, 拟稳态阶段的出现时间不受其影响。另外, 对比不同空间变导流关系曲线可以发现, 在相同的缝端和缝口导流能力情况下, 指数变化对典型曲线的降低幅度最大, 线性关系最小, 对数关系居中。
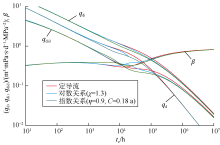
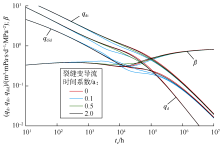
采用相同的储集层参数, 单独考虑裂缝时间变导流的影响。假定裂缝初始导流能力为200× 10-3 μ m2· m, 生产1年后导流能力值衰减至20× 10-3 μ m2· m, 随后基本稳定。分别根据对数和指数变化关系计算时间变导流能力对Blasingame典型曲线的影响(见图4)。分析计算结果可知, 相比于标准定导流典型曲线, 裂缝时间变导流能力对产量递减曲线的影响比较明显, 其主要影响在中期, 表现为产量曲线及产量积分曲线下掉, β 曲线上升, 形成S型。与空间变导流的影响类似, 时间变导流对典型曲线晚期的影响非常小, 从晚期β 曲线重合可知时间变导流同样不会影响储集层的压力扩散速度。此外, 对比对数关系与指数关系条件下的典型曲线可知, 对数关系下的典型曲线光滑度不如指数关系, 另外对数关系对典型曲线的影响幅度要小于指数关系, 这是因为对数关系整个过程的变化率比较平稳, 而指数关系的变化率由大变小。
以指数变导流关系为例来分析变导流系数对典型曲线的影响。图5为设定变导流时间系数为0.1 a, 不同变导流衰减系数条件下典型曲线对比。图6为设定变导流衰减系数为0.9, 不同变导流时间系数条件下的典型曲线对比。由计算结果可知, 裂缝变导流衰减系数越大, 产量曲线及产量积分曲线下掉的幅度越大, S型曲线越明显。裂缝变导流时间系数越大, 即裂缝导流能力衰减速度越小, 产量曲线及产量积分曲线下掉的开始时间越晚, 其对典型曲线的影响也越小, 当变导流时间系数很大时, 其影响很难辨别, 基本可以忽略。由此可知时间变导流模型中裂缝衰减系数控制典型曲线下掉的幅度大小, 而时间系数控制着典型曲线下掉的时间早晚。这一特点对于时间变导流裂缝井的产量递减曲线拟合具有重要指导意义。
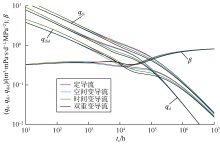
图7为不同裂缝变导流条件下的Blasingame曲线对比, 其中空间变导流和时间变导流均采用指数变化关系, 变导流系数bs值为2, η 值为0.9, C值为0.2 a。对比曲线可知, 典型曲线早期定导流曲线与时间变导流曲线重合, 而空间变导流曲线与双重变导流曲线重合, 这说明典型曲线早期主要受空间变导流的影响; 典型曲线中期空间变导流曲线与双重变导流相差较大, 而时间变导流曲线与双重变导流曲线差别较小, 这说明典型曲线中期受时间变导流和空间变导流双重影响, 但时间变导流起主导作用; 典型曲线晚期基本不受变导流的影响, 所有曲线基本重合。综合对空间变导流和时间变导流的单因素影响分析可知, 同时考虑空间变导流和时间变导流条件下的Blasingame曲线是两者效应的叠加。
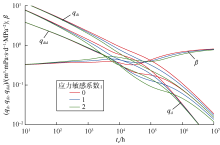
致密气储集层实际生产井中可能会存在裂缝双重变导流和应力敏感共同作用的情况, 为此在模型中同时考虑裂缝双重变导流和地层应力敏感效应。假定上覆岩石压力为60 MPa, 空间变导流和时间变导流均采用指数变化关系, 变导流系数bs值为2, η 值为0.9, C值为0.2 a, 分别计算双重变导流作用下不同应力敏感系数的Blasingame典型曲线(见图8)。对比可知, 不同应力敏感系数条件下的曲线在早期阶段基本重合, 但一段时间后曲线差异逐渐加大。与时间变导流的影响类似, 应力敏感效应会造成中后期阶段产量递减典型曲线值减小, 应力敏感系数越大曲线值减小的幅度越大。与时间变导流效应不同的是, 应力敏感会使得地层渗透率减小, 由此减缓压力扩散的速度, 使得边界响应的时间推迟, 图中β 曲线后期能够清晰地反映出该特征, 应力敏感效应越强拟稳态开始的时间越晚, 这种特点可用于区分应力敏感和时间变导流。
另外, 晚期进入拟稳态后, 变导流能力效应和应力敏感效应影响极小, 即:变导流能力效应和应力敏感效应不会对井控动态储量的拟合结果产生影响。
采用本文建立的致密气储集层双重变导流渗流模型对苏里格气田S1井的生产数据进行现代产量递减分析, 并与常规模型的拟合结果进行对比来说明新模型的可靠性与实用性。该井原始储集层压力为32 MPa, 储集层温度为107 ℃, 孔隙度13.7%, 有效厚度为5.3 m, 含气饱和度74%, 天然气相对密度0.6, 生产时间约2.5 a, 累计产气量848× 104 m3。
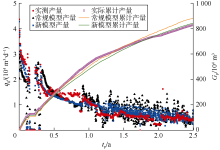
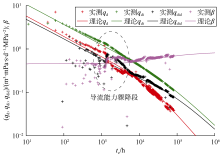
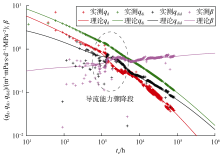
S1井全历史日产量及累计产量曲线的拟合效果见图9, 可以看出, 新模型对产量的拟合程度更高。常规模型与新模型的产量递减典型曲线拟合效果见图10、图11, 从图中实测Blasingame产量曲线可知, 该井在生产时间约1 000 h后产量曲线突然下掉, 产量曲线具有明显的S型特征, 非常符合时间变导流效应的特点。从图11中可以看出, 考虑双重变导流效应和应力敏感效应可以对典型曲线以及全历史产量曲线进行比较理想的拟合, 而常规模型无法对裂缝导流能力骤降段进行拟合(见图10), 只能通过加大裂缝半长、裂缝导流能力, 减小储集层渗透率来大致拟合早期典型曲线的变化趋势, 因此其解释的裂缝半长及裂缝导流能力都严重偏大。由此可见, 新模型比常规模型方法更实用、精度更高。
此外, 对比井控半径及井控储量可知(见表1), 两者解释的结果基本一致, 这进一步说明了变导流效应和应力敏感效应均不会对井控动态储量的拟合结果产生较大影响。从解释得到的变导流系数可知, 该井在早期生产过程中导流能力衰减幅度非常大, 时间变导流衰减系数达到了0.989, 这也是造成产量快速递减的主要原因。
| 表1 苏里格气田S1井的产量递减分析结果 |
建立了考虑裂缝空间、时间双重变导流和应力敏感效应的致密气压裂直井渗流的新型数学模型; 推导出一种新的指数型时间变导流表征公式, 变导流系数物理意义更明确; 采用混合有限元方法对模型进行求解, 获得新模型的Blasingame典型曲线。
裂缝变导流及应力敏感效应对Blasingame曲线的影响表现出不同的特点:空间变导流效应主要表现为降低早期典型曲线值; 时间变导流效应会使产量及产量积分曲线下掉, 形成S型典型曲线; 双重变导流则是两者效应的叠加; 时间、空间变导流效应均不会延缓地层进入拟稳态阶段的时间。应力敏感会降低曲线值, 但不会使曲线陡降; 应力敏感会延缓地层进入拟稳态阶段的时间。忽略变导流效应和应力敏感效应, 不会对井控动态储量的计算结果产生较大影响, 但会给裂缝、储集层参数解释带来较大误差。
经苏里格气田致密气压裂井的常规现代产量递减分析与新模型对比, 证实新方法可靠实用, 且比常规模型精度更高, 可用于存在裂缝变导流效应的致密气压裂井现代产量递减分析。
符号注释:
as, bs, cs— — 不同空间变导流变化关系的回归系数, 无因次; A— — 三角形网格单元面积, m2; b— — 气体滑脱因子, MPa; bi, bj, bk, ci, cj, ck— — 有限元单元系数, m-1; C— — 裂缝变导流时间系数, a; Ct— — 综合压缩系数, MPa-1; Fc— — 随空间及时间而变的裂缝导流能力, 10-3 μ m2· m; Fc0— — 缝口处裂缝的导流能力, 10-3 μ m2· m; Fci— — 裂缝初始导流能力, 10-3 μ m2· m; Fci0— — 缝口处裂缝初始导流能力, 10-3 μ m2· m; Fcl— — 随裂缝长度变化的导流能力, 10-3 μ m2· m; Fcr— — 裂缝残余导流能力, 10-3 μ m2· m; Fct— — 随时间变化的导流能力, 10-3 μ m2· m; Feq— — 流体流动方程; G— — 井控地质储量, 104 m3; Gp— — 累计产量, 104 m3; h— — 储集层有效厚度, m; i, j, k— — 三角形网格结点序号; j(k)— — j或k; Kf— — 裂缝渗透率, 10-3 μ m2; Kg— — 视渗透率, 10-3 μ m2; Kr— — 储集层渗透率, 10-3 μ m2; Kri— — 储集层初始渗透率, 10-3 μ m2; K∞ — — 绝对渗透率, 10-3 μ m2; l— — 裂缝控制方程坐标, m; lD— — 距缝口的无因次距离, lD=l/xf; L— — 裂缝一维网格长度, m; n— — 时间节点; p— — 压力, MPa; $\bar{p}$— — 储集层平均压力, MPa; pi— — 原始储集层压力, MPa; pm— — 储集层压力, MPa; qd, qdi, qdid— — 规整化产量、产量积分、产量积分导数, m3· mPa· s/(d· MPa2); qf— — 单位时间内从单位体积储集层进入裂缝的标准状况下的流体体积, d-1; qg— — 天然气产量, 104 m3/d; qsc— — 标准状况下气体产量, m3/d; Sp— — 渗透率应力敏感系数, 无因次; t— — 生产时间, h; tc— — 物质平衡时间, h; tp— — 气井生产时间, a; T— — 储集层温度, K; wf— — 裂缝宽度, m; x, y— — 储集层控制方程坐标, m; xf— — 裂缝半长, m; Z— — 气体偏差因子, 无因次; Zi— — 初始状态气体偏差因子, 无因次; ${{\alpha }_{1}}$— — 量纲换算系数, 277.8, 无因次; ${{\alpha }_{2}}$— — 量纲换算系数, 0.004, 无因次; ${{\alpha }_{3}}$— — 量纲换算系数, 0.008 MPa/K; β — — 规整化产量积分导数与规整化产量积分之比, 无因次; γ — — 时间变导流指数变化关系的回归系数, h-1; Γ in— — 内边界; Γ out— — 外边界; Δ t— — 时间步长, h; η — — 裂缝变导流衰减系数, 无因次; μ — — 气体黏度, mPa· s; σ — — 上覆岩石应力, MPa; ${{\sigma }_{\text{e}}}$— — 储集层有效应力, MPa; ${{\sigma }_{\text{ei}}}$— — 储集层初始有效应力, MPa; ϕ — — 有效孔隙度, %; χ — — 时间变导流对数变化关系的回归系数, 无因次; ψ — — 拟压力, MPa2/(mPa· s); ψ i— — 初始拟压力, MPa2/(mPa· s); ψ w— — 井底拟压力, MPa2/(mPa· s); $\frac{\partial \psi }{\partial N}$— — 沿Γ 单位外法线方向N的方向导数; Ω — — 整个流动区域; Ω m— — 储集层流动区域; ${{\overline{\Omega }}_{\text{f}}}$— — 裂缝流动区域。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|