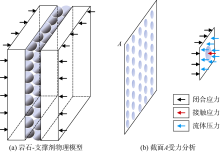
取支撑剂与岩石的接触截面A（见图1）进行分析, 其截面积为A_t。在该截面上作用有流体压力和支撑剂接触应力^[14]。根据受力平衡关系可得：

$\sigma_{c}A_{t}=\sigma_{p}A_{p}+p_{f}(A_{t}-A_{p})$（1）

图1

	Figure Option ViewDownloadNew Window
	图1 岩石-支撑剂受力分析图

（1）式中接触应力表示与岩石接触的支撑剂承受的应力大小, 为分析岩石-支撑剂体系内单个支撑剂的受力状态, 需确定与裂缝面接触的支撑剂分布状态。裂缝内支撑剂分布包括3种形式^[15]：单层稀疏分布、单层紧密分布和多层分布（见图2）。对于多层分布的支撑剂, 受闭合应力影响, 支撑剂在缝内处于压实状态, 因此多层分布状态下与岩石接触的支撑剂可视为单层紧密分布。多层分布的支撑剂接触应力分析与单层紧密分布支撑剂接触应力分析相同。

图2

	Figure Option ViewDownloadNew Window
	图2 支撑剂分布形式示意图

采用支撑剂面密度描述支撑剂分布状态。支撑剂面密度为单位面积内与岩石接触的支撑剂数量, 即：

${{n}_{t}}=\frac{{{N}_{t}}}{{{A}_{t}}}$ （2）

受岩石表面粗糙度和支撑剂粒径分布影响, 实际嵌入裂缝表面的支撑剂数量小于支撑剂总量^{[16, 17]}。定义支撑剂嵌入比例ε 为支撑剂嵌入数量与单层支撑剂（与岩石表面接触的支撑剂）总量之比, 即：

$\varepsilon =\frac{N}{{{N}_{t}}}=\frac{n}{{{n}_{t}}}$ （3）

单个支撑剂平均嵌入面积为：

${{A}_{pe}}=\frac{{{A}_{p}}}{N}$ （4）

联立（1）式— （4）式, 得到单个支撑剂平均接触应力为：

${{\sigma }_{p}}=\frac{{{\sigma }_{c}}-\left( 1-\varepsilon {{n}_{t}}{{A}_{pe}} \right){{p}_{f}}}{\varepsilon {{n}_{t}}{{A}_{pe}}}$ （5）

（5）式描述了接触应力与嵌入面积、嵌入量及外载荷的关系。由于外载荷、流体压力和支撑剂分布为已知量, 接触应力的求解关键在于嵌入面积的确定。

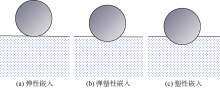
支撑剂嵌入岩体的过程可描述为圆球在法向载荷作用下与半无限空间体的接触力学问题。随着支撑剂嵌入深度的增加, 岩体和支撑剂接触位置的局部变形经历3种阶段— — 弹性阶段、弹塑性阶段和塑性阶段（见图3）。建立支撑剂嵌入过程的本构模型, 包括嵌入深度与外载荷的关系、嵌入深度与接触面积的关系, 是分析支撑剂嵌入深度的重要步骤。其中接触面积为支撑剂嵌入岩石的横截面积。

图3

	Figure Option ViewDownloadNew Window
	图3 支撑剂嵌入阶段示意图

1.2.1 弹性嵌入

支撑剂与岩石的接触面积较小时, 局部变形满足弹性变形。根据Hertz理论^[18], 支撑剂嵌入岩石的深度与平均接触应力的关系为：

$\sigma _{p, e}^{{}}=\frac{4{E}'}{3\pi }{{\left( \frac{d}{R} \right)}^{{1}/{2}\; }}$ （6）

广义弹性模量满足如下关系式^[18]：

$\frac{1}{{{E}'}}=\frac{1-\upsilon _{r}^{2}}{{{E}_{r}}}+\frac{1-\upsilon _{p}^{2}}{{{E}_{p}}}$ （7）

弹性嵌入阶段, 支撑剂嵌入岩石的接触面积与嵌入深度的关系为^[19]：

$A_{p, e}^{{}}=\pi Rd$ （8）

当支撑剂与岩石的接触应力达到1.1倍岩石屈服应力时, 岩石开始发生弹塑性变形^[19]。因此, 根据（6）式可得弹性阶段最大嵌入深度为：

${{d}_{c1}}={{\left( \frac{3.3\pi {{\sigma }_{\text{y}}}}{4{E}'} \right)}^{2}}R$ （9）

值得注意的是, 根据（9）式确定的弹性阶段最大嵌入深度是理论值。

1.2.2 塑性嵌入

由于弹塑性阶段的力学特征参数值主要以数值解为主, 解析公式需要根据弹性和塑性解进行插值建立, 因此首先描述塑性阶段变形, 再给出弹塑性嵌入的本构方程。

当接触应力达到岩石硬度时, 岩石开始发生塑性变形^[20], 并维持恒定的接触应力。材料硬度一般为屈服应力的3倍^[21], 因此塑性阶段接触应力为：

$\sigma _{p, p}^{{}}=3{{\sigma }_{\text{y}}}$ （10）

塑性阶段支撑剂嵌入岩石的接触面积与嵌入深度的关系为^[22]：

$A_{p, p}^{{}}=2\pi Rd$ （11）

岩石发生塑性变形的临界嵌入深度的准确确定需借助纳米压痕实验。为方便理论计算, 本文采用固体材料发生塑性变形的临界嵌入深度计算方法进行计算。对于固体材料, 理论和实验研究表明, 开始发生塑性变形的临界嵌入深度一般为弹性阶段最大嵌入深度的82.5倍^{[23, 24]}。因此, 塑性变形的临界嵌入深度为：

${{d}_{c2}}=82.5{{d}_{c1}}=\frac{56.15{{\pi }^{2}}\sigma _{\text{y}}^{\text{2}}R}{{{{{E}'}}^{2}}}$ （12）

需要注意的是, 根据（12）式确定的发生塑性变形的临界嵌入深度是基于均质固体材料假设的理论结果。对于实际岩石, 考虑其沉积演化等复杂过程的影响, 发生塑性变形的临界嵌入深度可能会有变化, 准确值需通过纳米压痕实验确定。

1.2.3 弹塑性嵌入

当d_c1≤ d≤ d_c2时, 接触区域处于弹塑性变形阶段^{[25, 26, 27]}。弹塑性变形阶段属于纯弹性和塑性变形的过渡阶段, 但力学机理较为复杂, 难以得到理论解。采用有限元等数值方法可以获得数值解^[21], 但数值方法计算量较大, 不利于工程应用。因此, 本文采用插值方法建立弹塑性阶段的本构方程, 方法简单, 便于计算分析。

根据Francis^[28]的实验研究结果, 弹塑性阶段接触应力可描述为：

$\sigma _{p, ep}^{{}}={{a}_{1}}+{{a}_{2}}\ln d$ （13）

根据[d_c1, d_c2]端点的应力连续性条件可以确定系数a₁、a₂, 由此得到：

$\sigma _{p, ep}^{{}}={{\sigma }_{\text{y}}}\left[ 1.1+2.9\frac{\ln \left( {d}/{{{d}_{c1}}}\; \right)}{\ln \left( {{{d}_{c2}}}/{{{d}_{c1}}}\; \right)} \right]$ （14）

由于弹塑性阶段为弹性和塑性的过渡阶段, 因此可假设弹塑性阶段接触面积与嵌入深度的关系为：

$A_{p, ep}^{{}}=c\left( d \right)\pi Rd$ （15）

采用三次样条插值法确定c(d)的表达式, 令：

$c\left( d \right)={{c}_{1}}{{d}^{3}}+{{c}_{2}}{{d}^{2}}+{{c}_{3}}d+{{c}_{4}}$ （16）

连续性条件为：

$\left\{ \begin{align} & A_{p, e}^{{}}\left( {{d}_{\text{c}1}} \right)=A_{p, ep}^{{}}\left( {{d}_{c1}} \right) \\ & A_{p, p}^{{}}\left( {{d}_{\text{c}2}} \right)=A_{p, ep}^{{}}\left( {{d}_{c2}} \right) \\ & A{{_{p, e}^{{}}}^{\prime }}\left( {{d}_{\text{c}1}} \right)=A{{_{p, ep}^{{}}}^{\prime }}\left( {{d}_{c1}} \right) \\ & A{{_{p, p}^{{}}}^{\prime }}\left( {{d}_{\text{c}2}} \right)=A{{_{p, ep}^{{}}}^{\prime }}\left( {{d}_{c2}} \right) \\ \end{align} \right.$ （17）

求解方程组（17）得到：

$c\left( d \right)=1-2{{\left( \frac{d-{{d}_{c1}}}{{{d}_{c2}}-{{d}_{c1}}} \right)}^{3}}+3{{\left( \frac{d-{{d}_{c1}}}{{{d}_{c2}}-{{d}_{c1}}} \right)}^{2}}$ （18）

将（18）式代入（15）式可得：

$A_{p, ep}^{{}}=\pi Rd\left[ 1-2{{\left( \frac{d-{{d}_{c1}}}{{{d}_{c2}}-{{d}_{c1}}} \right)}^{3}}+3{{\left( \frac{d-{{d}_{c1}}}{{{d}_{c2}}-{{d}_{c1}}} \right)}^{2}} \right]$ （19）

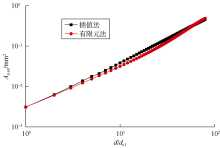
为分析插值方法的可靠性, 将插值法计算结果与Kogut等^[27]的有限元法计算结果对比（见图4）, 可以发现两者较为接近, 平均误差为5.71%, 说明插值方法具有较高的工程计算精度。

图4

	Figure Option ViewDownloadNew Window
	图4 插值结果和有限元结果对比

支撑剂嵌入深度的计算方法取决于支撑剂与岩石的嵌入变形阶段, 而变形阶段也是待确定的, 因此采用试算法求解支撑剂嵌入深度。首先根据岩石和支撑剂基本参数计算临界嵌入深度d_c1和d_c2。假设支撑剂嵌入处于弹性阶段, 则联立（5）式、（6）式和（8）式, 得到关于d的非线性方程F₁(d), 再采用牛顿法求得弹性嵌入深度, 若其值小于等于d_c1, 则假设正确。否则假设支撑剂嵌入处于弹塑性阶段, 联立（5）式、（14）式和（19）式, 得到关于d的非线性方程F₂(d), 再采用牛顿法求得弹塑性嵌入深度, 若其值小于d_c2, 则假设正确。否则支撑剂嵌入处于塑性阶段, 联立（5）式、（10）式和（11）式, 得到关于d的线性方程F₃(d), 从而求得支撑剂嵌入深度。采用Matlab软件编程实现上述求解过程。

支撑剂铺置浓度为单位面积的支撑剂质量, 根据支撑剂颗粒密度和体积可得到支撑剂铺置浓度与面密度的转化关系：

${{n}_{t}}=\frac{3{{c}_{p}}}{4\pi \rho {{R}^{3}}}$ （20）

本文所用支撑剂达到最大面密度时的支撑剂铺置浓度为0.95 kg/m²。当铺置浓度大于0.95 kg/m²时, 支撑剂呈现多层分布形式, 但与岩石表面接触的支撑剂面密度仍为单层紧密铺置时的最大面密度, 因此继续增大浓度不会增加与岩石表面接触的承压支撑剂数量。如图6所示, 当支撑剂浓度大于1.00 kg/m²时, 支撑剂嵌入深度和接触应力不再发生变化, 与前述分析一致。图6a显示, 不同缝内流体压力条件下, 支撑剂浓度0.25 kg/m²时的嵌入深度是1.00 kg/m²时的嵌入深度的2~3倍, 即当支撑剂为单层稀疏分布时, 支撑剂浓度越大, 支撑剂嵌入深度越小。

图6

	Figure Option ViewDownloadNew Window
	图6 不同铺置浓度的支撑剂嵌入特征

图6b显示, 在本文算例条件下, 不同支撑剂浓度下的接触应力均大于岩石屈服应力, 并小于3倍岩石屈服应力, 表明支撑剂嵌入主要发生于弹塑性变形阶段。同时, 流体压力为0~55 MPa时, 接触应力变化缓慢, 流体压力为55~65 MPa时, 接触应力变化显著。在闭合应力60 MPa、流体压力为零的条件下, 不同支撑剂浓度下的接触应力为287~315 MPa, 平均值约为闭合应力的5倍。由于支撑剂嵌入深度较小, 接触面积远小于闭合应力作用面积, 根据（1）式可以得到接触应力远大于闭合应力。需要注意的是, 实验测试支撑剂破碎时的应力为闭合应力, 并不是接触应力, 因此接触应力较高并不能说明支撑剂发生破碎。

图7中支撑剂嵌入深度与接触应力随流体压力的变化规律与图6类似。相同条件下, 支撑剂嵌入深度和接触应力随嵌入比例减小而增大。支撑剂嵌入比例为1时, 承压支撑剂密度最大, 单个颗粒的接触应力最小, 因此嵌入深度最小。嵌入比例受支撑剂粒径分布影响, 粒径分布分散时嵌入比例较小, 而粒径分布集中的支撑剂嵌入比例会趋近于1, 因此采用粒径均一或分布相对集中的支撑剂有利于减小支撑剂嵌入深度。对于段塞加砂工艺, 支撑剂分布会出现局部支撑, 嵌入比例会减小, 从而增大了嵌入深度。因此, 段塞加砂工艺要注重后期支撑剂嵌入的分析, 在压裂设计阶段可以提高支撑剂浓度来减小嵌入深度。

图7

	Figure Option ViewDownloadNew Window
	图7 不同嵌入比例的支撑剂嵌入特征

当流体压力大于等于闭合应力时, 支撑剂接触应力为零, 不发生嵌入; 随着流体返排和生产进行, 裂缝内流体压力不断减小, 作用在支撑剂上的接触应力不断增加, 嵌入深度逐渐增大。图8显示, 流体压力为零的条件下, 与闭合应力为50 MPa时相比, 闭合应力为65 MPa时嵌入深度增大25.6%; 在本文算例中闭合应力条件（60 MPa）下, 与缝内流体压力为40 MPa时相比, 缝内流体压力为零时嵌入深度增大127.5%。因此, 高闭合应力情况（如深井压裂）下支撑剂嵌入会更加显著; 生产过程中流体压力下降会显著增大支撑剂嵌入深度, 在进行产能递减分析时不能忽视流体压力下降导致的支撑剂嵌入问题。

图8

	Figure Option ViewDownloadNew Window
	图8 不同闭合应力的支撑剂嵌入特征

图9a显示, 相同条件下, 减小粒径会增大支撑剂嵌入深度。图9b显示, 不同粒径的支撑剂主要发生弹塑性嵌入, 接触应力受支撑剂粒径影响, 粒径越小, 嵌入面积越小, 接触应力则越大。因此, 采用小粒径支撑剂时需要注意支撑剂嵌入引起的缝宽变化。

图9

	Figure Option ViewDownloadNew Window
	图9 不同粒径的支撑剂嵌入特征

图10a显示, 减小岩石与支撑剂弹性模量比值会增大支撑剂嵌入深度。对于煤岩、塑性页岩等, 较低的弹性模量势必带来较大的嵌入深度, 与实验结果^{[4, 5, 29]}一致。图10b显示, 相同条件下, 岩石与支撑剂弹性模量比值越大, 接触应力越大。这是因为相同外载与内压作用下, 支撑剂所受的接触应力与接触面积成反比, 岩石弹性模量较低时支撑剂嵌入深度较大, 接触面积较大, 接触应力减小。

图10

	Figure Option ViewDownloadNew Window
	图10 不同岩石与支撑剂弹性模量比值的支撑剂嵌入特征