0 引言
“水平钻井+分段多簇压裂”工艺是实现非常规油气储层人工改造和效益开发的关键技术，其目标是沿水平段上多簇射孔的开启裂缝注入支撑剂形成有效渗流通道[1-2]。现场监测结果表明多裂缝起裂效率并不高，在大量促进多裂缝均衡改造研究基础上，目前形成了极限限流、非均匀布孔和暂堵转向等压裂工艺[3-5]，但大多重点关注缝内携砂液流动行为，较少考虑井筒内砂液运移和孔眼动态磨蚀过程，默认所有孔眼进砂浓度等于井口注入浓度。然而，现场试验与理论分析均发现井筒中支撑剂并不能完全沿着流线轨迹运移，并且孔眼磨蚀现象非常严重，各簇孔眼进液效率并不等同于进砂效率[6-8]。忽略井筒砂液运移和孔眼磨蚀过程极大限制了当前裂缝扩展与支撑剂运移模拟分析的可靠性，更不能准确解释非均匀进液、进砂和孔眼磨蚀等监测结果。因此，开展携砂液体由井口注入到井筒-孔眼-裂缝中运移的全过程研究，对深入认识多裂缝竞争扩展机制、解释现场监测数据、提升压裂工艺参数适应性具有重要意义。
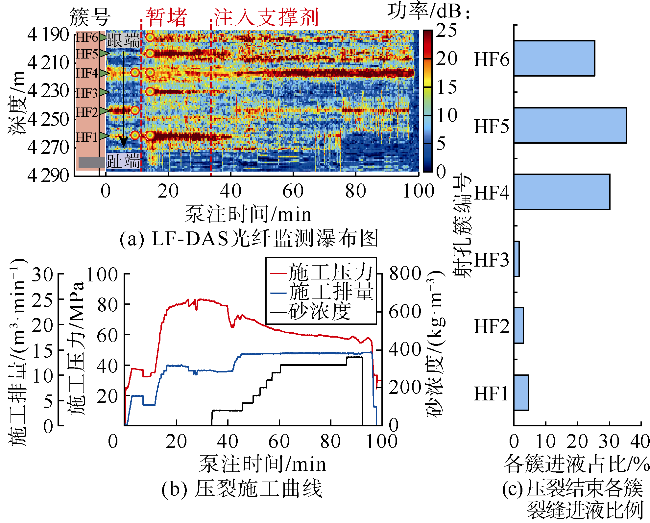
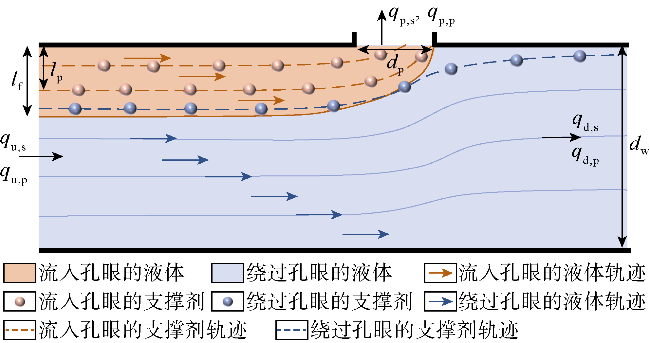
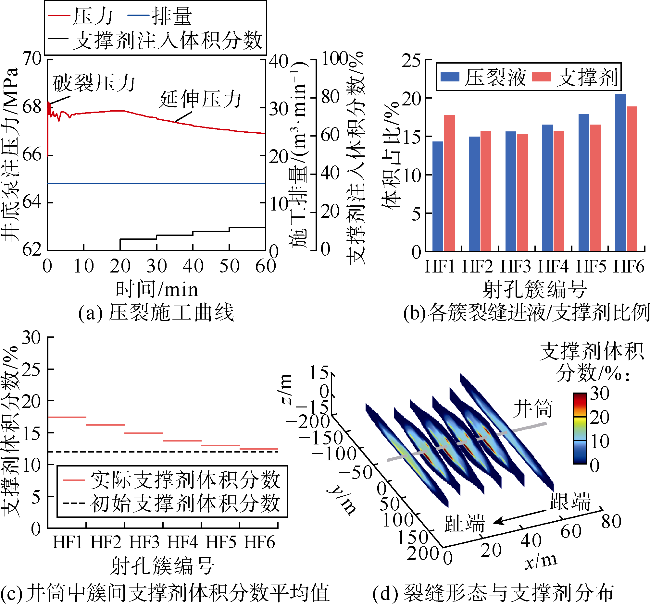
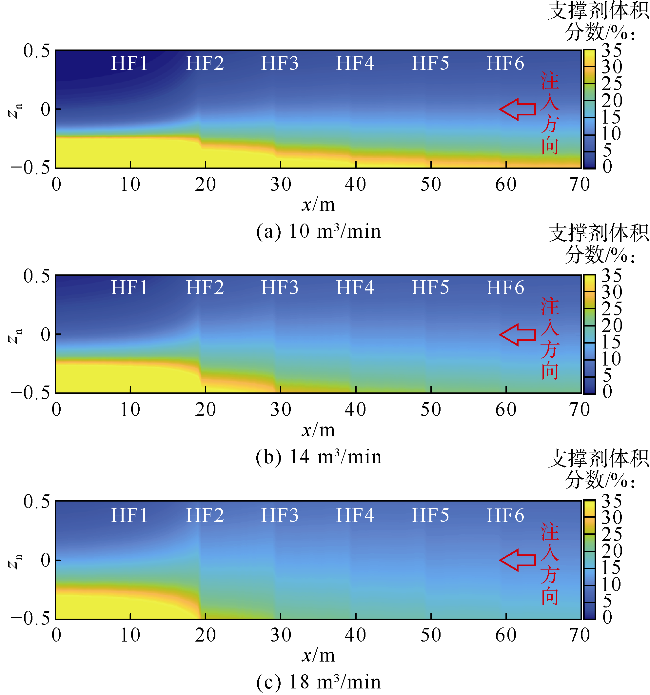
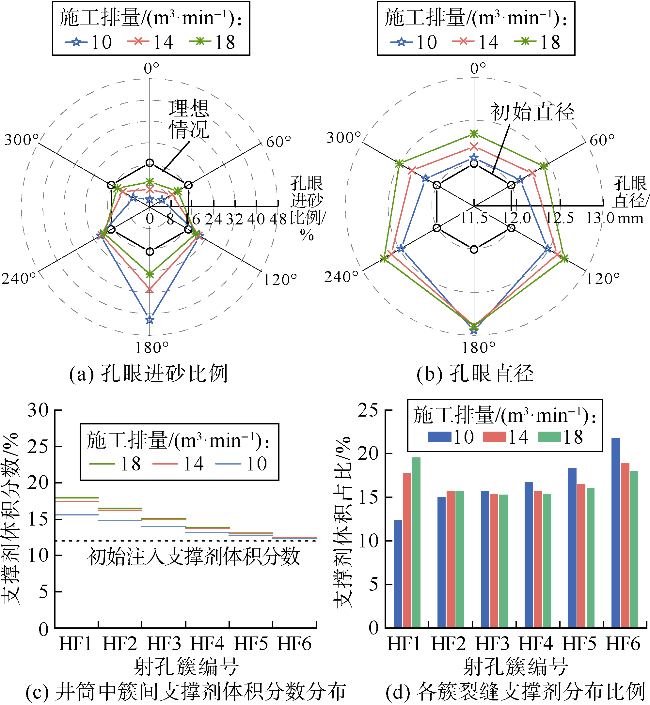
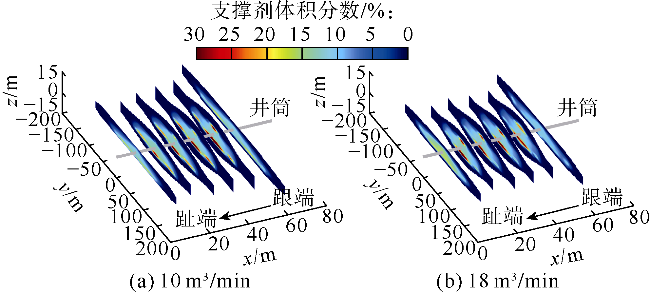
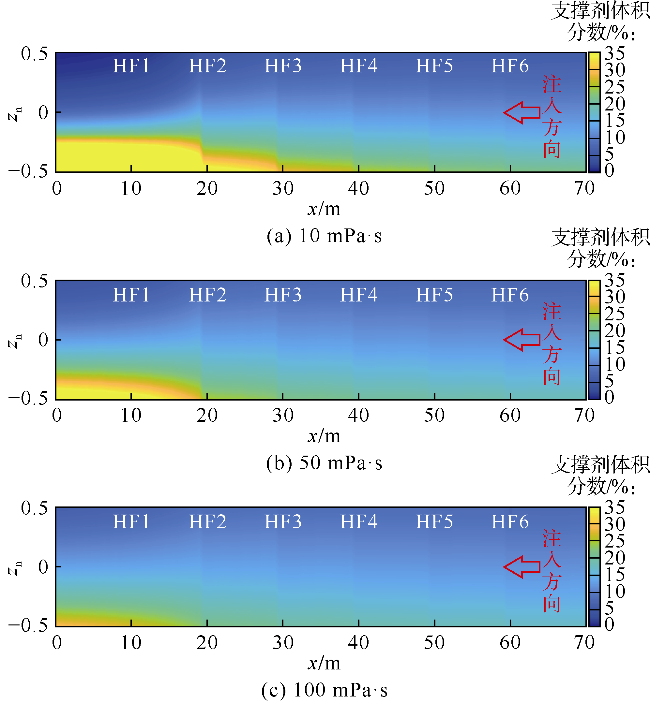
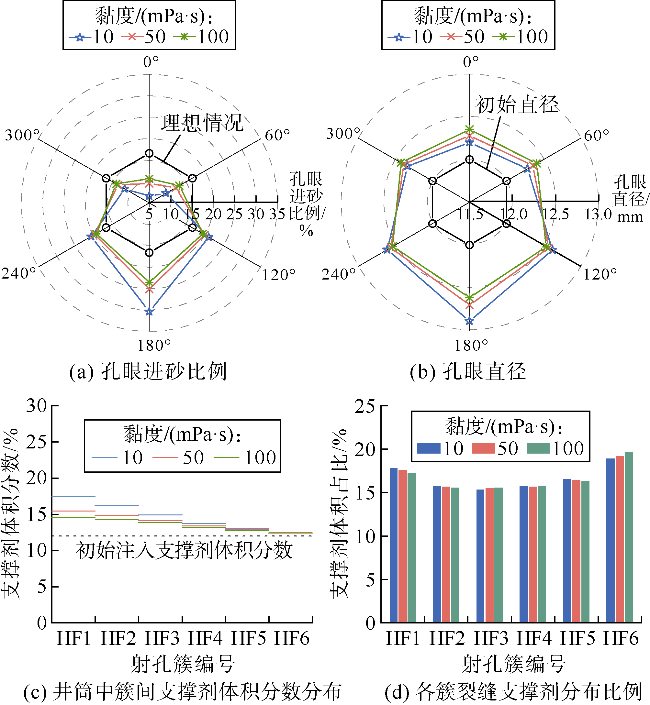
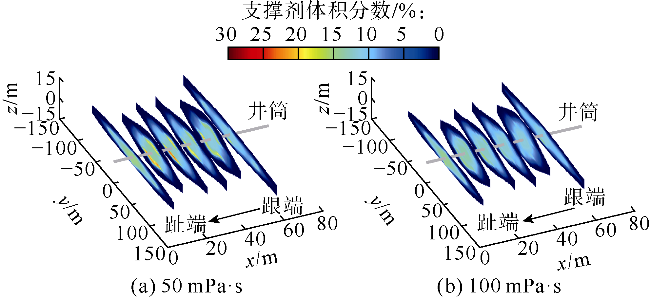
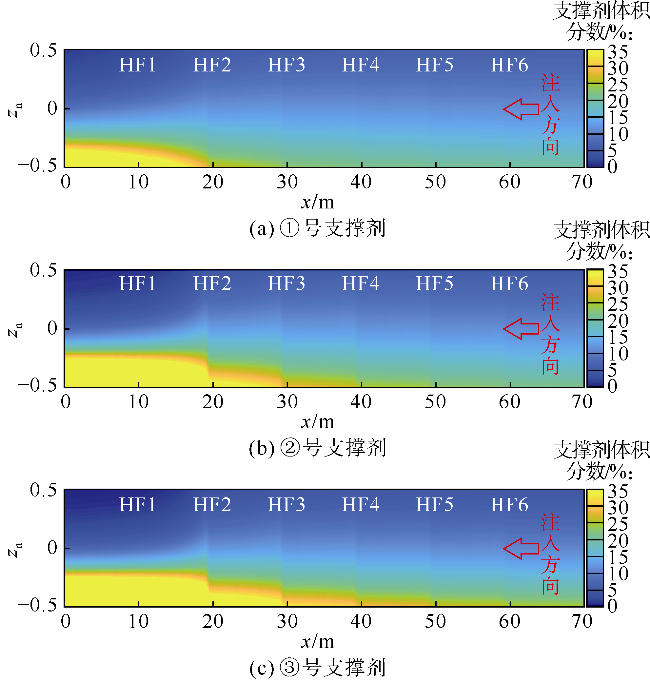
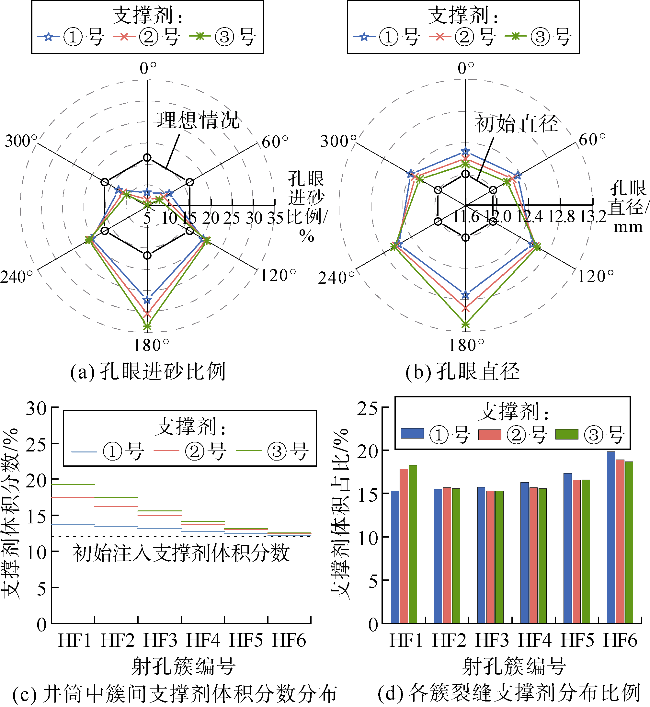
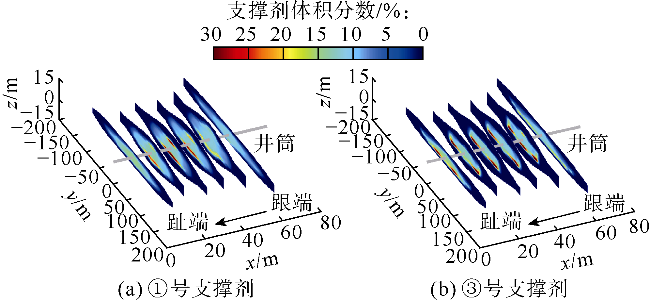
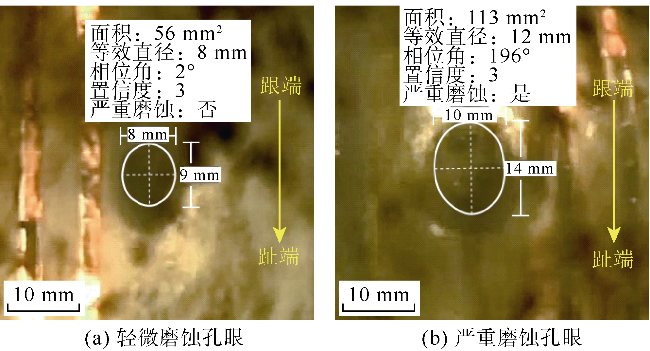
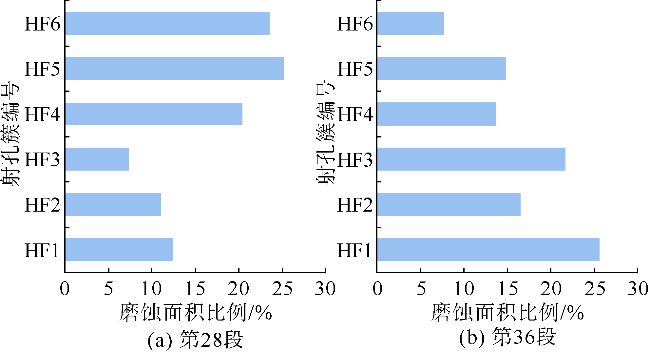
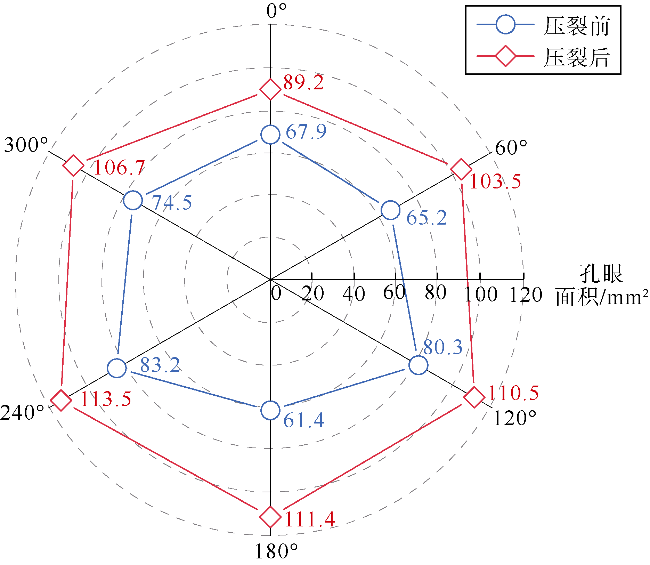
光纤监测结果发现，泵注过程中部分射孔簇停止进液，采用限流和暂堵等措施并未能完全解决非均匀改造问题[9-10]；压后鹰眼成像和示踪剂检测结果表明，压裂段内簇间支撑剂分布通常呈非均匀状态[10-11]；生产阶段产液剖面监测发现各簇裂缝改造程度与压后产液能力密切相关[12-13]。尽管非均衡改造已成为现场多种监测手段取得的共识，但对各簇裂缝改造程度的定量评价仍然较为粗糙，缺乏对进液及进砂比例的甄别。砂液运移管流模拟实验发现，低排量条件下支撑剂呈跟端倾向分布，而高排量注入时为趾端倾向，这归因于颗粒惯性作用引起支撑剂偏离流线轨迹而错过射孔孔眼，导致下游射孔簇砂浓度增加[14-15]。此外，水平管道中存在支撑剂沉降现象，低排量、低黏度和高密度颗粒条件下最为明显[8,16]。主流的井筒砂液运移数值模型由计算流体动力学方法（CFD）结合不同的固相颗粒描述模型（如离散元、离散相和欧拉颗粒模型）建立[17-19]。数值模拟结果表明颗粒不会完全跟随流体运移，簇间和不同相位孔眼间的进砂浓度甚至相差数十倍[20]。考虑到CFD方法计算成本高且模拟尺度有限，有学者基于大量CFD模拟结果建立了代理模型，通过分析孔眼进液比例推断进砂量，从而避免繁琐的CFD模拟计算[21-22]。但这些代理模型均是基于固定实验参数条件下模拟结果建立的，对于不同地层条件、完井参数、模拟尺度不具有普适性。更重要的是，上述研究着重关注井筒中混砂液运移过程，限定射孔出口压力边界条件，没有考虑孔眼动态磨蚀以及多裂缝竞争扩展过程的影响；而现有商业压裂软件或自主压裂模型则较少考虑井筒内携砂液体运移过程[23-24]。
携砂液体在井筒、孔眼、裂缝中的运移是一个复杂的连续物理过程，需要开展砂液注入全过程分析。本文以准噶尔盆地吉木萨尔凹陷二叠系芦草沟组页岩油为例，首先根据压裂现场分布式光纤监测和井下鹰眼成像结果评价各簇砂液分布与孔眼磨蚀规律，然后建立井筒-孔眼-裂缝全耦合压裂数值模型，开展携砂液体运移全过程模拟与主控因素分析，以全面认识和解释各簇孔眼非均匀进液、进砂、动态磨蚀、多裂缝竞争扩展以及支撑剂运移铺置机制。
1 水力压裂现场监测试验
1.1 页岩油储层特征
1.2 现场压裂施工与监测试验概况
吉木萨尔页岩油区块先后在两口先导试验井JHW1和JHW2开展了井下鹰眼成像和本井管外低频分布式光纤（LF-DAS）监测。试验井水平段长1 800 m，改造22段，簇间距离10 m，单段6簇，每簇以60°相位角射6孔或3孔，施工排量14 m3/min，用液强度30 m3/m，加砂强度3.0 m3/m。本井LF-DAS监测技术主要用于采集压裂过程中携砂液体在井筒中流动产生的声波或振动信号，并通过其强度信息来评价各段簇进液情况。井下鹰眼成像监测技术主要是在压裂施工结束后，采用连续油管下入特制的高精度摄像头进行连续成像，直接获取各段簇孔眼图像，通过计算磨蚀面积间接反映支撑剂进入量。值得说明的是，由于压裂监测试验并未统一规划，两口井各采用了一种监测措施开展试验，最新的JHW2试验井主要运用光纤监测方法评价变排量和投球暂堵措施对改善各簇液量分布的有效性，而最早的JHW1试验井采用鹰眼成像技术评价常规压裂完井方案中各簇孔眼的起裂效率。通过光纤监测获取了试验井中所有段簇的动态进液信号，而在鹰眼成像监测井中，受下入深度影响，只获取了最浅的13个压裂段的孔眼图像数据。
1.3 监测结果及分析
1.3.1 LF-DAS监测
LF-DAS监测技术将获取的声波信号通过泵注时间-监测深度（时空）动态显示，可以直观反映声波信号的时空变化，便于分析泵注过程中各段簇进液的活跃程度，监测信号越强，表示进液程度越高，裂缝开启及扩展规模越大。通过光纤监测瀑布图、压裂施工曲线、裂缝进液占比（见图1）可以看出：①初始阶段裂缝起裂并不均衡，只有一半射孔簇被有效开启，这是因为注入排量较低，无法克服簇间非均质性的影响；②第12 min进行投球暂堵和提升排量，可以看出跟端两簇被进一步激活，同时5个射孔簇均有较强的信号响应，射孔簇起裂效率达到了较高水平；随着继续泵注，信号强度分布几乎没有变化，表明各簇进液较为均匀；③加入支撑剂后，靠近趾端方向的射孔簇逐渐丢失信号，而跟端方向3个射孔簇的信号进一步加强，说明大部分携砂液体向跟端3簇裂缝分流，进液非均衡程度增加；④支撑剂注入是导致各簇液量分布发生变化的直接原因，支撑剂注入后，井筒趾端方向砂浓度过高，诱导砂堵现象发生，阻碍趾端射孔簇携砂液体进入，最终停止进液，北美压裂现场试验中也发现了该现象[9]；⑤井筒中支撑剂与压裂液体运移轨迹并不相同，笼统归为携砂液体运移可能导致分析结果错误，更无法准确解释各簇裂缝非均衡改造现象。
1.3.2 井下鹰眼成像监测
已有研究表明孔眼磨蚀面积与进砂量呈正比关系[7,11]，由磨蚀面积分布可知簇间进砂量分布并不均匀，多裂缝改造程度不均衡。由于井下鹰眼成像只能在施工结束后进行一次性成像，其结果难以反映井筒及孔眼中砂液运移的动态过程，无法还原各种支撑剂簇间分布模式的形成机制。如图3a中，趾端簇改造明显不足，但不能确定这是由储层非均质还是缝口砂堵导致的。统计所有段簇孔眼的磨蚀面积，并按60°相位角分布取平均值，绘制不同相位孔眼磨蚀面积雷达图，可以发现磨蚀程度存在明显相位倾向，即井筒底部（井筒横截面下半部分，相位角为90°~270°）的孔眼磨蚀程度更高，而井筒顶部（井筒截面上半部分，相位角为0°~90°、270°~360°）的磨蚀程度较低（见图4）。臧传贞等[27]认为这是完井时射孔枪不居中导致孔眼初始直径存在相位倾向，进而导致不同的磨蚀程度。本试验井中采用了等径射孔弹射孔，但压裂后孔眼磨蚀程度仍然存在明显的底部相位倾向，分析认为这是因为井筒中支撑剂沉降作用改变了不同相位孔眼的进砂量所致。因此，井下鹰眼成像结果也再次说明井筒中支撑剂颗粒和压裂液体运移轨迹并不一致，并且这对各簇孔眼进砂比例具有显著影响。
2 井筒-孔眼-裂缝全耦合压裂数值模拟
尽管现场监测试验证实了井筒各簇砂液非均匀分布、孔眼动态磨蚀和多裂缝竞争扩展现象普遍存在，但难以精确还原该动态连续过程，需建立井筒-孔眼-裂缝全耦合压裂数值模型开展全过程模拟与主控因素分析。
2.1 数学模型
2.1.1 井筒携砂液体运移
射孔井筒中携砂液体运移模型包括支撑剂在井筒中运移和转向进入孔眼两部分，前者确定井筒中固体颗粒体积浓度和运移速度分布，后者用于求解各簇孔眼进砂效率[6]。井筒中颗粒体积守恒方程为：
$\begin{array}{c} \frac{\partial \bar{\phi}}{\partial t}+\frac{\partial}{\partial x}\left(\frac{4 \bar{v}_{\mathrm{w}}}{\pi} \int_{-1 / 2}^{1 / 2} \sqrt{1-4 z_{\mathrm{n}}^{2}} \phi v_{\mathrm{n} x} \mathrm{~d} z_{\mathrm{n}}\right)+ \\ \sum_{n=1}^{N_{\mathrm{p}}} \frac{4 q_{\mathrm{p}, n}}{\pi d_{\mathrm{w}}^{2}} \delta_{1}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{inj}}\right)=0 \end{array}$
井筒中流体为全紊态流动，粒子微观运动通过表观黏度表征，颗粒在垂向上的动力行为由线性化动量平衡方程控制，其沉降作用由表观重力指数（Ga）衡量[6]：
$\frac{\partial G_{\mathrm{a}}}{\partial t}+\bar{v}_{\mathrm{w}} \frac{\partial G_{\mathrm{a}}}{\partial x}+\frac{G_{\mathrm{a}}-G}{t_{\mathrm{G}}}=0$
根据横向上颗粒平均浓度分布和表观重力指数，可确定纵向上颗粒浓度剖面[6]：
$\left\{\begin{array}{l} \frac{\mathrm{d}}{\mathrm{~d} z_{\mathrm{n}}}\left\{\frac{\eta_{\mathrm{n}}(\phi)}{\left[\eta_{\mathrm{s}}(\phi)\right]^{1 / 2}}+\frac{\phi}{\left[\eta_{\mathrm{s}}(\phi)\right]^{1 / 2}} T\right\}=-G_{\mathrm{a}} I^{2} \phi \\ \frac{4}{\pi} \int_{-1 / 2}^{1 / 2} S \phi \mathrm{~d} z_{\mathrm{n}}=\bar{\phi} \\ I=\frac{4}{\pi} \int_{-1 / 2}^{1 / 2} \frac{S}{\eta_{\mathrm{s}}(\phi)^{1 / 4}} \mathrm{~d} z_{\mathrm{n}} \end{array}\right.$
其中$S=\sqrt{1-4 z_{\mathrm{n}}^{2}}$
考虑能量均匀耗散可进一步推导运移速度剖面分布：
$v_{\mathrm{nx}}=\frac{1}{\eta_{\mathrm{s}}(\phi)^{1 / 4} I}$
基于井筒中支撑剂浓度和速度剖面，进一步确定各簇孔眼进砂量。首先根据井筒各簇液量分布确定每个孔眼的液体吸入半径（lf），其被隐式地表示为[6]：
$\frac{4}{\pi d_{\mathrm{w}}^{2}} \int_{A_{\mathrm{f}}\left(f_{\mathrm{f}}\right)} v_{\mathrm{nx}} \mathrm{~d} A=\frac{q_{\mathrm{p}, \mathrm{~s}}}{q_{\mathrm{u}, \mathrm{~s}}}$
$\begin{aligned} s= & \frac{p_{\mathrm{T}} l_{\mathrm{np}} d_{\mathrm{w}}}{\tau\left(p_{3}^{2}-1\right)} \frac{p_{1} p_{2}}{p_{1}+p_{2}}\left\{p _ { 3 } \operatorname { l g } \left[p_{3} \cosh (\tau)+\right.\right. \\ & \left.\sinh (\tau)]-\tau-p_{3} \lg \left(p_{3}\right)\right\} \end{aligned}$
其中$p_{1}=\frac{q_{\mathrm{u}, \mathrm{~s}}-q_{\mathrm{p}, \mathrm{~s}}}{q_{\mathrm{u}, \mathrm{~s}}} \quad p_{2}=\frac{R_{*}^{2}}{2 R_{\mathrm{a}}} \quad p_{3}=\frac{p_{1} \sqrt{1+R_{*}^{2}}}{p_{1}+p_{2}}$
根据滑移距离和孔眼形态可推得颗粒吸入半径（lp）：
$\frac{\int_{A_{\mathrm{p}}\left(l_{\mathrm{p}}\right)} v_{\mathrm{n} x} \mathrm{~d} A_{\mathrm{p}}}{\int_{A_{\mathrm{f}}\left(l_{\mathrm{f}}\right)} v_{\mathrm{n} x} \mathrm{~d} A_{\mathrm{f}}}=\Gamma\left(1-S_{\mathrm{n}}\right)$
其中$\Gamma\left(s_{\mathrm{n}}\right)=1+\frac{4 \varepsilon}{\pi} s_{\mathrm{n}}^{2}-\frac{2 \varepsilon+\sin (2 \varepsilon)}{\pi} \quad \varepsilon=\arccos \left(s_{\mathrm{n}}\right)$
最后用颗粒吸入半径确定通过射孔孔眼的支撑剂通量（qp,p）为[6]：
$q_{\mathrm{p}, \mathrm{p}}=\frac{\int_{A_{\mathrm{p}}\left(l_{\mathrm{p}}\right)} \phi v_{\mathrm{n} x} \mathrm{~d} A_{\mathrm{p}}}{\int_{A_{\mathrm{f}}\left(l_{\mathrm{f}}\right)} v_{\mathrm{n} x} \mathrm{~d} A_{\mathrm{f}}} q_{\mathrm{p}, \mathrm{~s}}$
2.1.2 射孔孔眼磨蚀
$\left\{\begin{array}{l} \frac{\mathrm{d} D_{\mathrm{u}}}{\mathrm{~d} t}=\alpha C v_{\mathrm{p}}^{2} \\ \frac{\mathrm{~d} D_{\mathrm{d}}}{\mathrm{~d} t}=\alpha C\left(v_{\mathrm{p}}^{2}+\gamma \bar{v}_{\mathrm{w}}^{2}\right) \end{array}\right.$
孔眼流量系数用于衡量液体通过孔眼能力，一般为0.7~0.9，其变化方程为：
$\frac{\mathrm{d} C_{\mathrm{d}}}{\mathrm{~d} t}=\beta C v_{\mathrm{p}}^{2}\left(1-\frac{C_{\mathrm{d}}}{C_{\mathrm{d}, \max }}\right)$
2.1.3 岩石弹性变形
$\left\{\begin{array}{l} \sigma_{\mathrm{sL}}^{i}=\sum_{j=1}^{N} A_{\mathrm{sL}, \mathrm{sL}}^{i, j} D_{1}^{j}+\sum_{j=1}^{N} A_{\mathrm{sL}, \mathrm{nn}}^{i, j} D_{3}^{j} \\ \sigma_{\mathrm{nn}}^{i}=\sum_{j=1}^{N} A_{\mathrm{nn}, \mathrm{sL}}^{i, j} D_{1}^{j}+\sum_{j=1}^{N} A_{\mathrm{nn}, \mathrm{nn}}^{i, j} D_{3}^{j} \end{array}\right.$
结合远场地应力和缝内流体压力边界条件，可以得到完整的固体变形方程。
2.1.4 缝内流体流动
水平井筒中各簇液量动态分布遵循基尔霍夫电流定律，满足液体体积守恒和压力平衡条件。水力裂缝中携砂液体运移视为平行板间流体流动，每簇裂缝的润滑方程可由质量守恒和动量守恒理论推得：
$\frac{\partial w}{\partial t}-\frac{1}{12 \mu_{\mathrm{f}}} \nabla\left(w^{3} \hat{Q}_{\mathrm{s}} \nabla p\right)+\frac{2 C_{\mathrm{L}}}{\sqrt{t-t_{0}}}=Q_{k} \delta_{2}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{inj}}\right)$
通过双欧拉法描述缝内支撑剂运移过程，压裂液与支撑剂颗粒视为固液连续相，缝内支撑剂分布由固体颗粒体积分数表征[32]。各簇缝内支撑剂质量守恒方程为：
$\frac{\partial w \phi_{\mathrm{n}}}{\partial t}+\frac{\partial q_{\mathrm{p}, x}}{\partial x}+\frac{\partial q_{\mathrm{p}, z}}{\partial z}=\phi_{k} Q_{k} \delta_{2}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{inj}}\right)$
缝长和缝高方向上支撑剂通量可以考虑支撑剂运移对流、重力沉降和桥接作用。根据实际物理过程，每簇裂缝入口液量和砂量由井筒携砂液体运移模型给定。
2.1.5 裂缝扩展准则
水力裂缝尖端在不同时间和空间尺度上存在多种行为，受断裂、岩石变形、流体流动及滤失等影响，表现为黏性、韧性或滤失扩展机制。为了高效捕捉裂缝尖端扩展行为，采用无需网格加密的多尺度尖端渐进解作为裂缝扩展准则[33]。裂缝尖端临界宽度用隐式表达：
$\begin{array}{r} w_{\mathrm{n}}^{3}-1-\frac{3}{2} \tilde{b}\left(w_{\mathrm{n}}^{2}-1\right)+3 \tilde{b}^{2}\left(w_{\mathrm{n}}-1\right)- \\ 3 \tilde{b}^{3} \ln \left(\frac{\tilde{b}+w_{\mathrm{n}}}{\tilde{b}+1}\right)=3 C_{1}(\xi)\left(\frac{r}{l}\right)^{1 / 2} \end{array}$
其中$w_{\mathrm{n}}=\frac{E^{\prime} w_{\mathrm{c}}}{K^{\prime} r^{1 / 2}} \quad l=\left(\frac{K^{\prime 3}}{12 \mu_{\mathrm{f}} E^{\prime 2} v}\right)^{2} \quad \tilde{b}=\frac{C_{2}(\xi)}{C_{1}(\xi)} \frac{4 C_{\mathrm{L}} E^{\prime}}{v^{1 / 2} K^{\prime}}$
水力裂缝扩展方向通过最大周向应力准则判断，根据Ⅰ-Ⅱ混合型裂缝尖端的主应力场，可以得到裂缝扩展时相对原方向的偏转角度为[34]：
$\theta=\arctan \left(\frac{K_{\mathrm{I}} \pm \sqrt{K_{\mathrm{I}}^{2}+8 K_{\mathrm{II}}^{2}}}{4 K_{\mathrm{II}}}\right)$
裂缝偏转扩展过程中可能导致相交合并行为，考虑不同网格单元间距小于单位长度时发生合并，裂缝交点单元满足压力连续和质量守恒条件[35]。
2.1.6 数值模型求解
井筒-射孔-裂缝全耦合压裂模型包括井筒携砂液体运移、孔眼动态磨蚀、裂缝扩展及缝内支撑剂运移3个主要模块。井筒颗粒体积守恒方程和重力沉降模型通过显式时间差分和迎风格式离散，支撑剂纵向浓度分布方程通过有限差分格式求解，确定井筒中颗粒浓度和速度场后，迭代求解液体和支撑剂吸入半径方程，获得各簇孔眼进液和进砂量。孔眼动态磨蚀模型通过Runge-Kutta方法求解，确定加砂阶段孔眼直径和流量系数变化[36]。岩石固体变形由位移不连续方法计算，缝内流体流动通过有限体积法离散，流固耦合方程采用显式大步长方法求解，可以得到水力裂缝宽度和压力场[37]。在此基础上，通过有限差分法离散支撑剂质量守恒方程，并显式求解获得缝内支撑剂体积分数分布[38]。
2.2 数值模型准确性验证
井筒砂液运移模型的准确性可通过混砂液体管道运移实验结果和CFD数值模拟结果进行验证。Gillies在不同管径、粒径、排量和砂浓度条件下开展了混砂液运移实验，管道装置包含入口段和观察段，调节入口段长度确保砂液流经后达到稳定流动状态，固定观察段于入口段末端，记录稳定状态下的实验结果，得到颗粒浓度和速度分布剖面[39]。根据两组典型实验（实验1、实验2）参数[39]开展水平管道砂液运移数值模拟：实验1，颗粒粒径0.3 mm，颗粒密度2 650 kg/m3，管道直径53.5 mm，支撑剂注入体积分数18%，液体流动速度1.8 m/s；实验2，颗粒粒径0.3 mm，颗粒密度2 650 kg/m3，管道直径2 263.0 mm，支撑剂注入体积分数25%，液体流动速度3.8 m/s。从模拟结果可以看出颗粒沉降作用明显，管道底部砂浓度更高，本模型获得的支撑剂体积分数剖面与物理模拟实验结果吻合（见图6a）。采用射孔井筒中携砂液体运移的CFD数值模拟结果[19]进一步验证模型可靠性，模拟结果显示孔眼进砂效率（qp,p/qu,p）对射孔相位角高度敏感，井筒底部孔眼进砂效率明显更高，且本文模拟结果与CFD数值模拟结果吻合度较高（见图6b）。此外，裂缝扩展和缝内支撑剂运移模型准确性在前期工作中已经被充分验证[37,40-42]。
2.3 数值模拟结果
2.3.1 基本案例
根据吉木萨尔页岩油区块先导试验井地质和工程参数建立数值模型，具体参数如表1所示。水平井每段以10 m簇间距设置6个射孔簇，每簇以60°相位角螺旋射6孔，各孔眼初始直径均为12 mm。水平井分段压裂过程中，除了第1段裂缝扩展不受段间诱导应力干扰作用外，后续所有压裂段均受先压裂缝影响。因此，在本文所有案例模拟中，均考虑前一压裂段裂缝的诱导应力干扰作用。各压裂段趾端簇到跟端簇依次编号为HF1—HF6，采用恒定排量和阶梯式加砂方式压裂施工。
表1 井筒-孔眼-裂缝全耦合压裂模型关键参数 |
| 参数 | 取值 | 参数 | 取值 |
|---|---|---|---|
| 弹性模量 | 36 GPa | 簇间距 | 10 m |
| 泊松比 | 0.25 | 单簇孔数 | 6 |
| 断裂韧性 | 1.56 MPa·m0.5 | 射孔相位角 | 60° |
| 储层厚度 | 20 m | 初始孔眼直径 | 12 mm |
| 最小水平主应力 | 60 MPa | 孔眼流量系数 | 0.70 |
| 水平应力差 | 10 MPa | 施工排量 | 14 m3/min |
| 层间应力差 | 5 MPa | 压裂液黏度 | 10 mPa·s |
| 水平段长 | 1 800 m | 压裂液密度 | 1 000 kg/m3 |
| 井筒直径 | 0.12 m | 支撑剂密度 | 2 650 kg/m3 |
| 压裂段长 | 70 m | 支撑剂注入体积分数 | 8%~12% |
| 单段簇数 | 6 | 支撑剂粒径 | 0.55/0.27 mm |
由井筒支撑剂体积分数剖面可以看出簇间和不同相位孔眼间的砂浓度分布差异明显，靠近跟端方向3簇（HF4—HF6）的颗粒浓度分布较为均匀，井筒底部砂浓度略高，但未形成明显砂堤，而接近趾端方向3簇（HF1—HF3）支撑剂重力沉降作用逐渐增强，井筒中出现砂液分层现象，底部砂浓度明显更高（见图7）。这是因为压裂段中携砂液体运移为变质量流动，沿注入方向砂液流速逐渐降低，液体悬砂能力减弱。井筒截面非均匀的砂浓度分布必然影响不同相位孔眼的进砂浓度。底部孔眼进砂浓度更高，孔眼磨蚀作用最为强烈，随孔眼直径和流量系数变大，孔眼摩阻降低，则允许更多砂液进入，逐渐加剧不同相位孔眼进液、进砂和磨蚀程度的差异。
泵注结束后，统计所有射孔簇不同相位的孔眼进液比例、进砂比例和磨蚀程度，并按60°相位角分布取平均值后绘制雷达图（见图8），可以看出井筒顶部3个相位孔眼进液比例均低于理想情况，而底部3个相位孔眼进液比例均高于理想情况，最底部孔眼进液比例最高，达到17.5%。对于支撑剂来说，受沉降作用影响，不同相位孔眼的进砂比例差异更为严重，72.1%的支撑剂颗粒由井筒底部3个相位孔眼流出，其中最底部孔眼进砂比例占30.4%，导致其磨蚀后的平均孔眼直径达12.89 mm，远大于顶部0°相位孔眼的12.20 mm，最底部孔眼流量系数也接近最大值0.9。对比图4与图8c，可以发现模拟结果很好地复现了井下鹰眼监测得到的非均匀孔眼磨蚀现象，证实了数值模型的可靠性。
支撑剂颗粒由井筒转向进入射孔孔眼过程是影响簇间砂量分布以及各簇裂缝进液、进砂效率的重要环节：①从压裂施工曲线上看，因孔眼磨蚀作用降低了孔眼摩阻，加砂阶段泵注压力明显降低（见图9a），同时因先压裂段的应力干扰作用，最终簇间砂液分布并不一致，各簇液量分布呈明显的跟端倾向（见图9b）。②靠近跟端的4簇裂缝（HF3—HF6）进砂比例低于进液比例，而趾端两簇裂缝（HF1—HF2）的进砂比例则高于进液比例。这是因为越靠近跟端方向，井筒中砂液运移速度越快，支撑剂更易偏离流线轨迹而错过射孔孔眼，导致下游射孔簇砂浓度逐渐增加（见图9c）。③在给定的水平应力差条件下，裂缝偏转受限，几乎呈近平面形态扩展，且受应力干扰作用，多簇裂缝表现为非均匀扩展现象（见图9d）。④簇间砂液分布比例直接影响缝内的实际铺砂浓度，跟端簇裂缝内铺砂浓度较低，而趾端缝内铺砂浓度明显更高。此外，缝内支撑剂主要铺置在近缝口区域，底部沉沙现象明显，而裂缝前缘宽度窄而铺砂较少。
2.3.2 施工排量的影响
高排量缓解了井筒中颗粒的沉降作用，不同相位孔眼的进砂比例和磨蚀程度更加均匀，相位倾向减轻。随着泵注排量由10 m3/min增加到18 m3/min，最顶部的0°相位孔眼与最底部180°相位孔眼的进砂比例差异由39.1%降低到了15.4%、磨蚀后孔眼直径差异由0.88 mm降低到了0.54 mm（见图11a、图11b），这说明提升排量促进了顶部孔眼进砂。尽管高排量减轻了孔眼直径扩大的相位倾向，但提升排量增强了孔眼磨蚀速率，造成更严重的磨蚀[36]，压裂后所有孔眼直径几乎都比低排量注入时大。高排量注入增强了颗粒运移的惯性作用，上游射孔簇进砂效率降低，井筒下游平均砂浓度逐渐增加（见图11c、图11d）。排量由10 m3/min增加到18 m3/min，趾端簇的平均支撑剂体积分数由15.6%增加到18.0%，且进砂比例由12.4%增加到19.6%，而跟端簇进砂比例反而由21.8%降低到18.0%。高排量注入时，更多的支撑剂被冲向趾端，簇间砂量分布呈趾端倾向。低排量下各簇支撑剂分布呈跟端倾向是因为：①各簇液量分布本身呈跟端倾向，且颗粒运移惯性效应更弱，颗粒进入孔眼效率较高，使得跟端簇进砂比例较高；②低排量下颗粒沉降作用更强，井筒底部孔眼支撑剂体积分数高于井口注入支撑剂体积分数，这增强了上游射孔簇进砂比例。
2.3.3 液体黏度的影响
从不同相位孔眼的进砂比例和磨蚀后的直径来看，增加压裂液黏度能够取得更高进砂效率：①液体黏度增加，促进了井筒上部孔眼进砂，降低了相位倾向（见图14a、图14b），液体黏度由10 mPa·s增加到100 mPa·s，最顶部的0°相位孔眼与最底部180°相位井眼的进砂比例差异由23.8%降低到了12.8%、最终孔眼直径差异由0.52 mm降低到了0.23 mm。②液体黏度与固体颗粒惯性指数呈反比，增加液体黏度降低了颗粒运移的惯性效应，支撑剂更易追随流线轨迹进入孔眼，簇间砂液比例更加一致。③液体黏度由10 mPa·s增加到100 mPa·s，井筒中跟端到趾端方向的支撑剂体积分数增加趋势明显降低，趾端平均支撑剂体积分数由17.4%降低到14.5%（见图14c）。④液体黏度增加，尽管趾端簇裂缝进砂比例降低，跟端簇裂缝进砂比例增加，但整体变化幅度并不剧烈（见图14d），这是因为在14 m3/min泵注排量下，携砂液流速对颗粒运移惯性效应的影响占主导地位，黏度提升的影响不足以改变颗粒运移的整体趋势[6]。
2.3.4 支撑剂粒径的影响
支撑剂粒径越大，不同相位孔眼进砂比例和磨蚀程度差异越明显。支撑剂粒径由0.380/0.212 mm增加到0.830/0.380 mm，最顶部的0°相位孔眼与最底部180°相位井眼的进砂比例差异由18.8%增加到28.1%，磨蚀后孔眼直径差异由0.43 mm增加到了0.97 mm，说明大粒径支撑剂增加了井筒底部孔眼进砂量和磨蚀程度，相位倾向更强（见图17a、图17b）。支撑剂粒径由0.380/0.212 mm增加到0.830/0.380 mm，支撑剂沿井筒下游射孔簇聚集现象更明显，井筒中从跟端到趾端各簇支撑剂体积分数增加趋势更快，如趾端簇的平均支撑剂体积分数由13%增加到19%（见图17c）。这是因为支撑剂粒径增加，颗粒运移惯性效应加强，上游射孔簇进砂比例降低，而下游趾端射孔簇进砂量增加（见图17d）。这与Snider等[8]的射孔井筒砂液运移物模实验的认识一致。
3 结论
水平井多簇压裂过程中，井筒中支撑剂与压裂液体运移轨迹并不一致，各簇砂液分布比例存在显著差异，孔眼进砂效率不等于进液效率。孔眼磨蚀现象非常普遍，且孔眼磨蚀程度和进砂比例具有明显相位倾向。
井筒中支撑剂运移受颗粒运移惯性效应和重力沉降作用共同影响。靠近井筒跟端，压裂液流速大，惯性效应占主导，颗粒转向进入孔眼能力弱，导致簇间砂量非均匀分布。靠近井筒趾端，压裂液流速降低，重力沉降作用增强，导致孔眼进液、进砂和磨蚀相位倾向性增强。
大排量注入能够缓解井筒中的颗粒沉降作用，减轻孔眼进砂及磨蚀的相位倾向，但强惯性效应导致靠近井筒跟端射孔簇进砂效率降低，支撑剂向井筒趾端方向集聚并进入裂缝。高黏液体悬砂能力强，井筒与缝内铺砂更均匀。支撑剂粒径越大，簇间、孔间进砂比例差异越大，缝内铺砂范围更小。
符号注释：
A——面积，m2；Af——孔眼进液半径范围内的井筒截面积，m2；Ap——孔眼进砂半径范围内的井筒截面积，m2；Ann,sL、Ann,nn、AsL,nn、AsL,sL——影响因子系数，Pa/m；$\tilde{b}$——与C1，C2相关的函数，无因次；C——压裂液中支撑剂含量，kg/m3；C1，C2——与ξ相关的函数，无因次；Cd——孔眼流量系数，无因次；Cd,max——最大容许孔眼流量系数，无因次；CL——流体滤失系数，m/s0.5；dp——孔眼直径，m；dw——井筒直径，m；D1，D3——裂缝单元位移不连续量，m；Dd——平行于流线方向的孔眼直径，m；Du——垂直于流线方向的孔眼直径，m；$E^{\prime}$——平面应变弹性模量，Pa；G——重力指数，无因次；Ga——表观重力指数，无因次；i，j——裂缝网格单元序号；I——中间变量；k——裂缝簇编号；KⅠ——Ⅰ型裂缝应力强度因子，Pa·m0.5；KⅡ——Ⅱ型裂缝应力强度因子，Pa·m0.5；KⅠc——Ⅰ型裂缝断裂韧性，Pa·m0.5；$K^{\prime}$——标度断裂韧性，取值$\sqrt{\frac{32}{\pi}} K_{\mathrm{Ic}}$，Pa·m0.5；l——裂缝尖端长度，m；lf——孔眼进液半径，m；lp——孔眼进砂半径，m；lnp——归一化孔眼进砂半径，无因次；n——射孔孔眼编号；N——裂缝网格单元数量；Np——每簇射孔数量；p——缝内流体压力，Pa；p1，p2，p3——中间变量；pT——模型标定参数，取值为1.3，无因次；qd,s——孔眼下游的压裂液通量，m3/s；qd,p——孔眼下游的支撑剂通量，m3/s；qp,n——第n个孔眼的支撑剂通量，m3/s；qp,s——进入孔眼的压裂液通量，m3/s；qp,p——进入孔眼的支撑剂通量，m3/s；qp,x——缝内x方向上支撑剂通量，m2/s；qp,z——缝内z方向上支撑剂通量，m2/s；qu,s——孔眼上游的压裂液通量，m3/s；qu,p——孔眼上游的支撑剂通量，m3/s；Qk——第k簇裂缝注入排量，m3/s；$\hat{Q}_{\mathrm{s}}$——描述支撑剂对流体流动影响的函数，无因次；r——与裂缝尖端距离，m；Ra，R——与颗粒雷诺数相关的函数，无因次；s——颗粒滑移距离，m；sn——归一化颗粒滑移距离，无因次；S——井筒形状因子函数，无因次；t——时间，s；t0——裂缝网格单元开始滤失的时间，s；tG——时间松弛因子，s；T——衡量湍流效应强度的函数，无因次；v——裂缝扩展速度，m/s；vp——压裂液通过孔眼的流速，m/s；$\overline{\mathbf{v}}_{w}$——井筒内液体平均流速，m/s；vnx——井筒内x方向归一化液体流速，无因次； w——裂缝宽度，m；wc——临界裂缝宽度，m；wn——归一化裂缝宽度，无因次；x，y，z——全局坐标，m；x——x方向坐标向量，m；xinj——注入点坐标向量，m；yn，zn——y、z归一化坐标，无因次；α——标定孔眼直径的参数，（m2·s）/kg；β——标定孔眼流量系数的参数，（m·s）/kg；γ——标定孔眼磨蚀程度的参数，无因次；μf——压裂液黏度，Pa·s；Г——孔眼进砂剖面的形状因子函数，无因次；δ1（x-xinj）——一维狄拉克函数，m−1；δ2（x-xinj）——二维狄拉克函数，m−2；ε——与归一化颗粒滑移距离sn相关的函数，无因次；ξ——与归一化裂缝宽度wn相关的函数，取值0~1/3；$\eta_{\mathrm{s}}(\phi)$，$\eta_{\mathrm{n}}(\phi)$——与支撑剂体积分数相关的函数，无因次；θ——裂缝扩展偏转角，（°）；σsL——裂缝单元诱导横向切应力，MPa；σnn——裂缝单元诱导法向应力，MPa；τ——无因次颗粒转向时间；$\phi$——支撑剂体积分数，%；$\phi_{\mathrm{n}}$——归一化支撑剂体积分数，无因次；$\bar{\phi}$——井筒内支撑剂体积分数平均值，%；$\phi_{\mathrm{k}}$——第k簇裂缝支撑剂注入体积分数，%。