石油勘探与开发 >

2025 , Vol. 52 >Issue 4: 907 - 918

DOI: https://doi.org/10.11698/PED.20240715

油气田开发

基于Transformer算法的智能完井异常检测方法

  • ARANHA Esteves Pedro , 1, 2 ,
  • POLICARPO Angelica Nara 2 ,
  • SAMPAIO Augusto Marcio 2
展开
  • 1 巴西国家石油公司，里约热内卢 20231-030，巴西
  • 2 圣保罗大学理工学院采矿与石油工程系，圣保罗 05508-030，巴西

ARANHA Esteves Pedro（1985-），男，巴西人，圣保罗大学理工学院采矿与石油工程系在读博士研究生、巴西国家石油公司技术顾问，主要从事机器学习、数字孪生、钻井、油井完整性等方面的研究工作。地址：Departamento de Engenharia de Minas e de Petroleo, Escola Politecnica, Universidade de Sao Paulo, São Paulo 05508-030, Brasil。E-mail:

Copy editor: 胡苇玮

收稿日期: 2024-11-09

  修回日期: 2025-07-21

  网络出版日期: 2025-07-23

收起

A Transformer-based approach for anomaly detection in intelligent well completions

  • ARANHA Esteves Pedro , 1, 2 ,
  • POLICARPO Angelica Nara 2 ,
  • SAMPAIO Augusto Marcio 2
Expand
  • 1 Petrobras, Rio de Janeiro 20231-030, Brazil
  • 2 Departamento de Engenharia de Minas e de Petroleo, Escola Politecnica, Universidade de Sao Paulo, São Paulo 05508-030, Brasil

Received date: 2024-11-09

  Revised date: 2025-07-21

  Online published: 2025-07-23

Fold

摘要

提出了一种多变量石油生产时间序列数据异常检测方法，基于Transformer算法识别智能完井过程中与层段控制阀相关的异常事件，并开展应用实例分析。Transformer算法能够有效处理数据漂移、捕捉复杂规律，因此在时间序列异常检测方面具有显著优势；采用的自注意力机制能够使相关模型适应数据分布随时间发生的漂移，从而弹性应对时间序列数据的可能变化；能够高效识别复杂的时间依赖关系和长程交互作用，而传统模型通常难以实现这一功能。在桑托斯盆地盐下油藏超深水井中进行了现场测试，结果表明：模型实现了层段控制阀异常的早期识别，从而最大限度地减少非生产时间并保护井筒完整性；准确率达到0.954 4，平衡准确率为0.969 4，F1分数为0.957 4，与以往研究中采用的模型相比提升显著。

关键词： 异常检测; 智能完井; 层段控制阀; 井筒完整性; 油井监测; 深度学习; Transformer算法

本文引用格式

ARANHA Esteves Pedro , POLICARPO Angelica Nara , SAMPAIO Augusto Marcio . 基于Transformer算法的智能完井异常检测方法[J]. 石油勘探与开发, 2025 , 52(4) : 907 -918 . DOI: 10.11698/PED.20240715

Abstract

This study introduces a novel methodology and makes case studies for anomaly detection in multivariate oil production time-series data, utilizing a supervised Transformer algorithm to identify spurious events related to interval control valves (ICVs) in intelligent well completions (IWC). Transformer algorithms present significant advantages in time-series anomaly detection, primarily due to their ability to handle data drift and capture complex patterns effectively. Their self-attention mechanism allows these models to adapt to shifts in data distribution over time, ensuring resilience against changes that can occur in time-series data. Additionally, Transformers excel at identifying intricate temporal dependencies and long-range interactions, which are often challenging for traditional models. Field tests conducted in the ultradeep water subsea wells of the Santos Basin further validate the model’s capability for early anomaly identification of ICVs, minimizing non-productive time and safeguarding well integrity. The model achieved an accuracy of 0.954 4, a balanced accuracy of 0.969 4 and an F1-Score of 0.957 4, representing significant improvements over previous literature models.

Key words： anomaly detection; intelligent well completion; interval control valve; well integrity; oil well monitoring; deep learning; Transformer algorithm

0 引言

过去16年间，桑托斯盆地已经成功部署了200多个智能完井（IWC）系统，用于盐下油藏开发[1-2]。智能完井系统在油藏管理中发挥着广泛作用，覆盖各个方面，如注气、控制水气比、实施水气交替注入循环、优化排水、平衡注采、完整性测试、使用层段控制阀作为临时封隔工具、注入油藏动态研究示踪剂以及清除油管中的水合物等[2]。
盐下油藏典型智能完井设计采用273.1 mm×250.8 mm（10 ¾″×9 ⅞″）生产套管组合。下放完井管柱之前，使用油管输送射孔或电缆输送射孔等技术开展射孔作业[1-2]。近期在几口井的裸眼完井作业中，配套使用了多位液压型层段控制阀（ICV），这些控制阀能够远程控制2~3个层段的注采作业。通过3~4条专用控制管线操控这些控制阀，其中1条用于关闭所有阀门，称为共闭线，而其余控制管线则分别用于打开各个阀门。在设置了共闭线的情况下，为了防止层段控制阀意外移动，必须遵守特定的操作流程。各层段和完井管柱均配备了专用的温压传感器以及井下化学剂注入系统。多路控制水下采油树与井下控制管线相连接，为温压传感器提供电力和通信，确保油井作业的有效监测和控制。
在生产阶段，检测到智能完井系统一些异常和故障，常见的情况包括层段控制阀意外移动、阀门循环困难、液压模块故障、结垢、层段控制阀被卡或泄漏、气体流经控制管线时生成水合物引起管道堵塞，导致原油产量下降、增加钻机修井作业成本等[2]。数字孪生技术通过捕捉井设备的热力学特征和负荷，可对井筒完整性实施有效、实时监测，但是该技术无法捕捉与地下或控制系统相关的潜在异常问题，如设备故障或阀门虚假关闭[3-4]。对于海上油井，由于钻机干预的相关成本较高，井下异常早期监测尤为重要。因此，需要引入先进的机器学习方法，主动预测上述异常问题，降低产量损失、确保井筒完整性。
近期，许多学者重点针对基于重建的时间序列异常检测方法开展了研究，这种方法首先将时间序列数据转换为本征向量，然后对其进行重建，通过高重建误差来检测异常。MALHOTRA等[5]使用自编码器学习正常数据的分布，GEIGER等[6]通过TadGAN对这种方法进行了升级，利用生成对抗网络（GAN）开展时间序列异常检测。有学者将K-最近邻算法（K-NN）和浮动窗口算法用于检测井下安全阀（DHSV）关闭、产量损失、管线阻塞和控制阀关闭等问题，并验证了这些方法在实际应用中的可行性，但是它们在处理复杂的层段控制阀故障问题方面表现欠佳[7]。还有学者使用随机森林算法和贝叶斯模型开展状态监控（CBM），成功识别了8类操作问题，准确率超过94%，然而该方法难以满足层段控制阀故障应急处置的要求，在解决复杂问题的时效性方面尚存在不足[8]。一些学者指出，决策树在故障分类方面发挥了有效作用，但无法用于准确检测井下安全阀的虚假关闭问题；基于长短期记忆（LSTM）自编码器和支持向量机（SVM）分类器创建的异常检测模型在慢动态故障检测方面表现出更好的性能，但不足以解决智能完井系统内的多种层段控制阀故障问题[9-10]。近期关于孤立森林、单类支持向量机（OCSVM）、局部离群因子（LOF）、椭圆包络线和自编码器（含前馈及长短期记忆结构）等方法的对比研究结果显示，局部离群因子在各种应用场景中的表现最优[11]。这些方法在一般异常检测方面都具有一定的准确性，但对于其能否有效适用于智能完井层段控制阀异常问题的检测，尚未开展专门的研究[12]。无监督机器学习算法（特别是局部离群因子）在识别井下安全阀虚假关闭方面具有较高的准确率，但尚未能成功识别智能完井作业中层段控制阀异常问题[13]。有学者研究发现将深度学习自编码器与基于规则的方法相结合用于异常检测，能够提高作业安全性，降低与非生产时间和维修相关的成本，然而这种方法未能捕捉智能完井作业中层段控制阀故障[14]。
相比之下，Transformer算法在多个领域的序列数据分析中均发挥了显著效用[15-16]。该算法最初是为自然语言处理而开发的，在长序列时间序列预测中表现出卓越的性能[17-19]。Transformer算法基于自注意力机制，使其模型架构能够适应数据分布随时间的漂移，从而弹性应对时间序列数据中的潜在变化。Transformer算法能够高效识别复杂的时间依赖关系和长程交互作用，而传统模型通常难以实现这一功能。与循环神经网络不同，Transformer网络架构可以并行处理整个序列，提高了训练和推理速度，因此更适用于大型数据集。其输入表示具有灵活性，能够适应各种特征类型，增强了复杂时间序列数据的建模效果。此外，Transformer算法通过其注意力机制收集丰富的上下文信息，从而准确识别某些易被忽视的异常。因此，该算法是检测时间序列数据中异常模式和特征的一个强大工具。
鉴于现有方法无法捕捉智能完井中层段控制阀的复杂故障，本研究提出了一种基于Transformer算法的时间序列数据异常检测方法，并在桑托斯盆地盐下油藏开展了应用。

1 方法

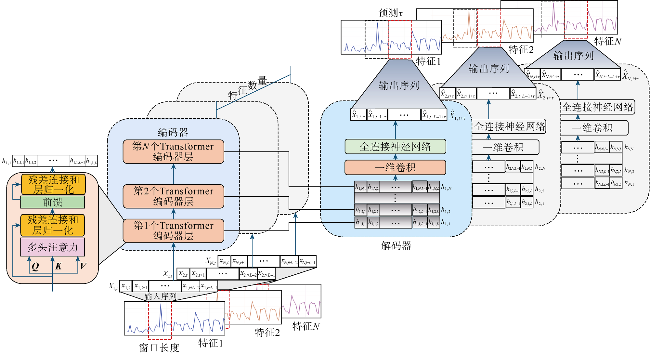
1.1 时间序列Transformer模型

本文提出了一种基于Transformer算法的时间序列异常检测方法，并构建了相关的时间序列预测模型，模型架构如图1所示。该模型由1个编码器和1个解码器构成。编码器从多个Transformer编码器层学习建立层次表示，而解码器对该层次表示进行集成。目标是尽可能减小预测序列与实际序列之间的预测误差，从而学习训练集中主体正常数据的分布。
图1 本文时间序列Transformer模型的架构
在时间序列数据中，每个时间戳的输入参数（如温度、压力、阀门传感器读数）与过去和未来时间戳之间均有依赖关系。基于自注意力机制的模型可以灵活地计算这些依赖关系，而自注意力机制是Transformer算法的1个关键特征。模型的输入序列包含多个向量，每个向量代表1个词元（token）。对于每个输入向量，在训练过程中学习得到3个不同的线性投影，即查询（Q）、键（K）和值（V）。将每个查询向量分别与所有键向量进行点积运算，即可得到1个注意力分数（Attention Score）矩阵。使用Softmax函数（或归一化指数函数）对注意力分数进行归一化处理，得到注意力权重（Attention Weight），这些权重代表每个词元应该给予其他词元的注意力大小。对于每个查询向量，将注意力权重与值向量进行加权求和，由此得到新的输入序列表示形式。
多头注意力机制是自注意力机制的一种扩展形式，基于这一机制的模型可以同时关注时间序列数据的不同方面。多头注意力机制中的每个头（下文称“注意力头”）能够学习捕捉数据中不同类型的时间关系或模式。例如，有些注意力头关注长期趋势，而有些则关注短期波动或季节性模式。每个注意力头独立运行，对应不同的查询、键和值矩阵。将这些注意力头的输出进行合并，然后进行线性变换，从而获得更全面的时间序列表征。
为了准备用于连续预测的时间序列数据，本文将输入序列分割成长度为L的窗口。这些窗口采用滑动机制创建，步长为1。例如，对于特征1，可得到窗口X1,t={x1,t，x1,t+1，…，x1,t+L−1}，其中t为开始时刻。
每个窗口通过编码器中的N个Transformer编码器层进行处理得到新的序列。例如，对于特征1的窗口X1,t，经第1个Transformer编码器层处理后序列转换为h1,1={h1,1,1，h1,1,2，…，h1,1,L}，再经第2个Transformer编码器层处理后序列转换为h1,2={h1,2,1，h1,2,2，…，h1,2,L}，依次类推，经第N个Transformer编码器层处理后序列最终转换为h1,N={h1,N,1，h1,N,2，…，h1,N,L}。
每个Transformer编码器层均采用掩蔽多头自注意力来捕捉序列内的依赖关系，通过掩蔽注意力矩阵的上三角元素来确保之后不会出现信息泄漏。为了有效地捕捉与层段控制阀故障时间序列特性识别等任务相关的特征，本文汇总了通过各Transformer编码器层学习到的特征。为此，将经各Transformer编码器层处理后的序列（如特征1的h1,1，h1,2，…，h1,N）堆叠（stack），形成最终编码器输出。这种方法集成了序列中较低层的局部细节和较高层的全局依赖关系。
解码器接收最终编码器输出并利用一维卷积神经网络（1D CNN）来组合分层信息。与传统循环神经网络相比，一维卷积神经网络能够利用更少的参数有效捕捉非时变特征，增强了在时间序列建模中的适用性。基于一维卷积神经网络的输出，通过全连接神经网络预测得到模型输出序列（如特征1输出的 X ^ 1 , t + τ）。
编码和解码过程之间的这种综合联系，结合注意力机制，能够增强模型捕捉和预测层段控制阀故障时间序列特性的能力，最终提高其在异常检测任务中的有效性。

1.2 训练和异常检测

本文使用均方误差（MSE）作为损失函数来训练模型。该损失函数计算实际序列（窗口）和预测序列（输出序列）相应元素之间的平方差，并根据序列长度（L）和编码器维数（d）进行归一化处理。训练后，模型可以学习训练集中正常数据的分布。将特征1—N的损失函数求和再除以N即可得到总损失（Total Loss）。
为了实时检测异常，将每个时间戳的预测误差量化为异常分数（Anomaly Score）。根据所有维数的实际值与预测值之间的欧几里德距离计算得出异常分数。
在推理阶段，模型以最近的L个时间戳Xt−L+1={xt−L+1，xt−L+2，…，xt}作为输入，并预测未来τ个时间步长后的序列Xt−L+1+τ={xt−L+1+τ，xt−L+2+τ，…，xt+τ}。基于最后的预测值，实时计算异常分数。为了确定数据点是否异常，根据高斯分布假设，基于重建误差的均值（μ）和标准差（σ）来设置阈值（T），其公式如下：
T = μ + k σ
（1）式中k是确定均值容差区间的参数。基于容差区间的可接受标准可用于序列和非序列数据集，因为该方法旨在涵盖设定置信水平下的数据集中的特定部分。以这种方式利用正态分布的特性是异常检测中的一种公认方法[20-21]。例如，根据均值与3个标准差（k=3）之和设定阈值，由此，落入99.7%范围之外的所有数据点均可视为异常。如果某实例的异常分数超过T，则将其标记为异常。这种方法利用训练后的模型，根据学习的正常模式，对输入的时间序列数据实施连续监测和评估，从而实现有效的实时异常检测。这种方法虽然简单，但结果可靠且不会给实时监测增加计算成本。
除了可用属性之外，基于Transformer模型还可以很便捷地通过计算特征值来进行异常检测。这些特征值包括环空井下压力计（PDG）之间的压差以及管柱内井下压力计之间的压差。压差变化可能与流量变化有关，表明1个或多个层段控制阀的位置可能发生偏移或关闭，而将传感器数据作为单独的特征进行分析则无法有效捕捉这种现象。

1.3 性能评估指标

分类算法的性能评估涉及几个关键指标，包括准确率（ACC）、精确率（PR）、召回率（REC）、特异性（SP）、F1分数、平衡准确率（ACCb）和实例识别百分比（IIP）。
准确率是基本指标，表示正确分类样本（正常样本和故障样本）在总数据集中的占比，其计算方法为真正例（TP）和真负例（TN）数目之和除以样本总数。其中，TP和TN分别表示正确地识别为正常和故障的实例。
精确率体现的是真正例在所有预测正例中的占比，有助于衡量算法的故障识别精确性，其计算方法为真正例数目除以真正例与假正例（FP）数目之和。其中，FP表示错误地识别为故障的实例。
召回率为真正例在所有实际正例中的占比，在工业应用中具有重要作用，其计算方法为真正例数目除以真正例与假负例（FN）数目之和。其中，FN表示错误地识别为正常的实例。
特异性评估算法正确识别出所有实际负例中的真负例的能力，是对假正例评估的一种补充，其计算方法为真负例数目除以真负例与假正例数目之和。
F1分数为精确率和召回率的调和平均值，是一种平衡度量，尤其适用于存在类别不平衡的场景。
对于不平衡数据的情况，准确率可能无法反映模型的真实性能。这时，可以使用平衡准确率，其为召回率与特异性的算术平均值。
此外，实例识别百分比衡量模型正确识别测试集中特定类别实例的能力，其值为1.0表示完美识别了所有测试实例。

1.4 模型参数设置

本文使用公共数据集和监测系统真实数据对模型的性能进行优化。受计算条件约束，重点探索了几种超参数组合，而没有详细测试每一种可能性。研究中采用了Python 3.9程序，并使用最小-最大归一化方法对数据进行归一化处理。
对于公共数据集，首先定义训练窗口和预测窗口。训练窗口每个属性包含60个样本，对应60 s时间段，预测窗口覆盖后续60 s时间段。根据这种设置，可以在可控条件下，基于明确界定的时间间隔评估模型性能。
监测系统真实数据的获取频率较低，每30 s采集1次数据点信息。因此，训练阶段每个属性包含60个样本，对应30 min时间段。测试阶段使用60个样本评估后续30 min内的模型性能。与公共数据集相比，这种方法考虑了数据频率和时序动态的固有差异。
本文采用网格搜索方法确定层数和注意力头数，而其他超参数（如学习率和批量大小）的选择则考虑了计算可行性和验证数据集的损失标准。基于性能指标（准确率和F1分数），对每个超参数组合进行评估。表1列出了公共数据集和智能完井现场实例真实数据使用的超参数。
表1 采用不同数据集进行模型训练和测试时的超参数
数据集 层数 输入
特征数		 头数 L τ 学习率 迭代
次数
公共数据集 16 3 3 60 60 0.001 20
真实数据 16 4~12 4~12 60 60 0.001 10

2 实例分析

首先，利用前文介绍的超参数、训练过程和异常检测方法，基于公共数据集[12]初步评估本文模型的性能，并与现有文献中使用的其他模型进行比较。然后，将该模型应用到桑托斯盆地盐下油藏采用智能完井技术的油井，验证本文模型在复杂场景中应用的有效性。

2.1 基于公共数据集的模型性能评估

目前，业内缺乏智能完井系统和层段控制阀相关事件的公共数据。使用公共数据集[12]中正常生产条件下（公共数据集中的类别0）的油井数据初步训练和验证本文提出的模型。然后，将本文模型与其他模型进行对比，重点研究公共数据集中的井下安全阀虚假关闭事件（公共数据集中的类别2）。通过自动检测这些关闭事件，可以及时采取纠正措施，避免产量损失和额外成本。使用的关键属性参数包括水下采油树温压传感器和井下压力计所测参数（见表2），温压传感器、井下压力计和井下安全阀位置如图2所示。公共数据集中数据采集时间间隔为1 s。故障的瞬态和稳态统一为单个异常状态，即进行二元分类（正常和故障）。变量监测数据中没有非数字（NaN）值；但有少量没有标签的数据点（即类别列中的NaN值），对于这些样本，故障瞬态与稳态之间的过渡时段数据被视为故障状态，其余数据则判定为正常状态。
表2 公共数据集中的可用属性
属性 说明 单位
P-TPT 温压传感器所测压力 Pa
T-TPT 温压传感器所测温度 ℃
P-PDG 井下压力计所测压力 Pa
图2 与生产平台相连的海上油井示意图[12]
将本文模型与以往类似研究中使用的方法进行比较，重点分析随机森林[8]、决策树[9]、长短期记忆自编码器[10]、决策图+长短期记忆自编码器[14]和局部离群因子[13]等算法。值得注意的是，决策图+长短期记忆自编码器[14]和局部离群因子[13]方法对井下安全阀虚假关闭事件的检测效果非常好。
表3列出了使用本文模型对公共数据库中井下安全阀虚假关闭事件[12]进行检测的性能验证结果，主要涉及准确率、F1分数和平衡准确率3个指标。表4为本文模型与其他模型的性能对比，主要涉及准确率、F1分数和实例识别百分比3个指标。在所用数据集相同的条件下，本文Transformer模型的准确率约为0.986，长短期记忆自编码器和局部离群因子模型为0.999，决策图+长短期记忆自编码器模型为0.989，随机森林模型为0.871，决策树模型为0.600。从F1分数指标来看，局部离群因子模型和决策图+长短期记忆自编码器模型的效果最好，本文Transformer模型和长短期记忆自编码器模型次之，但二者均明显优于决策树模型。从实例识别百分比指标来看，本文Transformer模型、局部离群因子模型、决策图+长短期记忆自编码器模型和长短期记忆自编码器模型都成功识别了正常和故障实例，而随机森林模型效果较差。
表3 本文模型对公共数据集中井下安全阀虚假关闭事件[12]识别效果汇总表
序号 数据集名称 准确率 F1分数 平衡准确率
1 WELL-00002_20131104014101.csv 0.993 2 0.994 2 0.986 1
2 WELL-00003_20141122214325.csv 0.993 6 0.995 7 0.983 2
3 WELL-00003_20170728150240.csv 0.991 2 0.993 4 0.980 6
4 WELL-00003_20180206182917.csv 0.987 9 0.993 2 0.942 0
5 WELL-00009_20170313160804.csv 0.991 3 0.990 9 0.982 7
7 WELL-00011_20140515110134.csv 0.971 6 0.985 5 0.950 0
8 WELL-00011_20140530100015.csv 0.969 5 0.980 2 0.937 7
10 WELL-00011_20140720120102.csv 0.994 9 0.993 9 0.995 7
11 WELL-00011_20140726180015.csv 0.982 5 0.988 3 0.966 6
13 WELL-00011_20140916060300.csv 0.997 1 0.995 8 0.997 8
14 WELL-00011_20140921200031.csv 0.981 6 0.987 7 0.964 0
15 WELL-00011_20140928100056.csv 0.989 2 0.985 2 0.991 5
16 WELL-00011_20140929170028.csv 0.977 7 0.982 8 0.969 2
17 WELL-00011_20140929220121.csv 0.991 7 0.984 4 0.994 4
18 WELL-00011_20141005170056.csv 0.993 9 0.994 7 0.992 9
19 WELL-00011_20141006160121.csv 0.989 3 0.986 5 0.991 2
20 WELL-00012_20170320033022.csv 0.964 7 0.968 6 0.961 1
21 WELL-00012_20170320143144.csv 0.982 0 0.980 5 0.983 5
22 WELL-00013_20170329020229.csv 0.994 2 0.995 4 0.992 1
平均值 0.986 1 0.988 2 0.976 9
表4 本文Transformer模型与其他模型对公共数据集中井下安全阀虚假关闭事件[12]识别效果的对比
分类算法 准确率 F1分数 实例识别百分比
随机森林 0.870 8 0.58
决策树 0.600 0 0.490 0
长短期记忆自编码器 0.999 2 0.936 0 1.00
决策图+长短期记忆自编码器 0.989 4 0.991 7 1.00
局部离群因子 0.999 1 0.996 9 1.00
Transformer 0.986 1 0.988 2 1.00

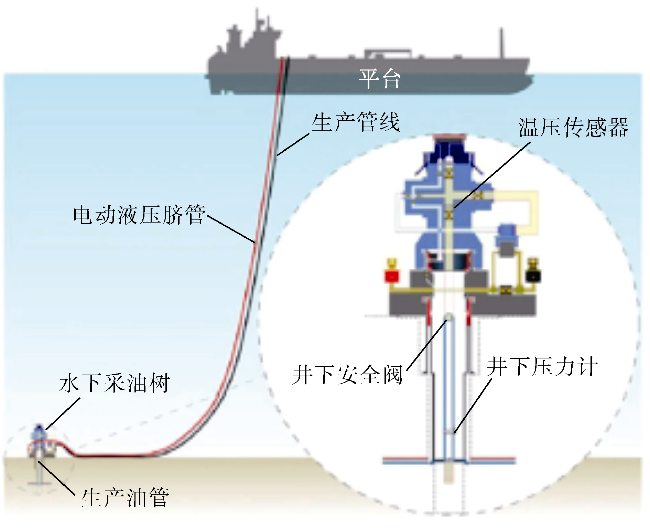
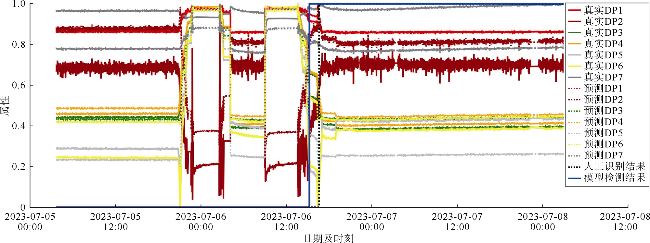
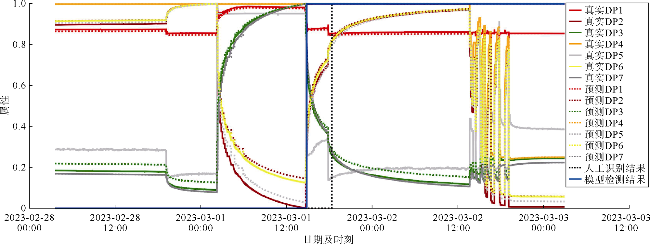
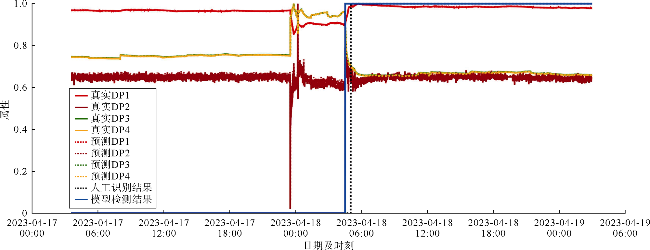
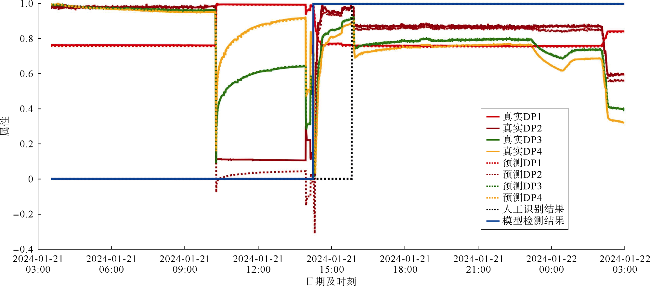
2.2 巴西海上盐下油藏超深水井实例应用

使用公共数据集对模型进行评估后，将其应用于巴西桑托斯盆地海上盐下油藏的水下生产井和注入井，这些井配置了多路水下采油树和智能完井系统[22]。训练过程中，使用每口井的3个月生产数据，重点关注正常条件下开井、关井或注采速度变化前后2 h内的时间段。训练过程没有考虑持续的稳态生产期，以便优先捕捉层段控制阀操作期间的异常。由于生产井和注入井的流态和特征不同，因此分别采用了单独的训练集。训练中使用了80%的数据作为训练集，以尽量减少损失，而其余20%的数据作为验证集。表5列出了主要的传感器参数，包括水下采油树温压传感器读数、井下压力计读数以及注采管线的地面压力和节流位置，以往油藏模型研究和实时监测也使用了这些属性参数[23-24]。表5中数据的采集时间间隔为30 s。
表5 智能完井油井的可用属性
属性名称 说明 单位
P-TPT 温压传感器所测压力 Pa
T-TPT 温压传感器所测温度 ℃
P-PDG 井下压力计所测压力 Pa
P-U-PDG 上层井下压力计所测压力 Pa
P-I-PDG 中层井下压力计所测压力 Pa
P-L-PDG 下层井下压力计所测压力 Pa
T-PDG 井下压力计所测温度 ℃
T-U-PDG 上层井下压力计所测温度 ℃
T-I-PDG 中层井下压力计所测温度 ℃
T-L-PDG 下层井下压力计所测温度 ℃
P-SURFACE 注采管线的地面压力 Pa
CHOKE 注采管线的节流位置 %
计算了表5中以下传感器之间的压差：P-TPT与P-PDG、P-PDG与P-L-PDG、P-PDG与P-U-PDG、P-L-PDG与P-U-PDG。针对油井具有3个注采层的情况，还计算了P-PDG与P-I-PDG、P-L-PDG与P-I-PDG、P-I-PDG与P-U-PDG之间的压差。表6列出了可用的计算属性。
表6 智能完井油井的计算属性
属性名称 说明 单位
DP1 温压传感器与井下压力计之间的压差 Pa
DP2 井下压力计与上层井下压力计之间的压差 Pa
DP3 井下压力计与下层井下压力计之间的压差 Pa
DP4 上层井下压力计与下层井下压力计之间的压差 Pa
DP5 井下压力计与中层井下压力计之间的压差 Pa
DP6 下层井下压力计与中层井下压力计之间的压差 Pa
DP7 中层井下压力计与上层井下压力计之间的压差 Pa
通过计算不同储层环空井下压力计以及管柱内井下压力计之间的压差，可以判断压差的波动或稳定状态。压差波动可能与流量变化有关，表明1个或多个层段控制阀的位置可能发生了偏移或关闭。另外，这种方法对源自传感器的噪声不太敏感，对于机器学习模型可能更有效。
鉴于Transformer模型允许使用多种输入特征，评估了以下几种配置下的模型性能：①TRANS-A模型，考虑了表5中所有传感器的数据，共12个特征；②TRANS-B模型，仅考虑水下采油树的压力传感器和井底的井下压力计数据，共4个或5个特征（取决于油井有2个还是3个注采层）；③TRANS-C模型，考虑压力传感器数据和表6中的计算压差，共8个或12个特征（取决于油井有2个还是3个注采层）；④TRANS-D模型，仅考虑表6中的计算压差，共4个或7个特征（取决于油井有2个还是3个注采层）。
对2022年底至2024年桑托斯盆地盐下油藏生产作业进行了监测分析，从6口井获得8个异常实例，以验证本文模型在层段控制阀故障检测方面的有效性和适用性。这6口井包括：①1号井，超深水（2 119 m）采油井，垂直钻至5 243 m，配备层段控制阀，生产层段4 898~5 129 m；②2号井，超深水（2 128 m）注水井，垂直钻至5 275 m，配备层段控制阀，注水层段4 917~5 180 m；③3号井，超深水（1 900 m）水气交替注入井，定向钻至6 111 m，配备层段控制阀，注入层段5 585~5 895 m；④4号井，超深水（2 027 m）水气交替注入井，垂直钻至5 933 m，配备层段控制阀，注入层段5 591~5 871 m；⑤5号井，超深水（2 125 m）采油井，裸眼完井，定向钻至5 343 m，配备层段控制阀，生产层段5 152~5 255 m；⑥6号井，超深水（2 183 m）水气交替注入井，裸眼完井，定向钻至5 538 m，配备层段控制阀，注入层段5 362~5 530 m。1号井、2号井、5号井、6号井有2个注采层，3号井、4号井有3个注采层。基于以上不同井况，可以验证本文模型在不同井深、井眼轨迹和作业配置条件下的鲁棒性。在获得的8个异常实例中，4个源于生产井（1号井、5号井），而其余4个源于注入井（2号井、3号井、4号井、6号井）。
将4种输入特征配置下的模型分别应用于8个实例，由表7所示的各性能指标可以看出，TRANS-D模型的性能优于其他3种模型。这可能是因为，该模型以各压力计之间的计算压差作为输入特征，与将压力计数据直接作为输入特征相比，能更有效地捕捉层段控制阀位置的偏移或关闭现象。图3—图8显示了TRANS-D模型的检测结果，并与人工识别结果进行了比较。
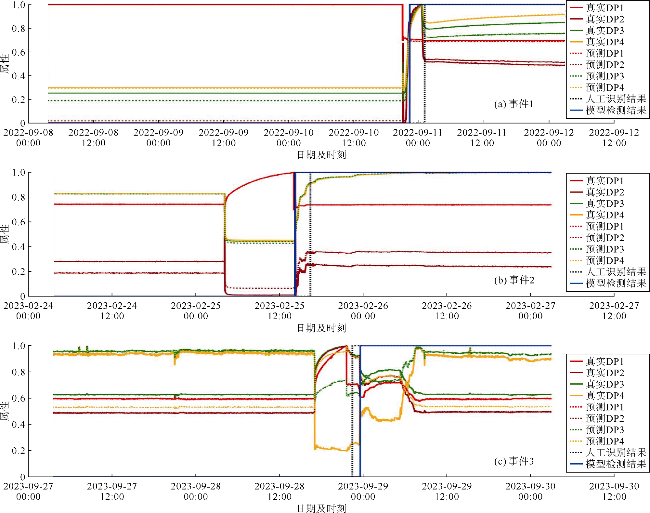
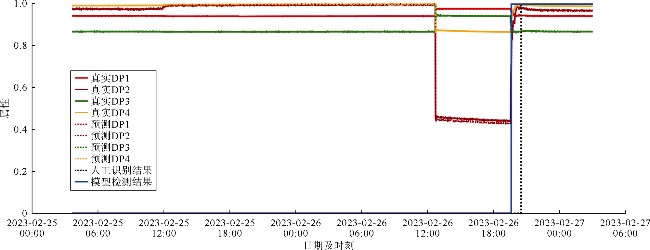
表7 本文模型实例研究结果
实例 模型 准确率 平衡准确率 F1分数
1号井事件1 TRANS-A 0.951 8 0.970 9 0.927 4
TRANS-B 0.951 9 0.970 9 0.927 6
TRANS-C 0.950 8 0.970 2 0.925 8
TRANS-D 0.964 2 0.979 4 0.947 5
1号井事件2 TRANS-A 0.914 5 0.923 5 0.924 5
TRANS-B 0.821 8 0.833 1 0.848 8
TRANS-C 0.912 2 0.921 3 0.922 5
TRANS-D 0.962 5 0.970 3 0.969 2
1号井事件3 TRANS-A 0.937 7 0.959 5 0.940 7
TRANS-B 0.910 8 0.937 0 0.910 8
TRANS-C 0.933 3 0.955 8 0.935 7
TRANS-D 0.970 2 0.979 1 0.978 7
2号井事件 TRANS-A 0.969 6 0.988 4 0.931 8
TRANS-B 0.826 5 0.904 6 0.624 4
TRANS-C 0.826 5 0.904 6 0.624 4
TRANS-D 0.970 4 0.988 9 0.934 6
3号井事件 TRANS-A 0.799 7 0.812 5 0.831 8
TRANS-B 0.800 5 0.813 3 0.832 4
TRANS-C 0.745 9 0.760 2 0.794 6
TRANS-D 0.974 0 0.981 6 0.980 6
4号井事件 TRANS-A * * *
TRANS-B 0.661 5 0.645 5 0.450 8
TRANS-C 0.903 9 0.931 6 0.924 3
TRANS-D 0.902 6 0.930 3 0.923 1
5号井事件 TRANS-A 0.465 6 0.507 0 0.636 2
TRANS-B 0.874 4 0.891 8 0.888 5
TRANS-C 0.891 6 0.908 0 0.903 6
TRANS-D 0.978 8 0.990 0 0.988 5
6号井事件 TRANS-A 0.908 3 0.931 4 0.929 5
TRANS-B 0.900 0 0.923 3 0.921 8
TRANS-C 0.900 0 0.923 3 0.921 8
TRANS-D 0.912 8 0.935 8 0.937 5

注：“*”表示模型未检测到异常

图3 1号井TRANS-D模型检测结果和人工识别结果对比
图4 2号井TRANS-D模型检测结果和人工识别结果对比
图5 3号井TRANS-D模型检测结果和人工识别结果对比
图6 4号井TRANS-D模型检测结果和人工识别结果对比
图7 5号井TRANS-D模型检测结果和人工识别结果对比
图8 6号井TRANS-D模型检测结果和人工识别结果对比
图3显示1号井异常事件模型检测和人工识别结果对比。可以看出，TRANS-D模型能够有效检测与下层层段控制阀相关的异常。事件1（见图3a）中，2022年9月10日晚上22:29，基于真实和预测压差，准确识别到1个异常。为解决该问题，作业人员随即实施层段控制阀循环。2022年9月11日凌晨01:04，通过人工识别确认了该事件。该事件展示了TRANS-D模型的快速检测能力，有助于作业人员及时采取干预措施，降低生产中断风险。事件2（见图3b）中，2023年2月25日下午14:17，模型检测到异常，作业人员启动阀门循环以解决该问题，通过人工识别于当天下午16:24确认这一异常。该事件说明了TRANS-D模型的异常预警能力，有助于作业人员采取主动维护措施，保障作业连续性。事件3（见图3c）中，2023年9月28日晚上23:28，模型检测到异常，与晚上22:20的人工识别结果非常接近。模型检测和人工识别均证实该事件为下层层段控制阀虚假关闭，且二者几乎同步，证明了模型在识别关键异常方面的一致性，及其在实时监测应用中的可靠性。在该事件中，异常检测避免油井（日产量约为3 500 m3）生产中断4 h，节省成本约40万美元。
图4显示了2号井2023年2月25日到2023年2月27日期间的异常事件。2023年2月26日晚上19:30，模型识别出异常，并将其准确分类为虚假关闭事件。2023年2月26日晚上20:28，通过人工识别确认了该事件。据此，作业人员启动阀门循环，重启作业程序，恢复安全生产条件。
图5显示了3号井2023年7月5日到2023年7月8日期间的异常事件。2023年7月6日下午15:13，模型检测到异常，将其分类为下层层段控制阀虚假关闭。2023年7月6日下午16:47才通过人工识别验证了该事件，证明了模型在作业场景中的早期检测能力。
图6显示了4号井2023年2月28日到2023年3月3日期间的异常事件。2023年3月1日下午14:45，模型识别到异常，指示层段控制阀可能存在问题。随后，作业人员启动阀门循环解决了该问题。2023年3月1日下午18:25，通过人工识别验证了该事件。可见，模型自动检测与人工干预有效协作，可以保持作业完整性。
图7显示了5号井2023年4月17日到2023年4月19日期间的异常事件。2023年4月18日早上04:36，模型准确识别到异常，指示层段控制阀虚假关闭，作业人员随即启动阀门循环。2023年4月18日早上05:00，通过人工识别验证了该事件。由此，确保了快速采取纠正措施，最大限度地减少了生产中断。
图8显示了6号井的异常事件。2024年1月21日下午14:16，模型识别出异常，指示可能为层段控制阀故障，作业人员通过启动阀门循环及时解决了该问题。当天下午15:43，通过人工识别确认了该事件。该实例揭示了模型在海上复杂作业环境下检测异常的可靠性，有助于作业人员及时采取纠正措施，保证作业效率。
以上对桑托斯盆地盐下油藏各井多个异常事件的数据分析结果表明，本文模型能够有效检测和分类异常事件，特别是层段控制阀的虚假关闭。例如，在1号井中，模型检测识别了3个异常事件，而通过人工识别，确认这些异常为层段控制阀虚假关闭。在2，3，4，5，6号井中，也同样成功检测到异常事件，且每个事件中均是模型首先准确识别到异常，然后由作业人员进行人工确认，并采取相应的纠正措施。这样的操作程序能够促进井筒完整性管理，并且有助于更好地设定作业条件，延长油井寿命[25]。以压差为输入特征对决策图+长短期记忆、局部离群因子和TRANS-D模型的检测结果进行对比，由表8可见，TRANS-D模型在检测层段控制阀虚假关闭方面表现出卓越的性能，在真实生产场景中的准确率超过0.9。TRANS-D模型预测层段控制阀关闭或部分关闭事件的平衡准确率达到0.969 4，F1分数达到0.957 4，表明该模型在准确识别关键操作异常方面具有效性，有助于保持生产效率，防止生产中断造成巨大的成本损失。相对来看，决策图+长短期记忆自编码器和局部离群因子模型无法达到理想的效果。
表8 决策图+长短期记忆自编码器、局部离群因子和TRANS-D模型智能完井层段控制阀虚假活动事件检测结果对比
实例 决策图+长短期记忆自编码器模型 局部离群因子模型 TRANS-D模型
准确率 平衡准确率 F1分数 准确率 平衡准确率 F1分数 准确率 平衡准确率 F1分数
1号井事件1 0.630 6 0.701 2 0.561 1 0.682 1 0.781 0 0.636 3 0.964 2 0.979 4 0.947 5
1号井事件2 0.816 7 0.811 9 0.768 6 0.828 6 0.834 1 0.853 9 0.962 5 0.970 3 0.969 2
1号井事件3 0.762 5 0.732 6 0.769 6 0.706 0 0.753 2 0.733 9 0.970 2 0.979 1 0.978 7
2号井事件 0.382 9 0.224 2 0 0.308 6 0.596 8 0.295 3 0.970 4 0.988 9 0.934 6
3号井事件 0.814 3 0.775 3 0.863 8 0.892 7 0.847 2 0.926 7 0.974 0 0.981 6 0.980 6
4号井事件 0.727 1 0.733 9 0.734 4 0.472 9 0.500 0 0.642 8 0.902 6 0.930 3 0.923 1
5号井事件 0.669 7 0.689 1 0.739 3 0.484 0 0.510 2 0.649 6 0.978 8 0.990 0 0.988 5
6号井事件 0.705 0 0.713 0 0.766 7 0.768 1 0.775 7 0.817 9 0.912 8 0.935 8 0.937 5
平均值 0.688 6 0.672 6 0.650 4 0.642 8 0.699 7 0.694 5 0.954 4 0.969 4 0.957 4
利用本文模型的快速异常检测优势，作业人员能够即时解决与生产或注入相关的问题。层段控制阀关闭的主要影响包括降低产量或注入量，随着时间的推移，这种产量或注入量降低会影响作业效率和井筒完整性，从而导致高昂的修井干预成本。如果采用人工识别方法，有时可能需要延迟超过1 d的时间，可能产生巨大的经济成本。本文模型在桑托斯盆地盐下油藏各种井型和作业条件下的应用效果验证了它的鲁棒性和适应性，展示了该模型在海上复杂环境中实现监测和层段控制阀故障检测方面的应用潜力。
尽管本文模型在以上8个实例中均展示出良好的应用效果，并且已经应用于大约200口采用智能完井系统的井中，但该模型仍有局限性。模型训练要求具有合理的具备开关井条件的初始作业期，以及一段稳定的作业期，还需要几个小时来进行井数据训练。此外，训练后的模型需要生产井或注入井的特定数据来分析正常作业条件。考虑到储层条件、流体性质和管柱配置的不同，这些要求限制了模型在其他配备层段控制阀的油井中的适用性。

3 结论

基于Transformer算法建立了石油生产相关多元时间序列数据异常检测模型，旨在识别智能完井层段控制阀和井下安全阀相关的异常事件。测试结果表明，与以往研究中采用的决策图+长短期记忆自编码器、局部离群因子等方法相比，本文以压差为输入特征的模型应用效果更优，在层段控制阀完全关闭或部分关闭预测方面的准确率达到0.954 4、平衡准确率达到0.969 4、F1分数达到0.957 4，证实了模型的准确性和可靠性。此外，本文模型在检测井下安全阀虚假关闭方面表现出很高的准确率，使用公共数据集时，其准确率约0.986，与其他模型相当，甚至超过了部分模型。
选取桑托斯盆地盐下油藏的8个异常实例进行了分析，其中4个异常源于生产井，4个异常源于注入井，说明本文模型能够适应不同的作业环境，证明了其在海上盐下油藏条件下的可靠性和有效性。利用模型的快速异常检测优势，作业人员能够及时解决与生产或注入相关的问题，从而减轻与层段控制阀异常相关的影响。本文模型不仅能够提高作业效率，而且是确保海上油气作业经济可行性和安全性的重要工具。模型可大规模推广部署到智能完井系统中，并有望适应其他复杂井控系统或多元故障检测场景。
未来需将本文模型从异常检测扩展到异常预测，通过持续反馈机制强化其在主动作业管理中的适用性。需要设计1个通用模型，可以使用多口井数据进行训练，从而大大拓宽模型的适用性。将模型集成到数字孪生框架中，有望增强井筒完整性监测效果。数字孪生技术可以提供合成传感器功能，促进井况的实时模拟和监测，结合模型的强大异常检测功能，强化预测性维护策略。通过二者的集成，不断适应作业环境的变化，进一步扩大模型在持续、高效海上油井作业中的应用。
符号注释：
h1,1，h1,2，h1,N——窗口X1,t经第1个、第2个、第N个Transformer编码器层处理后得到的新序列；h1,1,1，h1,1,2，…，h1,1,L——序列h1,1中包含的数据；h1,2,1，h1,2,2，…，h1,2,L——序列h1,2中包含的数据；h1,N,1，h1,N,2，…，h1,N,L——序列h1,N中包含的数据；k——确定均值容差区间的参数；L——窗口长度；N——特征数量；Q，K，V——查询、键和值向量；t——开始时间点编号；T——阈值；x1,t，x1,t+1，…，x1,t+L−1——窗口X1,t中包含的数据；x2,t，x2,t+1，…，x2,t+L−1——窗口X2,t中包含的数据；xN,t，xN,t+1，…，xN,t+L−1——窗口XN,t中包含的数据； x ^ 1 , t + τ， x ^ 1 , t + 1 + τ，…， x ^ 1 , t + L − 1 + τ——输出序列 X ^ 1 , t + τ中包含的数据； x ^ 2 , t + τ， x ^ 2 , t + 1 + τ，…， x ^ 2 , t + L − 1 + τ——输出序列 X ^ 2 , t + τ中包含的数据； x ^ N , t + τ， x ^ N , t + 1 + τ…， x ^ N , t + L − 1 + τ——输出序列 X ^ N , t + τ中包含的数据；X1,t，X2,t，XN,t——由特征1、特征2、特征N输入序列创建的窗口； X ^ 1 , t + τ， X ^ 2 , t + τ， X ^ N , t + τ——特征1、特征2、特征N的输出序列；μ，σ——重建误差的均值和标准差；τ——预测窗口长度。

感谢巴西国家石油公司、科学计算与可视化实验室（LCCV）、油藏模拟与管理实验室（LASG）和圣保罗大学理工学院对本文研究工作的支持。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
SCHNITZLER E, SILVA FILHO D A, MARQUES F H, et al. Road to success and lessons learned in intelligent completion installations at the Santos Basin pre-salt cluster[R]. SPE 174725-MS, 2015.

[2]
SCHNITZLER E, FERREIRA GONÇALEZ L, SAVOLDI ROMAN R, et al. 100th Intelligent completion installation: A milestone in brazilian pre-salt development[R]. SPE 195935-MS, 2019.

[3]
ANJOS J L, ARANHA P E, MARTINS A L, et al. Digital twin for well integrity with real time surveillance[R]. OTC 30574-MS, 2020.

[4]
ARANHA P E, SCHNITZLER E, MOREIRA N, et al. Field life extension: Real time well integrity management[R]. OTC 31816-MS, 2022.

[5]
MALHOTRA P, VIG L, SHROFF G, et al. Long short term memory networks for anomaly detection in time series[R]. Bruges: ESANN 2015 Proceedings, European Symposium on Artificial Neural Networks, Computational Intelligenceand Machine Learning, 2015: 89-94.

[6]
GEIGER A, LIU D Y, ALNEGHEIMISH S, et al. TadGAN: Time series anomaly detection using generative adversarial networks[R]. Atlanta:2020 IEEE International Conference on Big Data (Big Data), 2020: 33-43.

[7]
VARGAS R E V, MUNARO C J, CIARELLI P M, et al. Proposal for two classifiers of offshore naturally flowing wells events using k-nearest neighbors, sliding windows and time multiscale[R]. Taipei:2017 6th International Symposium on Advanced Control of Industrial Processes (AdCONIP), 2017: 209-214.

[8]
MARINS M A, BARROS B D, SANTOS I H, et al. Fault detection and classification in oil wells and production/service lines using random forest[J]. Journal of Petroleum Science and Engineering, 2021, 197: 107879.

[9]
TURAN E M, JÄSCHKE J. Classification of undesirable events in oil well operation[R]. Strbske Pleso:2021 23rd International Conference on Process Control (PC), 2021: 157-162.

[10]
MACHADO A P F, VARGAS R E V, CIARELLI P M, et al. Improving performance of one-class classifiers applied to anomaly detection in oil wells[J]. Journal of Petroleum Science and Engineering, 2022, 218: 110983.

[11]
FERNANDES W, Jr, KOMATI K S, ASSIS DE SOUZA GAZOLLI K. Anomaly detection in oil-producing wells: A comparative study of one-class classifiers in a multivariate time series dataset[J]. Journal of Petroleum Exploration and Production Technology, 2024, 14(1): 343-363.

[12]
VARGAS V R E, MUNARO C J, CIARELLI P M, et al. A realistic and public dataset with rare undesirable real events in oil wells[J]. Journal of Petroleum Science and Engineering, 2019, 181: 106223.

[13]
ARANHA P E, POLICARPO N A, SAMPAIO M A. Unsupervised machine learning model for predicting anomalies in subsurface safety valves and application in offshore wells during oil production[J]. Journal of Petroleum Exploration and Production Technology, 2024, 14(2): 567-581.

[14]
ARANHA P E, LOPES L G O, PARANHOS SOBRINHO E S, et al. A system to detect oilwell anomalies using deep learning and decision diagram dual approach[J]. SPE Journal, 2024, 29(3): 1540-1553.

[15]
DOSOVITSKIY A, BEYER L, KOLESNIKOV A, et al. An image is worth 16×16 words: Transformers for image recognition at scale[R]. Virtual: International Conference on Learning Representations, 2021: 1-21.

[16]
HUANG C Z A, VASWANI A, USZKOREIT J, et al. Music transformer[DB/OL]. (2018-12-12)[2024-10-06]. https://arxiv.org/abs/1809.04281.

[17]
WU N, GREEN B, BEN X, et al. Deep transformer models for time series forecasting: The influenza prevalence case[DB/OL]. (2020-01-23) [2024-10-20]. https://arxiv.org/abs/2001.08317.

[18]
ZHOU H Y, ZHANG S H, PENG J Q, et al. Informer: Beyond efficient transformer for long sequence time-series forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(12): 11106-11115.

[19]
KIM J, KANG H, KANG P. Time-series anomaly detection with stacked Transformer representations and 1D convolutional network[J]. Engineering Applications of Artificial Intelligence, 2023, 120: 105964.

[20]
SATHE S, AGGARWAL C. LODES: Local density meets spectral outlier detection[C]// VENKATASUBRAMANIAN S C, MEIRA W. Proceedings of the 2016 SIAM International Conference on Data Mining. Philadelphia: Society for Industrial and Applied Mathematics, 2016: 171-179.

[21]
NAKAO T, HANAOKA S, NOMURA Y, et al. Unsupervised deep anomaly detection in chest radiographs[J]. Journal of Digital Imaging, 2021, 34(2): 418-427.

DOI PMID

[22]
CARPENTER C. Intelligent completion installations instrumental in Brazilian presalt development[J]. Journal of Petroleum Technology, 2020, 72(5): 59-60.

[23]
PARI M N, KABIR A H, MOTAHHARI S M, et al. Smart well-benefits, types of sensors, challenges, economic consideration, and application in fractured reservoir[R]. SPE 126093-MS, 2009.

[24]
KLUTH E L E, VARNHAM M P, CLOWES J R, et al. Advanced sensor infrastructure for real time reservoir monitoring[R]. SPE 65152-MS, 2000.

[25]
MOREIRA N, LAZARO A F, MINUCCI F R, et al. Well integrity management based on new operating limits: A new method for extending the well lifespan and changes in operating conditions[R]. OTC 35440-MS, 2024.

Options
文章导航

/

〈 〉

版权所有：《石油勘探与开发》编辑部；《石油勘探与开发（英文）》编辑部
地址：北京市海淀区学院路20号，中国石油勘探开发研究院数据中心605室　

京ICP备15044687号    技术支持：北京玛格泰克科技发展有限公司