0 引言
关于冲击过程中能量的利用，现有评估体系主要依赖破岩比能这一单一指标[18]。冲击实验表明：锥齿相比于球齿更能有效降低破岩比能，但传统的实验手段并不能实时分析冲击过程中破岩比能的动态传递规律[19-21]。为突破实验限制，学者构建了冲锤-钻头-岩石耦合动力学模型，分析了动态冲击过程中能量的传递以及各部件的能量吸收情况，其中发现矩形波具有最优能量传递效率[22]，热力耦合作用会使能量利用率降低[23]。尽管现有研究探讨了冲击钻井中能量的传递过程，但多将冲击系统的各部件视为整体能量单元进行计算，未能深入解析各部件的能量组成，同时对能量传递过程中各子能量的大小与演化规律缺乏系统性研究，限制了对冲击钻井系统内部复杂相互作用的深入理解。
本文以干热岩为研究对象，基于有限元-离散元（Finite-Discrete Element Method，FDEM）方法，构建轴向冲击破岩三维数值模型，并提出一种针对冲击破岩系统的能量计算方法。通过霍普金森压杆冲击实验验证数值模型及能量计算方法的可靠性。在此基础上，重点探讨了锥齿前倾角、岩石温度及冲击速度对破岩机理和能量传递的影响规律，旨在为干热岩高效冲击钻井提供理论依据与工程优化指导。
1 数学模型
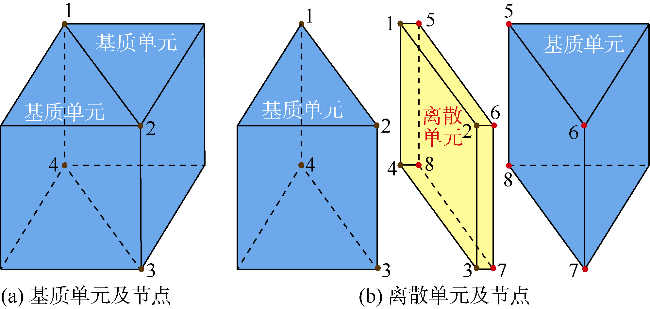
1.1 岩石损伤破坏基本理论
1.2 能量分析原理
在轴向冲击系统的动力学分析中，动能反映系统各组成部分因运动而具有的能量，其变化与外部冲击载荷的施加密切相关。在此背景下，通过分析模型中各节点的速度和质量，可以准确地量化整体动能的变化。其计算公式如下[29]：
冲击载荷施加于冲击系统时，会引发冲杆、砧板及岩石的弹性变形，从而转换为弹性应变能。其数值大小与材料的弹性模量、应变程度以及体积密切相关。计算公式如下[30]：
在冲击钻井中，接触能通常与接触表面之间的相互作用力、摩擦力以及材料的弹性和塑性变形密切相关。接触能主要指分离的四面体单元之间重叠部分所储存的弹性能，根据接触力所做的功来计算。计算公式如下[27]：
断裂能是指材料发生断裂时所需的能量，通常用于描述材料抵抗裂纹扩展的能力。在冲击破岩过程中，断裂能是评估岩石破碎特性和钻进效率的重要参数，不仅影响钻头与岩石之间的相互作用，还直接关系到钻井过程中能量的有效利用。计算公式如下[27]：
摩擦能是确定钻头与岩石之间以及岩石内部相互作用的关键因素，对于评估钻进效率、控制钻井参数及优化设计具有重要意义。摩擦能定义为接触面上摩擦力作用所消耗的能量，通常基于接触表面上的摩擦力和相对位移进行计算。计算公式如下[31]：
1.3 参数标定
轴向冲击破岩数值模型建立需要确定部分宏观物理力学参数以及微观力学参数。现阶段主要采用试错法进行参数标定[32]，本文对花岗岩样品单轴压缩测试和巴西劈裂测试数据进行数值模拟拟合，从而校准岩石力学参数。
2 模型验证
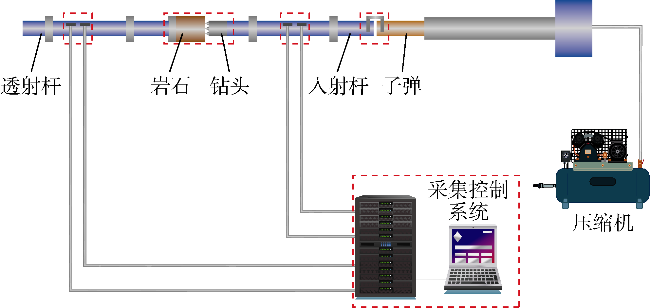
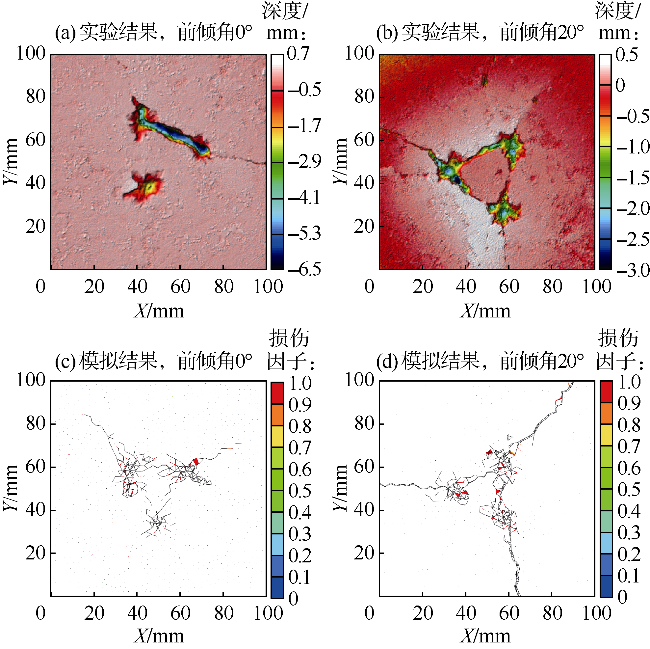
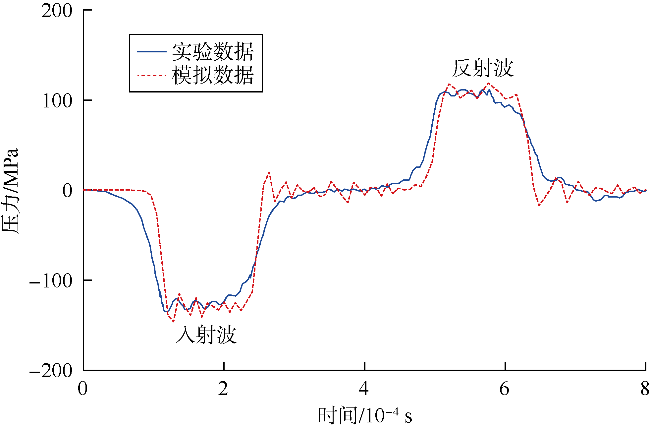
2.1 岩石破坏规律与应力波传递验证
为验证基于FDEM理论构建的冲击破岩数值模型在模拟岩石动态损伤断裂过程及应力波传播规律方面的可靠性，设计并开展匹配的冲击破岩实验，对比相同冲击条件下数值模型预测的岩石最终破坏形态与实验结果的一致性，以验证模型捕捉岩石损伤演化与宏观失效的能力；同时对比实验与模拟中关键位置的应力波曲线，以验证模型模拟弹性波在结构中传播、反射及相互作用的准确性。
建立霍普金森压杆冲击破岩数值模拟的几何模型（见图5）。模型包括4个主要部分：子弹、入射杆、钻头和岩石，其尺寸与实验设备保持一致，并设定岩石底面所有点的自由度为固定。为提升计算效率并保证模型可靠性，假设：①岩石是各向同性材料；②将钻头视为刚体，且忽略磨损；③冲击过程中不考虑运动部件的横向位移。
为了确保模拟与实验条件的一致性，设定子弹的初始速度为6 m/s。结果表明：与前倾角为0°的钻头相比，前倾角为20°的钻头在冲击破岩后，岩石表面同时形成了破碎坑和向外扩展的裂纹（见图6）。数值模拟与实验得到的岩石破坏规律基本一致，验证了模型在冲击载荷下捕捉岩石破坏规律的准确性。
以前倾角为20°的锥形齿钻头冲击破岩为例，分析其冲击过程中的应力波传递规律。结果表明，无论是入射波还是反射波，均呈现出矩形波形（见图7）。实验与数值模拟结果变化趋势相似，且入射波和反射波的峰值几乎相等，说明本文建立的数值模型具有较高的准确性。
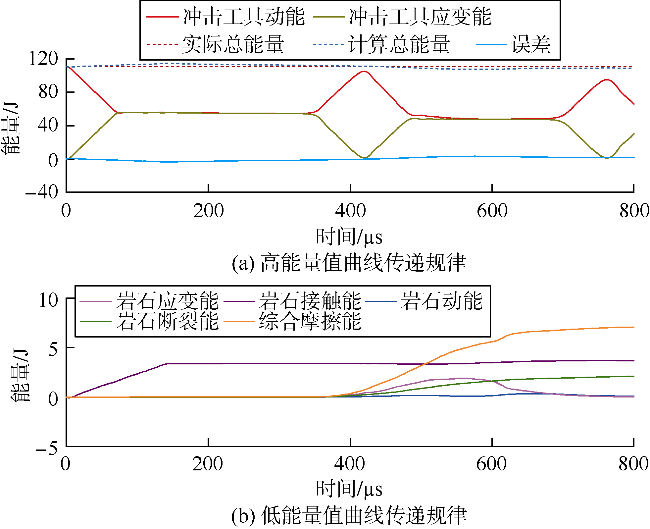
2.2 能量计算方法验证
基于能量守恒原理，冲击系统的总能量应保持恒定。在冲击过程中，系统的实际总能量（即子弹初始动能）将动态转化为冲击工具动能（除岩石外的部件动能）、岩石应变能、岩石接触能、岩石断裂能以及综合摩擦能（含钻头-岩石界面摩擦及岩石内部摩擦）。利用前述能量计算公式，在数值模拟的每个时间步长实时计算并累加上述关键能量分量，得到计算总能量。通过对比计算总能量与实际总能量的差值，验证能量计算方法的准确性。
以子弹初始速度6 m/s、前倾角为20°的锥形齿钻头冲击破岩为例，计算所得各能量分量的动态演化过程及其求和得到的计算总能量（见图8）。实际总能量为子弹在给定初始速度下的动能，其值为111 J。误差为计算总能量与实际总能量之间的差值。结果表明，在整个冲击过程，计算总能量与实际总能量的最大误差为3.3%，验证了能量计算方法的准确性。
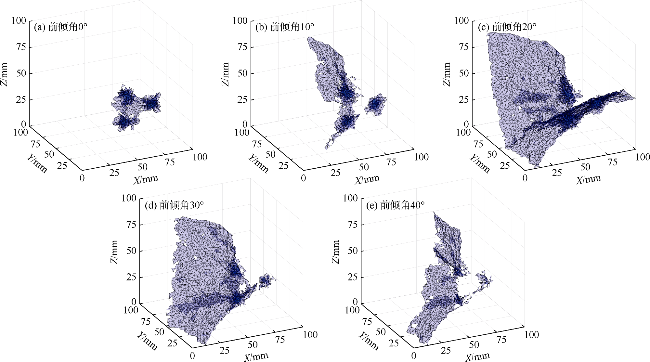
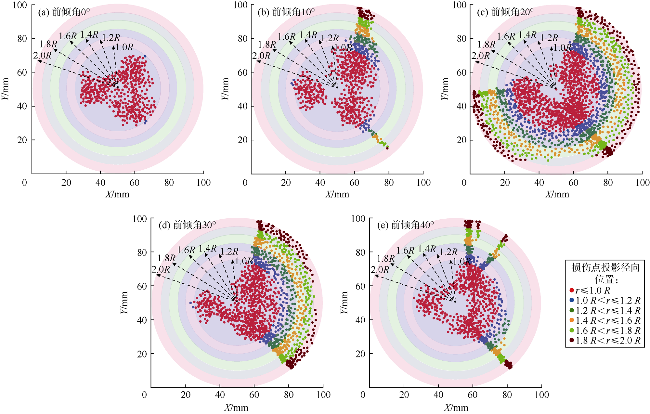
3 轴向冲击破岩数值模拟
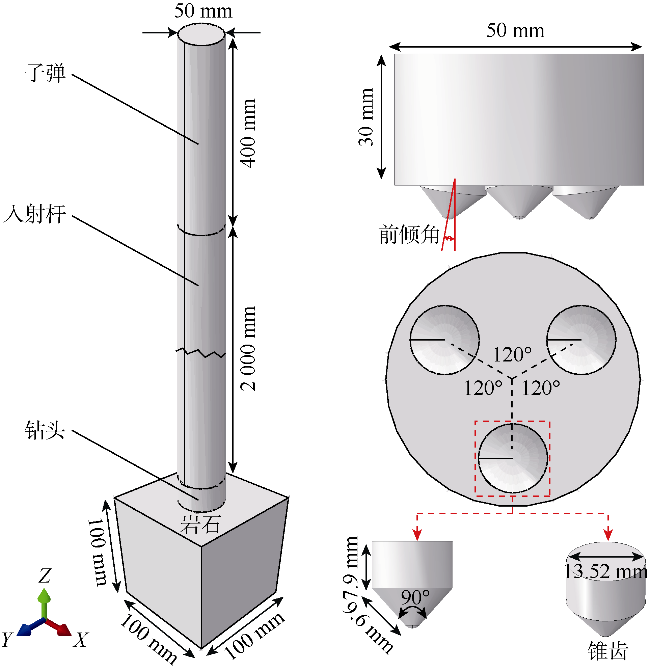
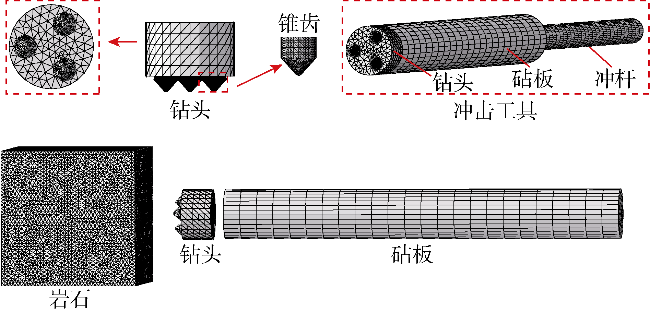
3.1 模拟方案
在冲击破岩数值模拟方法及能量计算方法得到验证后，建立了轴向冲击破岩系统模型（见图9）。在霍普金森压杆冲击模型的基础上，调整冲杆的直径为25 mm、长度为300 mm，调整砧板的直径为50 mm、长度为400 mm，其余参数保持不变。冲杆和砧板被视为弹性变形体，钻头则假设为刚性体。冲杆和砧板采用六面体网格进行结构化划分，而钻头、岩石则采用四面体网格进行非结构化网格划分。岩石单元网格尺寸为1.5 mm，并全局嵌入黏聚力单元。岩石底部设置为固定边界条件，冲杆预设初始速度后冲击砧板，砧板再冲击钻头，最终钻头破碎岩石。
基于构建的轴向冲击破岩三维数值模型，设定了不同的锥齿前倾角、岩石温度和冲击速度开展模拟，旨在探讨其对岩石破碎机理及能量传递规律的影响，具体分为3个模拟方案：①设定冲击速度为6 m/s，岩石温度为300 ℃，改变前倾角为0°，10°，20°，30°，40°；②设定冲击速度为6 m/s，前倾角为20°，改变岩石温度为25，100，200，300，400 ℃；③设定岩石温度为300 ℃，前倾角为20°，改变冲击速度为4，5，6，7 m/s。
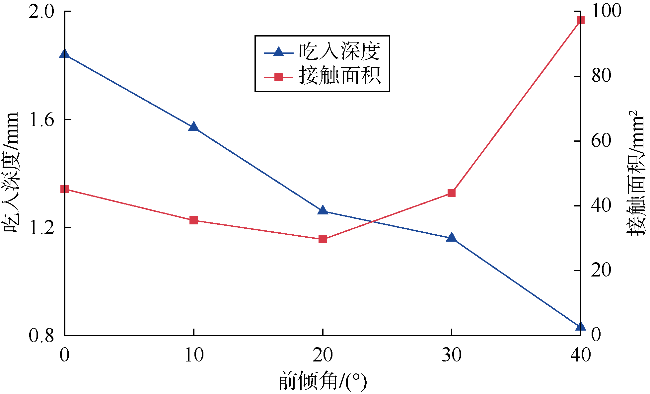
3.2 模拟结果
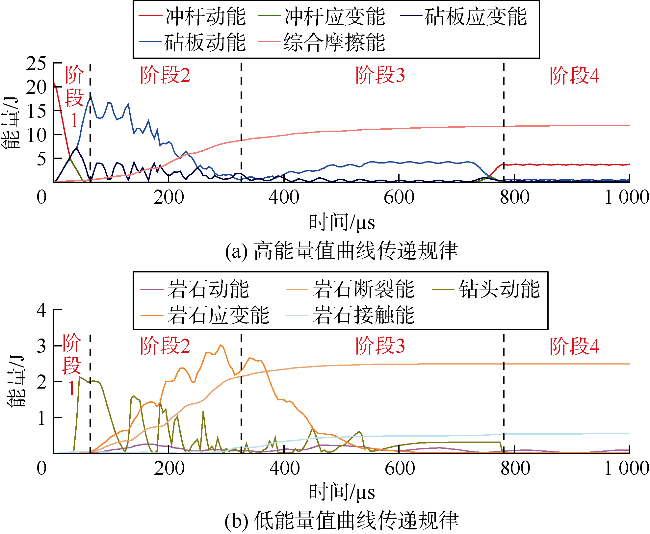
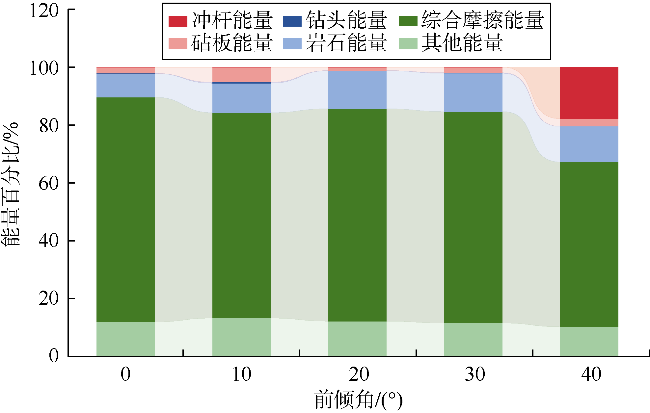
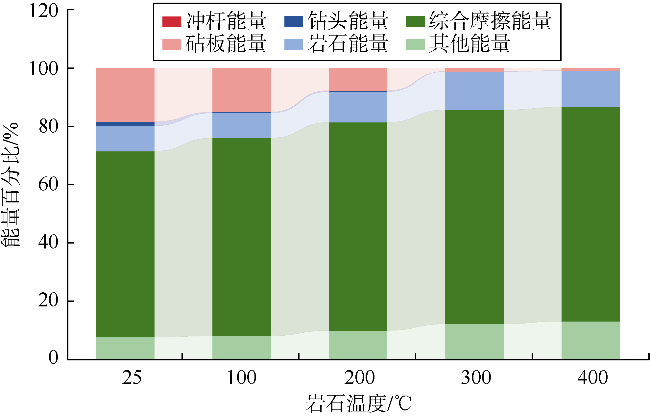
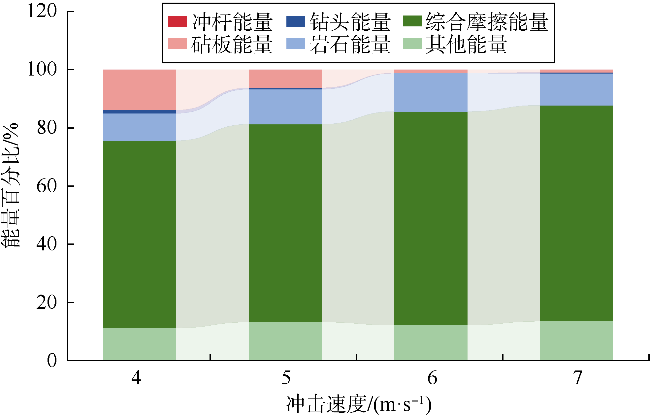
3.2.1 能量传递及分配规律分析
以锥齿前倾角40°、岩石温度300 ℃、冲击速度6 m/s的模拟条件为例，分析轴向冲击过程的能量传递规律。由图10可见，能量传递可分为4个阶段：①0~65 μs，冲杆的大部分能量转化为砧板的动能和应变能、钻头的动能。②65~325 μs，砧板的动能和应变能、钻头的动能转化为岩石应变能、岩石断裂能和综合摩擦能。③325~780 μs，钻头反弹，岩石中储存的应变能主要转化为钻头和砧板的动能。④780~1 000 μs，砧板撞击冲杆，使砧板的动能转化为冲杆的动能。
在冲击破岩过程中，提高岩石断裂能的占比是提升有效能量利用率的关键。相反，摩擦耗能不利于岩石破碎，应尽可能降低其比例。统计分析了不同锥齿前倾角、岩石温度及冲击速度下岩石断裂能与综合摩擦能的占比（见表3）。数据显示，在整个冲击过程中，用于岩石破碎的断裂能占比为7.52%~12.51%，而综合摩擦耗能占比高达57.26%~78.10%，表明冲击能量的有效利用率较低。未来研究可结合数字图像相关技术（DIC）与声发射三维定位，深入揭示能量耗散路径，以期减少无效能量损耗。
表3 不同模拟方案下岩石断裂能及综合摩擦能占比 |
| 模拟参数 | 取值 | 岩石断裂能占比/% | 综合摩擦能占比/% |
|---|---|---|---|
| 前倾角 | 0° | 7.52 | 78.10 |
| 10° | 9.77 | 71.38 | |
| 20° | 12.51 | 73.82 | |
| 30° | 12.03 | 73.48 | |
| 40° | 11.95 | 57.26 | |
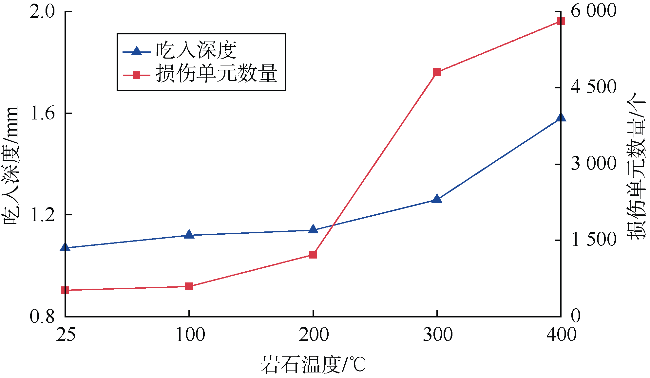
| 岩石温度 | 25 ℃ | 8.68 | 64.17 |
| 100 ℃ | 8.53 | 68.21 | |
| 200 ℃ | 10.39 | 71.75 | |
| 300 ℃ | 12.51 | 73.82 | |
| 400 ℃ | 11.87 | 73.82 | |
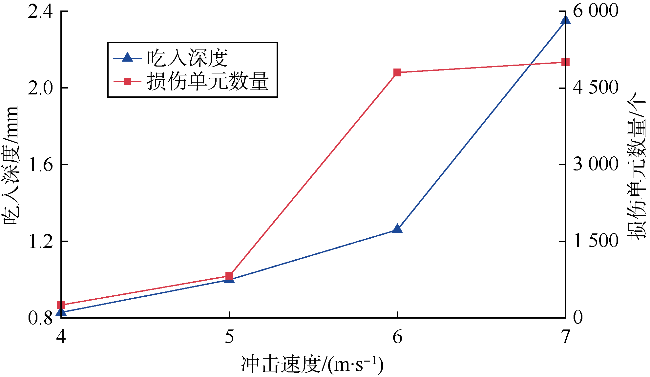
| 冲击速度 | 4 m/s | 9.35 | 64.74 |
| 5 m/s | 11.78 | 68.38 | |
| 6 m/s | 12.51 | 73.82 | |
| 7 m/s | 10.28 | 74.64 |
3.2.2 不同锥齿前倾角的影响
提取方案①模拟结果中不同冲击角度下的岩石损伤单元，并绘制裂缝形态（见图11）。图中颜色越深，代表损伤单元的重叠与嵌入程度越显著。结果表明：①低前倾角锥齿钻头冲击过程中，岩石破坏主要发生在锥齿底部，且损伤范围主要集中在一个钻头直径范围内。②锥齿前倾角增大，岩石破坏范围逐渐向外扩展，当锥齿前倾角为20°时，岩石损伤在径向和轴向范围达到最大。③前倾角进一步增大至30°时，岩石破坏程度逐渐减小，且损伤的范围也逐渐缩小。进一步提取损伤单元节点，并将其投影至井底平面（见图12）。以井底中心为圆心，假设钻头半径范围（1.0R）为井底，超过1.0R的部分则视为井周范围。当锥齿前倾角为0°时，岩石损伤范围集中在1.0R范围内。随着前倾角增大，冲击能量由轴向分解至径向，导致岩石损伤向井周扩展。当前倾角为20°，岩石的损伤范围达到2.0R。然而，锥齿前倾角超过20°时，岩石的损伤范围逐渐减小。
3.2.3 不同岩石温度的影响
按方案②设定参数计算锥齿的吃入深度及岩石损伤单元数量（见图15）。可以看到：当岩石温度不超过200 ℃时，吃入深度和损伤单元数量变化较为平缓。而在岩石温度达到400 ℃时，损伤单元的数量和吃入深度分别是常温（25 ℃）的11.2倍和1.5倍，说明温度对冲击破岩具有显著影响。
3.2.4 不同冲击速度的影响
按方案③设定参数计算不同冲击速度下锥齿吃入岩石的深度以及岩石损伤单元数量（见图17）。结果表明：冲击速度为7 m/s时，锥齿的吃入深度达到2.35 mm，是4 m/s时（0.83 mm）的2.8倍。同时，冲击速度为7 m/s时的岩石损伤单元数量为5 003个，是4 m/s时（254个）的19.7倍。这说明提高冲击速度，可显著提高岩石的破坏程度。值得注意的是，尽管冲击速度从6 m/s提升至7 m/s，锥齿的吃入深度增加了86.5%，但损伤单元数仅提升了4.1%。这表明冲击速度与岩石破坏程度并非完全正相关，而是存在最优冲击速度。
4 结论
在干热岩锥形齿钻头轴向冲击破岩过程中，能量消耗主要集中在钻头与岩石接触的第2阶段。用于岩石破碎的能量比例仅为7.52%~12.51%，表明冲击能量利用率普遍较低。可通过优化冲击参数、齿形及冲击工具结构，提高干热岩冲击钻井能量利用率。
锥齿前倾角过大或过小均不利于岩石对冲击能量的有效利用，从而降低岩石的破坏效果，锥齿前倾角存在最优值。高温环境不利于冲击破岩过程中岩石对能量的吸收与传递。提高冲击速度可加剧岩石的破坏程度，但冲击速度过高，摩擦损耗增加，岩石吸收能量占比下降，其破坏程度并不能大幅提升，说明冲击速度也存在最优值。
符号注释：
di——节点i的位移，m；Ec——接触能，J；Ee——弹性应变能，J；Efc——摩擦能，J；Efr——断裂能，J；Ek——动能，J；Fc——接触力，N；Ff,i——节点摩擦力，N；Ffr——作用在离散单元上的力，N；i——节点索引；mi——节点i的质量，kg；n——节点总数；vi——节点i的速度，m/s；V——体积，m3；R——微钻头半径，m；r——损伤点投影径向位置，m；X，Y，Z——空间坐标，m；ε——单元应变张量，无因次；σ——单元应力张量，MPa。