石油勘探与开发 >

2025 , Vol. 52 >Issue 3: 638 - 652

DOI: https://doi.org/10.11698/PED.20240518

油气勘探

黏土矿物包壳对砂岩储层质量的影响：基于多相场的数值模拟实验

  • KUMAR Akash , 1, 2 ,
  • SPÄTH Michael 1 ,
  • PRAJAPATI Nishant 1 ,
  • BUSCH Benjamin 3 ,
  • SCHNEIDER Daniel 1, 4 ,
  • HILGERS Christoph 3 ,
  • NESTLER Britta 1, 2, 4
展开
  • 1 卡尔斯鲁厄理工学院纳米技术研究所，卡尔斯鲁厄 76344，德国
  • 2 卡尔斯鲁厄理工学院应用材料研究所微观结构建模与仿真系，卡尔斯鲁厄 76131，德国
  • 3 卡尔斯鲁厄理工学院应用地球科学研究所构造地质学和构造学系，卡尔斯鲁厄 76131，德国
  • 4 卡尔斯鲁厄应用技术大学数字材料科学研究所，卡尔斯鲁厄 76133，德国

KUMAR Akash（1988-），男，印度人，硕士，卡尔斯鲁厄理工学院纳米技术研究所在读博士研究生，主要从事应用地球科学领域的多物理模拟（数值模拟）研究。地址：德国卡尔斯鲁厄市福乐姆街道7号，卡尔斯鲁厄理工学院应用材料研究所微观结构建模与仿真系，邮政编码：76131。E-mail：

Copy editor: 谷江锐

收稿日期: 2024-08-16

  修回日期: 2025-05-15

  网络出版日期: 2025-05-19

收起

Impact of clay coating on sandstone reservoir quality: A multiphase-field investigation by numerical simulation

  • KUMAR Akash , 1, 2 ,
  • SPÄTH Michael 1 ,
  • PRAJAPATI Nishant 1 ,
  • BUSCH Benjamin 3 ,
  • SCHNEIDER Daniel 1, 4 ,
  • HILGERS Christoph 3 ,
  • NESTLER Britta 1, 2, 4
Expand
  • 1 Institute of Nanotechnology (INT), Karlsruhe Institute of Technology (KIT), Karlsruhe 76344, Germany
  • 2 Institute for Applied Materials - Microstructure Modelling and Simulation (IAM-MMS), Karlsruhe Institute of Technology (KIT), Karlsruhe 76131, Germany
  • 3 Structural Geology and Tectonics, Institute of Applied Geosciences (AGW-SGT), Karlsruhe Institute of Technology (KIT), Karlsruhe 76131, Germany
  • 4 Institute for Digital Materials Science (IDM), Karlsruhe University of Applied Sciences, Karlsruhe 76133, Germany

Received date: 2024-08-16

  Revised date: 2025-05-15

  Online published: 2025-05-19

Fold

摘要

石英颗粒表面的黏土包壳是决定砂岩储层孔隙度和渗透率大小的关键因素，直接影响碎屑岩储层质量。基于共轴石英胶结的多相场模型，通过数值模拟实验研究黏土包壳参数对砂岩储层中石英胶结量、孔隙度、渗透率及其相互关系的影响。研究主要取得5项进展：①为了在三维数字砂岩模型的石英颗粒上模拟出逼近实际的各种黏土包壳形态，研发了一套新的预处理工作流程。②分别对发育石英单颗粒和多颗粒的砂岩开展共轴生长胶结的数值模拟实验，揭示出控制石英胶结量的主要包壳参数，即暴露锥面的生长方向、包壳覆盖率和包壳形态等。③黏土包壳形态对胶结具有显著影响，其中层状包壳形态的胶结速度较快；包壳覆盖率与砂岩孔隙度和渗透率呈正相关关系。④石英颗粒结晶垂直方向上胶结物生长速度最小，演化中后期斜角方向生长速度较水平方向更快。⑤动态演化过程模拟结果与实际对比验证显示，20，40 d后的包壳形态模拟结果与天然样品中观察到的形态高度相似，证实了包壳三维数值建模新方法的有效性。该套黏土包壳数值模拟方法和研究成果有助于改进砂岩储层表征结果和预测模型。

关键词： 石英胶结; 黏土矿物包壳; 颗粒包壳; 相场建模; 砂岩; 储层质量; 石英次生加大

本文引用格式

KUMAR Akash , SPÄTH Michael , PRAJAPATI Nishant , BUSCH Benjamin , SCHNEIDER Daniel , HILGERS Christoph , NESTLER Britta . 黏土矿物包壳对砂岩储层质量的影响：基于多相场的数值模拟实验[J]. 石油勘探与开发, 2025 , 52(3) : 638 -652 . DOI: 10.11698/PED.20240518

Abstract

The presence of clay coatings on the surfaces of quartz grains can play a pivotal role in determining the porosity and permeability of sandstone reservoirs, thus directly impacting their reservoir quality. This study employs a multiphase-field model of syntaxial quartz cementation to explore the effects of clay coatings on quartz cement volumes, porosity, permeability, and their interrelations in sandstone formations. To generate various patterns of clay coatings on quartz grains within three-dimensional (3D) digital sandstone grain packs, a pre-processing toolchain is developed. Through numerical simulation experiments involving syntaxial overgrowth cementation on both single crystals and multigrain packs, the main coating parameters controlling quartz cement volume are elucidated. Such parameters include the growth of exposed pyramidal faces, lateral encasement, coating coverage, and coating pattern, etc. The coating pattern has a remarkable impact on cementation, with the layered coatings corresponding to fast cement growth rates. The coating coverage is positively correlated with the porosity and permeability of sandstone. The cement growth rate of quartz crystals is the lowest in the vertical orientation, and in the middle to late stages of evolution, it is faster in the diagonal orientation than in the horizontal orientation. Through comparing the simulated results of dynamic evolution process with the actual features, it is found that the simulated coating patterns after 20 and 40 d show clear similarities with laboratory physical experiments and natural samples, proving the validity of the proposed three-dimensional numerical modeling of coatings. The methodology and findings presented contribute to improved reservoir characterization and predictive modeling of sandstone formations.

Key words： quartz cementation; clay coating; grain coating; phase-field modeling; sandstone; reservoir quality; quartz overgrowth

0 引言

砂岩储层质量优劣对油气和地热资源勘探至关重要。影响砂岩储层质量的关键因素是粒度和碎屑组成[1]，而压实、胶结和溶蚀等成岩作用也会改变这些因素。不连续成核或颗粒上的黏土矿物包壳（简称颗粒包壳）能够减少共轴生长胶结物，有助于提高储层质量。颗粒包壳抑制石英次生加大，不但有助于保持深埋砂岩的孔隙度[2-3]，而且随着孔隙结构的变化还会影响渗透率[4]。
颗粒包壳根据结构分成切向型和径向型，根据形成时间分成碎屑型或自生型，其性质在成岩过程和黏土矿物重结晶过程中会发生变化[5]。切向型黏土矿物包壳通常出现在颗粒接触处，表明在压实前形成。径向型黏土矿物包壳通常形成于碎屑颗粒或切向型黏土相成岩过程中[6]，但也可能在新近沉积的矿床中生成[7-8]，或与潜水带的近地表成岩作用有关[9]。
天然样品和模拟结果均表明，由于砂岩样品的颗粒包壳覆盖导致颗粒表面积减少，降低了石英胶结物含量[10-11]。前人对岩石样品[8,12 -13]、实验数据[14]和岩心[11,15 -16]中颗粒包壳的覆盖率进行了量化分析，结果显示，颗粒包壳覆盖率与共轴生长胶结物减少之间存在一定的相关性[11,15,17 -20]。颗粒包壳对石英胶结的影响与特定的黏土矿物类型无关，例如绿泥石包壳[11]和伊利石包壳[20]数量都与石英胶结量呈负相关。本研究不考虑黏土矿物本身对所建模型的影响。
数值模拟对于研究砂岩中各种岩石矿物性质如何影响储层质量的关键参数至关重要[10,21 -22]。Lander等[10]通过数值模拟和室内实验研究了石英胶结物的生长特征，发现颗粒大小、多结晶属性和黏土包壳对生长速度和胶结量会产生影响。他们使用Prism2D软件，通过二维模拟成功获取了石英的生长趋势和黏土包壳表面的真实结构，计算效率较高。但二维模拟过分简化了一些重要步骤，导致其仍然存在局限性：例如将晶体旋转限制在平面内运动，不能准确表达流体的流动特性，使得在晶体接触点完全阻止流动。而三维模拟允许非均质晶体定向，通过准确预测流体的流动特征，能够真实地表征自然岩石结构。这些优点使得三维模拟更适用于储层岩石特征的综合分析。
Prajapati等[21-22]使用多相场方法进行了大量三维模拟研究，模拟共轴生长胶结特征，分析其对砂岩孔隙度和渗透率关系的影响，重建了单颗粒和多颗粒砂岩中的石英胶结结构，恢复了孔隙度和渗透率的关系。然而，Prajapati等[22]没有全面分析黏土包壳如何影响石英共轴胶结作用及其对后续储层表征结果的影响。多相场模型在模拟各种矿物生长和溶解过程方面表现出了良好的性能，包括石英胶结生长[22-25]、方解石沉淀[26-27]、钾矾沉淀[26-27]和石英晶体溶解，如晶面特征的溶解[28]和点蚀溶解[29]。这些研究和应用显示出多相场模型在模拟复杂地质过程中的适用性和潜力。
自生黏土矿物包壳可以从不完整的颗粒包壳结构动态演化到完整的包壳结构，反映了沉积、成岩[30]和黏土矿物再结晶[5]的自然过程。近年来，研究人员应用多相场方法解决成核不连续的问题。具体方法是基于黏土矿物包壳阻碍石英颗粒生长的观察结果[26,31]，降低假定包壳颗粒的生长速度。但是这种方法相对简单，也不完全准确。本文在Prajapati等[21-22]研究的基础上，使用多相场模型研究黏土包壳（成核不连续）对砂岩中石英胶结、孔隙度、渗透率及其相互关系的影响。通过模拟Lander等[10]“石英板”实验及参考样品中获得的石英晶体形态，验证存在成核不连续的多相场模型；采用二叠系Rotliegendes统和三叠系Buntsandstein统中伊利石颗粒包壳的天然样品，评估黏土包壳对石英共轴胶结生长的抑制作用，模拟过程中未考虑压实孔隙损失的影响；采用内部数值求解器PACE3D[32]生成黏土包壳颗粒的数值模拟方法，通过改变包壳参数，搭建出不同的数字黏土包壳石英晶体和多颗粒充填样品，对石英胶结开展系统的实验研究；通过流体流动模拟多颗粒充填样品的胶结过程，计算切向型黏土包壳样品的渗透率；利用实验结果分析各项包壳参数对胶结量、孔隙度、渗透率及其之间的关系的影响，以期获得黏土包壳对储层质量影响的认识。

1 实验样品

实验样品采自德国中北部和英国[15,17 -18]的二叠系Rotliegendes统和德国西南部和法国东部[19,33]的三叠系Buntsandstein统（见图1）。尽管2个研究区域的埋藏史差异很大[20]，但成核不连续对共轴生长胶结物的影响具有可比性。三叠系Buntsandstein统的样品（最大埋深为2 200 m，最高地层温度为118 ℃）和二叠系Rotliegendes统的样品（最大埋深为4 800m，最高地层温度为178 ℃）含有切向和径向的伊利石颗粒包壳结构（见图1）。观测颗粒包壳覆盖率为10%~95%，石英共轴胶结物含量为0.3%~22.3%。此外，还选择样品单独评估了颗粒包壳覆盖率与晶间体积接触率[18]，揭示了颗粒包壳对成核不连续的影响。根据北海盆地二叠系Rotliegendes统的地层水数据，SiO2含量为0.45%~1.69%[34]。如果实测SiO2含量与基于Manning[35]的研究结果计算的SiO2饱和度相关，则德国西南部上莱茵地堑三叠系Buntsandstein统[36]的SiO2含量为1.13%~2.79%[35]。
图1 颗粒包壳对石英胶结物含量影响的薄片图像（左为单偏光，右为正交偏光）

（a）、（b）德国西南部上莱茵地堑及其周围地堑肩部区域，三叠系Buntsandstein统，完全被伊利石包裹的颗粒（白色箭头）缺乏石英共轴生长胶结物，未完全包裹的颗粒（红色箭头）是共轴生长胶结物的基质，保留了丰富的粒间孔隙；（c）、（d）北德意志盆地，二叠系Rotliegendes统，完全被伊利石包裹的颗粒（白色箭头）缺乏石英共轴生长胶结物，未完全包裹的颗粒（红色箭头）是共轴生长胶结物的基质，保留了丰富的粒间孔隙；（e）、（f）德国西南部上莱茵地堑，三叠系Buntsandstein统，未完全（着色）赤铁矿颗粒包壳（蓝色箭头）未抑制石英共轴胶结物的沉淀，粒间孔隙度小于颗粒包壳较好的样品；（g）、（h）北德意志盆地，二叠系Rotliegendes统，未完全（着色）赤铁矿颗粒包壳（蓝色箭头）未抑制石英共轴胶结物的沉淀

由于天然样品通常含有多种矿物，因此很难确定单个矿物对储层整体质量的具体影响。目前的参数和模拟研究有助于评估各类矿物和共生相互作用的具体影响，从而更深入地认识储层特征。

2 模拟方法

基于Nestler等[37]的研究，解释了石英砂岩中共轴生长胶结的多相场模型的数学方程，Späth等[24]和Prajapati等[28]也使用了该模型；讨论了在三维数字砂岩模型中模拟石英颗粒黏土包壳的预处理工作流程；描述了计算渗透率的流体流动模型方程。

2.1 共轴石英胶结的多相场数值模型

考虑一个物理域Ω，包括N−1个固相（每个相代表一个石英颗粒）和一个流体相（过饱和SiO2），使用一组相场ϕ(x,t)=[ϕ1(x,t),…, ϕN(x,t)]， φ α x , t为x∈Ω、t∈ ℝ 0 +处相α∈[1，2，…，N]的相场， φ α ∈ 0 , 1。颗粒之间或颗粒与流体之间的界面由一个有限宽度的扩散区域表示。在颗粒α与流体或其他颗粒共享的界面区域内，相场参数ϕα从颗粒外部的0渐变为颗粒内部的1。颗粒的形态和位置由ϕα为0.5的等值线决定。按照惯例，最后一个相α等于N时对应于流体相。系统的亥姆霍兹自由能（F）表示为体积能（Fbulk）与界面能（Fintf）贡献之和。其计算式如下：
F φ , ∇ φ = F b u l k + F i n t f = ∫ Ω f b u l k φ + ε a φ , ∇ φ + 1 ε ω φ d Ω
其中， f b u l k φ是体自由能密度，可表示为
f b u l k φ = ∑ α = 1 N f α h φ α
作为相特征自由能密度fα的插值，插值函数h(ϕα)=ϕα。固相和流相之间自由能密度的差异为界面提供了驱动力，为石英胶结物的生长提供了化学驱动力。式（1）中的第2项和第3项表示梯度 ε a φ , ∇ φ和势ω(ϕ)/ε的能量密度，共同表示界面能量密度。ε是控制漫射界面宽度的长度比例参数。梯度能量密度对扩散界面产生相关的能量是不利的，它的数学公式表示为
ε a φ , ∇ φ = ε ∑ α = 1 N ∑ β = 1 N γ α β a α β 2 φ , ∇ φ q α β 2       α < β
式中，γαβ为α-β界面的界面能，表示与α-β界面正交的广义梯度向量。石英晶体受地球化学和物理生长环境的影响，呈现出不同的生长形态。为了准确模拟这些棱角分明的多面晶体，采用一种由分段函数定义的强各向异性面型表面能。利用晶面的各向异性函数 a α β φ , ∇ φ模拟晶面的形成
$a_{\alpha \beta}(\boldsymbol{\phi}, \nabla \boldsymbol{\phi})=\max _{1 \leqslant k \leqslant n_{\alpha \beta}} \hat{\boldsymbol{n}}_{\alpha \beta} \boldsymbol{\eta}_{k, \alpha \beta}$
其中 n ^ α β = q α β / q α β
上述表面能各向异性公式为模拟二维和三维不同形态的多面晶体提供了一个通用的框架。当缺少界面驱动力时，势能密度部分形成了一个阻止自动相变的屏障。对于这项工作，选择了多障碍型势能密度的如下形式：
$\frac{1}{\varepsilon} \omega(\boldsymbol{\phi})=\left\{\begin{array}{ll}\frac{1}{\varepsilon}\left(\frac{16}{\pi^{2}} \sum_{\alpha \beta} \gamma_{\alpha \beta} \phi_{\alpha} \phi_{\beta}+\sum_{\alpha \beta \delta} \gamma_{\alpha \beta \delta} \phi_{\alpha} \phi_{\beta} \phi_{\delta}\right) & \boldsymbol{\phi} \in G \\\infty & \boldsymbol{\phi} \notin G\end{array}\right.$
由（6）式得到体相的锐能量极小值。
$G=\boldsymbol{\phi} \in \mathbb{R}^{N} \mid\left\{\sum_{\alpha=1}^{N} \phi_{\alpha}=1, \phi_{\alpha} \geqslant 0\right\}$
与ϕαϕβϕδ成比例的项避免在两项界面中出现虚假的第3相。通过能量泛函的变分推导，确定了提供自由能局部最小值的相场控制演化方程。为了解决不同相位的不同生长速度而产生多相区域的插值问题，使用了Steinbach[38]提出的公式。这种方法能够为每个相分配不同的流动性（生长速度）。演变方程表示为：
$\begin{array}{l}\frac{\partial \phi_{\alpha}}{\partial t}= \\-\frac{1}{N \varepsilon} \sum_{\substack{\beta=1 \\\beta \neq \alpha}}^{N}\left\{M_{\alpha \beta}(\hat{\boldsymbol{n}})\left[\frac{\delta F_{\text {intf }}}{\delta \phi_{\alpha}}-\frac{\delta F_{\text {intf }}}{\delta \phi_{\beta}}-\frac{8 \sqrt{\phi_{\alpha} \phi_{\beta}}}{\pi}\left(\frac{\delta F_{\text {bulk }}}{\delta \phi_{\beta}}-\frac{\delta F_{\text {bulk }}}{\delta \phi_{\alpha}}\right)\right]\right\} \\\alpha=1 \cdots N .\end{array}$
α-β界面的流动系数 M α β n ^决定了界面动力，表示为：
M α β n ^ = M 0 ,   α β a k i n ,   α β n ^
M 0 ,   α β反映了附着动力的差异。 a k i n ,   α β n ^考虑了生长速度的方向相关性，可以表示为：

a k i n ,   α β n ^ = 1 + δ max k n ^ ⋅ η k i n ,   k − max k − 1 n ^ ⋅ η k i n , k ⋅

max k n ^ ⋅ η k i n ,   k（k=1, 2, …, nkin）
根据Wendler等[23]的研究，该函数通过各向异性强度参数δ来反映晶面生成前石英生长较快的趋势，通过各向异性动能角的位置向量集 η k i n ,   k反映不同晶面相对生长速度的不同。模型方程在并行多物理场计算框架PACE3D中运行，有关PACE3D优化和并行化策略的详细信息，可参阅Hötzer等[32]的研究。本文使用的模拟参数集如表1所示。表中参数的有因次数值根据Prajapati等[22]的结果修正。毛管和动力各向异性形态的位置向量集 η c a p ,   k和 η k i n ,   k见文献[23]。整套数据集可参见文献[39]。
表1 用于多相场数值模拟的参数（据文献[25]修改）
模型参数 符号 无因次数值 有因次数值
网格单元大小 Δx 0.5 0.5 µm
时间步长 Δt 0.001 45 87.5 s
石英-液体界面能密度 γql 1 0.36 J/m2
黏土-液体界面能密度 γcl 0.03 0.010 8 J/m2
石英-石英界面能密度 γqq 1.91 0.687 6 J/m2
黏土-黏土界面能密度 γcc 0.42 0.151 2 J/m2
高阶界面能密度 γαβδ 25 9 J/m2
长度 ε 1.1 1.1 µm
石英-液体界面动能系数 μ 0 , q l 1.0 4.65×10−17 m4/(J•s)
石英胶结的驱动力 Δfql −0.294 −1.0×105 J/m3
动能各向异性强度 δ 115

2.2 石英表面黏土包壳的数值模拟

黏土矿物的存在对于碎屑石英颗粒界面和粒间孔隙空间起分隔作用，抑制石英的次生加大[40]。因此，将黏土矿物定义为建模框架中的惰性相。为了生成含有用户定义的厚度、体积分数和形态（例如：连续的、随机分布的）的数字黏土包壳，研发了一个预处理工作流程，包括以下2个步骤。
第1步，对于计算域中的石英颗粒相，根据界面区域的相场值ϕgrain生成给定厚度的全黏土包壳（见图2）。
图2 数字黏土包壳工作流程示意图
第2步，根据以下步骤生成连续型包壳（单面、层状）和随机分布包壳。连续型包壳：对于单面黏土包壳（见图2），将用户定义区域中的黏土相替换为液相，用户定义区域被空间平面分隔。使用用户定义的空间平面，可以生成层状包壳（见图2）。随机分布包壳：对于给定体积分数的黏土包壳的随机形态，建立迭代预处理算法。当黏土体积分数大于用户自定义值时，执行以下操作：①随机选择数值域黏土相中的一个空间点，该点作为用户定义半径的球体的中心。②用液相代替这个球形区域内形成的黏土相。计算整个区域中黏土包壳的体积分数。如果体积分数不在用户定义的范围内，则转到步骤第1步；否则，退出迭代循环。
利用这套工作流程，可以在任意真实形态的颗粒上生成不同厚度、形态和覆盖率的包壳。在充满液相的计算域中生成的黏土包壳石英颗粒可作为模拟胶结物各向异性生长的初始数值设置。图2显示了在不规则形态颗粒上生成的随机分布包壳形态。
惰性黏土相通过设定黏土-液体界面不流动进行计算。在数值方法中，将它转化为黏土矿物-液体体系的流动系数 M 0 ,   c l 。从本质上看，这表明在石英生长模拟过程中黏土相（相场参数ϕclay）不发生演化，根据演化方程，得出下式：
∂ φ clay ∂ t = 0
图3为建模工作流程的示意图。利用扩散界面区域的相场参数ϕgrain等值线，在颗粒上生成给定厚度的完整黏土包壳（见图3a、图3b）。随后，使用笔者研发的预处理工作流程生成用户定义的包壳形态（见图3c）。最后，使用多相场模型模拟各向异性石英次生加大（见图3d）。
图3 建模工作流程示意图（灰色越深表示石英的相场参数越大；黄色越深表示黏土矿物的相场参数越大）

（a）随机形态的颗粒；（b）给定厚度（相场参数以ϕclay表示）的完整黏土矿物包壳相；（c）采用预处理工作流程生成的覆膜形态；（d）模拟局部覆膜颗粒上石英次生加大

2.3 用于渗透率计算的流体动态模型

采用计算流体动态分析方法计算不同胶结阶段的黏土包壳砂岩的渗透率。为此，假设为层流，采用Stokes方程，数学表达式为：
μ d Δ u − ∇ p = 0
∇ ⋅ u = 0
在x方向上施加恒定压降，所有其他边界都设置为自由滑移边界条件。液体与颗粒/黏土体系的接触具有无滑移边界条件。渗透率（K）由达西定律计算：
K = μ d u ¯ ∇ p
考虑到域大小与前期研究相对应，因此本研究的流体流动模拟也采用了前期研究中的无因次参数。

3 结果和讨论

首先通过复制之前室内实验和观测天然样品的晶体形态来验证石英生长模型，然后通过无约束的单晶生长模拟，探索包壳参数（如晶体生长方向、覆盖率和包壳形态）对胶结量的影响。此外，还进行了一系列具有不同包壳形态和覆盖率的多颗粒充填样品模拟，以分析胶结量、孔隙度和渗透率的变化。这种采用多相场的数值模拟的方法不仅加深了黏土包壳对储层物性影响的理解，而且适用于储层表征和资源勘探等研究。

3.1 数值模型与物理实验模型和天然样品间相似性对比验证

3.1.1 实验验证

Lander等[10]研究发现在适当控制的实验室条件下成核不连续对石英次生加大具有影响，具体实验是在压力69 MPa和温度300~350 ℃下进行的。虽然Lander等[10]的研究没有提供与石英颗粒胶结相关的SiO2浓度或饱和指数的具体信息，但前期研究表明，自然环境条件下的饱和指数通常在0.45~2.79[34-36,41]。该指标对于确定达到平衡时的速度至关重要，并直接影响石英胶结需要的化学驱动力[22-23]。在开展石英生长建模研究时，研究人员通常采用合理的假设来减少模拟时间和计算成本，通过简化假设条件，优化计算资源，同时保持模拟过程的完整性[21-23,25]。本次研究采用的石英生长模拟参数与Prajapati等[22]使用的参数类似，即在压力为44 MPa、温度为150 ℃、饱和指数为6的条件下用数字方式模拟石英颗粒的胶结过程。Wendler等[23]和Prajapati等[22]的研究为上述假设的可靠性及其对自然现象精确重现的影响提供了有价值的信息。通过采用类似的模拟条件并做出可靠的假设，研究人员可以高效模拟复杂的自然过程，如石英胶结，同时合理控制计算需求，仿真再现长期的地质过程。在尝试模拟时，假设流体相对于SiO2过饱和是合理的。
首先，模拟了前人的石英板实验[10]，随后将本次模拟结果与前人实验结果进行了比较，以验证包含了惰性相的石英胶结模型。参考了Lander等[10]开展的最小铜网格实验，其实验装置采用了铜网一侧间距为20 µm的长度为42 µm的方孔；而本次模拟实验采用了3×3网格，如图4a。模拟域为406Δx×650Δy×406Δz（Δx、Δy、Δz的值均为0.5 μm）。在y方向上，厚度为20 μm的2个固体层分别代表石英板（灰色）和带方孔的铜网（铜色）。y方向上的其余区域充满了SiO2过饱和液相，为了使可视化清晰，图4a中没有显示。该模拟设置可以确保孔尺寸和网格间距与参考实验匹配。模拟结果与Lander等[10]的实验结果在晶体生长形态方面非常相似（见图4）。
图4 Lander等的“石英板次生加大”实验与本次模拟实验结果的对比
利用表1给出的参数，开展了石英晶体生长的相场数值模拟。图4a为石英过生长的不同阶段。随着石英胶结物在孔洞中生长，具有晶面的单晶体按照自面体形态形成。在模拟实验后期，由于晶体生长方向相同，而且在该方向上生长较快，单晶体横向上逐渐聚合（见图4a）。模拟结果与前人实验结果在晶体生长形态方面有明显的相似之处（见图4）。如前所述，本次模拟实验方法（基于Prajapati等[22]的实验）使用的温度、压力和过饱和条件不同于Lander等[10]所进行的实验，精确再现了石英胶结的形态特征，与实验观察结果一致，凸显了模型具有捕捉胶结过程基本特征的能力。Lander等[10]未提供SiO2过饱和液的具体浓度数据，因此无法对石英胶结物生长速度进行直接量化比较；但验证结果表明晶体生长形态相似，说明模型有较强的预测能力，为认识石英胶结过程奠定了坚实的基础。Prajapati等[22]和Wendler等[23]研究认为该模型适用于纯石英体系。
然而，采用石英和黏土验证模型的物理生长速度（例如Lander等[10]的实验，用铜模拟黏土矿物）存在挑战。在这类实验中，通过增加补充矿物加快生长速度，形成了多组分流体。本研究采用“纯”SiO2过饱和液获得的结果无法与上述复杂实验结果进行直接比较。
虽然多相场数值模拟方法适用于多组分和不同浓度的模拟，但由于计算成本较高，本次研究暂不考虑。对于包壳石英，有效的量化数据有限，即使有，其成分往往不明确或过于复杂，无法直接比较。考虑到上述限制条件，笔者的重点是数字模拟与室内实验的定性比较，争取实现二者的一致性结果。值得注意的是，目前的工作依据Prajapati等[22]提供的数据集，已经建立了一个有效的框架，可以有效用于各种储层质量表征。

3.1.2 天然样品验证

在存在部分包壳颗粒的天然样品中，内部生长分区明显。Buntsandstein统样品的薄片显微照片见图5a，显示颗粒包壳区域（红色箭头表示）和无包壳颗粒表面（绿色箭头表示）。图5b为相同颗粒和次生加大的冷阴极发光图像。在颗粒包壳覆盖不完全的区域内，共轴石英次生加大在包壳横向包裹颗粒前显示分区生长（深蓝色和亮蓝色，红色虚线范围）。这一分析重点关注孔隙表面粗糙度随地质时间的演变，并强调了成核不连续可能对储层质量的影响。沉淀物增加了孔隙表面的粗糙度，并可能改变流体的生产特征，而不是在孔隙旁产生一个光滑晶体面[42]。本研究假设的过饱和指数较高，使石英胶结过程加快了大约10倍，但不会改变自然石英胶结现象的其他方面。
图5 Buntsandstein统样品薄片显微照片及相场数值模拟结果

（a）Buntsandstein统样品中的部分覆膜石英颗粒：覆膜颗粒（红色箭头）和未覆膜颗粒（绿色箭头）；（b）与a相同颗粒，在颗粒未完全覆盖的区域，共轴石英次生加大在包壳横向聚合前出现分区生长（深蓝色和亮蓝色，红色虚线范围），冷阴极发光；（c）相场模拟结果说明了部分黏土矿物颗粒内部生长区随时间的演变：最初沉淀发生在未被黏土矿物覆盖的地方，随后出现颗粒包壳相的侧向，与天然样品中发生的现象类似

为了验证模型的预测能力，在模拟域中考虑了有包壳和无包壳的相似颗粒表面。该结构包括直径为100 μm的球形石英颗粒，局部包壳随机分布，浸入过饱和液相中，初始状态如图5c中的二维平面所示（为清楚展示省略了液相）。模拟域尺寸为300Δx×600Δy×300Δz（Δx、Δy、Δz的值均为0.5 μm）。利用表1中列出的参数模拟石英过生长，用不同灰度表示。值得注意的是，初始的沉淀发生在颗粒的无包壳部分，随后发生颗粒包壳相的侧向包裹，这在天然实例中也能观察到。与天然样品不同，模拟生长不受约束，导致在后期阶段形成晶面。

3.2 讨论

本节探讨了包壳参数如何影响胶结量。通过模拟无约束条件下黏土包壳单颗粒的次生加大胶结，研究了这些参数的影响。所有的模拟都使用表1中给出的参数。

3.2.1 石英颗粒结晶方向对砂岩胶结速度和数量的影响

石英晶体的棱柱形生长习性为沿c轴快速生长，直到晶面完成。在晶面上，锥体和棱柱体晶面以自面体形态发展。前人研究显示锥面比棱柱面生长速度快[10]。石英的这些生长趋势都在文献[22-23]的模型中有所反映。利用前文阐述的数字预处理工作流程，在足够大的模拟域内生成了连续单面包壳、覆盖率达50%、直径为100 μm的球形颗粒（见图6）。本文研究了石英基底颗粒相对于黏土包壳表面的3个不同的c轴方向，即：水平（0°）、垂直（90°）和对角线（45°）。模拟的石英次生加大特征以及胶结量的时间演变如图11所示，胶结物生长速度在垂直方向最低。对于对角和水平2个方向，注意到时间和胶结量的动态变化。在早期阶段（tsim最长为40 d），对角方向和水平方向的胶结量差异不大，因为这2个方向都形成自面体形态。到tsim为45 d时，通过对角线方向的横向包裹出现了更多的锥面，导致该方向的生长速度加快。
图6 3个方向模拟石英次生加大及胶结量随时间演变曲线
随后，在tsim为75 d时，在水平方向上也观察到快速生长的锥面发生横向包裹，加快了胶结物的生长速度。因此，在模拟阶段结束时（tsim为100 d），c轴在水平方向的颗粒积累了更多的胶结物。研究揭示了暴露锥面的生长和通过横向包裹作用产生新锥面之间的相互作用。

3.2.2 包壳覆盖率对砂岩胶结速度和数量的影响

模拟实验有1个假设和1个前置条件：①在一个足够大的模拟域中有一个粒径为92 μm、形态随机的数字球形石英颗粒；②在这个数字球形颗粒上用黏土产生不同的覆盖率，即占球形表面积20%，50%和80%的包壳。石英颗粒的生长方向如图7所示。随后，使用表1列出的参数模拟3种情况下的石英次生加大情况（见图7a）。正如预期的那样，与覆盖率较高的颗粒相比，覆盖率较低的颗粒具有较大的胶结量。图7a显示了所有3种情况下胶结量随时间的演变。减少黏土包壳的覆盖率导致胶结量增加和生长速度加快，这是由于在包壳较少的胶结物中，供胶结物生长的表面积较大。此外，这些曲线在初始生长阶段（tsim大约为2 d时，即晶面形成阶段）显示非线性特征。一旦石英表面上的所有晶面完全形成，生长就会以线性趋势进行，直到tsim为30 d（见图7a）。然而，图7b表明，如果模拟运行超过30 d，则图7a中胶结物生长的非线性特征将变得明显。图7b中的“随机分布覆盖”颗粒的曲线支持了这一推断，该曲线与图7a中的“50%黏土包壳”曲线匹配。由于计算成本高，没有进一步分析tsim超过30 d的第1种情况，主要关注包壳覆盖率的影响。
图7 任意形态石英颗粒上的次生加大胶结随时间变化的特征

3.2.3 包壳形态对砂岩胶结速度和数量的影响

为了研究石英颗粒上的包壳形态如何影响胶结物的生长速度和数量，研究了50%覆盖率下3种不同的包壳形态，初始状态如图7b左图所示。为简便起见，将3种形态分别称为层状包壳、随机包壳和半覆盖包壳。模型参数如表1所列，模拟结果如图6所示。胶结量随时间的变化见图6b，可以观察到从初期到中期（tsim为0~20 d），胶结量的增加幅度相似。在后期（30 d后），当晶面完全形成时，取决于是否存在生长更快的自由晶面，会发生进一步生长差异。对于层状包壳，生长速度较快的面比其他情况下的表面积要大，导致在模拟结束时（即大约60 d），胶结量更大。模拟结果表明，在次生加大的后期阶段，包壳形态的影响更明显，特别是形成光滑面时，包壳横向包围并继续扩展。在早期阶段，包壳形态的影响相对较小。即使黏土矿物包壳覆盖的表面积都是50%，沉淀的石英胶结物的体积也会随着时间的推移而变化。一般来说，黏土包壳随机分布的颗粒含较低的石英胶结量，与其他情况相比，可能是因为可容纳胶结物的未覆盖区域较小，表明更大的未覆盖区域可形成更多的次生加大胶结物。
在覆盖率均为50%的情况下模拟了3种随机包壳形态的胶结物生长特征。模拟参数如表1所列，模拟结果如图8所示，可以看出新生长胶结物随时间发生变化。在初始阶段（即tsim为0~25 d时），3种包壳形态下的净胶结物增加量没有明显差异。然而，到了中间阶段（tsim为25~100 d时），包壳形态的影响变得比较明显，净胶结量也出现了明显差异。最终，在胶结物完全堵塞孔隙空间的后期阶段，3种情况下胶结物增量逐渐趋于一致。
图8 3种覆膜分布形态下胶结物生长量随时间变化的曲线（数字砂岩的黏土矿物包壳覆盖率均为50%，黏土矿物包壳分布形态不同）

3.2.4 黏土包壳对储层质量的影响

通过开展系统的模拟研究，验证了共轴生长和黏土包壳覆盖率对岩石物理性质的影响，包括胶结物含量、孔隙度、渗透率及其相互关系。模拟采用数字砂岩在计算区域1 000Δx×1 000Δy×1 000Δz（Δx、Δy、Δz值为0.5 μm）中进行，见图8、图9。两次模拟的数字砂岩完全相同，均由464个颗粒组成，晶体生长方向随机（见图9），平均颗粒大小为80 μm，初始孔隙度为25%。
图9 Buntsandstein统样品的薄片显微图片与黏土矿物包壳覆盖率对岩石物理性质影响的模拟
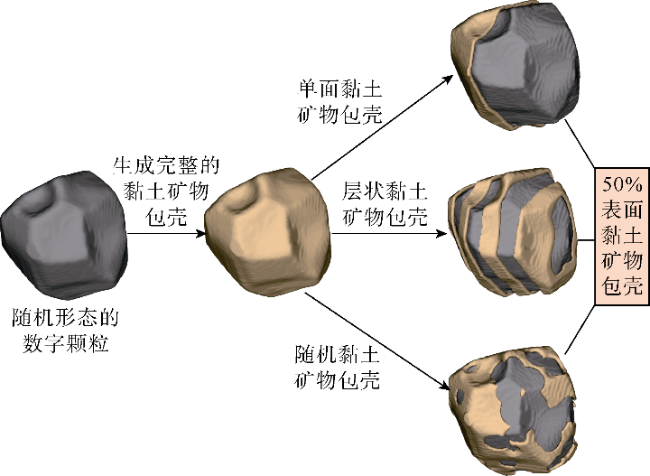
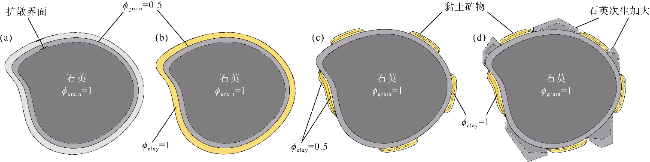
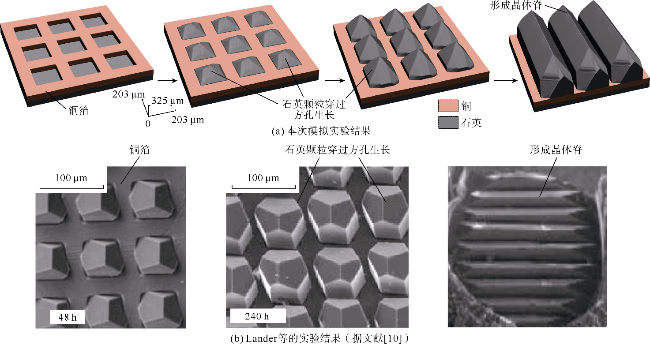
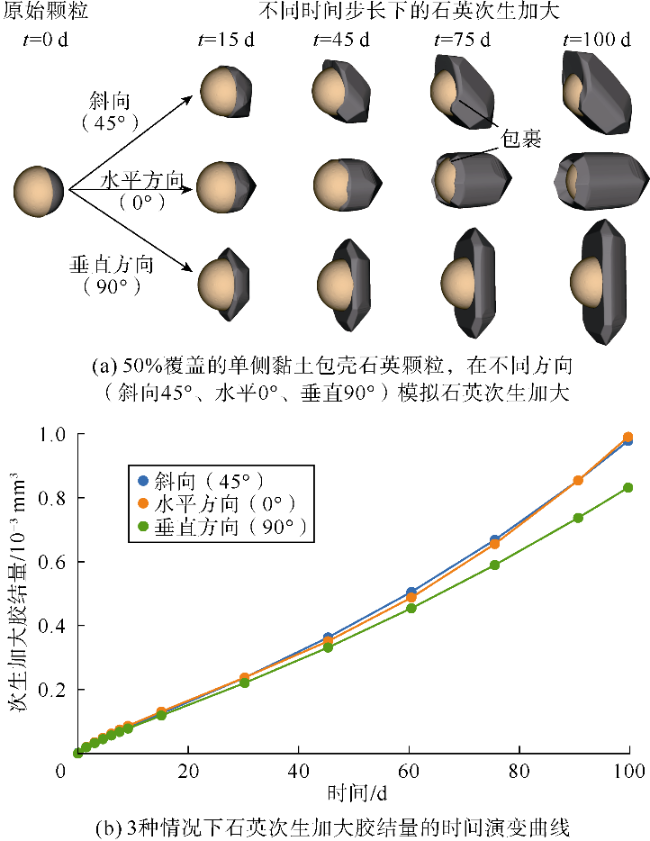
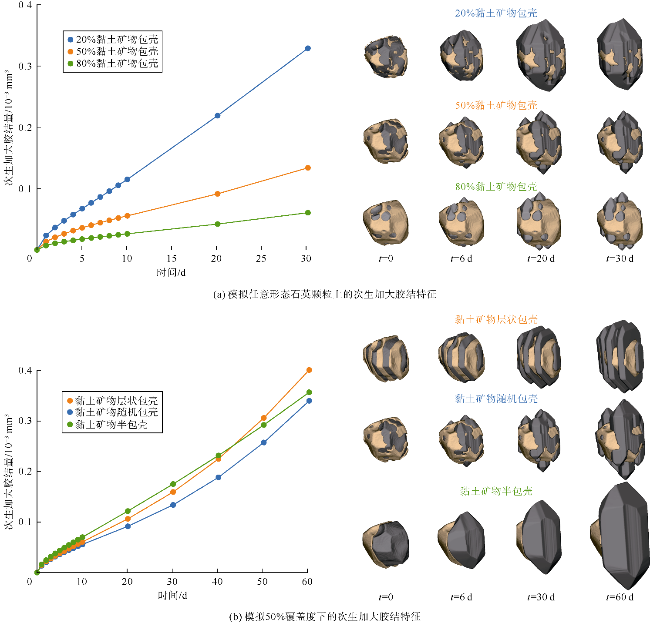
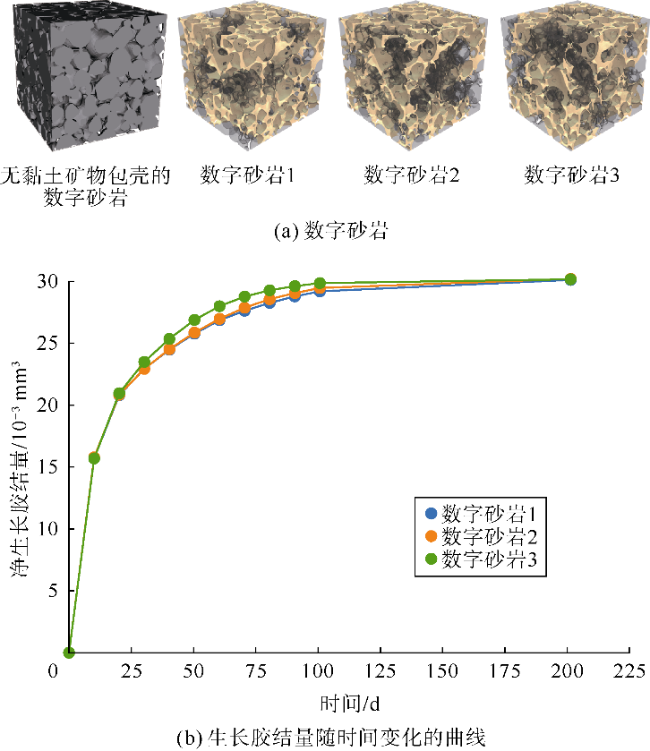
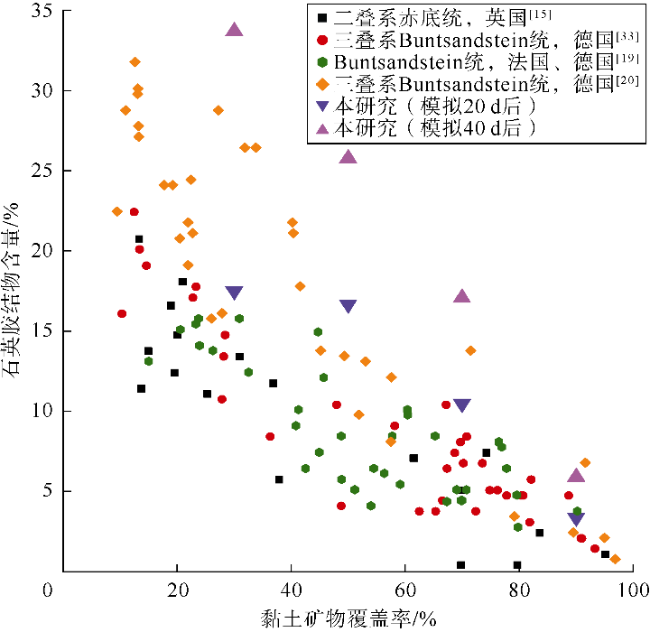
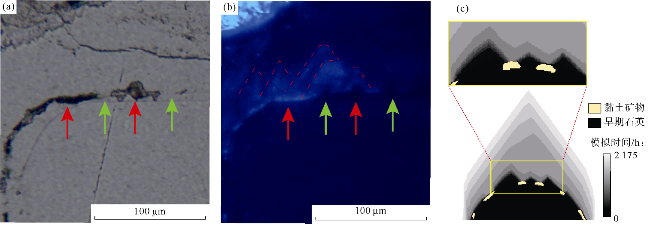
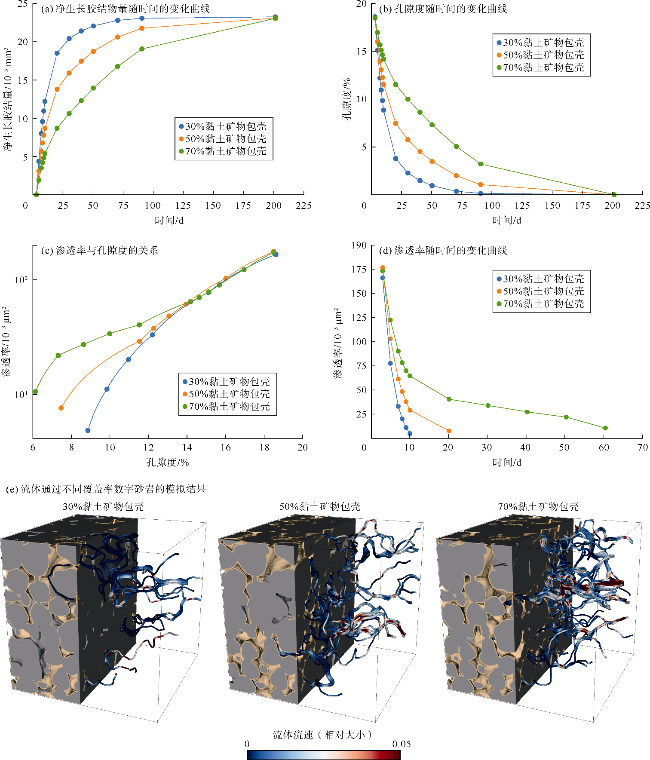
在数字砂岩的颗粒上生成3种不同覆盖率（30%，50%和70%）的随机黏土包壳形态，如图9b所示。黏土相的分布同样如图9b所示。采用表1所列的模拟参数，模拟3个砂样不同时间阶段的胶结物生长特征（见图9c—图9e）。包壳覆盖率较高的砂样胶结程度较低，因此在所有阶段都具有较高的孔隙空间。在模拟时间达到40 d后，孔隙空间的差异最为明显。在胶结物生长、孔隙空间和黏土包壳方面，模拟得到的黏土包壳微观结构与天然样品相似（见图9a）。图10a、图10b是胶结量和孔隙度随时间的变化曲线，可以看出在包壳覆盖率较低的砂岩中，由于胶结物生长的表面积较大，孔隙度降低得更快。这一点从图10a的胶结量随时间变化曲线也可以发现。速度流线描述了胶结大约10 d后，通过3种不同包壳覆盖率砂岩的流体流动情况，与包壳覆盖率较低的砂岩相比，包壳覆盖率较高的砂岩的孔隙连通性较好（见图10e）。该结论也与现场调查和室内实验结果一致，表明具有较高颗粒包壳覆盖率的样品在相同孔隙度下通常具有较高的渗透率[13]。然而，在其他天然样品系列中很少发现这种理想的相关性，可能由于以下因素造成：其他天然样品中含有堵塞孔隙空间的其他非石英胶结物；黏土矿物包壳结构（切向型、径向型或孔隙桥接型）也会影响渗透率[4]；已证实伊利石颗粒包壳可能增强压力溶解，进一步降低孔隙度和渗透率[17,20]。
图10 不同覆膜覆盖率下数字砂岩净生长胶结量、孔隙度、渗透率随时间的变化
根据本次研究的流体流动模型和流动参数[22]，对不同阶段模拟后的砂样进行了流体动力学分析。孔隙度相同时，包壳覆盖率高的砂岩渗透性好于覆盖率低的砂岩（见图10c）。覆盖率较高的砂岩孔隙中沉淀的胶结物较少，反之亦然。因此，新生长的胶结物只会堵塞附近的孔隙空间，而有黏土包壳的区域则不受影响。因此，包壳覆盖率较大的砂岩具有较高的渗透率（见图10d、图10e）。
无包壳或部分包壳覆盖颗粒样品上形成的石英次生加大胶结结构可能会影响孔隙表面粗糙度，从而影响润湿性质，也可能影响地下流体的流动性[41]。

3.2.5 与天然样品的对比

有关天然砂岩样品中石英胶结物含量和包壳覆盖率的数据，也可以从现场调查结果获得[15,19 -20]。这对评估结果形成了支撑，即颗粒包壳覆盖率是控制不同研究区域、不同流体作用和不同热演化史的石英共轴胶结物生长有效面积的主要控制因素。20 d后的模拟结果与天然样品的实测结果总体上具有很好的相关性（见图11）。而且，对于取自上莱茵地堑Buntsandstein统的样品，经历了高温热辐射，尽管流体作用相似，但包壳覆盖率低（小于40%）的样品（见图11的橙色菱形）比相同颗粒包壳覆盖率下经历较弱热辐射的样品（见图11的红色圈）具有较高的石英胶结物含量。40 d后（见图11紫色三角形）的模拟结果与20 d后（见图11蓝色三角形）的模拟结果相拟合，其中较强的热场作用也会导致较大的石英胶结量。这证明了本文提出的建模方法和数字工作流程是有效的。因此，利用上述模拟方法可以开展可变颗粒包壳覆盖率情况的钻前储层评估，评估新生长胶结物的含量，推测热场作用对有利储层孔隙度和渗透率的影响。与前期颗粒溶解[29]、单晶和多晶石英颗粒影响生长形态与生长量[21-22]和裂缝胶结形成[24,26 -27,43]的分析流程相结合，将是使用数字岩石模型进行钻前储层质量评估的宝贵补充。
图11 各种天然样品及数字砂岩模型模拟20 d和40 d后的石英胶结物含量与黏土矿物覆盖率的关系

4 结论和前景展望

本文揭示了黏土包壳对砂岩中共轴生长胶结及其储层性质的影响方式，并在黏土包壳建模方面有2项进展：①修正了前人的多相场模型，计算了各类黏土包壳的惰性相，新创立的建模方法能够重现Lander等[10]在“石英板”实验中观察到的石英次生加大形态。②研发了一种新的数字预处理工作流程，在多颗粒充填样品中的石英颗粒上生成真实的黏土包壳，能够系统地模拟和分析不同覆膜参数的影响。
实际研究中通常无法获得黏土包壳参数，即方向、覆盖率和包壳形态等参数特征，并且在前期的室内实验和建模文献中也未有报道。通过本次数值研究对单颗粒和多颗粒充填体中的一系列生长模拟，揭示出这些包壳参数对储层质量的相对重要性。
值得注意的是，黏土包壳的覆盖率是胶结量和生长速度的决定性因素，其次是与黏土包壳和形态相关的c轴方向。研究发现，石英颗粒结晶垂直方向上胶结物生长速度最小，实验中后期对角线方向的包壳生长速度较水平方向更快。黏土包壳形态对胶结的显著影响主要发生在储层成岩演化晚期，层状包壳形态的胶结速度更快；包壳覆盖率与砂岩孔隙度和渗透率呈正相关关系。
动态演化过程模拟结果和对比验证显示，多颗粒充填体中的模拟生长与室内实验及天然样品中观察到的形态高度相似，特别是在它们如何包裹黏土包壳和占据孔隙空间方面，证实了包壳三维数值模拟新方法的有效性。分析这些模拟产生的数值数据集，并通过胶结量、孔隙度和渗透率随时间演变的曲线揭示出胶结过程中储层性质动态变化的宝贵信息。
在相同孔隙度情况下，包壳覆盖率较高的砂岩渗透率高于覆盖率较低的砂岩渗透率，这是由于新胶结物局部生长在无包壳覆盖的颗粒表面，有利于堵塞渗流通道。
此外，在同样暴露于过饱和流体中20 d（模拟时间）后，模拟石英胶结物含量与天然样品的实测结果具有很好的一致性，说明本文的模拟结果具有较高的可靠性。
本研究是对Prajapati等[21-22]研究工作的补充，有助于认识黏土包壳砂岩，提供储层物性演化的见解。未来笔者构建的方法可以扩展到其他含惰性相的地质系统，如石英脉和钙质灰岩。此外，由于模型没有明确地将包壳划分为原生成因或成岩成因，这是未来研究的领域，将进一步加深对储层动态演化的认识，提高储层表征和预测的准确性，最终使从事地下资源勘探和管理的各方受益。
致谢：感谢亥姆霍兹协会对MTET: 38.04.04项目建模和模拟研究工作的资助，感谢巴符州通过bwHPC给予的支持，感谢卡尔斯鲁厄理工学院Lukas Schöller教授对本研究中颗粒填充数据生成的协助以及对论文的意见和建议。
符号注释：
a——梯度能密度函数，J/m4； a k i n ,   α β n ^——α-β界面动力各向异性函数；fα——相α的体自由能密度，J/m3；fbulk——体自由能密度，J/m3；Δfql——石英胶结的驱动力，J/m3；F——亥姆霍兹自由能，J；Fbulk——体自由能，J；Fintf——界面自由能，J；G——吉布斯函数；h——体自由能密度插值函数；K——渗透率，m2；k——从1到nαβ之间的1个数； M α β n ^——α-β界面流动系数，m4/（J·s）； M 0 ,   c l ——黏土矿物-液体界面动力流动系数，m4/（J·s）； M 0 ,   α β ——α-β界面动力流动系数，m4/（J·s）；N——相态数量；nαβ——各向异性方向的数量； n ^——单位法向量； n ^ α β——α-β界面的单位法向量；qαβ——与α-β界面垂直的广义相场梯度向量；t——时间，s；Δt——时间步长，s；u——液体流速向量，m/s； u ¯——液体平均流速向量，m/s；x——位置向量，m；Δx，Δy，Δz——网格单元大小，μm；tsim——模拟时间，d；ϕα，ϕβ，ϕγ——相α、β、γ的相场参数；ϕ(x,t)——位置x、时间t对应的相场向量；ϕclay——黏土的相场参数；Ω——物理域体积，m3；ε——长度，m；ω——势能密度函数，J/m2；γcc——黏土-黏土界面的界面能密度，J/m2；γcl——黏土-液体界面的界面能密度，J/m2；γql——石英-液体界面的界面能密度，J/m2；γqq——石英-石英界面的界面能密度，J/m2；γαβ——α-β界面的界面能密度，J/m2；γαβδ——高阶界面能密度，J/m2；ηαβ——α-β界面各向异性形态的顶点向量集； η c a p ,   k ——毛细管各向异性形态的顶点向量集； η k i n ,   k ——动力各向异性形态的顶点向量集；μd——动力黏度， Pa·s； μ 0 ,   q l ——石英-液体界面动能系数，m4/（J·s）； ∇ p——压力梯度，Pa/m； ℝ 0 +——非负实数集合； ℝ N——1组实数；δ——动能各向异性强度。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
AJDUKIEWICZ J M, LANDER R H. Sandstone reservoir quality prediction: The state of the art[J]. AAPG Bulletin, 2010, 94(8): 1083-1091.

[2]
HEALD M T, LARESE R E. Influence of coatings on quartz cementation[J]. Journal of Sedimentary Research, 1974, 44(4): 1269-1274.

[3]
PITTMAN E D, LARESE R E, HEALD M T. Clay coats: Occurrence and relevance to preservation of porosity in sandstones[M]//HOUSEKNECHT D W, PITTMAN E D. Origin, Diagenesis, and Petrophysics of Clay Minerals in Sandstones. Tulsa: SEPM Society for Sedimentary Geology, 1992: 241-255.

[4]
HOWARD J J. Influence of authigenic-clay minerals on permeability[M]//HOUSEKNECHT D W, PITTMAN E D. Origin, diagenesis, and petrophysics of clay minerals in sandstones. Tulsa: SEPM Society for Sedimentary Geology, 1992: 257-264.

[5]
AAGAARD P, JAHREN J S, HARSTAD A O, et al. Formation of grain-coating chlorite in sandstones. Laboratory synthesized vs. natural oc-currences[J]. Clay Minerals, 2000, 35(1): 261-269.

[6]
LIEWIG N, CLAUER N. K-Ar dating of varied microtextural illite in Permian gas reservoirs, northern Germany[J]. Clay Minerals, 2000, 35(1): 271-281.

[7]
ESCH W L, AJDUKIEWICZ J M, REYNOLDS A C. Early grain-coat formation in Chaco dune field, New Mexico: Insight into formation mechanisms, distribution, and implications for predictive modeling to assist in deep play identification[R]. San Antonio:2008 AAPG Annual Convention, 2008: 90078.

[8]
BUSCH B. Pilot study on provenance and depositional controls on clay mineral coatings in active fluvio-eolian systems, western USA[J]. Sedimentary Geology, 2020, 406: 105721.

[9]
AJDUKIEWICZ J M, NICHOLSON P H, ESCH W L. Prediction of deep reservoir quality using early diagenetic process models in the Jurassic Norphlet Formation, Gulf of Mexico[J]. AAPG Bulletin, 2010, 94(8): 1189-1227.

[10]
LANDER R H, LARESE R E, BONNELL L M. Toward more accurate quartz cement models: The importance of euhedral versus noneuhedral growth rates[J]. AAPG Bulletin, 2008, 92(11): 1537-1563.

[11]
BLOCH S, LANDER R H, BONNELL L. Anomalously high porosity and permeability in deeply buried sandstone reservoirs: Origin and pre-dictability[J]. AAPG Bulletin, 2002, 86(2): 301-328.

[12]
WOOLDRIDGE L J, WORDEN R H, GRIFFITHS J, et al. How to quantify clay-coat grain coverage in modern and ancient sediments[J]. Journal of Sedimentary Research, 2019, 89(2): 135-146.

DOI

[13]
BUSCH B, HILGERS C, ADELMANN D. Reservoir quality controls on Rotliegend fluvio-aeolian wells in Germany and the Netherlands, Southern Permian Basin: Impact of grain coatings and cements[J]. Marine and Petroleum Geology, 2020, 112: 104075.

[14]
VERHAGEN I T E, CRISÓSTOMO-FIGUEROA A, UTLEY J E P. Abrasion of detrital grain-coating clays during sediment transport: Implications for diagenetic clay coats[J]. Sedimentary Geology, 2020, 403: 105653.

[15]
BUSCH B, HILGERS C, GRONEN L, et al. Cementation and structural diagenesis of fluvio-aeolian Rotliegend sandstones, northern England[J]. Journal of the Geological Society, 2017, 174(5): 855-868.

[16]
FRANKS S G, PANTANO J. A simple, effective petrographic method for quantifying percent clay or other grain-coat coverage in sandstones[J]. Journal of Sedimentary Research, 2021, 91(2): 221-227.

[17]
MONSEES A C, BUSCH B, SCHÖNER N, et al. Rock typing of diagenetically induced heterogeneities: A case study from a deeply-buried clastic Rotliegend reservoir of the Northern German Basin[J]. Marine and Petroleum Geology, 2020, 113: 104163.

[18]
MONSEES A C, BUSCH B, HILGERS C. Compaction control on diagenesis and reservoir quality development in red bed sandstones: A case study of Permian Rotliegend sandstones[J]. International Journal of Earth Sciences, 2021, 110(5): 1683-1711.

[19]
BUSCH B, ADELMANN D, HERRMANN R, et al. Controls on compactional behavior and reservoir quality in a Triassic Buntsandstein reservoir, Upper Rhine Graben, SW Germany[J]. Marine and Petroleum Geology, 2022, 136: 105437.

[20]
BUSCH B, BÖCKER J, HILGERS C. Improved reservoir quality assessment by evaluating illite grain coatings, quartz cementation, and com-paction: Case study from the Buntsandstein, Upper Rhine Graben, Germany[J]. Geoenergy Science and Engineering, 2024, 241: 213141.

[21]
PRAJAPATI N, SELZER M, NESTLER B, et al. Three-dimensional phase-field investigation of pore space cementation and permeability in quartz sandstone[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(8): 6378-6396.

[22]
PRAJAPATI N, GONZALEZ A A, SELZER M, et al. Quartz cementation in polycrystalline sandstone: Insights from phase-field simulations[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(2): e2019JB019137.

[23]
WENDLER F, OKAMOTO A, BLUM P. Phase-field modeling of epitaxial growth of polycrystalline quartz veins in hydrothermal experiments[J]. Geofluids, 2016, 16(2): 211-230.

[24]
SPÄTH M, URAI J L, NESTLER B. Formation of radiator structures in quartz veins-phase-field modeling of multi-crack sealing[J]. Journal of Structural Geology, 2022, 158: 104576.

[25]
ANKIT K, URAI J L, NESTLER B. Microstructural evolution in bitaxial crack-seal veins: A phase-field study[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(5): 3096-3118.

[26]
SPÄTH M, SPRUŽENIECE L, URAI J L, et al. Kinematics of crystal growth in single-seal syntaxial veins in limestone: A phase-field study[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(10): e2021JB022106.

[27]
PRAJAPATI N, SELZER M, NESTLER B. Computational modeling of calcite cementation in saline limestone aquifers: A phase-field study[J]. Geothermal Energy, 2017, 5(1): 15.

[28]
PRAJAPATI N, SPÄTH M, KNECHT L, et al. Quantitative phase-field modeling of faceted crystal dissolution processes[J]. Crystal Growth & Design, 2021, 21(6): 3266-3279.

[29]
KUMAR A, PRAJAPATI N, SPÄTH M, et al. Qualitative dissolution modeling of etch-pit formation on the K-feldspar surface through phase-field approach[J]. Journal of Geophysical Research: Solid Earth, 2023, 128(4): e2022JB025749.

[30]
TAMBURELLI S, DI GIULIO A, AMADORI C, et al. New constraint on burial and thermal history of Devonian reservoir sandstones in the Illizi-Ghadames Basin (North Africa) through diagenetic numerical modelling[J]. Marine and Petroleum Geology, 2022, 145: 105903.

[31]
SPRUŽENIECE L, SPÄTH M, URAI J L, et al. Wide-blocky veins explained by dependency of crystal growth rate on fracture surface type: Insights from phase-field modeling[J]. Geology, 2021, 49(6): 641-646.

[32]
HÖTZER J, REITER A, HIERL H, et al. The parallel multi-physics phase-field framework PACE3D[J]. Journal of Computational Science, 2018, 26: 1-12.

[33]
BUSCH B, SPITZNER A D, ADELMANN D, et al. The significance of outcrop analog data for reservoir quality assessment: A comparative case study of Lower Triassic Buntsandstein sandstones in the upper Rhine graben[J]. Marine and Petroleum Geology, 2022, 141: 105701.

[34]
BUSCH B, OKAMOTO A, GARBEV K, et al. Experimental fracture sealing in reservoir sandstones and its relation to rock texture[J]. Journal of Structural Geology, 2021, 153: 104447.

[35]
MANNING C E. The solubility of quartz in H2O in the lower crust and upper mantle[J]. Geochimica et Cosmochimica Acta, 1994, 58(22): 4831-4839.

[36]
SANJUAN B, MILLOT R, INNOCENT C, et al. Major geochemical characteristics of geothermal brines from the Upper Rhine Graben granitic basement with constraints on temperature and circulation[J]. Chemical Geology, 2016, 428: 27-47.

[37]
NESTLER B, GARCKE H, STINNER B. Multicomponent alloy solidification: Phase-field modeling and simulations[J]. Physical Review E, 2005, 71(4): 041609.

[38]
STEINBACH I. Phase-field models in materials science[J]. Modelling and Simulation in Materials Science and Engineering, 2009, 17(7): 073001.

[39]
KUMAR A, SPÄTH M, PRAJAPATI N, et al. Dataset for phase-field simulation showcasing impact of clay-coating on sandstone reservoir[DB/OL]. (2024-06-07)[2024-10-10]. https://doi.org/10.5281/zenodo.11506190.

[40]
CHARLAFTIS D, DOBSON K J, JONES S J, et al. Experimental simulation of burial diagenesis and subsequent 2D-3D characterization of sandstone reservoir quality[J]. Frontiers in Earth Science, 2022, 10: 766145.

[41]
WARREN E A, SMALLEY C P, HOWARTH R. Part 4: Compositional variations of North Sea formation waters[J]. Geological Society, London, Memoirs, 1994, 15(1): 119-208.

[42]
SARI A, AL MASKARI N S, SAEEDI A, et al. Impact of surface roughness on wettability of oil-brine-calcite system at sub-pore scale[J]. Journal of Molecular Liquids, 2020, 299: 112107.

[43]
SPÄTH M, SELZER M, BUSCH B, et al. Phase-field simulations of epitaxial crystal growth in open fractures with reactive lateral flow[J]. Water Resources Research, 2023, 59(8): e2023WR034605.

Options
文章导航

/

〈 〉

版权所有：《石油勘探与开发》编辑部；《石油勘探与开发（英文）》编辑部
地址：北京市海淀区学院路20号，中国石油勘探开发研究院数据中心605室　

京ICP备15044687号    技术支持：北京玛格泰克科技发展有限公司