0 引言
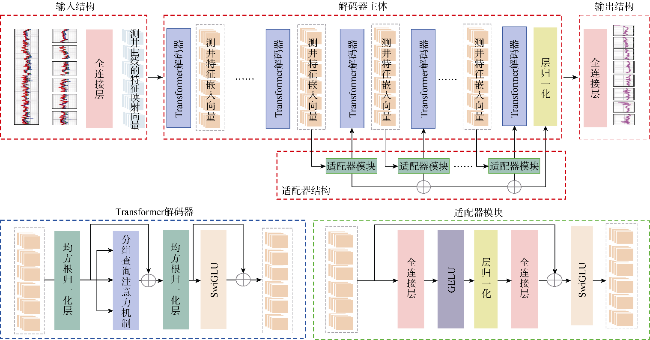
1 原理与方法
2 实验
2.1 数据预处理
表1 数据清洗后的测井数据统计表 |
| 指标 | 密度/ (kg·m-3) | 中子 孔隙度/% | 声波时差/ (μs·m-1) | 地层电阻率/ (Ω·m) | 自然伽马/ API |
|---|---|---|---|---|---|
| 均值 | 2 515.66 | 20.93 | 189.82 | 8.81 | 132.53 |
| 标准差 | 150.07 | 14.82 | 128.33 | 9.49 | 57.37 |
| 中位数 | 2 526.19 | 16.60 | 162.99 | 4.15 | 121.01 |
| 最小值 | 2 097.80 | 0 | 0 | 0 | 0 |
| 最大值 | 2 954.30 | 63.7 | 691.71 | 44.66 | 293.39 |
| 偏度 | -0.39 | 1.03 | 0.27 | 1.40 | 0.70 |
| 峰度 | 0.07 | 0.48 | -1.64 | 1.37 | -0.005 5 |
2.2 模型训练与参数设置
表2 盖亚模型的超参数表 |
| 参数 | 设置结果 | 参数 | 设置结果 |
|---|---|---|---|
| 优化器 | Adam | 序列长度 | 40 |
| 损失函数 | MAE | 解码器层数(Decoder Layers) | 32 |
| 最大迭代次数 | 150 | 全连接层数(FC Dimension) | 4 096 |
| 峰值学习率 | 0.000 1 | 注意力头数(Attention Heads) | 32 |
| 学习率调度器的预设因子 | 0.9 | 键/值头数(Key/Value Heads) | 8 |
| 批数量(Batch Size) | 256 | 激活函数 | SwiGLU和GELU |
2.3 实验结果
2.3.1 对比实验
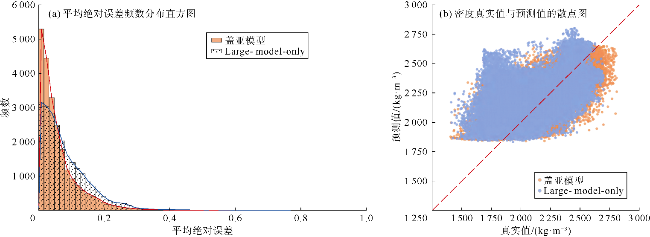
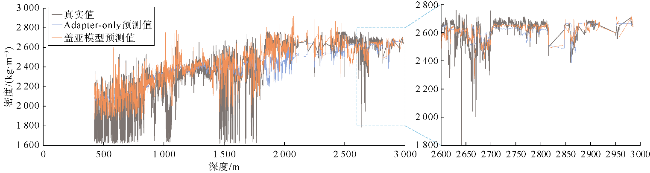
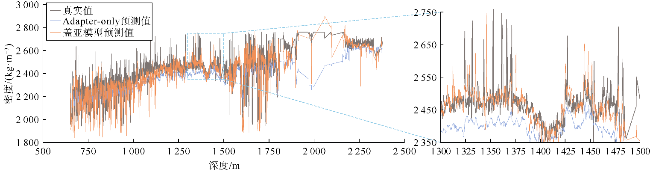
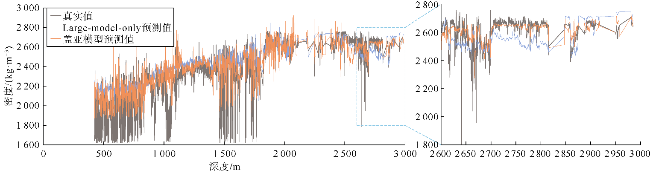
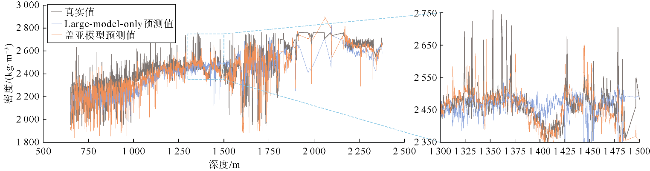
2.3.2 消融实验
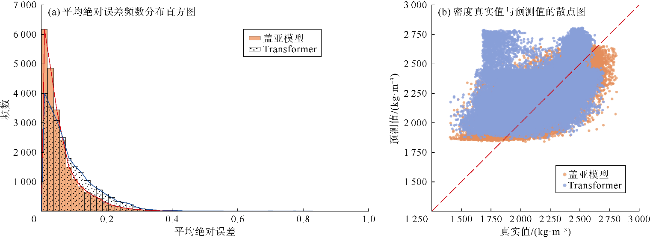
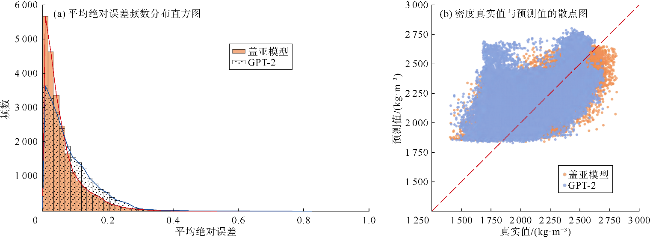
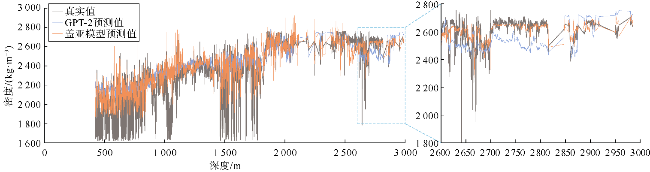
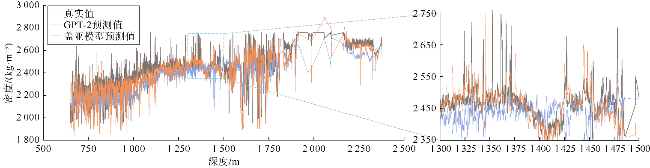
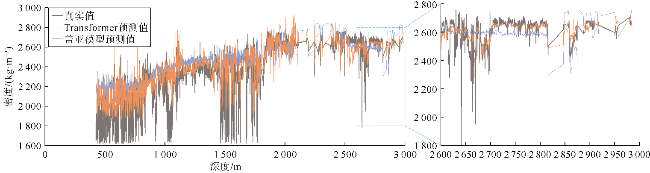
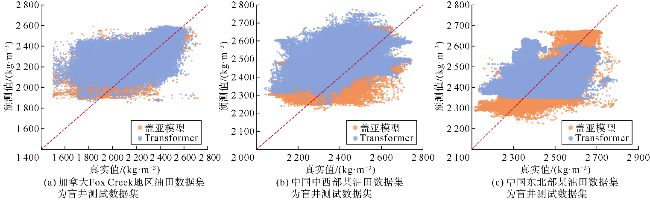
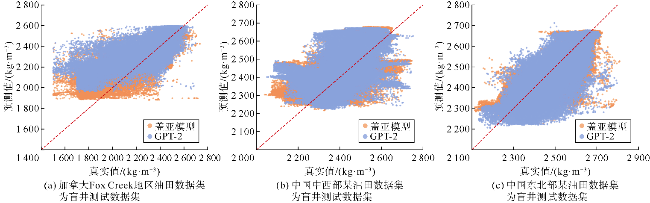
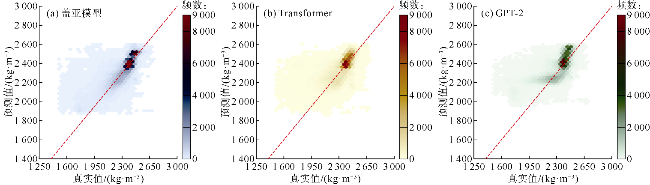
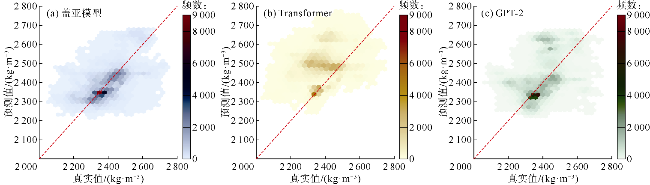
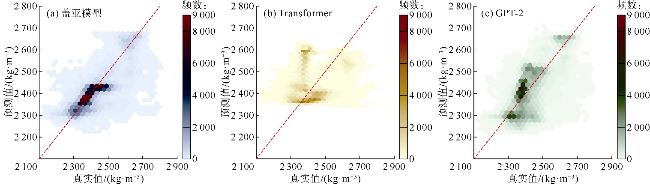
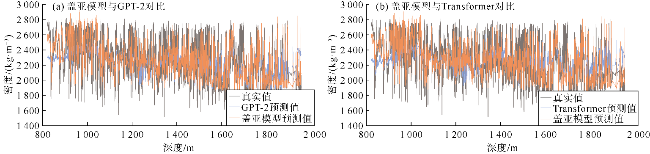
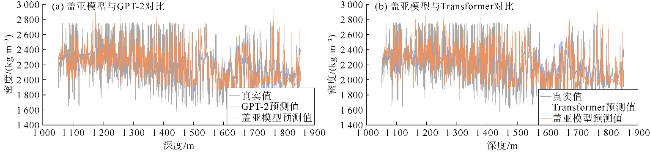
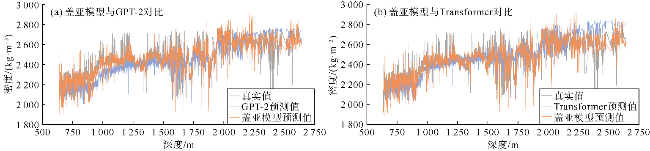
2.3.3 泛化性实验
表4 泛化性实验的误差指标 |
| 盲区 | 模型 | 均方误差 | 平均绝对误差 | 均方根误差 |
|---|---|---|---|---|
| 加拿大 Fox Creek 地区 | 盖亚模型 | 0.046 | 0.147 | 0.217 |
| Transformer | 0.215 | 0.379 | 0.464 | |
| GPT-2 | 0.094 | 0.231 | 0.308 | |
| 中国中西部 某油田 | 盖亚模型 | 0.108 | 0.234 | 0.329 |
| Transformer | 0.384 | 0.492 | 0.620 | |
| GPT-2 | 0.209 | 0.342 | 0.457 | |
| 中国东北部 某油田 | 盖亚模型 | 0.280 | 0.313 | 0.529 |
| Transformer | 0.618 | 0.500 | 0.786 | |
| GPT-2 | 0.487 | 0.441 | 0.698 |
表5 跨油藏泛化性实验的误差指标 |
| 井号 | 模型 | 均方误差 | 平均绝对误差 | 均方根误差 |
|---|---|---|---|---|
| 井1 | 盖亚模型 | 0.014 4 | 0.08 | 0.12 |
| GPT-2 | 0.025 6 | 0.12 | 0.16 | |
| Transformer | 0.028 9 | 0.14 | 0.17 | |
| 井2 | 盖亚模型 | 0.014 4 | 0.09 | 0.12 |
| GPT-2 | 0.016 9 | 0.10 | 0.13 | |
| Transformer | 0.019 6 | 0.12 | 0.14 | |
| 井3 | 盖亚模型 | 0.003 6 | 0.04 | 0.06 |
| GPT-2 | 0.008 1 | 0.07 | 0.09 | |
| Transformer | 0.010 0 | 0.08 | 0.10 |