石油勘探与开发 >

2025 , Vol. 52 >Issue 2: 451 - 462

DOI: https://doi.org/10.11698/PED.20240757

石油工程

基于热流固耦合作用的深水裂缝性地层高温高压井关井求压方法

  • 陈刚 , 1 ,
  • 王志远 , 1 ,
  • 孙小辉 2 ,
  • 钟杰 1 ,
  • 张剑波 1 ,
  • 刘雪琪 1 ,
  • 张明伟 1 ,
  • 孙宝江 1
展开
  • 1 中国石油大学（华东）石油工程学院，山东青岛 266580
  • 2 中国石油大学（华东）计算机科学与技术学院，山东青岛 266580
王志远（1981-），男，山东泰安人，博士，中国石油大学（华东）教授，主要从事井筒压力控制和天然气水合物开发等相关研究。地址：山东省青岛市黄岛区长江西路66号，中国石油大学（华东）石油工程学院，邮政编码：266580。E-mail：

陈刚（1997-），男，山东淄博人，中国石油大学（华东）在读博士，主要从事深水钻井相关研究。地址：山东省青岛市黄岛区长江西路66号，中国石油大学（华东）石油工程学院，邮政编码：266580。E-mail：

Copy editor: 刘恋

收稿日期: 2024-12-07

  修回日期: 2025-03-21

  网络出版日期: 2025-04-17

基金资助

国家自然科学基金联合基金重点项目“深水控压钻完井地层-井筒多场耦合机理与压力调控”(U21B2069)

山东省重点研发计划项目“深水复杂钻井多相流动模拟关键技术与监测装备”(2022CXGC020407)

国家自然科学基金基础科学中心项目“超深特深层油气钻采流动调控”(52288101)

收起

A shut-in pressure calculation method for high-temperature high-pressure wells in deepwater fractured formations based on thermo-hydro-mechanical coupling

  • CHEN Gang , 1 ,
  • WANG Zhiyuan , 1 ,
  • SUN Xiaohui 2 ,
  • ZHONG Jie 1 ,
  • ZHANG Jianbo 1 ,
  • LIU Xueqi 1 ,
  • ZHANG Mingwei 1 ,
  • SUN Baojiang 1
Expand
  • 1 School of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China
  • 2 College of Computer Science and Technology, China University of Petroleum (East China), Qingdao 266580, China

Received date: 2024-12-07

  Revised date: 2025-03-21

  Online published: 2025-04-17

Fold

摘要

综合考虑温度、压力对深水裂缝性地层高温高压井井内流体密度的影响和地层裂缝变形对关井续流作用的影响，耦合关井温度场模型、裂缝变形模型和气体流动模型，建立考虑热流固耦合作用的关井井筒压力计算模型，分析地温梯度、井底压差、钻井液池增量和井涌指数对井口套压的影响规律，并基于耦合模型计算结果建立高温高压井关井求压图版。研究表明：地温梯度、井底压差、钻井液池增量与井口套压呈正相关关系，井涌指数越大压力攀升越快而最大套压保持稳定；与实例井数据对比验证表明，耦合模型计算关井后井筒恢复压力准确率达95%以上，根据关井求压图版求取目标井口套压和目标关井时间的准确率分别为97.2%和98.3%。采用该方法能够在高温高压井关井后准确求取地层压力，为后续井控措施提供依据，保证深水深层油气安全高效开发。

关键词： 热流固耦合; 高温高压井; 关井求压; 裂缝性地层; 深水

本文引用格式

陈刚 , 王志远 , 孙小辉 , 钟杰 , 张剑波 , 刘雪琪 , 张明伟 , 孙宝江 . 基于热流固耦合作用的深水裂缝性地层高温高压井关井求压方法[J]. 石油勘探与开发, 2025 , 52(2) : 451 -462 . DOI: 10.11698/PED.20240757

Abstract

By comprehensively considering the influences of temperature and pressure on fluid density in high temperature and high pressure (HTHP) wells in deepwater fractured formations and the effects of formation fracture deformation on well shut-in afterflow, this study couples the shut-in temperature field model, fracture deformation model, and gas flow model to establish a wellbore pressure calculation model incorporating thermo-hydro-mechanical coupling effects. The research analyzes the governing patterns of geothermal gradient, bottomhole pressure difference, drilling fluid pit gain, and kick index on casing head pressure, and establishes a shut-in pressure determination chart for HPHT wells based on coupled model calculation results. The study results show: geothermal gradient, bottomhole pressure difference, and drilling fluid pit gain exhibit positive correlations with casing head pressure; higher kick indices accelerate pressure rising rates while maintaining a constant maximum casing pressure; validation against field case data demonstrates over 95% accuracy in predicting wellbore pressure recovery after shut-in, with the pressure determination chart achieving 97.2% accuracy in target casing head pressure prediction and 98.3% accuracy in target shut-in time. This method enables accurate acquisition of formation pressure after HPHT well shut-in, providing reliable technical support for subsequent well control measures and ensuring safe and efficient development of deepwater and deep hydrocarbon reservoirs.

Key words： thermo-hydro-mechanical coupling; high temperature and high pressure well; shut-in pressure calculation; fractured formation; deepwater

0 引言

近10年间，海洋新增油气储量占全球新增储量的60%，其中，深水—超深水区域新增储量占海洋新增储量的61.99%，深水油气资源勘探开发逐渐成为油气开发的重点方向[1⇓-3]。深水高温高压井通常水深超过500 m，井底温度高于150 ℃，地层孔隙压力超过69 MPa[4]。深水高温高压井钻井时，由于地层信息难以获取、井内多相流动规律不明导致井筒压力计算具有较大的不确定性，极易引发井漏、井涌甚至井喷[5⇓⇓⇓-9]。准确计算井筒压力、及时有效反演地层压力对保障深水深层油气安全高效开发有重大意义。
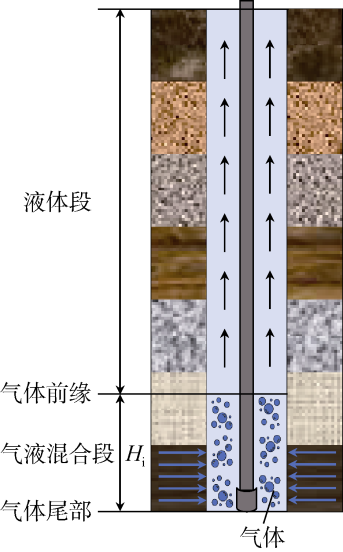
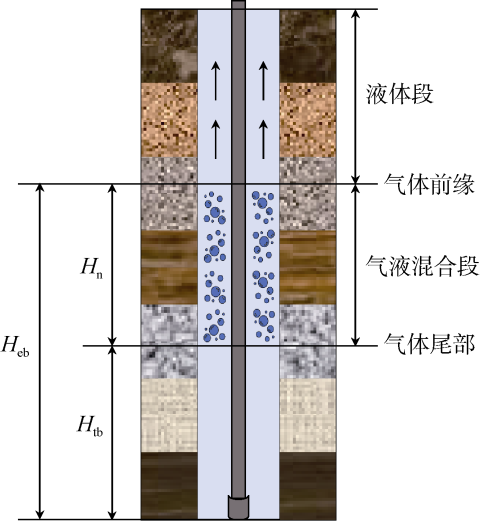
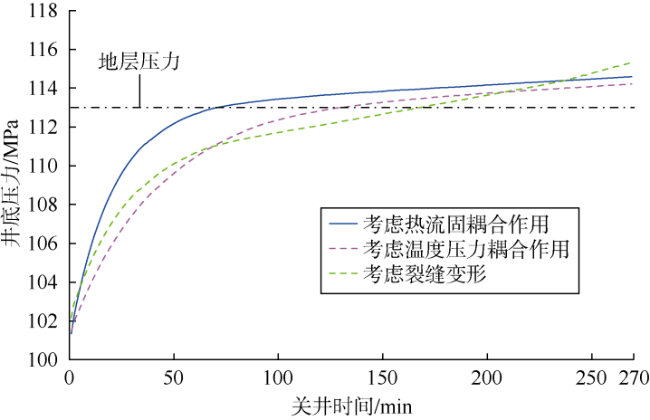
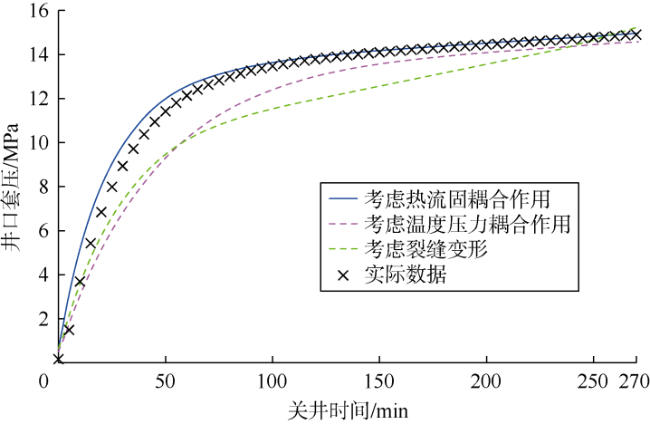
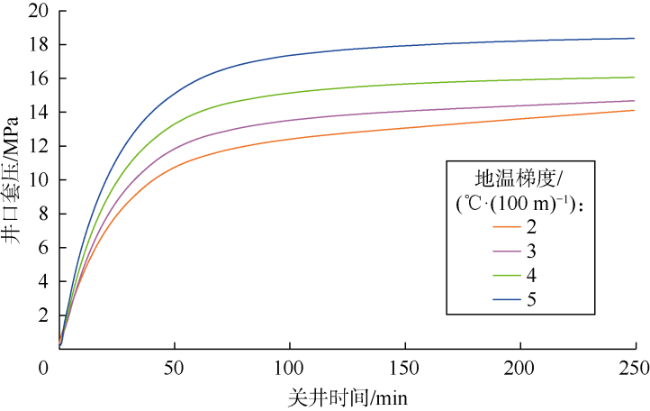
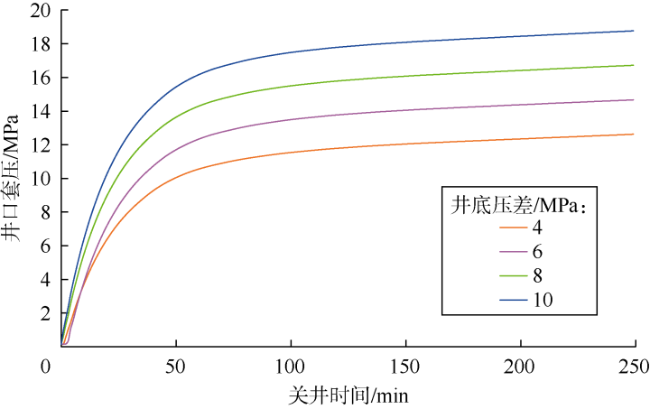
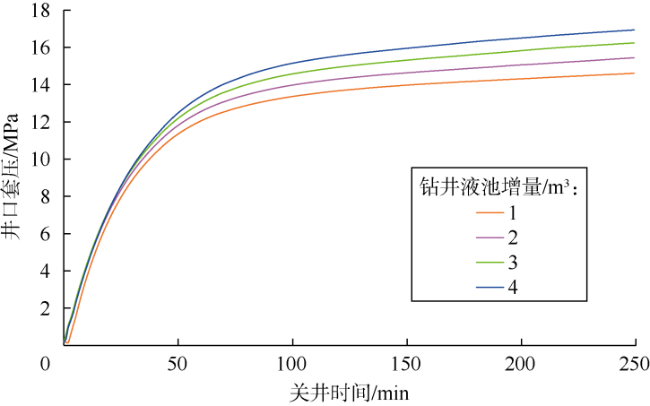
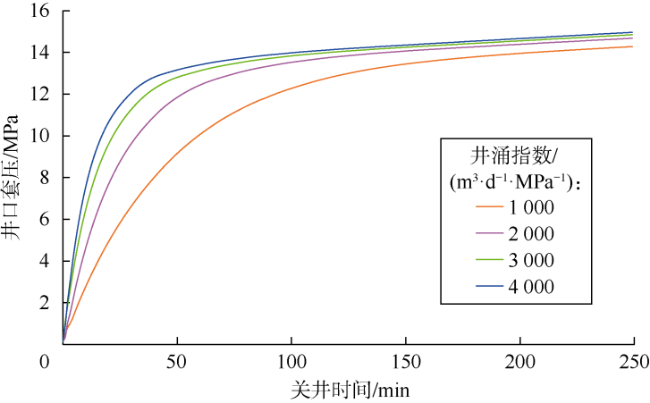
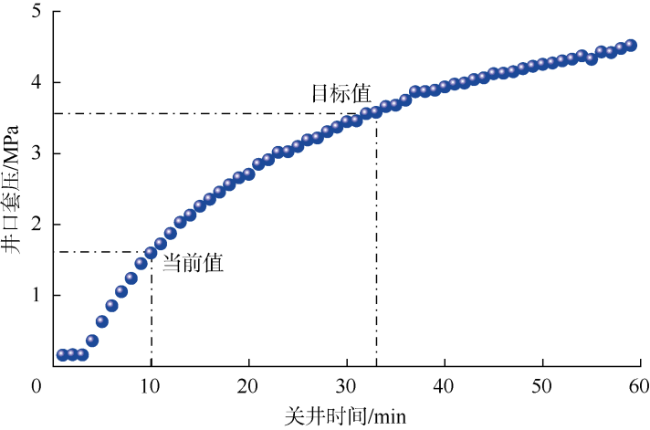
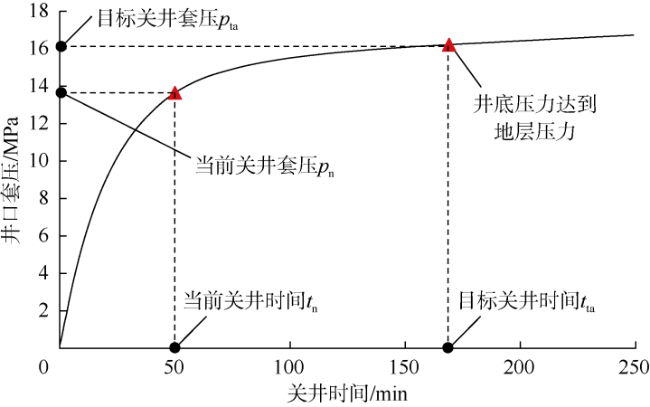
实际钻井过程中，钻井液池增量超过1 m3时需立即关井以控制井涌，并通过关井压力求取地层压力，然后根据地层压力的大小实施压井或其他井控措施[10]。传统关井求压方法一般认为气侵关井10~15 min后井底压力与地层压力相等，该阶段立压或套压趋于平稳或近似直线上升，此时小排量开泵直至开启钻杆浮阀，依据U型管原理读取井口立压或套压，然后根据井口压力和静液柱压力计算地层压力[11]。因此，准确判断井底压力上升至与地层压力相等的时间是关井求压的重要依据。诸多学者对关井后井筒压力的计算进行了研究，刘凯等[12]考虑井筒续流作用建立了溢流和关井压力计算模型；Leblanc等[13]同时考虑井筒续流作用和气体滑脱上升作用建立了关井压力计算模型；Zheng等[14]比较了9种温度-压力耦合算法，建立了关井条件下的非稳态温压耦合模型，分析了气水比、传热系数等因素的影响规律；Zhu等[15]基于多相流动模型，考虑地层渗透率、井底压差、钻井液流变性等因素，建立了关井气体侵入速率模型和气体运移模型；Zhang等[16]建立了关井条件下受悬浮气体影响的井筒压力计算方法；Xu等[17]耦合温度场和压力场，建立了高温高压斜井关井温压耦合模型；任美鹏等[18]基于渗流理论和多相流理论，建立了气侵后关井压力计算模型，并提出立管压力读取方法；田冷等[19]结合试井解释理论，建立了低渗透油藏生产井关井测压时间的压力计算方法；Maki[20]考虑静水压力损失，建立了由关井井口压力反推井底压力的计算方法。以上研究聚焦于考虑续流作用、气体运移膨胀效应、井筒内气体分布并耦合井筒温度场以求解关井井筒压力，但其与地层耦合机制主要采用静态渗透率和固定地层压力的简化假设，难以表征复杂地层的动态变化，存在一定局限性。此外，瞬时关井[21]、压力恢复异常[22]、注水井关井[23]等特定工况下的关井压力计算和关井求压方法研究虽有一定进展，但与复杂地层条件的耦合仍存在不足。尤其在深水裂缝性地层的高温高压井中，裂缝内气体流动为非达西流动，且裂缝由于应力敏感发生变形从而对关井续流阶段的压力恢复和流体流动行为产生影响[24]；同时，地层高温高压影响关井井筒内流体物性，温度场、压力场和渗流场相互耦合作用，现有模型无法准确计算其关井井筒压力，沿用传统关井求压方法容易造成二次事故。
因此，本文在现有关井压力计算模型的基础上考虑深水高温高压对钻井液密度的影响和地层裂缝变形对续流作用的影响，建立考虑热流固耦合作用的裂缝性地层高温高压井关井压力计算模型，分析地温梯度、井底压差、钻井液池增量和井涌指数对井筒压力的影响规律，并基于建立的耦合模型构建关井求压图版，形成深水裂缝性地层高温高压井关井求压方法，为保障裂缝性地层高温高压井井控安全提供了理论支撑。

1 考虑热流固耦合作用的关井井筒压力计算模型

深水裂缝性地层高温高压井关井过程中，在井底压差的作用下，裂缝内气体侵入井筒，导致裂缝内孔隙压力降低，有效应力增大，裂缝被压缩而发生闭合；裂缝闭合会挤压内部气体，使得孔隙压力有所回升，为气体持续侵入提供驱动力。在此过程中，深水低温和地层高温形成的大温度梯度会加速气体运移膨胀和钻井液热膨胀作用，两者协同使得井筒压力逐渐上升；随着井筒压力上升，井筒和地层之间的压差逐渐减小，从而反向抑制气体侵入。因此，深水裂缝性地层高温高压井关井时，受热传递（温度场）、气体运移（渗流场）、裂缝变形（应力场）的动态耦合作用，其井筒压力变化规律与常规井有明显不同。

1.1 关井井筒-地层热流固耦合作用机理

1.1.1 裂缝变形模型

由于裂缝性地层存在应力敏感性，气侵过程中裂缝闭合量动态变化[25]，且对关井过程中续流作用下的气侵速率和井筒压力有一定影响。地层中裂缝的应力状态会影响裂缝的闭合状态，二维裂缝主要受垂向和水平方向的外部力和内部孔隙压力的作用，外部作用力和内部作用力的平衡共同维持裂缝的稳定性[26]。本文为了简化模型，假设地层裂缝为单条径向二维裂缝。在地层稳定状态下，裂缝满足有效应力定理，考虑裂缝夹角的裂缝有效应力为：
${{\sigma }_{\text{f}}}=\left( 1-\frac{1-2\nu }{1-\nu }{{\sin }^{2}}\theta \right)\left( {{\rho }_{\text{ov}}}gh-{{p}_{\text{f}}} \right)$
裂缝中的气体侵入井筒，裂缝孔隙压力减小，其应力平衡被打破，裂缝会出现闭合现象，此时裂缝上下表面的间距逐渐减小。依据赫兹弹性理论[27]，裂缝有效应力与闭合量之间的关系为：
${{\sigma }_{\text{f}}}=\frac{2}{3}{{a}_{\text{d}}}\psi \frac{E}{\left( 1-{{\nu }^{2}} \right)}{{R}^{\frac{1}{2}}}\int_{{{b}_{0}}-\delta }^{\infty }{{{\left( m-{{b}_{0}}+\delta \right)}^{\frac{3}{2}}}}\varphi (m)\text{d}m$
依据Greenwood & Williamson（G & W）模型，裂缝表面微凸体的高度分布符合正态分布[28]：
$\varphi (m)=\frac{1}{\sqrt{2\pi }\xi }{{\text{e}}^{-\frac{{{\left( z-\eta \right)}^{2}}}{2{{\xi }^{2}}}}}$
将上式代入（2）可得：
${{\sigma }_{\text{f}}}=\frac{2}{3}{{a}_{\text{d}}}\psi \frac{E}{\left( 1-{{\nu }^{2}} \right)}{{R}^{\frac{1}{2}}}{{\int_{{{b}_{0}}-\delta }^{\infty }{\left( m-{{b}_{0}}+\delta \right)}}^{\frac{3}{2}}}\frac{1}{\sqrt{2\pi }\xi }{{\text{e}}^{-\frac{{{\left( m-\eta \right)}^{2}}}{2{{\xi }^{2}}}}}\text{d}m$

1.1.2 考虑裂缝变形的气体流动模型

钻井过程中裂缝被激活，关井初期裂缝内流体侵入井筒，以往研究将裂缝内流动等效为达西流动，与实际裂缝内流体流动有一定偏差[29]。因此，本文假设裂缝内流体流动为非达西流动，裂缝内流体为单相气体（天然气），裂缝外边界连接气藏。
根据质量守恒定律可知气体流动连续性方程为：
$\frac{1}{L}\frac{\partial \left( L{{\rho }_{\text{g}}}{{v}_{\text{g}}} \right)}{\partial L}+\frac{\partial {{\rho }_{\text{g}}}}{\partial t}=0$
Forchheimer公式的运动方程为[30]：
$\frac{\partial {{p}_{\text{f}}}}{\partial L}=-\frac{\mu }{K}{{v}_{\text{g}}}-\beta \rho {{v}_{\text{g}}}^{2}$
其中，Forchheimer系数采用经验公式获取[31]：
$\beta =\frac{8.594\times {{10}^{10}}}{{{\left( {{10}^{-15}}K \right)}^{1.1045}}}$
将裂缝变形模型（（3）式）和裂缝内气体流动模型（（4）—（5）式）联立，进行耦合求解。初始时刻裂缝内压力处处相等，裂缝内、外边界分别为井底和气藏，确立边界条件为：
$\left\{ \begin{array}{*{35}{l}} {{p}_{\text{f}}}(t,0)={{p}_{\text{w}}} \\ {{p}_{\text{f}}}(t,{{L}_{\text{m}}})={{p}_{\text{r}}} \\\end{array} \right.$
利用求解得到的气体流动速度计算地层气体侵入井筒流量[32]：
$Q(t)=2\pi {{r}_{\text{w}}}{{v}_{0}}(t){{b}_{\text{h}}}(t)$

1.1.3 关井温度场模型

深水高温高压井发生气侵后关井，关井期间井内流体处于静止状态，虽然无流体流动引发的摩擦生热，但井内流体与周围海水、地层之间存在热量传递[33]。假设关井初始温度场为钻井循环稳定时的温度场，钻杆温度等于环空温度，忽略水泥环和套管在热量传递过程中的热损失，考虑井壁在热量传递过程中的热损失，建立关井后节流管线段井筒温度场模型（见（8）式）、地层段井筒环空温度场模型（见（9）式）和环境温度模型（见（10）式），其中海水温度计算见参考文献[34]。
$\frac{{{T}_{\text{a}}}-{{T}_{\text{sea}}}}{\frac{\ln \left( {{r}_{\text{ro}}}/{{r}_{\text{ri}}} \right)}{2{{k}_{\text{l}}}}+\frac{1}{{{h}_{\text{so}}}{{r}_{\text{ro}}}}}={{\rho }_{\text{l}}}{{c}_{\text{l}}}r_{\text{ri}}^{2}\frac{\partial {{T}_{\text{a}}}}{\partial t}$
$\frac{2{{k}_{\text{s}}}{{h}_{\text{wa}}}{{r}_{\text{w}}}\left( {{T}_{\text{s}}}-{{T}_{\text{a}}} \right)}{{{f}_{\text{D}}}{{h}_{\text{wa}}}{{r}_{\text{w}}}+{{k}_{\text{s}}}}={{\rho }_{\text{l}}}{{c}_{\text{l}}}\left( r_{\text{w}}^{2}-r_{\text{p}}^{2} \right)\frac{\partial {{T}_{\text{a}}}}{\partial t}$
根据Hasan & Kabir公式得到无因次参数为：
$\left\{ \begin{array}{*{35}{l}} {{f}_{\text{D}}}(t)=1.281\sqrt{{{t}_{\text{D}}}}\left( 1-0.3\sqrt{{{t}_{\text{D}}}} \right)\quad \,1\times {{10}^{-10}}\le {{t}_{\text{D}}}\le 1.5 \\ {{f}_{\text{D}}}(t)=\left( 0.4063+0.5\ln {{t}_{\text{D}}} \right)\left( 1+\frac{0.6}{{{t}_{\text{D}}}} \right)\quad \,{{t}_{\text{D}}}1.5 \\\end{array} \right.$
其中 ${{t}_{\text{D}}}=\frac{{{k}_{\text{s}}}}{{{\rho }_{\text{s}}}{{c}_{\text{s}}}}\frac{t}{r_{\text{w}}^{2}}$
$\frac{\partial {{T}_{\text{s}}}}{\partial t}={{\alpha }_{\text{s}}}\left( \frac{{{\partial }^{2}}{{T}_{\text{s}}}}{\partial {{r}^{2}}}+\frac{1}{r}\frac{\partial {{T}_{\text{s}}}}{\partial r}+\frac{{{\partial }^{2}}{{T}_{\text{s}}}}{\partial {{z}^{2}}} \right)$
其中 ${{\alpha }_{\text{s}}}=\frac{{{k}_{\text{s}}}}{{{\rho }_{\text{s}}}{{c}_{\text{s}}}}$

1.1.4 不同温压下钻井液密度计算模型

在深水高温高压井中，井筒内钻井液密度直接影响井眼内静液柱压力的准确计算[35]。通常利用复合模型（机理模型）和经验模型（数据驱动模型）模拟钻井液密度在不同温压条件下的变化规律，复合模型考虑钻井液中各组分性能随温度和压力变化的特征，需精确获取多组分物性参数并求解多变量耦合方程，适用于新型钻井液研发；而经验模型直接通过实验测量目标钻井液在不同温压下的密度数据，拟合温压与密度的映射关系，无需解析组分特性或复杂方程，且精度在可接受范围内[36⇓⇓-39]。在深水钻井过程中通常使用水基钻井液，因此选择水基钻井液密度经验模型计算不同温度和压力下的钻井液密度[40]：
$\begin{align} & {{\rho }_{\text{l}}}\left( p,T \right)={{\rho }_{\text{li}}}\left( p,T \right)\exp \left( -2.678\times {{10}^{-6}}{{T}^{2}}-1.78\times {{10}^{-4}}T+ \right. \\ & \left. 4.92\times {{10}^{-4}}p+2.257\times {{10}^{-7}}pT+1.36\times {{10}^{-3}} \right) \\ \end{align}$

1.2 关井井筒压力计算模型

负压差气侵关井期间，在续流效应、气体运移膨胀效应和钻井液漏失效应的共同作用下，井筒内压力会发生变化[41]。由于地层裂缝在应力变化下发生闭合，钻井液漏失量相对较小，因此本文忽略钻井液漏失的影响。综合考虑环境温压对钻井液密度的影响和地层裂缝变形对续流期间气体侵入的影响，建立深水裂缝性地层高温高压井关井井筒压力计算模型。

1.2.1 续流作用

在关井初期，井底压力小于地层压力，地层气体在压差作用下侵入井筒，井筒内原有流体被压缩，井筒容积膨胀，井筒内压力升高。在高温高压井中，钻井液密度随温度和压力的变化也会影响井筒内静液柱压力的大小。当井底压力接近地层压力时，气体停止侵入。考虑井筒容积膨胀、井内流体的可压缩性和膨胀性，由质量守恒定律可得侵入井筒的气体体积为：
${{V}_{\text{gs}}}={{V}_{\text{g}}}{{C}_{\text{g}}}\Delta {{p}_{\text{w}}}+{{V}_{\text{l}}}{{C}_{\text{l}}}\Delta {{p}_{\text{w}}}+{{V}_{\text{o}}}{{C}_{\text{o}}}\Delta {{p}_{\text{w}}}$
其中 $\begin{align} & {{V}_{\text{gs}}}=\int_{0}^{t}{Q\left( t \right)\text{d}t} \\ & {{V}_{\text{l}}}={{V}_{\text{o}}}-{{V}_{\text{g}}} \\ \end{align}$
如图1所示，在续流效应的作用下，井筒内气体含量增大并逐渐形成气柱，根据井筒内气液分布可分为气液混合段和液体段。气体尾部压力为：
${{p}_{\text{t}}}={{p}_{\text{w}}}$
图1 关井续流作用示意图（蓝色箭头表示气体从地层侵入井筒，黑色箭头表示气体在井筒中运移）
气体前缘压力为：
${{p}_{\text{e}}}={{p}_{\text{w}}}-\left[ {{\rho }_{\text{g}}}{{E}_{\text{g}}}+\left( 1-{{E}_{\text{g}}} \right){{\rho }_{\text{l}}} \right]g{{H}_{\text{i}}}$
液体段特定深度处压力为：
${{p}_{\text{o}}}={{p}_{\text{e}}}-{{\rho }_{\text{l}}}g\left( z-{{H}_{\text{i}}} \right)$

1.2.2 气体运移膨胀

由于侵入井筒的气体密度小于钻井液，依据重力分离原理，气体会发生滑脱逐渐向上运移。运移过程中，气体受到温度和压力的影响，体积发生膨胀，导致井筒内压力升高。考虑井筒容积膨胀、井内流体的可压缩性和膨胀性，由质量守恒定律可得气体膨胀增加的体积为：
$\Delta {{V}_{\text{g}}}={{V}_{\text{l}}}{{C}_{\text{l}}}\Delta {{p}_{\text{w}}}+{{V}_{\text{o}}}{{C}_{\text{o}}}\Delta {{p}_{\text{w}}}-\Delta {{V}_{\text{l}}}$
其中 $\Delta {{V}_{\text{l}}}=\frac{{{\rho }_{\text{lb}}}{{V}_{\text{l}}}}{{{\rho }_{\text{l}}}\left( p,T \right)}-{{V}_{\text{l}}}$
如图2所示，随着气体的运移，其在井筒中的分布也会发生变化，依据单位时间内气体位置的变化可知：
$\left\{ \begin{array}{*{35}{l}} {{H}_{\text{tb}}}={{v}_{1}}\Delta t \\ {{H}_{\text{eb}}}={{v}_{2}}\Delta t+{{H}_{\text{i}}} \\ {{H}_{n}}={{H}_{\text{eb}}}-{{H}_{\text{tb}}} \\ \end{array} \right.$
图2 关井后气体运移膨胀示意图
根据气体在井筒中的分布计算相应位置处的井筒压力，气体尾部压力为：
${{p}_{\text{t}}}={{p}_{\text{w}}}-{{\rho }_{\text{l}}}g{{H}_{\text{tb}}}$
气体前缘压力为：
${{p}_{\text{e}}}={{p}_{\text{t}}}-\left[ {{\rho }_{\text{g}}}{{E}_{\text{g}}}+\left( 1-{{E}_{\text{g}}} \right){{\rho }_{\text{l}}} \right]g{{H}_{\text{n}}}$
液体段特定深度处压力为：
${{p}_{\text{o}}}={{p}_{\text{e}}}-{{\rho }_{\text{l}}}g\left( z-{{H}_{\text{eb}}} \right)$

2 考虑热流固耦合作用的关井井筒压力计算模型求解

2.1 求解方法

本文构建的关井井筒压力计算模型具有强非线性，采用数值方法进行迭代求解[42⇓-44]。初始时刻参数包括关井前裂缝孔隙压力、钻井液密度、井筒温度和井筒压力，具体计算步骤如下。
①根据实测裂缝孔隙压力pf计算裂缝有效应力σf，从而计算裂缝闭合量，结合裂缝内气体流动模型得到裂缝内气体流动速度vg，求取单位时间步长内的气侵量Vgs,ts；②估算井底压力pw1，计算井筒内气体压缩体积、液体压缩体积和井筒膨胀体积，三者相加得到总体积变化量$\Delta {{V}_{1,ts}}$；③判断$\left| \Delta {{V}_{\text{1},\text{ts}}}-{{V}_{\text{gs},\text{ts}}} \right|$是否小于1×10−6 m3，如果满足则进入下一步，不满足则返回步骤②，重新估算井底压力；④判断$\left| {{p}_{\text{w1}}}-{{p}_{\text{f}}} \right|$是否小于1× 10−5 MPa，如果满足则续流作用阶段结束，进入下一步，如果不满足则返回步骤①计算下一单位时间步长内的气侵量；⑤气体运移膨胀阶段初始时刻以续流作用阶段结束值（井底压力和侵入井筒的气体体积）为初值，计算续流结束时气液混合段高度Hi；⑥根据气体上升速度计算后续时刻气体尾部上升高度Htb、气体前缘上升高度Heb和气液混合段高度Hn；⑦估算井底压力pw2，利用气体状态方程获得气体运移膨胀阶段的气体体积，根据上一阶段的气体体积计算单位时间步长内气体膨胀体积ΔVg,ts。计算钻井液压缩体积、井筒膨胀体积、钻井液受热膨胀体积，三者相加得到总体积变化量$\Delta {{V}_{2,ts}}$；⑧判断$\left| \Delta {{V}_{2,\text{ts}}}-\Delta {{V}_{\text{g},\text{ts}}} \right|$是否小于1×10−6 m3，如果满足则进入下一步，不满足则返回步骤⑦，重新估算井底压力；⑨判断气体前缘上升高度Heb是否到达井深深度，如果是，则计算下一步，如果不是则返回步骤⑥进行下一时间步长计算；⑩由井底压力pw2计算整个井筒压力分布。

2.2 模型验证与计算

X-1井是中国南海珠江口盆地白云凹陷一口深水深层井，该地区深部地层发育断裂，且具有地温梯度高、裂缝孔隙压力大的特征。利用该井数据对本文关井井筒压力计算模型进行验证，基础参数如表1所示。
表1 X-1井基础参数
参数 参数值 参数 参数值
水深 1 000 m 钻井液密度 1 350 kg/m3
井深 7 800 m 地层压力 113 MPa
裸眼井筒半径 0.153 m 井口温度 20 ℃
钻井液黏度 20 mPa·s 地温梯度 3.5 ℃/100 m

2.2.1 模型验证

如图3所示，关井期间井底压力随时间呈上升趋势，在一定时间内恢复至地层压力。考虑热流固耦合作用时，井底压力曲线恢复最快，表明温度、流体流动和裂缝变形的多场耦合作用显著加快了井底压力恢复；仅考虑裂缝变形时，关井初期裂缝逐渐闭合导致井底压力急剧上升，后期由于裂缝稳定而缓慢上升；仅考虑温压耦合作用时，井底压力整体上升更为平缓。
图3 关井期间井底压力随关井时间变化曲线
如图4所示，井口套压的变化趋势与井底压力几乎相同，曲线整体较为平滑，呈上升趋势，无明显拐点。另外，考虑热流固耦合作用的压力模型计算结果与实际数据的吻合率达到95%以上，有良好的一致性。
图4 关井期间井口套压随关井时间变化曲线

2.2.2 计算结果分析

不同初始井底压差条件下气体侵入流量随时间的变化曲线如图5所示，与不考虑裂缝变形相比，在相同时间和压差条件下，考虑裂缝变形的气侵速率更快，气侵量更大。同一压差条件下，裂缝内孔隙压力随气体侵入时间而下降，裂缝受到的有效应力变大并逐渐闭合，裂缝内气体侵入井筒的速率大幅减小；但随着裂缝内气体被压缩，孔隙压力逐渐恢复，气体侵入速率的减小幅度降低。另外，初始井底压差越大，初始气体侵入速率越大，相同时间内气体侵入流量下降速率越快。实际施工过程中初始井底压差较大时，可以通过提高井筒液柱压力减缓地层气体侵入，防止气侵量过大导致的井控问题。
图5 不同初始井底压差下气体侵入流量随时间变化曲线
气体侵入井筒后在井筒内滑脱运移，图6为不同关井时间下井筒内自由气相含气率变化曲线。关井初期（0~40 min），自由气含气率曲线在井筒底部存在“波峰”，这是因为关井初期地层气体在井底压差的作用下由井底地层侵入井筒，导致井底含气率不断升高。随着关井时间的增加，自由气在井筒内持续上升，井底附近的含气率逐渐下降。
图6 不同关井时间条件下井筒自由气含气率分布（对应时间内4 000 m以浅自由气含气率为0）
不同关井时间条件下井筒环空温度和环境温度变化如图7所示。在钻井循环过程中，海水段节流管线内的流体温度整体高于海水温度；发生气侵关井后，由于井筒内流体与海水之间发生热交换，节流管线内流体温度逐渐降低，紧邻节流管线的海水温度逐渐升高，关井10 min后两者趋于相等（见图7a）。循环结束后地层段井筒环空内流体温度与地层温度之间差距较大；随着气侵关井时间延长，地层高温气体持续侵入井筒，且井筒环空内流体与地层之间发生热交换，导致井筒环空温度逐渐升高，紧邻井筒附近的地层温度逐渐降低，关井40 min后两者趋于相等（见图7b）。
图7 不同关井时间下井筒环空温度和环境温度剖面
以表1中常温常压下钻井液密度为初始密度，计算不同温度（4~220 ℃）和压力（10~120 MPa）条件下的钻井液密度（见图8），在相同温度下，压力增大时钻井液密度增大，反映了其压缩性；在相同压力下，温度升高时钻井液密度减小，反映其热膨胀性。钻井液压缩性和热膨胀性受温度和压力的影响而发生变化[45]，随着压力升高，钻井液压缩性和热膨胀性均变化较小；而温度升高时，钻井液压缩性变化较小，热膨胀性增强。故随着温度和压力的同时升高，尤其是温度变化范围较大时，钻井液热膨胀效应比压缩效应更为显著。因此，深水高温高压井关井时，钻井液热膨胀作用对井筒压力的影响更大。
图8 不同温度和压力下的钻井液密度
在实际钻井过程中，将井口套压视为井口安全的重要指标。因此，本文计算了不同地温梯度、井底压差、钻井液池增量、井涌指数下的井口套压并分析其变化规律。井底压差（6 MPa）、钻井液池增量（1.6 m3）、井涌指数（2 000 m3/（d·MPa））恒定，相同关井时间内，地温梯度越大，井口套压越高（见图9）；这是因为地层温度越高，井筒温度越高，钻井液热膨胀和气体膨胀作用越明显，导致井口套压更高。
图9 不同地温梯度下的井口套压变化曲线
地温梯度（3 ℃/100 m）、钻井液池增量（1.6 m3）、井涌指数（2 000 m3/（d·MPa））恒定，相同关井时间内，井底压差越大，井口套压越高（见图10）；归因于井底压差越大，地层气体侵入井筒速率越快，侵入量越多，气体膨胀作用越明显，导致井口套压越高。
图10 不同井底压差下的井口套压变化曲线
地温梯度（3 ℃/100 m）、井底压差（6 MPa）、井涌指数（2 000 m3/（d·MPa））恒定，关井相同时间内钻井液池增量越大，井口套压越高（见图11）；钻井液池增量由地层气体侵入造成，钻井液池增量越大说明地层气体侵入量越大，气体膨胀作用越明显，导致井口套压越高。
图11 不同钻井液池增量下的井口套压变化曲线
本文采用井涌指数表征钻井过程中单位压力、单位时间条件下的气体侵入量。井涌指数可以通过邻井数据获取，或根据钻井液池增量和所钻地层渗透率、储层厚度等参数计算得到。地温梯度（3 ℃/100 m）、井底压差（6 MPa）、钻井液池增量（1.6 m3）恒定，相同关井时间内，井涌指数越大，井口套压上升越快，归因于井涌指数越大地层气体侵入速率越快（见图12）；由于计算条件中不同井涌指数下的钻井液池增量相同，则气体总侵入量相同，因此对应的最大套压几乎相同。
图12 不同井涌指数下的井口套压变化曲线

3 考虑热流固耦合作用的高温高压井关井求压方法

3.1 关井求压图版

3.1.1 参数定义

根据考虑热流固耦合作用的关井井筒压力计算模型，可以预测不同参数条件下的井口套压和关井时间。通过定义井口套压比（见（21）式）和关井时间比（见（22）式），可以依据当前的井口套压和关井时间反推目标井口套压和时间（井底压力上升至与地层压力相等时的井口套压为目标井口套压，对应关井时间为目标关井时间），如图13所示。
${{R}_{\text{p}}}=\frac{{{p}_{\text{n}}}}{{{p}_{\text{ta}}}}\times 100%$
${{R}_{\text{t}}}=\frac{{{t}_{\text{n}}}}{{{t}_{ta}}}\times 100%$
图13 井口套压比和关井时间比参数定义示意图

3.1.2 因素相关性分析

在相同关井时间（10 min）条件下，计算了不同地温梯度、井底压差、钻井液池增量和井涌指数下的井口套压比和关井时间比（见图14），此时地层压力取X-1井地层压力。
图14 不同参数对井口套压比和关井时间比的影响
由图可知，各参数对井口套压比和关井时间比的影响存在差异：①地温梯度主要影响井筒内气体运移膨胀和钻井液热膨胀作用，当超过临界值（5 ℃/100 m）时，气体运移膨胀和钻井液热膨胀的叠加效应急剧加强，井筒压力短时间内快速上升，导致井口套压比和关井时间比均明显增大；②虽然井底压差直接影响气体侵入速率和侵入量，但由于目标关井套压升高和目标关井时间变长，井口套压比和关井时间比变化不明显；③钻井液池增量越大，说明关井前侵入井筒的气体越多，在井筒内更容易形成气柱，减缓了关井压力波的传递，导致井口套压上升有滞后性，从而使得井口套压比和关井时间比降低；④井涌指数越大，气侵速率越快，侵入量越大，气体运移膨胀作用越强，井口套压上升越快，因此井口套压比和关井时间比均表现为上升趋势。综上，关井时间相同的情况下，钻井液池增量、地温梯度和井涌指数3个参数对井口套压比和关井时间比的影响较大，而井底压差的影响较小。

3.1.3 关井求压图版

基于因素相关性分析，选择钻井液池增量、地温梯度和井涌指数3个参数构建关井求压图版，即任意选择1个参数恒定，建立另外两个参数与井口套压比和关井时间比的关系图。以地温梯度恒定为3 ℃/100 m为例，关井时间为10 min时在相同钻井液池增量条件下，井涌指数越大，井口套压比和关井时间比越大（见图15和图16），这是由于井涌指数越大，地层气体侵入速率越快，侵入量越大，导致井筒压力相同时间内上升更快，即井口套压比和关井时间比越大。因此，在已知井涌指数和钻井液池增量的条件下，可根据图版查找对应的井口套压比和关井时间比。如井涌指数为4 000 m3/（d·MPa）、钻井液池增量为1 m3时，查图版可知井口套压比为72%，关井时间比为43%，由此可推算出目标井口套压和目标关井时间。现场技术人员可以通过关井至目标关井时间，小排量开泵顶开钻杆浮阀，读取立压，计算其与静液柱压力之和即为地层压力；考虑关井时间过长容易发生二次事故，套压与立压由于U型管效应相差较小，也可以将目标井口套压作为立压，计算得到地层压力。
图15 不同井涌指数和钻井液池增量下的井口套压比
图16 不同井涌指数和钻井液池增量下的关井时间比
基于本文建立的关井井筒压力计算模型，结合井口套压比和关井时间比，可以绘制不同关井时间、不同参数组合及不同参数范围下的求压图版。

3.2 案例验证

X-2井位于中国南海珠江口盆地白云凹陷，该井钻进至4 383 m时发生溢流，随即关井。采用X-2井实际关井井口套压数据验证关井求压图版，该井的基础参数如表2所示。
表2 X-2井基础参数
参数 参数值 参数 参数值
水深 814.8 m 当前关井时间 10 min
设计井深 5 129 m 当前井口套压 1.59 MPa
井涌指数 2 000 m3/(d·MPa) 钻井液池增量 1 m3
地温梯度 3 ℃/100 m 地层压力 55 MPa
如图17所示，X-2井关井期间井口套压呈上升趋势。实测数据显示，关井33 min时该井井底压力上升至与地层压力相等，此时对应的井口套压为3.58 MPa，但由于钻井液热膨胀和气体运移膨胀的叠加作用，井筒压力持续升高。伴随气体逐渐向井口运移，井筒温度场趋于稳定，压力增长速率缓慢减小。整个关井过程中井口套压变化曲线未出现明显拐点，导致传统关井求压方法不适用。X-2井井涌指数为2 000 m3/（d·MPa）、钻井液池增量为1 m3时，由本文求压图版可知井口套压比为45.2%、关井时间比为29.5%，根据当前井口套压1.59 MPa、当前关井时间10 min，可推算目标井口套压为3.52 MPa、目标关井时间为33.9 min。
图17 X-2井关井期间井口套压实测数据
将图版反推结果与实际测量值进行对比可知，利用本文建立的关井求压图版预测的目标井口套压准确率为97.2%，目标关井时间准确率为98.3%，误差均在可接受范围内，证明该图版能够为高温高压井关井求压提供支持，保障高温高压井井控安全。

4 结论

综合考虑裂缝内气体非达西流动、裂缝变形和钻井液热膨胀效应，建立了深水裂缝性地层高温高压井关井井筒压力计算模型。关井井筒压力计算模型结果与X-1井关井期间井口套压实测数据的吻合率达95%以上。关井初期较短时间内，裂缝变形显著促进地层气体侵入，使得气侵速率更快，气侵量更大；深水高温高压井关井期间，节流管线内流体温度逐渐降低，地层段井筒环空温度逐渐升高；随着压力升高，钻井液压缩性和热膨胀性均变化较小，而温度升高时，钻井液压缩性变化较小，热膨胀性增强，表明在高温高压且温度变化范围较大的情况下，钻井液的热膨胀效应更为显著，从而影响井筒压力。地温梯度增大加剧了钻井液热膨胀和气体膨胀，使井口套压升高；井底压差增加会加速气体侵入，导致套压上升；钻井液池增量直接反映气体总侵入量，与套压呈正相关关系；井涌指数越大压力攀升越快，但最大套压由总侵入量决定而保持稳定。
基于因素相关性分析结果，选择钻井液池增量、地温梯度和井涌指数3个参数构建关井求压图版，关井求压图版对X-2井关井期间井口套压预测准确率为97.2%、关井时间预测准确率为98.3%。采用本文关井求压方法能够在高温高压井关井后准确求取地层压力，为后续井控措施提供依据，保证深水深层油气安全高效开发。
符号注释：
ad——微凸体密度，mm−2；bh(t)——t时刻裂缝水力等效开度，m；b0——裂缝初始开度，mm；cl，cs——钻井液、地层岩石的比热容，J/（kg·K）；Cg，Cl，Co——气体、钻井液和井筒压缩系数，MPa−1；E——岩石弹性模量，Pa；Eg——气液混合段截面含气率，无因次；g——重力加速度，m/s2；h——深度，m；hso——海水与节流管外表面之间的换热系数，W/（m2·K）；hwa——井壁与环空之间的换热系数，W/（m2·K）；Heb——气体前缘距井底高度，m；Hi——续流阶段气液混合段高度，m；Hn——气体运移阶段气液混合段的高度，m；Htb——气体尾部距井底高度，m；kl——节流管线导热系数，W/（m·K）；ks——地层导热系数，W/（m·K）；K——裂缝等效渗透率，m2；L——裂缝径向长度，m；Lm——裂缝最大径向长度，m；m——裂缝接触面上的微凸体高度，mm；p——压力，Pa；pe——气体前缘压力，Pa；pf——裂缝内流体压力，Pa；pn——当前关井套压，Pa；po——液体段压力，Pa；pr——气藏压力，Pa；pt——气体尾部压力，Pa；pta——目标关井套压，Pa；pw——井底压力，Pa；Q(t)——气体侵入井筒流量，m3/s；r——距离井壁的径向距离，m；rp——钻杆外径，m；rri——节流管内径，m；rro——节流管外径，m；rw——井筒半径，m；R——微凸体期望半径，mm；Rp——井口套压比，%；Rt——关井时间比，%；t——关井时间，s；Δt——单位时间步，s；tn——当前关井时间，min；tta——目标关井时间，min；T——温度，℃；Ta——井筒环空温度，K；Ts——地层温度，K；Tsea——海水温度，K；vg——裂缝内气体流动速度，m/s；v0(t)——t时刻井壁处气体流速，m/s；v1——气体尾部上升速度，m/s；v2——气体前缘上升速度，m/s；Vg——关井前侵入井筒气体体积，m3；ΔVg——气体膨胀增加的体积，m3；Vgs——关井后侵入井筒气体体积，m3；Vl——井筒内钻井液体积，m3；ΔVl——钻井液受热膨胀增加的体积，m3；Vo——井筒容积，m3；ΔV1——井筒内气体压缩体积、液体压缩体积和井筒膨胀体积相加的总体积变化量，m3；ΔV2——钻井液压缩体积、井筒膨胀体积、钻井液受热膨胀体积相加的总体积变化量，m3；z——井深，m；αs——地层热扩散系数，m2/s；β——Forchheimer系数，m−1；δ——裂缝闭合量，mm；η——微凸体高度期望值，mm；θ——裂缝倾角，（°）；μ——天然气黏度，Pa·s；υ——岩石泊松比，无因次；ξ——微凸体高度分布标准差，mm；ρg——气体密度，kg/m3；ρl——钻井液密度，kg/m3；ρlb——关井前的钻井液密度，kg/m3；ρli——常温常压下钻井液密度，kg/m3；ρov——上覆岩层密度，kg/m3；ρs——地层岩石密度，kg/m3；φ(m)——裂缝面微凸体高度分布函数，mm−1；σf——裂缝有效应力，Pa；ψ——剪切应力校正因子，无因次。下标：ts——单位时间步长。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
温志新, 王建君, 王兆明, 等. 世界深水油气勘探形势分析与思考[J]. 石油勘探与开发, 2023, 50(5): 924-936.

DOI

WEN Zhixin, WANG Jianjun, WANG Zhaoming, et al. Analysis of the world deepwater oil and gas exploration situation[J]. Petroleum Exploration and Development, 2023, 50(5): 924-936.

[2]
王作乾, 范喆, 陈希, 等. 2023年度全球油气开发现状、形势及启示[J]. 石油勘探与开发, 2024, 51(6): 1331-1346.

DOI

WANG Zuoqian, FAN Zhe, CHEN Xi, et al. Global oil and gas development situation, trends and enlightenment in 2023[J]. Petroleum Exploration and Development, 2024, 51(6): 1331-1346.

[3]
KONG Q W, WANG Z Y, PEI J H, et al. An improved high-efficiency anti-agglomerant for avoiding hydrate flow barriers in high water-cut systems: Flowloop investigation and mechanisms[J/OL]. Science China Chemistry, 2024: 1-21(2024-11-04)[2025-02-25]. https://doi.org/10.1007/s11426-024-2371-9.

[4]
杜威, 鹿传世, 李占东, 等. 南海西部深水高温高压固井挑战与实践[J]. 广东化工, 2017, 44(14): 93-94.

DU Wei, LU Chuanshi, LI Zhandong, et al. Deepwater HTHP cementing challenge and practice in southwest China Sea[J]. Guangdong Chemical Industry, 2017, 44(14): 93-94.

[5]
李中, 殷志明, 田得强. 深远海超深水钻井井控风险防控技术研究进展[J]. 钻采工艺, 2024, 47(4): 8-17.

LI Zhong, YIN Zhiming, TIAN Deqiang. Research progress on well control risk management technology for deep sea and ultra-deep water drilling[J]. Drilling & Production Technology, 2024, 47(4): 8-17.

[6]
杨进, 傅超, 刘书杰, 等. 中国深水钻井关键技术与装备现状及展望[J]. 世界石油工业, 2024, 31(4): 69-80.

YANG Jin, FU Chao, LIU Shujie, et al. Current status and prospects of key technologies and equipment for deepwater drilling in China[J]. World Petroleum Industry, 2024, 31(4): 69-80.

[7]
焦阳. 南海深水井控难点分析与应对技术措施[J]. 中国石油和化工标准与质量, 2023, 43(19): 169-171.

JIAO Yang. Analysis of difficulties in deep well control and technical measures[J]. China Petroleum and Chemical Standard and Quality, 2023, 43(19): 169-171.

[8]
张来斌, 谢仁军, 殷启帅. 深水油气开采风险评估及安全控制技术进展与发展建议[J]. 石油钻探技术, 2023, 51(4): 55-65.

ZHANG Laibin, XIE Renjun, YIN Qishuai. Technical progress and development suggestions for risk assessment and safety control of deep-water oil and gas exploitation[J]. Petroleum Drilling Techniques, 2023, 51(4): 55-65.

[9]
罗鸣, 吴江, 陈浩东, 等. 南海西部窄安全密度窗口超高温高压钻井技术[J]. 石油钻探技术, 2019, 47(1): 8-12.

LUO Ming, WU Jiang, CHEN Haodong, et al. Ultra-high temperature high pressure drilling technology for narrow safety density window strata in the western South China[J]. Petroleum Drilling Techniques, 2019, 47(1): 8-12.

[10]
董星亮, 曹式敬, 唐海雄, 等. 海洋钻井手册[M]. 北京: 石油工业出版社, 2011.

DONG Xingliang, CAO Shijing, TANG Haixiong, et al. Offshore drilling manual[M]. Beijing: Petroleum Industry Press, 2011.

[11]
李相方, 庄湘琦. 关井压力恢复和读取时机分析[J]. 石油学报, 2002, 23(5): 110-112.

DOI

LI Xiangfang, ZHUANG Xiangqi. Analysis on the pressure build-up and its recording time after shut-in[J]. Acta Petrolei Sinica, 2002, 23(5): 110-112.

DOI

[12]
刘凯, 郝俊芳. 溢流和关井过程中的数学处理[J]. 石油钻采工艺, 1989, 11(5): 1-8.

LIU Kai, HAO Junfang. Mathematical processing during overflow and well closure processes[J]. Oil Drilling & Production Technology, 1989, 11(5): 1-8.

[13]
LEBLANC J L, LEWIS R L. A mathematical model of a gas kick[J]. Journal of Petroleum Technology, 1968, 20(8): 888-898.

[14]
ZHENG J, LI J H, WANG W X, et al. Establishment and application of temperature-pressure coupling model for opening and closing wells in HTHP gas wells[J]. Energy Exploration & Exploitation, 2024, 42(4): 1359-1385.

[15]
ZHU H F, XIANG M, LIN Z Q, et al. Study on the mechanism of gas intrusion and its transportation in a wellbore under shut-in conditions[J]. Energies, 2024, 17(1): 242.

[16]
ZHANG Z, SUN B J, WANG Z Y, et al. A wellbore pressure calculation method considering gas suspension in wellbore shut-in condition[R]. SPE 205768-MS, 2021.

[17]
XU J, DING C, WU Z, et al. Prediction pressure and temperature in shut-in procedures for HTHP deviated wells[J]. Petroleum Science and Technology, 2013, 31(21): 2258-2271.

[18]
任美鹏, 李相方, 刘书杰, 等. 钻井井喷关井期间井筒压力变化特征[J]. 中国石油大学学报(自然科学版), 2015, 39(3): 113-119.

REN Meipeng, LI Xiangfang, LIU Shujie, et al. Characteristics of wellbore pressure change during shut-in after blowout[J]. Journal of China University of Petroleum (Edition of Natural Science), 2015, 39(3): 113-119.

[19]
田冷, 何顺利, 李秀生, 等. 低渗透油藏生产井关井测压时间的计算与应用[J]. 石油勘探与开发, 2007, 34(2): 226-229.

TIAN Leng, HE Shunli, LI Xiusheng, et al. Calculating method of shut-in time for pressure survey in production wells in low permeability oil reservoirs and its application[J]. Petroleum Exploration and Development, 2007, 34(2): 226-229.

[20]
MAKI S. Prediction of shut-in bottom-hole pressure from wellhead pressure considering transient behaviour of hydrostatic pressure loss during shut-in[R]. IPTC 21241-MS, 2021.

[21]
张智, 王嘉伟, 李炎军, 等. 高产气井瞬时关井对油管内流体流动的影响[J]. 石油勘探与开发, 2020, 47(3): 600-607.

DOI

ZHANG Zhi, WANG Jiawei, LI Yanjun, et al. Effects of instantaneous shut-in of high production gas well on fluid flow in tubing[J]. Petroleum Exploration and Development, 2020, 47(3): 600-607.

[22]
李洋, 柴德民, 罗水发, 等. 压力恢复异常资料试井分析方法[J]. 油气井测试, 2024, 33(5): 1-7.

LI Yang, CHAI Demin, LUO Shuifa, et al. Well test analysis method for abnormal pressure build-up data[J]. Well Testing, 2024, 33(5): 1-7.

[23]
靳心伟, 刘英宪, 赵靖康, 等. 一种利用注水井关井压力曲线计算地层超压值的新方法[J]. 复杂油气藏, 2023, 16(4): 439-443.

JIN Xinwei, LIU Yingxian, ZHAO Jingkang, et al. A new method for calculating formation overpressure value by using shut-in pressure curves of injection wells[J]. Complex Hydrocarbon Reservoirs, 2023, 16(4): 439-443.

[24]
刘森. 碳酸盐岩裂缝性地层溢流侵入机理研究[D]. 成都: 西南石油大学, 2019.

LIU Sen. Study on the mechanism of overflow and intrusion in fractured formations of carbonate rocks[D]. Chengdu: Southwest Petroleum University, 2019.

[25]
夏玫沁. 裂缝闭合规律及其渗流特征研究[D]. 西安: 西安石油大学, 2015.

XIA Meiqin. Research of crack closure law and seepage mechanisms[D]. Xi’an: Xi’an Shiyou University, 2015.

[26]
程汉列, 武博, 郭旭, 等. 不同微观条件下的天然裂缝闭合特征对比分析[J]. 河南理工大学学报(自然科学版), 2017, 36(5): 29-34.

CHENG Hanlie, WU Bo, GUO Xu, et al. Comparative analysis of natural fracture closure characteristics of different reservoir in microscopic conditions[J]. Journal of Henan Polytechnic University (Natural Science), 2017, 36(5): 29-34.

[27]
BROWN S R, SCHOLZ C H. Closure of rock joints[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B5): 4939-4948.

[28]
GREENWOOD J A, TRIPP J H. The elastic contact of rough spheres[J]. Journal of Applied Mechanics, 1967, 34(1): 153-159.

[29]
RANJITH P G, VIETE D R. Applicability of the “cubic law” for non-Darcian fracture flow[J]. Journal of Petroleum Science and Engineering, 2011, 78(2): 321-327.

[30]
FORCHHEIMER P. Wasserbewegung durch boden[J]. Zeitschrift des Vereines Deutscher Ingenieure, 1901, 45(50): 1781-1788.

[31]
FIROOZABADI A, KATZ D L. An analysis of high-velocity gas flow through porous media[J]. Journal of Petroleum Technology, 1979, 31(2): 211-216.

[32]
何世明, 刘森, 赵转玲, 等. 裂缝性地层溢流侵入动态规律研究[J]. 石油钻探技术, 2018, 46(6): 26-32.

HE Shiming, LIU Sen, ZHAO Zhuanling, et al. The dynamic laws of overflow intrusion in fractured formations[J]. Petroleum Drilling Techniques, 2018, 46(6): 26-32.

[33]
曹砚锋, 邹明华, 陈欢, 等. 海上气举井筒温度预测模型及影响因素研究[J]. 北京石油化工学院学报, 2024, 32(2): 31-37.

CAO Yanfeng, ZOU Minghua, CHEN Huan, et al. Research on offshore gas lift wellbore temperature prediction model and influencing factors[J]. Journal of Beijing Institute of Petrochemical Technology, 2024, 32(2): 31-37.

[34]
高永海. 深水油气钻探井筒多相流动与井控的研究[D]. 青岛: 中国石油大学(华东), 2007.

GAO Yonghai. Study on multi-phase flow in wellbore and well control in deep water drilling[D]. Qingdao: China University of Petroleum (East China), 2007.

[35]
管志川. 温度和压力对深水钻井油基钻井液液柱压力的影响[J]. 中国石油大学学报(自然科学版), 2003, 27(4): 48-52.

GUAN Zhichuan. Effect of temperature and pressure on fluid column pressure of wellbore drilling fluid in deep-water drilling with oil-based drilling fluid[J]. Journal of China University of Petroleum (Edition of Natural Science), 2003, 27(4): 48-52.

[36]
张波涛, 刘书杰, 徐一龙. 等. 南海深水大温压域钻井液密度预测新模型[J]. 中国海上油气, 2025, 37(2): 240-246.

ZHANG Botao, LIU Shujie, XU Yilong. et al. New model for predicting density of drilling fluids employed in regions of South China Sea with high temperature and pressure[J]. China Offshore Oil and Gas, 2025, 37(2): 240-246.

[37]
罗宇维, 朱江林, 李东, 等. 温度和压力对井内流体密度的影响[J]. 石油钻探技术, 2012, 40(2): 30-34.

LUO Yuwei, ZHU Jianglin, LI Dong, et al. The impact of temperature & pressure on borehole fluids density[J]. Petroleum Drilling Techniques, 2012, 40(2): 30-34.

[38]
宋洵成, 王振飞, 韦龙贵, 等. 温度压力与钻井液密度相互影响规律研究[J]. 内蒙古石油化工, 2012, 38(5): 1-3.

SONG Xuncheng, WANG Zhenfei, WEI Longgui, et al. Interrelationship between temperature-pressure and drilling fluids density[J]. Inner Mongolia Petrochemical Industry, 2012, 38(5): 1-3.

[39]
汪海阁, 刘岩生, 杨立平. 高温高压井中温度和压力对钻井液密度的影响[J]. 钻采工艺, 2000, 23(1): 56-60.

WANG Haige, LIU Yansheng, YANG Liping. Effect of temperature and pressure on drilling fluid density in HTHP wells[J]. Drilling & Production Technology, 2000, 23(1): 56-60.

[40]
赵向阳, 杨顺辉, 郑德帅. 水基钻井液高温高压密度预测新模型[J]. 科学技术与工程, 2013, 13(15): 4334-4338.

ZHAO Xiangyang, YANG Shunhui, ZHENG Deshuai. A new HPHT density forecast model of water drilling fluid[J]. Science Technology and Engineering, 2013, 13(15): 4334-4338.

[41]
郭艳利. 深水钻井关井气侵机理及井筒压力变化规律研究[D]. 青岛: 中国石油大学(华东), 2018.

GUO Yanli. Study on gas invasion mechanism and wellbore pressure during well shut-in in deepwater drilling[D]. Qingdao: China University of Petroleum (East China), 2018.

[42]
宋荣荣, 孙宝江, 刘晓兰, 等. 井筒气侵后井底压力变化的计算分析[J]. 断块油气田, 2011, 18(4): 486-488.

SONG Rongrong, SUN Baojiang, LIU Xiaolan, et al. Calculation and analysis of bottomhole pressure in wellbore after gas invasion[J]. Fault-Block Oil and Gas Field, 2011, 18(4): 486-488.

[43]
侯绪田. 多相流井筒压力分布规律探讨[J]. 石油钻探技术, 2004, 32(4): 32-34.

HOU Xutian. The study on the wellbore pressure under multiphase flow condition[J]. Petroleum Drilling Techniques, 2004, 32(4): 32-34.

[44]
WANG X, LIU H, ZHAO M, et al. Study on multiphase flow modeling and parameter optimization design for bullheading[J]. Geoenergy Science and Engineering, 2024, 245: 213519.

[45]
ADAMS A J, MACEACHRAN A. Impact on casing design of thermal expansion of fluids in confined annuli[J]. SPE Drilling & Completion, 1994, 9(3): 210-216.

Options
文章导航

/

〈 〉

版权所有：《石油勘探与开发》编辑部；《石油勘探与开发（英文）》编辑部
地址：北京市海淀区学院路20号，中国石油勘探开发研究院数据中心605室　

京ICP备15044687号    技术支持：北京玛格泰克科技发展有限公司