0 引言
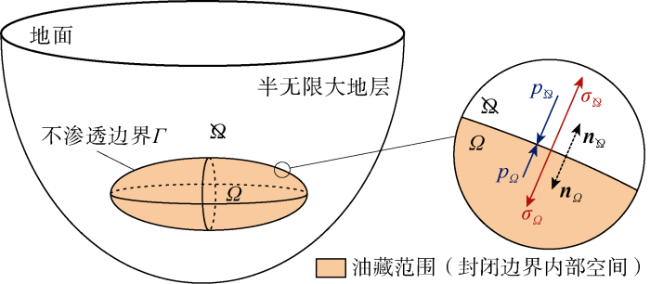
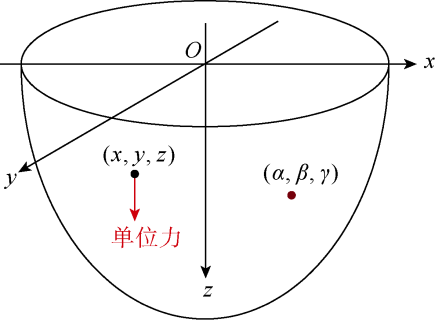
1 基本方程
2 开发诱导变形等效力模型
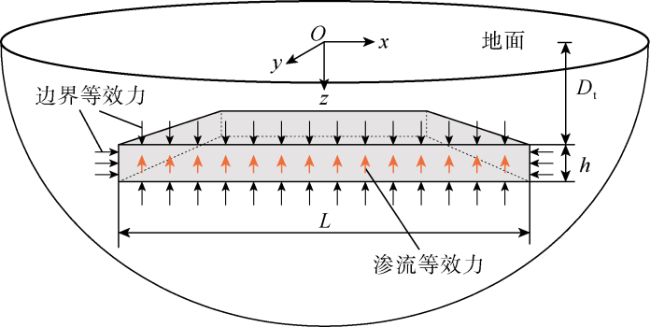
2.1 渗流等效力
2.2 边界等效力
2.3 解析求解方法
2.4 体积边界元数值求解方法
3 模型验证与测试
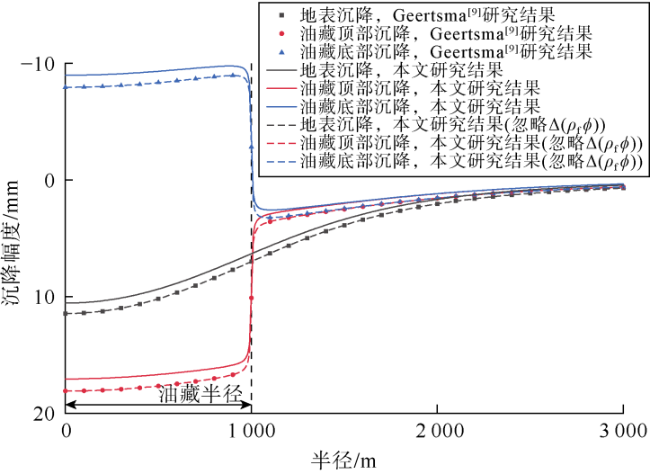
3.1 解析解验证
表1 用于解析解验证的油藏参数 |
| 参数名称 | 参数值 | 参数名称 | 参数值 |
|---|---|---|---|
| 骨架材料体积模量 | 35 000 MPa | 油藏厚度 | 10 m |
| 岩石表观体积模量 | 2 000 MPa | 油藏顶深 | 1 000 m |
| 岩石表观剪切模量 | 1 200 MPa | 油藏半径 | 1 000 m |
| 岩石表观泊松比 | 0.25 | 原始地层压力 | 30 MPa |
| 岩石孔隙度 | 20% | 油藏压力增量 | -10 MPa |
| 流体密度 (参考压力) | 800 kg/m3 (30 MPa) | 综合压缩系数 | 3×10-3 MPa-1 |
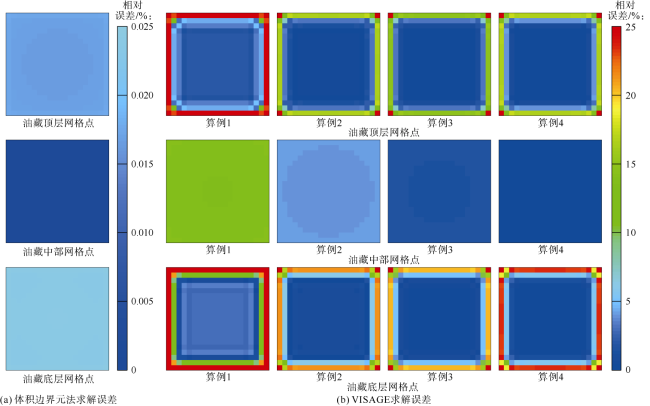
3.2 商业模拟器对比测试
表3 VISAGE模型参数设置 |
| 算例 | 水平方向 延伸倍数 | 水平方向 延伸网格数 | 油藏上部 延伸网格数 | 油藏下部延伸所至深度/m | 油藏下部 延伸网格数 |
|---|---|---|---|---|---|
| 算例1 | 3 | 5 | 15 | 6 400 | 20 |
| 算例2 | 10 | 20 | 20 | 15 000 | 50 |
| 算例3 | 30 | 30 | 20 | 30 000 | 70 |
| 算例4 | 100 | 50 | 40 | 140 000 | 90 |
表4 不同模拟方法求解油藏网格位移性能对比 |
| 方法 | 网格数 | 求解 时间/min | 最小 误差/% | 最大 误差/% | 平均 误差/% |
|---|---|---|---|---|---|
| 体积边界元法 | 31.0 | 2.5×10-14 | 0.024 | 0.008 2 | |
| VISAGE(算例1) | 40 960 | 0.6 | 0.650 00 | 67.210 | 10.770 0 |
| VISAGE(算例2) | 288 300 | 7.0 | 0.100 00 | 47.380 | 5.150 0 |
| VISAGE(算例3) | 638 780 | 21.5 | 0.027 00 | 45.360 | 4.050 0 |
| VISAGE(算例4) | 2 009 340 | 149.2 | 0.000 33 | 51.530 | 4.150 0 |
表5 不同模拟方法求解地表沉降性能对比 |
| 方法 | 顶层网格 厚度/m | 最小 误差/% | 最大 误差/% | 平均 误差/% |
|---|---|---|---|---|
| 体积边界元法 | 2.15×10-13 | 1.95×10-12 | 1.11×10-12 | |
| VISAGE(算例1) | 668.2 | 0.10 | 2.33 | 1.21 |
| VISAGE(算例2) | 464.0 | 1.83 | 3.25 | 2.72 |
| VISAGE(算例3) | 464.0 | 3.00 | 4.08 | 3.68 |
| VISAGE(算例4) | 216.6 | 1.76 | 2.22 | 2.05 |
表6 考虑流体密度及饱和度变化时不同方法求解误差对比 |
| 位置 | 方法 | 最小 误差/% | 最大 误差/% | 平均 误差/% |
|---|---|---|---|---|
| 油藏 | 体积边界元法 | 0.25×10-4 | 0.023 | 0.008 |
| VISAGE(算例1) | 0.39 | 83.400 | 25.680 | |
| VISAGE(算例2) | 2.07 | 103.860 | 29.390 | |
| VISAGE(算例3) | 0.43 | 109.230 | 30.650 | |
| VISAGE(算例4) | 1.58 | 112.240 | 31.890 | |
| 地面 | 体积边界元法 | 4.54×10-13 | 2.50×10-12 | 1.67×10-12 |
| VISAGE(算例1) | 18.24 | 18.51 | 18.34 | |
| VISAGE(算例2) | 19.57 | 21.33 | 20.15 | |
| VISAGE(算例3) | 20.54 | 22.73 | 21.27 | |
| VISAGE(算例4) | 18.38 | 21.25 | 19.37 |