0 引言
1 数学模型
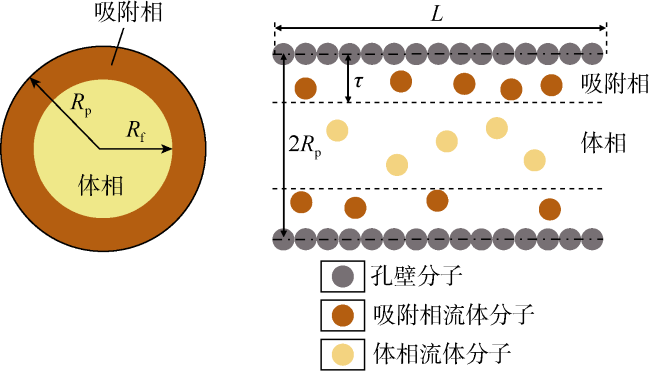
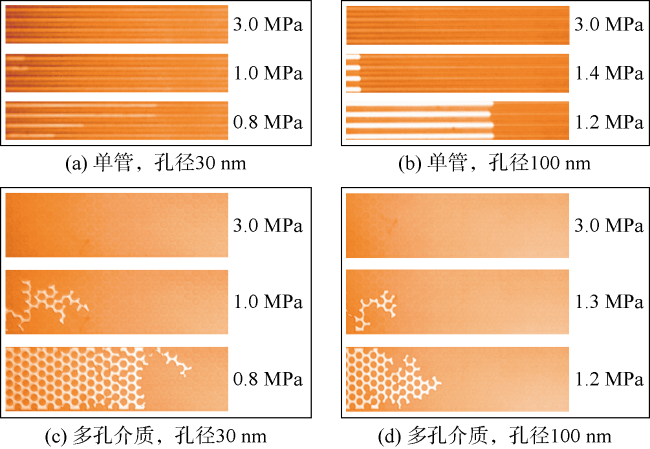
1.1 流体分子与孔壁间的相互作用
1.2 有效摩尔体积修正
1.3 多影响因素条件下的PR状态方程修正
1.4 吸附相-气相-液相三相相平衡计算
1.4.1 多组分Langmuir吸附模型
1.4.2 压缩因子和逸度计算
$\left[ \frac{2\sum\limits_{j=1}^{N}{{{x}_{j}}\left( 1-{{k}_{ij}} \right)\sqrt{{{a}_{i}}{{a}_{j}}}}}{a}-\frac{{{b}_{i}}}{b} \right]\ln \frac{Z+\left( \sqrt{2}+1 \right)B}{Z-\left( \sqrt{2}-1 \right)B}$
1.4.3 毛管压力计算
1.4.4 三相相平衡计算
2 模型验证
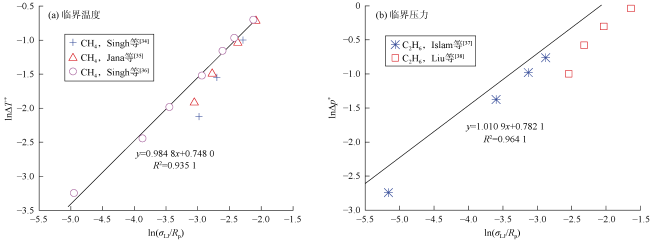
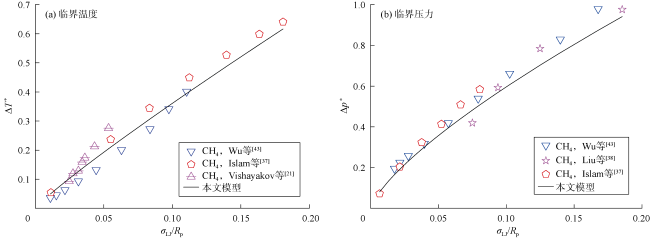
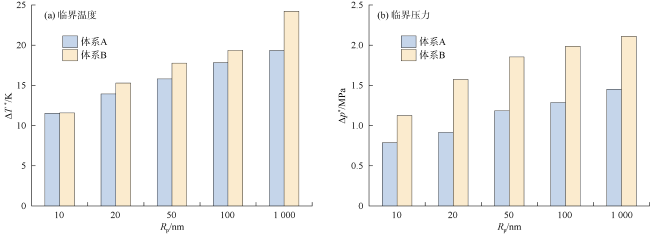
2.1 临界性质验证
2.2 泡点压力验证
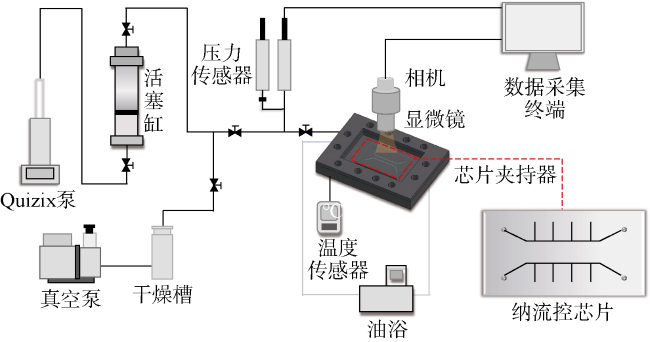
2.2.1 实验装置
2.2.2 实验步骤
2.2.3 实验结果与理论计算结果对比
3 模型计算及分析
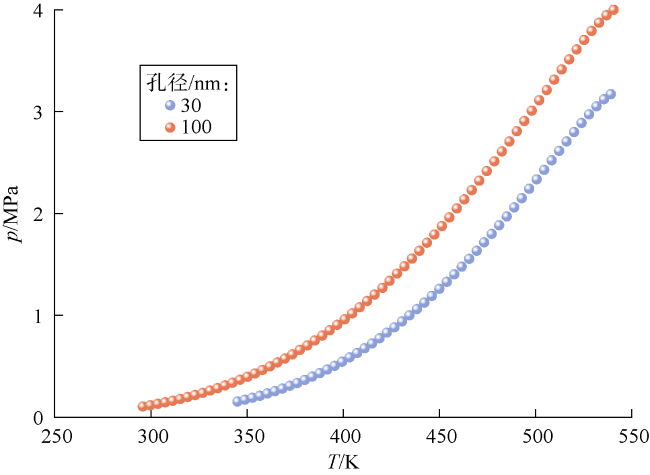
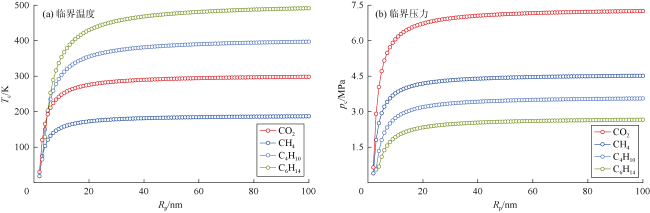
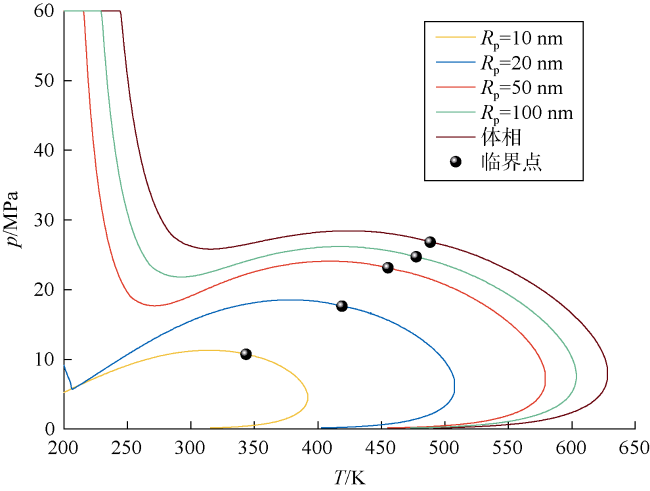
3.1 单组分临界性质变化规律
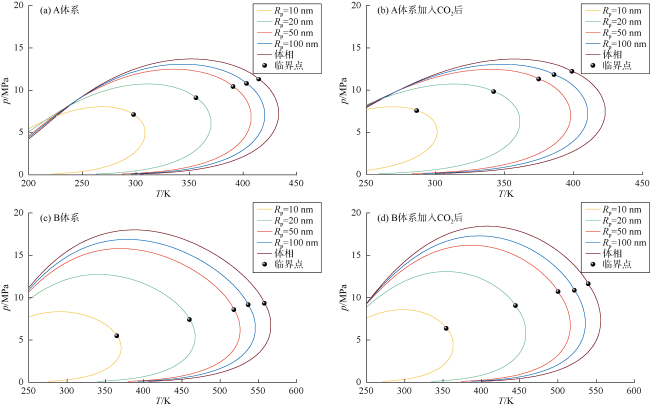
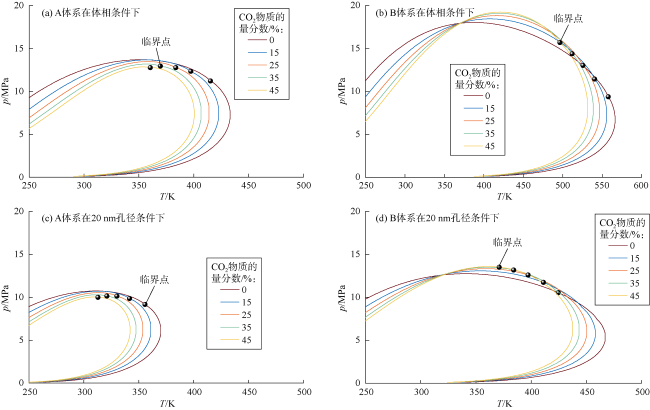
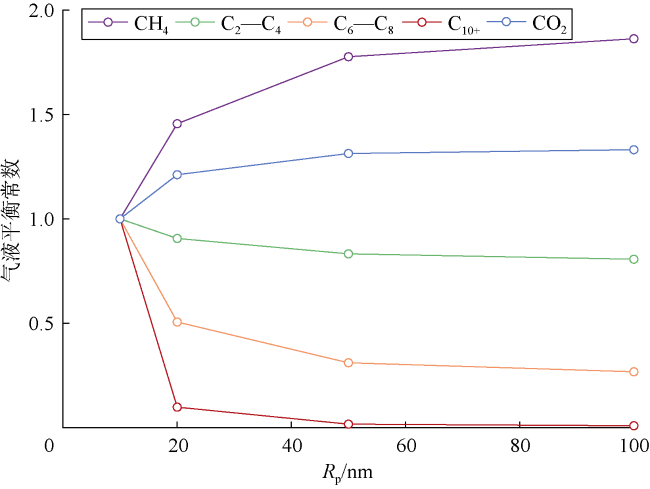
3.2 CO2-页岩油相行为分析
表1 各组分参数统计表 |
| 组分 | 相对分子 质量 | 临界 压力/MPa | 临界 温度/K | 偏心 因子 | 等张比容/ (N1/4•m11/4•mol-1) |
|---|---|---|---|---|---|
| CO2 | 44.010 | 7.382 | 304.19 | 0.198 | 82.00 |
| CH4 | 16.040 | 4.599 | 190.56 | 0.011 | 74.00 |
| C4H10 | 58.123 | 3.648 | 408.14 | 0.177 | 185.32 |
| C6H14 | 86.177 | 3.025 | 507.60 | 0.301 | 276.71 |
| C8H18 | 114.231 | 2.490 | 568.70 | 0.399 | 359.33 |
| C10H22 | 142.285 | 2.110 | 617.70 | 0.492 | 440.69 |
4 矿场应用
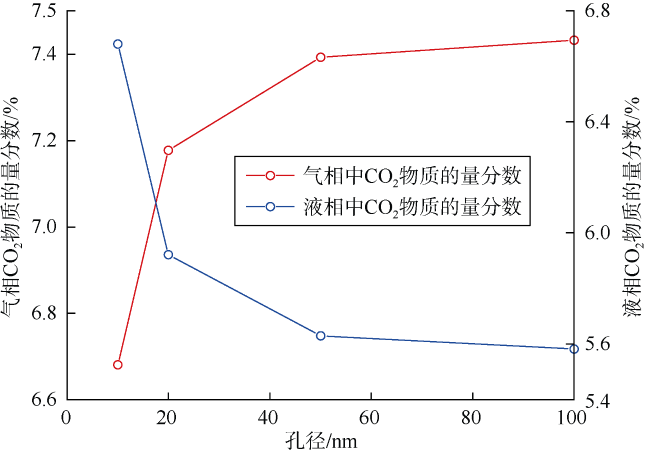
4.1 古龙A区块页岩储层流体相态特征
表2 大庆古龙A区块页岩储层流体组分参数统计表 |
| 组分 | 物质的 量分数/% | 相对分子质量 | 临界 压力/MPa | 临界 温度/K | 偏心 因子 | 等张比容/ (N1/4•m11/4•mol-1) |
|---|---|---|---|---|---|---|
| CO2 | 6.03 | 44.01 | 7.382 | 304.19 | 0.198 | 82.000 |
| CH4 | 43.25 | 16.04 | 4.599 | 190.56 | 0.011 | 74.000 |
| C2—C4 | 23.01 | 42.82 | 4.310 | 363.30 | 0.143 | 145.200 |
| C6—C8 | 19.56 | 98.05 | 2.941 | 531.56 | 0.316 | 291.600 |
| C10+ | 8.15 | 200.00 | 2.180 | 788.74 | 0.687 | 683.300 |