石油勘探与开发 >

2024 , Vol. 51 >Issue 6: 1384 - 1394

DOI: https://doi.org/10.11698/PED.20240488

石油工程

干热岩柔性压裂裂缝起裂与扩展规律

  • 周小夏 ,
  • 李根生 ,
  • 马正超 ,
  • 黄中伟 ,
  • 张旭 ,
  • 田守嶒 ,
  • 邹文超 ,
  • 王天宇
展开
  • 油气资源与工程全国重点实验室，中国石油大学（北京），北京 102249
王天宇（1991-），男，河北保定人，博士，中国石油大学（北京）副教授，主要从事非常规油气钻完井增产理论与方法研究。地址：北京市昌平区府学路18号，中国石油大学（北京）石油工程学院，邮政编码：102249。E-mail：

周小夏（1999-），男，四川广元人，现为中国石油大学（北京）在读博士，主要从事干热岩柔性造储的数值模拟与实验研究。地址：北京市昌平区府学路18号，中国石油大学（北京）石油工程学院，邮政编码：102249。E-mail：

Copy editor: 刘恋

收稿日期: 2024-07-30

  修回日期: 2024-11-19

  网络出版日期: 2024-12-10

基金资助

国家自然科学基金重大项目课题“高温岩体复杂缝网造储理论与技术”(52192621)

收起

Fracture initiation and propagation in soft hydraulic fracturing of hot dry rock

  • ZHOU Xiaoxia ,
  • LI Gensheng ,
  • MA Zhengchao ,
  • HUANG Zhongwei ,
  • ZHANG Xu ,
  • TIAN Shouceng ,
  • ZOU Wenchao ,
  • WANG Tianyu
Expand
  • State Key Laboratory of Petroleum Resources and Engineering, China University of Petroleum (Beijing), Beijing 102249, China

Received date: 2024-07-30

  Revised date: 2024-11-19

  Online published: 2024-12-10

Fold

摘要

考虑岩石热孔隙弹性效应、循环载荷下岩石强度疲劳劣化本构关系、弹脆性破坏准则和井筒应力叠加效应，建立并验证了热流固-疲劳损伤耦合的干热岩柔性水力压裂裂缝扩展数值模型，在此基础上开展数值模拟研究，探究不同温度和循环载荷共同作用下干热岩裂缝起裂及扩展特征。研究表明：①周期注入、流体渗透、孔隙压力累积与岩石强度劣化共同引发柔性压裂岩石疲劳破坏；②干热岩柔性压裂裂缝扩展模式由温差和循环载荷共同控制，温差越大，热应力越强，利于形成复杂缝网；循环载荷降低，热应力波及范围增大，循环载荷为90%pb和80%pb（pb为常规水力压裂时岩石破裂压力）时，改造面积相较于常规水力压裂分别提升88.33%和120%（注入温度为25 ℃）；③随着循环载荷的进一步降低，储层改造效果减弱，循环载荷降低至70%pb时，距离井筒较远处流体压力无法达到岩石最低破裂压力，不会产生宏观水力裂缝。

关键词： 干热岩; 柔性压裂; 热流固-疲劳损伤耦合; 热应力; 疲劳劣化; 裂缝扩展

本文引用格式

周小夏 , 李根生 , 马正超 , 黄中伟 , 张旭 , 田守嶒 , 邹文超 , 王天宇 . 干热岩柔性压裂裂缝起裂与扩展规律[J]. 石油勘探与开发, 2024 , 51(6) : 1384 -1394 . DOI: 10.11698/PED.20240488

Abstract

By considering the thermo poroelastic effects of rock, the constitutive relationship of fatigue deterioration of rock under cyclic loading, elastic-brittle failure criteria and wellbore stress superposition effects, a thermal-hydraulic-mechanical-fatigue damage coupled model for fracture propagation during soft hydraulic fracturing in hot dry rock (HDR) was established and validated. Based on this model, numerical simulations were conducted to investigate the fracture initiation and propagation characteristics in HDR under the combined effects of different temperatures and cyclic loading. The results are obtained in three aspects. First, cyclic injection, fluid infiltration, pore pressure accumulation, and rock strength deterioration collectively induce fatigue damage of rocks during soft hydraulic fracturing. Second, the fracture propagation pattern of soft hydraulic fracturing in HDR is jointly controlled by temperature difference and cyclic loading. A larger temperature difference generates stronger thermal stress, facilitating the formation of complex fracture networks. As cyclic loading decreases, the influence range of thermal stress expands. When the cyclic loading is 90%pb and 80%pb (where pb is the breakdown pressure during conventional hydraulic fracturing), the stimulated reservoir area increases by 88.33% and 120%, respectively, compared to conventional hydraulic fracturing (with an injection temperature of 25 ℃). Third, as cyclic loading is further reduced, the reservoir stimulation efficiency diminishes. When the cyclic loading decreases to 70%pb, the fluid pressure cannot reach the minimum breakdown pressure of the rock, resulting in no macroscopic hydraulic fractures.

Key words： hot dry rock; soft hydraulic fracturing; thermal-hydraulic-mechanical-fatigue damage coupling; thermal stress; fatigue deterioration; fracture propagation

0 引言

干热岩地热资源储量大、分布广，是一种具有独特优势的清洁可再生能源[1⇓-3]。增强型地热系统（EGS）是开发干热岩的主要技术，其原理为通过水力压裂等方式形成人工热储，提高地热储层的渗透率，建立高导流换热通道，实现高效、经济取热[4-5]。常规水力压裂通过压裂液的连续注入，使井底压力高于储层破裂压力，形成人工裂缝；但在干热岩造储过程中存在破裂压力高、裂缝形态单一的难题，严重制约干热岩地热资源的高效取热，实际开发过程中的高破裂压力甚至会诱发地震[6⇓-8]。干热岩柔性造储有望降低储层破裂压力，提高改造体积，实现高效安全造储，对干热岩地热资源经济高效开发具有重要意义[9-10]。
柔性水力压裂（又称循环水力压裂、脉冲水力压裂）技术作为一种新型的注液方法，采用循环注入的方式，保持注入流体压力低于岩石破裂压力，在井底形成循环载荷，使岩石不断经受加载-卸载过程，促使岩石力学性能降低，诱导岩石疲劳破坏，有利于降低起裂压力、形成复杂缝网和减少诱发地震风险[11-12]。李全贵等[13-14]研究了煤岩在循环水力压裂下裂缝形态的演化规律，结果表明煤岩内部在循环载荷下出现多个破裂面从而形成复杂裂缝网络，且最低循环压力为常规连续注入压力的85%。翟成等[15]针对煤岩开展了不同循环参数（频率、压力）下柔性压裂室内实验，发现在循环载荷条件下煤岩孔隙产生“压缩-膨胀-压缩”的周期作用，使得煤岩呈现疲劳破坏，形成裂缝网络。Wei等[16]通过室内实验和数值模拟探究了不同脉冲水压下砂岩强度劣化特征及岩石断裂机制，得到了相应条件下砂岩抗拉强度劣化曲线。Zang等[17⇓-19]通过对比泵入能量与地震释放能量，发现循环水力压裂能降低引发事件的总数和更大震级事件的发生概率，同时对该注液方式在地热储层中的应用进行了讨论；在后续研究中Zang等[6]开展了花岗岩室内及矿场实验，证实柔性水力压裂能降低破裂压力、改变岩石的断裂模式、提高储层渗透率。Zhuang等[20]开展了常规连续注入、逐步连续注入、循环渐进注入、逐步增压、逐步脉冲增压、循环脉冲增压共6种注入方式下的花岗岩真三轴水力压裂实验，其中循环脉冲增压的注入方式具有控制水力裂缝延伸的潜力；Zhuang等[21]进一步研究了不同循环压力加载比下的花岗岩柔性水力压裂，结果表明柔性水力压裂可降低破裂压力，且加压阶段产生的局部裂纹更多。尽管已有学者基于流固耦合对柔性水力压裂开展了相关研究，但考虑高温高应力条件下干热岩柔性水力压裂的研究较少，因此亟需开展热流固-疲劳损伤耦合下的干热岩柔性水力压裂裂缝的起裂与扩展研究。
本研究引入周期载荷函数与岩石强度劣化本构关系，建立考虑井筒应力叠加效应、岩石热孔隙弹性效应、弹脆性破坏准则和基岩周期载荷下疲劳劣化的热流固-疲劳损伤耦合裂缝扩展数值模型，通过与微裂缝扩展实验结果、动态响应解析解和热固结现象对比，验证数值模型的准确性。在此基础上，开展热流固-疲劳损伤耦合作用下的干热岩柔性水力压裂数值模拟研究，探究不同温度和循环载荷共同作用下干热岩裂缝起裂及扩展特征，以揭示干热岩柔性压裂机理和裂缝扩展规律。

1 干热岩柔性水力压裂模型

1.1 干热岩柔性造储方法

干热岩储层具有高温高应力、地层渗透性差、无水或含水极少的特点，导致储层改造困难。EGS是开发干热岩地热资源的重要手段，主要流程包括钻井沟通地热储层、压裂造储形成渗流通道、循环工质高效取热。其中，压裂造储技术用于形成高导流水力裂缝沟通注采井，为取热工质提供渗流传热通道，但该技术在EGS工业化推广应用方面仍极具挑战[22⇓⇓⇓-26]：①缝网改造体积小，压裂过程产生单一主裂缝，对天然裂缝的激活程度低，难以形成复杂缝网；②压裂改造过程中，超高破裂压力引起的应力扰动导致附近断层活化失稳，形成高震级事件，妨碍EGS安全稳定运行。因此，干热岩高效、安全压裂是影响其高效开发利用的关键技术，周期循环注入流体诱导岩石疲劳致裂的柔性水力压裂造储方法可以提高造储体积并降低压裂过程中诱发地震的风险。相比常规压裂短时大排量注入，柔性造储方法采用的注入压力/排量振荡的长周期泵注方式可始终保持注入流体压力低于岩石破裂压力，在反复加载-卸载的过程中使得岩石力学性能降低，诱导岩石疲劳破坏，减小破裂压力，形成复杂裂缝网络（见图1）。
图1 干热岩柔性水力压裂造储机理示意图

1.2 模型假设

数值模型基于以下基本假设：①岩石基质中压力传递连续、各向同性，横波与纵波的速度传递保持一致；②裂缝扩展视为准静态；③压裂液不与储层发生化学反应；④压裂液为单相，始终保持液态；⑤温度场中传热通过对流换热和热传导实现，且满足局部热平衡。

1.3 模型控制方程

本文采用有限元法建立柔性水力压裂裂缝扩展模型，引入了周期载荷函数与岩石强度劣化本构关系。使用COMSOL Multiphysics数值模拟软件对全耦合热流固-疲劳损伤模型进行数值求解，模拟温度场、渗流场、应力场以及岩石损伤4个物理场耦合作用下干热岩储层裂缝的起裂扩展过程。

1.3.1 热流固耦合模型控制方程

考虑应力影响的干热岩内流体流动质量守恒方程为[27]：
$ \rho_{\mathrm{w}} S \frac{\partial p}{\partial t}-\nabla \cdot \frac{\rho_{\mathrm{w}} K_{\mathrm{r}}}{\mu_{\mathrm{f}}} \nabla p=-q_{\mathrm{m}}-\rho_{\mathrm{w}} \alpha_{\mathrm{B}} \frac{\partial \varepsilon_{\mathrm{vol}}}{\partial t}$
其中 $ S=\phi_{\mathrm{r}} \chi_{\mathrm{f}}+\left(\alpha_{\mathrm{B}}-\phi_{\mathrm{r}}\right) \frac{1-\alpha_{\mathrm{B}}}{K_{\mathrm{d}}}$
考虑热对流和热传导作用的干热岩内热量传递能量守恒方程为[28]：
$ \begin{array}{l} {\left[\phi_{\mathrm{r}} \rho_{\mathrm{w}} C_{\mathrm{w}}+\left(1-\phi_{\mathrm{r}}\right) \rho_{\mathrm{r}} C_{\mathrm{r}}\right] \frac{\partial T}{\partial t}+\rho_{\mathrm{w}} C_{\mathrm{w}} v_{\mathrm{w}} \nabla T-} \\ \nabla \cdot\left\{\left[\phi_{\mathrm{r}} \lambda_{\mathrm{w}}+\left(1-\phi_{\mathrm{r}}\right) \lambda_{\mathrm{r}}\right] \nabla T\right\}=W \end{array}$
考虑热应力和孔隙弹性效应的应力-应变方程如下[29]：
$ G \nabla^{2} u_{i}+(\lambda+G) u_{j, j i}^{\prime \prime}-\alpha_{\mathrm{B}} p_{i}^{\prime}-\alpha_{T} K\left(T_{i}^{\prime}-T_{0, i}^{\prime}\right)+F_{i}=0$

1.3.2 干热岩破裂准则和疲劳损伤演化方程

采用最大拉应力准则和Mohr-Coulomb准则来界定岩石拉伸破裂和剪切破裂（拉伸为正，压缩为负），方程如下[30]：
$ \left\{\begin{array}{l} F_{1}=\sigma_{1}-f_{\mathrm{t} 0} \\ F_{2}=-\sigma_{3}+\sigma_{1} \frac{1+\sin \theta}{1-\sin \theta}-f_{\mathrm{co}} \end{array}\right.$
当岩石发生拉伸破坏时（F1≥0），损伤变量Ds的控制方程如下[31]：
$ D_{s}=\left\{\begin{array}{ll} 0 & \varepsilon<\varepsilon_{\mathrm{t} 0} \\ 1- & \frac{f_{\mathrm{tr}}}{\varepsilon E_{0}} \quad \varepsilon_{\mathrm{t} 0} \leqslant \varepsilon<\varepsilon_{\mathrm{tv}} \\ 1 & \varepsilon_{\mathrm{tv}} \leqslant \varepsilon \end{array}\right.$
其中 εtu=ηεt0
当岩石发生剪切破坏时（F2≥0），损伤变量Ds的控制方程如下：
$ D_{\mathrm{s}}=\left\{\begin{array}{l} 0 \varepsilon_{\mathrm{c} 0}<\varepsilon \\ 1+\frac{f_{\mathrm{cr}}}{\varepsilon E_{0}} \quad \varepsilon \leqslant \varepsilon_{\mathrm{c} 0} \end{array}\right.$
传统的裂缝扩展模型仅考虑单调载荷下的裂缝扩展；在柔性压裂过程中，循环载荷会降低岩石的力学性能，因此需要对单调载荷作用下的裂缝扩展本构关系进行修正。本文将疲劳损伤引入脆性本构模型，用于表征循环载荷下引起的岩石强度退化。
循环加载n次后的岩石强度为[32]：
$ \sigma_{0, n}=\left(1-D_{\mathrm{f}}\right) \sigma_{0}$
通过引入真实干热岩（本文取花岗岩）疲劳本构关系模拟岩石在循环载荷作用下的疲劳破坏效应，定量表征了由疲劳引起的岩石强度退化，控制方程如
下[33]：
$ \frac{\sigma_{\max }}{\sigma_{0}}=A \log _{10} N+B$
其中，A和B为经验参数，受加载频率、样本量、温度和岩石饱和度的影响，一般由实验数据拟合得到。由花岗岩疲劳实验拟合得到A和B分别为−0.107和0.977[34]。
在给定的载荷比（σmax/σ0）条件下，将（8）式转换为（9）式计算疲劳寿命N：
$ N=10^{\frac{\sigma_{\max } / \sigma_{0}-B}{A}}$
在最大加载应力σmax条件下，n次循环的疲劳损伤为[35]：
$ D_{\mathrm{f}}=\frac{\sigma_{0}-\sigma_{\max }}{\sigma_{0}} \frac{n}{N}$
基于细观损伤力学，在循环载荷条件下，岩石疲劳劣化，损伤后岩石力学性能发生退化。压裂过程中弹性模量的控制方程如下[36]：
$ E=E_{0}\left(1-\frac{n}{N}\right)\left(1-D_{f}\right)$
压裂过程中干热岩的孔隙度随应力变化，渗透率随岩石损伤增大而增大，控制方程分别为[37-38]：
$ \phi_{\mathrm{r}}=\left(\phi_{\mathrm{r} 0}-\phi_{\mathrm{re}}\right) \exp \left(-\alpha_{\phi} \sigma_{\mathrm{eff}}\right)+\phi_{\mathrm{re}}$
$ K_{\mathrm{r}}=K_{0}\left(\frac{\phi_{\mathrm{r}}}{\phi_{\mathrm{r} 0}}\right)^{3} \exp \left(\alpha_{K} D_{\mathrm{f}}\right)$

2 模型验证

2.1 柔性水力压裂裂缝扩展模型验证

为验证数值模型模拟裂缝扩展的可靠性，本文采用常规水力压裂和柔性水力压裂的室内实验结果与模拟结果进行对比。基于真三轴水力压裂实验系统（见图2），对边长为0.1 m的立方体花岗岩露头进行常温条件下的常规水力压裂和柔性水力压裂，柔性水力压裂循环载荷为常规连续注入破裂压力（pb）的80%或90%（见图3a），其他参数如表1所示。
图2 真三轴水力压裂实验装置示意图
图3 常规水力压裂和柔性水力压裂的流体注入方式（a）以及室内实验和数值模拟裂缝扩展结果对比（b）
表1 初始条件及物性参数表[39]
类别 参数名称 符号 数值
初始条件 储层初始温度 T0 200 ℃
孔隙压力 p 0.1 MPa
注入流量 qs 0.02 kg/(m3·s)
频率 f 1 Hz
垂直地应力 σv 10 MPa
最大水平主应力 σH 8 MPa
最小水平主应力 σh 5 MPa
干热岩储层 密度 ρr 2 650 kg/m3
抗压强度 fc0 200 MPa
抗拉强度 ft0 10 MPa
初始弹性模量 E0 60 GPa
泊松比 υ 0.25
导热系数 λr 3 W/(m·K)
等压热容 Cr 1 000 J/(kg·K)
孔隙度 ϕr 1%
渗透率 K0 1×10−18 m2
热膨胀系数 αT 2×10−6 K−1
注入流体 密度 ρw 1 000 kg/m3
导热系数 λw 0.5 W/(m·K)
等压比热容 Cw 4 200 J/(kg·K)
黏度 μf 0.001 Pa·s
基于室内实验，建立了干热岩柔性水力压裂数值模型，模拟直井条件下裂缝起裂与扩展过程。模型为0.1 m×0.1 m×0.1 m，中心井筒直径设置为0.016 m，地应力通过外部载荷施加，σH，σh，σv分别设置为8，5，10 MPa（见图4a）。外边界设置为无流动和隔热边界，井筒周围设置为压力和热交换边界，模拟干热岩柔性水力压裂过程中循环载荷引起的岩石力学性能疲劳劣化和温差引起的热应力作用，模拟结果取最大、最小水平主应力方向截面进行分析。压裂过程中，注入流体初始温度为25 ℃，循环载荷为80%pb，90%pb，通过控制最大、最小循环载荷以保证施加稳定的循环载荷，直至裂缝扩展到边界，相关初始条件及物性参数如表1所示。
图4 干热岩柔性水力压裂数值模型（a）和有限元网格剖分示意图（b）
为确定裂缝起裂位置以及延伸方向，采用有限元方法对数学模型进行离散求解（见图4b），并对渗流场、温度场、应力场以及岩石损伤破裂准则进行耦合求解。柔性水力压裂裂缝扩展模型采用非结构化网格进行空间离散，平均单元尺寸为0.5 mm（模型特征长度的1/200）。基于隐式向后差分方法计算压力、温度、应力及损伤的时空演化过程。
图3b对比了室内实验和数值模拟得到的常规水力压裂和柔性水力压裂诱导的裂缝扩展形态。其中，常规压裂仅诱导出双翼裂缝，裂缝形态单一；柔性压裂井筒周围产生多条微裂缝，同时部分微裂缝扩展延伸，形成多条水力裂缝，裂缝形态相对复杂。常规水力压裂和柔性水力压裂裂缝形态数值模拟结果与实验结果基本吻合，验证了本文数值模型模拟裂缝扩展的准确性。

2.2 柔性水力压裂动态响应模型验证

相较于常规水力压裂，柔性压裂的压裂液注入方式为循环注入，储层内部呈现动态应力响应。为进一步验证模型的有效性，通过模拟30~50 MPa循环注入条件下监测点（距井筒内壁0.12 m）径向应力、周向应力以及孔隙压力随时间的变化情况，验证了所建立模型动态响应和数值求解的有效性。图5a—图5c为不同时刻（0~10 s）监测点径向应力、周向应力以及孔隙压力随时间的变化图，其中数值解通过模型计算获得，解析解采用Senjuntichai等[40]通过Biot’s多孔弹性动力学方程在拉普拉斯变换空间中推导出的径向应力、周向应力和孔隙压力公式进行计算。结果表明数值解与解析解吻合较好，验证了模型数值求解方法的准确性。
图5 径向应力、周向应力以及孔隙压力随时间的变化

2.3 热流固耦合模型验证

通过模拟热固结现象引起的土柱温度、位移和孔隙压力随时间的变化情况，验证所建立模型热流固耦合的准确性。参考白冰的相关研究[41]，本文采用相同的模型设置进行热固结模拟。模型中假定所有边界都是绝热和封闭边界，除顶面外的其他边界均采用辊支撑边界约束（即不存在法向位移）；设置土柱上表面施加压缩载荷为10 kPa，温差50 ℃，孔隙压力10 kPa。图6a—图6c为不同时刻（1×10−1~1×105 s）土柱温度、位移和孔隙压力的变化图，其中数值解通过模型计算获得，解析解采用Bai等[42]推导出的热流固耦合公式进行计算。结果表明数值解与解析解基本一致，验证了本文建立的热流固耦合模型及数值求解方法的准确性。
图6 热固结模型土柱温度、位移和孔隙压力随时间的变化（z—监测点高度）

3 裂缝起裂与扩展数值模拟研究

3.1 裂缝起裂与扩展特征

图7展示了注入温度为25 ℃时常规水力压裂和柔性水力压裂数值模拟结果，其中常规水力压裂以恒定速率连续注入，直至岩石发生破裂；柔性水力压裂通过周期变化的注入速率提供循环载荷，循环载荷在90%pb或80%pb与0之间交替，每个循环周期为1 s （1 Hz），通过设置最大注入压力来控制循环载荷峰值。从图7可以看出，常规水力压裂在较短时间内达到破裂压力（11.3 MPa），裂缝起裂并迅速扩展，损伤面积达到最大；柔性水力压裂通过施加0~90%pb或0~80%pb循环压裂，损伤面积随着循环注入时间增大而逐步增大；相较于常规水力压裂，柔性水力压裂的损伤面积分别提升了88.33%和120%。
图7 岩石损伤面积随注入周期的演化规律图
图8展示了干热岩储层的温度、孔隙压力和疲劳损伤分布随时间的演化情况，t取0.1t0，0.8t0，1.0t0，其中t0表示整个压裂过程所用时间。①t=0.1t0为裂缝扩展初期，由温度场变化图观察到高温储层由于低温压裂液的注入诱发热应力，并集中于井筒部分。受热应力影响，井筒周围萌生较多微裂缝。随着压裂时间的延续，t=1.0t0时裂缝延伸至远离热应力区域，地应力场开始主导裂缝延伸，即扩展方向垂直于最小水平主应力。此外，由于柔性水力压裂的注入过程比常规水力压裂时间更长，注入流体与高温岩石接触时间更长，热应力影响范围更广。②从渗流场变化图可以看出，压裂初期流体渗流区域为圆形；随着压裂时间的增加，注入流体逐渐渗入，孔隙压力增大，在岩石中产生局部裂缝。在压裂后期，裂缝沿最大水平主应力方向扩展，渗流区域由圆形变为椭圆形，流体渗流方向与裂缝扩展方向一致。③疲劳损伤变化图展示了压裂过程中岩石弹性模量和裂缝形态的变化情况。常规水力压裂岩石的弹性模量仅在裂缝处呈现降低趋势，即弹性模量随着岩石破坏逐渐减小，当岩石完全破坏时，弹性模量降至0。而柔性水力压裂岩石的弹性模量不仅在裂缝处出现降低，随着注入时间的延长和多次循环注入，岩石的弹性模量出现整体劣化，使岩石在较低的压力下发生破裂。综上所述，经过较长时间的多次流体循环后，柔性水力压裂下的岩石在流体渗透、孔隙压力累积和力学性能劣化的共同作用下发生疲劳破坏。
图8 常规和柔性水力压裂条件下温度场、渗流场和疲劳损伤随压裂时间的变化

3.2 孔隙压力分布及其演化

柔性水力压裂下岩石孔隙压力分布和演化规律与常规水力压裂不同。通过记录岩石起裂前至井筒不同距离（10，15，20，25，30 mm）处孔隙压力随时间的演变，进而研究岩石内孔隙压力分布及其时空演化规律。注入温度200 ℃条件下，常规水力压裂和柔性水力压裂过程中孔隙压力随注入时间与至井筒距离的变化曲线如图9所示。在压裂过程中，随着循环注入周期的增加，流体逐渐向井眼外渗透，孔隙压力逐渐升高；同时，孔隙压力随着至井眼中心距离的增大而减小。另外，水平地应力差和岩石基质的渗透率也会影响孔隙压力场的分布[20]。
图9 不同注入方式下孔隙压力随时间的变化
常规水力压裂时，至井筒不同距离的孔隙压力都随注入时间单调增加（见图9a）。在岩石起裂前，任意时刻岩石孔隙压力均随至井筒距离增大而降低。而对于柔性水力压裂，孔隙压力会随着压裂液的循环注入呈现出周期性的增大和减小，显示出更大的波及范围（见图9b—图9c）。同时，随着至井筒距离的增大，孔隙压力的周期变化会出现明显的滞后性，即不同至井筒距离下达到孔隙压力峰值的时间不同，形成压力波动，有利于岩石破坏。

3.3 热应力和疲劳劣化耦合作用下裂缝扩展模式与应力场重构特征

为阐明热应力及疲劳劣化耦合作用下的裂缝扩展模式与应力场重构特征，对比分析了不同流体注入温度（25，100，200 ℃）下常规连续注入和不同循环载荷（取常规连续注入破裂压力的90%，80%，70%）注入条件下的岩石破裂裂缝形态（见图10）以及应力场扰动分布（见图11）。常规连续注入条件下，流体注入温度越低岩石破裂压力越低，裂缝形态越复杂，应力扰动越大。当注入温度为200 ℃时，仅形成沿最大水平主应力扩展的两条双翼裂缝，应力扰动范围小，破裂压力为17.2 MPa；当注入温度为25 ℃时，井筒周围产生大量微裂缝，有利于岩石起裂，同时在流体的持续注入下形成5条沿不同方向扩展的水力裂缝，最终破裂压力降低了34.30%，改造面积提升了45.41%。
图10 不同温度和循环载荷下干热岩常规和柔性水力压裂裂缝形态及热应力分布图（取1 000个循环周期为注入极限）
图11 不同温度和循环载荷下干热岩常规和柔性水力压裂应力扰动图
柔性水力压裂过程中，随着注入周期延长和注入流体温度的逐渐降低，出现更多条裂缝和更复杂的裂缝形态。主要是因为长时间的循环注入延长了冷流体与高温岩石的作用时间，增大了热应力的作用范围，有利于热破裂的发生；同时，多次的循环注入促使岩石发生疲劳劣化，岩石力学性能变差，造成破裂压力降低，形成复杂的裂缝网络。
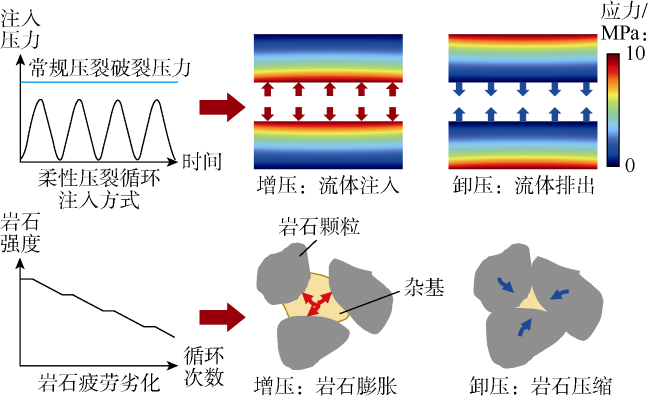
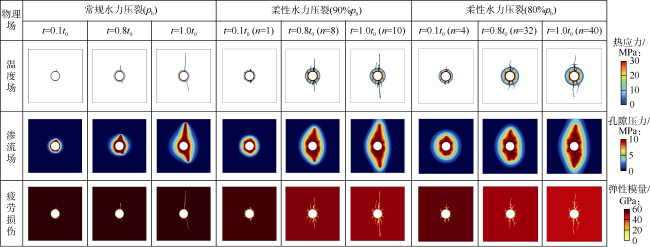
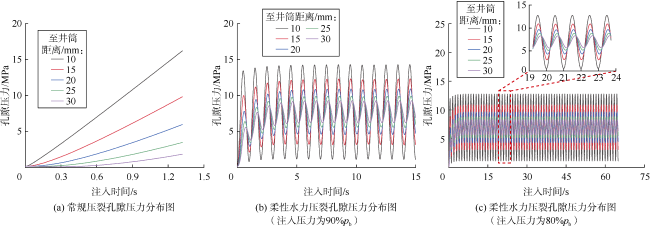
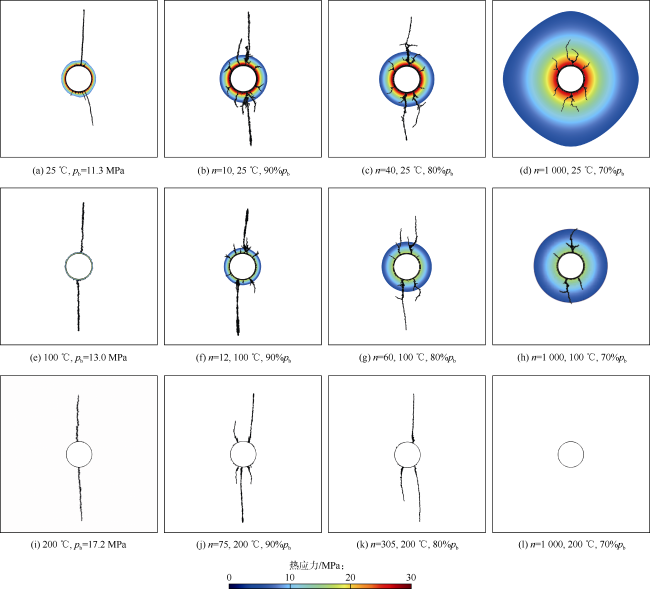
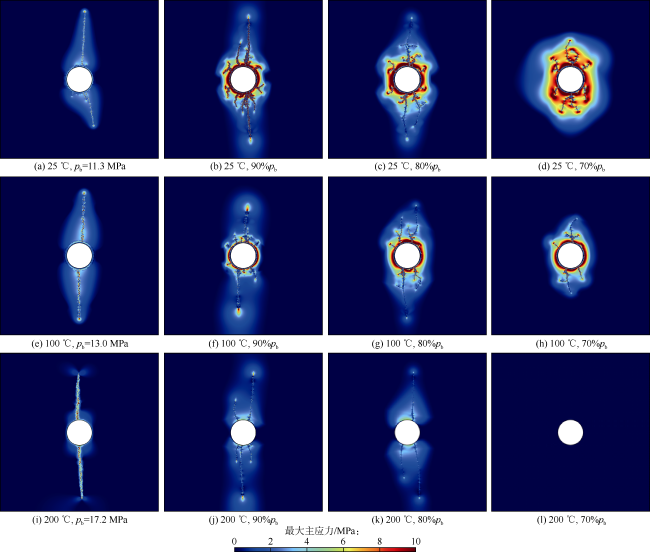
分析热应力及疲劳劣化耦合作用下裂缝形态和应力场演化发现：①当注入温度为25 ℃时，低温压裂液与井筒附近高温岩石的较大温差产生热应力进而诱导热破裂和剧烈的应力扰动（见图10和图11中井筒附近红色应力区），促使井筒周围萌生大量微裂缝。当循环载荷为90%pb时，循环注入10个周期后水力裂缝便延伸至边界附近。井筒附近岩石在热应力和疲劳劣化的共同作用下，沿各个方向形成多条水力裂缝，相较于常规水力压裂改造面积提升88.33%，同时裂缝扩展过程中出现分叉现象，表明循环注入会改变裂缝的扩展模式。当循环载荷为80%pb时，相较于90%pb下产生的主水力裂缝更多、分支裂缝迂曲度更大且各方向延伸更长，改造面积提升16.81%；相较于常规水力压裂改造面积提升120%。但水力裂缝延伸至边界需要40个注入周期，表明更低的循环注入压力虽然能诱发多个扭曲和复杂的裂缝，同时可能需要更长的注入时间。然而，当循环载荷降为70%pb时，循环注入1 000个周期后水力裂缝仍未扩展至边界，仅在井筒附近出现沿各个方向扩展的水力裂缝。这是由于在过低的循环载荷条件下，距离井筒较远位置的流体压力较低，即使在长时间的循环载荷作用下岩石力学性能发生疲劳劣化，流体压力仍然不能达到岩石最低的破裂压力，因此未能出现宏观水力裂缝。Zhuang等[21]的室内实验也验证了循环注入压力低于某个特定值时，岩石将不会出现宏观水力裂缝。②当注入温度为100 ℃时，温差减小，诱导热应力减小，井筒周围应力扰动减弱，热破裂引起的微裂缝减少（见图10e—图10h）。在相同的循环载荷下，注入温度为100 ℃时水力裂缝延伸至边界所需的循环周期要多于注入温度为25 ℃时所需的循环周期，并且随着循环载荷降低，所需周期成倍增加。相比注入温度为25 ℃的压裂条件，注入温度为100 ℃产生的水力裂缝数量减少、迂曲度更小且裂缝形态更加单一，90%pb，80%pb，70%pb条件下改造面积分别降低7.96%，29.02%，19.81%。③当注入温度为200 ℃时，压裂液与岩石温度一致，热应力消失，仅存在疲劳作用（见图10i—图10l）。相较于常规水力压裂的双翼裂缝，90%pb和80%pb循环载荷作用下，岩石出现分支裂缝和多条主裂缝。在70%pb循环载荷条件下，循环注入1 000个周期后岩石未发生破裂。
综上所述，相较于常规水力压裂，柔性水力压裂可使破裂压力降低10%~30%。温差增大，热应力增强；循环载荷降低，热应力波及范围增大，当注入温度为25 ℃时，循环载荷为90%pb和80%pb的柔性水力压裂相较于常规水力压裂改造面积分别提升88.33%和120%。但随着循环载荷的进一步降低，储层改造效果减弱，循环载荷降低至70%pb时，距离井筒较远处流体压力不能达到岩石最低的破裂压力，在有限循环注入周期内（1 000）岩石难以出现宏观水力裂缝。

4 结论

通过长时间的循环注入，柔性水力压裂在井筒附近形成了周期变化的孔隙压力场，相较于常规水力压裂产生的波及范围更广，导致岩石力学性能出现疲劳劣化，促使岩石在较低的压力下发生破裂；随着与井筒距离的增大，孔隙压力的周期变化会出现明显滞后性，形成压力波动，有利于岩石破坏。
相较于常规水力压裂，柔性水力压裂减小破裂压力10%~30%。温差增大，热应力增强；循环载荷降低，热应力波及范围增大，当注入温度为25 ℃时，循环载荷为90%pb和80%pb的柔性水力压裂相较于常规水力压裂改造面积分别提升88.33%和120%。但随着循环载荷的进一步降低，储层改造效果减弱，循环载荷降低至70%pb时，距离井筒较远处流体压力不能达到岩石最低的破裂压力，在有限循环注入周期内（1 000）岩石难以出现宏观水力裂缝。
符号注释：
A，B——疲劳参数，无因次；Cr——岩石的比热容，J/（kg·K）；Cw——流体的比热容，J/（kg·K）；Df——岩石在循环加载后的疲劳损伤参数，无因次；Ds——表征岩石在水力压裂过程中单元发生完全破坏的损伤变量，无因次，Ds=0代表岩石未发生损伤，Ds=1代表岩石完全破坏；E——弹性模量，Pa；E0——岩石初始弹性模量，Pa；f——频率，Hz；fcr——岩石残余压缩强度，Pa；fc0——岩石单轴抗压强度，Pa；ftr——岩石残余拉伸强度，Pa；ft0——岩石单轴抗拉强度，Pa；Fi——体积力在i方向的分量，Pa/m；F1，F2——应力状态函数，Pa；G——剪切模量，Pa；i，j——直角坐标系方向，取x，y，z，m；K——体积模量，Pa；K0——初始渗透率，m2；Kd——排水体积模量，Pa；Kr——岩石渗透率，m2；n——循环加载次数；N——最大循环加载次数，即疲劳寿命；p——孔隙压力，Pa；pb——常规水力压裂时岩石的破裂压力，MPa；pi°——压力对空间坐标的偏导数，Pa/m；qs——注入流量，0.02 kg/（m3·s）；qm——源/汇项，kg/（m3·s）；S——储水系数，Pa−1；t——时间，s；t0——整个压裂过程所用时间，s；T——实时温度，K；Ti°——温度对空间坐标的偏导数，K/m；Tin——注入温度，℃；T0——初始温度，K；T°0,i——初始温度对空间坐标的偏导数，K/m；u——岩石位移，m；ui——岩石位移在i方向上的分量，m；uj,ji——位移的二阶偏导数，m−1；vw——流体速度，m/s；W——冷流体与热岩石之间的热交换，W/m3；X，Y，Z——真三轴实验的3个方向；αB——Biot’s系数，无因次；αK——岩石损伤后的渗透率变化系数，本文取值为5[38]；αT——热膨胀系数，K−1；αϕ——孔隙度影响系数，Pa−1，本文取值为5×10−8[33]；ε——应变，无因次；εc0——剪切破坏时对应的最大压缩主应变，无因次；εt0——单元发生损伤时最大拉伸主应变，无因次；εtu——岩石极限拉伸应变，无因次；εvol——体积应变，无因次；η——极限应变系数，无因次；θ——岩石内摩擦角，（°）；λ——Lame常数，Pa；λr——岩石导热系数，W/（m·K）；λw——流体导热系数，W/（m·K）；μf——注入流体黏度，Pa·s；υ——泊松比，无因次；ρr——岩石密度，kg/m3；ρw——注入流体密度，kg/m3；σeff——平均有效应力，Pa；σh——最小水平主应力，MPa；σH——最大水平主应力，MPa；σmax——循环加载周期内最大应力，Pa；σv——垂直地应力，MPa；σ0——岩石初始强度，Pa；σ0,n——n次循环后的岩石强度，Pa；σ1——最大主应力，Pa；σ3——最小主应力，Pa；$ \chi_{\mathrm{f}}$——流体压缩系数，Pa−1；ϕr——岩石孔隙度，%；ϕre——残余孔隙度，%；ϕr0——初始孔隙度，%。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
李根生, 宋先知, 石宇, 等. 智慧地热田技术研究现状与系统构建方案[J]. 石油勘探与开发, 2024, 51(4): 899-909.

DOI

LI Gensheng, SONG Xianzhi, SHI Yu, et al. Current status and construction scheme of smart geothermal field technology[J]. Petroleum Exploration and Development, 2024, 51(4): 899-909.

[2]
谢和平. “深部岩体力学与开采理论”研究构想与预期成果展望[J]. 工程科学与技术, 2017, 49(2): 1-16.

XIE Heping. Research framework and anticipated results of deep rock mechanics and mining theory[J]. Advanced Engineering Sciences, 2017, 49(2): 1-16.

[3]
多吉, 王贵玲. 加大深部热能探采技术攻关持续推进地热资源规模化开发[J]. 科技导报, 2022, 40(20): 1.

DUO Ji, WANG Guiling. Enhancing deep thermal energy exploration and extraction technology to promote the large-scale development of geothermal resources[J]. Science & Technology Review, 2022, 40(20): 1.

[4]
赵鹏, 朱海燕, 李根生, 等. 青海共和盆地干热岩注采大尺度物理模拟实验[J]. 石油勘探与开发, 2024, 51(3): 646-654.

DOI

ZHAO Peng, ZHU Haiyan, LI Gensheng, et al. Large-scale physical simulation of injection and production of hot dry rock in Gonghe Basin, Qinghai Province, China[J]. Petroleum Exploration and Development, 2024, 51(3): 646-654.

[5]
王天宇, 周小夏, 李根生, 等. 基于热—流—固耦合的多分支径向井地热开发模型及其取热效果分析[J]. 天然气工业, 2023, 43(3): 133-144.

WANG Tianyu, ZHOU Xiaoxia, LI Gensheng, et al. Geothermal development model of multilateral radial well and its heat extraction effect analysis based on thermal-hydraulic-mechanical coupling[J]. Natural Gas Industry, 2023, 43(3): 133-144.

[6]
ZANG A, ZIMMERMANN G, HOFMANN H, et al. How to reduce fluid-injection-induced seismicity[J]. Rock Mechanics and Rock Engineering, 2019, 52(2): 475-493.

DOI

[7]
MCGARR A, BEKINS B, BURKARDT N, et al. Coping with earthquakes induced by fluid injection[J]. Science, 2015, 347(6224): 830-831.

[8]
GIARDINI D. Geothermal quake risks must be faced[J]. Nature, 2009, 462(7275): 848-849.

[9]
JI Y L, ZHUANG L, WU W, et al. Cyclic water injection potentially mitigates seismic risks by promoting slow and stable slip of a natural fracture in granite[J]. Rock Mechanics and Rock Engineering, 2021, 54(10): 5389-5405.

[10]
YANG Y, HU D, WANG H, et al. Experimental study on SC-CO2 fracturing of granite under real-time high temperature and true triaxial stress[J]. International Journal of Rock Mechanics and Mining Sciences, 2024, 183: 105889.

[11]
JINGNA X, JUN X, GUANHUA N, et al. Effects of pulse wave on the variation of coal pore structure in pulsating hydraulic fracturing process of coal seam[J]. Fuel, 2020, 264: 116906.

[12]
ZHUANG L, KIM K Y, JUNG S G, et al. Cyclic hydraulic fracturing of pocheon granite cores and its impact on breakdown pressure, acoustic emission amplitudes and injectivity[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 122: 104065.

[13]
LI Q G, LIN B Q, ZHAI C. The effect of pulse frequency on the fracture extension during hydraulic fracturing[J]. Journal of Natural Gas Science and Engineering, 2014, 21: 296-303.

[14]
李全贵. 脉动载荷下煤体裂隙演化规律及其在瓦斯抽采中的应用研究[D]. 徐州: 中国矿业大学, 2015.

LI Quangui. Research on the evolution law of coal fracture under pulse loading and its application on gas extraction[D]. Xuzhou: China University of Mining and Technology, 2015.

[15]
翟成, 李贤忠, 李全贵. 煤层脉动水力压裂卸压增透技术研究与应用[J]. 煤炭学报, 2011, 36(12): 1996-2001.

ZHAI Cheng, LI Xianzhong, LI Quangui. Research and application of coal seam pulse hydraulic fracturing technology[J]. Journal of China Coal Society, 2011, 36(12): 1996-2001.

[16]
WEI C, LI S C, YU L Y, et al. Study on mechanism of strength deterioration of rock-like specimen and fracture damage deterioration model under pulse hydraulic fracturing[J]. Rock Mechanics and Rock Engineering, 2023, 56(7): 4959-4973.

[17]
ZANG A, YOON J S, STEPHANSSON O, et al. Fatigue hydraulic fracturing by cyclic reservoir treatment enhances permeability and reduces induced seismicity[J]. Geophysical Journal International, 2013, 195(2): 1282-1287.

[18]
ZANG A, STEPHANSSON O, STENBERG L, et al. Hydraulic fracture monitoring in hard rock at 410 m depth with an advanced fluid-injection protocol and extensive sensor array[J]. Geophysical Journal International, 2017, 208(2): 790-813.

[19]
ZANG A, STEPHANSSON O, ZIMMERMANN G. Keynote: Fatigue hydraulic fracturing[R]. ISRM-EUROCK 2017-142, 2017.

[20]
ZHUANG L, JUNG S G, DIAZ M, et al. Laboratory true triaxial hydraulic fracturing of granite under six fluid injection schemes and grain-scale fracture observations[J]. Rock Mechanics and Rock Engineering, 2020, 53(10): 4329-4344.

[21]
ZHUANG L, SUN C L, HOFMANN H, et al. Comparison of fatigue hydraulic fracturing of granite cores subjected to creep and cyclic injection[J]. Rock Mechanics and Rock Engineering, 2024, 57(8): 5465-5481.

[22]
李根生, 武晓光, 宋先知, 等. 干热岩地热资源开采技术现状与挑战[J]. 石油科学通报, 2022, 7(3): 343-364.

LI Gensheng, WU Xiaoguang, SONG Xianzhi, et al. Status and challenges of hot dry rock geothermal resource exploitation[J]. Petroleum Science Bulletin, 2022, 7(3): 343-364.

[23]
亢方超, 唐春安, 李迎春, 等. 增强地热系统研究现状: 挑战与机遇[J]. 工程科学学报, 2022, 44(10): 1767-1777.

KANG Fangchao, TANG Chun’an, LI Yingchun, et al. Challenges and opportunities of enhanced geothermal systems: A review[J]. Chinese Journal of Engineering, 2022, 44(10): 1767-1777.

[24]
荀杨, 苏博, 翟梁皓, 等. 干热岩储层改造技术研究进展[J]. 长春工程学院学报(自然科学版), 2023, 24(3): 81-86.

XUN Yang, SU Bo, ZHAI Lianghao, et al. Progress in research on modification technology of hot dry rock reservoir[J]. Journal of Changchun Institute of Technology (Natural Sciences Edition), 2023, 24(3): 81-86.

[25]
解经宇, 王丹, 李宁, 等. 干热岩压裂建造人工热储发展现状及建议[J]. 地质科技通报, 2022, 41(3): 321-329.

XIE Jingyu, WANG Dan, LI Ning, et al. Development status and suggestions of hot dry rock hydraulic fracturing for building geothermal reservoirs[J]. Bulletin of Geological Science and Technology, 2022, 41(3): 321-329.

[26]
刘贺娟, 童荣琛, 侯正猛, 等. 地下流体注采诱发地震综述及对深部高温岩体地热开发的影响[J]. 工程科学与技术, 2022, 54(1): 83-96.

LIU Hejuan, TONG Rongchen, HOU Zhengmeng, et al. Review of induced seismicity caused by subsurface fluid injection and production and impacts on the geothermal energy production from deep high temperature rock[J]. Advanced Engineering Sciences, 2022, 54(1): 83-96.

[27]
郭建春, 任冀川, 王世彬, 等. 裂缝性致密碳酸盐岩储层酸压多场耦合数值模拟与应用[J]. 石油学报, 2020, 41(10): 1219-1228.

DOI

GUO Jianchun, REN Jichuan, WANG Shibin, et al. Numerical simulation and application of multi-field coupling of acid fracturing in fractured tight carbonate reservoirs[J]. Acta Petrolei Sinica, 2020, 41(10): 1219-1228.

DOI

[28]
AKDAS S B, ONUR M. Analytical solutions for predicting and optimizing geothermal energy extraction from an enhanced geothermal system with a multiple hydraulically fractured horizontal-well doublet[J]. Renewable Energy, 2022, 181: 567-580.

[29]
JIRÁSEK M, BAUER M. Numerical aspects of the crack band approach[J]. Computers & Structures, 2012, 110/111: 60-78.

[30]
LI T J, LI L C, TANG C A, et al. A coupled hydraulic-mechanical- damage geotechnical model for simulation of fracture propagation in geological media during hydraulic fracturing[J]. Journal of Petroleum Science and Engineering, 2019, 173: 1390-1416.

[31]
WEI C H, ZHU W C, CHEN S K, et al. A coupled thermal- hydrological-mechanical damage model and its numerical simulations of damage evolution in APSE[J]. Materials, 2016, 9(11): 841.

[32]
LIU Y, DAI F, FAN P X, et al. Experimental investigation of the influence of joint geometric configurations on the mechanical properties of intermittent jointed rock models under cyclic uniaxial compression[J]. Rock Mechanics and Rock Engineering, 2017, 50(6): 1453-1471.

[33]
CERFONTAINE B, COLLIN F. Cyclic and fatigue behavior of rock materials: Review, interpretation and research perspectives[J]. Rock Mechanics and Rock Engineering, 2018, 51(2): 391-414.

[34]
XI X, YANG S T, MCDERMOTT C I, et al. Modeling rock fracture induced by hydraulic pulses[J]. Rock Mechanics and Rock Engineering, 2021, 54(8): 3977-3994.

[35]
NOJAVAN S, SCHESSER D, YANG Q D. An in situ fatigue-CZM for unified crack initiation and propagation in composites under cyclic loading[J]. Composite Structures, 2016, 146: 34-49.

[36]
WEI C H, ZHU W C, YU Q L, et al. Numerical simulation of excavation damaged zone under coupled thermal-mechanical conditions with varying mechanical parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 75: 169-181.

[37]
余莉, 彭海旺, 李国伟, 等. 花岗岩高温-水冷循环作用下的试验研究[J]. 岩土力学, 2021, 42(4): 1025-1035.

YU Li, PENG Haiwang, LI Guowei, et al. Experimental study on granite under high temperature-water cooling cycle[J]. Rock and Soil Mechanics, 2021, 42(4): 1025-1035.

[38]
ZHANG W, GUO T K, QU Z Q, et al. Research of fracture initiation and propagation in HDR fracturing under thermal stress from meso-damage perspective[J]. Energy, 2019, 178: 508-521.

[39]
ZHANG X, HUANG Z W, LI G S, et al. Enhancing reservoir stimulation and heat extraction performance for fractured geothermal reservoirs: Utilization of novel multilateral wells[J]. Energy, 2024, 291: 130410.

[40]
SENJUNTICHAI T, RAJAPAKSE R. Transient response of a circular cavity in a poroelastic medium[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1993, 17(6): 357-383.

[41]
白冰. 岩土颗粒介质非等温一维热固结特性研究[J]. 工程力学, 2005, 22(5): 186-191.

BAI Bing. One-dimensional thermal consolidation characteristics of geotechnical media under non-isothermal condition[J]. Engineering Mechanics, 2005, 22(5): 186-191.

[42]
BAI M, ROEGIERS J C. Fluid flow and heat flow in deformable fractured porous media[J]. International Journal of Engineering Science, 1994, 32(10): 1615-1633.

Options
文章导航

/

〈 〉

版权所有：《石油勘探与开发》编辑部；《石油勘探与开发（英文）》编辑部
地址：北京市海淀区学院路20号，中国石油勘探开发研究院数据中心605室　

京ICP备15044687号    技术支持：北京玛格泰克科技发展有限公司