0 引言
超深—特深井钻井过程中钻柱具有超大长细比，处于超大轴向力、大扭矩、高温高压等极端载荷环境，受狭长井筒的限制，振动特征非常复杂，使得钻柱安全性和钻井效率面临严峻挑战[3⇓⇓-6]。长期以来，钻柱振动引起的失效问题备受关注，国内外学者通过各种方法对钻柱的动力学特性开展了深入研究。Jansen[7]采用集中质量模型研究了底部钻具组合（BHA）的涡动特征，基于此，Di等[8]对预弯曲动力学防斜打快技术的机理进行研究，分析了钻压、转速及BHA结构参数对钻头动态侧向力的影响。Dykstra[9]基于Himilton原理，考虑钻柱的几何非线性和接触非线性，推导出钻柱动力学有限元模型，分别计算了钻柱的静态解、动力学稳态解和瞬态解；祝效华等[10]建立了三维井眼全井钻柱动力学有限元模型，采用Wilson-θ逐步积分法研究了具有不确定性和动态边界的大型非线性系统；Hu等[11]以空间曲梁单元为基础建立钻柱动力学有限元模型，实现了超7 000 m钻柱的动力学特性分析。Cheng等[12]基于绝对节点坐标法建立了全井钻柱系统多体动力学模型，实现了钻柱黏滑、涡动、动态屈曲、跳钻等井下动力学特性模拟。随着钻柱振动研究的深入和测量技术的进步，新的振动现象（如高频扭转振荡）和新的失效形式（如电子元件故障）不断显现[13⇓⇓-16]，钻柱动力学研究需要进一步拓展，方能满足实际钻井工程的安全要求。
在塔里木油田超深井钻井作业中，常常遇到井下钻具接头的二次上扣问题，说明井下存在动态冲击扭矩，严重影响钻井作业安全。目前少有关于特深井钻具接头三维力学分析的文献，其中陈锋等[17]研究了适用于特深井的双台肩钻杆接头合理副台肩间隙问题。为了保证中国首口超万米特深井——SDTK1井的钻具安全，测量了具有相同上部井筒尺寸的塔里木油田格探1井（GT1井）钻铤螺纹接头台肩处的二次上扣量，并分析了二次上扣后钻具接头的应力特征，为寻找有效保障措施提供依据。鉴于目前无法直接测量井下动态冲击扭矩，本文采用等效冲击扭矩评价钻铤接头二次上扣的载荷特征，利用钻铤接头内、外螺纹台肩处的环向相对偏移量反映二次上扣特征，结合有限元分析确定井下等效冲击扭矩与相对偏移量的关系式，作为根据相对偏移量快速确定井下等效冲击扭矩的预测模型。在SDTK1井二开井段对该方法进行了二次验证，并将其应用于后续钻井作业的井下等效冲击扭矩预测。
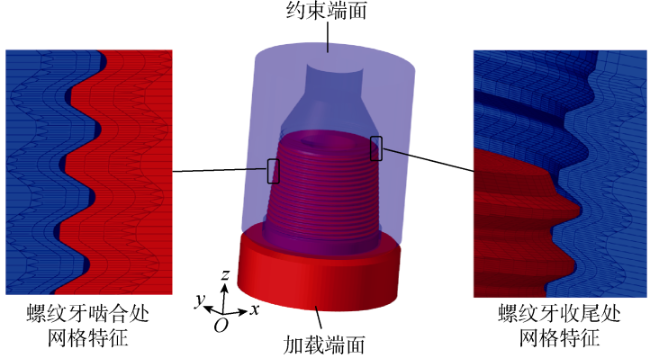
1 钻铤接头三维弹塑性有限元模型
1.1 分析方法
钻铤接头由内、外螺纹通过三维空间螺旋曲面啮合而成，台肩面之间和螺纹牙啮合面之间的接触关系非常复杂，其三维力学计算涉及接触条件高度非线性的问题。本文采用显式动力学计算方法求解动力学方程，即应用一个增量步的动力学状态计算下一个增量步的动力学状态且无需迭代，求解运动方程时不需要进行矩阵求逆，能有效计算复杂载荷作用下钻铤接头的三维应力。钻铤接头的动力学平衡方程为：
采用中心差分方法进行求解，用位移表示加速度和速度[18]：
将（2）式和（3）式代入t时刻的动力学平衡方程，可得中心差分法的递推公式：
求解（4）式可得（t+Δt）时刻的节点位移ut+Δt，将ut+Δt代入几何方程与本构方程即可获得（t+Δt）时刻的单元应变与单元应力。
1.2 网格划分和材料参数
二次上扣过程是上扣后的钻具接头内、外螺纹在井下复杂载荷作用下的位移变化过程。GT1井二开井段第2趟钻使用如下BHA进行钻进作业：17″（431.8 mm）聚晶金刚石复合片（PDC）钻头+241.0 mm旋转导向钻井系统Power-V+螺杆钻具+17″（431.8 mm）倒划眼稳定器+9″（228.6 mm）钻铤×3根+转换接头+8″（203.2 mm）浮阀+ 8″（203.2 mm）钻铤×13根+8″（203.2 mm）随钻震击器+8″（203.2 mm）挠性接头+8″（203.2 mm）钻铤×5根。现场统计资料表明，二次上扣主要发生在BHA。本趟BHA包括203.2 mm和228.6 mm两种规格的钻铤。与228.6 mm钻铤相比，203.2 mm钻铤接头的抗冲击能力较弱，因此仅建立203.2 mm钻铤接头的三维弹塑性有限元模型。利用非线性有限元分析软件ABAQUS计算上扣扭矩、轴向力和不同井下冲击扭矩作用下203.2 mm钻铤接头的力学性能，分析不同井下冲击扭矩作用下钻铤接头的井下上扣特性。
203.2 mm钻铤NC56接头的基本尺寸如表1 所示。为了准确模拟复合载荷作用下钻铤接头的应力特征，考虑螺纹牙的螺旋升角，采用六面体网格划分以保证计算精度，在螺纹牙啮合区域布置细密网格。整个有限元模型的单元数为66.2×104，节点数为75.7×104，计算时选用的单元类型为C3D8I，网格划分如图1 所示。在台肩啮合面、螺纹啮合面处定义接触，以模拟外载荷作用下外螺纹、内螺纹之间的相互作用。在外螺纹端面处建立分布式节点耦合，以施加外载荷；在内螺纹端面处建立运动式节点耦合，以施加约束。
表2 真实应力-塑性应变关系 |
| 真实应力/ MPa | 塑性 应变 | 真实应力/ MPa | 塑性 应变 | 真实应力/ MPa | 塑性 应变 |
|---|---|---|---|---|---|
| 758.0 | 0 | 953.7 | 0.025 | 1 063.6 | 0.065 |
| 790.1 | 0.000 5 | 971.3 | 0.030 | 1 072.4 | 0.070 |
| 818.3 | 0.001 0 | 987.6 | 0.035 | 1 079.8 | 0.075 |
| 878.5 | 0.006 0 | 1 003.3 | 0.040 | 1 086.1 | 0.080 |
| 891.3 | 0.009 0 | 1 017.6 | 0.045 | 1 091.2 | 0.085 |
| 905.2 | 0.012 0 | 1 030.9 | 0.050 | 1 095.1 | 0.097 |
| 920.8 | 0.016 0 | 1 043.0 | 0.055 | ||
| 940.1 | 0.021 0 | 1 054.3 | 0.060 |
钻铤接头应力分布不均匀，当外载荷达到特定数值时，存在严重应力集中的区域首先进入塑性状态，此时线弹性应力-应变关系已不再适用。因此，本研究引入非线性的应力-应变关系，采用von Mises屈服准则[18]：
其中
材料的初始屈服应力σso可通过单轴拉伸实验获取。材料发生屈服后，本文采用von Mises流动法则描述塑性应变增量在各个方向上的分量和应力增量分量之间的关系，并选用各向同性硬化模型模拟复杂载荷作用下钻具接头的材料硬化特性。
整个有限元分析包含3个分析步：在第1个分析步中对NC56钻铤接头进行上扣预紧，上扣扭矩参照API（美国石油学会）标准设定为65 kN·m；考虑到近钻头位置的钻铤接头在动态钻压的作用下承受轴向压缩载荷作用，在第2个分析步中对模型施加120 kN的轴向压缩载荷；第3个分析步中对模型施加井下等效冲击扭矩（0~120 kN·m），以分析不同井下等效冲击扭矩作用下外螺纹、内螺纹相对转动情况。需要注意的是，等效冲击扭矩与井下实际的动态冲击扭矩不同，是一种准静态加载条件下的等效扭矩，即二者产生等效的上扣量。
2 钻铤接头三维弹塑性有限元分析
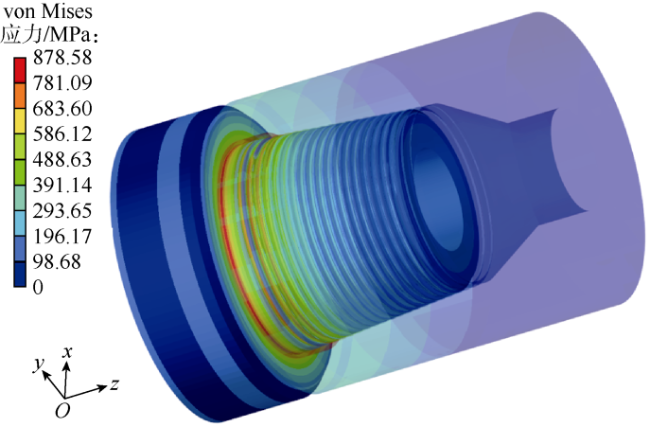
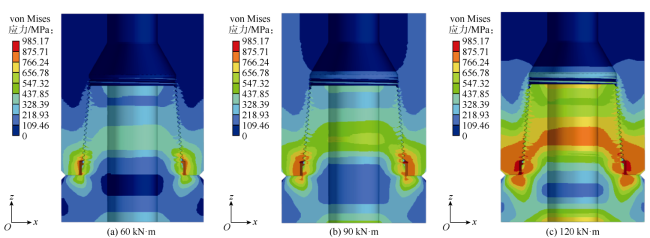
2.1 上扣扭矩作用下钻铤接头的三维应力特征
在65 kN·m上扣扭矩作用下钻铤接头的von Mises应力分布云图如图2 所示。分析结果表明，上扣预紧作用下钻铤接头应力分布不均匀，台肩及靠近台肩的啮合螺纹牙处应力水平较高，von Mises应力最大值为878.58 MPa，出现在外螺纹近台肩第1个啮合螺纹牙处。
在钻铤接头旋转中心建立柱坐标系，将位移计算结果转换至该柱坐标系中得到钻铤接头环向相对位移，分析上扣扭矩作用下内、外螺纹间的相对转动（见图3 ）。上扣过程中钻铤接头内螺纹端部约束固定，外螺纹端部施加上扣扭矩，此时外螺纹会相对内螺纹旋进预紧，产生相对位移。在65 kN·m上扣扭矩作用下，钻铤接头内、外螺纹台肩处的环向相对位移为50.0 mm。将上扣扭矩单独造成的环向相对位移称为基准偏移量，在此基础上其他载荷引起的偏移量增量称为相对偏移量。
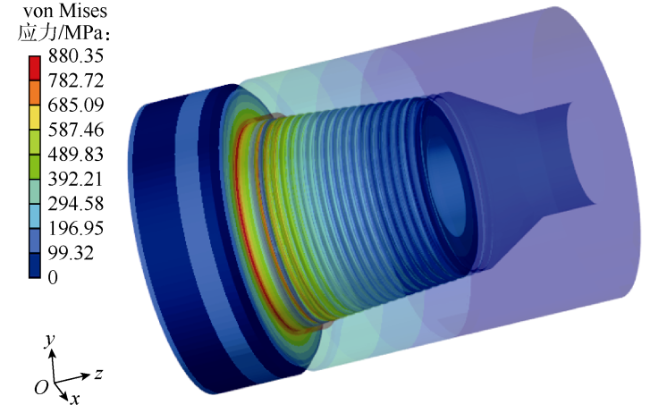
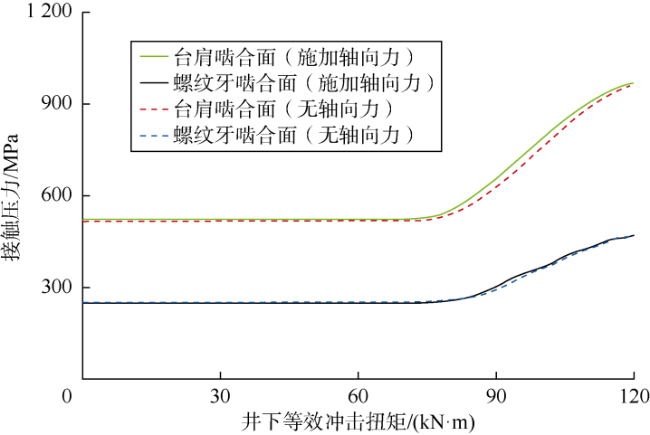
2.2 上扣扭矩和轴向压缩载荷作用下钻铤接头的应力特征
实际钻井作业中，靠近钻头位置的钻铤接头所受轴向压缩载荷相对较大，而靠近钻柱中和点的钻铤接头承受轴向压缩载荷相对较小，因此需要探明所施加的轴向载荷是否会影响上扣后钻铤接头的应力特征。在65 kN·m上扣扭矩的基础上对钻铤接头施加120 kN轴向压缩载荷，此时钻铤接头的von Mises应力分布云图如图4 所示。分析结果表明，与单独施加上扣扭矩相比（见图2 ），增加轴向压缩载荷作用后钻铤接头应力分布变化不大，最大von Mises应力依然出现在外螺纹近台肩第1个啮合螺纹牙处，应力值为880.35 MPa。采用同样的方法建立柱坐标系、提取环向相对位移，65 kN·m上扣扭矩和120 kN轴向压缩载荷作用下，钻铤接头内、外螺纹台肩处的环向相对位移为50.0 mm，与基准偏移量相同，说明120 kN轴向压缩载荷未引起内螺纹、外螺纹出现相对偏移，即相对偏移量为0。
轴向压缩载荷为0，120 kN时，钻铤接头在不同井下等效冲击扭矩作用下各啮合面之间的接触压力变化特征如图5 所示。可以看出，压缩载荷的施加对螺纹牙啮合面、台肩啮合面上接触压力变化规律影响较小，轴向力的增加没有明显改变接头的应力特征。因此，利用120 kN轴向压缩载荷进行偏移量计算可以代表实际情况，误差小。
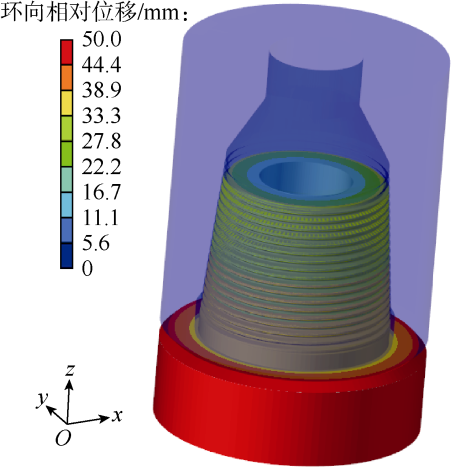
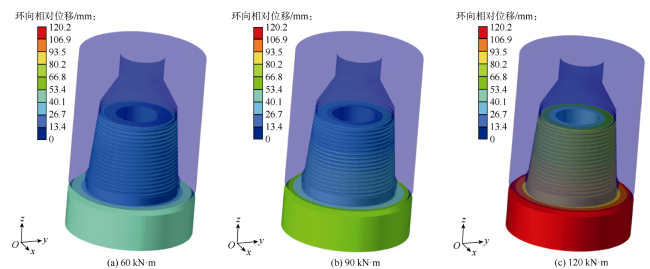
2.3 井下等效冲击扭矩作用下钻铤接头的三维应力特征及内、外螺纹相对偏移量
在上扣扭矩和轴向压缩载荷作用的基础上对模型施加不同的井下等效冲击扭矩，以获取井下等效冲击扭矩作用下钻铤接头的位移及应力分布特征。井下等效冲击扭矩分别为60，90，120 kN·m时，钻铤接头内、外螺纹的von Mises应力分布云图如图6 所示。对比可见，井下等效冲击扭矩越大，台肩和靠近台肩的螺纹牙处von Mises应力水平越高；应力峰值均出现在外螺纹近台肩第1个啮合螺纹牙处，井下等效冲击扭矩为60，90，120 kN·m时，von Mises应力峰值分别为878.8，917.3，985.2 MPa。
不同井下等效冲击扭矩作用下内、外螺纹间的相对转动情况如图7 所示。计算结果表明，在60，90，120 kN·m井下等效冲击扭矩作用下钻铤接头内、外螺纹台肩处的环向相对位移最大值分别为50.1，61.8，120.2 mm，则相对偏移量分别为0.1，11.8，70.2 mm。冲击扭矩的加载是一个连续的过程，实际计算时涉及计算点较多，考虑实际情况下的相对偏移量一般小于40.0 mm，本文参照该偏移量范围对计算结果进行回归，得到井下等效冲击扭矩与内、外螺纹台肩处相对偏移量的关系曲线（见图8 ）。
由图可见，当井下等效冲击扭矩小于65 kN·m时，钻铤接头内、外螺纹台肩处的相对偏移量几乎为0，此时接头仍处于较好的上扣预紧状态。当井下等效冲击扭矩超过65 kN·m时钻铤接头的上扣预紧平衡状态被打破，钻铤接头内、外螺纹之间产生明显的相对偏移量。因此，对井下等效冲击扭矩超过65 kN·m的数据进行拟合，得到（6）式。拟合曲线的相关系数为0.998，参与回归的计算点共23个。
（T≥65 kN·m）
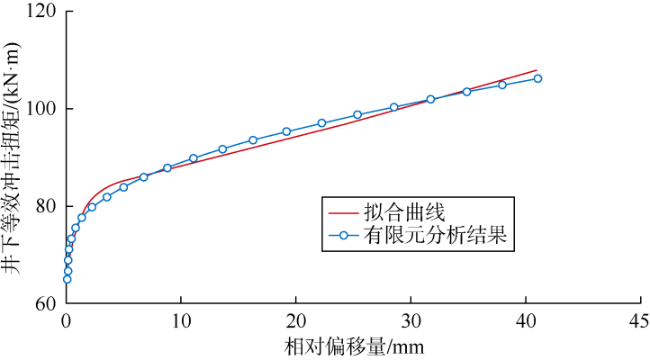
3 钻铤接头井下等效冲击扭矩预测
根据（6）式，可以由接头内、外螺纹台肩处的环向相对偏移量反算井下等效冲击扭矩。因此，下钻前在前述BHA中203.2 mm钻铤接头上以刻痕作为标记，待起钻时测量刻痕标记偏移量大小，即相对偏移量。GT1井第2趟钻具组合中除钻头、Power-V、扶正器、228.6 mm钻铤用B型钳外，其他钻具均采用液气大钳按照API标准推荐上扣扭矩进行上扣，确保测量结果不受上扣扭矩的影响。
GT1井的完井井深为5 180 m，二开17″（431.8 mm）井眼的井深为530~3 580 m，二开第2趟钻钻具组合所钻井段为2 877~3 580 m。钻井过程中，钻压为60~120 kN，地面转速为60 r/min。起钻后发现NC611×NC560转换接头和203.2 mm浮阀接头内、外螺纹台肩处相对偏移量为13 mm，203.2 mm浮阀接头与203.2 mm钻铤接头内、外螺纹台肩处相对偏移量为4 mm（见图9 、图10 ）。
现场测试结果表明，BHA中不同位置的钻铤接头发生了二次上扣现象。同时，不同位置的钻铤接头内、外螺纹台肩处的环向相对偏移量不尽相同，证明不同位置的钻铤承受不同的冲击扭矩作用，且大于上扣扭矩。根据（6）式可得，转换接头和浮阀间的相对偏移量为13 mm时，对应的井下等效冲击扭矩为90.05 kN·m，而该接头的现场卸扣扭矩为90.00 kN·m，因此理论计算结果与实测卸扣扭矩的误差仅为0.06%。浮阀与203.2 mm钻铤间的实测偏移量为4 mm，此时对应的井下等效冲击扭矩为84.35 kN·m，而该接头现场卸扣扭矩为80.00 kN·m，理论计算结果与实测结果的误差为5.44%。上述结果证明了本文计算方法的准确性。
SDTK1井于2023年5月30日开钻，并于2023年6月1日开始进行二开井段第2趟钻的钻井作业，所用BHA为：431.8 mm PDC钻头+241.0 mm Power-V+螺杆+431.8 mm稳定器+228.6 mm钻铤×6根+转换接头+ 203.2 mm钻铤×6根+浮阀+203.2 mm钻铤×6根+203.2 mm随钻震击器+203.2 mm钻铤×3根。该趟钻所用的钻压和地面转速为60 kN和60 r/min。为了提高接头的抗扭能力，将部分203.2 mm钻铤接头的上扣扭矩提高到71 kN·m。下钻时在203.2 mm钻铤接头处进行刻痕标记，起钻后发现203.2 mm钻铤接头的标记均发生了偏移。表3 中列出了部分203.2 mm钻铤接头内、外螺纹台肩处的相对偏移量。
表3 SDTK1井二开第2趟钻钻铤接头内、外螺纹台肩处相对偏移量及对应的井下等效冲击扭矩 |
| 203.2 mm钻铤接头刻痕位置 | 扣型 | 上扣扭矩/ （kN·m） | 相对偏移量/ mm | 卸扣扭矩/ （kN·m） | 井下等效冲击扭矩/ （kN·m） | 井下等效冲击扭矩与 卸扣扭矩的相对误差/% |
|---|---|---|---|---|---|---|
| 第3根下端 | NC56 | 71 | 18 | 94 | 93.03 | −1.03 |
| 第7根下端 | NC56 | 69 | 18 | 101 | 93.03 | −7.89 |
| 第8根下端 | NC56 | 71 | 15 | 91 | 91.23 | 0.25 |
| 第10根下端 | NC56 | 71 | 19 | 96 | 93.64 | −2.46 |
如表3 所示，SDTK1井二开第2趟钻所用钻具组合中由钻头向上第3根203.2 mm钻铤下端的相对偏移量为18 mm，由（6）式计算对应的井下等效冲击扭矩为93.03 kN·m，与卸扣扭矩的相对误差仅为−1.03%；第8根203.2 mm钻铤下端及第10根203.2 mm钻铤接头的相对偏移量分别为15，19 mm，对应的井下等效冲击扭矩为91.23，93.64 kN·m，与卸扣扭矩的相对误差分别为0.25%和−2.46%。第7根钻铤下端与浮阀连接处（即浮阀上端）的上扣扭矩为69 kN·m，测得的相对偏移量为18 mm，计算井下等效冲击扭矩为93.03 kN·m，与卸扣扭矩的相对误差为−7.89%，在4个测点中相对误差最大，可能与不同的上扣扭矩及浮阀有关。上述结果再次表明，（6）式具有较高的预测精度。实际操作中，铁钻工卸扣时测量的数据波动范围较大，获取准确的卸扣扭矩费时费力，采用（6）式可以根据相对偏移量快速获取井下等效冲击扭矩的大小。通过测量SDTK1井二开井段第3趟钻203.2 mm钻铤接头相对偏移量，计算出井下等效冲击扭矩（见表4 ）。
表4 SDTK1井二开第3趟钻203.2 mm钻铤NC56接头内、外螺纹台肩处相对偏移量及对应的井下等效冲击扭矩 |
| 203.2 mm钻铤 接头刻痕位置 | 上扣扭矩/ (kN·m) | 相对偏移量/ mm | 井下等效冲击 扭矩/(kN·m) |
|---|---|---|---|
| 第3根下端 | 71 | 12 | 89.17 |
| 第5根下端 | 71 | 19 | 93.16 |
| 第6根下端 | 71 | 22 | 94.93 |
| 第9根下端 | 71 | 1 | 75.78 |
上述结果表明，SDTK1井二开第3趟钻203.2 mm钻铤接头处承受了较大的井下冲击扭矩作用，给钻铤接头带来安全隐患。另外，不同位置的钻铤承受了不同的井下冲击扭矩，一方面说明井下钻铤的运动特征十分复杂，另一方面说明相对偏移量受多种因素影响，包括冲击扭矩大小、测量精度、上扣扭矩是否按标准准确施加及接头螺纹间的接触状态等。
上述方法在SDTK1井后续井段钻井中得到很好应用，较好地评价了钻铤接头承受的井下等效冲击扭矩。在SDTK1井四开钻井中，多趟钻出现了钻具接头的二次上扣现象，并且在钻铤接头或加重钻杆接头内螺纹中形成微裂纹，其中第4趟钻所用21根7″（177.8 mm）钻铤中有17根钻铤接头内螺纹出现微裂纹（见图11 ）。为了排除钻铤接头失效隐患，确保井下安全，采用了以下3项措施：①更换已出现微裂纹的钻铤；②在确保上扣扭矩满足要求的前提下，采用具有更高抗扭能力的双台肩接头DS56[20]，提高钻具接头的抗冲击扭矩能力，使微裂纹出现的频率大幅度减少；③优化钻柱结构参数和钻井参数，减小钻柱振动，降低井下冲击扭矩。
4 结论
复杂载荷作用下钻铤接头应力分布不均匀，台肩处和靠近台肩的螺纹牙处von Mises应力水平相对较高，是钻铤接头的薄弱位置。对于按API标准上扣的203.2 mm钻铤接头，当井下等效冲击扭矩超过65 kN·m时，钻铤接头的上扣预紧平衡被打破，钻铤接头发生二次上扣，内、外螺纹台肩处相对偏移量随井下等效冲击扭矩的增大而增加。根据接头内、外螺纹台肩处相对偏移量，通过有限元分析可实现井下等效冲击扭矩的反演，并形成井下等效冲击扭矩的快速预测方法。SDTK1井井下存在较大的冲击扭矩，井下载荷复杂，需要采取有效措施提高接头的抗冲击扭矩能力或降低井下冲击扭矩：一是采用双台肩钻铤螺纹接头代替单台肩钻铤螺纹接头；二是优化钻柱结构参数和钻井参数，减小钻柱振动，降低井下冲击扭矩。
符号注释：
a(t)——t时刻系统的节点加速度向量，m/s2；C——系统的阻尼矩阵，N/（m·s−1）； ——应力函数；K——系统的刚度矩阵，N/m；M——系统的质量矩阵，kg；Q(t)——t时刻系统的节点载荷向量，N；sij——偏应力张量，MPa；t——时间，s；Δt——计算时间步长，s；T——钻铤接头受到的井下等效冲击扭矩，kN·m；u——系统的位移，m；u(t)——t时刻系统的节点位移，m；v(t)——t时刻节点速度向量，m/s；x，y，z——柱坐标系3个方向；δij——Kronecker符号，无因次；ξ——钻井过程中钻铤接头内、外螺纹台肩处的相对偏移量，mm；σm——平均正应力，MPa；σso——材料的初始屈服应力，MPa；σ11，σ22，σ33——3个方向的主应力，MPa。下标：i，j——可分别取值1，2，3，表征不同的应力分量。