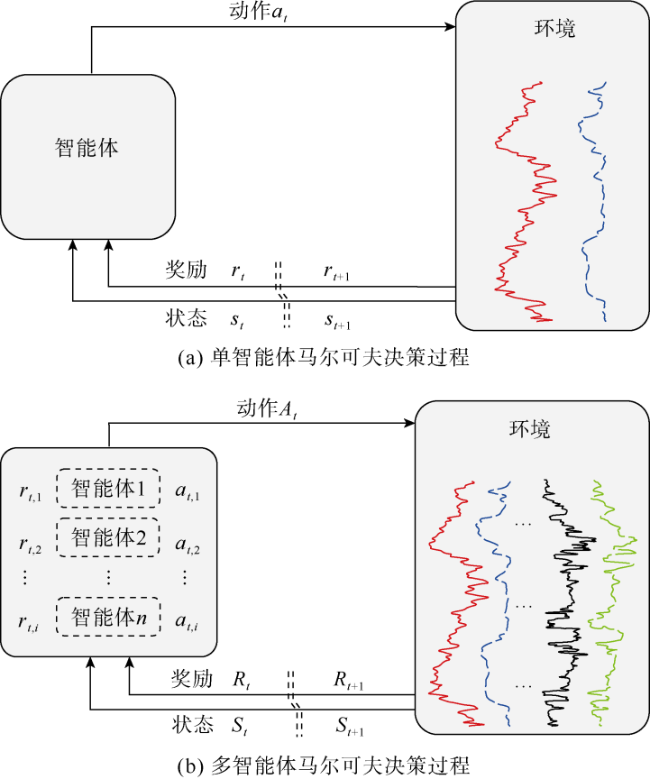
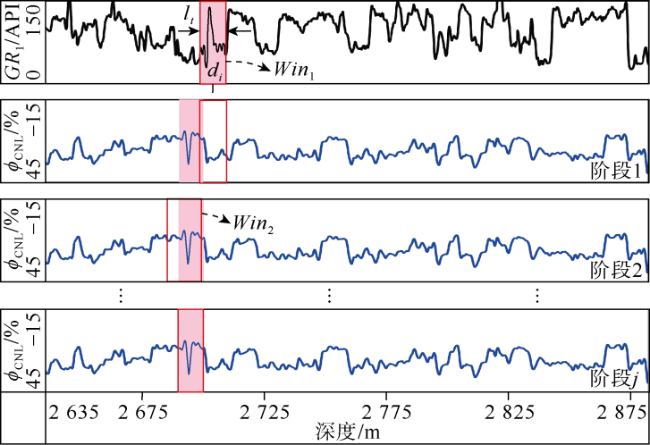
这样多智能体进行深度校正任务时,
t时刻每个智能体通过观察当前双滑动窗口输入的测井曲线特征序列获得一个深度匹配状态。第1类智能体(负责
GR曲线之间的深度校正)按照预设顺序先做出决策,即根据
ε-greedy策略
[26]选择一个动作
作用于环境。随后第2类智能体(负责
ϕCNL、
ρ、Δ
t等与
GR1之间的深度校正)基于第1种智能体的决策结果选择一个动作
作用于被校正的测井曲线。
t时刻,每一个智能体与环境交互后可以更新到下一时间步状态
和获得一个反馈奖励
。然后经验回放池
收集并存储智能体在每一个时间
t的经验样本
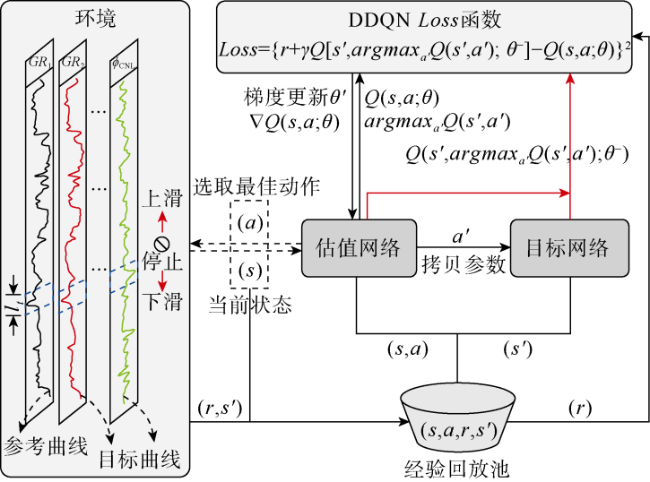
。如
图3所示,在模型训练过程中,DDQN随机从经验池
Dt中选取一小批样本数据,通过估值网络计算当前状态下选择动作
的
Q值
Q(
s,
a;
θ),并利用目标网络估计下一状态下选择动作
的价值
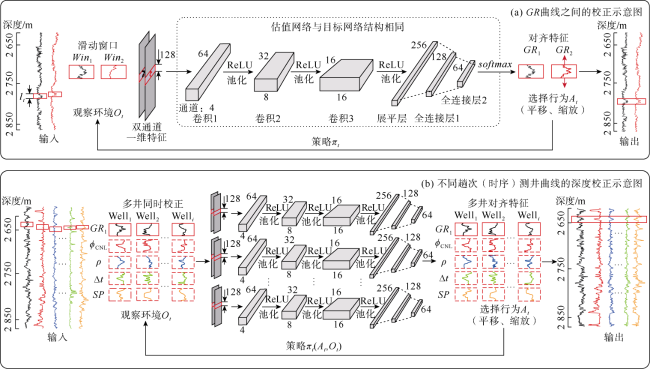
。这种双网络结构具有相同的架构,都包含有3层卷积神经网络(见
图4),每个卷积层之后使用一个非线性激活函数ReLU和一个最大池化层,并通过全连接层来整合特征输出动作
Q值。然后,通过损失函数((5)式)计算当前策略下估值网络
Q值与目标网络
Q值之间的差异。通过最小化损失函数,用于指导神经网络的优化,从而学习到更优的匹配策略。最后,通过随机梯度下降法((6)式)将当前估值网络参数
更新到
以进行下一轮训练学习。重复上述过程,最终每个智能体能学习到如何采取最优的动作完成多条测井曲线深度匹配。