0 引言
CO2注入地下多孔介质的过程中，至少涉及到以下几个方面的基本问题：①多孔介质流动，地下岩石为具有复杂孔喉结构的多孔介质，因而涉及到多孔介质内的流动问题；②传质（多组分传输），地层水离子组分复杂，在与CO2和岩石的相互作用中，离子组分浓度可能发生变化，即存在多个组分的传输问题；③溶解（非均相化学反应），CO2可能与岩石部分矿物发生化学溶解反应，导致岩石孔喉结构变化，这属于非均相化学反应问题；④沉淀生成，CO2与地层水接触后可能导致某些无机盐过饱和结晶析出，此外，溶解作用可能诱发矿物颗粒从主矿物体脱落，生成新的沉淀；⑤沉淀运移，生成的沉淀在水动力的作用下会与流体一起运移，还可能发生沉淀沉积和再启动现象。因此，CO2-水-岩系统涉及到CO2、地层水、岩石之间的相互作用，其中，溶解和沉淀作用将导致岩石的孔隙度和渗透率发生改变，而沉淀运移则可能严重影响岩石的渗流能力（如堵塞喉道），这些物理化学过程的耦合作用可能导致储集层物性发生剧烈变化。对这些过程的微观作用机制认识不明确、缺乏有效的模拟表征方法，将导致储集层宏观孔渗参数变化规律预测不准确，进而使得埋存容量、注采能力、埋存封闭性等一系列参数的评价不可靠[6]，影响CCUS和CCS工业注采方案制定及安全评估的可靠性。
溶解—沉淀—沉淀运移是一种孔隙尺度行为，传统岩心渗流实验往往难以直观刻画其作用过程（如离子浓度变化、孔隙形貌演化、沉淀运移追踪等），导致对储集层物性参数变化规律认识不清。基于孔隙尺度微观渗流模拟，可以得到流体、离子、压力等在孔隙空间的三维分布，且能显性观察到多孔介质固体形貌随反应的变化，是连接宏观尺度与微观尺度的桥梁。开展CO2-水-岩系统的孔隙尺度模拟，有助于确定溶解、沉淀和沉淀运移的发生条件与判据，量化其对渗流规律的影响，为宏观数值模拟提供基础参数。
本文以CCUS及CCS技术中出现的CO2-水-岩系统为背景，系统综述CO2-水-岩复杂作用机理、多孔介质反应输运（溶解、沉淀及沉淀运移）微观模拟、CO2-水-岩系统微观模拟3个方面的研究现状，讨论国内外相关研究的优缺点，梳理目前研究存在的主要问题及技术瓶颈，并针对性地提出未来研究方向。
1 CO2-水-岩复杂作用机理
CO2-水-岩系统是一个耦合了流动、传质、溶解、沉淀、沉淀运移等过程的复杂渗流体系，如图1 所示。CO2注入地下与地层水接触后，首先在气相压力的作用下溶解在水中。CO2在水中的溶解度与压力呈正比，与温度、地层水矿化度呈反比[7]。溶解度主要采用Henry常数计算，较常用的还有一些经验公式[8]。CO2溶解于水后，主要以自由分子的形式存在，仅部分CO2与水结合形成H2CO3（见（1）式）。CO2在水中的溶解反应是一个平衡的过程，在没有催化剂时该反应需要很长时间才能达到平衡[9]。该溶解反应会释放出H+，导致溶液的pH值降低，且降低程度随着CO2溶解度的增加而增加[10]。在常温常压下，CO2饱和溶液的pH值为5.6。在酸性环境下，大多数矿物的化学性质不稳定，H+与这些矿物进行一系列的化学反应，产生溶解现象，并可能伴随释放出新的成垢离子（如Ca2+、Mg2+等）。同时，当CO2溶于水形成H2CO3后，由于解离作用，会进一步生成HCO3-和CO32-（见（2）式、（3）式），这些离子与成垢离子互相作用，产生沉淀现象。因此，CO2-水-岩相互作用会导致溶解和沉淀过程同时发生。
$\mathrm{CO}_{2}(\mathrm{~g})+\mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{H}_{2} \mathrm{CO}_{3}(\mathrm{aq})$
$\mathrm{H}_{2} \mathrm{CO}_{3} \rightleftharpoons \mathrm{H}^{+}+\mathrm{HCO}_{3}^{-}$
$\mathrm{HCO}_{3}^{-} \rightleftharpoons \mathrm{H}^{+}+\mathrm{CO}_{3}^{2-}$
CO2-水-岩石系统作用机理研究主要通过静态溶解实验和动态岩心驱替实验开展[11]。通过矿物组分分析、扫描成像、流体组分分析等手段，监测反应前后或反应过程中的矿物组分变化、孔喉变化及最终导致的岩心孔隙度、渗透率变化等信息。
1.1 矿物溶解
由于储集层中的许多岩石矿物（方解石、白云石、长石等）和胶结物化学性质不稳定，在与CO2、地层水形成的弱酸性流体接触时，会在化学反应的作用下发生溶解，如表1 所示。部分学者的实验结果表明，CO2-水-岩反应导致岩石孔隙度和渗透率增加。那金等[12]、Cui等[13]、丁茜等[14]采用碳酸盐岩岩心开展了一系列储集层条件下的溶解实验和岩心驱替实验，结果表明CO2在地层水的作用下对岩石矿物产生了强烈的溶蚀现象，增加了岩心的孔隙度和渗透率。孔隙度、渗透率增加的现象不仅出现在碳酸盐岩实验中，在砂岩实验中也有发现。李四海等[15]将砂岩岩心用CO2水溶液浸泡后，岩心产生了强烈的溶蚀作用，表现为方解石和白云石含量显著降低、溶蚀孔隙数量增多、原孔径变大，最终导致孔隙度和渗透率也相应增大。需要说明的是，不同矿物的反应速率会有几个数量级的差异[16-17]，因此，目前开展的相关室内实验受到时间尺度限制，一些速率较慢（几百至几千年）的反应在室内实验中可能无法观测到，不利于评估地质时间尺度下CO2对储集层孔隙度、渗透率的影响。
表1 CO2水溶液与部分矿物的化学反应 |
| 矿物类型 | 矿物名称 | 化学式 | 与CO2水溶液产生的化学反应 |
|---|---|---|---|
| 碳 酸 盐 | 方解石 | CaCO3 | CaCO3+CO2+H2O→Ca(HCO3)2[18] |
| 白云石 | CaR(CO3)2 | CaR(CO3)2+2CO2+2H2O→Ca(HCO3)2+R(HCO3)2[19] | |
| 菱镁矿、菱铁矿、菱锰矿 | R(CO3)2 | R(CO3)2+CO2+H2O→R(HCO3)2[19] | |
| 长石 | 钠长石 | NaAlSi3O8 | 2NaAlSi3O8+2CO2+3H2O→Al2Si2O5(OH)4+2Na++4SiO4+2HCO3-[19]，NaAlSi3O8+CO2+H2O→NaAlCO3(OH)2+3SiO4[20] |
| 钙长石 | CaAl2Si2O8 | CaAl2Si2O8+2CO2+3H2O→Al2Si2O5(OH)4+CaCO3[18] | |
| 钾长石 | KAlSi3O8 | 2KAlSi3O8+2CO2+3H2O→Al2Si2O5(OH)4+2K++4SiO4+2HCO3-[21] | |
| 黏土 | 伊利石 | K0.6Mg0.25Al2.3Si3.5O10(OH)2 | K0.6Mg0.25Al2.3Si3.5O10(OH)2+8H+→5H2O+0.6K++0.25Mg2++2.3Al3++3.5SiO2[13] |
| 绿泥石 | A5Al2Si3O10(OH)8 | A5Al2Si3O10(OH)8+5CaCO3+5CO2→5CaA(CO3)2+Al2Si2O5(OH)4+SiO2+2H2O[22] |
注：R为Mg/Fe/Mn，A为Mg/Fe |
1.2 矿物沉淀及运移
矿物溶解可能伴随产生次生矿物和溶解诱发的矿物颗粒脱落，这些沉淀可能在水动力作用下运移堵塞孔隙，导致岩石渗透率降低，且影响程度远大于对孔隙度的影响。于志超等[23]开展了地层条件下（100 ℃，24 MPa）饱和CO2地层水的驱替实验，发现实验过程中砂岩岩心的孔隙度基本不变但渗透率持续降低，认为是新生成的次生矿物和碳酸盐胶结物溶解释放出的黏土颗粒运移堵塞孔隙造成。Mohamed等[24]对砂岩的CO2驱替实验结果表明岩心的渗透率降低了55%，认为有如下两种因素导致岩心渗透率降低：①CO2-水-岩反应产生沉淀物运移堵塞孔隙；②部分胶结物发生反应溶解导致附着的黏土颗粒运移堵塞孔隙。Chen等[25]在60 ℃、20 MPa条件下对渗透率为100×10-3 μm2的砂岩开展饱和CO2水的驱替实验，发现岩心的孔隙度增加了1.8个百分点、渗透率降低了5.1%，这是碳酸盐胶结物溶解后诱发的颗粒运移引起的。Nunez等[26]通过串联2个白云岩岩心研究注CO2后近井筒和远井筒区域的溶解和沉淀特征，发现第1个岩心的孔隙度、渗透率都有所增加，而第2个岩心孔隙度基本不变，第1个岩心所形成的次生矿物运移到第2个岩心产生孔隙堵塞现象，最终使得远井筒区域渗透率降低。Wang等[27]研究发现CO2饱和水注入砂岩后，碳酸盐矿物溶解既会导致渗透率增加，也会诱发颗粒运移降低渗透率，地层水盐度较低时，溶蚀作用占主导地位，渗透率增加，而地层水盐度较高时，颗粒脱落运移显著，渗透率降低。
1.3 蒸发结晶
当干燥的超临界CO2注入矿化度较高的储集层时，会导致地层水蒸发进入CO2，当地层水中的盐浓度超过其溶解度极限时，易结晶析出，生成无机盐沉淀[28-29]。具体而言，存在如图2 所示的4个机理[30]：①CO2注入储集层形成两相流，即超临界CO2相和含盐地层水相。超临界CO2驱替地层水后，地层水以水膜、水桥等形式形成残余水。在干燥的超临界CO2持续流动作用下，这些含盐残余水开始蒸发。随着水的蒸发，CO2的相对渗透率增加，将进一步促进蒸发。②由于驱替前缘的干燥蒸发作用，会与远端高含水区产生毛管压力梯度，当该梯度超过注入压力梯度时，地层水回流至蒸发前缘，导致蒸发持续发生[31]；③随着水被蒸发进入超临界CO2中，残余水中的盐浓度增加，也会导致盐从干燥前缘向地层水侧扩散[32]。一旦盐浓度因蒸发达到其溶解度极限，盐将从溶液中析出，形成沉淀物。④沉淀的盐对盐水有很强的亲和力，诱导远距离的盐水向蒸发前缘移动、蒸发，进一步导致沉淀增加[33]，类似于毛细管抽吸作用。因此，当干燥的CO2注入到高矿化度储集层中时，一般从注入端到储集层端会形成3个典型区域：产生大量沉淀的干燥区域、CO2驱替地层水的两相流区域、地层水单相流动区域。
2 多孔介质反应输运的微观模拟
相对于室内实验，基于等比例微观模型的数值模拟具有可重复性好、灵活性高、成本低等优势。CO2-水-岩系统是一种典型的物理化学过程耦合的输运系统，溶解、沉淀及沉淀运移是该系统区别于其他流体运移系统最显著的特征，下面分别对这些机理的微观模拟研究进展予以阐述。
2.1 溶解的模拟
对于包含溶解作用的流体输运系统，需要求解的方程包括：流体的流动方程、流体组分的对流扩散方程（传质方程）、固相发生溶解的化学反应方程以及描述固体溶解的几何形状演变方程。学者们提出了一系列方法来求解这些方程（见表2 ）：第1类为传统计算流体力学（CFD）的离散方法[36⇓⇓-39]，例如有限体积（FV）和有限差分（FD）方法；第2类为采用拉格朗日方法描述流动与传质的粒子法[40⇓-42]，例如光滑粒子流体动力学方法（SPH）和移动粒子半隐式法（MPS）；第3类为混合计算方法[43-44]，例如采用FD求解流动方程、采用随机移动法（RW）刻画溶质的传输[43]。传统CFD方法的计算量较大，但是近年来随着计算机性能的提高及非结构化网格的成熟，该类方法也逐渐用于模拟反应流体的输运过程。粒子法的无网格特性使其非常适合模拟紊流、自由表面流、多相流等，但对反应流输运模拟的相关报道还较少。对于混合类计算方法，学者们往往利用一些成熟的软件包或者某种方法在计算效率上的优势，采用不同计算方法求解不同的场方程，但是随着计算机性能的提高及算法的成熟，越来越多地采用单一计算方法求解多物理化学场问题。近些年还发展了一种非贴体网格模拟方法——格子玻尔兹曼法（LBM）[45⇓⇓-48]，这种方法不需要随着各相区域的运移变化而重构或调整计算网格。相对于常规的CFD方法，LBM具有不受限于流体连续性假设、易于考虑微观力学特征、对复杂多孔介质适应性好、并行简单等优势，因此，越来越多学者开始采用LBM模拟多孔介质中的流动和反应过程。
表2 溶解反应流的微观模拟方法 |
| 作者 | 计算方法 | 网格形态 | 界面更新方法 |
|---|---|---|---|
| Molins等[36] | CFD（FV） | 直角网格 | LS |
| Xu等[37] | CFD（FD） | PF，LS | |
| Oltéan等[38] | CFD | 非结构网格 | ALE |
| Bracconi[39] | CFD (FV) | VOF | |
| Tartakovsky等[40] | SPH | SPH | |
| Xu等[41] | SPH | PF | |
| Ovaysi等[42] | MPS | 显性表征 | |
| Sallès等[43] | CFD（FD）+RW | 直角网格 | 固相平衡临界值 |
| Pereira-Nunes等[44] | CFD（FV）+PT | 直角网格 | 固相平衡临界值 |
| Szymczak等[45] | LBM | 固相平衡临界值 | |
| Kang等[46-47] | LBM | VOP | |
| Chen等[48] | LBM | VOP |
在孔隙尺度的多孔介质反应输运模拟中，首先要解决显性表征流体相与固体相空间分布的问题。若采用传统CFD方法，需要采用合适的技术追踪或捕获相界面，例如水平集法（LS）[36]、相场法（PF）[37]、流体体积法（VOF）[39]和任意拉格朗日-欧拉方法（Arbitrary Lagrangian-Eulerian，ALE）[38]。当采用这些方法模拟溶解时，需要根据反应不断地更新流固界面或重构网格，从而捕捉固体边界随时间空间的演化。但是，由于多孔介质内固体边界形状复杂，传统数值方法处理变化的固体边界难度较大。LBM是以分子运动论为基础的介观数值方法，能高效处理任意形状的固体边界，无需追踪、捕获或重构复杂的相界面，模拟多孔介质中的复杂流动优势明显，笔者团队将传统LBM拓展至页岩纳米多孔介质流体传输模拟[49⇓-51]。当采用LBM模拟溶解时，发展了一些简单高效的界面更新法，例如固相平衡临界值法、像元体积法（VOP）等[45⇓⇓-48]。在化学反应输运模拟中，需要解决的另一个问题即为化学反应对流体组分浓度的影响。当反应发生在溶液体相不同组分之间时（均相反应），通过在LBM方程中添加源汇项处理；当反应发生在溶液组分与固体表面之间时（非均相反应），在LBM中有3种代表性的处理方法：①Kang等[46-47]在流固界面采用He等[52]的热力学边界表征非均相反应边界；②Patel等[53]提出了一种伪均质方法，通过在流固边界相邻的流体节点添加源汇项表征非均相反应对流体组分的影响；③郭照立团队[54]提出了一种处理非均相反应的局部反应边界格式，该格式在反弹格式的基础上考虑了化学反应消耗与反应可逆的影响。
2.2 沉淀的模拟
在多孔介质的模拟中，沉淀是溶解的一个反过程，在模拟中的处理方法是相似的，包括边界处理方法、化学反应对流体组分浓度影响的处理方法等。因此，沉淀模拟的关键在于对不同物理化学作用导致的沉淀过程予以刻画。对于CO2-水-岩系统，沉淀的生成主要包含无机盐的析出和非反应矿物的脱落，沉淀在多孔介质中将严重改变流体的流动路径[55]，必须对沉淀的生成位置精确模拟。因此，需要根据无机盐析出和非反应矿物脱落的机理，深入分析沉淀生成机理，从而实现对沉淀的合理模拟。
无机盐的析出是溶液过饱和后结晶核形成和结晶体生长的过程。成核可以在液体内发生，称为均相成核，也可以在液体和固体界面发生，称为异相成核。成核是控制矿物沉淀的初步生长过程，是一个概率性过程，晶体可以在存在类似条件（如表面性质、过饱和度和温度）的任何地方发生成核[56]。概率性的成核导致沉淀物在多孔介质不同空间生成，影响流体渗流能力，需要采用概率性方法或基于合理物理基础的尺度化表示方法来表征。目前，针对无机盐沉淀的数值模拟中，一般假设无机盐的成核发生在浓度达到一定阈值时[48,57]，未考虑概率性的成核过程。近年来，基于经典成核理论（CNT）中的指数成核速率方程（见（4）式），建立了一些新的动力学模型和公式来表征成核过程。有学者尝试利用CNT在沉淀模拟中预测概率性的成核行为。Li等[58]将CNT耦合进连续尺度的模拟器中刻画方解石的沉淀，模拟了CO2储存过程中井筒水泥的化学变化。Prasianakis等[59]将孔隙尺度的反应传输求解器与CNT耦合，展示了均相和异相沉淀动力学对多孔介质演化的影响。Hellevang等[60]通过实验对玄武岩柱上次生矿物生长的空间分布进行了研究，认为需要开发新的概率成核方法表征无机盐的随机成核过程。Fazeli等[61]建立了一个新的基于CNT的概率成核模型，并将其耦合进孔隙尺度的反应输运求解器中，模拟了多孔介质中的矿物成核和生长，利用单组分矿物反应对不同的过饱和度、生长速率和流速进行了模拟。Masoudi等[62]进一步拓展该模型来模拟富含CO2相中微米级无机盐晶体的形成，以及它们对孔隙形态和渗透率变化的影响。因此，针对无机盐的析出，需要模拟无机盐的成核过程，表征成核相与原固相的差异性生长。确定晶体的成核与生长表征方法后，与溶解类似，不仅需要更新无机盐析出后的流-固几何界面，还要通过添加源汇项至浓度扩散方程，考虑沉淀（晶体成核与生长）对流体离子浓度的影响。
$\ln \tau_{\mathrm{N}}=\frac{\beta V^{2} k_{\mathrm{B}}^{-3} \sigma^{3}}{T^{3}(\ln \Omega)^{2}}-\ln k_{\mathrm{N}}$
非反应矿物的脱落可以分为两种类型：类型Ⅰ，非反应矿物周边矿物溶解导致直接脱落；类型Ⅱ，矿物溶解导致胶结薄弱面在水动力作用下发生剪切脱落，如图5 所示。对于类型Ⅰ，可以利用标定函数判断，若非反应矿物在某时间步不与主岩体连接，则认为非反应矿物脱落，形成了沉淀物，例如Liu等[63]使用Hoshen-Kopelman算法[64]来判断脱落矿物与主岩体的关系，从而识别反应过程中溶解导致的矿物脱落。对于类型Ⅱ，首先对全局空间进行位置搜索，判断潜在的胶结薄弱点，分析矿物胶结薄弱点的受力情况。当流速达到一定值（临界流速）时，流体对矿物颗粒的拖曳力（Fd）的扭矩足以克服接触力（Fc1）、胶结力（Fc2）和吸附力（Fa）合力的扭矩，则认为矿物发生脱落、形成沉淀物，如图5 所示。因此，首先根据不同矿物的反应速率，采用矿物溶解模拟方法开展模拟计算，在每个计算时间步判断是否有类型Ⅰ或类型Ⅱ的沉淀物生成，若有，则对沉淀物进行运移、沉积与再启动的后续模拟。对于类型Ⅱ的模拟目前尚未见到相关报道。
2.3 沉淀运移的模拟
CO2-水-岩系统可能产生沉淀，沉淀在水动力的作用下运移，可能堵塞孔喉，严重降低多孔介质渗流能力。沉淀运移与溶液中颗粒运移现象在本质上一致，而颗粒运移的模拟方法在文献中的报道较多，一般分为Euler-Euler法和Euler-Lagrange法[65]。Euler-Euler法将流体和颗粒都视为连续相，Euler-Lagrange法则是将流体处理为连续相而将颗粒视为离散相，通过追踪每个颗粒的运动轨迹予以精细表征。在Euler-Lagrange法中，离散元方法（DEM）在研究颗粒流时考虑颗粒与流体之间的作用力，具备明显优势，被广泛应用[66⇓-68]。DEM的基本思想是将离散介质当作单元体，不同单元体之间通过角、面或边等发生接触，单元体的运动（包括平动和转动）受牛顿第二定律控制，单元体之间的接触力由合适的接触模型计算[69]。线性接触模型是最基本的接触模型，在该模型中计算颗粒间接触力和力矩时均将其简化为正比于变形量，大幅简化了整个接触力及力矩变化的模拟。对于岩石颗粒系统，常用的接触模型还有线性平行键模型、平面节理模型和软键模型[65]，这些模型简化了颗粒间的复杂非线性接触过程、降低了计算量，适合特定的工程问题。
目前大部分的DEM模拟基于球形颗粒展开，而CO2-水-岩系统产生的沉淀一般为非球形颗粒。相比于球形颗粒，非球形颗粒DEM模拟的难点主要体现在以下两方面[70]：①非球形颗粒之间的接触判断更为复杂，并且当颗粒形状发生变化时，其碰撞接触算法也随之改变；②非球形颗粒之间的受力解析难以达到较高精度。目前对非球形颗粒形状的描述方法可分为多体组合方法和精确几何形状描述方法[71]。多体组合方法采用球体或者其他形状的基本单元构造复杂颗粒形状，该方法的优势在于构造单元间的接触判断相对简单，需要协调几何形状的描述精度与模拟计算效率。精确几何形状描述方法是严格基于颗粒的几何形状进行颗粒碰撞判断，接触判断更加复杂，其优点在于颗粒接触判断精度高，其计算量与颗粒数目及接触判断算法的复杂程度相关，能够较好地拓展到存在尺寸差异的非球形颗粒体系模拟中。
与溶解或沉淀类似，DEM也可以与传统CFD、粒子法（如SPH）、LBM等方法耦合模拟颗粒流[72]，如图6 所示。考虑到LBM模拟多孔介质流动的优势，这里仅对LBM-DEM流固耦合模拟的研究现状予以综述。在早期LBM研究中[73]，为建立流体-颗粒的相互作用体系，当颗粒边界与流体网格相交时，固体颗粒的数值边界被认为处于LBM晶格的中点，但该方法无法准确耦合和计算流固相互作用力，可能在颗粒快速移动时导致流体曳力数值的振荡。Noble等[74]提出了浸入式移动边界方法（IMB），认为固体颗粒上的拉格朗日点位于颗粒边界和流体网格的交叉点处，应采用流体网格单元被颗粒覆盖的面积分数（即固体体积分数）来计算流固相互作用力。在处理复杂移动边界问题时，近年来，越来越引人注意的方法是由Peskin[75]提出的用于血液细胞流动模拟的浸入边界法（IBM），在该方法中一个颗粒由一组独立的点表示，拉格朗日点的位置可以简单地通过颗粒的位置和取向得出，颗粒的总作用力和扭矩通过加和颗粒上所有拉格朗日点的动量变化得到。该方法最初应用于球形颗粒的LBM-DEM流固耦合模拟，后来逐渐拓展到二维非球形颗粒[76]和三维非球形颗粒[77]的流动模拟中。
3 CO2-水-岩系统的微观模拟
由于LBM在模拟多物理化学反应输运系统方面具有明显优势，近些年，已经有学者开始尝试采用LBM模拟CO2-水-岩系统，并得到了一些重要的进展与认识。
对于溶解的模拟，通常采用溶解反应动力学模型预测溶解速率，孔隙尺度矿物溶解/沉淀速率可以用过渡态理论（TST）来描述。所有矿物的反应速率都可用如下一般形式表示[78]：
$R_{m}=-k_{m}\left(1-\frac{Q_{\mathrm{s}}}{K_{\mathrm{eq}}}\right)^{n}$
根据（5）式，室温25 ℃条件下方解石矿物在CO2酸性环境中的溶解/沉淀速率可以表示为：
$R=\left(k_{1} \alpha_{\mathrm{H}^{+}}+k_{2} \alpha_{\mathrm{H}_{2} \mathrm{CO}_{3}}+k_{3}\right)\left(1-\frac{\alpha_{\mathrm{Ca}^{2+}} \alpha_{\mathrm{CO}_{3}^{2-}}}{K_{\mathrm{eq}^{2}, \mathrm{CaCO}_{3}}}\right)$
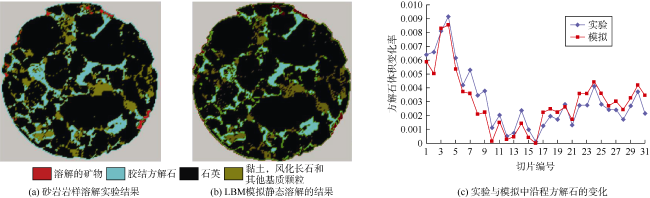
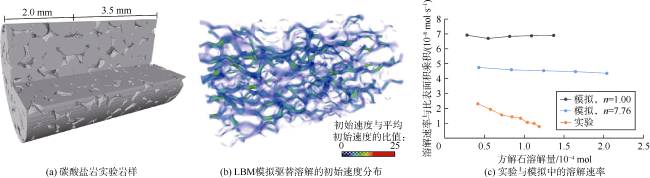
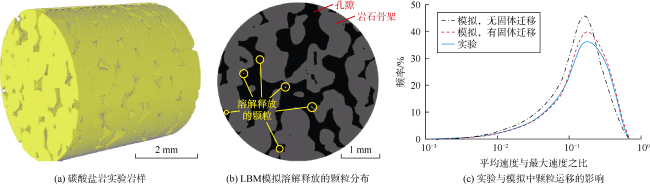
除了上述计算方法以外，也有学者直接采用地球化学模拟器PhreeqcRM获取反应速率。不论是直接采用LBM模拟还是采用LBM与其他CFD离散方法结合（如FV、FE、FD等），再结合数字岩心技术与并行处理技术，基本可以在岩心尺度上实现对CO2-水-岩系统溶解反应的三维孔喉空间模拟，定量评价溶解导致的孔喉变化、孔隙度变化及渗透率变化。在静态溶解模拟方面，Gao等[81]将砂岩中的方解石胶结物考虑为可溶解、其他矿物考虑为不可溶解，利用LBM模拟了CO2-水-岩静态溶解过程，还与前人[82]开展的溶解实验进行了对比，如图7 所示。模型实现了碳酸溶液与方解石长达1 440 d的反应过程（直到达到反应平衡状态）模拟，由于方解石被溶解，岩心孔隙度从1.1%增加到10.7%。他们发现方解石在岩心中的空间展布位置非常重要，由于部分方解石未与酸性流体直接接触，导致仍有超过三分之一的方解石未溶解。在动态溶解模拟方面，采用Patel等[53]建立的LBM伪均质反应边界，Fazeli等[83]模拟了碳酸盐岩岩样注入CO2饱和盐水后的裂缝溶解演化过程，结果表明，流动路径上存在的非反应性矿物可以限制渗透率的增加，单矿物多孔介质中常用的孔隙度和渗透率立方关系在多矿物多孔介质中失效。An等[84]为了模拟岩心尺度的CO2-水-岩反应，将LBM与地球化学模拟器PhreeqcRM耦合，评价了不同注入速率、压力和温度下孔隙度和渗透率随时间的演变关系，随着流速的增加，岩石中的溶解作用更加均匀，认为高注入速率下的渗透率增幅要比低注入速率下的更大。Xie等[85]利用LBM处理流体流动和组分输运，利用VOP法处理反应造成的边界演化，模拟CO2埋存过程中碳酸钙的溶解过程，阐明压差对碳酸钙溶解的影响随温度的增加而减弱，根据温度和压力之间的关系绘制了碳酸钙溶解模式的图版，认为高温和高注入速率下注入CO2有助于其实现溶解埋存。Ju等[86]采用考虑了化学反应消耗与反应可逆影响的局部反应边界格式，模拟了CO2地下咸水层封存中的对流混合过程，分析了流固溶解反应及H2S杂质组分对系统稳定性的影响。
在矿物溶解的化学反应模拟中，重要矿物地球化学反应相关参数（平衡常数、反应速率常数等）的数值不确定，是限制数值模拟准确性的主要因素。例如，Gray等[87]指出在利用LBM模拟CO2饱和溶液时，需要考虑溶解反应的非线性动力学模型（（5）式中的n不为1）和多组分扩散系数模型，即便如此，在与Menke等[88]碳酸盐岩实验结果对比时，发现模拟结果快几倍（见图8 ），认为是模型一些关键参数的不确定性引起的。此外，实验中溶解速率与时间呈平方根关系，而模拟中溶解速率与时间近似线性相关，认为可能是CT扫描精度无法捕捉一些更小孔隙中的离子扩散作用，导致模拟中的溶解速率更高。在孔隙尺度的反应模拟中，往往对一些反应速率较慢的过程考虑为不反应，可能低估部分矿物的反应速率。而在长时间、宏观尺度的模拟中，往往对一些快速反应的矿物（如CaCO3）处理为平衡相，这又可能高估实际多孔介质中的反应速率。
在沉淀生成及运移模拟方面，除了前文提到的无机盐结晶沉淀模拟研究以外，还有如下学者开展了CO2-水-岩系统的沉淀模拟。Jiang等[57]采用颜色LBM求解两相流动方程、FV求解组分输运方程，考虑无机盐的沉淀出现在浓度达到一定阈值时，模拟发现沉淀引起的孔隙结构变化显著降低了多孔介质的绝对渗透率，且对非润湿相相对渗透率的影响大于对润湿相相对渗透率的影响。Liu等[63]利用LBM求解流动方程、FV求解组分输运方程，通过Stokes定律的简化方法，将受溶解释放的颗粒迁移耦合至LBM反应输运模型，探索性地模拟了固体沉淀的运移过程，如图9 所示。通过与在线X射线断层扫描仪（Micro-CT）监测的动态岩心驱替实验结果对比，发现模拟结果可以很好地匹配不同时间步下沿驱替方向的孔隙度变化。通过对碳酸盐岩多孔介质的大量模拟，发现了渗透率和孔隙度之间的幂律关系，同时也探讨了由于溶解释放而引起的固体颗粒迁移对渗透率的影响。Parvan等开展了相似的模拟研究[89]，但是在模拟中假设所有固体与流体之间的表面都可以进行反应，忽略了岩石表面的化学非均质特征以及有效的反应接触面。除了针对单一矿物沉淀的研究存在不确定性以外，还有学者指出，溶解反应后生成的部分次生矿物的种类难以确定、生成量难以量化、反应动力学参数缺失，导致部分次生矿物的模拟难度大，也可能对化学反应模拟结果产生较大影响[90]。
4 存在的问题及建议
①CO2-水-岩石系统中复杂作用机理（溶解、沉淀与沉淀运移等）的解耦合。CO2注入储集层打破地层水与岩石间的物理化学平衡，产生溶解、沉淀和沉淀运移等现象，它们的综合作用导致储集层渗透率可能出现增大、减少、波动变化等复杂结果。溶解—沉淀—沉淀运移是一种孔隙尺度行为，传统岩心渗流实验往往难以直观刻画其作用过程（如离子浓度变化、孔隙形貌演化、沉淀运移追踪等），导致对储集层物性参数变化规律认识不清、预测难度大。因此，还需要进一步深入剖析CO2-水-岩石系统中溶解、沉淀与沉淀运移的耦合渗流作用机理。具体而言，可以通过不同实验设备及可视化手段对各种复杂机理（溶解、沉淀和沉淀运移）解耦合，系统研究各个机理的作用特征及规律。例如，借助静态溶解实验，分析多矿物差异溶解规律；借助刻蚀玻璃实验，捕捉地层水过饱和沉淀（结晶）及沉淀运移规律；借助岩心在线驱替实验，分析驱替条件下的溶解、沉淀及沉淀运移规律。
②多矿物差异性反应的反应系数测量及微观表征方法。总体而言，相对于传统CFD或拉格朗日描述的粒子法等方法，LBM在模拟多孔介质内的复杂流动方面具有明显优势，包括易处理复杂边界、易捕捉相界面及易并行等。针对反应输运流，可以通过在LBM方程中添加源汇项并结合恰当的边界更新法，实现溶液中均相反应和流固接触面非均相反应的表征，已在各种物理化学反应流中得到了广泛应用。在CO2-水-岩系统中，CO2水溶液与不同地层水组分、不同矿物之间可能发生反应，且反应速率存在差异。需要针对性地开展不同温度、压力环境下，CO2水溶液与离子组分、矿物组分之间的反应速率标定实验，提高实验测试的准确性，降低主要矿物地球化学反应相关参数（平衡常数、反应速率常数等）的数值不确定性，最终增加表征组分交换流动方程的数值预测可靠性。
③晶体成核和矿物脱落作用下的沉淀生成机理及表征。沉淀的生成位置、大小及运移能力直接影响多孔介质的渗流能力，因此，沉淀生成表征是CO2-水-岩系统微观模拟成功与否的关键。沉淀的生成包含无机盐的析出和非反应矿物的脱落，其中，无机盐的结晶成核受概率成核理论控制，且晶体生长也遵循一定的规律，但目前的相关研究报道对结晶沉淀的表征过于简化，将结晶成核和晶体生长简单处理为一个随机过程。受周边矿物溶解和胶结薄弱处破坏的诱导，非反应矿物从主固相体脱落是生成沉淀的另一个重要机理，但目前尚未发现相关机理及表征方法的研究。因此，需要基于晶体成核理论预测无机盐的生成过程、提出非反应矿物脱落的判别方法，从而建立可靠的沉淀生成表征方法。
④不规则、多类型、变数量、变形状沉淀条件下的沉淀-流体相互作用模拟方法。沉淀（颗粒）在多孔介质中的运移是影响CO2-水-岩系统渗透率的关键因素。DEM是多孔介质颗粒流模拟最常用的处理方法，结合IBM法，可以实现LBM体系下的颗粒-流体相互作用模拟。CO2-水-岩系统的颗粒运移模拟主要存在3个方面的特殊性：沉淀的产生方式多样（次生矿物、矿物颗粒脱落）；沉淀的形状一般不规则；生成的沉淀在运移过程中可能消失（溶解），也即沉淀的数量和大小在运移过程中可能变化。因此，需要针对不同的沉淀生成机理和沉淀的几何特征，建立不规则、多类型、变数量、变形状沉淀条件下的沉淀-流体相互作用模拟方法。
⑤CO2-水-岩系统中多物理化学过程的耦合渗流机制。近年来，已有学者采用LBM模拟CO2-水-岩系统的反应流，但建立的模拟方法主要针对某一个或某几个物理化学过程，然而CO2注入储集层中是一个多相（气/水/油）、多组分（CO2水溶液，H+，HCO3−，CO32−和OH−等）、非均相/均相化学反应的过程，对这些复杂过程实现全耦合模拟是一个具有挑战性的问题。CO2-水-岩系统中的各个物理化学过程之间相互耦合、相互影响，例如，矿物的溶解可能诱导周边矿物脱落产生沉淀，沉淀运移后暴露的新鲜矿物面接触CO2后可能产生新的溶解。根据文献调研结果，目前针对该问题的研究主要针对上述某一个或某几个物理化学过程，若未有效协调各机理之间的耦合关系，将导致模拟结果与室内实验结果存在较大差异。因此，需要有机衔接各个物理化学过程之间的模拟边界条件、协调各机理的耦合关系，从而定量评价溶解、沉淀、沉淀运移对孔隙度、渗透率影响。
5 结论
CO2注入地下后，打破地层水与岩石之间的物理化学平衡，产生溶解、沉淀及沉淀运移等特殊现象，影响CO2注入性、盖层封堵性及埋存可靠性。目前基于宏观高温高压静态实验、岩心渗流实验等方法，难以从本质上深入认识CO2-水-岩系统的溶解—沉淀—沉淀运移耦合作用机制，无法有效预测宏观孔渗参数的复杂变化。开展这些特殊物理化学过程的耦合渗流机制及微观模拟研究，是量化物理化学反应导致的多孔介质孔喉结构变化、预测复杂渗透率变化规律的有效手段。
CO2-水-岩系统溶解—沉淀—沉淀运移的耦合渗流机制及微观模拟的研究，尚需要解决一些关键的科学问题。例如，考虑CO2溶于地层水与不同矿物之间发生的差异溶解反应，建立非均相矿物溶解的模拟方法；针对不同类型的沉淀生成机理（如化学反应产生的次生矿物、溶解诱发的矿物颗粒脱落），建立合理的沉淀生成表征方法；建立不规则、多类型、变数量、变形状沉淀条件下的沉淀-流体相互作用模拟方法；有机衔接各个物理化学过程之间的模拟边界条件，协调各机理的耦合关系。合理解决这些问题，可以实现碳埋存多孔介质内溶解—沉淀—沉淀运移的可视化模拟。
在未来研究中，还需要深入结合室内可视化实验与微观模拟，通过静态溶解实验、刻蚀玻璃实验及岩心在线驱替实验对溶解—沉淀—沉淀运移解耦合，为各过程的微观模拟方法提供验证数据。例如，以LBM和DEM为基本模拟手段处理流动、传质和沉淀运移过程，在其中耦合基于溶解动力学的非均相矿物溶解模拟方法、基于晶体成核理论和矿物脱落判别法的沉淀生成模拟方法，形成溶解—沉淀—沉淀运移耦合渗流的微观模拟技术，实现CO2-水-岩系统渗流相关参数的定量预测，为CCUS和CCS工业活动的安全、高效实施提供理论依据与技术支撑。
符号注释：
Fa——流体与矿物颗粒间的吸附力，N；Fc1——流体与矿物颗粒间的接触力，N；Fc2——流体与矿物颗粒间的胶结力，N；Fd——流体对矿物颗粒的拖曳力，N；Keq,CaCO3——CaCO3的反应平衡常数，无因次；kB——玻尔兹曼常数，取值为1.38×10-23 J/K；km——第m种矿物的反应速率常数，mol/（m2·s）；kN——成核速率常数，1/（m2·s）；Keq——反应平衡常数，无因次；n——反应级数；Qs——离子活度乘积，无因次；R——方解石矿物在CO2酸性环境中的溶解/沉淀速率，mol/（m2·s）；Rm——第m种矿物的反应速率，mol/（m2·s）；T——绝对温度，K；V——成核相的体积，m3；$\alpha_{\mathrm{H}^{+}}$，$\alpha_{\mathrm{H}_{2} \mathrm{CO}_{3}}$，$\alpha_{\mathrm{Ca}^{2+}}$，$\alpha_{\mathrm{CO}_{3}^{2-}}$——H+、H2CO3、Ca2+、CO32－的活度，无因次；β——几何因子，无因次；σ——成核相与基底之间的界面自由能，J/m2；τN——诱导时间，（m2·s）；Ω——过饱和度，%。