0 引言
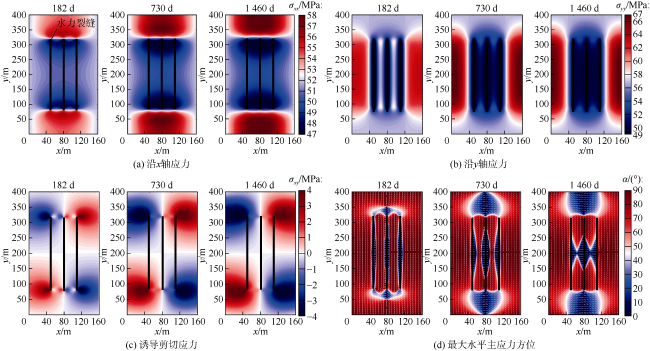
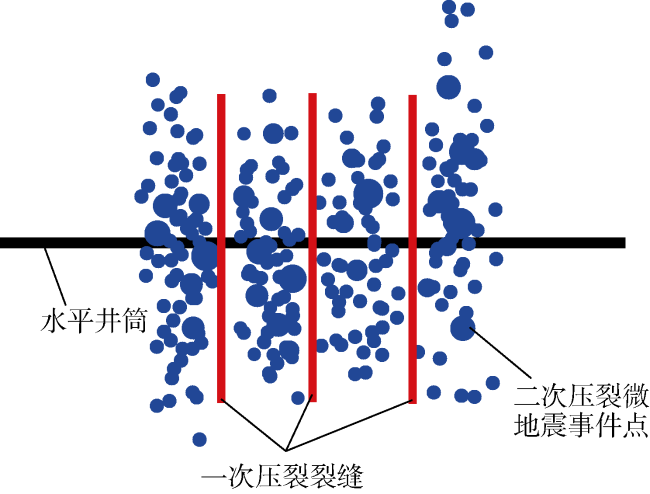
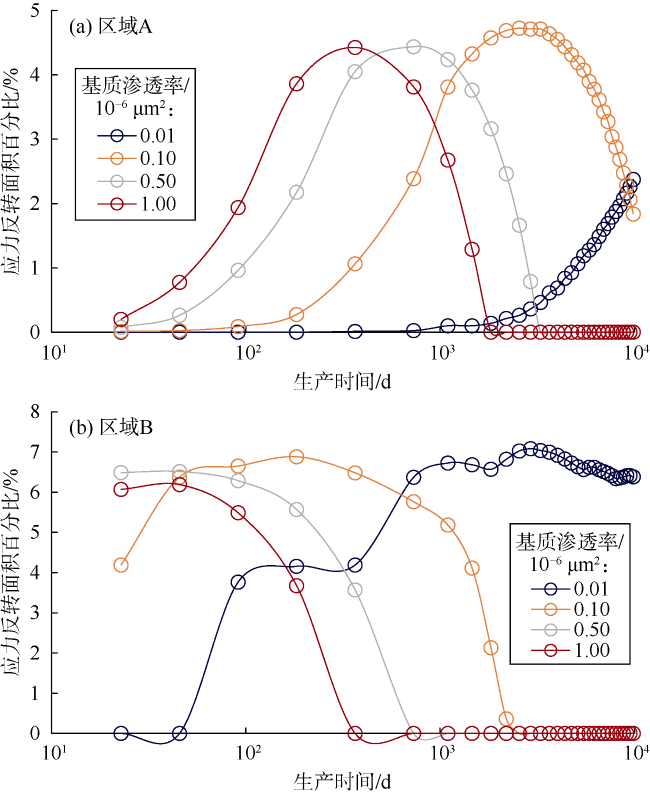
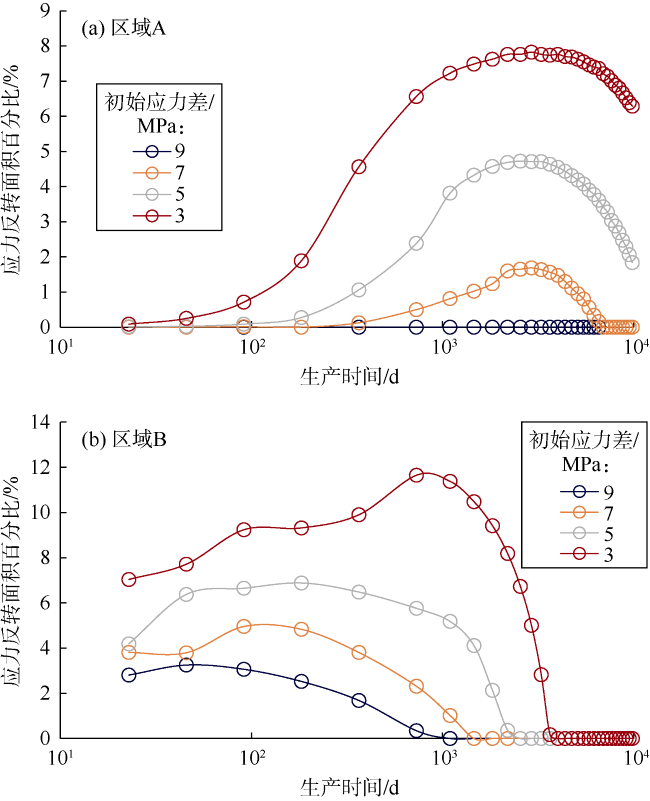
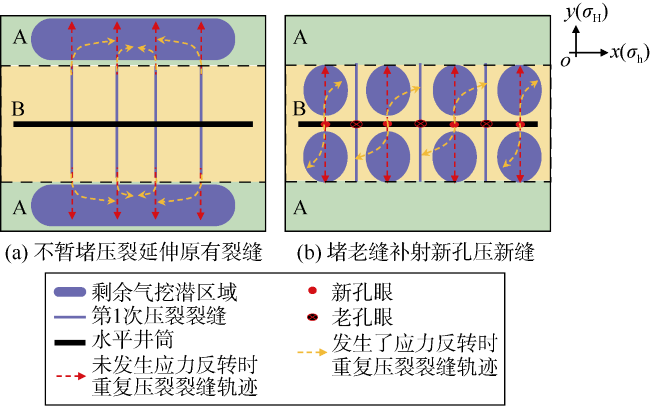
早在20世纪90年代，Elbel等[4]首次通过实验证明油气井初次压裂可令主应力方向发生90°反转。随后Wright等[5]基于多孔介质弹性力学，从储集层压实、裂缝滑移等角度阐释了孔隙压力降低诱导应力场变化的内在机制。Gupta等[6]认为应力场变化与油藏开发存在联系，油藏初始水平主应力差越小越有利于地应力反转产生。Roussel等[7]验证了应力反转现象，并认为加密井周围主应力方向发生了90°反转。Safari等发现由于水平井的应力重新定向，加密井压裂过程中水力裂缝可能发生弯曲也可能形成直缝，主要取决于主应力的转向情况，但并未给出加密井压裂时机优选方法[8-9]。Sangnimnuan等[10]基于嵌入离散裂缝模型建立了渗流-地质力学耦合模型，用于表征具有复杂几何形状裂缝的非常规油气储集层中压力衰竭诱导的应力场，得到了与Gupta相似的结论。Kumar等[11]建立了三维全耦模型，模拟了生产引起的应力重定向行为，得到了受应力转向影响的加密井裂缝扩展轨迹。Sangnimnuan等[12]通过研究裂缝性储集层衰竭后的压力和应力分布，认为应力反转对重复压裂方式选择有重要影响，但未讨论重复压裂时机的优选。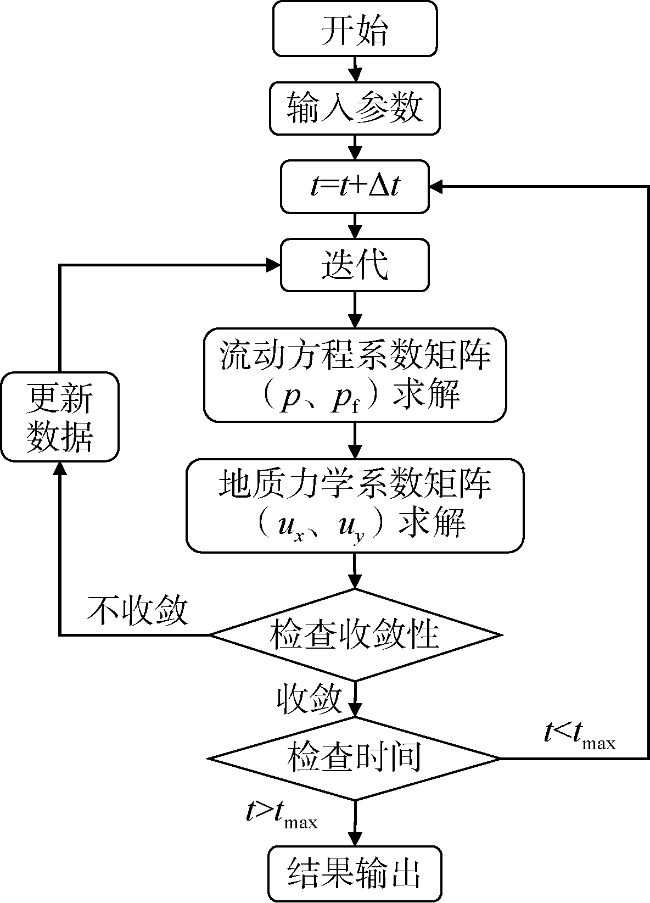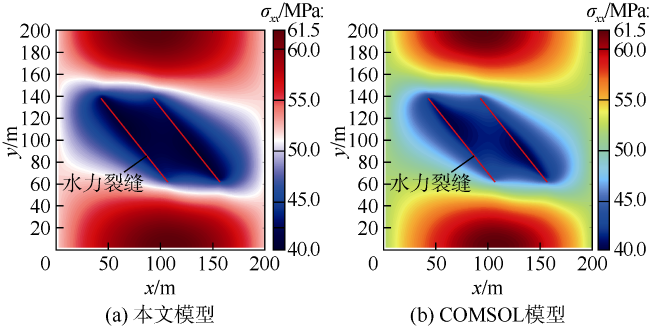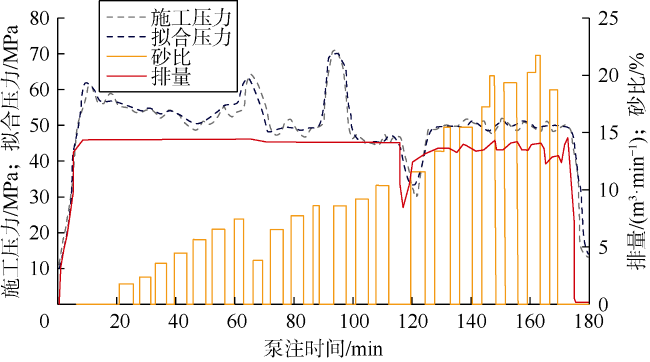Ibáñez等[13]研发了集成多学科方法的工作流程，可筛选合适的候选井，并采用地质力学建模评估候选井进行重复压裂的可行性。朱海燕等将Eclipse和ABAQUS相结合，提出了一套致密砂岩储集层注采开发过程中储集层多物理场四维地应力演化数值模拟方法[14-15]。夏阳等[16]建立了应力场演化预测模型，揭示了纵向非均质页岩储集层层内、层间开采诱导地应力演化规律。郭建春等也指出生产诱导应力场的变化对重复压裂设计非常重要，但并未从应力演化角度确定重复压裂的最佳时机[17-18]。
综上可知，目前老井重复压裂在时机优选上还存在应力重定向规律不明确、优化方法不完善的问题。本文基于多孔介质弹性力学理论、嵌入式离散裂缝模型及有限体积法，推导并建立了考虑页岩气微观流动机制的渗流-地质力学耦合模型，并采用四川盆地涪陵页岩气中资料研究了生产时间、地层渗透性、初始地层应力差等对应力重定向演化规律、重复压裂时机优选的影响。
1 老井重复压裂时机优化
早期对页岩气储集层改造认识不足，中国页岩气井存在压裂施工规模与排量不合理、簇间距较大等问题，部分页岩气井产能衰竭快、采收率和经济效益低，重复压裂成为目前老井剩余气挖潜的重要措施。
1.1 页岩气井重复压裂时机优化方法
根据重复压裂挖潜目标区域的不同，常用的重复压裂方式包括：不暂堵压裂延伸原有水力裂缝，简称为方式Ⅰ（见图1a ），主要挖潜水力裂缝端部以远区域（区域A）的剩余气；暂堵老孔眼，补射新孔眼，压裂新裂缝，简称为方式Ⅱ（见图1b ），主要挖潜水力裂缝内部及附近区域（区域B）的剩余气。开采时间不同，储集层不同区域应力重定向程度差异较大，不同重复压裂方式获得的裂缝轨迹也不同。裂缝端部和井筒附近未发生主应力反转时，裂缝轨迹一般沿图中红色虚线箭头扩展（垂直于井筒方向）穿过目标挖潜区；裂缝端部和井筒附近主应力反转后，裂缝轨迹一般沿图中黄色虚线箭头扩展（平行于水平最大主应力方向）与第1次压裂裂缝汇合。可见，当裂缝端部和井筒附近主应力未反转或应力转向程度较弱时（水平最大主应力与水平井筒之间夹角接近90°），实施重复压裂才具有较高的改造成功率。
根据上述分析，页岩气储集层老井重复压裂时机优化可按5个步骤进行：①基于储集层参数构建地质模型；②采用现场压裂压力数据反演裂缝参数；③根据产量数据拟合储集层应力演化过程；④建立应力反转面积百分比与开采时间的关系；⑤结合单井生产情况及开发需求，综合开展重复压裂时机优选。
1.2 基于孔弹性理论的渗流-地质力学耦合模型
线弹性储集层应力平衡方程可以表示为[19]：
$\nabla \cdot \boldsymbol{\sigma}+\rho_{\mathrm{r}} g=0$
根据Biot孔弹性介质理论，适用于多孔介质固体的孔弹性方程为[19]：
$\boldsymbol{\sigma}-\boldsymbol{\sigma}_{0}=\boldsymbol{C}_{\mathrm{dr}}: \boldsymbol{\varepsilon}-b\left(p-p_{0}\right) \boldsymbol{I}$
$\frac{1}{\rho_{\mathrm{g}}}\left(m-m_{0}\right)=b \varepsilon_{\mathrm{v}}+\frac{1}{M}\left(p-p_{0}\right)$
其中：
$\begin{array}{c}b=1-\frac{K_{\mathrm{dr}}}{K_{\mathrm{s}}} \quad \frac{1}{M}=\phi c_{\mathrm{g}}+\frac{b-\phi}{K_{\mathrm{s}}} \\K_{\mathrm{dr}}=\frac{E(1-v)}{(1+v)(1-2 v)} \quad \boldsymbol{\varepsilon}=\frac{1}{2}\left[\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{\mathrm{T}}\right]\end{array}$
将应力张量σ迹的三分之一σv=Tr（σ）/3代入（2）式可以得到新的应力应变关系：
$\left(\sigma_{\mathrm{v}}-\sigma_{\mathrm{v}, 0}\right)+b\left(p-p_{0}\right)=K_{\mathrm{dr}} \varepsilon_{\mathrm{v}}$
将（2）、（3）、（4）式代入到（1）式中，并忽略重力项的影响，应力平衡方程可以表示为：
$\begin{array}{r}\nabla \cdot\left[\mu \nabla \boldsymbol{u}+\mu(\nabla \boldsymbol{u})^{\mathrm{T}}+\boldsymbol{I} \lambda T_{\mathrm{r}}(\nabla \boldsymbol{u})\right]+ \\\nabla \cdot \boldsymbol{\sigma}_{0}-b \nabla p+b \nabla p_{0}=0\end{array}$
小变形假设下，流体质量守恒方程为：
$\frac{\partial m}{\partial t}+\rho_{\mathrm{g}} \nabla \cdot \boldsymbol{v}=\rho_{\mathrm{g}} q$
将（3）式代入（6）式可得地层压力与应变表示的质量守恒方程：
$\frac{1}{M} \frac{\partial p}{\partial t}+b \frac{\partial \varepsilon_{\mathrm{v}}}{\partial t}+\nabla \cdot \boldsymbol{v}=q$
考虑页岩气吸附对孔隙度的影响，对Biot模量进行修正，则有[20]：
$\frac{1}{M}=\phi c_{\mathrm{g}}+\frac{b-\phi}{K_{\mathrm{s}}} \frac{m_{\mathrm{ad}}}{\rho_{\mathrm{g}}}$
考虑页岩气在基质孔隙内的多种渗流机制，流动速度v可以表示为[21]:
$\boldsymbol{v}=-\frac{\prod_{i} F_{\mathrm{app}, i} \boldsymbol{K}}{\mu_{\mathrm{g}}} \nabla p$
将（8）、（9）式代入（7）式可得：
$\begin{array}{c}\left(\phi c_{\mathrm{g}}+\frac{b-\phi}{K_{\mathrm{s}}} \frac{m_{\mathrm{ad}}}{\rho_{\mathrm{g}}}\right) \frac{\partial p}{\partial t}+b \frac{\partial \varepsilon_{\mathrm{v}}}{\partial t}+ \\\nabla \cdot\left(-\frac{\prod_{i} F_{\mathrm{app}, i} \boldsymbol{K}}{\mu_{\mathrm{g}}} \nabla p\right)=q\end{array}$
$\begin{array}{c}\left(\phi c_{\mathrm{g}}+\frac{b-\phi}{K_{\mathrm{s}}} \frac{m_{\mathrm{ad}}}{\rho_{\mathrm{g}}}+\frac{b^{2}}{K_{\mathrm{dr}}}\right) \frac{\partial p}{\partial t}+\frac{b^{2}}{K_{\mathrm{dr}}} \frac{\partial \sigma_{\mathrm{v}}}{\partial t}- \\\nabla \cdot\left(\frac{\prod_{i} F_{\mathrm{app}, i} \boldsymbol{K}}{\mu_{\mathrm{g}}} \nabla p\right)=q\end{array}$
将（11）式改写为含位移的形式：
$\begin{array}{r}\left(\phi c_{\mathrm{g}}+\frac{b-\phi}{K_{\mathrm{s}}} \frac{m_{\mathrm{ad}}}{\rho_{\mathrm{g}}}+\frac{b^{2}}{K_{\mathrm{dr}}}\right) \frac{\partial p_{n}}{\partial t}-\frac{b^{2}}{K_{\mathrm{dr}}} \frac{\partial p_{n-1}}{\partial t}+ \\b \frac{\partial(\nabla \cdot \boldsymbol{u})}{\partial t}-\nabla \cdot\left(\frac{\prod_{i} F_{\mathrm{app}, i} \boldsymbol{K}}{\mu_{\mathrm{g}}} \nabla p_{n}\right)=q\end{array}$
（5）、（12）式即为基于Biot理论的渗流与地质力学耦合模型主要求解方程。
1.3 页岩气微观渗流机理
采用单层Langmuir等温线和多层BET（Brunauer- Emmett-Teller）等温线模拟页岩储集层干酪根上吸附
$m_{\mathrm{ad}, \mathrm{L}}=\rho_{\mathrm{r}} \rho_{\mathrm{gsc}} \frac{p V_{\mathrm{L}}}{p+p_{\mathrm{L}}}$
$m_{\mathrm{ad}, \mathrm{B}}=\rho_{\mathrm{r}} \rho_{\mathrm{gsc}} \frac{V_{\mathrm{m}} C p_{\mathrm{r}}}{1-p_{\mathrm{r}}}\left[\frac{1-(d+1) p_{\mathrm{r}}^{d}+d p_{\mathrm{r}}^{d+1}}{1+(C-1) p_{\mathrm{r}}-C p_{\mathrm{r}}^{d+1}}\right]$
其中
$p_{\mathrm{r}}=\frac{p}{p_{\mathrm{s}}} \quad p_{\mathrm{s}}=\exp \left(7.7437-\frac{1306.5485}{19.4362+T_{\mathrm{m}}}\right)$
$F_{\text {app }}=(1+\beta K n)\left(1+\frac{4 K n}{1+K n}\right)$
其中
$K n=\frac{\mu_{\mathrm{g}}}{2.8284 p} \sqrt{\frac{\pi R T_{\mathrm{m}}}{2 M_{\mathrm{g}}} \frac{\phi}{K}} \quad \beta=\frac{128}{15 \pi^{2}} \tan ^{-1}\left(4 K n^{0.4}\right)$
1.4 渗流-地质力学全耦合模型
嵌入式离散裂缝模型的核心思想是采用结构化网格分别独立建立基质与裂缝对应的模拟域，通过非相邻传导率建立两者间的流动关系[26]。对于任意裂缝单元及对应的基质单元，两者间的体积流量可以表示为：
$q_{\mathrm{f}-\mathrm{m}}=\lambda_{\mathrm{t}} T_{\mathrm{f}-\mathrm{m}} \Delta p$
传导率主要受基质与裂缝段渗透率和几何形状的影响，于是有[27]：
$T_{\mathrm{f}-\mathrm{m}}=\frac{2 A_{\mathrm{f}}(\boldsymbol{K} \cdot \boldsymbol{n}) \cdot \boldsymbol{n}}{d_{\mathrm{f}-\mathrm{m}}}$
对于两条相交裂缝而言，相交裂缝单元之间的传导率可以表示为[28]：
$T_{\mathrm{f}-\mathrm{f}}=\frac{T_{1} T_{2}}{T_{1}+T_{2}}$
将基质与裂缝间的流量交换项（16）式代入到（12）式中，可得考虑裂缝系统影响的基质内流动方程：
$\begin{array}{c}\left(\phi c_{\mathrm{g}}+\frac{b-\phi}{K_{\mathrm{s}}} \frac{m_{\mathrm{ad}}}{\rho_{\mathrm{g}}}+\frac{b^{2}}{K_{\mathrm{dr}}}\right) \frac{\partial p_{n}}{\partial t}-\frac{b^{2}}{K_{\mathrm{dr}}} \frac{\partial p_{n-1}}{\partial t}+b \frac{\partial(\nabla \cdot \boldsymbol{u})}{\partial t}- \\\nabla \cdot\left(\frac{\prod_{i} F_{\mathrm{app}, i} \boldsymbol{K}}{\mu_{\mathrm{g}}} \nabla p^{n}\right)+\frac{\lambda_{\mathrm{t}} T_{\mathrm{f}-\mathrm{m}}\left(p_{\mathrm{f}, n}-p_{n}\right)}{V_{\mathrm{c}}}=q\end{array}$
同理可得裂缝内的流动方程：
$\begin{array}{c}\left(\frac{1}{M_{\mathrm{f}}}+\frac{b^{2}}{K_{\mathrm{dr}}}\right) \frac{\partial p_{\mathrm{f}, n}}{\partial t}-\frac{b^{2}}{K_{\mathrm{dr}}} \frac{\partial p_{\mathrm{f}, n-1}}{\partial t}-\nabla \cdot\left(\frac{\boldsymbol{K}_{\mathrm{f}}}{\mu_{\mathrm{g}}} \nabla p_{\mathrm{f}, n}\right)+ \\\frac{\lambda_{\mathrm{t}} T_{\mathrm{f}-\mathrm{m}}\left(p_{n}-p_{\mathrm{f}, n}\right)}{V_{\mathrm{c}}}+\frac{\lambda_{\mathrm{t}} T_{\mathrm{f}-\mathrm{f}}\left(p_{\mathrm{f} 1, n}-p_{\mathrm{f} 2, n}\right)}{V_{\mathrm{c}}}=q\end{array}$
结合（2）、（3）、（5）、（19）及（20）式可得沿y轴方向的应力σyy、沿x轴方向的应力σxx及诱导剪切应力σxy。根据下述方程，可计算最大、最小水平主应力（σH、σh）及其方位角α：
$\left\{\begin{array}{l}\sigma_{\mathrm{H}}=\frac{\sigma_{x x}+\sigma_{y y}}{2}+\sqrt{\left(\frac{\sigma_{x x}-\sigma_{y y}}{2}\right)^{2}+\sigma_{x y}^{2}} \\\sigma_{\mathrm{h}}=\frac{\sigma_{x x}+\sigma_{y y}}{2}-\sqrt{\left(\frac{\sigma_{x x}-\sigma_{y y}}{2}\right)^{2}+\sigma_{x y}^{2}}\end{array}\right.$
$\tan \alpha=\frac{\sigma_{\mathrm{H}}-\sigma_{x x}}{\sigma_{x y}}$
1.5 模型求解
2 模型验证
为验证本文模型的准确性，利用本文模型和COMSOL商业软件，分别使用结构化和非结构化网格，建立了两个具有50°倾角、两簇裂缝的物理模型。两个模型尺寸均为200 m×200 m×20 m，输入表1 中的参数，设置边界上的法向位移为0进行模拟，得到生产5年后沿x轴方向的应力分布（见图3 ）。对比可以看出，受地层压力降低的影响，σxx在裂缝附近均出现较大程度降低，而在裂缝端部以远区域大幅增加，两种方法模拟的应力分布非常接近，证实本文模型计算应力精度较高。
表1 模型验证主要输入参数 |
| 参数 | 取值 | 参数 | 值 |
|---|---|---|---|
| 初始地层压力 | 38 MPa | 裂缝半长 | 100 m |
| 兰格缪尔压力 | 4 MPa | 基质渗透率 | 300×10−9 μm2 |
| 地层温度 | 343.15 K | 裂缝渗透率 | 2 μm2 |
| 兰格缪尔体积 | 0.018 m3/kg | 裂缝宽度 | 1×10−3 m |
| 基质孔隙度 | 6% | 井底压力 | 18 MPa |
| 基质压缩系数 | 1.0×10−3 MPa−1 | 模拟时间 | 5 年 |
| 裂缝孔隙度 | 100% | 沿x轴应力 | 52 MPa |
| 弹性模量 | 29 GPa | 沿y轴应力 | 55 MPa |
| 泊松比 | 0.13 | 沿z轴应力 | 56 MPa |
| Biot常数 | 0.8 |
3 应用实例
3.1 重复压裂时机优选
四川盆地涪陵页岩气田W1水平井志留系龙马溪组储集层连续厚度38 m，平均垂深2 400 m，压力梯度为1.2 MPa/100 m，水平井段长1 600 m，井间距400 m。压裂设计方案表明该井平均孔隙度4.8%，平均渗透率0.035×10−6 μm2，平均泊松比0.18，平均弹性模量41 GPa，初始水平最小主应力52 MPa，初始应力差为5 MPa。该井第6段压裂设计段长120 m，压裂3簇，由于加砂困难，为减小应力干扰，簇间距设计为40 m；设计施工排量14 m3/min，设计总液量1 600 m3。利用该井第6段现场压裂施工曲线（见图5 ）采用Meyer压裂设计软件拟合得该压裂段平均有效裂缝半长118 m，平均裂缝导流能力为15 μm2·cm。W1井生产3年后，产能出现了较大程度递减，为进一步提升单井开发效果，计划进行重复压裂。根据地质力学参数、裂缝参数，建立页岩气生产物理模型，模型尺寸400 m×160 m×38 m。
考虑到W1井生产3年后产能已经出现大幅降低，显然生产2 000 d或10 000 d后再实施重复压裂不能满足气井效益开发的需求。综合考虑重复压裂最佳时间及现场实际情况，决定采取关井或注入流体等恢复地层压力的方式，使得目标区域A、区域B内应力恢复到初始状态，保证裂缝轨迹到达理想位置。W1井在生产1 255 d时关井，关井约30 d后，按方式Ⅱ实施了重复压裂。重复压裂微地震监测（见图8 ）显示，二次压裂微地震事件信号点主要集中在一次压裂裂缝之间，表明重复压裂形成的新裂缝未与老缝相交并穿越目标剩余气区，证明本次重复压裂改造成功。
3.2 重复压裂时机影响因素
3.2.1 渗透率的影响
采用W1井模型，设定基质渗透率为0.01×10−6，0.10×10−6，0.50×10−6，1.00×10−6 μm2，模拟生产时间与区域A、区域B内应力反转面积百分比的关系曲线（见图9 ）。可以看出：①随生产时间延长，不同基质渗透率条件下区域A内应力反转面积百分比表现出不同的变化趋势，当基质渗透率大于0.01×10−6 μm2时，曲线先上升后下降；当基质渗透率等于0.01×10−6 μm2， 曲线单调上升。分析原因认为，基质渗透率低至0.01× 10−6 μm2时，页岩气流动困难，且持续时间长，模拟时间范围内的数据不足以反应区域A内应力反转的全过程。②随生产时间延长，不同基质渗透率条件下区域B应力反转面积百分比曲线则均基本表现为先上升后下降的趋势。这主要是因为区域B总体距人工裂缝近，页岩气流动距离较短，地层压力下降快，应力变化也快，一方面模拟时间可以反映区域B内应力反转的全过程，另一方面可以看到，与区域A相比，相同基质渗透率条件下曲线出现峰值的时间缩短。③随着基质渗透率的增加，区域A、区域B曲线出现峰值的时间缩短，应力反转消失的时间同样缩短，采取重复压裂措施的时机越早。④基质渗透率为0.1×10−6~1.0×10−6 μm2时，区域A重复压裂方式Ⅰ的最佳时间为1 460~10 000 d，区域B重复压裂方式Ⅱ的最佳时间为182~2 190 d。⑤基质渗透率降低到0.01×10−6 μm2时，重复压裂的理论最佳时间将远超10 000 d，这种条件下，单井产能降低快，为保证经济性，可采取关井或注气补能等措施恢复应力，提前实施重复压裂。
3.2.2 初始应力差的影响
采用W1井模型，设置初始应力差为3，5，7，9 MPa，模拟生产时间与应力反转面积百分比的关系曲线（见图10 ）。由图可见：①初始应力差越大，应力反转面积百分比曲线先上升后下降、最终归零（恢复到初始状态）所需的时间越短，开展重复压裂的最佳时间越早。②由于区域B距人工裂缝近，相同初始应力差条件下，曲线出现峰值、曲线归零的时间比区域A短。③初始应力差为3~7 MPa时，区域A重复压裂方式Ⅰ的最佳时间需要大于6 570 d，初始应力差达到9 MPa时，曲线持续为0，始终未出现应力反转，随时可实施重复压裂。④对于区域B内的挖潜气区，重复压裂方式Ⅱ的最佳时间为730~3 650 d。⑤在相同基质渗透率和初始应力差下，排除人为因素干扰，重复压裂方式Ⅰ的最佳时间比方式Ⅱ晚。
3.2.3 天然裂缝分布的影响
采用W1井模型，随机生成400条长30 m、渗透率0.01 μm2的天然裂缝，设置天然裂缝逼近角为80°，60°，40°，20°，模拟裂缝逼近角对最大水平主应力方位的影响（见图11 ），得到生产时间与应力反转面积百分比的关系曲线（见图12 ）。对比分析可知：①天然裂缝逼近角越大，区域B越难发生应力反转、开展重复压裂的最佳时间越早，区域A越易发生应力反转、开展重复压裂的最佳时间越晚。②区域A实施重复压裂方式Ⅰ的最佳时间为1 825~3 650 d；区域B实施重复压裂方式Ⅱ的最佳时间为152~1 460 d。
4 结论
受地层压力衰竭影响，页岩气压裂井附近应力反转面积百分比随时间的延长先增加后减小，且距人工裂缝越近的区域，应力反转面积百分比曲线出现峰值的时间越短，最终归零（恢复到初始状态）的时间也越短。
页岩气井重复压裂的最佳时间受基质渗透率、初始应力差、天然裂缝逼近角的影响。基质渗透率、初始应力差越大，应力反转面积百分比曲线出现峰值、恢复到初始状态的时间越短，采取重复压裂措施的最佳时间越早。天然裂缝逼近角越大，裂缝附近越难发生应力反转、重复压裂最佳时间越早，裂缝端部以远区域越易发生应力反转、重复压裂最佳时间越晚。
基质渗透率很小的页岩气储集层，其单井产能下降快，为保证经济性，可采取关井或注气补能等措施恢复应力，提前实施重复压裂。
符号注释：
Af——基质单元与裂缝单元的相交面积，m2；b——Biot系数，无因次；cg——页岩气压缩系数，Pa−1；C——BET吸附常数，无因次；Cdr——四阶弹性张量，Pa；d——BET吸附分子层数；df-m——基质单元到裂缝平面的平均法向距离，m；E——岩石弹性模量，Pa；Fapp——页岩气渗透率的修正因子，无因次；g——重力加速度，m/s2；I——单位张量，无因次；K——基质渗透率张量，m2；K——基质渗透率，m2；Kf——裂缝渗透率张量，m2；Kdr——干燥岩石的体积模量，Pa；Ks——岩石体积模量，Pa；Kn——努森数（Knudsen number），无因次；m——单位岩石体积内流体质量，kg/m3；mad——单位基质体积的吸附气量，kg/m3；mad,L，mad,B——基于单层Langmuir等温线、多层BET等温线的吸附气量，kg/m3；M——Biot模量，Pa；Mf——裂缝模拟域内的Biot模量，Pa；Mg——页岩气摩尔质量，kg/mol；n——时间步；n——裂缝面的法向向量，无因次；p——流体压力，Pa；pf、pf1、pf2——裂缝、裂缝1、裂缝2内流体压力，Pa；pr——中间变量，无因次；ps——拟饱和压力，Pa；pL——兰格缪尔压力，Pa；Δp——基质与裂缝单元之间的压力差，Pa；q——流体源汇项，s−1；qf-m——裂缝单元与对应基质单元之间的流量，m3/s；R——玻尔兹曼常数，J/（K·mol）；t——时间，s；tmax——模拟的最大时间，s；Δt——时间步长，s；Tm——储集层温度，K； T1，T2——裂缝单元1和裂缝单元2的传导率，m3；Tf-f——相交裂缝单元之间的传导率，m3；Tf-m——裂缝单元与基质单元之间的传导率，m3；Tr——矩阵的迹（矩阵主对角线上所有元素之和）；u——位移张量，m；ux，uy——沿x、y轴方向的位移，m；v——流动速度，m/s；Vc——基质单元体积，m3；VL——兰格缪尔体积，m3/kg；Vm——BET吸附体积，m3/kg；α——最大水平主应力与x轴的夹角（最大水平主应力的方位），初始状态方位为90°，（°）；β——稀疏参数，无因次；ε——二阶应变张量，无因次；εv——体积应变，无因次；λt——相对流度，（Pa·s）−1；λ、μ——第一、第二拉梅常数，Pa；μg——页岩气的黏度，Pa·s；V——泊松比，无因次；ρg——页岩气密度，kg/m3；ρgsc——吸附气密度，kg/m3；ρr——岩石密度，kg/m3；σ——总应力张量，Pa；σh，σH——水平最小、最大主应力，Pa；σxx，σyy，σxy——沿x轴方向应力、沿y轴方向应力及剪切诱导应力，Pa；σv——应力张量σ迹的三分之一，Pa；ϕ——页岩孔隙度，%。下标：0——初始参考状态；i——基质单元编号。