0 引言
煤层气作为重要的非常规能源，其高效开采对能源供应和碳减排具有重要意义[1]。由于煤层强度低，钻井过程中受钻井液软化和地应力作用，井壁稳定性难以长期维持。超临界二氧化碳（SC-CO2）作为极具应用潜力的钻井液，与常规的水基钻井液相比，能够避免由于“水力化”措施引起的井壁失稳和水锁效应等。此外，CO2不仅可以与煤基质发生萃取溶解作用增大煤孔隙裂隙发育程度，从而提高低渗煤层的透气性，而且其吸附岩石的效率远大于甲烷，能够在实现煤层气驱替的同时有效封存CO2，促进“碳中和”目标的实现[2-3]。SC-CO2射流钻井技术的破岩深度是水射流的1.65~7.85倍，有效提高了钻井效率，但其能耗高、系统复杂，限制了其工程推广应用[4-5]。提高SC-CO2射流破煤效率，降低破煤压力，是降低能耗、简化系统装备的关键。自激振荡SC-CO2射流能够产生高于连续射流的脉冲压力，已被证实能够提高破煤效率[6]。除了脉冲压力，脉冲频率也是影响自激振荡SC-CO2射流破煤效率的关键因素[7]。
学者们对薄煤、开采面煤体及不同尺寸煤样的固有频率展开研究，频率范围多为0~2 000 Hz[8⇓-10]。当冲击频率与煤的固有频率一致或呈整数倍关系时，射流与煤形成共振，破坏效果得到明显提升。岩石的固有频率与射流冲击频率对岩石介质能量响应的振动周期起决定性作用，而且动静载荷冲击作用能够扩大岩石的响应范围和载荷的作用区域，加剧岩石振动的剧烈程度，促进岩石破碎[11]。随着静态载荷、动态载荷和冲击频率的增加，岩石破坏程度增加，并且当冲击频率和岩石自身固有频率接近时，岩石的破坏程度达到最大值[12]。采用共振钻头进行破岩，钻进速度可比常规旋转钻头提高近5倍[13]。因此，采用共振钻头破岩是钻井技术发展的重要方向之一。
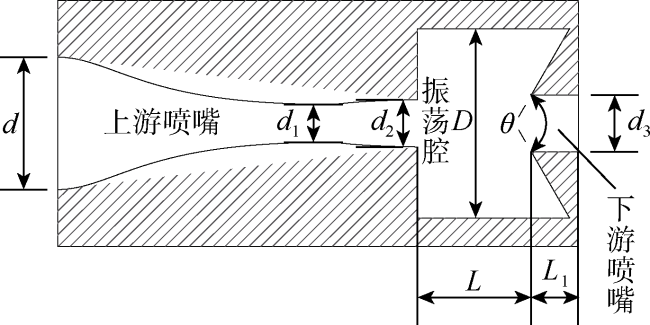
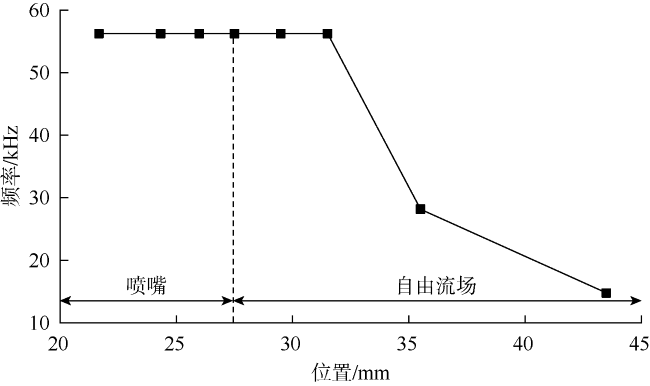
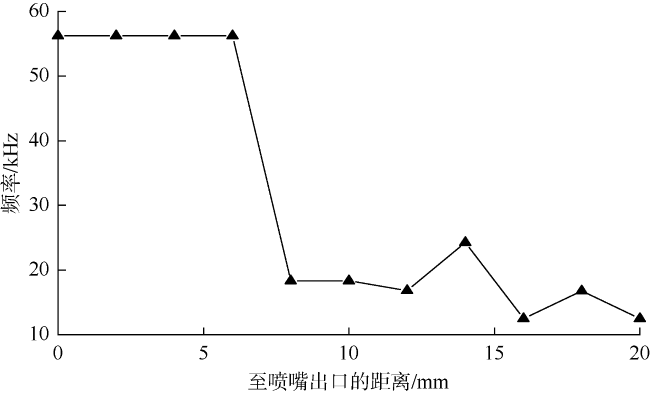
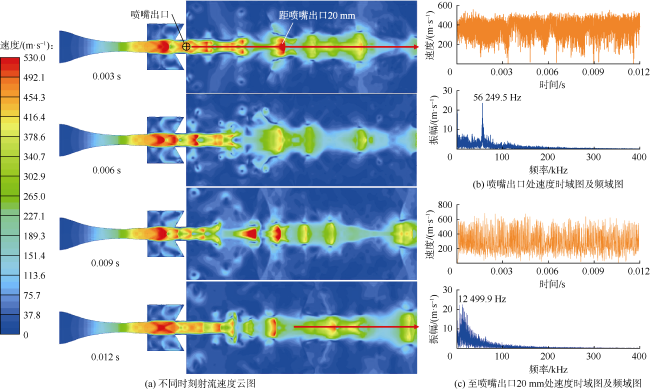
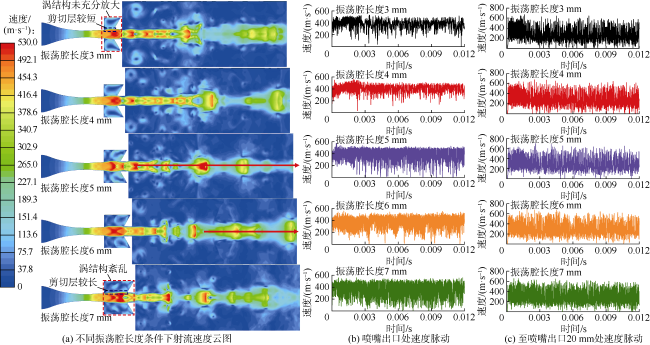
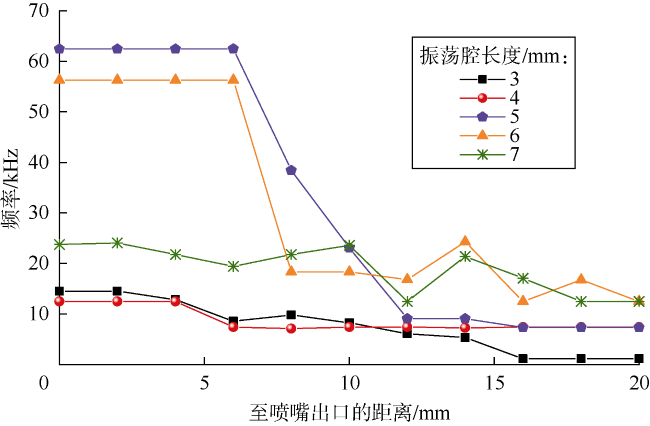
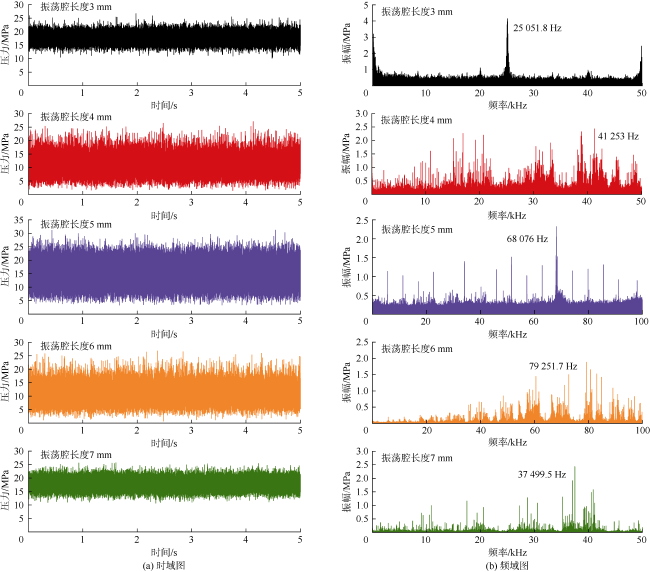
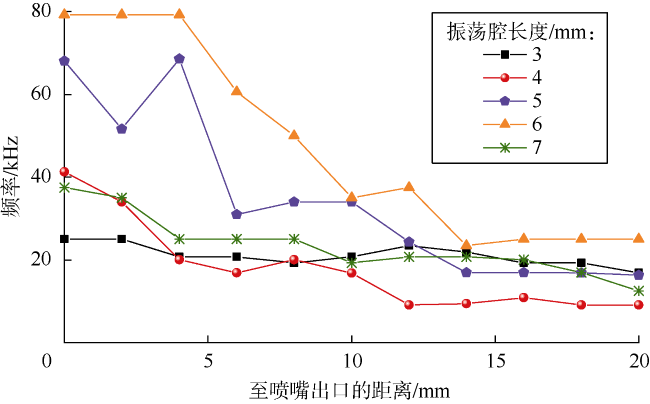
射流脉冲频率与脉冲幅值耦合作用于岩石，其中裂纹初生主要由其频率决定[7]，且岩石冲蚀深度随脉冲频率的增大呈现先增大后减小的趋势，存在一个最优频率范围[14]。为使自激振荡射流冲击频率在最优频率范围内，可通过改变自激振荡喷嘴结构实现频率的调制[15-16]。自激振荡喷嘴产生脉冲射流的关键在于能够形成稳定的剪切层，并将剪切层控制在合理的厚度和长度范围内[17]。涡结构生成后，在剪切层内运动和反馈过程中能够充分发展，形成拟序结构并发展成具有一定频率的脉冲射流。改变振荡腔腔径比、前后喷嘴结构和碰撞壁角度等参数能够影响喷嘴内部剪切层内涡结构的反馈与放大规律，从而改变射流冲击频率[18-19]。目前的研究均通过监测喷嘴内部压力信号的脉冲特征来反映脉冲频率，对于频率的调制均针对喷嘴内部的射流脉冲频率[20⇓⇓-23]。但是，射流冲击破岩时形成共振作用的频率为射流作用于岩石表面的冲击频率，由于环境压力、温度等的变化，两个频率可能并不一致。笔者前期研究表明，连续SC-CO2射流的压力和速度均存在明显的波动规律，脉动频率在1.3 kHz内[24-25]。对于SC-CO2射流，射流结构及环境的变化使射流的脉冲特征不断发生变化，频率会随之改变。通过改变喷嘴结构调节射流脉冲频率并不能直接得到共振破岩所需冲击频率。
为了得到自激振荡脉冲SC-CO2射流谐振破煤适用冲击频率，本文采用大涡模拟研究自激振荡脉冲SC-CO2射流在喷嘴内部以及自由流场中的形成及发展过程，分析射流冲击频率变化规律。此外，采用自主研制的自激振荡脉冲SC-CO2射流频率测试装置开展实验，研究不同条件下的射流冲击频率变化规律。将数值模拟结果和实验结果相结合进行分析。
1 数值模拟
1.1 物理模型
自激振荡喷嘴结构如图1 所示，由上游喷嘴（Laval喷嘴）、Helmholtz振荡腔及下游喷嘴组成，结构参数如表1 所示。
1.2 大涡模拟
自激振荡脉冲射流的形成及发展与涡结构的有序生成和拟序结构的形成密切相关。相较于雷诺平均模拟和直接数值模拟，大涡模拟能够精准求解某尺度以上的湍流运动，进而捕捉非稳态平衡过程中出现的大尺度效应和拟序结构。故本文采用大涡模拟研究自激振荡脉冲SC-CO2射流的形成及发展过程，监测射流速度随时间的变化关系，通过快速傅里叶变换将时域信号转换为频域信号后进行寻峰操作得到射流主频，分析射流冲击频率变化规律。
1.2.1 控制方程
大涡模拟采用滤波函数根据尺度大小划分涡环，直接求解得到大涡流动的运动方程，采用亚格子尺度模型来体现小涡。基于N-S方程滤波后得到可压缩理想气体的连续性方程、动量方程、能量方程，具体参见文献[6,26]。亚格子尺度模型选择WALE模型，其涡流黏度在层流剪切流区域为零，可以正确处理近壁层流体的流场模拟，涡流黏度模型参见文献[27-28]。SC-CO2物性方程是数值模拟计算中的一个关键难题。笔者前期采用分区拟合的方式构建了SC-CO2定压比热容、导热系数和黏度的理论计算模型，并通过用户自定义函数（UDF）和多项式将其与Fluent软件相结合构建SC-CO2物性参数数值计算模型[29]，如（1）式—（3）式所示。
定压比热容的计算模型为：
${{C}_{\text{p}}}=\left\{ \begin{align} & 184\ 1-0.000\ 1T\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( T\le 273\ \text{K} \right) \\ & 0.064\ 09{{\text{e}}^{-{{\left( \frac{T-318.9}{5.577} \right)}^{2}}}}+0.103{{\text{e}}^{-{{\left( \frac{T-324.5}{12.75} \right)}^{2}}}}+1.896{{\text{e}}^{-{{\left( \frac{T-329.1}{375.8} \right)}^{2}}}}+0.250\ 5{{\text{e}}^{-{{\left( \frac{T-334.4}{32.15} \right)}^{2}}}}\quad \quad \quad \left( 273\ \text{K}T\le 374\ \text{K} \right) \\ & 192\ 7-0.000\ 1{{T}^{^{^{^{^{^{{}}}}}}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( T374\ \text{K} \right) \\\end{align} \right.$ （1）
导热系数的计算模型为：
$k=0.845\ 8-0.003\ 649T+1.033\times {{10}^{-6}}{{T}^{2}}+$ $1.513\times {{10}^{-8}}{{T}^{3}}-1.8\times {{10}^{-11}}{{T}^{4}}$
黏度的计算模型为：
$\mu =3.293\ 34-0.028\ 831T+9.732\times {{10}^{-5}}{{T}^{2}}-$ $1.479\ 05\times {{10}^{-7}}{{T}^{3}}+8.509\ 3\times {{10}^{-1}}{{T}^{4}}$
1.2.2 网格划分及边界条件
将物理模型简化为二维轴对称结构（见图2 ），采用ANSYS Meshing进行四边形结构化网格划分，设置网格最小尺寸为0.000 1 m，对壁面进行3级加密提高网格质量。设置入口压力为45 MPa，入口温度为453 K，出口压力10 MPa，出口温度为353 K，壁面绝热无滑移。时间步长设置为1×10-7 s，每个时间步长内迭代20次，计算总时长为0.012 s。边界条件如图2 所示。
1.2.3 数值模拟方案
为了监测自激振荡脉冲SC-CO2射流在喷嘴内部以及自由流场中不同位置处的瞬时速度变化，设置监测点位置如表2 所示[30]。为了监测至喷嘴出口不同距离处和不同振荡腔长度下射流速度随时间的变化关系，在喷嘴出口外每隔2 mm等间距设置监测点，监测点与喷嘴出口距离依次为0，2，4，6，8，10，12，14，16，18，20 mm，振荡腔长度分为设置为3，4，5，6，7 mm。
表2 喷嘴内部以及自由流场中监测点位置（振荡腔长度6 mm） |
| 监测点 序号 | 位置（x，y）/ （mm，mm） | 监测点 序号 | 位置（x，y）/ （mm，mm） |
|---|---|---|---|
| 1 | （21.673，4.95） | 5 | （29.500，0） |
| 2 | (24.327，4.95) | 6 | （31.500，0） |
| 3 | （26.000，3.25） | 7 | （35.500，0） |
| 4 | （27.500，0） | 8 | （43.500，0） |
1.3 喷嘴和自由流场中自激振荡脉冲SC-CO2射流冲击频率差异
自激振荡脉冲SC-CO2射流的形成与发展过程受喷嘴结构以及流场结构影响，使射流在喷嘴内部和自由流场中的频率不同（见图3 ）。在自激振荡喷嘴内部，SC-CO2经振荡腔扰动生成涡结构，在碰撞壁作用下形成压力扰动波并以声速向上游传播，当其相位与射流初始振荡相位一致时，射流振荡被叠加放大形成频率为56 249.5 Hz的A波[31]，其在喷嘴内部的频率相同。在喷嘴出口处，射流发展仅与喷嘴结构相关，其频率与喷嘴内部扰动频率保持一致。SC-CO2具有可压缩性，射流由喷嘴喷出后受外界环境与流体间压力梯度的影响形成激波，使射流速度、压力等发生脉动（B波）[6]。随着射流的发展，A波与B波叠加形成C波[32]，使自由流场中的射流冲击频率变为14 749.9 Hz。由于脉冲射流谐振破岩时与煤岩体发生共振作用的是冲击在煤岩表面的射流频率，在进行谐振破岩研究时，应调制自由流场中的射流冲击频率而不是喷嘴内部的频率。
1.4 至喷嘴出口不同距离处自激振荡脉冲SC-CO2射流冲击频率变化规律
由图4 可知，随着至喷嘴出口距离的增加，自激振荡脉冲SC-CO2射流冲击频率整体呈现振荡式下降趋势。如图5 所示，SC-CO2流体受自激振荡喷嘴结构的扰动，使射流速度发生明显的脉动，在喷嘴出口处形成频率为56 249.5 Hz的扰动波。射流由喷嘴喷出后，射流冲击频率发生变化，使射流在喷嘴内部和喷嘴外部的频率不一致。笔者前期研究表明，由于SC-CO2的可压缩性，SC-CO2连续射流在喷嘴外部受外界环境影响形成激波，使射流速度、压力等参数产生波动，具有脉动频率[24-25]。喷嘴出口外射流速度、压力等参数波动与喷嘴出口内的射流扰动波叠加后影响射流冲击频率。随着至喷嘴出口距离的增加，射流发生能量耗散，射流流场结构不断发生变化，改变射流压力、速度等参数波动[32]，进而使射流冲击频率在射流轴向上逐渐减小至12 499.9 Hz。
1.5 振荡腔长度对自激振荡脉冲SC-CO2射流冲击频率的影响规律
由图6 可知，随着振荡腔长度的增加，在喷嘴内部自激振荡脉冲SC-CO2射流扰动形成的频率总体上呈现先增加后减小的趋势，由喷嘴喷出后，随着至喷嘴出口距离的增加，射流冲击频率整体呈现振荡性减小趋势。振荡腔长度为3 mm和4 mm时，自激振荡脉冲SC-CO2射流在喷嘴内部自激形成的频率为14 499.9，12 499.9 Hz，随着至喷嘴出口距离增加至20 mm，冲击频率逐渐减小至1 166.7，7 416.6 Hz；振荡腔长度为5 mm时喷嘴出口处的射流频率（即射流由喷嘴自激形成的频率）增加至62 416.1 Hz，随着至喷嘴出口距离的增加冲击频率整体呈现振荡性减小的趋势；振荡腔长度为6 mm和7 mm时，喷嘴出口处的射流频率为56 249.5，23 749.8 Hz，随着至喷嘴出口距离增加至20 mm，射流冲击频率均减小至12 499.9 Hz。振荡腔长度影响喷嘴内部涡结构的反馈，振荡腔长度过短时，振荡腔内部剪切层长度较短，使涡结构不能充分放大；振荡腔长度过长时，剪切层长度较长，涡结构在发展与反馈的过程中会不断破碎消散，使涡结构反馈紊乱。如图7 所示，增加振荡腔长度，喷嘴内部涡结构的反馈效果先增强后减弱，影响扰动波的反馈周期，使喷嘴出口处的速度波形发生变化，喷嘴出口处的射流频率呈现先增加后减小的趋势。射流由喷嘴喷出后受外界环境影响产生的速度、压力等参数波动与喷嘴内部形成的扰动波叠加后改变射流冲击频率，射流在发展过程中会发生能量耗散，改变不同位置处的参数波形，使射流轴向上冲击频率逐渐减小。由于不同振荡腔长度条件下射流由喷嘴自激形成的扰动波不同，其与喷嘴出口外射流压力、速度等参数波形叠加后使不同振荡腔条件下射流轴向位置处的冲击频率亦不相同。因此通过调整振荡腔长度能够实现射流冲击频率的调节。
2 实验验证
2.1 实验系统
为验证自激振荡脉冲SC-CO2射流的冲击频率变化规律数值模拟结果，采用SC-CO2射流制备系统和高频压力传感器及高频信号采集系统进行自激振荡脉冲SC-CO2射流的频率测试实验。实验通过高频压力传感器及高频信号采集系统完成自激振荡脉冲SC-CO2射流冲击压力的实时采集及存储，对其进行快速傅里叶转换后得到射流冲击频率。
SC-CO2射流制备系统由CO2供应系统、液化系统、增压系统、升温系统及中控系统组成。系统包括CO2储气瓶、冷浴箱、风冷式制冷压缩机、储罐以及柱塞式高压泵、热浴箱、加热缓冲罐和总控制柜等。高频压力传感器及高频信号采集系统由高频压力传感器、高频信号采集卡及数据分析软件组成。高频压力传感器采用压电式压力传感器，压力量程为0~100 MPa，传感器固有频率不小于200 kHz，频带宽度为0.5~100.0 kHz，抗冲击力5 000 g，工作温度为-40~125 ℃。高频信号采集卡的最大采样速率为500×103次/s（500 ksps），采样精度为16 bit。
2.2 实验方案
分别采用振荡腔长度为3，4，5，6，7 mm的自激振荡喷嘴开展自激振荡脉冲SC-CO2射流冲击频率测试实验。实验入口压力为45 MPa，温度为453 K。环境压力为10 MPa，温度为353 K。设置数据采集频率为200 kHz，采集时间为5 s，监测点位置与数值模拟一致。
2.3 实验结果及分析
由图8 、图9 可知，振荡腔长度为6 mm时，自激振荡脉冲SC-CO2射流在喷嘴内自激形成的频率为79 251.7 Hz，振幅为1.89 MPa，射流由喷嘴喷出后，随着至喷嘴出口距离的增加射流冲击频率逐渐减小至25 004.4 Hz。振荡腔长度为3 mm时，喷嘴出口处的射流频率为25 051.8 Hz，振幅为4.14 MPa，由喷嘴喷出后随着射流的发展，冲击频率整体呈现振荡性减小的趋势，逐渐降低至16 898.2 Hz。振荡腔长度为4，5，7 mm时，涡结构反馈效果较差，喷嘴出口处射流初始冲击波的脉动周期较大，自激振荡脉冲SC-CO2射流在喷嘴出口处的冲击频率较小，分别为41 253.0，68 076.0，37 499.5 Hz，振幅分别为2.43，2.32，2.47 MPa，随着射流的发展，射流冲击频率分别降低至9 098.1，16 290.0，12 496.4 Hz。可见，在本文所用喷嘴结构条件下，改变振荡腔长度可使SC-CO2经喷嘴结构扰动形成的自激振荡脉冲SC-CO2射流呈现高频微幅冲击振动破岩特征。随着振荡腔长度的增加，喷嘴出口处的射流频率整体呈现先增加后减小的趋势，随着至喷嘴出口距离的增加射流冲击频率整体呈现振荡性减小趋势。上述结论与数值模拟结论相一致，验证了自激振荡脉冲SC-CO2射流冲击频率变化规律的正确性。在实际工程应用中，不同激励频率条件下煤岩的谐振频率存在差异，可通过调节振荡腔长度改变射流频率实现谐振破煤效果。以煤固有频率为35 Hz为例[8]，采用振荡腔长度为6 mm的自激振荡喷嘴在0 mm靶距处破岩时，射流冲击频率约为煤固有频率的2 264.3倍。为提高射流破煤效果，可调节振荡腔长度至5 mm，使射流冲击频率为煤岩固有频率的1 945倍，实现谐振破煤。
3 结论
自激振荡脉冲SC-CO2射流在喷嘴内形成后，随着射流的形成和发展，脉冲频率并不会保持不变，而是随着射流结构的变化而变化。在射流轴向上，脉冲频率随射流不断发展而逐渐降低。在进行谐振破岩研究时，应调制自由流场中的射流冲击频率而不是喷嘴内部的频率。
在自激振荡喷嘴内，SC-CO2自激产生脉冲波动（A波），脉冲频率与喷嘴结构有关。SC-CO2在喷嘴喷出后形成射流，受CO2可压缩性的影响，射流在喷嘴出口处形成激波，使射流速度、压力和温度等参数剧烈振荡产生波动（B波），脉冲频率与射流流场结构有关。在射流形成和发展过程中A波和B波发生叠加形成C波，C波频率受喷嘴结构和射流流场结构耦合控制。本文所用振荡腔长度为6 mm的喷嘴出口处的射流频率为79 251.7 Hz，在自由流场中，射流频率逐渐降低至25 004.4 Hz，射流频率整体呈现减小趋势。
随着振荡腔长度的增加，喷嘴内部频率呈现先增加后减小的趋势，由喷嘴喷出后轴向上射流冲击频率逐渐降低。在实际工程应用中，可通过调节振荡腔长度来调节射流冲击频率，实现谐振破煤。
符号注释：
Cp——定压比热容，J/（kg·K）；d——上游喷嘴入口直径，mm；d1——上游喷嘴喉部直径，mm；d2——上游喷嘴出口直径，mm；d3——下游喷嘴直径，mm；D——振荡腔直径，mm；k——导热系数，W/（m·K）；L——振荡腔长度，mm；L1——下游喷嘴长度，mm；T——温度，K；x，y——直角坐标系，mm；μ——黏度，Pa·s；θ——碰撞壁角度，（°）。